【期末押题卷】2024-2025学年数学七年级下册苏科版(2024)
文档属性
| 名称 | 【期末押题卷】2024-2025学年数学七年级下册苏科版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 981.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 20:55:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【期末押题卷】2024-2025学年数学七年级下册苏科版(2024)
一.选择题(共8小题)
1.(2024秋 靖西市期末)下列银行标志是轴对称图形的是( )
A. B.
C. D.
2.(2024秋 怀仁市期末)下列计算正确的是( )
A.b4 b4=2b4 B.(m3)5=m8
C.(﹣2a)3=﹣8a3 D.x16÷x4=x4
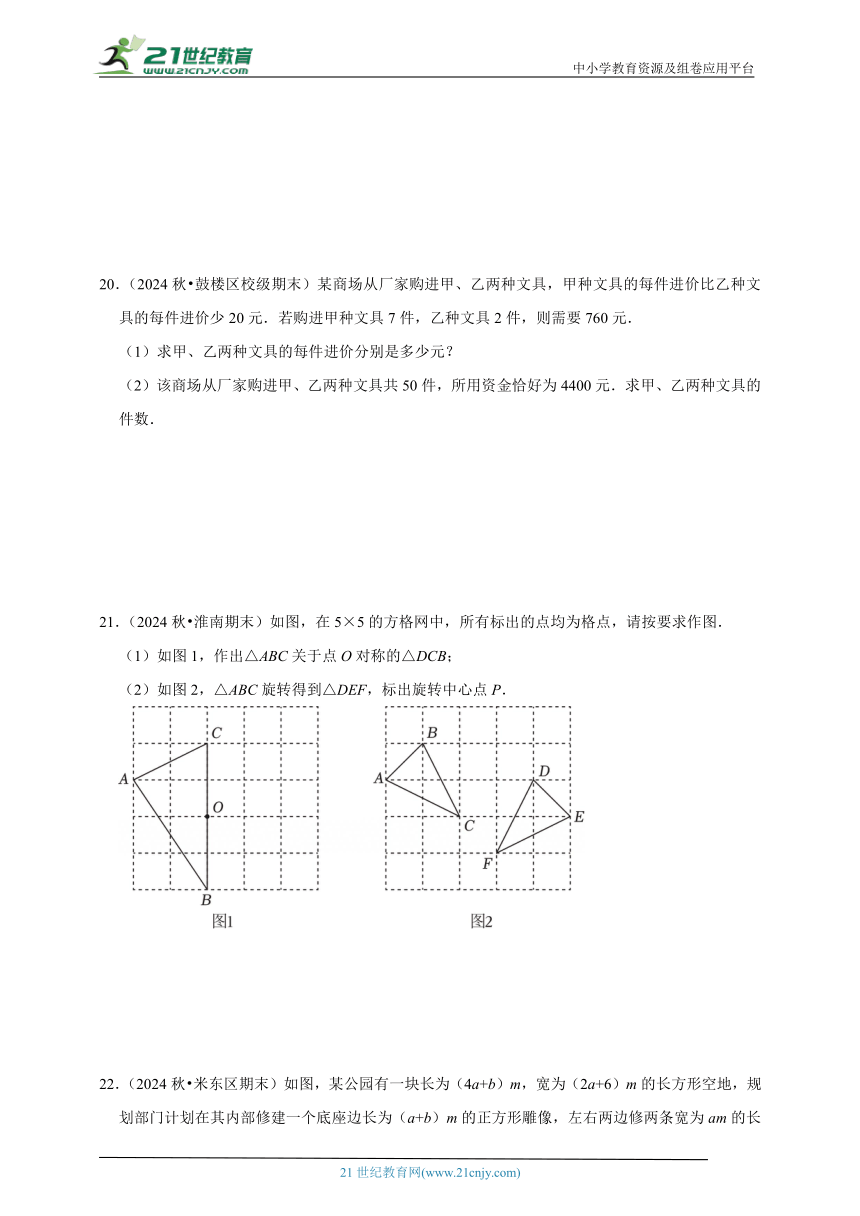
3.(2024秋 鄄城县期末)下列命题中,是真命题的是( )
A.相等的两个角是对顶角
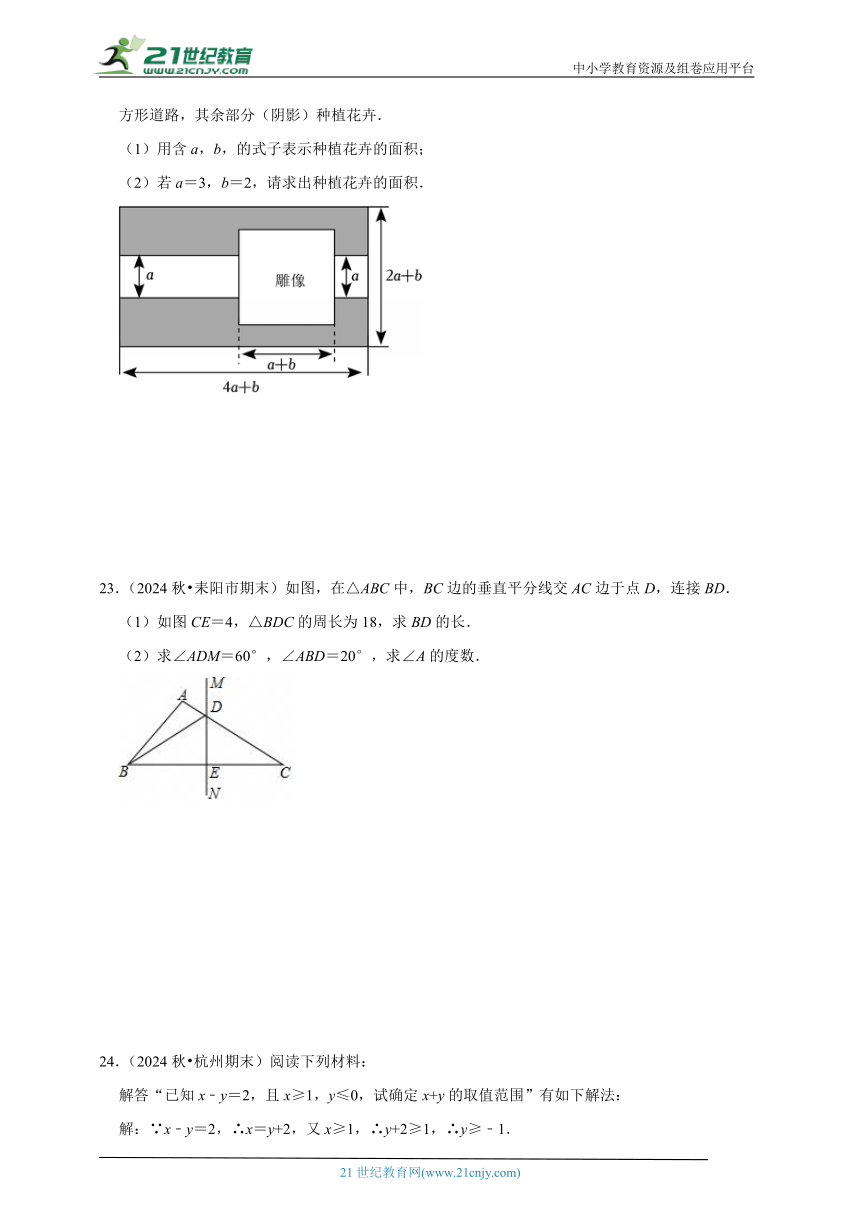
B.同位角相等
C.若|a|=|b|,则a=b
D.平行于同一条直线的两条直线平行
4.(2024秋 临澧县期末)已知x,y满足方程组,则(x+y)2025的值为( )
A.2025 B.﹣1 C.1 D.﹣2025
5.(2024春 沾化区期末)《九章算术》中有这样一道题:“今有善行者一百步,不善行者六十步.今不善行者先行一百步,善行者追之,问几何步及之?”意思是:走路快的人走100步时,走路慢的人只走60步,走路慢的人先走100步,走路快的人要走多少步才能追上?设走路快的人走x步才能追上走路慢的人,此时走路慢的人走了y步,则可列方程组为( )
A. B.
C. D.
6.(2023秋 海珠区期末)把如图的五角星绕着它的中心旋转一定角度后与自身重合,则这个旋转角度可能是( )
A.36° B.72° C.90° D.108°
7.(2024秋 济宁期末)如果(x+b)(ax﹣1)展开后不含x的一次项,且常数项为﹣2,那么ab的值为( )
A. B.4 C.0 D.﹣4
8.(2024秋 冠县期末)如图,在△ABC中,以点A为圆心,AC的长为半径作圆弧交BC于点D,再分别以点B和点D为圆心,大于的长为半径作圆弧,两弧分别交于点M和点N,连接MN交AB于点E.若AB=9,AC=7,则△ADE的周长为( )
A.22 B.20 C.18 D.16
二.填空题(共8小题)
9.(2024秋 石狮市期末)若am=2,an=5,则am﹣n= .
10.(2024秋 凉州区期末) .
11.(2024秋 临澧县期末)将方程x﹣2y=6变形为用含x的代数式表示y的形式是y= .
12.(2024秋 桑植县期末)如图,在△ABC中,DE垂直平分BC,若AB=8,AC=10,则△ABD的周长等于 .
13.(2024秋 临澧县期末)若关于m,n的二元一次方程组的解是,那么关于x,y的二元一次方程组的解是 .
14.(2024秋 金沙县期末)第24届冬季奥林匹克运动会将于2022年02月04日至2022年02月20日在中华人民共和国北京市和张家口市联合举行,这是中国历史上第一次举办冬季奥运会冬奥会吉祥物“冰墩墩”和“雪容融”陶制品分为小套装和大套装两种已知购买2个小套装和购买1个大套装,共需220元;购买3个小套装和2个大套装,共需390元,则大套装的单价为 元.
15.(2024秋 娄底期末)不等式组的解集为x<3a+2,则a的取值范围是 .
16.(2024秋 临海市期末)如图,标号为①,②,③,④的四个长方形以不重叠的方式围成长方形EFGH.已知①和②全等,③和④全等,且这四个长方形的面积都是6.设AM=a,MD=b,且a2﹣8ab+16b2=0.则S长方形EFGH为 .
三.解答题(共9小题)
17.(2024秋 鄂州期末)计算:
(1);
(2)(x+4)(2x﹣1).
18.(2024秋 海淀区校级期末)解方程组:.
19.(2023春 海淀区期末)解不等式组:.
20.(2024秋 鼓楼区校级期末)某商场从厂家购进甲、乙两种文具,甲种文具的每件进价比乙种文具的每件进价少20元.若购进甲种文具7件,乙种文具2件,则需要760元.
(1)求甲、乙两种文具的每件进价分别是多少元?
(2)该商场从厂家购进甲、乙两种文具共50件,所用资金恰好为4400元.求甲、乙两种文具的件数.
21.(2024秋 淮南期末)如图,在5×5的方格网中,所有标出的点均为格点,请按要求作图.
(1)如图1,作出△ABC关于点O对称的△DCB;
(2)如图2,△ABC旋转得到△DEF,标出旋转中心点P.
22.(2024秋 米东区期末)如图,某公园有一块长为(4a+b)m,宽为(2a+6)m的长方形空地,规划部门计划在其内部修建一个底座边长为(a+b)m的正方形雕像,左右两边修两条宽为am的长方形道路,其余部分(阴影)种植花卉.
(1)用含a,b,的式子表示种植花卉的面积;
(2)若a=3,b=2,请求出种植花卉的面积.
23.(2024秋 耒阳市期末)如图,在△ABC中,BC边的垂直平分线交AC边于点D,连接BD.
(1)如图CE=4,△BDC的周长为18,求BD的长.
(2)求∠ADM=60°,∠ABD=20°,求∠A的度数.
24.(2024秋 杭州期末)阅读下列材料:
解答“已知x﹣y=2,且x≥1,y≤0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,∴x=y+2,又x≥1,∴y+2≥1,∴y≥﹣1.
又y≤0,∴﹣1≤y≤0①
不等式①三者同加2,得1≤y+2≤2.即1≤x≤2②
①+②得,0≤x+y≤2.
问题:
(1)已知x﹣y=3,且x>2,y<1,求x+y的取值范围;
(2)一家具生产企业,生产学生用的课桌椅,一张桌子的售价比一把椅子高50元,若一张桌子的售价不低于120元,一把椅子的售价不超过90元,求出售一套桌椅(一张桌子+一把椅子)定价的范围(定价用w表示).
25.(2024秋 天元区期末)数学方法:
解方程组:,若设2x+y=m,x﹣2y=n,则原方程组可化为,解方程组得,所以,解方程组得,我们把某个式子看成一个整体,用一个字母去替代它,这种解方程组的方法叫做换元法.
(1)直接填空:已知关于x,y的二元一次方程组,的解为,那么关于m、n的二元一次方程组的解为: .
(2)知识迁移:请用这种方法解方程组.
(3)拓展应用:已知关于x,y的二元一次方程组的解为,求关于x,y的方程组的解.
【期末押题卷】2024-2025学年数学七年级下册苏科版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C D B A B A D
一.选择题(共8小题)
1.(2024秋 靖西市期末)下列银行标志是轴对称图形的是( )
A. B.
C. D.
【解答】解:选项A、C、D均不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项B能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
故选:B.
2.(2024秋 怀仁市期末)下列计算正确的是( )
A.b4 b4=2b4 B.(m3)5=m8
C.(﹣2a)3=﹣8a3 D.x16÷x4=x4
【解答】解:A、b4 4=b8,故该项不正确,不符合题意;
B、(m3)5=m15,故该项不正确,不符合题意;
C、(﹣2a)3=﹣8a3,故该项正确,符合题意;
D、x16÷x4=x12,故该项不正确,不符合题意;
故选:C.
3.(2024秋 鄄城县期末)下列命题中,是真命题的是( )
A.相等的两个角是对顶角
B.同位角相等
C.若|a|=|b|,则a=b
D.平行于同一条直线的两条直线平行
【解答】解:等的两个角不一定是对顶角,故A是假命题,不符合题意;
同位角不一定相等,故B是假命题,不符合题意;
若|a|=|b|,则a=b或a=﹣b,故C是假命题,不符合题意;
平行于同一条直线的两条直线平行,故D是真命题,符合题意;
故选:D.
4.(2024秋 临澧县期末)已知x,y满足方程组,则(x+y)2025的值为( )
A.2025 B.﹣1 C.1 D.﹣2025
【解答】解:,
①+②,得3x+3y=﹣3,
∴x+y=﹣1,
∴(x+y)2025=(﹣1)2025=﹣1,
故选:B.
5.(2024春 沾化区期末)《九章算术》中有这样一道题:“今有善行者一百步,不善行者六十步.今不善行者先行一百步,善行者追之,问几何步及之?”意思是:走路快的人走100步时,走路慢的人只走60步,走路慢的人先走100步,走路快的人要走多少步才能追上?设走路快的人走x步才能追上走路慢的人,此时走路慢的人走了y步,则可列方程组为( )
A. B.
C. D.
【解答】解:由题意可得,
,
故选:A.
6.(2023秋 海珠区期末)把如图的五角星绕着它的中心旋转一定角度后与自身重合,则这个旋转角度可能是( )
A.36° B.72° C.90° D.108°
【解答】解:五角星可以被中心发出的射线分成5个全等的部分,
因而旋转的角度是360°÷5=72°,
故选:B.
7.(2024秋 济宁期末)如果(x+b)(ax﹣1)展开后不含x的一次项,且常数项为﹣2,那么ab的值为( )
A. B.4 C.0 D.﹣4
【解答】解:∵(x+b)(ax﹣1)=ax2+(ab﹣1)x﹣b,
又∵展开式中不含x的一次项,且常数项为﹣2,
∴,
解得:,
∴.
故选:A.
8.(2024秋 冠县期末)如图,在△ABC中,以点A为圆心,AC的长为半径作圆弧交BC于点D,再分别以点B和点D为圆心,大于的长为半径作圆弧,两弧分别交于点M和点N,连接MN交AB于点E.若AB=9,AC=7,则△ADE的周长为( )
A.22 B.20 C.18 D.16
【解答】解:由作图可知AD=AC,
∵分别以点B和点D为圆心,大于的长为半径作圆弧,两弧分别交于点M和点N,连接MN交AB于点E.
∴MN垂直平分BD,
∴BE=DE,
∴△ADE的周长为AD+AE+DE=AC+AE+BE=AC+AB,
∵AB=9,AC=7,
∴△ADE的周长为9+7=16,
故选:D.
二.填空题(共8小题)
9.(2024秋 石狮市期末)若am=2,an=5,则am﹣n= .
【解答】解:∵am=2,an=5,
∴am﹣n=am÷an.
故填.
10.(2024秋 凉州区期末) ﹣1.5 .
【解答】解:()2007×(1.5)2008÷(﹣1)2009,
=()2007×(1.5)2007×1.5÷(﹣1),
=(1.5)2007×1.5×(﹣1),
=﹣1.5.
11.(2024秋 临澧县期末)将方程x﹣2y=6变形为用含x的代数式表示y的形式是y= .
【解答】解:方程x﹣2y=6,
2y=x﹣6,
解得:y,
故答案为:.
12.(2024秋 桑植县期末)如图,在△ABC中,DE垂直平分BC,若AB=8,AC=10,则△ABD的周长等于 18 .
【解答】解:∵DE垂直平分BC,
∴DB=DC,
∵AB=8,AC=10,
∴△ABD的周长=AB+AD+DB=AB+AD+DC=AB+AC=8+10=18,
故答案为:18.
13.(2024秋 临澧县期末)若关于m,n的二元一次方程组的解是,那么关于x,y的二元一次方程组的解是 .
【解答】解:方法一:
∵的解是,
∴,
解得:
把代入,
∴化简可得:
解得:,
故答案为:
方法二:
∵二元一次方程组的解是,
∴关于x,y的二元一次方程组中,
解得,
故答案为:
14.(2024秋 金沙县期末)第24届冬季奥林匹克运动会将于2022年02月04日至2022年02月20日在中华人民共和国北京市和张家口市联合举行,这是中国历史上第一次举办冬季奥运会冬奥会吉祥物“冰墩墩”和“雪容融”陶制品分为小套装和大套装两种已知购买2个小套装和购买1个大套装,共需220元;购买3个小套装和2个大套装,共需390元,则大套装的单价为 120 元.
【解答】解:设大套装的单价为x元,小套装的单价为y元,
依题意可得:,
解得,
∴大套装的单价为120元.
故答案为:120.
15.(2024秋 娄底期末)不等式组的解集为x<3a+2,则a的取值范围是 a≤﹣3 .
【解答】解:解这个不等式组为x<3a+2,
则3a+2≤a﹣4,
解这个不等式得a≤﹣3
故答案a≤﹣3.
16.(2024秋 临海市期末)如图,标号为①,②,③,④的四个长方形以不重叠的方式围成长方形EFGH.已知①和②全等,③和④全等,且这四个长方形的面积都是6.设AM=a,MD=b,且a2﹣8ab+16b2=0.则S长方形EFGH为 13.5 .
【解答】解:∵AM=a,MD=b,①和②全等,③和④全等,且这四个长方形的面积都是6,
∴MH,MG,
∴HG=MG﹣MH,EH=AM﹣MD=a﹣b,
∴S长方形EFGH=HG EH,
∵a2﹣8ab+16b2=0,
∴(a﹣4b)2=0,
∴a=4b,
∴S长方形EFGH13.5.
三.解答题(共9小题)
17.(2024秋 鄂州期末)计算:
(1);
(2)(x+4)(2x﹣1).
【解答】解:(1)
=9+1﹣2
=8;
(2)(x+4)(2x﹣1)
=2x2﹣x+8x﹣4
=2x2+7x﹣4.
18.(2024秋 海淀区校级期末)解方程组:.
【解答】解:由方程2x﹣y=7,得:y=2x﹣7,
将y=2x﹣7代入3x+2y=0,得:3x+2(2x﹣7)=0,
解得:x=2,
将x=2代入y=2x﹣7得:y=﹣3,
∴原方程组的解为:.
19.(2023春 海淀区期末)解不等式组:.
【解答】解:解不等式3(x﹣1)<2x+1,得x<4,
解不等式1≥x,得x,
所以原不等式组的解集为x<4.
20.(2024秋 鼓楼区校级期末)某商场从厂家购进甲、乙两种文具,甲种文具的每件进价比乙种文具的每件进价少20元.若购进甲种文具7件,乙种文具2件,则需要760元.
(1)求甲、乙两种文具的每件进价分别是多少元?
(2)该商场从厂家购进甲、乙两种文具共50件,所用资金恰好为4400元.求甲、乙两种文具的件数.
【解答】解:(1)设甲种文具每件进价为x元,则乙种文具每件进价为(x+20)元,
由题意得:7x+2(x+20)=760,
解得:x=80,
∴x+20=80+20=100,
答:甲种文具每件进价为80元,乙种文具每件进价为100元;
(2)设商场从厂家购进甲种文具a件,购进乙种文具b件,
由题意得:,
解得:,
答:商场从厂家购进甲种文具30件,乙种文具20件.
21.(2024秋 淮南期末)如图,在5×5的方格网中,所有标出的点均为格点,请按要求作图.
(1)如图1,作出△ABC关于点O对称的△DCB;
(2)如图2,△ABC旋转得到△DEF,标出旋转中心点P.
【解答】解:(1)如图1中,△DCB即为所求;
(2)如图2中,点P即为所求.
22.(2024秋 米东区期末)如图,某公园有一块长为(4a+b)m,宽为(2a+6)m的长方形空地,规划部门计划在其内部修建一个底座边长为(a+b)m的正方形雕像,左右两边修两条宽为am的长方形道路,其余部分(阴影)种植花卉.
(1)用含a,b,的式子表示种植花卉的面积;
(2)若a=3,b=2,请求出种植花卉的面积.
【解答】解:(1)种植花卉=(4a+b)(2a+b)﹣(a+b)2﹣a[4a+b﹣(a+b)],
=8a2+4ab+2ab+b2﹣a2﹣2ab﹣b2﹣3a2,
=(4a2+4ab)(m2);
(2)当a=3,b=2,
原式=4×32+4×3×2=60(m2).
23.(2024秋 耒阳市期末)如图,在△ABC中,BC边的垂直平分线交AC边于点D,连接BD.
(1)如图CE=4,△BDC的周长为18,求BD的长.
(2)求∠ADM=60°,∠ABD=20°,求∠A的度数.
【解答】解:(1)∵MN垂直平分BC,
∴DC=BD,
CE=EB,
又∵EC=4,
∴BE=4,
又∵△BDC的周长=18,
∴BD+DC=10,
∴BD=5;
(2)∵∠ADM=60°,
∴∠CDN=60°,
又∵MN垂直平分BC,
∴∠DNC=90°,
∴∠C=30°,
又∵∠C=∠DBC=30°,
∠ABD=20°,
∴∠ABC=50°,
∴∠A=180°﹣∠C﹣∠ABC=100°.
24.(2024秋 杭州期末)阅读下列材料:
解答“已知x﹣y=2,且x≥1,y≤0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,∴x=y+2,又x≥1,∴y+2≥1,∴y≥﹣1.
又y≤0,∴﹣1≤y≤0①
不等式①三者同加2,得1≤y+2≤2.即1≤x≤2②
①+②得,0≤x+y≤2.
问题:
(1)已知x﹣y=3,且x>2,y<1,求x+y的取值范围;
(2)一家具生产企业,生产学生用的课桌椅,一张桌子的售价比一把椅子高50元,若一张桌子的售价不低于120元,一把椅子的售价不超过90元,求出售一套桌椅(一张桌子+一把椅子)定价的范围(定价用w表示).
【解答】解:(1)∵x﹣y=3,
∴y=x﹣3,
又∵y<1,
∴x﹣3<1,
∴x<4.
又∵x>2,
∴2<x<4,①
同理得:﹣1<y<1,②
由①+②得:2﹣1<x+y<4+1,
∴1<x+y<5.
(2)设每张椅子的价格为x元,则每张桌子的价格为(x+50)元,
由已知可知:,
解得70≤x≤90,
140≤2x≤180,
190≤2x+50≤230,
∵w=2x+50,
∴190≤w≤230,
答:出售一套桌椅(一张桌子+一把椅子)定价的范围190≤w≤230.
25.(2024秋 天元区期末)数学方法:
解方程组:,若设2x+y=m,x﹣2y=n,则原方程组可化为,解方程组得,所以,解方程组得,我们把某个式子看成一个整体,用一个字母去替代它,这种解方程组的方法叫做换元法.
(1)直接填空:已知关于x,y的二元一次方程组,的解为,那么关于m、n的二元一次方程组的解为: .
(2)知识迁移:请用这种方法解方程组.
(3)拓展应用:已知关于x,y的二元一次方程组的解为,求关于x,y的方程组的解.
【解答】解:(1)设m+n=x,m﹣n=y,则原方程组可化为,
∵的解为,
∴,
解得,
故答案为:;
(2)设,,则原方程组可化为,
解得,
即有,
解得,
即:方程组的解为;
(3)设,,则原方程组可化为,
化简,得,
∵关于x,y的二元一次方程组的解为,
∴,即有,
解得:.
故方程组的解为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【期末押题卷】2024-2025学年数学七年级下册苏科版(2024)
一.选择题(共8小题)
1.(2024秋 靖西市期末)下列银行标志是轴对称图形的是( )
A. B.
C. D.
2.(2024秋 怀仁市期末)下列计算正确的是( )
A.b4 b4=2b4 B.(m3)5=m8
C.(﹣2a)3=﹣8a3 D.x16÷x4=x4
3.(2024秋 鄄城县期末)下列命题中,是真命题的是( )
A.相等的两个角是对顶角
B.同位角相等
C.若|a|=|b|,则a=b
D.平行于同一条直线的两条直线平行
4.(2024秋 临澧县期末)已知x,y满足方程组,则(x+y)2025的值为( )
A.2025 B.﹣1 C.1 D.﹣2025
5.(2024春 沾化区期末)《九章算术》中有这样一道题:“今有善行者一百步,不善行者六十步.今不善行者先行一百步,善行者追之,问几何步及之?”意思是:走路快的人走100步时,走路慢的人只走60步,走路慢的人先走100步,走路快的人要走多少步才能追上?设走路快的人走x步才能追上走路慢的人,此时走路慢的人走了y步,则可列方程组为( )
A. B.
C. D.
6.(2023秋 海珠区期末)把如图的五角星绕着它的中心旋转一定角度后与自身重合,则这个旋转角度可能是( )
A.36° B.72° C.90° D.108°
7.(2024秋 济宁期末)如果(x+b)(ax﹣1)展开后不含x的一次项,且常数项为﹣2,那么ab的值为( )
A. B.4 C.0 D.﹣4
8.(2024秋 冠县期末)如图,在△ABC中,以点A为圆心,AC的长为半径作圆弧交BC于点D,再分别以点B和点D为圆心,大于的长为半径作圆弧,两弧分别交于点M和点N,连接MN交AB于点E.若AB=9,AC=7,则△ADE的周长为( )
A.22 B.20 C.18 D.16
二.填空题(共8小题)
9.(2024秋 石狮市期末)若am=2,an=5,则am﹣n= .
10.(2024秋 凉州区期末) .
11.(2024秋 临澧县期末)将方程x﹣2y=6变形为用含x的代数式表示y的形式是y= .
12.(2024秋 桑植县期末)如图,在△ABC中,DE垂直平分BC,若AB=8,AC=10,则△ABD的周长等于 .
13.(2024秋 临澧县期末)若关于m,n的二元一次方程组的解是,那么关于x,y的二元一次方程组的解是 .
14.(2024秋 金沙县期末)第24届冬季奥林匹克运动会将于2022年02月04日至2022年02月20日在中华人民共和国北京市和张家口市联合举行,这是中国历史上第一次举办冬季奥运会冬奥会吉祥物“冰墩墩”和“雪容融”陶制品分为小套装和大套装两种已知购买2个小套装和购买1个大套装,共需220元;购买3个小套装和2个大套装,共需390元,则大套装的单价为 元.
15.(2024秋 娄底期末)不等式组的解集为x<3a+2,则a的取值范围是 .
16.(2024秋 临海市期末)如图,标号为①,②,③,④的四个长方形以不重叠的方式围成长方形EFGH.已知①和②全等,③和④全等,且这四个长方形的面积都是6.设AM=a,MD=b,且a2﹣8ab+16b2=0.则S长方形EFGH为 .
三.解答题(共9小题)
17.(2024秋 鄂州期末)计算:
(1);
(2)(x+4)(2x﹣1).
18.(2024秋 海淀区校级期末)解方程组:.
19.(2023春 海淀区期末)解不等式组:.
20.(2024秋 鼓楼区校级期末)某商场从厂家购进甲、乙两种文具,甲种文具的每件进价比乙种文具的每件进价少20元.若购进甲种文具7件,乙种文具2件,则需要760元.
(1)求甲、乙两种文具的每件进价分别是多少元?
(2)该商场从厂家购进甲、乙两种文具共50件,所用资金恰好为4400元.求甲、乙两种文具的件数.
21.(2024秋 淮南期末)如图,在5×5的方格网中,所有标出的点均为格点,请按要求作图.
(1)如图1,作出△ABC关于点O对称的△DCB;
(2)如图2,△ABC旋转得到△DEF,标出旋转中心点P.
22.(2024秋 米东区期末)如图,某公园有一块长为(4a+b)m,宽为(2a+6)m的长方形空地,规划部门计划在其内部修建一个底座边长为(a+b)m的正方形雕像,左右两边修两条宽为am的长方形道路,其余部分(阴影)种植花卉.
(1)用含a,b,的式子表示种植花卉的面积;
(2)若a=3,b=2,请求出种植花卉的面积.
23.(2024秋 耒阳市期末)如图,在△ABC中,BC边的垂直平分线交AC边于点D,连接BD.
(1)如图CE=4,△BDC的周长为18,求BD的长.
(2)求∠ADM=60°,∠ABD=20°,求∠A的度数.
24.(2024秋 杭州期末)阅读下列材料:
解答“已知x﹣y=2,且x≥1,y≤0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,∴x=y+2,又x≥1,∴y+2≥1,∴y≥﹣1.
又y≤0,∴﹣1≤y≤0①
不等式①三者同加2,得1≤y+2≤2.即1≤x≤2②
①+②得,0≤x+y≤2.
问题:
(1)已知x﹣y=3,且x>2,y<1,求x+y的取值范围;
(2)一家具生产企业,生产学生用的课桌椅,一张桌子的售价比一把椅子高50元,若一张桌子的售价不低于120元,一把椅子的售价不超过90元,求出售一套桌椅(一张桌子+一把椅子)定价的范围(定价用w表示).
25.(2024秋 天元区期末)数学方法:
解方程组:,若设2x+y=m,x﹣2y=n,则原方程组可化为,解方程组得,所以,解方程组得,我们把某个式子看成一个整体,用一个字母去替代它,这种解方程组的方法叫做换元法.
(1)直接填空:已知关于x,y的二元一次方程组,的解为,那么关于m、n的二元一次方程组的解为: .
(2)知识迁移:请用这种方法解方程组.
(3)拓展应用:已知关于x,y的二元一次方程组的解为,求关于x,y的方程组的解.
【期末押题卷】2024-2025学年数学七年级下册苏科版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C D B A B A D
一.选择题(共8小题)
1.(2024秋 靖西市期末)下列银行标志是轴对称图形的是( )
A. B.
C. D.
【解答】解:选项A、C、D均不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
选项B能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
故选:B.
2.(2024秋 怀仁市期末)下列计算正确的是( )
A.b4 b4=2b4 B.(m3)5=m8
C.(﹣2a)3=﹣8a3 D.x16÷x4=x4
【解答】解:A、b4 4=b8,故该项不正确,不符合题意;
B、(m3)5=m15,故该项不正确,不符合题意;
C、(﹣2a)3=﹣8a3,故该项正确,符合题意;
D、x16÷x4=x12,故该项不正确,不符合题意;
故选:C.
3.(2024秋 鄄城县期末)下列命题中,是真命题的是( )
A.相等的两个角是对顶角
B.同位角相等
C.若|a|=|b|,则a=b
D.平行于同一条直线的两条直线平行
【解答】解:等的两个角不一定是对顶角,故A是假命题,不符合题意;
同位角不一定相等,故B是假命题,不符合题意;
若|a|=|b|,则a=b或a=﹣b,故C是假命题,不符合题意;
平行于同一条直线的两条直线平行,故D是真命题,符合题意;
故选:D.
4.(2024秋 临澧县期末)已知x,y满足方程组,则(x+y)2025的值为( )
A.2025 B.﹣1 C.1 D.﹣2025
【解答】解:,
①+②,得3x+3y=﹣3,
∴x+y=﹣1,
∴(x+y)2025=(﹣1)2025=﹣1,
故选:B.
5.(2024春 沾化区期末)《九章算术》中有这样一道题:“今有善行者一百步,不善行者六十步.今不善行者先行一百步,善行者追之,问几何步及之?”意思是:走路快的人走100步时,走路慢的人只走60步,走路慢的人先走100步,走路快的人要走多少步才能追上?设走路快的人走x步才能追上走路慢的人,此时走路慢的人走了y步,则可列方程组为( )
A. B.
C. D.
【解答】解:由题意可得,
,
故选:A.
6.(2023秋 海珠区期末)把如图的五角星绕着它的中心旋转一定角度后与自身重合,则这个旋转角度可能是( )
A.36° B.72° C.90° D.108°
【解答】解:五角星可以被中心发出的射线分成5个全等的部分,
因而旋转的角度是360°÷5=72°,
故选:B.
7.(2024秋 济宁期末)如果(x+b)(ax﹣1)展开后不含x的一次项,且常数项为﹣2,那么ab的值为( )
A. B.4 C.0 D.﹣4
【解答】解:∵(x+b)(ax﹣1)=ax2+(ab﹣1)x﹣b,
又∵展开式中不含x的一次项,且常数项为﹣2,
∴,
解得:,
∴.
故选:A.
8.(2024秋 冠县期末)如图,在△ABC中,以点A为圆心,AC的长为半径作圆弧交BC于点D,再分别以点B和点D为圆心,大于的长为半径作圆弧,两弧分别交于点M和点N,连接MN交AB于点E.若AB=9,AC=7,则△ADE的周长为( )
A.22 B.20 C.18 D.16
【解答】解:由作图可知AD=AC,
∵分别以点B和点D为圆心,大于的长为半径作圆弧,两弧分别交于点M和点N,连接MN交AB于点E.
∴MN垂直平分BD,
∴BE=DE,
∴△ADE的周长为AD+AE+DE=AC+AE+BE=AC+AB,
∵AB=9,AC=7,
∴△ADE的周长为9+7=16,
故选:D.
二.填空题(共8小题)
9.(2024秋 石狮市期末)若am=2,an=5,则am﹣n= .
【解答】解:∵am=2,an=5,
∴am﹣n=am÷an.
故填.
10.(2024秋 凉州区期末) ﹣1.5 .
【解答】解:()2007×(1.5)2008÷(﹣1)2009,
=()2007×(1.5)2007×1.5÷(﹣1),
=(1.5)2007×1.5×(﹣1),
=﹣1.5.
11.(2024秋 临澧县期末)将方程x﹣2y=6变形为用含x的代数式表示y的形式是y= .
【解答】解:方程x﹣2y=6,
2y=x﹣6,
解得:y,
故答案为:.
12.(2024秋 桑植县期末)如图,在△ABC中,DE垂直平分BC,若AB=8,AC=10,则△ABD的周长等于 18 .
【解答】解:∵DE垂直平分BC,
∴DB=DC,
∵AB=8,AC=10,
∴△ABD的周长=AB+AD+DB=AB+AD+DC=AB+AC=8+10=18,
故答案为:18.
13.(2024秋 临澧县期末)若关于m,n的二元一次方程组的解是,那么关于x,y的二元一次方程组的解是 .
【解答】解:方法一:
∵的解是,
∴,
解得:
把代入,
∴化简可得:
解得:,
故答案为:
方法二:
∵二元一次方程组的解是,
∴关于x,y的二元一次方程组中,
解得,
故答案为:
14.(2024秋 金沙县期末)第24届冬季奥林匹克运动会将于2022年02月04日至2022年02月20日在中华人民共和国北京市和张家口市联合举行,这是中国历史上第一次举办冬季奥运会冬奥会吉祥物“冰墩墩”和“雪容融”陶制品分为小套装和大套装两种已知购买2个小套装和购买1个大套装,共需220元;购买3个小套装和2个大套装,共需390元,则大套装的单价为 120 元.
【解答】解:设大套装的单价为x元,小套装的单价为y元,
依题意可得:,
解得,
∴大套装的单价为120元.
故答案为:120.
15.(2024秋 娄底期末)不等式组的解集为x<3a+2,则a的取值范围是 a≤﹣3 .
【解答】解:解这个不等式组为x<3a+2,
则3a+2≤a﹣4,
解这个不等式得a≤﹣3
故答案a≤﹣3.
16.(2024秋 临海市期末)如图,标号为①,②,③,④的四个长方形以不重叠的方式围成长方形EFGH.已知①和②全等,③和④全等,且这四个长方形的面积都是6.设AM=a,MD=b,且a2﹣8ab+16b2=0.则S长方形EFGH为 13.5 .
【解答】解:∵AM=a,MD=b,①和②全等,③和④全等,且这四个长方形的面积都是6,
∴MH,MG,
∴HG=MG﹣MH,EH=AM﹣MD=a﹣b,
∴S长方形EFGH=HG EH,
∵a2﹣8ab+16b2=0,
∴(a﹣4b)2=0,
∴a=4b,
∴S长方形EFGH13.5.
三.解答题(共9小题)
17.(2024秋 鄂州期末)计算:
(1);
(2)(x+4)(2x﹣1).
【解答】解:(1)
=9+1﹣2
=8;
(2)(x+4)(2x﹣1)
=2x2﹣x+8x﹣4
=2x2+7x﹣4.
18.(2024秋 海淀区校级期末)解方程组:.
【解答】解:由方程2x﹣y=7,得:y=2x﹣7,
将y=2x﹣7代入3x+2y=0,得:3x+2(2x﹣7)=0,
解得:x=2,
将x=2代入y=2x﹣7得:y=﹣3,
∴原方程组的解为:.
19.(2023春 海淀区期末)解不等式组:.
【解答】解:解不等式3(x﹣1)<2x+1,得x<4,
解不等式1≥x,得x,
所以原不等式组的解集为x<4.
20.(2024秋 鼓楼区校级期末)某商场从厂家购进甲、乙两种文具,甲种文具的每件进价比乙种文具的每件进价少20元.若购进甲种文具7件,乙种文具2件,则需要760元.
(1)求甲、乙两种文具的每件进价分别是多少元?
(2)该商场从厂家购进甲、乙两种文具共50件,所用资金恰好为4400元.求甲、乙两种文具的件数.
【解答】解:(1)设甲种文具每件进价为x元,则乙种文具每件进价为(x+20)元,
由题意得:7x+2(x+20)=760,
解得:x=80,
∴x+20=80+20=100,
答:甲种文具每件进价为80元,乙种文具每件进价为100元;
(2)设商场从厂家购进甲种文具a件,购进乙种文具b件,
由题意得:,
解得:,
答:商场从厂家购进甲种文具30件,乙种文具20件.
21.(2024秋 淮南期末)如图,在5×5的方格网中,所有标出的点均为格点,请按要求作图.
(1)如图1,作出△ABC关于点O对称的△DCB;
(2)如图2,△ABC旋转得到△DEF,标出旋转中心点P.
【解答】解:(1)如图1中,△DCB即为所求;
(2)如图2中,点P即为所求.
22.(2024秋 米东区期末)如图,某公园有一块长为(4a+b)m,宽为(2a+6)m的长方形空地,规划部门计划在其内部修建一个底座边长为(a+b)m的正方形雕像,左右两边修两条宽为am的长方形道路,其余部分(阴影)种植花卉.
(1)用含a,b,的式子表示种植花卉的面积;
(2)若a=3,b=2,请求出种植花卉的面积.
【解答】解:(1)种植花卉=(4a+b)(2a+b)﹣(a+b)2﹣a[4a+b﹣(a+b)],
=8a2+4ab+2ab+b2﹣a2﹣2ab﹣b2﹣3a2,
=(4a2+4ab)(m2);
(2)当a=3,b=2,
原式=4×32+4×3×2=60(m2).
23.(2024秋 耒阳市期末)如图,在△ABC中,BC边的垂直平分线交AC边于点D,连接BD.
(1)如图CE=4,△BDC的周长为18,求BD的长.
(2)求∠ADM=60°,∠ABD=20°,求∠A的度数.
【解答】解:(1)∵MN垂直平分BC,
∴DC=BD,
CE=EB,
又∵EC=4,
∴BE=4,
又∵△BDC的周长=18,
∴BD+DC=10,
∴BD=5;
(2)∵∠ADM=60°,
∴∠CDN=60°,
又∵MN垂直平分BC,
∴∠DNC=90°,
∴∠C=30°,
又∵∠C=∠DBC=30°,
∠ABD=20°,
∴∠ABC=50°,
∴∠A=180°﹣∠C﹣∠ABC=100°.
24.(2024秋 杭州期末)阅读下列材料:
解答“已知x﹣y=2,且x≥1,y≤0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,∴x=y+2,又x≥1,∴y+2≥1,∴y≥﹣1.
又y≤0,∴﹣1≤y≤0①
不等式①三者同加2,得1≤y+2≤2.即1≤x≤2②
①+②得,0≤x+y≤2.
问题:
(1)已知x﹣y=3,且x>2,y<1,求x+y的取值范围;
(2)一家具生产企业,生产学生用的课桌椅,一张桌子的售价比一把椅子高50元,若一张桌子的售价不低于120元,一把椅子的售价不超过90元,求出售一套桌椅(一张桌子+一把椅子)定价的范围(定价用w表示).
【解答】解:(1)∵x﹣y=3,
∴y=x﹣3,
又∵y<1,
∴x﹣3<1,
∴x<4.
又∵x>2,
∴2<x<4,①
同理得:﹣1<y<1,②
由①+②得:2﹣1<x+y<4+1,
∴1<x+y<5.
(2)设每张椅子的价格为x元,则每张桌子的价格为(x+50)元,
由已知可知:,
解得70≤x≤90,
140≤2x≤180,
190≤2x+50≤230,
∵w=2x+50,
∴190≤w≤230,
答:出售一套桌椅(一张桌子+一把椅子)定价的范围190≤w≤230.
25.(2024秋 天元区期末)数学方法:
解方程组:,若设2x+y=m,x﹣2y=n,则原方程组可化为,解方程组得,所以,解方程组得,我们把某个式子看成一个整体,用一个字母去替代它,这种解方程组的方法叫做换元法.
(1)直接填空:已知关于x,y的二元一次方程组,的解为,那么关于m、n的二元一次方程组的解为: .
(2)知识迁移:请用这种方法解方程组.
(3)拓展应用:已知关于x,y的二元一次方程组的解为,求关于x,y的方程组的解.
【解答】解:(1)设m+n=x,m﹣n=y,则原方程组可化为,
∵的解为,
∴,
解得,
故答案为:;
(2)设,,则原方程组可化为,
解得,
即有,
解得,
即:方程组的解为;
(3)设,,则原方程组可化为,
化简,得,
∵关于x,y的二元一次方程组的解为,
∴,即有,
解得:.
故方程组的解为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
