期末复习卷-2024-2025学年数学七年级下册北师大版(2024)(含解析)
文档属性
| 名称 | 期末复习卷-2024-2025学年数学七年级下册北师大版(2024)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 21:01:31 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末复习卷-2024-2025学年数学七年级下册北师大版(2024)
一.选择题(共8小题)
1.2024年9月9日,工业和信息化部宣布中国首台氟化氩光刻机,实现套刻≤8nm技术,标志着我国在高端芯片制造领域取得了关键性进展.已知8纳米=0.000000008米,0.000000008用科学记数法可表示为( )
A.8×109 B.8×10﹣9 C.8×1010 D.8×10﹣10
2.如图,AB∥CD,∠CDE=130°,则∠A的度数为( )
A.70° B.65° C.50° D.40°
3.如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A. B.
C. D.
4.下列各式运算中结果是a6是( )
A.a3+a3 B.(a3)3 C.a12÷a2 D.a3 a3
5.观察下列作图痕迹,所作线段CD为△ABC的中线的是( )
A. B.
C. D.
6.已知m+n=4,m2﹣n2=﹣8,则m﹣n的值为( )
A.﹣4 B.﹣2 C.2 D.4
7.汉字是世界上最古老的文字之一,现存最早的汉字是公元前14世纪殷商时期的甲骨文,之后又产生了金文、小篆、隶书、草书、楷书、行书等多种字体,每种字体都有着鲜明的艺术特征.下面的汉字可以近似地看成轴对称图形的是( )
A. B. C. D.
8.将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
二.填空题(共6小题)
9.一个等腰三角形的一个角为50°,则它的顶角的度数是 .
10.围棋起源于中国,棋子分黑白两色.一个不透明的盒子中装有2个黑色棋子和4个白色棋子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到白色棋子的概率是 .
11.如图,点P到一条笔直的公路MN共有四条路径,若要用相同速度从点P走到公路,最快到达的路径是选择沿线段PB去公路,这一选择用到的数学知识是 .
12.水池中有若干吨水,开一个出水口将全池水放光,所用时间t(单位:h)与出水速度v(单位:T/h)之间的关系如表:
出水速度v(T/h) 10 8 5 4 2 …
t(h) 1 1.25 2 2.5 5 …
用式子表示t与v的关系是 .
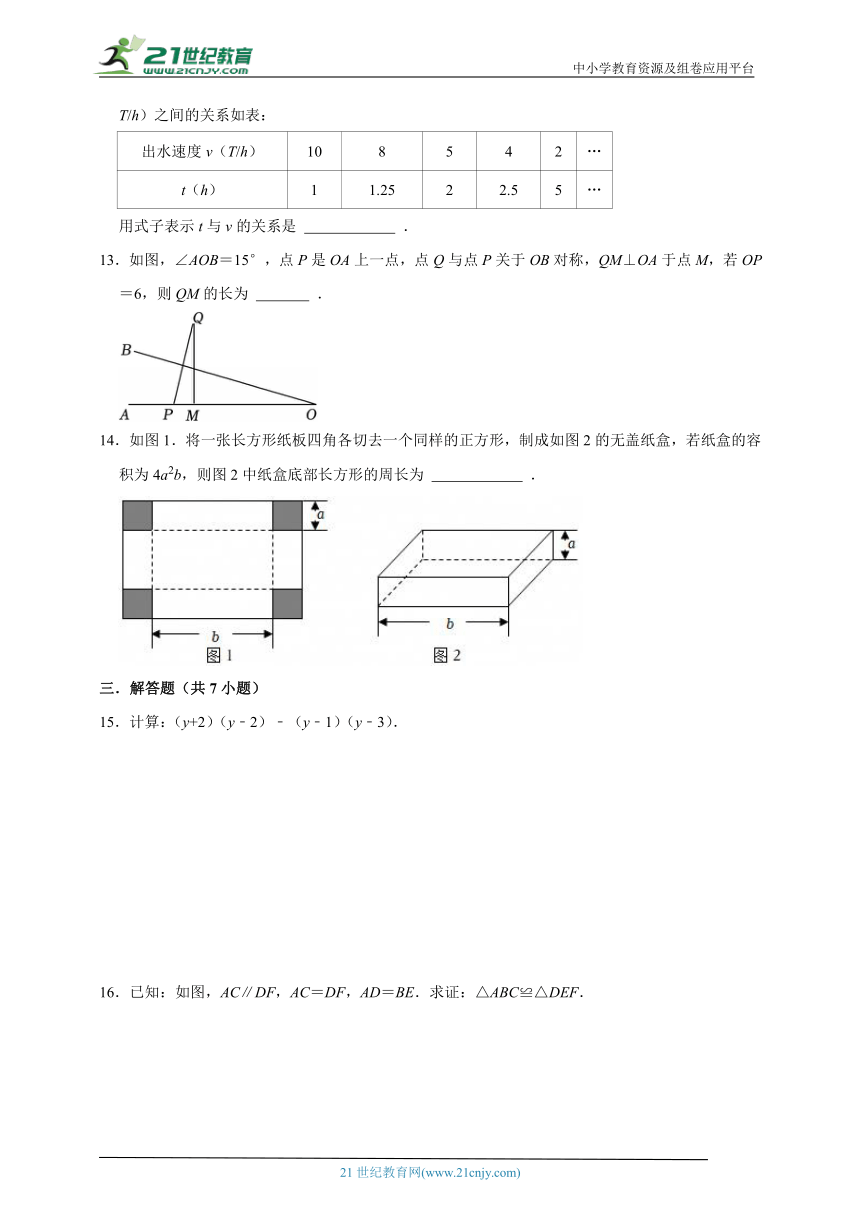
13.如图,∠AOB=15°,点P是OA上一点,点Q与点P关于OB对称,QM⊥OA于点M,若OP=6,则QM的长为 .
14.如图1.将一张长方形纸板四角各切去一个同样的正方形,制成如图2的无盖纸盒,若纸盒的容积为4a2b,则图2中纸盒底部长方形的周长为 .
三.解答题(共7小题)
15.计算:(y+2)(y﹣2)﹣(y﹣1)(y﹣3).
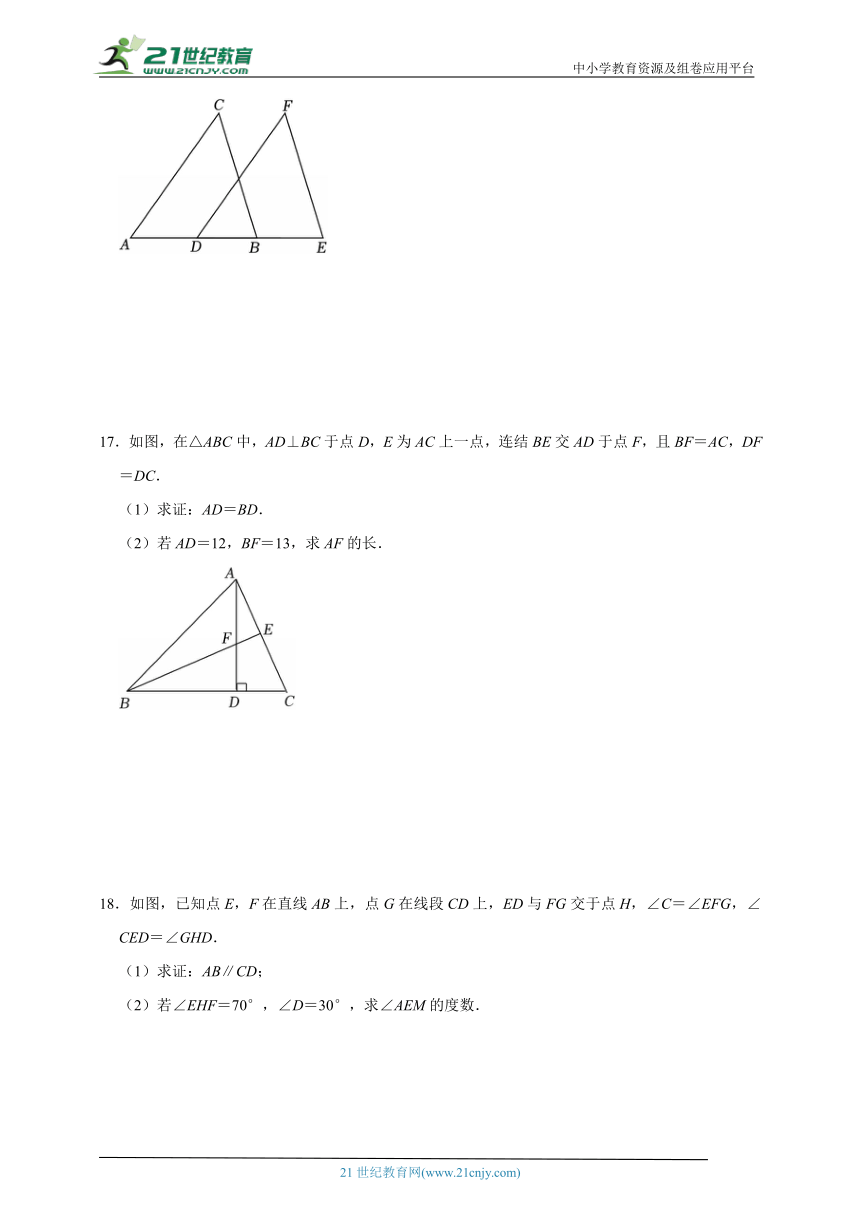
16.已知:如图,AC∥DF,AC=DF,AD=BE.求证:△ABC≌△DEF.
17.如图,在△ABC中,AD⊥BC于点D,E为AC上一点,连结BE交AD于点F,且BF=AC,DF=DC.
(1)求证:AD=BD.
(2)若AD=12,BF=13,求AF的长.
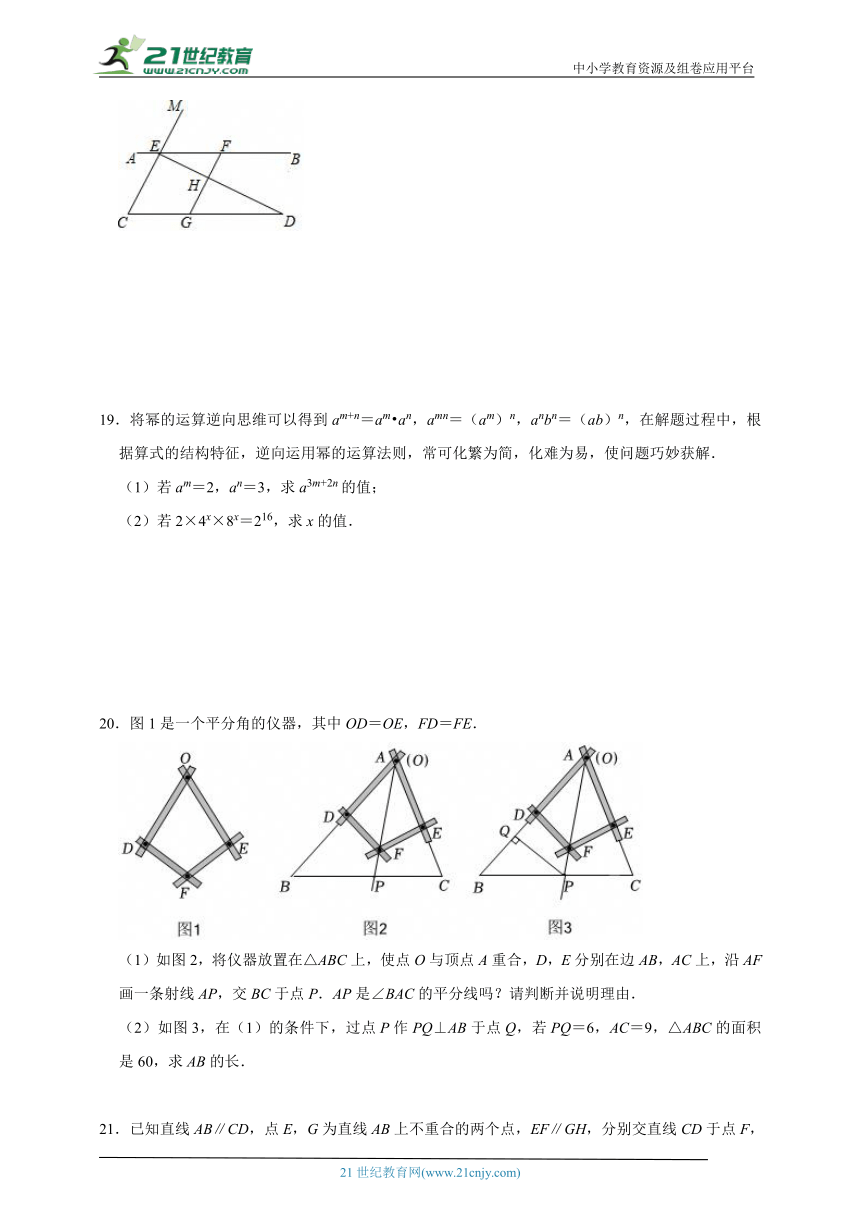
18.如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:AB∥CD;
(2)若∠EHF=70°,∠D=30°,求∠AEM的度数.
19.将幂的运算逆向思维可以得到am+n=am an,amn=(am)n,anbn=(ab)n,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解.
(1)若am=2,an=3,求a3m+2n的值;
(2)若2×4x×8x=216,求x的值.
20.图1是一个平分角的仪器,其中OD=OE,FD=FE.
(1)如图2,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P.AP是∠BAC的平分线吗?请判断并说明理由.
(2)如图3,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ=6,AC=9,△ABC的面积是60,求AB的长.
21.已知直线AB∥CD,点E,G为直线AB上不重合的两个点,EF∥GH,分别交直线CD于点F,H,EP平分∠AEF交CD于点P.
(1)如图1,试说明:∠PHG=∠FEG;
(2)如图1,若∠EPF:∠PHG=1:3,求∠EFD的大小.
(3)如图2,点M为线段GH延长线上一点,连结EM,FM.若∠HFM=∠HMF,试探索∠PEM与∠EMF的数量关系,并说明理由.
期末复习卷-2024-2025学年数学七年级下册北师大版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C D D B B B D
一.选择题(共8小题)
1.2024年9月9日,工业和信息化部宣布中国首台氟化氩光刻机,实现套刻≤8nm技术,标志着我国在高端芯片制造领域取得了关键性进展.已知8纳米=0.000000008米,0.000000008用科学记数法可表示为( )
A.8×109 B.8×10﹣9 C.8×1010 D.8×10﹣10
【解答】解:0.000000008=8×10﹣9.
故选:B.
2.如图,AB∥CD,∠CDE=130°,则∠A的度数为( )
A.70° B.65° C.50° D.40°
【解答】解:由题意知,∠CDA=180°﹣∠CDE=50°,
∵AB∥CD,
∴∠A=∠CDA=50°,
故选:C.
3.如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A. B.
C. D.
【解答】解:该蓄水池就是一个连通器.开始时注入甲池,乙池无水,当甲池中水位到达与乙池的连接处时,乙池才开始注水,所以A、B不正确,
此时甲池水位不变,所有水注入乙池,所以水位上升快.当乙池水位到达连接处时,所注入的水使甲乙两个水池同时升高,所以升高速度变慢.在乙池水位超过连通部分,甲和乙部分同时升高,但蓄水池底变小,此时比连通部分快.
故选:D.
4.下列各式运算中结果是a6是( )
A.a3+a3 B.(a3)3 C.a12÷a2 D.a3 a3
【解答】解:A、a3+a3=2a3,故此选项不合题意;
B、(a3)3=a9,故此选项不合题意;
C、a12÷a2=a10,故此选项不合题意;
D、a3 a3=a6,故此选项符合题意;
故选:D.
5.观察下列作图痕迹,所作线段CD为△ABC的中线的是( )
A. B.
C. D.
【解答】解:观察作图痕迹可知:
A.BC=BD,
所以A选项不符合题意;
B.CD为△ABC的边AB上的中线,
所以B选项符合题意;
C.CD是∠ACB的平分线,
所以C选项不符合题意;
D.CD⊥AB,但不平分,
所以D选项不符合题意.
故选:B.
6.已知m+n=4,m2﹣n2=﹣8,则m﹣n的值为( )
A.﹣4 B.﹣2 C.2 D.4
【解答】解:∵m2﹣n2=(m+n)(m﹣n)=﹣8,m+n=4,
∴m﹣n=﹣2.
故选:B.
7.汉字是世界上最古老的文字之一,现存最早的汉字是公元前14世纪殷商时期的甲骨文,之后又产生了金文、小篆、隶书、草书、楷书、行书等多种字体,每种字体都有着鲜明的艺术特征.下面的汉字可以近似地看成轴对称图形的是( )
A. B. C. D.
【解答】解:A选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
B选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
C选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
D选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
故选:B.
8.将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
【解答】解:如图所示,
∵长方形的两条长边平行,∠1=42°,
∴∠1=∠4=42°,∠4=∠5,
∴∠5=42°,
由折叠的性质可知,∠2=∠3,
∵∠2+∠3+∠5=180°,
∴∠2=69°,
故选:D.
二.填空题(共6小题)
9.一个等腰三角形的一个角为50°,则它的顶角的度数是 50°或80° .
【解答】解:(1)当50°角为顶角,顶角度数即为50°;
(2)当50°为底角时,顶角=180°﹣2×50°=80°.
故填50°或80°.
10.围棋起源于中国,棋子分黑白两色.一个不透明的盒子中装有2个黑色棋子和4个白色棋子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到白色棋子的概率是 .
【解答】解:∵一个不透明的盒子中装有2个黑色棋子和4个白色棋子,每个棋子除颜色外都相同,
∴任意摸出一个棋子,摸到白色棋子的概率是.
故答案为:.
11.如图,点P到一条笔直的公路MN共有四条路径,若要用相同速度从点P走到公路,最快到达的路径是选择沿线段PB去公路,这一选择用到的数学知识是 垂线段最短 .
【解答】解:∵PB⊥MN,
∴根据垂线段最短得出最快到达的路径是选择沿线段PB去公路,
故答案为:垂线段最短.
12.水池中有若干吨水,开一个出水口将全池水放光,所用时间t(单位:h)与出水速度v(单位:T/h)之间的关系如表:
出水速度v(T/h) 10 8 5 4 2 …
t(h) 1 1.25 2 2.5 5 …
用式子表示t与v的关系是 vt=10 .
【解答】解:由表格可知,vt=10.
故答案为:vt=10.
13.如图,∠AOB=15°,点P是OA上一点,点Q与点P关于OB对称,QM⊥OA于点M,若OP=6,则QM的长为 3 .
【解答】解:如图,连接OQ.
∵P与PQ关于OB对称,
∴∠AOB=∠QOB=15°,OQ=OP=6,
∴∠AOQ=30°,
∵QM⊥OA,
∴∠OMQ=90°,
∴QMOQ=3.
故答案为:3.
14.如图1.将一张长方形纸板四角各切去一个同样的正方形,制成如图2的无盖纸盒,若纸盒的容积为4a2b,则图2中纸盒底部长方形的周长为 8a+2b .
【解答】解:根据题意,得
纸盒底部长方形的宽为4a,
∴纸盒底部长方形的周长为:2(4a+b)=8a+2b.
故答案为:8a+2b.
三.解答题(共7小题)
15.计算:(y+2)(y﹣2)﹣(y﹣1)(y﹣3).
【解答】解:(y+2)(y﹣2)﹣(y﹣1)(y﹣3)
=y2﹣4﹣(y2﹣3y﹣y+3)
=y2﹣4﹣y2+3y+y﹣3
=4y﹣7.
16.已知:如图,AC∥DF,AC=DF,AD=BE.求证:△ABC≌△DEF.
【解答】证明:∵AC∥DF,
∴∠A=∠FDE
∵AD=BE,
∴AD+AE=BE+AE,即 AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
17.如图,在△ABC中,AD⊥BC于点D,E为AC上一点,连结BE交AD于点F,且BF=AC,DF=DC.
(1)求证:AD=BD.
(2)若AD=12,BF=13,求AF的长.
【解答】证明:(1)∵AD⊥BC,
∴∠BDA=∠ADC=90°,
∵BF=AC,DF=DC,
∴Rt△BFD≌Rt△ACD(HL),
∴AD=BD;
(2)∵AD=12,BF=13,
∴BD=12,
由勾股定理得:DF5,
∴AF=AD﹣DF=12﹣5=7.
18.如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:AB∥CD;
(2)若∠EHF=70°,∠D=30°,求∠AEM的度数.
【解答】解:(1)证明:∵∠CED=∠GHD,
∴CE∥GF,
∴∠C=∠DGF,
又∵∠C=∠EFG,
∴∠DGF=∠EFG,
∴AB∥CD;
(2)∵∠CED=∠GHD,∠GHD=∠EHF=70°,
∴∠CED=70°,
在△CDE中,∠CED=70°,∠D=30°,
∴∠C=180°﹣70°﹣30°=80°,
∵AB∥CD,
∴∠AEC=∠C=80°,
∴∠AEM=180°﹣∠AEC=180°﹣80°=100°.
答:∠AEM的度数为100°.
19.将幂的运算逆向思维可以得到am+n=am an,amn=(am)n,anbn=(ab)n,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解.
(1)若am=2,an=3,求a3m+2n的值;
(2)若2×4x×8x=216,求x的值.
【解答】解:(1)根据题意可知,am=2,an=3,
∴a3m+2n
=a3m a2n
=(am)3 (an)2
=23×32
=8×9
=72;
(2)∵2×4x×8x
=2×(22)x×(23)x
=21+2x+3x
=216,
∴1+2x+3x=16,
5x=15,
解得:x=3.
20.图1是一个平分角的仪器,其中OD=OE,FD=FE.
(1)如图2,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P.AP是∠BAC的平分线吗?请判断并说明理由.
(2)如图3,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ=6,AC=9,△ABC的面积是60,求AB的长.
【解答】解:(1)AP是∠BAC的平分线,
理由如下:∵OD=OE,FD=FE,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P.
∴AD=AE,AF=AF,DF=EF,
在△ADF和△AEF中,
,
∴△ADF≌△AEF(SSS),
∴∠DAF=∠EAF,
∴AP平分∠BAC.
(2)∵AP平分∠BAC,PQ⊥AB,
∴△APC的高等于PQ,
∵PQ=6.
∴S△APC=6×9÷2=27,
∵S△ABP=S△ABC﹣S△APC=33
∴AB=2S△ABP÷PQ=33×2÷6=11.
21.已知直线AB∥CD,点E,G为直线AB上不重合的两个点,EF∥GH,分别交直线CD于点F,H,EP平分∠AEF交CD于点P.
(1)如图1,试说明:∠PHG=∠FEG;
(2)如图1,若∠EPF:∠PHG=1:3,求∠EFD的大小.
(3)如图2,点M为线段GH延长线上一点,连结EM,FM.若∠HFM=∠HMF,试探索∠PEM与∠EMF的数量关系,并说明理由.
【解答】(1)证明:∵AB∥CD,
∴∠FEG=∠EFP,
∵EF∥GH,
∴∠EFP=∠PHG,
∴∠PHG=∠FEG;
(2)解:∵AB∥CD,
∴∠EPF=∠PEA,
∵EP平分∠AEF,
∴∠AEP∠AEF,
∴∠EPF∠AEF,
∵∠AEF+∠FEG=180°,
∴∠EPF(180°﹣∠FEG),
由(1)知∠PHG=∠FEG;
∴∠EPF(180°﹣∠PHG),
∵∠EPF:∠PHG=1:3,
可设∠EPF=x,则∠PHG=3x,
则x(180°﹣3x),
解得x=36°,
∴∠PHG=108°,
∵EF∥GH,
∴∠EFD+∠PHG=180°,
∴∠EFD=72°;
(3)解:∠PEM+∠EMF=90°;理由如下:
设∠EMF=α,∠EMG=β,则∠HFM=∠HMF=α+β,
∵EF∥GH,
∴∠EFM+∠HMF=180°,∠FEM=β,
∴∠EFM=180°﹣(α+β),
∴∠EFH=∠EFM﹣∠HFM=180°﹣2(α+β),
∵AB∥CD,
∴∠AEF=∠EFH=180°﹣2(α+β),
∵EP平分∠AEF,
∴∠PEF∠AEF=90°﹣α﹣β,
∴∠PEM=∠PEF+FEM=90°﹣α﹣β+β=90°﹣α,
∵∠EMF=α,
∴∠PEM=90°﹣∠EMF,
∴∠PEM+∠EMF=90°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末复习卷-2024-2025学年数学七年级下册北师大版(2024)
一.选择题(共8小题)
1.2024年9月9日,工业和信息化部宣布中国首台氟化氩光刻机,实现套刻≤8nm技术,标志着我国在高端芯片制造领域取得了关键性进展.已知8纳米=0.000000008米,0.000000008用科学记数法可表示为( )
A.8×109 B.8×10﹣9 C.8×1010 D.8×10﹣10
2.如图,AB∥CD,∠CDE=130°,则∠A的度数为( )
A.70° B.65° C.50° D.40°
3.如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A. B.
C. D.
4.下列各式运算中结果是a6是( )
A.a3+a3 B.(a3)3 C.a12÷a2 D.a3 a3
5.观察下列作图痕迹,所作线段CD为△ABC的中线的是( )
A. B.
C. D.
6.已知m+n=4,m2﹣n2=﹣8,则m﹣n的值为( )
A.﹣4 B.﹣2 C.2 D.4
7.汉字是世界上最古老的文字之一,现存最早的汉字是公元前14世纪殷商时期的甲骨文,之后又产生了金文、小篆、隶书、草书、楷书、行书等多种字体,每种字体都有着鲜明的艺术特征.下面的汉字可以近似地看成轴对称图形的是( )
A. B. C. D.
8.将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
二.填空题(共6小题)
9.一个等腰三角形的一个角为50°,则它的顶角的度数是 .
10.围棋起源于中国,棋子分黑白两色.一个不透明的盒子中装有2个黑色棋子和4个白色棋子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到白色棋子的概率是 .
11.如图,点P到一条笔直的公路MN共有四条路径,若要用相同速度从点P走到公路,最快到达的路径是选择沿线段PB去公路,这一选择用到的数学知识是 .
12.水池中有若干吨水,开一个出水口将全池水放光,所用时间t(单位:h)与出水速度v(单位:T/h)之间的关系如表:
出水速度v(T/h) 10 8 5 4 2 …
t(h) 1 1.25 2 2.5 5 …
用式子表示t与v的关系是 .
13.如图,∠AOB=15°,点P是OA上一点,点Q与点P关于OB对称,QM⊥OA于点M,若OP=6,则QM的长为 .
14.如图1.将一张长方形纸板四角各切去一个同样的正方形,制成如图2的无盖纸盒,若纸盒的容积为4a2b,则图2中纸盒底部长方形的周长为 .
三.解答题(共7小题)
15.计算:(y+2)(y﹣2)﹣(y﹣1)(y﹣3).
16.已知:如图,AC∥DF,AC=DF,AD=BE.求证:△ABC≌△DEF.
17.如图,在△ABC中,AD⊥BC于点D,E为AC上一点,连结BE交AD于点F,且BF=AC,DF=DC.
(1)求证:AD=BD.
(2)若AD=12,BF=13,求AF的长.
18.如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:AB∥CD;
(2)若∠EHF=70°,∠D=30°,求∠AEM的度数.
19.将幂的运算逆向思维可以得到am+n=am an,amn=(am)n,anbn=(ab)n,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解.
(1)若am=2,an=3,求a3m+2n的值;
(2)若2×4x×8x=216,求x的值.
20.图1是一个平分角的仪器,其中OD=OE,FD=FE.
(1)如图2,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P.AP是∠BAC的平分线吗?请判断并说明理由.
(2)如图3,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ=6,AC=9,△ABC的面积是60,求AB的长.
21.已知直线AB∥CD,点E,G为直线AB上不重合的两个点,EF∥GH,分别交直线CD于点F,H,EP平分∠AEF交CD于点P.
(1)如图1,试说明:∠PHG=∠FEG;
(2)如图1,若∠EPF:∠PHG=1:3,求∠EFD的大小.
(3)如图2,点M为线段GH延长线上一点,连结EM,FM.若∠HFM=∠HMF,试探索∠PEM与∠EMF的数量关系,并说明理由.
期末复习卷-2024-2025学年数学七年级下册北师大版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C D D B B B D
一.选择题(共8小题)
1.2024年9月9日,工业和信息化部宣布中国首台氟化氩光刻机,实现套刻≤8nm技术,标志着我国在高端芯片制造领域取得了关键性进展.已知8纳米=0.000000008米,0.000000008用科学记数法可表示为( )
A.8×109 B.8×10﹣9 C.8×1010 D.8×10﹣10
【解答】解:0.000000008=8×10﹣9.
故选:B.
2.如图,AB∥CD,∠CDE=130°,则∠A的度数为( )
A.70° B.65° C.50° D.40°
【解答】解:由题意知,∠CDA=180°﹣∠CDE=50°,
∵AB∥CD,
∴∠A=∠CDA=50°,
故选:C.
3.如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A. B.
C. D.
【解答】解:该蓄水池就是一个连通器.开始时注入甲池,乙池无水,当甲池中水位到达与乙池的连接处时,乙池才开始注水,所以A、B不正确,
此时甲池水位不变,所有水注入乙池,所以水位上升快.当乙池水位到达连接处时,所注入的水使甲乙两个水池同时升高,所以升高速度变慢.在乙池水位超过连通部分,甲和乙部分同时升高,但蓄水池底变小,此时比连通部分快.
故选:D.
4.下列各式运算中结果是a6是( )
A.a3+a3 B.(a3)3 C.a12÷a2 D.a3 a3
【解答】解:A、a3+a3=2a3,故此选项不合题意;
B、(a3)3=a9,故此选项不合题意;
C、a12÷a2=a10,故此选项不合题意;
D、a3 a3=a6,故此选项符合题意;
故选:D.
5.观察下列作图痕迹,所作线段CD为△ABC的中线的是( )
A. B.
C. D.
【解答】解:观察作图痕迹可知:
A.BC=BD,
所以A选项不符合题意;
B.CD为△ABC的边AB上的中线,
所以B选项符合题意;
C.CD是∠ACB的平分线,
所以C选项不符合题意;
D.CD⊥AB,但不平分,
所以D选项不符合题意.
故选:B.
6.已知m+n=4,m2﹣n2=﹣8,则m﹣n的值为( )
A.﹣4 B.﹣2 C.2 D.4
【解答】解:∵m2﹣n2=(m+n)(m﹣n)=﹣8,m+n=4,
∴m﹣n=﹣2.
故选:B.
7.汉字是世界上最古老的文字之一,现存最早的汉字是公元前14世纪殷商时期的甲骨文,之后又产生了金文、小篆、隶书、草书、楷书、行书等多种字体,每种字体都有着鲜明的艺术特征.下面的汉字可以近似地看成轴对称图形的是( )
A. B. C. D.
【解答】解:A选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
B选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
C选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
D选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
故选:B.
8.将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
【解答】解:如图所示,
∵长方形的两条长边平行,∠1=42°,
∴∠1=∠4=42°,∠4=∠5,
∴∠5=42°,
由折叠的性质可知,∠2=∠3,
∵∠2+∠3+∠5=180°,
∴∠2=69°,
故选:D.
二.填空题(共6小题)
9.一个等腰三角形的一个角为50°,则它的顶角的度数是 50°或80° .
【解答】解:(1)当50°角为顶角,顶角度数即为50°;
(2)当50°为底角时,顶角=180°﹣2×50°=80°.
故填50°或80°.
10.围棋起源于中国,棋子分黑白两色.一个不透明的盒子中装有2个黑色棋子和4个白色棋子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到白色棋子的概率是 .
【解答】解:∵一个不透明的盒子中装有2个黑色棋子和4个白色棋子,每个棋子除颜色外都相同,
∴任意摸出一个棋子,摸到白色棋子的概率是.
故答案为:.
11.如图,点P到一条笔直的公路MN共有四条路径,若要用相同速度从点P走到公路,最快到达的路径是选择沿线段PB去公路,这一选择用到的数学知识是 垂线段最短 .
【解答】解:∵PB⊥MN,
∴根据垂线段最短得出最快到达的路径是选择沿线段PB去公路,
故答案为:垂线段最短.
12.水池中有若干吨水,开一个出水口将全池水放光,所用时间t(单位:h)与出水速度v(单位:T/h)之间的关系如表:
出水速度v(T/h) 10 8 5 4 2 …
t(h) 1 1.25 2 2.5 5 …
用式子表示t与v的关系是 vt=10 .
【解答】解:由表格可知,vt=10.
故答案为:vt=10.
13.如图,∠AOB=15°,点P是OA上一点,点Q与点P关于OB对称,QM⊥OA于点M,若OP=6,则QM的长为 3 .
【解答】解:如图,连接OQ.
∵P与PQ关于OB对称,
∴∠AOB=∠QOB=15°,OQ=OP=6,
∴∠AOQ=30°,
∵QM⊥OA,
∴∠OMQ=90°,
∴QMOQ=3.
故答案为:3.
14.如图1.将一张长方形纸板四角各切去一个同样的正方形,制成如图2的无盖纸盒,若纸盒的容积为4a2b,则图2中纸盒底部长方形的周长为 8a+2b .
【解答】解:根据题意,得
纸盒底部长方形的宽为4a,
∴纸盒底部长方形的周长为:2(4a+b)=8a+2b.
故答案为:8a+2b.
三.解答题(共7小题)
15.计算:(y+2)(y﹣2)﹣(y﹣1)(y﹣3).
【解答】解:(y+2)(y﹣2)﹣(y﹣1)(y﹣3)
=y2﹣4﹣(y2﹣3y﹣y+3)
=y2﹣4﹣y2+3y+y﹣3
=4y﹣7.
16.已知:如图,AC∥DF,AC=DF,AD=BE.求证:△ABC≌△DEF.
【解答】证明:∵AC∥DF,
∴∠A=∠FDE
∵AD=BE,
∴AD+AE=BE+AE,即 AB=DE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
17.如图,在△ABC中,AD⊥BC于点D,E为AC上一点,连结BE交AD于点F,且BF=AC,DF=DC.
(1)求证:AD=BD.
(2)若AD=12,BF=13,求AF的长.
【解答】证明:(1)∵AD⊥BC,
∴∠BDA=∠ADC=90°,
∵BF=AC,DF=DC,
∴Rt△BFD≌Rt△ACD(HL),
∴AD=BD;
(2)∵AD=12,BF=13,
∴BD=12,
由勾股定理得:DF5,
∴AF=AD﹣DF=12﹣5=7.
18.如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:AB∥CD;
(2)若∠EHF=70°,∠D=30°,求∠AEM的度数.
【解答】解:(1)证明:∵∠CED=∠GHD,
∴CE∥GF,
∴∠C=∠DGF,
又∵∠C=∠EFG,
∴∠DGF=∠EFG,
∴AB∥CD;
(2)∵∠CED=∠GHD,∠GHD=∠EHF=70°,
∴∠CED=70°,
在△CDE中,∠CED=70°,∠D=30°,
∴∠C=180°﹣70°﹣30°=80°,
∵AB∥CD,
∴∠AEC=∠C=80°,
∴∠AEM=180°﹣∠AEC=180°﹣80°=100°.
答:∠AEM的度数为100°.
19.将幂的运算逆向思维可以得到am+n=am an,amn=(am)n,anbn=(ab)n,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解.
(1)若am=2,an=3,求a3m+2n的值;
(2)若2×4x×8x=216,求x的值.
【解答】解:(1)根据题意可知,am=2,an=3,
∴a3m+2n
=a3m a2n
=(am)3 (an)2
=23×32
=8×9
=72;
(2)∵2×4x×8x
=2×(22)x×(23)x
=21+2x+3x
=216,
∴1+2x+3x=16,
5x=15,
解得:x=3.
20.图1是一个平分角的仪器,其中OD=OE,FD=FE.
(1)如图2,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P.AP是∠BAC的平分线吗?请判断并说明理由.
(2)如图3,在(1)的条件下,过点P作PQ⊥AB于点Q,若PQ=6,AC=9,△ABC的面积是60,求AB的长.
【解答】解:(1)AP是∠BAC的平分线,
理由如下:∵OD=OE,FD=FE,将仪器放置在△ABC上,使点O与顶点A重合,D,E分别在边AB,AC上,沿AF画一条射线AP,交BC于点P.
∴AD=AE,AF=AF,DF=EF,
在△ADF和△AEF中,
,
∴△ADF≌△AEF(SSS),
∴∠DAF=∠EAF,
∴AP平分∠BAC.
(2)∵AP平分∠BAC,PQ⊥AB,
∴△APC的高等于PQ,
∵PQ=6.
∴S△APC=6×9÷2=27,
∵S△ABP=S△ABC﹣S△APC=33
∴AB=2S△ABP÷PQ=33×2÷6=11.
21.已知直线AB∥CD,点E,G为直线AB上不重合的两个点,EF∥GH,分别交直线CD于点F,H,EP平分∠AEF交CD于点P.
(1)如图1,试说明:∠PHG=∠FEG;
(2)如图1,若∠EPF:∠PHG=1:3,求∠EFD的大小.
(3)如图2,点M为线段GH延长线上一点,连结EM,FM.若∠HFM=∠HMF,试探索∠PEM与∠EMF的数量关系,并说明理由.
【解答】(1)证明:∵AB∥CD,
∴∠FEG=∠EFP,
∵EF∥GH,
∴∠EFP=∠PHG,
∴∠PHG=∠FEG;
(2)解:∵AB∥CD,
∴∠EPF=∠PEA,
∵EP平分∠AEF,
∴∠AEP∠AEF,
∴∠EPF∠AEF,
∵∠AEF+∠FEG=180°,
∴∠EPF(180°﹣∠FEG),
由(1)知∠PHG=∠FEG;
∴∠EPF(180°﹣∠PHG),
∵∠EPF:∠PHG=1:3,
可设∠EPF=x,则∠PHG=3x,
则x(180°﹣3x),
解得x=36°,
∴∠PHG=108°,
∵EF∥GH,
∴∠EFD+∠PHG=180°,
∴∠EFD=72°;
(3)解:∠PEM+∠EMF=90°;理由如下:
设∠EMF=α,∠EMG=β,则∠HFM=∠HMF=α+β,
∵EF∥GH,
∴∠EFM+∠HMF=180°,∠FEM=β,
∴∠EFM=180°﹣(α+β),
∴∠EFH=∠EFM﹣∠HFM=180°﹣2(α+β),
∵AB∥CD,
∴∠AEF=∠EFH=180°﹣2(α+β),
∵EP平分∠AEF,
∴∠PEF∠AEF=90°﹣α﹣β,
∴∠PEM=∠PEF+FEM=90°﹣α﹣β+β=90°﹣α,
∵∠EMF=α,
∴∠PEM=90°﹣∠EMF,
∴∠PEM+∠EMF=90°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
