江苏省南通市启东市2025届九年级下学期中考二模数学试卷(含详解)
文档属性
| 名称 | 江苏省南通市启东市2025届九年级下学期中考二模数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 08:56:46 | ||
图片预览




文档简介
2025年江苏省南通市启东市中考二模数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.2025的倒数是( )
A.2025 B. C. D.
2.下列运算正确的是( )
A. B.
C. D.
3.将一个含有角的直角三角板和一把直尺按如图方式放置,若,则的度数为( )
A. B.
C. D.
4.若一次函数的图象经过点,,则与的大小关系是( )
A. B. C. D.
5.在下面四个几何体中,其左视图不是中心对称图形的是( )
A. B. C. D.
6.已知是关于的一元二次方程的一个根,则的值为( )
A. B. C.5 D.7
7.如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在左、右两个最高位置时,细绳相应所成的角∠AOB为40°,那么小球在最高位置和最低位置时的高度差为( )
A.厘米 B.厘米
C.厘米 D.厘米
8.在献爱心活动中,五名同学捐款数分别是,,,,(单元:元),后来每人追加了元.追加后的5个数据与之前的5个数据相比,不变的是( )
A.平均数 B.众数 C.中位数 D.方差
9.如图,在等腰三角形中,,点D在上,连接,把绕点A逆时针旋转得到,使,连接,若,,则的长为( )
A. B. C. D.10
10.二次函数,若当时,,则当时,函数值的取值范围是( )
A. B. C. D.
二、填空题
11.量子点是一种重要的低维半导体材料,一般为球形或类球形,直径常在之间.用科学记数法表示是 (其中).
12.分解因式: .
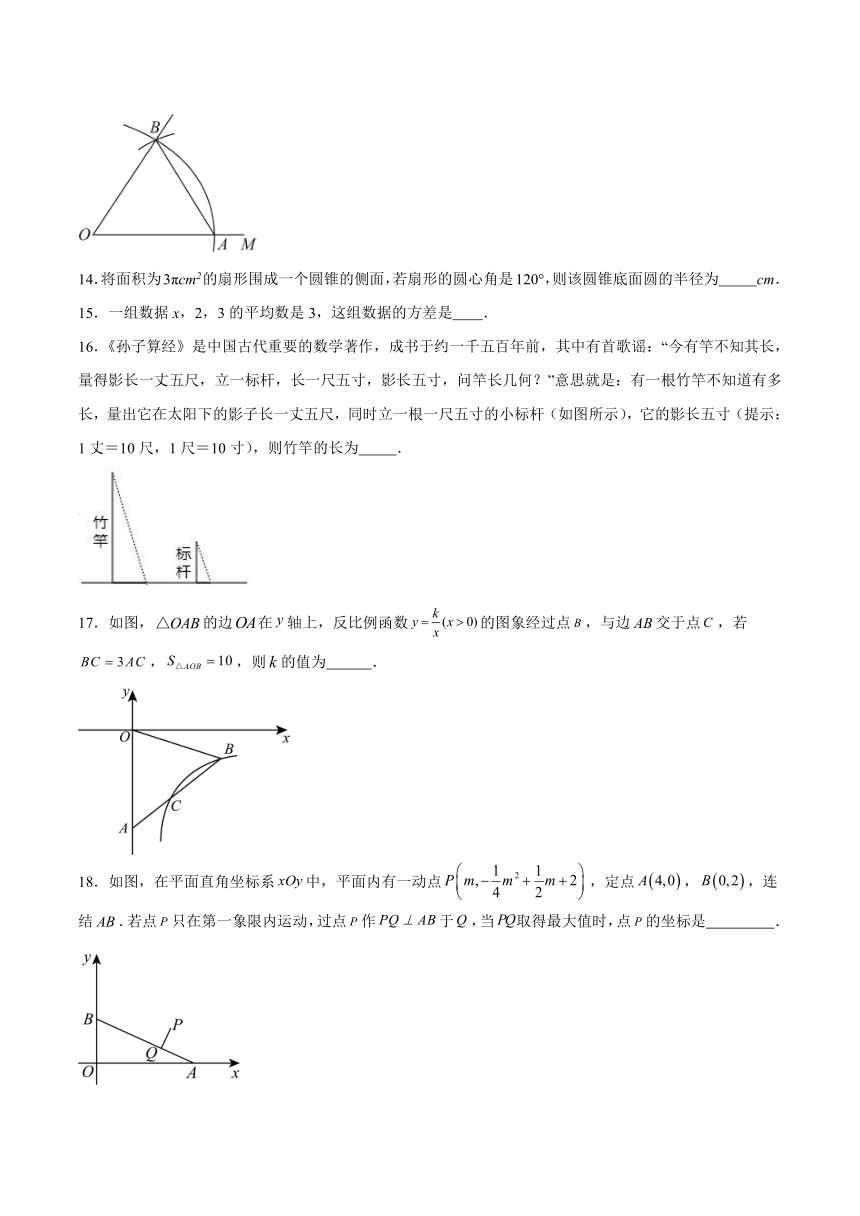
13.如图,以O为圆心,任意长为半径画弧,与射线OM相交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于 .
14.将面积为3πcm2的扇形围成一个圆锥的侧面,若扇形的圆心角是120°,则该圆锥底面圆的半径为 cm.
15.一组数据x,2,3的平均数是3,这组数据的方差是 .
16.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?”意思就是:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆(如图所示),它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为 .
17.如图,的边在轴上,反比例函数的图象经过点,与边交于点,若,,则的值为 .
18.如图,在平面直角坐标系中,平面内有一动点,定点,,连结.若点只在第一象限内运动,过点作于,当取得最大值时,点的坐标是 .
三、解答题
19.(1)计算:;
(2)解不等式组:.
20.【阅读材料】
老师的问题:
已知:如图,中,,是斜边上的中线,求作:菱形
小明的作法:
(1)取的中点,
(2)连接并延长到,使,
(3)连接,,四边形就是所求作的菱形;
【解答问题】
请根据材料中的信息,证明四边形是菱形.
21.某商品博览会在五一节期间举办了“五一不重”的活动,吸引了众多市民前来参观.商品博览会设置了A、B两个安检通道进入场馆内部,又设置了D、E、F三个离场通道.小明和小亮两名同学分别到博览会游玩.
(1)小明从A入口进入商品博览会的概率是 ;
(2)参观结束后,小明和小亮都从D出口走出博览会的概率是多少?(列表或画树状图)
22.如图,在中,.以为直径的圆分别交,于点,.过点作圆的切线交的延长线于点.
(1)求证:;
(2)如果,,求的长.
23.如图1、图2是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮筐D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮筐D到地面的距离.(精确到0.1米,参考数据:cos75°≈0.3,sin75°≈0.9,tan75°≈3.7,≈1.7,≈1.4)
24.某企业生产并销售某种产品,假设销售量与产量相等,图中的线段表示该产品每千克生产成本单位:元与产量单位:之间的函数关系;线段表示该产品销售价单位:元与产量单位:之间的函数关系,已知,.
(1)求线段所表示的与之间的函数表达式;
(2)若,该产品产量为多少时,获得的利润最大?最大利润是多少?
(3)若,该产品获得的利润最大利润是______.
25.已知关于x的二次函数(实数b,c为常数).
(1)若二次函数的图象经过点,对称轴为,求此二次函数的表达式;
(2)若,当时,二次函数的最小值为21,求b的值;
(3)记关于x的二次函数,若在(1)的条件下,当时,总有,求实数m的最小值.
26.如图,在矩形中,,,点E在上,连接、,相交于点G,作,交于点F,设.
【变中不变】
(1)明明发现:连接,当点E的位置在上发生变化时,的度数始终不变.经过思考,他整理出如下说理过程,请补充完整.
∵,且①_______;
∴;
∴即:;
又∵;
∴②_______;
∴;
∴;
在矩形中,;
∴;
∴③_______°,即度数不变.
【尝试应用】
(2)若,求的长;
【思维拓展】
(3)将绕着点E顺时针旋转得到,是否存在这样的x,使得有顶点落在直线上,若存在,请求出满足条件的x值;若不存在,请说明理由.
《2025年江苏省南通市启东市中考二模数学试题》参考答案
1.D
解:根据倒数的定义得2025的倒数为,
故选:D.
2.C
解:A、,故本选项错误,不符合题意;
B、,故本选项错误,不符合题意;
C、,故本选项正确,符合题意;
D、,故本选项错误,不符合题意;
故选:C
3.B
解:如图所示,
∵,
∴,
∴,
故选:B.
4.A
解:∵一次函数y=2x+1中,k=2>0,
∴y随着x的增大而增大.
∵点(-3,y1)和(4,y2)是一次函数y=2x+1图象上的两个点,-3<4,
∴y1<y2.
故选:A.
5.C
解:根据题意知,A选项左视图为正方形,是中心对称图形,故该选项不符合题意;
B选项左视图为圆,是中心对称图形,故该选项不符合题意;
C选项左视图为等腰三角形,不是中心对称图形,故该选项符合题意;
D选项左视图为矩形,是中心对称图形,故该选项不符合题意;
故选:C.
6.C
解:把代入关于的一元二次方程得:
,
,
故选:C
7.D
解:如图:过作于,
中,厘米,,
.
(厘米).
故选:D.
8.D
解:五名同学捐款数分别是,,,,(单位:元),后来每人追加了元.追加后的个数据与之前的个数据相比,不变的是方差;平均数,众数,中位数都会发生变化,
故选:D.
9.D
解:∵绕点A逆时针旋转得到,,
∴,,
又∵,
∴,
∴,
∵,
∴,
∵,,即,
∴,
∴,
∵,
∴.
故选:D.
10.B
解:由题意得,抛物线的对称轴为直线.
,
.
.
设与轴交点为,(其中,
即:,
当时,,且抛物线开口向上,
,
抛物线的对称轴为直线,或1时,,
,.
,
当,即时,随着的增大而减少,
当时,,
,
,
当时,,
,
当时,,
函数值的取值范围为.
故选:B.
11.
解:,
故答案为:.
12.
解:原式
,
故答案为:.
13.
∵以O为圆心,任意长为半径画弧,与射线OM交于点A,
∴OA=OB,
∵以A为圆心,AO长为半径画弧,两弧交于点B,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴sin∠AOB=sin60°=.
故答案为.
14.1
解:设圆锥的母线长为Rcm,底面圆的半径为rcm,
∵面积为3πcm2的扇形围成一个圆锥的侧面,扇形的圆心角是120°,
∴=3π,
解得:R=3,
由题意可得:2πr=,
解得:r=1.
故答案为:1.
15.
解:利用平均数的计算公式可得:,解得,
∴这组数据为4,2,3,
∴这组数据的方差为.
故答案为.
16.四丈五尺
解:设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,
∴由相似相似原理可知:
解得x=45(尺).
故答案为:四丈五尺.
17.
解:如图,作轴,垂足为,轴,垂足为,连接,
,,
,
由反比例函数值的几何意义可知:
,
设,则,
,
,
解得:.
故答案为:.
18.
解:依题得,点在的函数图象上,
且需满足,,
当时,,
当时,,
即定点,为函数与坐标轴的交点,
作轴,交于点,
设直线的解析式为,
将,代入可得,
解得,
即直线的解析式为,
,,
中,,
,
,
,
,
,
在中,,
当最长时,最长,
,则,
,,
,
,
,
,
,
当时,取最大值,
此时点的坐标为.
故答案为:.
19.(1);(2)
解:(1)原式
;
(2)由不等式,得,
由不等式,得,
∴不等式组的解集为.
20.见解析
证明:∵中,,是斜边上的中线,
∴,
∵,
∴,
∴
∴四边形是平行四边形,
∵,
∴四边形是菱形.
21.(1)
(2)
(1)解:∵一共有两个入口,每个入口被选择的概率相同,
∴小明从A入口进入商品博览会的概率是,
故答案为:;
(2)解:画树状图如下:
由树状图可知,一共有9种等可能性的结果数,其中小明和小亮都从D出口走出博览会的结果数有1种,
∴小明和小亮都从D出口走出博览会的概率为.
22.(1)见解析
(2)
(1)证明:,
,
又,
,
,
;
(2)解:连接,交于,
为的直径,
,
在中,,,
,
,,
,
,
在中, ,
,
为的切线,
,
,
,
,
,
,
,
,
.
23.2.9米
解:延长FE交CB的延长线于M,过A作AG⊥FM于G,
在Rt△ABC中,tan∠ACB=,
∴AB=BC tan75°=0.60×3.732=2.22,
∴GM=AB=2.22,
在Rt△AGF中,∵∠FAG=∠FHE=60°,sin∠FAG=,
∴sin60°==,
∴FG=2.125,
∴DM=FG+GM﹣DF≈2.9米.
答:篮筐D到地面的距离是2.9米.
24.(1)
(2)若,该产品产量为时,获得的利润最大,最大利润是元
(3)元
(1)解:设线段所表示的与之间的函数关系式为,
根据题意,得:,
解得:,
与之间的函数关系式为;
(2)解:若,设与之间的函数关系式为,
根据题意,得:,
解得:,
这个函数的表达式为:,
设产量为时,获得的利润为元,
根据题意,得:,
当时,取得最大值,最大值为,
答:若,该产品产量为时,获得的利润最大,最大利润是元;
(3)解:设,
由题意得:,
解得:,
这个函数的表达式为:,
,
,
,,
,即该抛物线对称轴在轴左侧,
当时,随的增大而增大,
当时,的值最大,元.
时,该产品产量为时,获得的利润最大,最大利润为元.
故答案为:元.
25.(1);(2)或4;(3)4.
解:(1)将点代入得:,
二次函数的对称轴为,
,解得,
则此二次函数的表达式为;
(2),即,
,
则此二次函数的对称轴为,
由题意,分以下三种情况:
①当,即时,
在内,随的增大而减小,
则当时,取得最小值,
因此有,
解得或(不符题设,舍去);
②当,即时,
在内,随的增大而减小;在内,随的增大而增大,
则当时,取得最小值,
因此有,
解得或(均不符题设,舍去);
③当,即时,
在内,随的增大而增大,
则当时,取得最小值,
因此有,
解得或(不符题设,舍去),
综上,的值为或4;
(3)由(1)可知,,
由得:,即,
令,
在内,随的增大而增大,
要使得当时,总有,则只需当时,即可,
因此有,
解得,
则实数的最小值为4.
26.(1);;;(2);(3)或或.
解:(1)∵,且;
∴;
∴即:;
又∵;
∴;
∴;
∴;
在矩形中,;
∴;
∴,即度数不变.
故答案为:;;;
(2)∵矩形中,,,
∴,,,
∵,
∴,
由(1)知,,
∴,
∴,即,
解得;
(2)存在,①当点与点重合时,点都在直线上,此时;
②当点落在直线上时,由旋转得,,,
过点作交分别为,
∴四边形为矩形,
∵,
∴,
∴,,,
∴,
由勾股定理得,
同理,
在中,,即,
整理得,
解得或,
∵,
∴不合题意,舍去,
∴;
③当点落在直线上时,过点作交分别为,
同理四边形为矩形,
∴,
由旋转得,,,
同理得,
∴,
∴,
∵,
∴,
∴,即,
整理得,
解得(舍去负值),
∴,
综上,或或.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.2025的倒数是( )
A.2025 B. C. D.
2.下列运算正确的是( )
A. B.
C. D.
3.将一个含有角的直角三角板和一把直尺按如图方式放置,若,则的度数为( )
A. B.
C. D.
4.若一次函数的图象经过点,,则与的大小关系是( )
A. B. C. D.
5.在下面四个几何体中,其左视图不是中心对称图形的是( )
A. B. C. D.
6.已知是关于的一元二次方程的一个根,则的值为( )
A. B. C.5 D.7
7.如图,一条细绳系着一个小球在平面内摆动.已知细绳从悬挂点O到球心的长度为50厘米,小球在左、右两个最高位置时,细绳相应所成的角∠AOB为40°,那么小球在最高位置和最低位置时的高度差为( )
A.厘米 B.厘米
C.厘米 D.厘米
8.在献爱心活动中,五名同学捐款数分别是,,,,(单元:元),后来每人追加了元.追加后的5个数据与之前的5个数据相比,不变的是( )
A.平均数 B.众数 C.中位数 D.方差
9.如图,在等腰三角形中,,点D在上,连接,把绕点A逆时针旋转得到,使,连接,若,,则的长为( )
A. B. C. D.10
10.二次函数,若当时,,则当时,函数值的取值范围是( )
A. B. C. D.
二、填空题
11.量子点是一种重要的低维半导体材料,一般为球形或类球形,直径常在之间.用科学记数法表示是 (其中).
12.分解因式: .
13.如图,以O为圆心,任意长为半径画弧,与射线OM相交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于 .
14.将面积为3πcm2的扇形围成一个圆锥的侧面,若扇形的圆心角是120°,则该圆锥底面圆的半径为 cm.
15.一组数据x,2,3的平均数是3,这组数据的方差是 .
16.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?”意思就是:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆(如图所示),它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为 .
17.如图,的边在轴上,反比例函数的图象经过点,与边交于点,若,,则的值为 .
18.如图,在平面直角坐标系中,平面内有一动点,定点,,连结.若点只在第一象限内运动,过点作于,当取得最大值时,点的坐标是 .
三、解答题
19.(1)计算:;
(2)解不等式组:.
20.【阅读材料】
老师的问题:
已知:如图,中,,是斜边上的中线,求作:菱形
小明的作法:
(1)取的中点,
(2)连接并延长到,使,
(3)连接,,四边形就是所求作的菱形;
【解答问题】
请根据材料中的信息,证明四边形是菱形.
21.某商品博览会在五一节期间举办了“五一不重”的活动,吸引了众多市民前来参观.商品博览会设置了A、B两个安检通道进入场馆内部,又设置了D、E、F三个离场通道.小明和小亮两名同学分别到博览会游玩.
(1)小明从A入口进入商品博览会的概率是 ;
(2)参观结束后,小明和小亮都从D出口走出博览会的概率是多少?(列表或画树状图)
22.如图,在中,.以为直径的圆分别交,于点,.过点作圆的切线交的延长线于点.
(1)求证:;
(2)如果,,求的长.
23.如图1、图2是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮筐D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮筐D到地面的距离.(精确到0.1米,参考数据:cos75°≈0.3,sin75°≈0.9,tan75°≈3.7,≈1.7,≈1.4)
24.某企业生产并销售某种产品,假设销售量与产量相等,图中的线段表示该产品每千克生产成本单位:元与产量单位:之间的函数关系;线段表示该产品销售价单位:元与产量单位:之间的函数关系,已知,.
(1)求线段所表示的与之间的函数表达式;
(2)若,该产品产量为多少时,获得的利润最大?最大利润是多少?
(3)若,该产品获得的利润最大利润是______.
25.已知关于x的二次函数(实数b,c为常数).
(1)若二次函数的图象经过点,对称轴为,求此二次函数的表达式;
(2)若,当时,二次函数的最小值为21,求b的值;
(3)记关于x的二次函数,若在(1)的条件下,当时,总有,求实数m的最小值.
26.如图,在矩形中,,,点E在上,连接、,相交于点G,作,交于点F,设.
【变中不变】
(1)明明发现:连接,当点E的位置在上发生变化时,的度数始终不变.经过思考,他整理出如下说理过程,请补充完整.
∵,且①_______;
∴;
∴即:;
又∵;
∴②_______;
∴;
∴;
在矩形中,;
∴;
∴③_______°,即度数不变.
【尝试应用】
(2)若,求的长;
【思维拓展】
(3)将绕着点E顺时针旋转得到,是否存在这样的x,使得有顶点落在直线上,若存在,请求出满足条件的x值;若不存在,请说明理由.
《2025年江苏省南通市启东市中考二模数学试题》参考答案
1.D
解:根据倒数的定义得2025的倒数为,
故选:D.
2.C
解:A、,故本选项错误,不符合题意;
B、,故本选项错误,不符合题意;
C、,故本选项正确,符合题意;
D、,故本选项错误,不符合题意;
故选:C
3.B
解:如图所示,
∵,
∴,
∴,
故选:B.
4.A
解:∵一次函数y=2x+1中,k=2>0,
∴y随着x的增大而增大.
∵点(-3,y1)和(4,y2)是一次函数y=2x+1图象上的两个点,-3<4,
∴y1<y2.
故选:A.
5.C
解:根据题意知,A选项左视图为正方形,是中心对称图形,故该选项不符合题意;
B选项左视图为圆,是中心对称图形,故该选项不符合题意;
C选项左视图为等腰三角形,不是中心对称图形,故该选项符合题意;
D选项左视图为矩形,是中心对称图形,故该选项不符合题意;
故选:C.
6.C
解:把代入关于的一元二次方程得:
,
,
故选:C
7.D
解:如图:过作于,
中,厘米,,
.
(厘米).
故选:D.
8.D
解:五名同学捐款数分别是,,,,(单位:元),后来每人追加了元.追加后的个数据与之前的个数据相比,不变的是方差;平均数,众数,中位数都会发生变化,
故选:D.
9.D
解:∵绕点A逆时针旋转得到,,
∴,,
又∵,
∴,
∴,
∵,
∴,
∵,,即,
∴,
∴,
∵,
∴.
故选:D.
10.B
解:由题意得,抛物线的对称轴为直线.
,
.
.
设与轴交点为,(其中,
即:,
当时,,且抛物线开口向上,
,
抛物线的对称轴为直线,或1时,,
,.
,
当,即时,随着的增大而减少,
当时,,
,
,
当时,,
,
当时,,
函数值的取值范围为.
故选:B.
11.
解:,
故答案为:.
12.
解:原式
,
故答案为:.
13.
∵以O为圆心,任意长为半径画弧,与射线OM交于点A,
∴OA=OB,
∵以A为圆心,AO长为半径画弧,两弧交于点B,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴sin∠AOB=sin60°=.
故答案为.
14.1
解:设圆锥的母线长为Rcm,底面圆的半径为rcm,
∵面积为3πcm2的扇形围成一个圆锥的侧面,扇形的圆心角是120°,
∴=3π,
解得:R=3,
由题意可得:2πr=,
解得:r=1.
故答案为:1.
15.
解:利用平均数的计算公式可得:,解得,
∴这组数据为4,2,3,
∴这组数据的方差为.
故答案为.
16.四丈五尺
解:设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,
∴由相似相似原理可知:
解得x=45(尺).
故答案为:四丈五尺.
17.
解:如图,作轴,垂足为,轴,垂足为,连接,
,,
,
由反比例函数值的几何意义可知:
,
设,则,
,
,
解得:.
故答案为:.
18.
解:依题得,点在的函数图象上,
且需满足,,
当时,,
当时,,
即定点,为函数与坐标轴的交点,
作轴,交于点,
设直线的解析式为,
将,代入可得,
解得,
即直线的解析式为,
,,
中,,
,
,
,
,
,
在中,,
当最长时,最长,
,则,
,,
,
,
,
,
,
当时,取最大值,
此时点的坐标为.
故答案为:.
19.(1);(2)
解:(1)原式
;
(2)由不等式,得,
由不等式,得,
∴不等式组的解集为.
20.见解析
证明:∵中,,是斜边上的中线,
∴,
∵,
∴,
∴
∴四边形是平行四边形,
∵,
∴四边形是菱形.
21.(1)
(2)
(1)解:∵一共有两个入口,每个入口被选择的概率相同,
∴小明从A入口进入商品博览会的概率是,
故答案为:;
(2)解:画树状图如下:
由树状图可知,一共有9种等可能性的结果数,其中小明和小亮都从D出口走出博览会的结果数有1种,
∴小明和小亮都从D出口走出博览会的概率为.
22.(1)见解析
(2)
(1)证明:,
,
又,
,
,
;
(2)解:连接,交于,
为的直径,
,
在中,,,
,
,,
,
,
在中, ,
,
为的切线,
,
,
,
,
,
,
,
,
.
23.2.9米
解:延长FE交CB的延长线于M,过A作AG⊥FM于G,
在Rt△ABC中,tan∠ACB=,
∴AB=BC tan75°=0.60×3.732=2.22,
∴GM=AB=2.22,
在Rt△AGF中,∵∠FAG=∠FHE=60°,sin∠FAG=,
∴sin60°==,
∴FG=2.125,
∴DM=FG+GM﹣DF≈2.9米.
答:篮筐D到地面的距离是2.9米.
24.(1)
(2)若,该产品产量为时,获得的利润最大,最大利润是元
(3)元
(1)解:设线段所表示的与之间的函数关系式为,
根据题意,得:,
解得:,
与之间的函数关系式为;
(2)解:若,设与之间的函数关系式为,
根据题意,得:,
解得:,
这个函数的表达式为:,
设产量为时,获得的利润为元,
根据题意,得:,
当时,取得最大值,最大值为,
答:若,该产品产量为时,获得的利润最大,最大利润是元;
(3)解:设,
由题意得:,
解得:,
这个函数的表达式为:,
,
,
,,
,即该抛物线对称轴在轴左侧,
当时,随的增大而增大,
当时,的值最大,元.
时,该产品产量为时,获得的利润最大,最大利润为元.
故答案为:元.
25.(1);(2)或4;(3)4.
解:(1)将点代入得:,
二次函数的对称轴为,
,解得,
则此二次函数的表达式为;
(2),即,
,
则此二次函数的对称轴为,
由题意,分以下三种情况:
①当,即时,
在内,随的增大而减小,
则当时,取得最小值,
因此有,
解得或(不符题设,舍去);
②当,即时,
在内,随的增大而减小;在内,随的增大而增大,
则当时,取得最小值,
因此有,
解得或(均不符题设,舍去);
③当,即时,
在内,随的增大而增大,
则当时,取得最小值,
因此有,
解得或(不符题设,舍去),
综上,的值为或4;
(3)由(1)可知,,
由得:,即,
令,
在内,随的增大而增大,
要使得当时,总有,则只需当时,即可,
因此有,
解得,
则实数的最小值为4.
26.(1);;;(2);(3)或或.
解:(1)∵,且;
∴;
∴即:;
又∵;
∴;
∴;
∴;
在矩形中,;
∴;
∴,即度数不变.
故答案为:;;;
(2)∵矩形中,,,
∴,,,
∵,
∴,
由(1)知,,
∴,
∴,即,
解得;
(2)存在,①当点与点重合时,点都在直线上,此时;
②当点落在直线上时,由旋转得,,,
过点作交分别为,
∴四边形为矩形,
∵,
∴,
∴,,,
∴,
由勾股定理得,
同理,
在中,,即,
整理得,
解得或,
∵,
∴不合题意,舍去,
∴;
③当点落在直线上时,过点作交分别为,
同理四边形为矩形,
∴,
由旋转得,,,
同理得,
∴,
∴,
∵,
∴,
∴,即,
整理得,
解得(舍去负值),
∴,
综上,或或.
同课章节目录
