20.2函数巩固强化练习（含解析）

中小学教育资源及组卷应用平台
20.2函数
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．下列变量之间是函数关系的有（ ）
①正方形的面积S与边长a；
②长方形的周长C与长a；
③圆的周长C与半径R；
④中的y与x．
A．1个 B．2个 C．3个 D．4个
2．某科技小组在网上获取了声音在空气中传播的速度与空气中的温度之间的关系的一些数据（如下表）：下列说法：①在这变化过程中，自变量是温度，因变量是声音的速度；②空气的温度越高声音传播的速度越快；③声音速度y（m/s）与温度x（℃）关系式可以是；④温度每升高10℃，声音速度增加6m/s．正确的有（ ）
温度x（℃） 20 10 0 10 20 30
声速y（m/s） 318 324 330 336 342 348
A．1个 B．2个 C．3个 D．4个
3．已知n边形的内角和公式是，则其中变量是（ ）
A． B．n C．和n D．，n和180°
4．下列变量之间的关系中，具有函数关系的有（ ）
①三角形的面积与底边 ②多边形的内角和与边数
③圆的面积与半径 ④y=中的y与x
A．1个 B．2个 C．3个 D．4个
5．自由下落物体下落的高度h与下落的时间t之间的关系为h=gt2（g=9.8m/s2），在这个变化中，变量为（　　）
A．h，t B．h，g C．t，g D．t
6．2021年春节期间，疫情形势复杂，王丽遵循“防疫当前，本地过年”的原则，给远在家乡的家人打电话拜年．电话费随着时间的变化而变化，在这个过程中，因变量是（ ）
A．王丽 B．电话费 C．时间 D．家人
7．在关系式中，下列说法：都是变量，、都是常量；的值随的值变化而变化；是变量，它的值可以与无关；与的关系不能用表格表示；与的关系还可以用列表法和图象法表示，其中说法正确的是（ ）
A． B． C． D．
8．下列曲线中，表示y是x的函数的是（ ）
A． B． C． D．
9．下列图象不能表示为的函数的是（ ）
A． B．
C． D．
10．判断下列各组中的两个函数是同一函数的为（）
⑴，；
⑵，；
⑶，；
⑷，；
⑸，
A．⑴⑵ B．⑵⑶ C．⑷ D．⑶⑸
11．给出解析式①，②，③，④，⑤，其中y是x的函数的有（ ）
A．1个 B．2个 C．3个 D．4个
12．某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据如下：
温度（℃） 0 10 20 30
声速（m/s） 318 324 330 336 342 348
下列说法错误的是（　）
A．在这个变化中，自变量是温度，声速是温度的函数
B．温度越低，声速越慢
C．当温度每升高时，声速增加
D．当空气温度为时，声音可以传播
二、填空题
13．下列式子中，y是x的函数关系的有 个．
①；②；③；④；
14．如图是济南市8月2日的气温随时间变化的图象，根据图象可知：在这一天中，气温T(℃) (填“是”或“不是”)时间t(时)的函数．
15．下表是根据某地区入学儿童人数编制的：
年份 2020 2021 2022 2023 2024 …
入学儿童人数/人 2930 2720 2520 2330 2140 …
上表反映了 个变量之间的关系，其中，自变量是 ，因变量是 ．
16．一般地，如果在一个变化过程中有两个变量x、y，并且对于变量x的每一个值，y都有唯一的值与它对应，那么我们称y是x的 ，其中x是 ．
17．果字成熟后从树上落到地面，它落下的高度与经过的时间有如下的关系：
时间（秒） 0.5 0.6 0.7 0.8 0.9 1
落下的高度（米）
如果果子经过2秒落到地上，那么此果子开始落下时离地面的高度大约是 米．
三、解答题
18．指出下列问题中的常量和变量：
(1)正方形的周长l与它的边长a之间的关系是；
(2)一台机器上的轮子的转速为60转/分，轮子旋转的转数n（单位：转）与时间t（单位：分）之间的关系为；
(3)小亮练习1500米长跑，他跑完全程所用的时间t（单位：秒）与他跑步的平均速度v（单位：米/秒）的关系为．
19．下列各题中分别有几个变量？你能将其中某个变量看成另一个变量的函数吗？若能，请指出自变量的取值范围．
（1）
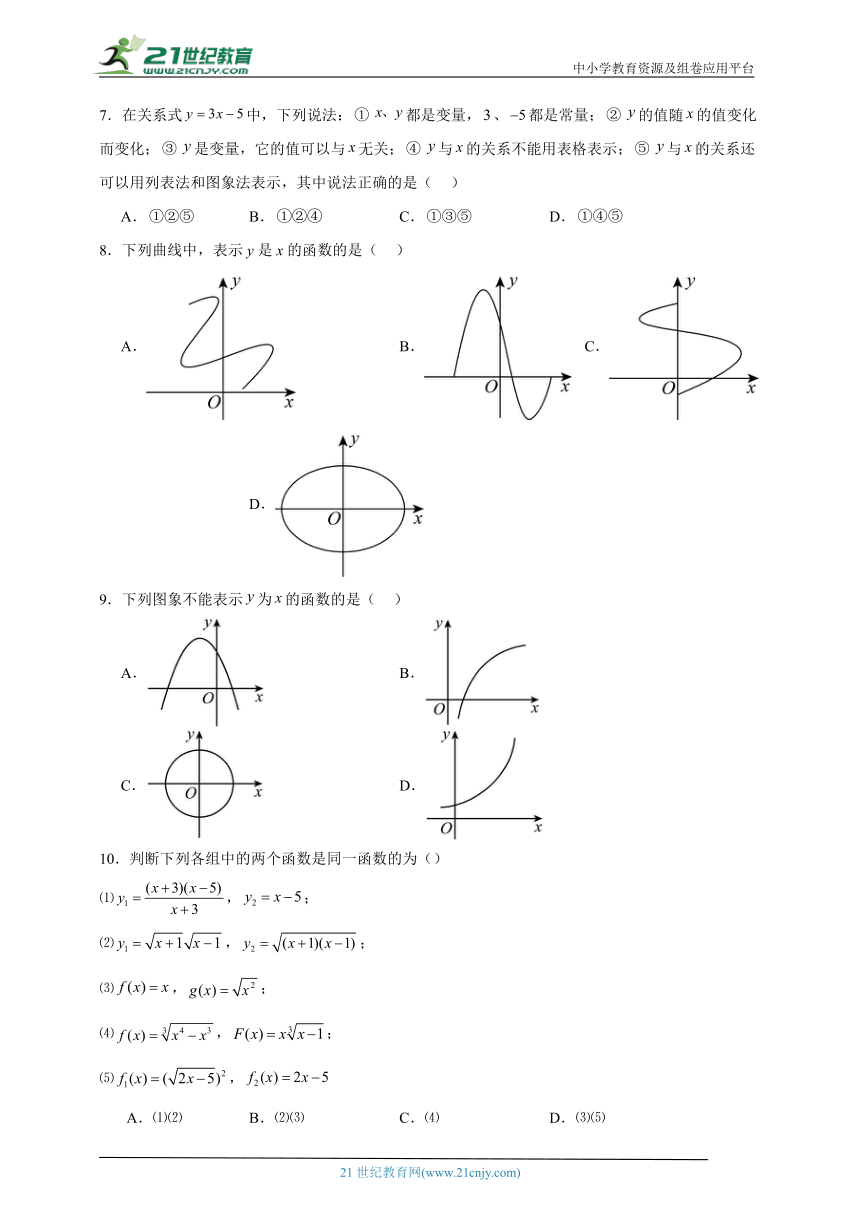
（2）在平整的路面上，某型号汽车紧急刹车后仍将滑行，一般地有经验公式，其中表示刹车前汽车的速度（单位：）．
（3）在国内投寄到外埠质量为以内的普通信函应付邮资如下表：
信件质量
邮资/元 1.20 2.40 3.60 4.80 6.00
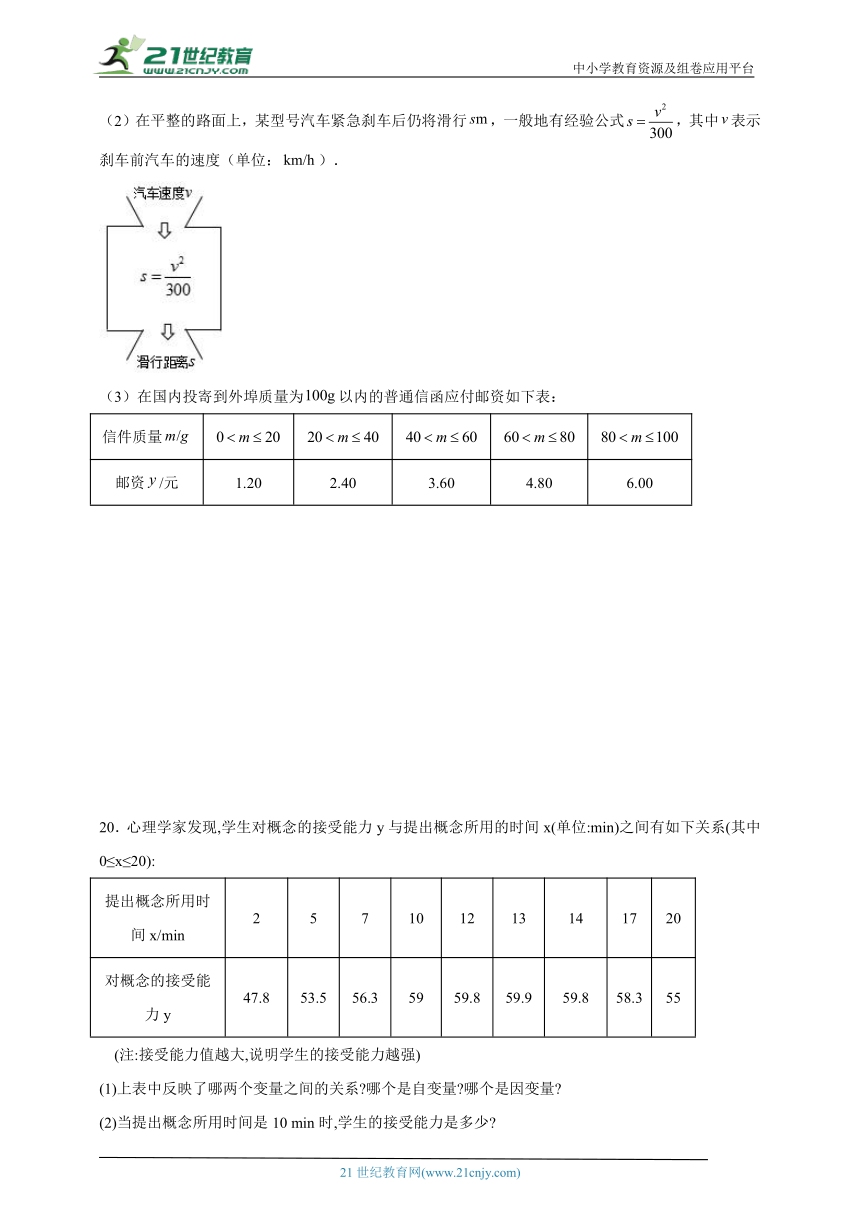
20．心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:min)之间有如下关系(其中0≤x≤20):
提出概念所用时间x/min 2 5 7 10 12 13 14 17 20
对概念的接受能力y 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
　(注:接受能力值越大,说明学生的接受能力越强)
(1)上表中反映了哪两个变量之间的关系 哪个是自变量 哪个是因变量
(2)当提出概念所用时间是10 min时,学生的接受能力是多少
(3)根据表格中的数据,你认为提出概念所用时间为多少时,学生的接受能力最强
(4)从表格中可知,当提出概念所用时间x在什么范围内时,学生的接受能力逐步增强 当提出概念所用时间x在什么范围内时,学生的接受能力逐步降低
21．研究表明，当钾肥和磷肥的施用量一定时，土豆的产量与氮肥的施用量有如下关系：
氮肥施用量/（千克/公顷） 0 34 67 101 135 202 259 336 404 471
土豆产量/（吨/公顷） 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 30.75
（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）当氮肥的施用量是101千克/公顷时，土豆的产量是多少？如果不施肥氮肥呢？
（3）根据表格中的数据，你认为氮肥的施用量是多少时比较适宜？说说你的理由．
（4）粗略说一说氮肥的施用量对土豆产量的影响.
22．下图是某物体的抛射曲线图，其中表示物体与抛射点之间的水平距离，表示物体的高度．
（1）这个图象反映了哪两个变量之间的关系？
（2）根据图象填表：
0 1 2 3 4 5 6
（3）当距离取之间的一个确定的值时，相应的高度确定吗？
（4）高度可以看成距离的函数吗？
23．父亲告诉小明：“距离地面越高，温度越低” ，并给小明出示了下面的表格．
距离地面高度（千米） 0 1 2 3 4 5
温度（°C） 20 14 8 2 –4 –10
根据上表，父亲还给小明出了下面几个问题，你和小明一起回答．
（1）上表反映了哪两个变量之间的关系？哪个是自变量？
（2）如果用h表示距离地面的高度，用t表示温度，那么随着h的变化，t是怎么变化的？
（3）你能猜出距离地面6千米的高空温度是多少吗？
24．某电动车厂2023年各月份生产电动车的数量情况如下表：
时间/月 1 2 3 4 5 6 7 8 9 10 11 12
月产量/万辆 8 8.5 9 10 11 12 10 9 10 10 10.5
(1)上表反应了哪两个变量之间的关系？
(2)哪个月份电动车的产量最高？哪个月份电动车的产量最低？
(3)从1月到6月，电动车的月产量随时间的增长而怎么变化？
《20.2函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C C A B A B C C
题号 11 12
答案 C C
1．C
【分析】根据函数的定义即可判断．
【详解】①正方形的面积，符合函数的概念，因此是函数关系；
②当长方形的宽也变化时，有3个变量，不符合函数的概念，因此不是函数关系；
③圆的周长，符合函数的概念，因此是函数关系；
④，符合函数的概念，因此是函数关系．
故选C．
【点睛】本题考查函数概念，需要理解：①有两个变量；②一个变量的数值随着另一个变量的数值的变化而发生变化；③对于自变量的每一个确定的值，函数值有且只有一个值与之对应.
2．D
【分析】根据因变量，自变量的定义即可判断①；根据表格中的数据即可判断②、③、④．
【详解】解：由表格可知随着温度的升高，声速越来越快，故②正确；
∴在这个变化过程中声速随着温度的变化而变化，
∴在这变化过程中，自变量是温度，因变量是声音的速度，故①正确；
由表格中的数据可知，温度每升高10℃，声音速度增加6m/s，故④正确；
∴，故③正确，
故选D．
【点睛】本题主要考查了求函数关系式，因变量，自变量的定义，以及用表格表示变量之间的关系，正确读懂表格中的数据是解题的关键．
3．C
【分析】本题考查了函数的概念及表示方法：一般地，如果在一个变化过程中，有两个变量，例如和，对于的每一个值，都有唯一的值与之对应，我们就说是自变量，是因变量，此时也称是的函数．
【详解】解：在多边形的内角和公式是边形的内角和是边数中，常量是和，变量是和，是的函数
故选：C．
4．C
【分析】此题是对函数概念的考查:
一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,
相应地就确定一个y值,那么我们称y是x的函数,其中x是自变量,
y是因变量.
要判断一个关系是不是函数关系,第一要看是不是一个变化过程,第二
要看在这个变化过程中是不是有两个变量,第三要看某一变量每取一个
确定的值,另一个变量是否有唯一确定的值与它对应.
【详解】解:对于①,设三角形的面积为S,底边为a,高为h,则有S=ah,由于h为变量,故不满足函数关系;
对于②,设多边形的内角和为y,边数为n(n≥3且n为整数则有y=(n-2)180°,满足函数关系;
对于③,设圆的面积为S,半径为r,则有S= πr2,满足函数关系;
对于④, 满足函数关系.故具有函数关系的有三个，答案为C
【点睛】函数关系是一一对应的，且只有两个变量是解题的关键，第①个含有三个变量底，高，面积．
5．A
【详解】试题解析：在这个变化中，变量为h、t.
故选A.
点睛：根据在一个变化的过程中，数值发生变化的量称为变量；数值始终不变的量称为常量进行分析．
6．B
【分析】根据因变量的定义：在某个变化过程中，一个变量会随着其他一个变量或几个变量的变化而变化，那么这个变量就叫做因变量．
【详解】解：∵随着时间的变化，电话费也在跟着变化，
∴在这个过程中，因变量是电话费，
故选B．
【点睛】本题主要考查了因变量的定义，熟知相关定义是解题的关键．
7．A
【分析】本题考查了函数的有关概念，根据函数的概念逐一判断即可，正确理解函数的概念是解题的关键．
【详解】是自变量，是因变量，故该说法正确；
值随值的变化而变化，故该说法正确；
是变量，随值的变化而变化，故该说法错误；
用关系式表示的可以用表格表示，故该说法错误；
与的关系还可以用列表法和图象法表示，故该说法正确，
综上所述：正确，错误，
故选：．
8．B
【分析】根据函数的定义，对于自变量x的每一个值，y都有唯一的值与它对应，即可判断．
【详解】解：A、对于自变量x的每一个值，y不是都有唯一的值与它对应，所以不能表示y是x的函数，故A不符合题意；
B、对于自变量x的每一个值，y都有唯一的值与它对应，所以能表示y是x的函数，故B符合题意；
C、对于自变量x的每一个值，y不是都有唯一的值与它对应，所以不能表示y是x的函数，故C不符合题意；
D、对于自变量x的每一个值，y不是都有唯一的值与它对应，所以不能表示y是x的函数，故D不符合题意；
故选：B．
【点睛】本题考查了函数的概念：在某一变化过程中，有两个变量x、y，一个量x变化，另一个量y随之变化，当x每取一个值，另一个量y就有唯一值与之相对应，这时，我们把x叫做自变量，y是x的函数，理解自变量与函数值的对应关系是正确判断的前提．
9．C
【分析】本题考查函数的概念，根据函数的概念即可得出答案．
【详解】解：由函数的概念可知，一个自变量x的值只能对应一个因变量y的值，
选项C中，一个自变量x的值可以对应两个因变量y的值，不符合函数的概念．
其他选项均符合函数的概念．
故选：C．
10．C
【详解】（1）定义域不同；（2）定义域不同；（3）对应法则不同；
（4）定义域相同，且对应法则相同；（5）定义域不同；
故选C.
11．C
【分析】对于两个变量x与y，y随x的变化而变化，对于x的每一个取值，都有唯一的y值与之对应，则称y是x的函数，其中x称为函数的自变量，y是因变量；根据函数的定义判断即可．
【详解】根据函数定义知，①③④都是函数，其余两个都不是函数，因为给定一个x的值1，及中y的值有两个，分别是1与-1，这不符合函数定义中y值的唯一性．
故是函数的有3个．
故选：C．
【点睛】本题考查了函数概念，关键和难点是理解函数概念．
12．C
【分析】本题考查函数的表示方法、常量与变量．根据自变量与函数的定义判断A即可；通过观察数据即可得出结论BC；根据C计算出空气温度为的声速，即此时每秒传播的距离即可判断D．
【详解】解：∵声速随温度的变化而变化，
∴自变量是温度，声速是温度的函数，
∴A正确，不符合题意；
从而表格数据可知，随着温度的降低，声速变慢，
∴B正确，不符合题意；
从数据可知，温度每升高时，声速增加，
∴C错误，符合题意；
由C可知，当空气温度为时，声速为，即当空气温度为时，声音每秒可以传播，
∴D正确，不符合题意．
故选：C．
13．3
【解析】略
14．是
【分析】根据函数的定义进行判断即可．
【详解】解：由图可知，气温T随着时间的变化而变化，对于每一个都有唯一确定的与之对应，所以气温T(℃)是时间t(时)的函数．
故答案为：是．
【点睛】本题考查函数的定义．熟练掌握函数的定义是解题的关键．注意，对于每一个自变量都有唯一确定的因变量与之对应．
15． 两 年份 入学儿童人数
【分析】本题主要考查了函数的概念，在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．首先根据表格，可得上表反映了两个变量（入学儿童人数和年份）之间的关系；然后根据自变量、因变量的含义，判断出自变量、因变量各是哪个即可．
【详解】解：∵入学儿童人数随着年份的变化而变化，
∴上表反映了两个变量之间的关系，其中，自变量是年份；因变量是入学儿童人数．
故答案为：两，年份，入学儿童人数．
16． 函数 自变量
【解析】略
17．20
【分析】分析表格中数据，得到物体自由下落的高度随着时间的增大而增大，与的关系为：，把代入，再进行计算即可．
【详解】解：由表格得，用时间表示高度的关系式为：，
当时，．
所以果子开始落下时离地面的高度大约是20米．
故答案为：20．
【点睛】本题考查了根据图表找规律，并应用规律解决问题，要求有较强的分析数据和描述数据的能力．能够正确找到和的关系是解题的关键．
18．(1)l、a为变量，4为常量
(2)n、t为变量，60为常量
(3)t、v为变量，1500为常量
【分析】本题考查了常量与变量，根据常量是变化过程中保持不变的量，变化过程中变化的量是变量，可得答案．
【详解】（1）解：根据题意可知：等式中，l、a为变量，4为常量；
（2）解：根据题意可知：等式中，n、t为变量，60为常量；
（3）解：根据题意可知：等式中，t、v为变量，1500为常量．
19．（1）（2）（3）都含有两个变量；（1）可将温度看成时间（可用字母表示）的函数，时间的取值范围是：；（2）可将看成的函数，的取值范围是：；（3）可将看成的函数，的取值范围是：
【分析】根据函数的定义可知，满足对于x的每一个取值，y都有唯一确定的值与之对应关系，据此即可得出答案，结合图像分析出自变量的取值范围即可；
【详解】（1）（2）（3）都含有两个变量；
（1）可将温度看成时间（可用字母表示）的函数，时间的取值范围是：；
（2）可将看成的函数，的取值范围是：；
（3）可将看成的函数，的取值范围是：
【点睛】本题主要考查了函数的定义．函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．
20．(1)反映了提出概念所用的时间x和对概念的接受能力y两个变量之间的关系;其中x是自变量,y是因变量.
(2) 59.
(3)所用时间为13 min时,学生的接受能力最强.
(4)当x在2至13的范围内,学生的接受能力逐步增强;当x在13至20的范围内,学生的接受能力逐步降低.
【详解】分析：(1)由条件可知两个变量是提出概念所用的时间和对概念的接受能力，对概念的接受能力随着时间的变化而变化；
(2)直接从表中读出提出概念时间是10时对应的接受能力；
(3)从表中读出接受能力最大时对应的时间；
(4)根据接受能力的增大和减小过程得到对应的x的范围.
本题解析： (1)提出概念所用的时间x和对概念接受能力y两个变量，其中x是自变量，y是因变量；
(2)提出概念10分钟时，学生的接受能力是59；
(3)学生接受能力最强是59.9，对应的时间是13，
所以提出概念13分钟时学生的接受能力最强；
(4)2分钟至13分钟时学生接受能力逐步增强，13分钟至20分钟时逐步降低.
点睛：用表格可以表示变量之间的关系，根据表格中的数据，可以对数据的变化趋势进行预测.因变量随着自变量的变化而变化.
21．（1）土豆的产量与氮肥的施用量，氮肥施用量是自变量，土豆产量是因变量；（2）32.29吨/公顷， 15.18吨/公顷；（3）336千克/公顷；（4）当氮肥的施用量低于336千克/公顷时，土豆产量随氮肥的施用量的增加而增产，当氮肥的施用量高于336千克/公顷时，土豆产量随氮肥的施用量的增加而减产．
【分析】（1）根据变量、自变量、因变量的定义，结合表格解答即可；
（2）直接从表格中找出施用氮肥和不用氮肥时对应的土豆产量；
（3）从表格中找出土豆的最高产量，此时施用氮肥量是最合适的；
（4）根据表格中土豆产量的增长和减少数量来说明氮肥的施用量对土豆产量的影响．
【详解】解：（1）上表反映了土豆的产量与氮肥的施用量的关系，氮肥施用量是自变量，土豆产量是因变量；
（2）由表可知：当氮肥的施用量是101千克/公顷时，土豆的产量是：32.29吨/公顷，
如果不施氮肥，土豆的产量是：15.18吨/公顷；
（3）当氮肥的施用量是336千克/公顷时，氮肥的施用量是比较适宜的，因为此时土豆产量最高，施肥太多或太少都会使土豆产量减产；
（4）当氮肥的施用量低于336千克/公顷时，土豆产量随氮肥的施用量的增加而增产，当氮肥的施用量高于336千克/公顷时，土豆产量随氮肥的施用量的增加而减产．
【点睛】本题主要考查了函数的定义和结合实际土豆产量和施用氮肥量确定函数关系．函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．
22．（1）反映了拋射距离与高度之间的关系；（2）2.0，2.5，2.65，2.5，2.0，1.2，0；（3）确定；（4）可以
【分析】（1）根据变量的定义，即可求解；
（2）根据图象填表即可；
（3）根据这一范围内对于任一个距离，对应的函数值高度是唯一的，即可得到相应的高度是确定的；
（4）根据函数的定义，即可求解．
【详解】解：（1）根据题意得：这个图象反映了高度与拋射水平距离之间的关系；
（2）根据图象填表如下：
0 1 2 3 4 5 6
2.0 2.5 2.65 2.5 2.0 1.2 0
（3）当距离取之间的一个确定的值时，相应的高度是确定的，
理由如下：因为这一范围内对于任一个距离，对应的函数值高度是唯一的，所以相应的高度是确定的；
（4）∵高度随距离的变化而变化，并且对于任一个距离，对应的函数值高度是唯一的，
∴高度可以看成距离的函数．
【点睛】本题主要考查了函数与变量，熟练掌握设在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应，那么就说y是x的函数，x是自变量是解题的关键．
23．（1）上表反映了温度和高度两个变量之间．高度是自变量，温度是因变量．
（2）如果用h表示距离地面的高度，用t表示温度，那么随着高度h的增大，温度t逐渐减小（或降低）．
（3）距离地面6千米的高空温度是-16℃．
【详解】（1）上表反映了温度和高度两个变量之间的关系．高度是自变量．
（2）如果用h表示距离地面的高度，用t表示温度，那么随着高度h的增大，温度t逐渐减小（或降低）．
（3）距离地面6千米的高空温度是–16°C．
24．(1)上表反应了时间和电动车的月产量之间的关系
(2)6月份产量最高，1月份产量最低
(3)从1月到6月，电动车的月产量随时间的增长而增长
【分析】本题考查了函数的表示方法—列表法，利用了函数的定义．
（1）根据函数的定义，可得答案；
（2）比较月产量的大小，可得答案；
（3）比较月产量的大小，可得答案．
【详解】（1）解：电动车的月产量y为随着时间的变化而变化，故上表反应了时间和电动车的月产量之间的关系；
（2）解：根据表格数据可得：六月份产量最高，一月份产量最低；
（3）解：根据表格数据可得：从1月到6月，电动车的月产量随时间的增长而增长．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)