18.3数据的整理与表示巩固强化练习(含解析)
文档属性
| 名称 | 18.3数据的整理与表示巩固强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 07:22:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
18.3数据的整理与表示
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为了描述某病人的体温变化情况,以下统计图最合适的是( )
A.扇形统计图 B.条形统计图 C.折线统计图 D.直方图
2.下图是上证指数2004年5月21日分时走势图,它属于( )
A.折线统计图
B.条形统计图
C.上部是这线统计图,下部是条形统计图
D.下半部不是统计图
3.某校为丰富学生的课余生活成立了兴趣小组,学生会对全校400名学生各自最喜欢的兴趣小组进行问卷调查后(每人选一种),绘制成如图所示的扇形统计图,选择球类的人数为( )
A.40人 B.60人 C.80人 D.100人
4.某校开展了“爱阅读”活动,七(1)班统计了1月~6月全班同学的课外阅读数量(单位:本),绘制了折线统计图(如图所示),则下列说法正确的是( )
A.6月份阅读数量最大 B.阅读数量超过40本的月份共有5个月
C.相邻的两个月中,1月到2月的月阅读数量增长最快 D.4月份阅读数量为38本
5.下列统计图能够显示数据变化趋势的是( )
A.条形图 B.扇形图
C.折线图 D.以上都正确
6.如图是我市6月份某7天的最高气温折线统计图,则这些最高气温的众数与中位数分别是()
A.26,30°C B.28°C,27°C
C.28°C,28°C D.27°C,28°C
7.如图是某校学生参加课外兴趣小组的人数占总人数比例的 统计图,则参加人数最多的课外兴趣小组是 ( )
A.音乐组 B.美术组 C.体育组 D.科技组
8.“长安十二时辰”是中国首个沉浸式唐风市井生活街区,呈现出一处淋漓尽致、多彩至极的唐朝时空,为反映该街区月份旅游人数的变化情况,最恰当的是( )
A.条形图 B.折线图 C.扇形图 D.统计表
9.某青年足球队12名队员的年龄情况如表所示,则出现次数最多的是( ).
A.19
B.20
C.21
D.22
10.一组数据:7,5,9,3,9,15,则这组数据的极差是( )
A.12 B.9 C.7 D.8
11.在一个扇形统计图中,某部分所对的圆心角为,则该部分占总体的百分比是( )
A. B. C. D.
12.刘老师从全校2000名学生每天体育锻炼时长的问卷中,随机抽取部分学生的答卷,并将结果统计后绘制成如图所示的条形统计图,其中一部分被墨迹遮盖.已知每天锻炼时长为1小时的学生人数占样本总人数的,则下列说法正确的是( )
A.抽取的学生人数小于
B.名学生是样本
C.被调查学生中,锻炼时长为1.5小时的人数最多
D.该校锻炼时长为2小时的学生约有名
二、填空题
13.你喜欢足球吗?下面是对某学校七年级学生的调查结果:
男同学 女同学
喜欢的人数 75 24
不喜欢的人数 15 36
则男同学中喜欢足球的人数占全体同学的百分比是 .
14.林丛同学调查了全班50名同学分别喜欢相声、小品、歌曲、舞蹈节目的情况,并制成下面的统计表:
最喜欢的节目类型 划记 人数 百分比
相声 正 13 26%
小品 正正正一 21 42%
歌曲 正正 10 28%
舞蹈 正一 6 12%
在上表所给的数据中,仅有一类节目的统计是完全正确的,则该项目统计类别是 .
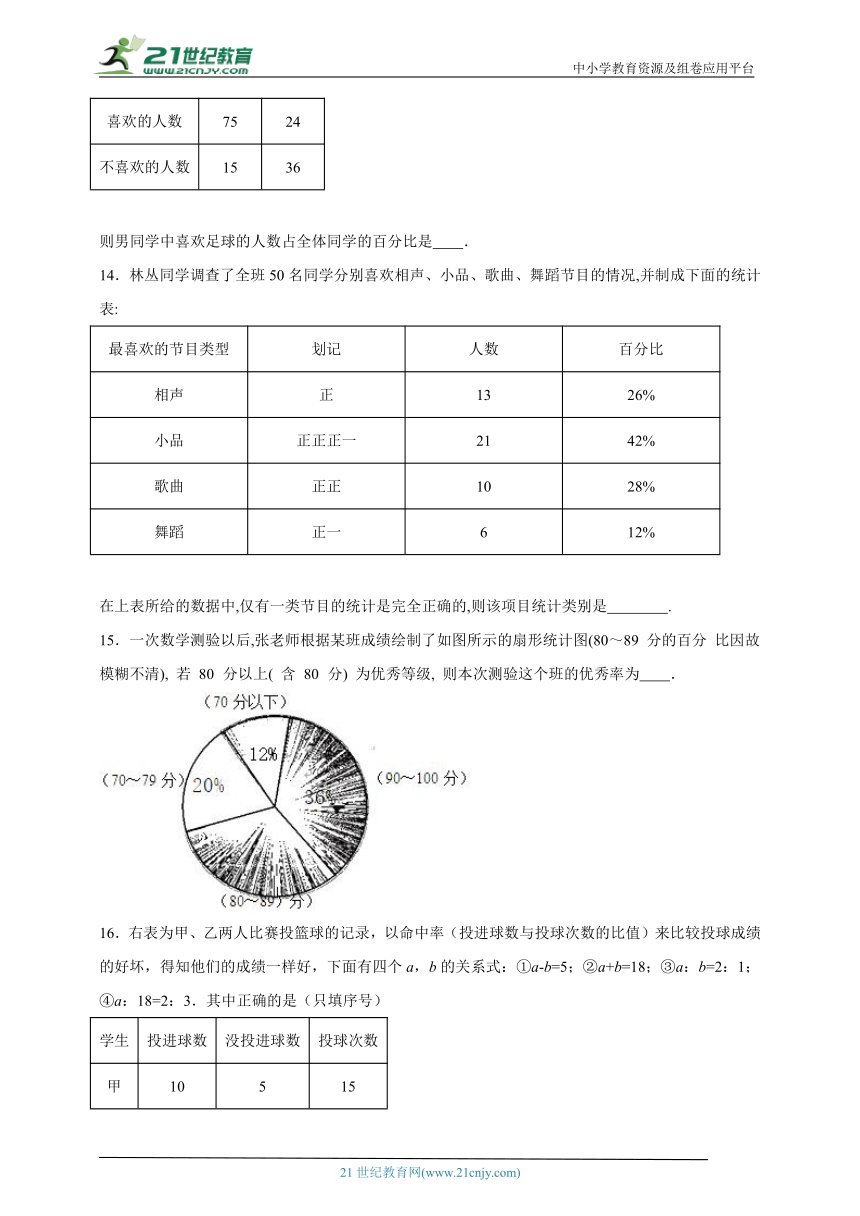
15.一次数学测验以后,张老师根据某班成绩绘制了如图所示的扇形统计图(80~89 分的百分 比因故模糊不清), 若 80 分以上( 含 80 分) 为优秀等级, 则本次测验这个班的优秀率为 .
16.右表为甲、乙两人比赛投篮球的记录,以命中率(投进球数与投球次数的比值)来比较投球成绩的好坏,得知他们的成绩一样好,下面有四个a,b的关系式:①a-b=5;②a+b=18;③a:b=2:1;④a:18=2:3.其中正确的是(只填序号)
学生 投进球数 没投进球数 投球次数
甲 10 5 15
乙 a b 18
17.如图,是2001年3月至2002年2月日本失业人口占劳动力总人口的比例统计图,从图中可以看出,在这段时间内失业率最高的月份是 ,这个月份的失业率是 ,你认为2001年3月份的失业率大约是 .
三、解答题
18.小刚家2009年和2010年的家庭支出如下:
(1)2010年总支出比2009年增加多少万元?增加的百分比是多少?
(2)2009年衣食方面支出的金额是多少?教育方面支出的金额是多少?
(3)2010年娱乐方面支出的金额比2009年增加了还是减少了?变化了多少?
19.北京和南京两城市月降水量统计表(单位:)
月份城市 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 11月 12月
北 京 26 59 90 264 287 707 1756 1822 487 188 60 53
南 京 288 481 688 866 964 1592 1875 1237 951 599 556 322
根据上表,回答下列问题:
(1)哪一个城市一年的降水量大?哪一个城市一年的降水量变化幅度大?
(2)两个城市在哪个月的降水量相差最大?差多少?
(3)哪几个月两城市的降水量相差在以内.
20.小丽一天中的体温变化情况如图:
(1)大约什么时候,小丽的体温最低?最低体温约是多少?
(2)什么时间内,小丽的体温在升高?
(3)什么时间内,小丽的体温在保持不变?
21.某家装公司为新建小区做家装设计,调查员设计如下问卷,对家装风格进行专项调查.
【收集数据】通过随机抽样调查50家客户,得到如下数据:
【整理、描述数据】调查员根据数据绘制了下面不完整的家装风格统计表
装修风格 划记 户数
正正正正正 25
正正正 ___________
___________ 5
正 5
合计 / 50
(1)补全统计表
【分析数据】
(2)根据抽样调查的结果,将估计出的整个小区的1000户家住户的家庭装修风格绘制成合适的统计图(绘制一种即可).
【得出结论】
(3)如果公司准备招聘10名装修设计师(每名装修设计师只擅长一种设计风格),根据统计数据预测招收种装修风格的设计师的人数.
22.某电视机专卖店在四个月的试销期内共销售了400台A、B两个品牌的电视机,试销结束后,专卖店只能经销其中的一个品牌,为作出决定,专卖店老板根据这四个月销售的情况,绘制了两幅统计图如图,请根据统计图提供的信息,解答下列问题:
(1)第四个月销量占总销量的百分比是______;
(2)在图2中补全表示B品牌电视机月销售量的折线;
(3)经计算,两个品牌电视机平均月销量相同,请你结合折线的走势进行简要分析,判断该专卖店应经销哪个品牌的电视机?
23.某村1993年开办了两个村办企业—塑料厂、纺织厂.两厂从1993年到2002年的获利情况如图所示,根据图象回答下列问题:
(1)哪几年两厂的获利额相同,是多少?
(2)找出两厂差额最大的年份,最大的差额是多少?
24.某水果批发市场新进一批水果,有苹果、西瓜、桃子和香蕉四个品种,统计后将结果绘制成条形图(如图),已知西瓜的重量占这批水果总重量的40%.
回答下列问题:
(1)这批水果总重量为 kg;
(2)请将条形图补充完整;
(3)若用扇形图表示统计结果,则桃子所对应扇形的圆心角为 度.
《18.3数据的整理与表示》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C D C C C C B A A
题号 11 12
答案 B C
1.C
【分析】根据题意,描述某病人某一天的体温变化情况最合适的应该反映变化趋势,则选取折线统计图,据此求解即可.
【详解】解:为了描述某病人某一天的体温变化情况,
∴最合适的统计图是折线统计图.
故选:C.
【点睛】本题考查了根据实际选取合适的统计图,理解题意是解题的关键.条形统计图的特点:能清楚的表示出数量的多少;折线统计图的特点:不但可以表示出数量的多少,而且能看出各种数量的增减变化情况;扇形统计图比较清楚地反映出部分与部分、部分与整体之间的数量关系.
2.C
【分析】根据统计图的性质找出其相对应的统计图名称. 如图所示,上半部分由折线组成所以为折线统计图,下半部分由长条形块面组成为条形统计图.
【详解】如图所示,上半部分由折线组成所以为折线统计图,下半部分由长条形块面组成为条形统计图.
【点睛】本题考查了条形统计图与折线统计图的知识,解题的关键是能根据统计图的性质找出其相对应的统计图名称.
3.D
【分析】根据扇形统计图中球类学生的占比乘以总人数,即可求解.
【详解】由扇形统计图可知,选择球类的人数占总人数的25%,
∴400×25%=100人,
故选:D.
【点睛】本题考查扇形统计图的概念,理解并运用扇形统计图中的信息是解题关键.
4.C
【分析】根据折线统计图中的数据,可判断各选项.
【详解】解:由统计图可得:2月份阅读数量最大,A错误,不符合题意;
阅读数量超过40本的月份有2、3、4、6月份,共有4个月,B错误,不符合题意;
相邻的两个月中,1月到2月的月阅读数量增长最快,C正确,符合题意;
4月份阅读数量为56本,D错误,不符合题意;
故选:C.
【点睛】本题主要考查了折线统计图,折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.从统计图中得到必要的信息是解决问题的关键.
5.C
【解析】略
6.C
【详解】根据7天的最高气温折线统计图,可得28°出现的次数最多,为3次,故最高气温的众数为28°;7天的最高气温按大小排列为:25°,26°,27°,28°,28°,28°,30°,故中位数为28°,故选C.
【考点】折线统计图;中位数;众数.
7.C
【分析】根据扇形统计图中扇形所占百分比越大,相应的人数越多,可得答案.
【详解】解:根据扇形统计图中扇形面积越大,所占的比例越重,相应的人数越多,由40%>25%>23%>12%,
所以体育组的人数最多
故选C
【点睛】本题考查了扇形统计图的特征,熟记扇形统计图的特征是解题的关键.
8.B
【分析】本题考查统计图的选择与应用.选择统计图时,应根据数据的性质和展示目的来决定.折线统计图在展示数据变化趋势方面具有优势,因此在反映旅游人数随时间变化的情况时,折线统计图是最恰当的选择.
【详解】解:A、条形统计图∶适用于比较数据之间的大小和差异,例如不同月份的旅游人数对比.故A不符合题意;
B、折线统计图∶适用于展示数据随时间变化的趋势,例如旅游人数在月份的变化趋势.故B符合题意;
C、扇形统计图∶适用于展示部分与整体的关系例如不同旅游项目所占的百分比.故C不符合题意;
D、统计表∶适用于展示具体数据,例如每个月的旅游人数.故D不符合题意;
故选:B.
9.A
【分析】求某青年足球队12名队员的年龄出现次数最多的,就是确定在调查结果中的A、B、C、D中哪个是众数.
【详解】解:A、年龄19,出现了4次,出现次数最多,符合题意;
B、年龄20,出现了3次,出现次数不是最多,不符合题意;
C、年龄21,出现了2次,出现次数不是最多,不符合题意;
D、年龄22,出现了2次,出现次数不是最多,不符合题意.
故选A.
【点睛】由于年龄19出现了4次,为众数,代表了这组数据的集中趋势,故可判断年龄19出现次数最多.
10.A
【分析】本题考查极差的定义,熟练掌握极差的定义是解题的关键,根据极差的定义:一组数据中最大数减去最小数的值,计算即可得到答案.
【详解】解:由题可得:这组数据中最大数为:,最小数为:3,
∴这组数据的极差为:,
故选:A.
11.B
【分析】利用该部分所对的圆心角为,圆心角占的百分比即为部分占总体的百分比,即可求出答案.
【详解】解:.
故选B.
【点睛】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与的比.
12.C
【分析】根据条形统计图相关数据即可进行判断.
【详解】解:A:抽取的学生人数为:(人),故A错误;
B:名学生的每天体育锻炼时长是样本,故B错误;
C:被调查学生中,锻炼时长为1.5小时的人数为:(人),人数最多,故C正确;
D:该校锻炼时长为2小时的学生约有:(人),故D错误;
故选:C
【点睛】本题考查由条形统计图推断结论.考查学生的数据处理能力.
13.50%
【分析】依据男同学中喜欢足球的人数除以全体同学的数量,即可得到百分比.
【详解】由题可得,男同学中喜欢足球的人数占全体同学的百分比是:=50%,
故答案为:50%.
【点睛】本题主要考查了统计表的应用,统计表是表现数字资料整理结果的最常用的一种表格.
14.舞蹈
【分析】由图表可知相声人数5,小品人数16,歌曲人数10,舞蹈人数6;然后根据划记的人数除以总人数,正确计算百分比,即可进行分析判断.
【详解】由统计表可得:
A、相声划记应为5人,则百分数应为×100%=10%,故错误;
B、小品划记应为16人,则百分数应为×100%=32%,故错误; C、歌曲划记为应10人,则百分数应为×100%=20%,故错误;
D、舞蹈的划记为6人是正确的,百分数为×100%=12%,百分数也正确,故正确.
故答案为舞蹈.
【点睛】本题考查统计表.主要是统计表的制作与从统计表中获取信息的能力.
15.68%
【详解】∵80分以上(含80分)为优秀等级,∴本次测验这个班的优秀率为1-20%-12%=68%.
16.②③④
【分析】本题考查学生对统计表的理解与运用.根据甲乙的命中率相同可求出a的值,进而求出b的值,可判断:①a-b=5;②a+b=18;③a:b=2:1;④a:18=2:3.四个关系式哪些正确.
【详解】解∵命中率相同,
,得a=12.
则b=18-12=6.
a-b=12-6=6,故①错误.
a+b=12+6=18,故②正确.
a:b=12:6=2:1,故③正确.
a:18=12:18=2:3,故④正确.
故答案为:②③④.
17. 2001年12月 5.6% 4.7%(5%左右即可)
【分析】根据统计图找出与题意相对应的答案.如这段时间内失业率最高的月份是折线的最高点.
【详解】根据上图可得:
这段时间内失业率最高的月份是2001年12月,
这个月份的失业率5.6%,你认为2001年3月份的失业率大约是4.7%.
故答案为:2001年12月,5. 6%,4.7%.
【点睛】本题考查了折线统计图的知识,读懂折线统计图是解题的关键.
18.(1)2010年总支出比2009年增加0.36万元,增加的百分比是;(2)2009年衣食方面支出的金额是0.54万元,教育方面支出的金额是0.54万元;(3)2010年比2009年减少了0. 054万元.
【分析】(1)由图可知2010年总支出和2009年总支出,相减即可得出增加的数,再用增加的数除以2009年总支出即可得出增加的百分比;
(2)2009年衣食方面支出的金额是2009年总支出乘衣食方面所占百分比,教育方面支出的金额是2009年总支出乘教育方面所占百分比;
(3)先分别求出2010年娱乐方面支出的金额和2009年娱乐方面支出的金额再相减即可.
【详解】解:(1)2010年总支出比2009年总支出增加万元,增加的百分比是;
(2)2009年衣食方面支出的金额是(万元),教育方面支出的金额是(万元);
(3)2010年娱乐方面支出的金额是(万元),
2009年娱乐方面的支出金额是(万元),
2010年比2009年减少了万元.
答:2010年总支出比2009年增加万元,增加的百分比是;
2009年衣食方面支出的金额是万元,教育方面支出的金额是万元;
2010年娱乐方面支出的金额比2009年减少了0. 054万元.
【点睛】此题考查了条形统计图,以及扇形统计图,读懂图得出相关信息是解本题的关键.
19.(1)南京一年的降水量大;北京一年的降水量变化幅度大.
(2)6月份;
(3)1月、7月、12月
【分析】(1)直接根据表格中的数据分析比较即可;
(2)分别把每个月的降水量作差比较,即可找到所对应的月份.
(3)分别把每个月的降水量作差比较,即可找到所对应的月份.
【详解】(1)解:北京一年的降水量为,
南京一年的降水量为,
所以南京一年的降水量大.
北京降水量的波动范围从到.
南京降水量的波动范围从到,
所以北京一年的降水量变化幅度大.
(2)1月降水量相差;
2月降水量相差
3月降水量相差;
4月降水量相差;
5月降水量相差;
6月降水量相差;
7月降水量相差;
8月降水量相差;
9月降水量相差;
10月降水量相差;
11月降水量相差;
12月降水量相差;
∴两个城市在6月的降水量相差最大,为.
(3)由(2)可知:1月、7月、12月两城市的降水量相差在以内.
20.(1)2时,36.2°C
(2)2~7时,9 ~12时
(3)12 ~17时
【分析】(1)根据图象确定出温度最高低的时间以及温度即可;
(2)找出温度随时间增大而升高的时间段即可;
(3)找出随时间增大而温度不变化的时间段即可.
【详解】解:(1)由折线统计图可知,大约2时,小丽的体温最低,最低体温约是36.2° C;
(2)由折线统计图可知,2~7时,9 ~12时,小丽的体温在升高;
(3)由折线统计图可知,12~ 17时,小丽的体温在保持不变.
【点睛】本题考查了折线统计图的实际应用,解题的关键是能够看懂折线统计图.
21.(1)见解析;(2)见解析;(3)5
【分析】本题主要考查了统计表、扇形统计图及其应用等知识,通过统计表获得所需信息是解题关键.
(1)根据统计表中的数据进行计算即可;
(2)根据抽样调查的结果,绘制成合适的统计图,如扇形统计图即可;
(3)根据抽样调查的结果中种装修风格所占比例,即可预测招收种装修风格的设计师的人数.
【详解】解:(1)补全的统计表为
装修风格 划记 户数
正正正正正 25
正正正 15
正 5
正 5
合计 / 50
(2)A.;
B.;
C.;
D.;
扇形统计图如图所示:
(3)∵,
∴种装修风格的设计师可招5人.
22.(1)30%
(2)见解析
(3)经销B品牌电视机,分析见解析
【分析】(1)用1减去其它部分的百分比即可求解;
(2)根据扇形图,可补全折线图;
(3)比较折线图,经销量好的那个品牌.
【详解】(1)解:分析扇形图可得:第四个月销量占总销量的百分比为:
1 (15%+30%+25%)=30%.
故答案为:30%.
(2)解:B品牌电视剧第3个月销量为(台),
B品牌电视剧第4个月销量为(台),
补全折线图,如图所示:
(3)解:由于月销量的平均水平相同,从折线的走势看,A品牌的月销量呈下降趋势,而B品牌的月销量呈上升趋势,所以该商店应经销B品牌电视机.
【点睛】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
23.(1)1995年、1998年、2000年分别是15万元、25万元、30万元;(2)2001年,15万元
【分析】根据统计图的相关知识即可找出与题意相对应的答案.如哪几年两厂的获利额相同,只需要找出图上两条线相交的点即可,以此类推两厂差额最大的年份是两条线分离最大的时候.
【详解】(1)1995年、1998年、2000年分别是15万元、25万元、30万元;
(2)2001年,15万元.
【点睛】本题考查了折线统计图的知识,解题的关键能看懂折线统计图并能根据题意找出相对应的答案.
24.(1)4000;(2)作图见解析;(3)90.
【分析】(1)设这批水果总重量为mkg,根据西瓜的重量占这批水果总重量的40%,列出方程即可解决.
(2)根据苹果的重量=总重量 西瓜的重量 桃子的重量 香蕉西瓜的重量,即可画出图形.
(3)根据圆心角=360°×百分比,即可解决问题.
【详解】(1)设这批水果总重量为mkg,
应用m 40%=1600,
解得:m=4000kg.
故答案为:4000.
(2)∵苹果的重量=总重量﹣西瓜的重量﹣桃子的重量﹣香蕉西瓜的重量=4000﹣1600﹣1000﹣200=1200,
条形图如图所示,
(3)∵桃子的重量占这批水果总重量的25%,∴桃子所对应扇形的圆心角为360°×25%=90°.
故答案为:90.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
18.3数据的整理与表示
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为了描述某病人的体温变化情况,以下统计图最合适的是( )
A.扇形统计图 B.条形统计图 C.折线统计图 D.直方图
2.下图是上证指数2004年5月21日分时走势图,它属于( )
A.折线统计图
B.条形统计图
C.上部是这线统计图,下部是条形统计图
D.下半部不是统计图
3.某校为丰富学生的课余生活成立了兴趣小组,学生会对全校400名学生各自最喜欢的兴趣小组进行问卷调查后(每人选一种),绘制成如图所示的扇形统计图,选择球类的人数为( )
A.40人 B.60人 C.80人 D.100人
4.某校开展了“爱阅读”活动,七(1)班统计了1月~6月全班同学的课外阅读数量(单位:本),绘制了折线统计图(如图所示),则下列说法正确的是( )
A.6月份阅读数量最大 B.阅读数量超过40本的月份共有5个月
C.相邻的两个月中,1月到2月的月阅读数量增长最快 D.4月份阅读数量为38本
5.下列统计图能够显示数据变化趋势的是( )
A.条形图 B.扇形图
C.折线图 D.以上都正确
6.如图是我市6月份某7天的最高气温折线统计图,则这些最高气温的众数与中位数分别是()
A.26,30°C B.28°C,27°C
C.28°C,28°C D.27°C,28°C
7.如图是某校学生参加课外兴趣小组的人数占总人数比例的 统计图,则参加人数最多的课外兴趣小组是 ( )
A.音乐组 B.美术组 C.体育组 D.科技组
8.“长安十二时辰”是中国首个沉浸式唐风市井生活街区,呈现出一处淋漓尽致、多彩至极的唐朝时空,为反映该街区月份旅游人数的变化情况,最恰当的是( )
A.条形图 B.折线图 C.扇形图 D.统计表
9.某青年足球队12名队员的年龄情况如表所示,则出现次数最多的是( ).
A.19
B.20
C.21
D.22
10.一组数据:7,5,9,3,9,15,则这组数据的极差是( )
A.12 B.9 C.7 D.8
11.在一个扇形统计图中,某部分所对的圆心角为,则该部分占总体的百分比是( )
A. B. C. D.
12.刘老师从全校2000名学生每天体育锻炼时长的问卷中,随机抽取部分学生的答卷,并将结果统计后绘制成如图所示的条形统计图,其中一部分被墨迹遮盖.已知每天锻炼时长为1小时的学生人数占样本总人数的,则下列说法正确的是( )
A.抽取的学生人数小于
B.名学生是样本
C.被调查学生中,锻炼时长为1.5小时的人数最多
D.该校锻炼时长为2小时的学生约有名
二、填空题
13.你喜欢足球吗?下面是对某学校七年级学生的调查结果:
男同学 女同学
喜欢的人数 75 24
不喜欢的人数 15 36
则男同学中喜欢足球的人数占全体同学的百分比是 .
14.林丛同学调查了全班50名同学分别喜欢相声、小品、歌曲、舞蹈节目的情况,并制成下面的统计表:
最喜欢的节目类型 划记 人数 百分比
相声 正 13 26%
小品 正正正一 21 42%
歌曲 正正 10 28%
舞蹈 正一 6 12%
在上表所给的数据中,仅有一类节目的统计是完全正确的,则该项目统计类别是 .
15.一次数学测验以后,张老师根据某班成绩绘制了如图所示的扇形统计图(80~89 分的百分 比因故模糊不清), 若 80 分以上( 含 80 分) 为优秀等级, 则本次测验这个班的优秀率为 .
16.右表为甲、乙两人比赛投篮球的记录,以命中率(投进球数与投球次数的比值)来比较投球成绩的好坏,得知他们的成绩一样好,下面有四个a,b的关系式:①a-b=5;②a+b=18;③a:b=2:1;④a:18=2:3.其中正确的是(只填序号)
学生 投进球数 没投进球数 投球次数
甲 10 5 15
乙 a b 18
17.如图,是2001年3月至2002年2月日本失业人口占劳动力总人口的比例统计图,从图中可以看出,在这段时间内失业率最高的月份是 ,这个月份的失业率是 ,你认为2001年3月份的失业率大约是 .
三、解答题
18.小刚家2009年和2010年的家庭支出如下:
(1)2010年总支出比2009年增加多少万元?增加的百分比是多少?
(2)2009年衣食方面支出的金额是多少?教育方面支出的金额是多少?
(3)2010年娱乐方面支出的金额比2009年增加了还是减少了?变化了多少?
19.北京和南京两城市月降水量统计表(单位:)
月份城市 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 11月 12月
北 京 26 59 90 264 287 707 1756 1822 487 188 60 53
南 京 288 481 688 866 964 1592 1875 1237 951 599 556 322
根据上表,回答下列问题:
(1)哪一个城市一年的降水量大?哪一个城市一年的降水量变化幅度大?
(2)两个城市在哪个月的降水量相差最大?差多少?
(3)哪几个月两城市的降水量相差在以内.
20.小丽一天中的体温变化情况如图:
(1)大约什么时候,小丽的体温最低?最低体温约是多少?
(2)什么时间内,小丽的体温在升高?
(3)什么时间内,小丽的体温在保持不变?
21.某家装公司为新建小区做家装设计,调查员设计如下问卷,对家装风格进行专项调查.
【收集数据】通过随机抽样调查50家客户,得到如下数据:
【整理、描述数据】调查员根据数据绘制了下面不完整的家装风格统计表
装修风格 划记 户数
正正正正正 25
正正正 ___________
___________ 5
正 5
合计 / 50
(1)补全统计表
【分析数据】
(2)根据抽样调查的结果,将估计出的整个小区的1000户家住户的家庭装修风格绘制成合适的统计图(绘制一种即可).
【得出结论】
(3)如果公司准备招聘10名装修设计师(每名装修设计师只擅长一种设计风格),根据统计数据预测招收种装修风格的设计师的人数.
22.某电视机专卖店在四个月的试销期内共销售了400台A、B两个品牌的电视机,试销结束后,专卖店只能经销其中的一个品牌,为作出决定,专卖店老板根据这四个月销售的情况,绘制了两幅统计图如图,请根据统计图提供的信息,解答下列问题:
(1)第四个月销量占总销量的百分比是______;
(2)在图2中补全表示B品牌电视机月销售量的折线;
(3)经计算,两个品牌电视机平均月销量相同,请你结合折线的走势进行简要分析,判断该专卖店应经销哪个品牌的电视机?
23.某村1993年开办了两个村办企业—塑料厂、纺织厂.两厂从1993年到2002年的获利情况如图所示,根据图象回答下列问题:
(1)哪几年两厂的获利额相同,是多少?
(2)找出两厂差额最大的年份,最大的差额是多少?
24.某水果批发市场新进一批水果,有苹果、西瓜、桃子和香蕉四个品种,统计后将结果绘制成条形图(如图),已知西瓜的重量占这批水果总重量的40%.
回答下列问题:
(1)这批水果总重量为 kg;
(2)请将条形图补充完整;
(3)若用扇形图表示统计结果,则桃子所对应扇形的圆心角为 度.
《18.3数据的整理与表示》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C D C C C C B A A
题号 11 12
答案 B C
1.C
【分析】根据题意,描述某病人某一天的体温变化情况最合适的应该反映变化趋势,则选取折线统计图,据此求解即可.
【详解】解:为了描述某病人某一天的体温变化情况,
∴最合适的统计图是折线统计图.
故选:C.
【点睛】本题考查了根据实际选取合适的统计图,理解题意是解题的关键.条形统计图的特点:能清楚的表示出数量的多少;折线统计图的特点:不但可以表示出数量的多少,而且能看出各种数量的增减变化情况;扇形统计图比较清楚地反映出部分与部分、部分与整体之间的数量关系.
2.C
【分析】根据统计图的性质找出其相对应的统计图名称. 如图所示,上半部分由折线组成所以为折线统计图,下半部分由长条形块面组成为条形统计图.
【详解】如图所示,上半部分由折线组成所以为折线统计图,下半部分由长条形块面组成为条形统计图.
【点睛】本题考查了条形统计图与折线统计图的知识,解题的关键是能根据统计图的性质找出其相对应的统计图名称.
3.D
【分析】根据扇形统计图中球类学生的占比乘以总人数,即可求解.
【详解】由扇形统计图可知,选择球类的人数占总人数的25%,
∴400×25%=100人,
故选:D.
【点睛】本题考查扇形统计图的概念,理解并运用扇形统计图中的信息是解题关键.
4.C
【分析】根据折线统计图中的数据,可判断各选项.
【详解】解:由统计图可得:2月份阅读数量最大,A错误,不符合题意;
阅读数量超过40本的月份有2、3、4、6月份,共有4个月,B错误,不符合题意;
相邻的两个月中,1月到2月的月阅读数量增长最快,C正确,符合题意;
4月份阅读数量为56本,D错误,不符合题意;
故选:C.
【点睛】本题主要考查了折线统计图,折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.从统计图中得到必要的信息是解决问题的关键.
5.C
【解析】略
6.C
【详解】根据7天的最高气温折线统计图,可得28°出现的次数最多,为3次,故最高气温的众数为28°;7天的最高气温按大小排列为:25°,26°,27°,28°,28°,28°,30°,故中位数为28°,故选C.
【考点】折线统计图;中位数;众数.
7.C
【分析】根据扇形统计图中扇形所占百分比越大,相应的人数越多,可得答案.
【详解】解:根据扇形统计图中扇形面积越大,所占的比例越重,相应的人数越多,由40%>25%>23%>12%,
所以体育组的人数最多
故选C
【点睛】本题考查了扇形统计图的特征,熟记扇形统计图的特征是解题的关键.
8.B
【分析】本题考查统计图的选择与应用.选择统计图时,应根据数据的性质和展示目的来决定.折线统计图在展示数据变化趋势方面具有优势,因此在反映旅游人数随时间变化的情况时,折线统计图是最恰当的选择.
【详解】解:A、条形统计图∶适用于比较数据之间的大小和差异,例如不同月份的旅游人数对比.故A不符合题意;
B、折线统计图∶适用于展示数据随时间变化的趋势,例如旅游人数在月份的变化趋势.故B符合题意;
C、扇形统计图∶适用于展示部分与整体的关系例如不同旅游项目所占的百分比.故C不符合题意;
D、统计表∶适用于展示具体数据,例如每个月的旅游人数.故D不符合题意;
故选:B.
9.A
【分析】求某青年足球队12名队员的年龄出现次数最多的,就是确定在调查结果中的A、B、C、D中哪个是众数.
【详解】解:A、年龄19,出现了4次,出现次数最多,符合题意;
B、年龄20,出现了3次,出现次数不是最多,不符合题意;
C、年龄21,出现了2次,出现次数不是最多,不符合题意;
D、年龄22,出现了2次,出现次数不是最多,不符合题意.
故选A.
【点睛】由于年龄19出现了4次,为众数,代表了这组数据的集中趋势,故可判断年龄19出现次数最多.
10.A
【分析】本题考查极差的定义,熟练掌握极差的定义是解题的关键,根据极差的定义:一组数据中最大数减去最小数的值,计算即可得到答案.
【详解】解:由题可得:这组数据中最大数为:,最小数为:3,
∴这组数据的极差为:,
故选:A.
11.B
【分析】利用该部分所对的圆心角为,圆心角占的百分比即为部分占总体的百分比,即可求出答案.
【详解】解:.
故选B.
【点睛】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与的比.
12.C
【分析】根据条形统计图相关数据即可进行判断.
【详解】解:A:抽取的学生人数为:(人),故A错误;
B:名学生的每天体育锻炼时长是样本,故B错误;
C:被调查学生中,锻炼时长为1.5小时的人数为:(人),人数最多,故C正确;
D:该校锻炼时长为2小时的学生约有:(人),故D错误;
故选:C
【点睛】本题考查由条形统计图推断结论.考查学生的数据处理能力.
13.50%
【分析】依据男同学中喜欢足球的人数除以全体同学的数量,即可得到百分比.
【详解】由题可得,男同学中喜欢足球的人数占全体同学的百分比是:=50%,
故答案为:50%.
【点睛】本题主要考查了统计表的应用,统计表是表现数字资料整理结果的最常用的一种表格.
14.舞蹈
【分析】由图表可知相声人数5,小品人数16,歌曲人数10,舞蹈人数6;然后根据划记的人数除以总人数,正确计算百分比,即可进行分析判断.
【详解】由统计表可得:
A、相声划记应为5人,则百分数应为×100%=10%,故错误;
B、小品划记应为16人,则百分数应为×100%=32%,故错误; C、歌曲划记为应10人,则百分数应为×100%=20%,故错误;
D、舞蹈的划记为6人是正确的,百分数为×100%=12%,百分数也正确,故正确.
故答案为舞蹈.
【点睛】本题考查统计表.主要是统计表的制作与从统计表中获取信息的能力.
15.68%
【详解】∵80分以上(含80分)为优秀等级,∴本次测验这个班的优秀率为1-20%-12%=68%.
16.②③④
【分析】本题考查学生对统计表的理解与运用.根据甲乙的命中率相同可求出a的值,进而求出b的值,可判断:①a-b=5;②a+b=18;③a:b=2:1;④a:18=2:3.四个关系式哪些正确.
【详解】解∵命中率相同,
,得a=12.
则b=18-12=6.
a-b=12-6=6,故①错误.
a+b=12+6=18,故②正确.
a:b=12:6=2:1,故③正确.
a:18=12:18=2:3,故④正确.
故答案为:②③④.
17. 2001年12月 5.6% 4.7%(5%左右即可)
【分析】根据统计图找出与题意相对应的答案.如这段时间内失业率最高的月份是折线的最高点.
【详解】根据上图可得:
这段时间内失业率最高的月份是2001年12月,
这个月份的失业率5.6%,你认为2001年3月份的失业率大约是4.7%.
故答案为:2001年12月,5. 6%,4.7%.
【点睛】本题考查了折线统计图的知识,读懂折线统计图是解题的关键.
18.(1)2010年总支出比2009年增加0.36万元,增加的百分比是;(2)2009年衣食方面支出的金额是0.54万元,教育方面支出的金额是0.54万元;(3)2010年比2009年减少了0. 054万元.
【分析】(1)由图可知2010年总支出和2009年总支出,相减即可得出增加的数,再用增加的数除以2009年总支出即可得出增加的百分比;
(2)2009年衣食方面支出的金额是2009年总支出乘衣食方面所占百分比,教育方面支出的金额是2009年总支出乘教育方面所占百分比;
(3)先分别求出2010年娱乐方面支出的金额和2009年娱乐方面支出的金额再相减即可.
【详解】解:(1)2010年总支出比2009年总支出增加万元,增加的百分比是;
(2)2009年衣食方面支出的金额是(万元),教育方面支出的金额是(万元);
(3)2010年娱乐方面支出的金额是(万元),
2009年娱乐方面的支出金额是(万元),
2010年比2009年减少了万元.
答:2010年总支出比2009年增加万元,增加的百分比是;
2009年衣食方面支出的金额是万元,教育方面支出的金额是万元;
2010年娱乐方面支出的金额比2009年减少了0. 054万元.
【点睛】此题考查了条形统计图,以及扇形统计图,读懂图得出相关信息是解本题的关键.
19.(1)南京一年的降水量大;北京一年的降水量变化幅度大.
(2)6月份;
(3)1月、7月、12月
【分析】(1)直接根据表格中的数据分析比较即可;
(2)分别把每个月的降水量作差比较,即可找到所对应的月份.
(3)分别把每个月的降水量作差比较,即可找到所对应的月份.
【详解】(1)解:北京一年的降水量为,
南京一年的降水量为,
所以南京一年的降水量大.
北京降水量的波动范围从到.
南京降水量的波动范围从到,
所以北京一年的降水量变化幅度大.
(2)1月降水量相差;
2月降水量相差
3月降水量相差;
4月降水量相差;
5月降水量相差;
6月降水量相差;
7月降水量相差;
8月降水量相差;
9月降水量相差;
10月降水量相差;
11月降水量相差;
12月降水量相差;
∴两个城市在6月的降水量相差最大,为.
(3)由(2)可知:1月、7月、12月两城市的降水量相差在以内.
20.(1)2时,36.2°C
(2)2~7时,9 ~12时
(3)12 ~17时
【分析】(1)根据图象确定出温度最高低的时间以及温度即可;
(2)找出温度随时间增大而升高的时间段即可;
(3)找出随时间增大而温度不变化的时间段即可.
【详解】解:(1)由折线统计图可知,大约2时,小丽的体温最低,最低体温约是36.2° C;
(2)由折线统计图可知,2~7时,9 ~12时,小丽的体温在升高;
(3)由折线统计图可知,12~ 17时,小丽的体温在保持不变.
【点睛】本题考查了折线统计图的实际应用,解题的关键是能够看懂折线统计图.
21.(1)见解析;(2)见解析;(3)5
【分析】本题主要考查了统计表、扇形统计图及其应用等知识,通过统计表获得所需信息是解题关键.
(1)根据统计表中的数据进行计算即可;
(2)根据抽样调查的结果,绘制成合适的统计图,如扇形统计图即可;
(3)根据抽样调查的结果中种装修风格所占比例,即可预测招收种装修风格的设计师的人数.
【详解】解:(1)补全的统计表为
装修风格 划记 户数
正正正正正 25
正正正 15
正 5
正 5
合计 / 50
(2)A.;
B.;
C.;
D.;
扇形统计图如图所示:
(3)∵,
∴种装修风格的设计师可招5人.
22.(1)30%
(2)见解析
(3)经销B品牌电视机,分析见解析
【分析】(1)用1减去其它部分的百分比即可求解;
(2)根据扇形图,可补全折线图;
(3)比较折线图,经销量好的那个品牌.
【详解】(1)解:分析扇形图可得:第四个月销量占总销量的百分比为:
1 (15%+30%+25%)=30%.
故答案为:30%.
(2)解:B品牌电视剧第3个月销量为(台),
B品牌电视剧第4个月销量为(台),
补全折线图,如图所示:
(3)解:由于月销量的平均水平相同,从折线的走势看,A品牌的月销量呈下降趋势,而B品牌的月销量呈上升趋势,所以该商店应经销B品牌电视机.
【点睛】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
23.(1)1995年、1998年、2000年分别是15万元、25万元、30万元;(2)2001年,15万元
【分析】根据统计图的相关知识即可找出与题意相对应的答案.如哪几年两厂的获利额相同,只需要找出图上两条线相交的点即可,以此类推两厂差额最大的年份是两条线分离最大的时候.
【详解】(1)1995年、1998年、2000年分别是15万元、25万元、30万元;
(2)2001年,15万元.
【点睛】本题考查了折线统计图的知识,解题的关键能看懂折线统计图并能根据题意找出相对应的答案.
24.(1)4000;(2)作图见解析;(3)90.
【分析】(1)设这批水果总重量为mkg,根据西瓜的重量占这批水果总重量的40%,列出方程即可解决.
(2)根据苹果的重量=总重量 西瓜的重量 桃子的重量 香蕉西瓜的重量,即可画出图形.
(3)根据圆心角=360°×百分比,即可解决问题.
【详解】(1)设这批水果总重量为mkg,
应用m 40%=1600,
解得:m=4000kg.
故答案为:4000.
(2)∵苹果的重量=总重量﹣西瓜的重量﹣桃子的重量﹣香蕉西瓜的重量=4000﹣1600﹣1000﹣200=1200,
条形图如图所示,
(3)∵桃子的重量占这批水果总重量的25%,∴桃子所对应扇形的圆心角为360°×25%=90°.
故答案为:90.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
