19.4坐标与图形的变化巩固强化练习(含解析)
文档属性
| 名称 | 19.4坐标与图形的变化巩固强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
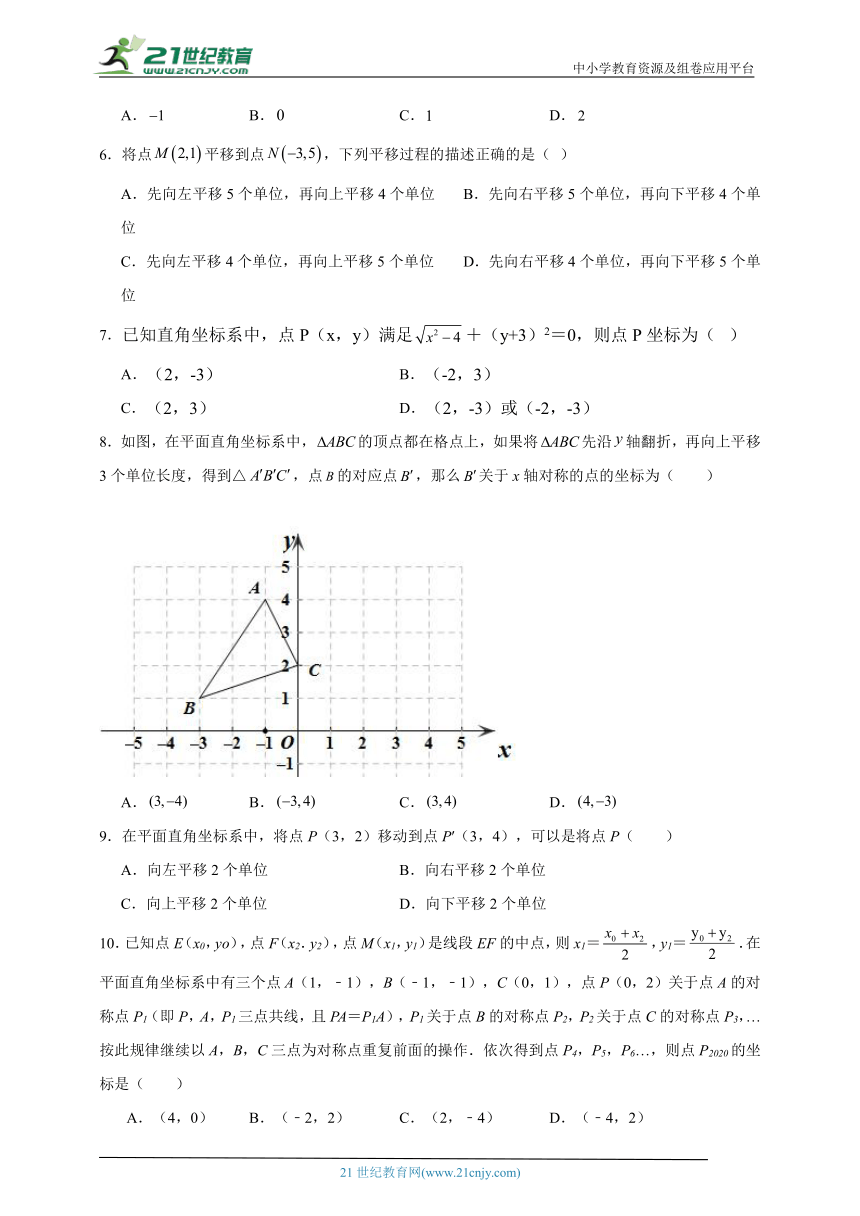
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
19.4坐标与图形的变化
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在平面直角坐标系中,关于垂直于y轴于点C(0,1)的直线成轴对称,已知点A坐标是,则点B的坐标是( )
A. B. C. D.
2.下列说法不正确的是( )
A.点一定在第二象限 B.点到轴的距离为2
C.若中,则点在轴上 D.若在轴上,则
3.点A的坐标为(1,2),把点A向右平移2个单位,再向下平移1个单位后得到A’,则点A’的坐标为( )
A.(0,4) B.(3,1) C.(﹣1,3) D.(2,0)
4.在平面直角坐标系中,把点向左平移2个单位,再向上平移1个单位,得到的点的坐标是( )
A. B. C. D.
5.如图, 的坐标为若将线段平移至,则的值为( )
A. B. C. D.
6.将点平移到点,下列平移过程的描述正确的是( )
A.先向左平移5个单位,再向上平移4个单位 B.先向右平移5个单位,再向下平移4个单位
C.先向左平移4个单位,再向上平移5个单位 D.先向右平移4个单位,再向下平移5个单位
7.已知直角坐标系中,点P(x,y)满足+(y+3)2=0,则点P坐标为( )
A.(2,-3) B.(-2,3)
C.(2,3) D.(2,-3)或(-2,-3)
8.如图,在平面直角坐标系中,的顶点都在格点上,如果将先沿轴翻折,再向上平移3个单位长度,得到△,点的对应点,那么关于x轴对称的点的坐标为( )
A. B. C. D.
9.在平面直角坐标系中,将点P(3,2)移动到点P′(3,4),可以是将点P( )
A.向左平移2个单位 B.向右平移2个单位
C.向上平移2个单位 D.向下平移2个单位
10.已知点E(x0,yo),点F(x2.y2),点M(x1,y1)是线段EF的中点,则x1=,y1=.在平面直角坐标系中有三个点A(1,﹣1),B(﹣1,﹣1),C(0,1),点P(0,2)关于点A的对称点P1(即P,A,P1三点共线,且PA=P1A),P1关于点B的对称点P2,P2关于点C的对称点P3,…按此规律继续以A,B,C三点为对称点重复前面的操作.依次得到点P4,P5,P6…,则点P2020的坐标是( )
A.(4,0) B.(﹣2,2) C.(2,﹣4) D.(﹣4,2)
11.如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,….照此规律,点P第100次跳动至点P100的坐标是( )
A.(﹣26,50) B.(﹣25,50)
C.(26,50) D.(25,50)
12.如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A1的坐标是( )
A.(6,1) B.(0,1) C.(0,-3) D.(6,-3)
二、填空题
13.在平面直角坐标系中,将点A(a,1)先向右平移3个单位,再向下平移2个单位,得到点B(5,b),则ab的值为 .
14.的三个顶点坐标分别是,,,将平移后得到,其中,,则点的坐标是 .
15.在平面直角坐标系中,点绕原点顺时针旋转所得点的坐标是 .
16.点A(-1,-3)关于x轴对称点的坐标是 ;关于原点对称的点坐标是 .
17.如图,在平面直角坐标系中,的顶点A在x轴的正半轴上,点B的坐标为(4,4),点C的坐标为(1,0),且,点P为斜边OB上的一个动点,则的最小值为 .
三、解答题
18.如图,在平面直角坐标系中,点A、B的坐标分别为、,且实数a、b满足.
(1)求A、B两点的坐标;
(2)如图1,已知坐标轴上有两动点P,Q同时出发,P点从A点出发沿x轴负方向以每秒2个单位长度的速度向点O匀速移动,Q点从O点出发沿y轴正方向以每秒1个单位长度的速度向点B匀速移动,点P到达O点整个运动随之结束.AB的中点C的坐标是,设运动时间为t秒.是否存在这样的t,使得的面积等于面积的2倍?若存在,请求出t的值;若不存在,请说明理由;
(3)如图2,在(2)的条件下,若,点G是第二象限中一点,并且y轴平分.点E是线段OB上一动点,连接AE交OC于点H,当点E在线段OB上运动的过程中,探究,,之间的数量关系,并证明你的结论(三角形的内角和为180°可以直接使用).
19.如图,把平移,使点A平移到点O.作出平移后的,并求的顶点坐标和平移的距离.
20.你能尽快说出如图所示图案上各个“顶点”的坐标吗?它们的坐标由什么特点?
21.把点向左平移3个单位,所得的点与点A关于y轴对称,求a的值.
22.如图所示,在平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A2B3与△B2A2B1关于点B2成中心对称.
(1)直接写出B1,B2,B3,的坐标分别为 , , ;
(2)连接A1B2,求A1B2的长.
23.在平面直角坐标系中,O为坐标原点,在四边形OABC中,顶点A(0,2),,,且点B在第一象限,△OAB是等边三角形.
(1)如图①,求点B的坐标;
(2)如图②,将四边形OABC沿直线EF折叠,使点A与点C重合,求点E,F的坐标;
(3)如图③,若将四边形OABC沿直线EF折叠,使,设点A对折后所对应的点为,△AEF与四边形EOBF的重叠面积为S,设点E的坐标为(0,m)(0<m<1),请直接写出S与m的函数关系式.
24.如图,先将三角形向左平移个单位长度,再向下平移个单位长度,得到三角形.
(1)画出三角形
(2)已知三角形内部一点的坐标为,若点随三角形一起平移,平移后点的对应点的坐标为,请求出,的值;
(3)求三角形面积;
(4)设线段与轴的交点为,则点的坐标为 .
《19.4坐标与图形的变化》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C B B B A D A C B
题号 11 12
答案 C B
1.C
【分析】由点C坐标可得对称轴为直线y=1,根据轴对称的性质可得直线y=1垂直平分线段AB,根据点A坐标即可得答案.
【详解】∵关于垂直于y轴于点C(0,1)的直线成轴对称,
∴对称轴为直线y=1,
∴直线y=1垂直平分线段AB,
∵A(4,4),
∴B(4,-2).
故选:C.
【点睛】本题主要考查了坐标的对称特点.解此类问题的关键是要掌握轴对称的性质:对称轴垂直平分对应点的连线.利用此性质可在坐标系中得到对应点的坐标.
2.C
【分析】A:第二象限的点满足(-,+),B:找出P点坐标即可确定与y轴的距离,C:xy=0,可确定x、y至少有一个为0来确定,D:根据x轴上点的坐标特征即可判定.
【详解】A:<0,>0,本选项说法正确;
B:P点到y轴距离是2,本选项说法正确;
C:xy=0,得到x、y至少有一个为0,P可能在x轴上,也可能在y轴上,本选项说法错误;
D:点P在x轴上,则y=0,本选项说法正确.
故选:C.
【点睛】本题考查坐标上点的特征.确定各个象限的点和坐标轴上点的特征是解决本题的关键.
3.B
【分析】直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
【详解】原来点的横坐标是1,纵坐标是2,向右平移2个单位再向下平移1个单位得到新点的横坐标是1+2=3,纵坐标为2-1=1.
则新坐标为(3,1).
故选B.
【点睛】本题主要考查了平移中点的变化规律:左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.
4.B
【分析】本题考查了点的平移中坐标变化规律,掌握点的平移规律:横坐标左减右加,纵坐标上加下减是解题的关键.
【详解】解:将点向左平移2个单位,再向上平移1个单位,
所得到的点的坐标为,
即,
故选:B.
5.B
【分析】直接利用平移中点的变化规律求解即可.
【详解】解:由B点平移前后的纵坐标分别为2、4,可得B点向上平移了2个单位,
由A点平移前后的横坐标分别是为1、3,可得A点向右平移了2个单位,
由此得线段AB的平移的过程是:向上平移2个单位,再向右平移2个单位,
所以点A、B均按此规律平移,
由此可得a=0+2=2,b=0+2=2,
∴a-b=2-2=0,
故选:B.
【点睛】本题考查了坐标系中点、线段的平移规律,解题的关键是掌握在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
6.A
【分析】根据在平面直角坐标系中坐标与图形变化-平移的规律进行判断.
【详解】解:点平移到点,
表示点M向左平移5个单位,再向上平移4个单位.
故选A.
【点睛】本题考查了坐标与图形变化-平移:在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.(即:横坐标,右移加,左移减;纵坐标,上移加,下移减.)
7.D
【详解】已知+(y+3)2=0,根据非负数的性质可得,y+3=0,解得x=±2,y=-3,所以点P坐标为(2,-3)或(-2,-3),故选D.
8.A
【分析】根据轴对称的性质和平移规律求解即可.
【详解】解:由平面直角坐标系中图形可知B( 3,1),将△ABC先沿y轴翻折得到B点对应点坐标为(3,1),再向上平移3个单位长度得到点的坐标为(3,1+3),则点B的对应点B'的坐标为(3,4),那么关于x轴对称的点的坐标为,
故选:A.
【点睛】此题主要考查了坐标与图形的变化 对称和平移,解决问题的关键是掌握点的坐标的变化规律.
9.C
【分析】横坐标,右移加,左移减;纵坐标,上移加,下移减可得结论.
【详解】解:将点向上平移2个单位长度得到的点坐标为,
故选:C.
【点睛】本题主要考查了坐标与图形的变化,解题的关键是掌握点的坐标的变化规律.
10.B
【分析】根据题意可得前6个点的坐标,即可发现规律每6个点一组为一个循环,根据2020÷6=336…4,进而可得点P2020的坐标.
【详解】解:∵A(1,﹣1),B(﹣1,﹣1),C(0,1),
点P(0,2)关于点A的对称点P1,
∴,,
解得x=2,y=﹣4,
所以点P1(2,﹣4);
同理:
P1关于点B的对称点P2,
所以P2(﹣4,2)
P2关于点C的对称点P3,
所以P3(4,0),
P4(﹣2,﹣2),
P5(0,0),
P6(0,2),
…,
发现规律:
每6个点一组为一个循环,
∴2020÷6=336…4,
所以点P2020的坐标是(﹣2,﹣2).
故选:B.
【点睛】本题考查了坐标与图形的变化-旋转、规律型-点的坐标、关于x轴、y轴对称的点的坐标,解决本题的关键是掌握旋转的性质.
11.C
【分析】解决本题的关键是分析出题目的规律,以奇数开头的相邻两个坐标的纵坐标是相同的,所以第100次跳动后,纵坐标为,其中4的倍数的跳动都在轴的右侧,那么第100次跳动得到的横坐标也在轴的右侧.横坐标为,横坐标为,横坐标为,以此类推可得到的横坐标.
【详解】解:经过观察可得:和的纵坐标均为,
和的纵坐标均为,
和的纵坐标均为,
∴可以推知和的纵坐标均为,
∵4的倍数的跳动都在轴的右侧,
∴第100次跳动得到的横坐标也在轴的右侧.横坐标为,横坐标为,横坐标为,
∴以此类推可得到:的横坐标为(是4的倍数),
∴点的横坐标为:,纵坐标为:,
∴点第100次跳动至点的坐标为
故选:.
【点睛】本题考查规律型:点的坐标,解题的关键是分析出题目的规律,找出题目中点的坐标的规律,属于中考常考题型.
12.B
【详解】∵四边形ABCD先向左平移3个单位,再向上平移2个单位,
∴点A也先向左平移3个单位,再向上平移2个单位,
∴由A(3,-1)可知,A′坐标为(0,1).故选B.
13.-2
【分析】根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得答案.
【详解】解:将点向右平移3个单位,再向下平移2个单位得到点,
则点的坐标为.
又∵点B的坐标为(5,b)
∴,
∴,
故答案为:.
【点睛】本题考查了坐标系中点的平移规律.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
14.
【分析】利用平移变换的性质求出平移得到的路径,即可求出答案.
【详解】解:由题意向上平移3个单位,再向左平移一个单位得到,
.
故答案为:.
【点睛】本题考查了坐标与图形的变化—平移,解题的关键是理解题意,熟练掌握平移的性质.
15.
【分析】本题考查了坐标与图形的变化-旋转,根据绕原点旋转后两点关于原点对称,再根据关于坐标原点对称的点的横坐标互为相反数,纵坐标互为相反数解答.
【详解】解:∵点绕原点旋转后所得点与点A关于坐标原点对称,
∴所得的点的横坐标为3,纵坐标为,
∴点的坐标为.
故答案为:.
16. (-1,3) (1,3)
【详解】根据题意得:得A点关于x轴对称的点的坐标为(-1,3);A点关于原点对称的点坐标为(1,3).
故答案为(-1,3);(1,3).
17.
【分析】作A关于OB的对称点D,连接CD交OB于P,连接AP,则此时的值最小,根据勾股定理求出CD,即可得出答案.
【详解】解:如下图,作A关于OB的对称点D,连接CD交OB于P,连接AP,则此时的值最小,
∵,
∴,
∵为直角三角形,且,
∴,
∴为等腰直角三角形,
又∵点B的坐标为(4,4),
∴点A的坐标为(4,0),
∴由对称性可知D点在y轴上,且坐标为(0,4),
∵点D的坐标为(4,4),点C的坐标为(1,0),
∴,,
∴在中,由勾股定理得,
即的最小值是.
故答案为:.
【点睛】本题主要考查了坐标与图形、等腰直角三角形的判定与性质、轴对称-最短路线问题、勾股定理等知识,解题的关键是求出P点的位置.
18.(1)A(16,0),B(0,12)
(2)存在,
(3)2∠GOB+∠BAE=∠OHA,理由见解析
【分析】(1)根据算术平方根的非负性列出二元一次方程组,解方程组得到答案;
(2)根据题意用t表示出OP、OQ,根据三角形的面积公式列出方程,解方程即可求出t;
(3)过点H作HF∥OG交x轴于F,根据平行线的性质得到∠OHF=∠GOH,证明HF∥AB,根据平行线的性质得到∠AHF=∠BAE,结合图形计算,证明结论.
【详解】(1)解:∵,
∴,
解得:,
∴A(16,0),B(0,12);
(2)解:解:存在t,使得△OCP的面积等于△OCQ面积的2倍
由(1)知,A(16,0),B(0,12),
∴OA=16,OB=12,
∵,
∴,
∵C(8,6),
∴,,
∵△OCP的面积等于△OCQ面积的2倍,
∴ ,解得:,
∴当时,△OCP的面积等于△OCQ面积的2倍;
(3)解:2∠GOB+∠BAE=∠OHA,理由如下:
∵∠COA+∠BOC=∠BOA=90°,
∴∠OBA+∠BAO=90°,
又∵∠COA=∠CAO,
∴∠OBA=∠BOC,
∵y轴平分∠GOC,
∴∠GOB=∠BOC,
∴∠GOB=∠OBA,
∴OG∥BA,
过点H作HF∥OG交x轴于F,
∴HF∥BA,
∴∠FHA=∠BAE,
∵OG∥FH,
∴∠GOC=∠FHO,
∴∠GOC+∠BAE=∠FHO+∠FHA,
即∠GOC+∠BAE=∠OHA,
∴2∠GOB+∠BAE=∠OHA.
【点睛】本题考查的是非负性的性质,三角形的面积公式,角平分线的定义,平行线的性质,正确作出辅助线是解本题的关键.
19.图形见解析,,
【分析】(1)根据平移的性质画出平移后的即可;
(2)根据各点在坐标系中的位置写出各点坐标,再由平移的性质即可.
【详解】解:如图,即为所求,
根据题意得:点,
平移的距离为.
【点睛】本题考查的是作图一平移变换,熟知图形平移不变性的性质是解答此题的关键.
20.答案不唯一,见解析
【分析】结合平面直角坐标系可确定坐标轴上点的坐标,确定第一象限内的点的坐标,再根据关于坐标轴及原点对称的点的坐标特征求解即可.
【详解】解:具体方法不唯一.例如,可以先写出坐标轴上四个点的坐标,,,;然后写第一象限的三个点的坐标,,;第二象限的三个点与第一象限的三个点关于y轴对称,所以只要将横坐标乘-1,纵坐标不变就可以得到,,;第四象限与第三象限的点,分别与第一象限、第二象限的点关于x轴对称,所以横坐标不变,纵坐标乘-1即可,分别为,,,,,.
【点睛】本题考查了平面直角坐标系内点的表示方法及对称点的坐标特征,解题的关键是掌握关于坐标轴及原点对称的点的坐标特征.
21.
【分析】根据点向左平移减可得平移后的点坐标,然后关于y轴对称的点的坐标特点列式计算即可.
【详解】解:点向左平移3个单位,可得.
∵所得的点与点A关于y轴对称,
∴ ,解得:.
【点睛】本题主要考查了关于y轴对称的点的坐标特点,掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.
22.(1);(2)
【分析】(1)由题意易得,然后问题可求解;
(2)过点作轴于点H,由题意易得,则有,然后根据勾股定理可求解.
【详解】解:(1)∵△OA1B1是边长为2的等边三角形,
∴,
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴,
同理可得,
∴,
∴;
故答案为;
(2)过点作轴于点H,如图所示:
∵△OA1B1是边长为2的等边三角形,
∴,
∴,
∴在中,,
∴在中,.
【点睛】本题主要考查平面直角坐标系中点的坐标、等边三角形的性质、中心对称的性质及勾股定理,熟练掌握上述知识是解题的关键.
23.(1)点B的坐标
(2)点E坐标为,点F坐标为
(3)(0<m<1)
【分析】(1)根据A的坐标得到OA的长,由B与C的横坐标相同得到BC垂直于x轴,再由三角形ABO为等边三角形,得到OA=OB=AB=2,且求出∠OBC为30度,在直角三角形OBC中,利用30度所对的直角边等于斜边的一半求出n的值,即可得点B的坐标;
(2)设点E坐标为(0,y),在中,根据勾股定理列方程即可解出y的值,进而得出过F作FM垂直于CB,设MB=x,求出∠MBF为60度,在直角三角形MBF中,利用30度所对的直角边等于斜边的一半表示出FB,再利用勾股定理表示出FM,在直角三角形MCF中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,进而求出点F坐标;
(3)当点E的坐标为(0,m)(0<m<1),可判断出点A'落在四边形EOBF外,重合部分面积两等边三角形与面积之差,表示出S与m关系式即可.
【详解】(1)解∶∵,,,
BC⊥x轴,OA=2,
∵△ABO为等边三角形,
∴OA=OB=AB=2,
∴在中,
∠BOC=30°,OB=2
∴,
∴点B的坐标.
(2)解∶设点E的坐标为(0,y),
由折叠的性质可得,
在中,,
解得:,则点E坐标为,
作FM⊥CB于点M,如下图
设,
∵,
在中,
,,
在中,
根据勾股定理得:,
解得:,
,
则点F坐标为.
(3)解:∵EF∥OB,
∴为等边三角形,
∴为等边三角形,
∵点E的坐标为(0,m)(0<m<1),
此时点A'落在四边形EOBF外时,如下图所示,
由题意可得,
,
∵,又,
是等边三角形,,
,
,
得(0<m<1)
【点睛】本题主要考查了翻折变换中折叠的性质,坐标与图形性质,等边三角形的性质,以及勾股定理,牢固掌握以上知识点和会作辅助线是做出本题的关键,此题是一道综合性较强的试题.
24.(1)作图见解析
(2),
(3)
(4)
【分析】(1)根据三角形平移的方向和单位长度分别作出,,的对应点,,,然后顺次连接即可;
(2)根据点平移的坐标变化规律:左减右加纵不变,上加下减横不变,构建方程组即可解决问题;
(3)利用分割法求出三角形的面积即可;
(4)设点,则,然后利用建立关于的方程,求解即可.
【详解】(1)解:∵将三角形向左平移个单位长度,再向下平移个单位长度,如图,
∴,,,
连接、、,
∴三角形即为所作;
(2)平移后点的对应点,
∵,
∴,
解:,
∴,;
(3),
∴三角形面积为;
(4)设点,
∴,
∵,
∴,
解得:,
∴点的坐标为,
故答案为:.
【点睛】本题考查作图—平移变换,点坐标平移的规律,两点间距离,三角形的面积等知识,解题的关键是熟练掌握基本知识,学会用分割法求三角形的面积.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
19.4坐标与图形的变化
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在平面直角坐标系中,关于垂直于y轴于点C(0,1)的直线成轴对称,已知点A坐标是,则点B的坐标是( )
A. B. C. D.
2.下列说法不正确的是( )
A.点一定在第二象限 B.点到轴的距离为2
C.若中,则点在轴上 D.若在轴上,则
3.点A的坐标为(1,2),把点A向右平移2个单位,再向下平移1个单位后得到A’,则点A’的坐标为( )
A.(0,4) B.(3,1) C.(﹣1,3) D.(2,0)
4.在平面直角坐标系中,把点向左平移2个单位,再向上平移1个单位,得到的点的坐标是( )
A. B. C. D.
5.如图, 的坐标为若将线段平移至,则的值为( )
A. B. C. D.
6.将点平移到点,下列平移过程的描述正确的是( )
A.先向左平移5个单位,再向上平移4个单位 B.先向右平移5个单位,再向下平移4个单位
C.先向左平移4个单位,再向上平移5个单位 D.先向右平移4个单位,再向下平移5个单位
7.已知直角坐标系中,点P(x,y)满足+(y+3)2=0,则点P坐标为( )
A.(2,-3) B.(-2,3)
C.(2,3) D.(2,-3)或(-2,-3)
8.如图,在平面直角坐标系中,的顶点都在格点上,如果将先沿轴翻折,再向上平移3个单位长度,得到△,点的对应点,那么关于x轴对称的点的坐标为( )
A. B. C. D.
9.在平面直角坐标系中,将点P(3,2)移动到点P′(3,4),可以是将点P( )
A.向左平移2个单位 B.向右平移2个单位
C.向上平移2个单位 D.向下平移2个单位
10.已知点E(x0,yo),点F(x2.y2),点M(x1,y1)是线段EF的中点,则x1=,y1=.在平面直角坐标系中有三个点A(1,﹣1),B(﹣1,﹣1),C(0,1),点P(0,2)关于点A的对称点P1(即P,A,P1三点共线,且PA=P1A),P1关于点B的对称点P2,P2关于点C的对称点P3,…按此规律继续以A,B,C三点为对称点重复前面的操作.依次得到点P4,P5,P6…,则点P2020的坐标是( )
A.(4,0) B.(﹣2,2) C.(2,﹣4) D.(﹣4,2)
11.如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,….照此规律,点P第100次跳动至点P100的坐标是( )
A.(﹣26,50) B.(﹣25,50)
C.(26,50) D.(25,50)
12.如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A1的坐标是( )
A.(6,1) B.(0,1) C.(0,-3) D.(6,-3)
二、填空题
13.在平面直角坐标系中,将点A(a,1)先向右平移3个单位,再向下平移2个单位,得到点B(5,b),则ab的值为 .
14.的三个顶点坐标分别是,,,将平移后得到,其中,,则点的坐标是 .
15.在平面直角坐标系中,点绕原点顺时针旋转所得点的坐标是 .
16.点A(-1,-3)关于x轴对称点的坐标是 ;关于原点对称的点坐标是 .
17.如图,在平面直角坐标系中,的顶点A在x轴的正半轴上,点B的坐标为(4,4),点C的坐标为(1,0),且,点P为斜边OB上的一个动点,则的最小值为 .
三、解答题
18.如图,在平面直角坐标系中,点A、B的坐标分别为、,且实数a、b满足.
(1)求A、B两点的坐标;
(2)如图1,已知坐标轴上有两动点P,Q同时出发,P点从A点出发沿x轴负方向以每秒2个单位长度的速度向点O匀速移动,Q点从O点出发沿y轴正方向以每秒1个单位长度的速度向点B匀速移动,点P到达O点整个运动随之结束.AB的中点C的坐标是,设运动时间为t秒.是否存在这样的t,使得的面积等于面积的2倍?若存在,请求出t的值;若不存在,请说明理由;
(3)如图2,在(2)的条件下,若,点G是第二象限中一点,并且y轴平分.点E是线段OB上一动点,连接AE交OC于点H,当点E在线段OB上运动的过程中,探究,,之间的数量关系,并证明你的结论(三角形的内角和为180°可以直接使用).
19.如图,把平移,使点A平移到点O.作出平移后的,并求的顶点坐标和平移的距离.
20.你能尽快说出如图所示图案上各个“顶点”的坐标吗?它们的坐标由什么特点?
21.把点向左平移3个单位,所得的点与点A关于y轴对称,求a的值.
22.如图所示,在平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A2B3与△B2A2B1关于点B2成中心对称.
(1)直接写出B1,B2,B3,的坐标分别为 , , ;
(2)连接A1B2,求A1B2的长.
23.在平面直角坐标系中,O为坐标原点,在四边形OABC中,顶点A(0,2),,,且点B在第一象限,△OAB是等边三角形.
(1)如图①,求点B的坐标;
(2)如图②,将四边形OABC沿直线EF折叠,使点A与点C重合,求点E,F的坐标;
(3)如图③,若将四边形OABC沿直线EF折叠,使,设点A对折后所对应的点为,△AEF与四边形EOBF的重叠面积为S,设点E的坐标为(0,m)(0<m<1),请直接写出S与m的函数关系式.
24.如图,先将三角形向左平移个单位长度,再向下平移个单位长度,得到三角形.
(1)画出三角形
(2)已知三角形内部一点的坐标为,若点随三角形一起平移,平移后点的对应点的坐标为,请求出,的值;
(3)求三角形面积;
(4)设线段与轴的交点为,则点的坐标为 .
《19.4坐标与图形的变化》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C B B B A D A C B
题号 11 12
答案 C B
1.C
【分析】由点C坐标可得对称轴为直线y=1,根据轴对称的性质可得直线y=1垂直平分线段AB,根据点A坐标即可得答案.
【详解】∵关于垂直于y轴于点C(0,1)的直线成轴对称,
∴对称轴为直线y=1,
∴直线y=1垂直平分线段AB,
∵A(4,4),
∴B(4,-2).
故选:C.
【点睛】本题主要考查了坐标的对称特点.解此类问题的关键是要掌握轴对称的性质:对称轴垂直平分对应点的连线.利用此性质可在坐标系中得到对应点的坐标.
2.C
【分析】A:第二象限的点满足(-,+),B:找出P点坐标即可确定与y轴的距离,C:xy=0,可确定x、y至少有一个为0来确定,D:根据x轴上点的坐标特征即可判定.
【详解】A:<0,>0,本选项说法正确;
B:P点到y轴距离是2,本选项说法正确;
C:xy=0,得到x、y至少有一个为0,P可能在x轴上,也可能在y轴上,本选项说法错误;
D:点P在x轴上,则y=0,本选项说法正确.
故选:C.
【点睛】本题考查坐标上点的特征.确定各个象限的点和坐标轴上点的特征是解决本题的关键.
3.B
【分析】直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
【详解】原来点的横坐标是1,纵坐标是2,向右平移2个单位再向下平移1个单位得到新点的横坐标是1+2=3,纵坐标为2-1=1.
则新坐标为(3,1).
故选B.
【点睛】本题主要考查了平移中点的变化规律:左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.
4.B
【分析】本题考查了点的平移中坐标变化规律,掌握点的平移规律:横坐标左减右加,纵坐标上加下减是解题的关键.
【详解】解:将点向左平移2个单位,再向上平移1个单位,
所得到的点的坐标为,
即,
故选:B.
5.B
【分析】直接利用平移中点的变化规律求解即可.
【详解】解:由B点平移前后的纵坐标分别为2、4,可得B点向上平移了2个单位,
由A点平移前后的横坐标分别是为1、3,可得A点向右平移了2个单位,
由此得线段AB的平移的过程是:向上平移2个单位,再向右平移2个单位,
所以点A、B均按此规律平移,
由此可得a=0+2=2,b=0+2=2,
∴a-b=2-2=0,
故选:B.
【点睛】本题考查了坐标系中点、线段的平移规律,解题的关键是掌握在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
6.A
【分析】根据在平面直角坐标系中坐标与图形变化-平移的规律进行判断.
【详解】解:点平移到点,
表示点M向左平移5个单位,再向上平移4个单位.
故选A.
【点睛】本题考查了坐标与图形变化-平移:在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.(即:横坐标,右移加,左移减;纵坐标,上移加,下移减.)
7.D
【详解】已知+(y+3)2=0,根据非负数的性质可得,y+3=0,解得x=±2,y=-3,所以点P坐标为(2,-3)或(-2,-3),故选D.
8.A
【分析】根据轴对称的性质和平移规律求解即可.
【详解】解:由平面直角坐标系中图形可知B( 3,1),将△ABC先沿y轴翻折得到B点对应点坐标为(3,1),再向上平移3个单位长度得到点的坐标为(3,1+3),则点B的对应点B'的坐标为(3,4),那么关于x轴对称的点的坐标为,
故选:A.
【点睛】此题主要考查了坐标与图形的变化 对称和平移,解决问题的关键是掌握点的坐标的变化规律.
9.C
【分析】横坐标,右移加,左移减;纵坐标,上移加,下移减可得结论.
【详解】解:将点向上平移2个单位长度得到的点坐标为,
故选:C.
【点睛】本题主要考查了坐标与图形的变化,解题的关键是掌握点的坐标的变化规律.
10.B
【分析】根据题意可得前6个点的坐标,即可发现规律每6个点一组为一个循环,根据2020÷6=336…4,进而可得点P2020的坐标.
【详解】解:∵A(1,﹣1),B(﹣1,﹣1),C(0,1),
点P(0,2)关于点A的对称点P1,
∴,,
解得x=2,y=﹣4,
所以点P1(2,﹣4);
同理:
P1关于点B的对称点P2,
所以P2(﹣4,2)
P2关于点C的对称点P3,
所以P3(4,0),
P4(﹣2,﹣2),
P5(0,0),
P6(0,2),
…,
发现规律:
每6个点一组为一个循环,
∴2020÷6=336…4,
所以点P2020的坐标是(﹣2,﹣2).
故选:B.
【点睛】本题考查了坐标与图形的变化-旋转、规律型-点的坐标、关于x轴、y轴对称的点的坐标,解决本题的关键是掌握旋转的性质.
11.C
【分析】解决本题的关键是分析出题目的规律,以奇数开头的相邻两个坐标的纵坐标是相同的,所以第100次跳动后,纵坐标为,其中4的倍数的跳动都在轴的右侧,那么第100次跳动得到的横坐标也在轴的右侧.横坐标为,横坐标为,横坐标为,以此类推可得到的横坐标.
【详解】解:经过观察可得:和的纵坐标均为,
和的纵坐标均为,
和的纵坐标均为,
∴可以推知和的纵坐标均为,
∵4的倍数的跳动都在轴的右侧,
∴第100次跳动得到的横坐标也在轴的右侧.横坐标为,横坐标为,横坐标为,
∴以此类推可得到:的横坐标为(是4的倍数),
∴点的横坐标为:,纵坐标为:,
∴点第100次跳动至点的坐标为
故选:.
【点睛】本题考查规律型:点的坐标,解题的关键是分析出题目的规律,找出题目中点的坐标的规律,属于中考常考题型.
12.B
【详解】∵四边形ABCD先向左平移3个单位,再向上平移2个单位,
∴点A也先向左平移3个单位,再向上平移2个单位,
∴由A(3,-1)可知,A′坐标为(0,1).故选B.
13.-2
【分析】根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得答案.
【详解】解:将点向右平移3个单位,再向下平移2个单位得到点,
则点的坐标为.
又∵点B的坐标为(5,b)
∴,
∴,
故答案为:.
【点睛】本题考查了坐标系中点的平移规律.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
14.
【分析】利用平移变换的性质求出平移得到的路径,即可求出答案.
【详解】解:由题意向上平移3个单位,再向左平移一个单位得到,
.
故答案为:.
【点睛】本题考查了坐标与图形的变化—平移,解题的关键是理解题意,熟练掌握平移的性质.
15.
【分析】本题考查了坐标与图形的变化-旋转,根据绕原点旋转后两点关于原点对称,再根据关于坐标原点对称的点的横坐标互为相反数,纵坐标互为相反数解答.
【详解】解:∵点绕原点旋转后所得点与点A关于坐标原点对称,
∴所得的点的横坐标为3,纵坐标为,
∴点的坐标为.
故答案为:.
16. (-1,3) (1,3)
【详解】根据题意得:得A点关于x轴对称的点的坐标为(-1,3);A点关于原点对称的点坐标为(1,3).
故答案为(-1,3);(1,3).
17.
【分析】作A关于OB的对称点D,连接CD交OB于P,连接AP,则此时的值最小,根据勾股定理求出CD,即可得出答案.
【详解】解:如下图,作A关于OB的对称点D,连接CD交OB于P,连接AP,则此时的值最小,
∵,
∴,
∵为直角三角形,且,
∴,
∴为等腰直角三角形,
又∵点B的坐标为(4,4),
∴点A的坐标为(4,0),
∴由对称性可知D点在y轴上,且坐标为(0,4),
∵点D的坐标为(4,4),点C的坐标为(1,0),
∴,,
∴在中,由勾股定理得,
即的最小值是.
故答案为:.
【点睛】本题主要考查了坐标与图形、等腰直角三角形的判定与性质、轴对称-最短路线问题、勾股定理等知识,解题的关键是求出P点的位置.
18.(1)A(16,0),B(0,12)
(2)存在,
(3)2∠GOB+∠BAE=∠OHA,理由见解析
【分析】(1)根据算术平方根的非负性列出二元一次方程组,解方程组得到答案;
(2)根据题意用t表示出OP、OQ,根据三角形的面积公式列出方程,解方程即可求出t;
(3)过点H作HF∥OG交x轴于F,根据平行线的性质得到∠OHF=∠GOH,证明HF∥AB,根据平行线的性质得到∠AHF=∠BAE,结合图形计算,证明结论.
【详解】(1)解:∵,
∴,
解得:,
∴A(16,0),B(0,12);
(2)解:解:存在t,使得△OCP的面积等于△OCQ面积的2倍
由(1)知,A(16,0),B(0,12),
∴OA=16,OB=12,
∵,
∴,
∵C(8,6),
∴,,
∵△OCP的面积等于△OCQ面积的2倍,
∴ ,解得:,
∴当时,△OCP的面积等于△OCQ面积的2倍;
(3)解:2∠GOB+∠BAE=∠OHA,理由如下:
∵∠COA+∠BOC=∠BOA=90°,
∴∠OBA+∠BAO=90°,
又∵∠COA=∠CAO,
∴∠OBA=∠BOC,
∵y轴平分∠GOC,
∴∠GOB=∠BOC,
∴∠GOB=∠OBA,
∴OG∥BA,
过点H作HF∥OG交x轴于F,
∴HF∥BA,
∴∠FHA=∠BAE,
∵OG∥FH,
∴∠GOC=∠FHO,
∴∠GOC+∠BAE=∠FHO+∠FHA,
即∠GOC+∠BAE=∠OHA,
∴2∠GOB+∠BAE=∠OHA.
【点睛】本题考查的是非负性的性质,三角形的面积公式,角平分线的定义,平行线的性质,正确作出辅助线是解本题的关键.
19.图形见解析,,
【分析】(1)根据平移的性质画出平移后的即可;
(2)根据各点在坐标系中的位置写出各点坐标,再由平移的性质即可.
【详解】解:如图,即为所求,
根据题意得:点,
平移的距离为.
【点睛】本题考查的是作图一平移变换,熟知图形平移不变性的性质是解答此题的关键.
20.答案不唯一,见解析
【分析】结合平面直角坐标系可确定坐标轴上点的坐标,确定第一象限内的点的坐标,再根据关于坐标轴及原点对称的点的坐标特征求解即可.
【详解】解:具体方法不唯一.例如,可以先写出坐标轴上四个点的坐标,,,;然后写第一象限的三个点的坐标,,;第二象限的三个点与第一象限的三个点关于y轴对称,所以只要将横坐标乘-1,纵坐标不变就可以得到,,;第四象限与第三象限的点,分别与第一象限、第二象限的点关于x轴对称,所以横坐标不变,纵坐标乘-1即可,分别为,,,,,.
【点睛】本题考查了平面直角坐标系内点的表示方法及对称点的坐标特征,解题的关键是掌握关于坐标轴及原点对称的点的坐标特征.
21.
【分析】根据点向左平移减可得平移后的点坐标,然后关于y轴对称的点的坐标特点列式计算即可.
【详解】解:点向左平移3个单位,可得.
∵所得的点与点A关于y轴对称,
∴ ,解得:.
【点睛】本题主要考查了关于y轴对称的点的坐标特点,掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.
22.(1);(2)
【分析】(1)由题意易得,然后问题可求解;
(2)过点作轴于点H,由题意易得,则有,然后根据勾股定理可求解.
【详解】解:(1)∵△OA1B1是边长为2的等边三角形,
∴,
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴,
同理可得,
∴,
∴;
故答案为;
(2)过点作轴于点H,如图所示:
∵△OA1B1是边长为2的等边三角形,
∴,
∴,
∴在中,,
∴在中,.
【点睛】本题主要考查平面直角坐标系中点的坐标、等边三角形的性质、中心对称的性质及勾股定理,熟练掌握上述知识是解题的关键.
23.(1)点B的坐标
(2)点E坐标为,点F坐标为
(3)(0<m<1)
【分析】(1)根据A的坐标得到OA的长,由B与C的横坐标相同得到BC垂直于x轴,再由三角形ABO为等边三角形,得到OA=OB=AB=2,且求出∠OBC为30度,在直角三角形OBC中,利用30度所对的直角边等于斜边的一半求出n的值,即可得点B的坐标;
(2)设点E坐标为(0,y),在中,根据勾股定理列方程即可解出y的值,进而得出过F作FM垂直于CB,设MB=x,求出∠MBF为60度,在直角三角形MBF中,利用30度所对的直角边等于斜边的一半表示出FB,再利用勾股定理表示出FM,在直角三角形MCF中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,进而求出点F坐标;
(3)当点E的坐标为(0,m)(0<m<1),可判断出点A'落在四边形EOBF外,重合部分面积两等边三角形与面积之差,表示出S与m关系式即可.
【详解】(1)解∶∵,,,
BC⊥x轴,OA=2,
∵△ABO为等边三角形,
∴OA=OB=AB=2,
∴在中,
∠BOC=30°,OB=2
∴,
∴点B的坐标.
(2)解∶设点E的坐标为(0,y),
由折叠的性质可得,
在中,,
解得:,则点E坐标为,
作FM⊥CB于点M,如下图
设,
∵,
在中,
,,
在中,
根据勾股定理得:,
解得:,
,
则点F坐标为.
(3)解:∵EF∥OB,
∴为等边三角形,
∴为等边三角形,
∵点E的坐标为(0,m)(0<m<1),
此时点A'落在四边形EOBF外时,如下图所示,
由题意可得,
,
∵,又,
是等边三角形,,
,
,
得(0<m<1)
【点睛】本题主要考查了翻折变换中折叠的性质,坐标与图形性质,等边三角形的性质,以及勾股定理,牢固掌握以上知识点和会作辅助线是做出本题的关键,此题是一道综合性较强的试题.
24.(1)作图见解析
(2),
(3)
(4)
【分析】(1)根据三角形平移的方向和单位长度分别作出,,的对应点,,,然后顺次连接即可;
(2)根据点平移的坐标变化规律:左减右加纵不变,上加下减横不变,构建方程组即可解决问题;
(3)利用分割法求出三角形的面积即可;
(4)设点,则,然后利用建立关于的方程,求解即可.
【详解】(1)解:∵将三角形向左平移个单位长度,再向下平移个单位长度,如图,
∴,,,
连接、、,
∴三角形即为所作;
(2)平移后点的对应点,
∵,
∴,
解:,
∴,;
(3),
∴三角形面积为;
(4)设点,
∴,
∵,
∴,
解得:,
∴点的坐标为,
故答案为:.
【点睛】本题考查作图—平移变换,点坐标平移的规律,两点间距离,三角形的面积等知识,解题的关键是熟练掌握基本知识,学会用分割法求三角形的面积.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
