第八单元数学广角——搭配(二)期末复习练 人教版数学三年级下册(含解析)
文档属性
| 名称 | 第八单元数学广角——搭配(二)期末复习练 人教版数学三年级下册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 119.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 16:32:47 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第八单元数学广角——搭配(二)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.把5件相同的礼物全部分给3个小朋友,使每个小朋友都分到礼物,分礼物的不同方法一共有( )种。
A.3 B.4 C.5 D.6
2.3个小朋友都单独和李老师、陈老师分别各拍一张照片,一共要拍( )张照片.
A.3 B.6 C.9
3.用4、2、0三个数可以组成( )个三位数.
A.4 B.5 C.6
4.书架上有4本不同的科技书和5本不同的文艺书,张梦想借两本不同类的书,共有( )种不同的借法.
A.20 B.15 C.9
5.用3、5、7这三个数字能组成( )个不同的三位数.
A.2个 B.3 个 C.4个 D.6个
6.商店里有5种水果,分别是香蕉、苹果、橘子、梨、西瓜。我想买其中的2种,有( )种买法。
A.6 B.8 C.10
7.有2件上衣3条裤子,有多少中不同的穿法( )
A.4种 B.5种 C.6种
8.3个好朋友见面,每两个人握1次手,一共要握( )次手.
A.6 B.4 C.3
9.在下图的棋盘上,把黑子移到A处,有( )种走法?请你推算出来(要求只能向上,向右)
A.18
B.20
C.22
10.用2、0、5、可以组成( )个三位数.
A.6 B.4 C.8
二、填空题
11.有6名同学,每2名同学握一次手,一共要握( )次手。
12.春季运动会,三年级四个班进行拔河比赛,每两个班比赛一场,一共要比( )场。
13.用4、5、6能组成( )个两位数,它们是( )、( )、( )、( )、( )、( )。
14.用1、2、3、4组成24个四位数,从大到小第8个数是 .
15.用数字卡片各2张,能组成 个不同的六位数.
三、判断题
16.聪聪在演讲比赛中获得了第1名,他和参加比赛的每个选手都握了一次手,一个握了10次,参加比赛的一共有10人.( )
17.有4位同学参加乒乓球比赛,每两人比赛一场,一共要比6场。( )
18.用2、3、5、0这四个数字能组成9个没有重复数字的两位数。( )
19.3个好朋友聚会,每两个人握一次手,一共要握6次。( )
20.妈妈向贝贝推荐了《少年智力开发报》、《中国少年报》、《小学生数学报》三种报纸。如果贝贝至少订阅一种,最多订阅三种,贝贝一共有7种不同的订阅方法。 。
四、计算题
21.直接写出得数.
40×50= 1.5+5= 20×18= 70÷5=
60+30= 54÷6= 6.5+0.05= 8.4-4=
22.列竖式计算.
58×35= 36×43=
5.37+15.3= 25.6-2.56=
五、解答题
23.甲、乙、丙、丁4人参加乒乓球小组赛,每2人 比赛一场,一共要比赛多少场?
24.用0、1、2可以组成几个不同的三位数,分别是什么?
25.在一个书架上有不同的数学参考书9本,不同的语文参考书6本,不同的英语参考书3本.现从中取出两本不同学科的参考书,有多少种不同的取法?
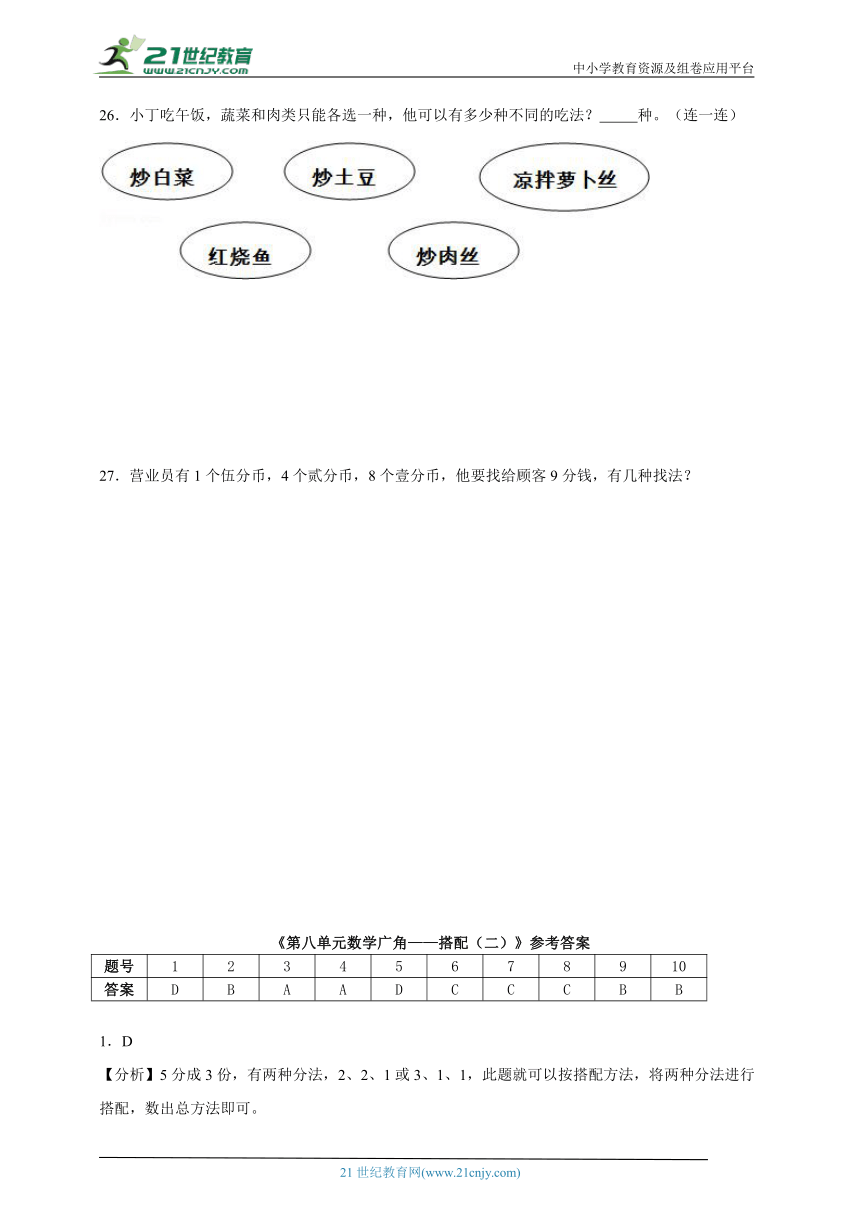
26.小丁吃午饭,蔬菜和肉类只能各选一种,他可以有多少种不同的吃法? 种。(连一连)
27.营业员有1个伍分币,4个贰分币,8个壹分币,他要找给顾客9分钱,有几种找法?
《第八单元数学广角——搭配(二)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A A D C C C B B
1.D
【分析】5分成3份,有两种分法,2、2、1或3、1、1,此题就可以按搭配方法,将两种分法进行搭配,数出总方法即可。
【详解】①一类是礼物被分成2,2,1,从3人中选出1人给1个礼物,故有3种方法,即:1+2+2,2+1+2,2+2+1;
②一类是礼物被分成3,1,1,从3人中选出1人给3个礼物,故有3种方法,即:3+1+1,1+1+3,1+3+1;
所以,一共有6种不同的方法。
故答案为:D
【点睛】本题考查分配问题,用列举法比较简单。
2.B
【详解】略
3.A
【详解】试题分析:写出用4、2、0可以组成的全部三位数即可求解.
解:用4、2、0可以组成的三位数有:
204,240,402,420;一共有4个;
故选A.
点评:写数时要注意0不能放在最高位,要按照一定的顺序写,不要重复和漏写.
4.A
【详解】任选一本科技书,文艺书有五种选法,四本科技书就有4×5=20种借法.
5.D
【详解】试题分析:分三种情况:①3在百位时;②5在百位时;③7在百位时;依次写出组成的三位数即可.
解::①3在百位时,有357、375;
②5在百位时,有537、573;
③7在百位时,有735、753;
一共有6个.
故选D.
点评:本题考查了简单的乘法原理:即做一件事情,完成它需要分成n个步骤,做第一步有M1种不同的方法,做第二步有M2种不同的方法,…,做第n步有Mn种不同的方法,那么完成这件事就有M1×M2×…×Mn种不同的方法.
6.C
【分析】此题可以这样列举:香蕉与剩下的进行搭配,香蕉和苹果、香蕉和橘子、香蕉和梨、香蕉和西瓜,共4种;苹果与剩下的搭配,苹果和橘子、苹果和梨、苹果和西瓜,共3种,橘子与剩下的搭配,橘子和梨、橘子和西瓜,共2种;梨和西瓜,用加法求一共有几种买法,据此解答。
【详解】4+3+2+1=10(种)
故答案为:C
【点睛】本题考查事物的简单搭配规律。
7.C
【详解】试题分析:上衣是从2件中选择1件,有2种选择的方法;再把裤子从3条种选择1条,有3种选择的方法,一共有2×3种不同的选择方法.
解:2×3=6(种);
答:有6种不同的穿法.
故选C.
点评:本题数据较少,也可以画图连线求解.
8.C
【详解】(3﹣1)×3÷2
=6÷2
=3(次)
答:一共握3次手.
故选:C.
9.B
【分析】先判断移到A处走的步数,然后判断向右或向上的步数,根据排序问题的解法列式计算即可;注意C(6,3)的计算方法,3表示6×5×4,三个数相乘,然后除以3×2×1就是所有的步数.
【详解】移动到A处共走6步,向上3步,向右3步;C(6,3),
所以6×5×4÷(3×2×1)=120÷6=20(种)
故答案为B
10.B
【详解】试题分析:先将能组成的三位数列举出来,再计算出一共有几个.
解:能组成的三位数有:250,205,502,520,共有4个.
故选B.
点评:解决本题时要注意0不能写在最高数位上.
11.15
【分析】6位同学,每个人都要和剩下的5人握手,要握5次,一共是6×5次,由于是两两之间握手,甲与乙握手和乙与甲握手是一样的,所以再除以2即可。
【详解】6×(6-1)÷2
=6×5÷2
=30÷2
=15(次)
【点睛】本题属于握手问题,当数据较大时可利用握手问题的公式:握手次数=人数×(人数-1)÷2求解。
12.6
【分析】两两之间进行比赛,每个班就要与其余3个班进行比赛,则进行3场比赛。4个班就要进行(4×3)场比赛,但每两个班之间只进行1场比赛,则实际进行了(4×3÷2)场比赛。
【详解】(4-1)×4÷2
=3×4÷2
=12÷2
=6(场)
因此,三年级四个班进行拔河比赛,每两个班比赛一场,一共要6场。
【点睛】本题考查搭配问题,要注意去掉重复计算的情况,如果班数比较少可以用枚举法解答,如果班数比较多可以用公式:比赛场数=n×(n-1)÷2解答。
13. 6 45 46 54 56 64 65
【解析】略
14.3421
【详解】试题分析:先排千位有4种排法;再排百位,有3种排法;再排十位,有2种排法;再排个位,有1种排法,共有4×3×2×1=24种;所以,这四个数字在千位上都有:24÷4=6个数,那么从大到小第8个数是应在千位上是3的数,并且是第二大的数(8﹣6=2),这个数为:3421;据此解答.
解:24÷4=6(个),
8﹣6=2(个);
所以,从大到小第8个数是应在千位上是3的数,并且是第二大的数,这个数为:3421.
故答案为3421.
点评:本题考查了乘法原理的灵活应用,关键明确从大到小第8个数的最高位上的数字是几.
15.90
【详解】试题分析:先确定最高位十万位上的数是2,则万位上有3种选择,再分别将剩下的数位上的可能选择利用树状图列举出来,计算出一共有多少种方法;因为十万位上还可能是3或4,方法和2在首位时方法一样,所以用2在首位的方法数再乘3即可.
解:如图所示:
2在首位时的方法一共有30种方法,则一共有30×3=90(种).
答:能组成90个不同的六位数.
故答案为90.
点评:解决本题主要借助树状图来解答,根据2在首位的排列方法,得出3、4在首位时的方法一样,进而得出结论.
16.×
【详解】略
17.√
【分析】4个人进行乒乓球比赛,每两人比赛一场,即每人都要与其他三人各赛一场,共赛3场,则4人共参赛4×3=12(场),由于比赛是在两人之间进行的,所以一共要比赛12÷2=6(场)。
【详解】4×(4-1)÷2
=4×3÷2
=12÷2
=6(场)
所以原题的说法判断正确。
故答案为:√
【点睛】此类赛制为单循环赛制,比赛场数=参赛人数×(人数-1)÷2。
18.√
【分析】先排十位,因为0不能放在十位上,所以十位上先排2,个位有三种情况;十位上排3,个位也有三种情况;十位上排5,个位也有三种情况,据此列举出组成没有重复数字的两位数,再进一步解答即可。
【详解】十位上是2,个位上可以是3、5、0,组成3个两位数,分别是:23、25、20;
十位上是3,个位上可以是2、5、0,组成3个两位数,分别是:32、35、30;
十位上是5,个位上可以是2、3、0,组成3个两位数,分别是:52、53、50;
一共组成3×3=9(个);所有原题的说法判断正确。
故答案为:√
【点睛】此题考查排列数,解答此题的关键是按一定的顺序列举,做到不重复,不遗漏;注意此题0不能放在十位上。
19.×
【分析】每个人都要和另外的2个人握一次手,3个人共握3×2=6次,由于每两人握手,应算作一次手,去掉重复的情况,实际只握了6÷2=3次,据此解答。
【详解】(3-1)×3÷2
=6÷2
=3(次)
故答案为:×
【点睛】本题是典型的握手问题,如果人数比较少,可以用枚举法解答;如果人数比较多,可以用公式:n(n-1)÷2解答。
20.√
【分析】分订阅1种,订阅2种,订阅3种进行讨论,求出每种的各有几种订法,再相加。
【详解】(1)订阅1种时:
是从3种报纸中任选1种,有3种选法;
(2)订阅2种时:
是从3种报纸中选2种订阅,即选出1种不订阅的,也有3种选法;
(3)订阅3种时:
3本全选,有1种选法;
3+3+1=7(种)。
故答案为正确。
【点睛】本题分情况讨论后,每一种情况都可以看成简单的组合问题。
21.2000 6.5 360 14
90 9 6.55 4.4
【详解】略
【点睛】本题考查学生整数和小数的运算能力。要求学生要看清题目中的数字和运算符号,认真计算,规范书写。特别是小数要保证是相同数位上的数字相加减。
22.
【详解】计算乘数是两位数的乘法时,先用乘数的个位上的数去乘另一个乘数,得数的末位与乘数的个位对齐,再用这个乘数的十位上的数去乘另一个乘数,所得数的末位与乘数的十位对齐,最后把各数位上的数相加即是最后得数;计算小数加减法,先把小数的小数点对齐(也就是把相同数位上的数对齐),再按照整数加减法的法则进行计算,最后,在得数里对齐横线上的小数点,点上小数点。
23.6场
【分析】由于每人都要和另外的(4-1)人比赛一次,则一共要比赛:4×3=12(场);又因为每两个人只比赛一场,去掉重复计算的情况,实际只有(12÷2)场,据此解答。
【详解】4-1=3(人)
4×3=12(次)
12÷2=6(场)
答:一共要比赛6场。
24.4个,210、201、120、201
【详解】试题分析:先排百位,因为0不能放在百位上,所以有2种排法;再排十位,有2种排法;再排个位,有1种排法,共有2×2×1=4种;据此例举即可.
解:根据分析可得,
共有2×2×1=4(个),
它们是:210、201;120、201;共4种;
答:用0、1、2可以组成4个不同的三位数,分别是210、201、120、201.
点评:本题考查了简单的乘法原理,由于情况数较少可以有枚举法解答,注意要按顺序写出,防止遗漏.
25.99种
【详解】试题分析:分情况讨论:
(1)选择拿语文书和数学书:
数学书有9种不同的拿法,语文书有6种不同的拿法,它们的积就是全部的拿法;
(2)选择语文书和英语书:
语文书有6种不同的拿法,英语书有3种不同的拿法,它们的积就是全部的拿法;
(3)选择数学书和英语书:
数学书有9种不同的拿法,英语书有3种不同的拿法,它们的积就是全部的拿法;
然后把这三种情况的数量加在一起即可.
解:9×6+9×3+6×3,
=54+27+18,
=81+18,
=99(种);
答:有99种不同的取法.
点评:本题先确定拿哪两种类型的书,再看这两种类型的书可以有多少种可能,进而求解.
26.连线见详解;
6
【分析】从二肉类中选一种有2种选法;从三种蔬菜中选一种有3种选法;共有2×3=6(种),据此解答。
【详解】连线如下:
2×3=6(种)
答:一共可以有种不同的吃法。
【点睛】本题考查了乘法原理,由于情况数较少可以有枚举法解答,注意要按顺序写出,防止遗漏。
27.7种
【分析】根据题意可知,一共有1个伍分币,4个贰分币,8个壹分币,要找9分钱,可以按照顺序依次列举出所有可能的找法。比如先列举出带伍分币的,再列举出不带伍分币,只带贰分币和壹分币的情况。据此解答。
【详解】可以找1个伍分币、2个贰分币,或者找1个伍分币、1个贰分币、2个壹分币,或者找1个伍分币、4个壹分币,或者找4个贰分币、1个壹分币,或者找3个贰分币、3个壹分币,或者找2个贰分币、5个壹分币,或者找1个贰分币、7个壹分币。
答:他要找给顾客9分钱,有7种找法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八单元数学广角——搭配(二)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.把5件相同的礼物全部分给3个小朋友,使每个小朋友都分到礼物,分礼物的不同方法一共有( )种。
A.3 B.4 C.5 D.6
2.3个小朋友都单独和李老师、陈老师分别各拍一张照片,一共要拍( )张照片.
A.3 B.6 C.9
3.用4、2、0三个数可以组成( )个三位数.
A.4 B.5 C.6
4.书架上有4本不同的科技书和5本不同的文艺书,张梦想借两本不同类的书,共有( )种不同的借法.
A.20 B.15 C.9
5.用3、5、7这三个数字能组成( )个不同的三位数.
A.2个 B.3 个 C.4个 D.6个
6.商店里有5种水果,分别是香蕉、苹果、橘子、梨、西瓜。我想买其中的2种,有( )种买法。
A.6 B.8 C.10
7.有2件上衣3条裤子,有多少中不同的穿法( )
A.4种 B.5种 C.6种
8.3个好朋友见面,每两个人握1次手,一共要握( )次手.
A.6 B.4 C.3
9.在下图的棋盘上,把黑子移到A处,有( )种走法?请你推算出来(要求只能向上,向右)
A.18
B.20
C.22
10.用2、0、5、可以组成( )个三位数.
A.6 B.4 C.8
二、填空题
11.有6名同学,每2名同学握一次手,一共要握( )次手。
12.春季运动会,三年级四个班进行拔河比赛,每两个班比赛一场,一共要比( )场。
13.用4、5、6能组成( )个两位数,它们是( )、( )、( )、( )、( )、( )。
14.用1、2、3、4组成24个四位数,从大到小第8个数是 .
15.用数字卡片各2张,能组成 个不同的六位数.
三、判断题
16.聪聪在演讲比赛中获得了第1名,他和参加比赛的每个选手都握了一次手,一个握了10次,参加比赛的一共有10人.( )
17.有4位同学参加乒乓球比赛,每两人比赛一场,一共要比6场。( )
18.用2、3、5、0这四个数字能组成9个没有重复数字的两位数。( )
19.3个好朋友聚会,每两个人握一次手,一共要握6次。( )
20.妈妈向贝贝推荐了《少年智力开发报》、《中国少年报》、《小学生数学报》三种报纸。如果贝贝至少订阅一种,最多订阅三种,贝贝一共有7种不同的订阅方法。 。
四、计算题
21.直接写出得数.
40×50= 1.5+5= 20×18= 70÷5=
60+30= 54÷6= 6.5+0.05= 8.4-4=
22.列竖式计算.
58×35= 36×43=
5.37+15.3= 25.6-2.56=
五、解答题
23.甲、乙、丙、丁4人参加乒乓球小组赛,每2人 比赛一场,一共要比赛多少场?
24.用0、1、2可以组成几个不同的三位数,分别是什么?
25.在一个书架上有不同的数学参考书9本,不同的语文参考书6本,不同的英语参考书3本.现从中取出两本不同学科的参考书,有多少种不同的取法?
26.小丁吃午饭,蔬菜和肉类只能各选一种,他可以有多少种不同的吃法? 种。(连一连)
27.营业员有1个伍分币,4个贰分币,8个壹分币,他要找给顾客9分钱,有几种找法?
《第八单元数学广角——搭配(二)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A A D C C C B B
1.D
【分析】5分成3份,有两种分法,2、2、1或3、1、1,此题就可以按搭配方法,将两种分法进行搭配,数出总方法即可。
【详解】①一类是礼物被分成2,2,1,从3人中选出1人给1个礼物,故有3种方法,即:1+2+2,2+1+2,2+2+1;
②一类是礼物被分成3,1,1,从3人中选出1人给3个礼物,故有3种方法,即:3+1+1,1+1+3,1+3+1;
所以,一共有6种不同的方法。
故答案为:D
【点睛】本题考查分配问题,用列举法比较简单。
2.B
【详解】略
3.A
【详解】试题分析:写出用4、2、0可以组成的全部三位数即可求解.
解:用4、2、0可以组成的三位数有:
204,240,402,420;一共有4个;
故选A.
点评:写数时要注意0不能放在最高位,要按照一定的顺序写,不要重复和漏写.
4.A
【详解】任选一本科技书,文艺书有五种选法,四本科技书就有4×5=20种借法.
5.D
【详解】试题分析:分三种情况:①3在百位时;②5在百位时;③7在百位时;依次写出组成的三位数即可.
解::①3在百位时,有357、375;
②5在百位时,有537、573;
③7在百位时,有735、753;
一共有6个.
故选D.
点评:本题考查了简单的乘法原理:即做一件事情,完成它需要分成n个步骤,做第一步有M1种不同的方法,做第二步有M2种不同的方法,…,做第n步有Mn种不同的方法,那么完成这件事就有M1×M2×…×Mn种不同的方法.
6.C
【分析】此题可以这样列举:香蕉与剩下的进行搭配,香蕉和苹果、香蕉和橘子、香蕉和梨、香蕉和西瓜,共4种;苹果与剩下的搭配,苹果和橘子、苹果和梨、苹果和西瓜,共3种,橘子与剩下的搭配,橘子和梨、橘子和西瓜,共2种;梨和西瓜,用加法求一共有几种买法,据此解答。
【详解】4+3+2+1=10(种)
故答案为:C
【点睛】本题考查事物的简单搭配规律。
7.C
【详解】试题分析:上衣是从2件中选择1件,有2种选择的方法;再把裤子从3条种选择1条,有3种选择的方法,一共有2×3种不同的选择方法.
解:2×3=6(种);
答:有6种不同的穿法.
故选C.
点评:本题数据较少,也可以画图连线求解.
8.C
【详解】(3﹣1)×3÷2
=6÷2
=3(次)
答:一共握3次手.
故选:C.
9.B
【分析】先判断移到A处走的步数,然后判断向右或向上的步数,根据排序问题的解法列式计算即可;注意C(6,3)的计算方法,3表示6×5×4,三个数相乘,然后除以3×2×1就是所有的步数.
【详解】移动到A处共走6步,向上3步,向右3步;C(6,3),
所以6×5×4÷(3×2×1)=120÷6=20(种)
故答案为B
10.B
【详解】试题分析:先将能组成的三位数列举出来,再计算出一共有几个.
解:能组成的三位数有:250,205,502,520,共有4个.
故选B.
点评:解决本题时要注意0不能写在最高数位上.
11.15
【分析】6位同学,每个人都要和剩下的5人握手,要握5次,一共是6×5次,由于是两两之间握手,甲与乙握手和乙与甲握手是一样的,所以再除以2即可。
【详解】6×(6-1)÷2
=6×5÷2
=30÷2
=15(次)
【点睛】本题属于握手问题,当数据较大时可利用握手问题的公式:握手次数=人数×(人数-1)÷2求解。
12.6
【分析】两两之间进行比赛,每个班就要与其余3个班进行比赛,则进行3场比赛。4个班就要进行(4×3)场比赛,但每两个班之间只进行1场比赛,则实际进行了(4×3÷2)场比赛。
【详解】(4-1)×4÷2
=3×4÷2
=12÷2
=6(场)
因此,三年级四个班进行拔河比赛,每两个班比赛一场,一共要6场。
【点睛】本题考查搭配问题,要注意去掉重复计算的情况,如果班数比较少可以用枚举法解答,如果班数比较多可以用公式:比赛场数=n×(n-1)÷2解答。
13. 6 45 46 54 56 64 65
【解析】略
14.3421
【详解】试题分析:先排千位有4种排法;再排百位,有3种排法;再排十位,有2种排法;再排个位,有1种排法,共有4×3×2×1=24种;所以,这四个数字在千位上都有:24÷4=6个数,那么从大到小第8个数是应在千位上是3的数,并且是第二大的数(8﹣6=2),这个数为:3421;据此解答.
解:24÷4=6(个),
8﹣6=2(个);
所以,从大到小第8个数是应在千位上是3的数,并且是第二大的数,这个数为:3421.
故答案为3421.
点评:本题考查了乘法原理的灵活应用,关键明确从大到小第8个数的最高位上的数字是几.
15.90
【详解】试题分析:先确定最高位十万位上的数是2,则万位上有3种选择,再分别将剩下的数位上的可能选择利用树状图列举出来,计算出一共有多少种方法;因为十万位上还可能是3或4,方法和2在首位时方法一样,所以用2在首位的方法数再乘3即可.
解:如图所示:
2在首位时的方法一共有30种方法,则一共有30×3=90(种).
答:能组成90个不同的六位数.
故答案为90.
点评:解决本题主要借助树状图来解答,根据2在首位的排列方法,得出3、4在首位时的方法一样,进而得出结论.
16.×
【详解】略
17.√
【分析】4个人进行乒乓球比赛,每两人比赛一场,即每人都要与其他三人各赛一场,共赛3场,则4人共参赛4×3=12(场),由于比赛是在两人之间进行的,所以一共要比赛12÷2=6(场)。
【详解】4×(4-1)÷2
=4×3÷2
=12÷2
=6(场)
所以原题的说法判断正确。
故答案为:√
【点睛】此类赛制为单循环赛制,比赛场数=参赛人数×(人数-1)÷2。
18.√
【分析】先排十位,因为0不能放在十位上,所以十位上先排2,个位有三种情况;十位上排3,个位也有三种情况;十位上排5,个位也有三种情况,据此列举出组成没有重复数字的两位数,再进一步解答即可。
【详解】十位上是2,个位上可以是3、5、0,组成3个两位数,分别是:23、25、20;
十位上是3,个位上可以是2、5、0,组成3个两位数,分别是:32、35、30;
十位上是5,个位上可以是2、3、0,组成3个两位数,分别是:52、53、50;
一共组成3×3=9(个);所有原题的说法判断正确。
故答案为:√
【点睛】此题考查排列数,解答此题的关键是按一定的顺序列举,做到不重复,不遗漏;注意此题0不能放在十位上。
19.×
【分析】每个人都要和另外的2个人握一次手,3个人共握3×2=6次,由于每两人握手,应算作一次手,去掉重复的情况,实际只握了6÷2=3次,据此解答。
【详解】(3-1)×3÷2
=6÷2
=3(次)
故答案为:×
【点睛】本题是典型的握手问题,如果人数比较少,可以用枚举法解答;如果人数比较多,可以用公式:n(n-1)÷2解答。
20.√
【分析】分订阅1种,订阅2种,订阅3种进行讨论,求出每种的各有几种订法,再相加。
【详解】(1)订阅1种时:
是从3种报纸中任选1种,有3种选法;
(2)订阅2种时:
是从3种报纸中选2种订阅,即选出1种不订阅的,也有3种选法;
(3)订阅3种时:
3本全选,有1种选法;
3+3+1=7(种)。
故答案为正确。
【点睛】本题分情况讨论后,每一种情况都可以看成简单的组合问题。
21.2000 6.5 360 14
90 9 6.55 4.4
【详解】略
【点睛】本题考查学生整数和小数的运算能力。要求学生要看清题目中的数字和运算符号,认真计算,规范书写。特别是小数要保证是相同数位上的数字相加减。
22.
【详解】计算乘数是两位数的乘法时,先用乘数的个位上的数去乘另一个乘数,得数的末位与乘数的个位对齐,再用这个乘数的十位上的数去乘另一个乘数,所得数的末位与乘数的十位对齐,最后把各数位上的数相加即是最后得数;计算小数加减法,先把小数的小数点对齐(也就是把相同数位上的数对齐),再按照整数加减法的法则进行计算,最后,在得数里对齐横线上的小数点,点上小数点。
23.6场
【分析】由于每人都要和另外的(4-1)人比赛一次,则一共要比赛:4×3=12(场);又因为每两个人只比赛一场,去掉重复计算的情况,实际只有(12÷2)场,据此解答。
【详解】4-1=3(人)
4×3=12(次)
12÷2=6(场)
答:一共要比赛6场。
24.4个,210、201、120、201
【详解】试题分析:先排百位,因为0不能放在百位上,所以有2种排法;再排十位,有2种排法;再排个位,有1种排法,共有2×2×1=4种;据此例举即可.
解:根据分析可得,
共有2×2×1=4(个),
它们是:210、201;120、201;共4种;
答:用0、1、2可以组成4个不同的三位数,分别是210、201、120、201.
点评:本题考查了简单的乘法原理,由于情况数较少可以有枚举法解答,注意要按顺序写出,防止遗漏.
25.99种
【详解】试题分析:分情况讨论:
(1)选择拿语文书和数学书:
数学书有9种不同的拿法,语文书有6种不同的拿法,它们的积就是全部的拿法;
(2)选择语文书和英语书:
语文书有6种不同的拿法,英语书有3种不同的拿法,它们的积就是全部的拿法;
(3)选择数学书和英语书:
数学书有9种不同的拿法,英语书有3种不同的拿法,它们的积就是全部的拿法;
然后把这三种情况的数量加在一起即可.
解:9×6+9×3+6×3,
=54+27+18,
=81+18,
=99(种);
答:有99种不同的取法.
点评:本题先确定拿哪两种类型的书,再看这两种类型的书可以有多少种可能,进而求解.
26.连线见详解;
6
【分析】从二肉类中选一种有2种选法;从三种蔬菜中选一种有3种选法;共有2×3=6(种),据此解答。
【详解】连线如下:
2×3=6(种)
答:一共可以有种不同的吃法。
【点睛】本题考查了乘法原理,由于情况数较少可以有枚举法解答,注意要按顺序写出,防止遗漏。
27.7种
【分析】根据题意可知,一共有1个伍分币,4个贰分币,8个壹分币,要找9分钱,可以按照顺序依次列举出所有可能的找法。比如先列举出带伍分币的,再列举出不带伍分币,只带贰分币和壹分币的情况。据此解答。
【详解】可以找1个伍分币、2个贰分币,或者找1个伍分币、1个贰分币、2个壹分币,或者找1个伍分币、4个壹分币,或者找4个贰分币、1个壹分币,或者找3个贰分币、3个壹分币,或者找2个贰分币、5个壹分币,或者找1个贰分币、7个壹分币。
答:他要找给顾客9分钱,有7种找法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
