【攻克压轴大题】2025年中考数学压轴题精选:一次函数(含解析)
文档属性
| 名称 | 【攻克压轴大题】2025年中考数学压轴题精选:一次函数(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 20:59:45 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
【攻克压轴大题】2025年中考数学压轴题精选:一次函数
1.(2025春 重庆期末)如图1,在平面直角坐标系中,直线l1交y轴于点A,交x轴于点B,∠ABO=30°.直线l2:yx+6经过点A,交x轴于点C.
(1)求直线l1的解析式;
(2)如图2,点D是y轴负半轴上一动点,点E是x轴上一动点,若S△ACD=10,求DEBE的最小值;
(3)如图3,点P是直线l2上的一个动点,过点P作y轴的平行线交直线l1于点Q,平面内有一个动点M,若以C,P,Q,M为顶点的四边形是菱形,请直接写出点M的坐标.
2.(2025春 长安区期末)如图1,在平面直角坐标系中,直线yx+4分别与x轴、y轴交于点A、点B,将△AOB绕坐标原点逆时针旋转90°得到△COD,直线CD交直线AB于点E.
(1)直线CD的函数表达式为 ;
(2)如图2,连接OE,过点O作OF⊥OE交直线CD于点F,求证:∠OEF=45°;
(3)若点P是直线DC上一点,点Q是x轴上一点(点Q不与点O重合),当△DPQ与△DOC全等时,直接写出点P的坐标.
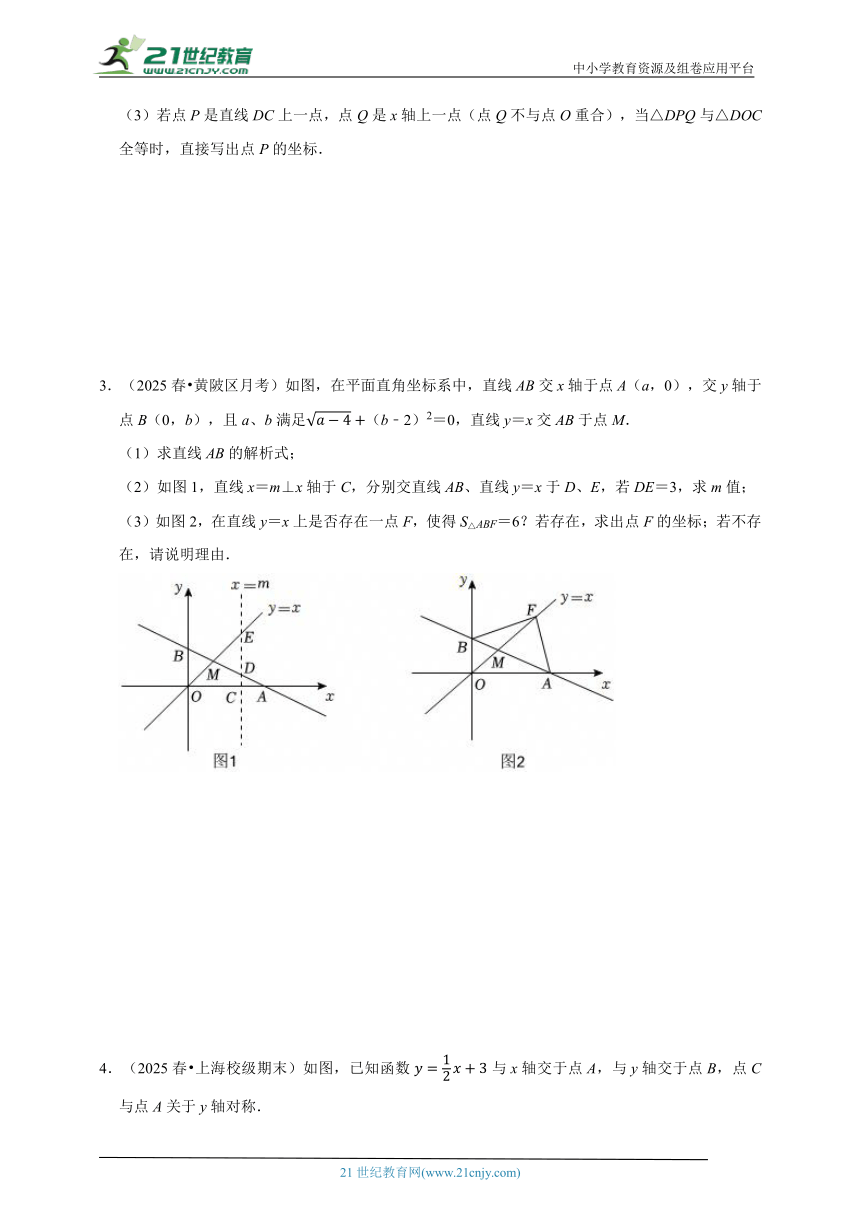
3.(2025春 黄陂区月考)如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足(b﹣2)2=0,直线y=x交AB于点M.
(1)求直线AB的解析式;
(2)如图1,直线x=m⊥x轴于C,分别交直线AB、直线y=x于D、E,若DE=3,求m值;
(3)如图2,在直线y=x上是否存在一点F,使得S△ABF=6?若存在,求出点F的坐标;若不存在,请说明理由.
4.(2025春 上海校级期末)如图,已知函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.
①点M在线段AO上,若△PQB的面积为2,求点P的坐标;
②点M在线段AC上运动的过程中,联结BM,若∠BMP=∠BAC,请直接写出点Q的坐标.
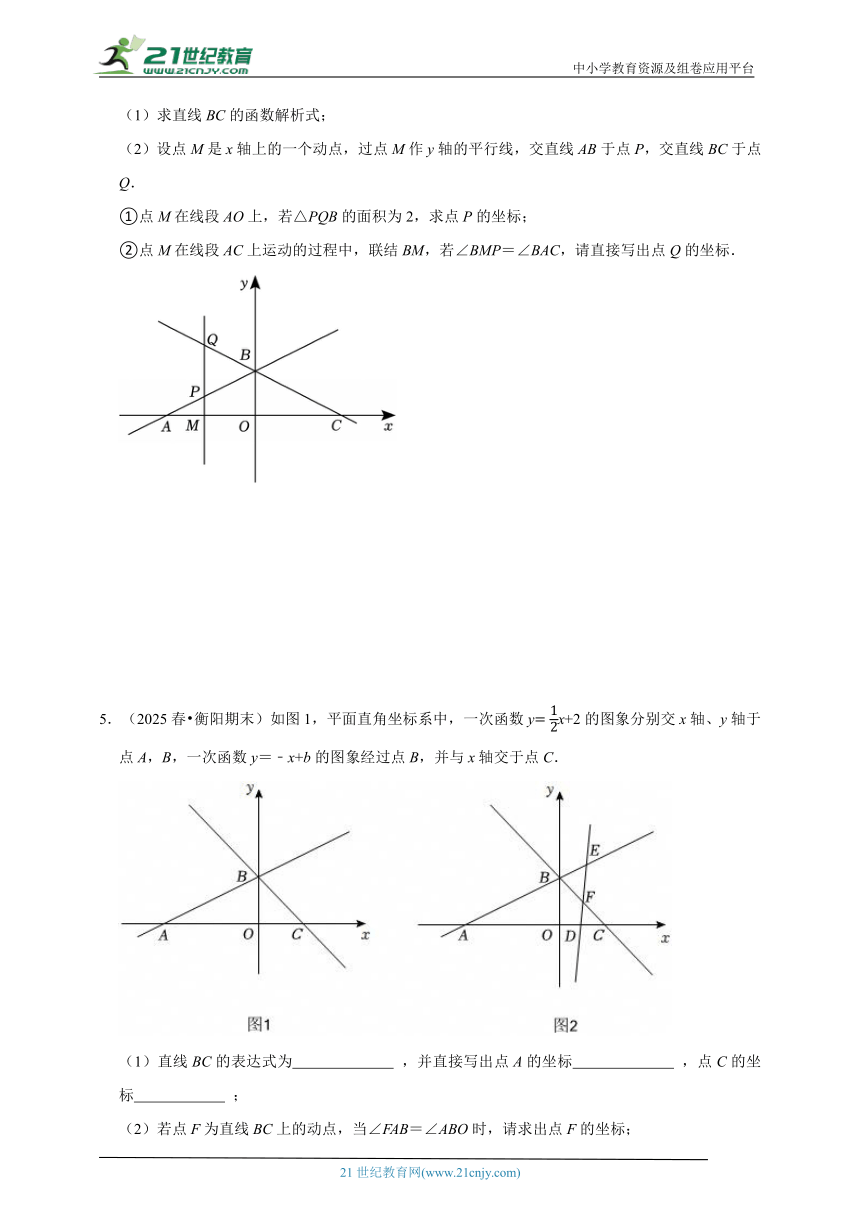
5.(2025春 衡阳期末)如图1,平面直角坐标系中,一次函数yx+2的图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C.
(1)直线BC的表达式为 ,并直接写出点A的坐标 ,点C的坐标 ;
(2)若点F为直线BC上的动点,当∠FAB=∠ABO时,请求出点F的坐标;
(3)如图2,已知点D(1,0),点F在直线BC上运动,连接DF,直线DF与直线AB交于点E,当△CDF与△BEF面积相等时,求出点E的坐标.
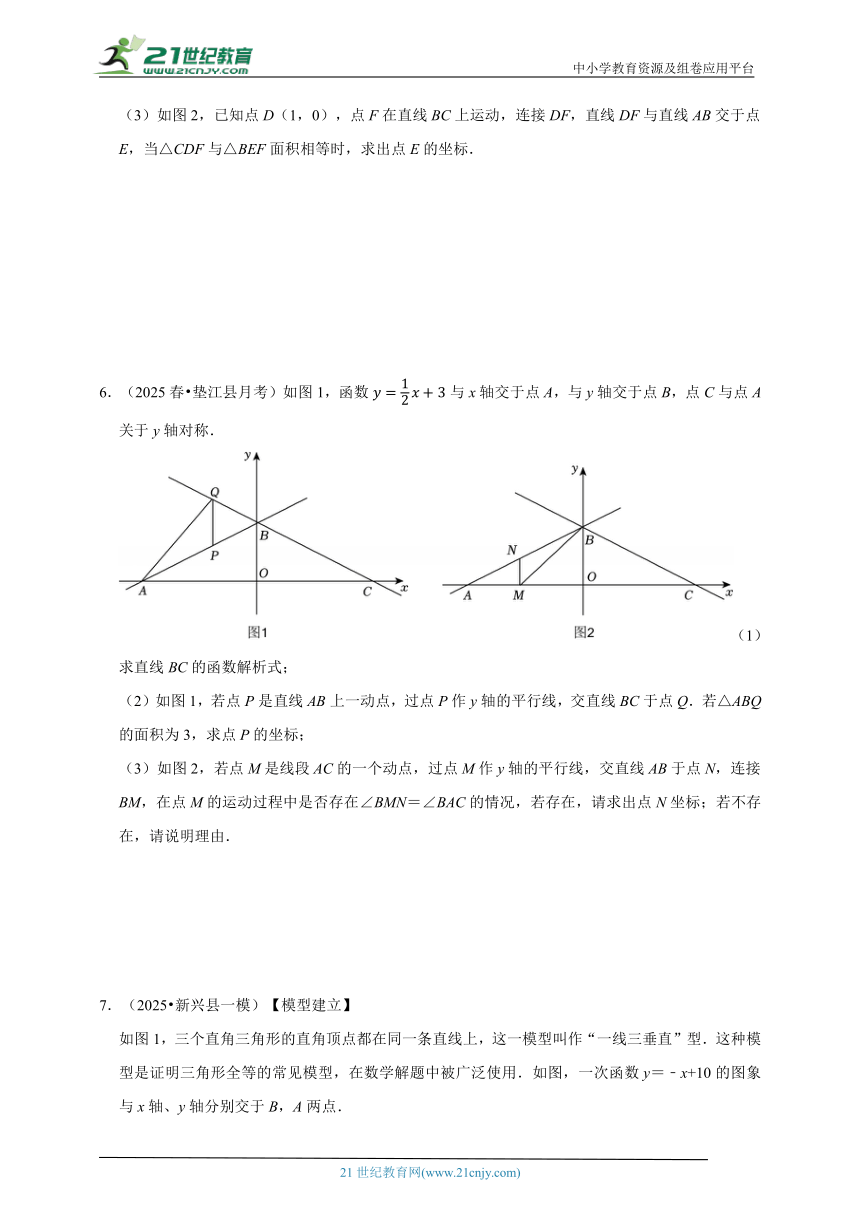
6.(2025春 垫江县月考)如图1,函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)如图1,若点P是直线AB上一动点,过点P作y轴的平行线,交直线BC于点Q.若△ABQ的面积为3,求点P的坐标;
(3)如图2,若点M是线段AC的一个动点,过点M作y轴的平行线,交直线AB于点N,连接BM,在点M的运动过程中是否存在∠BMN=∠BAC的情况,若存在,请求出点N坐标;若不存在,请说明理由.
7.(2025 新兴县一模)【模型建立】
如图1,三个直角三角形的直角顶点都在同一条直线上,这一模型叫作“一线三垂直”型.这种模型是证明三角形全等的常见模型,在数学解题中被广泛使用.如图,一次函数y=﹣x+10的图象与x轴、y轴分别交于B,A两点.
【模型探索】
(1)如图2,求证:△AOB是等腰直角三角形.
(2)如图3,M,N是直线y=kx上的两动点,连接BM,AN.若BM⊥MN,BM=6,求AN的长的最小值.
【模型应用】
(3)如图4,经过点B的直线与y轴交于点C,H为线段OB上的一点,作射线CH.若∠BCH=45°,求直线CH的函数解析式.
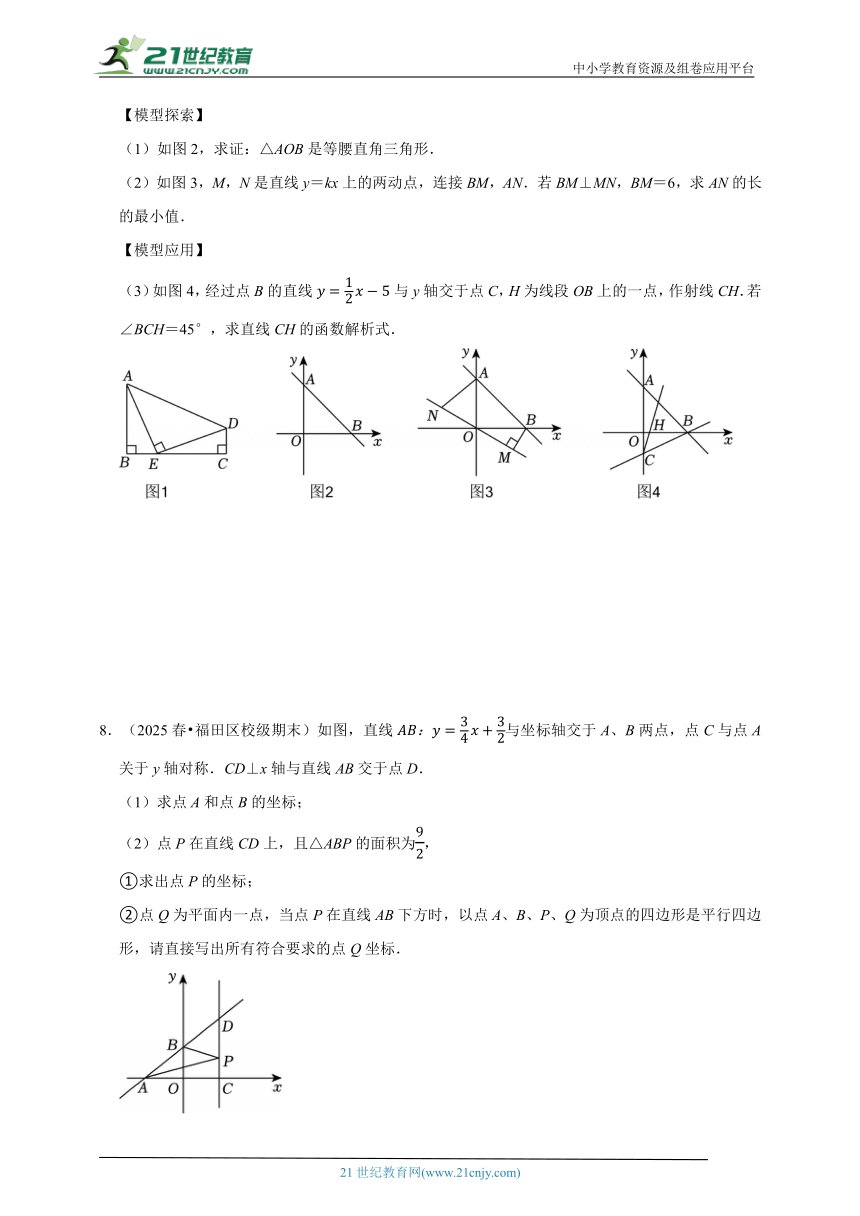
8.(2025春 福田区校级期末)如图,直线与坐标轴交于A、B两点,点C与点A关于y轴对称.CD⊥x轴与直线AB交于点D.
(1)求点A和点B的坐标;
(2)点P在直线CD上,且△ABP的面积为,
①求出点P的坐标;
②点Q为平面内一点,当点P在直线AB下方时,以点A、B、P、Q为顶点的四边形是平行四边形,请直接写出所有符合要求的点Q坐标.
9.(2025春 鲤城区校级期末)已知:如图,一次函数的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx﹣6的图象相交于点D,直线CD与y轴相交于点E.
(1)直线CD的函数表达式为: ;点D的坐标为 ;(直接写出结果)
(2)点Q为线段DE上的一个动点,连接BQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;
②点Q是否存在某个位置,将△BDE沿着直线BQ翻折,使得点D恰好落在直线AB下方的y轴上?若存在,请求出点Q的坐标;若不存在,请说明理由.
10.(2025春 万州区期末)如图1,函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)如图1,若点P是直线AB上一动点,过点P作y轴的平行线,交直线BC于点Q.若△ABQ的面积为3,求点P的坐标;
(3)如图2,若点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点N,连接BM,在点M的运动过程中是否存在∠BMN=∠BAC的情况,若存在,请求出点N坐标;若不存在,请说明理由.
11.(2024秋 寿阳县期末)综合与探究
如图,在平面直角坐标系中,直线m:y=x﹣1与x轴、y轴分别交于点A,B,直线n:y=﹣2x+b经过点A,并与y轴交于点C.
(1)求A,B两点的坐标及b的值.
(2)若动点P在直线AC上运动,
①当时,求点P的坐标;
②当点P与点C重合时,在第一象限内是否存在一点Q,使△APQ为等腰直角三角形,若存在直接写出点Q的坐标;若不存在说明理由.
12.(2025春 西山区校级期末)如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.
(1)若△APD为等腰直角三角形.
①求直线AP的函数解析式;
②在x轴上另有一点G的坐标为(2,0),请在直线AP上找一点M,使△GEM的周长最小,并求出此时点M的坐标和△GEM周长的最小值.
(2)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.
13.(2025春 法库县期末)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与y轴交于点D,与正比例函数y=2x的图象相交于点C,点C的横坐标为1.
【基本问题】
(1)求k,b的值;
【问题探究】
(2)①M为射线CB(点C除外)上一点,过点M作y轴的平行线交y=2x于点N,设点M的横坐标为m,线段MN的长度为W,请求出W与m之间的函数关系式;
②当MN<2DO时,直接写出m的取值范围.
【问题拓展】
(3)在x轴上是否存在一点P,满足△APC是等腰三角形?若存在请直接写出点P的坐标,若不存在,请说明理由.
14.(2025春 金牛区校级期末)如图,直线y=x+2与坐标轴交于A,B两点,点C坐标为,将B点向右平移4个单位,再向下平移1个单位得到点D,直线CD交直线AB于点E.
(1)求直线CD的表达式;
(2)点F是直线AB上第一象限内一点,在△EFD中有一个内角是45°,求点F的坐标;
(3)在(2)的条件下,当点F的横坐标大于时,作点B关于x轴的对称点B′,点P为直线FD上的一个动点,连接AP,点Q为线段AP的中点,连接B'Q,当AP+2B'Q最小时,求点Q的坐标.
15.(2025春 东城区期末)在平面直角坐标系中,给出如下定义:P为图形M上任意一点,如果点P到直线EF的距离等于图形M上任意两点距离的最大值时,那么点P称为直线EF的“伴随点”.例如:如图①,已知点A(1,2),B(3,2),P(2,2)在线段AB上,则点P是直线EF:x轴的“伴随点”.
(1)如图②,已知点A(1,0),B(3,0),P是线段AB上一点,直线EF过点G(﹣1,0),且与x轴的夹角∠FGO=30°,当点P是直线EF的“伴随点”时,点P的坐标为 ;
(2)如图③,x轴上方有一等边三角形ABC,BC⊥y轴,顶点A在y轴上且在BC上方,,点P是△ABC上一点,且点P是直线EF:x轴的“伴随点”,当点P到x轴的距离最小时,求等边三角形ABC的边长;
(3)如图④,以A(1,0),B(2,0),C(2,1)为顶点的正方形ABCD上始终存在点P,使得点P是直线EF:y=﹣x+b的“伴随点”,请直接写出b的取值范围.
【攻克压轴大题】2025年中考数学压轴题精选:一次函数
参考答案与试题解析
一.解答题(共15小题)
1.(2025春 重庆期末)如图1,在平面直角坐标系中,直线l1交y轴于点A,交x轴于点B,∠ABO=30°.直线l2:yx+6经过点A,交x轴于点C.
(1)求直线l1的解析式;
(2)如图2,点D是y轴负半轴上一动点,点E是x轴上一动点,若S△ACD=10,求DEBE的最小值;
(3)如图3,点P是直线l2上的一个动点,过点P作y轴的平行线交直线l1于点Q,平面内有一个动点M,若以C,P,Q,M为顶点的四边形是菱形,请直接写出点M的坐标.
【解答】解:(1)直线l2:yx+6经过点A,交x轴于点C,则点A、C的坐标分别为:(0,6)、(2,0),
在Rt△ABO中,OA=6,则AB=12,OB=6,即点B(﹣6,0),
设直线l1的解析式为:y=kx+6,
将点B的坐标代入上式得:0=﹣6k+6,则k,
则直线l1的解析式yx+6;
(2)S△ACD=10AD×COAD×2,
则AD=10,
过点D作DH⊥AB于点H,
∵∠ABC=30°,则HEBE,
此时DEBE=DE+HE=DH为最小,
在Rt△DHA中,∠BAO=60°,AD=10,
则AH=5,DH=5,
即DEBE的最小值为5;
(3)设点P(m,m+6),则点Q(m,m+6),点C(2,0),
则PQ=|m|,QC2=(m﹣2)2+(m+6)2,PC2=(m+6)2+(m﹣2)2,
当点P在AB的下方时,
则PQ=PC,即(|m|)2=(m+6)2+(m﹣2)2,
解得:m=12﹣6(不合题意的值已舍去),
则点P、Q的坐标分别为:(12﹣6,24﹣12)、(12﹣6,4),
由中点坐标公式得,点M(﹣2,1624);
当点P在AB的上方时,则PQ=CQ,
即(|m|)2=(m﹣2)2+(m+6)2,
解得:m=﹣2(不合题意的值已舍去),
则点P、Q的坐标分别为:(﹣2,12)、(﹣2,4),
由中点坐标公式得,点M(2,8);
综上,M(﹣2,1624)或(2,8).
2.(2025春 长安区期末)如图1,在平面直角坐标系中,直线yx+4分别与x轴、y轴交于点A、点B,将△AOB绕坐标原点逆时针旋转90°得到△COD,直线CD交直线AB于点E.
(1)直线CD的函数表达式为 yx+3 ;
(2)如图2,连接OE,过点O作OF⊥OE交直线CD于点F,求证:∠OEF=45°;
(3)若点P是直线DC上一点,点Q是x轴上一点(点Q不与点O重合),当△DPQ与△DOC全等时,直接写出点P的坐标.
【解答】(1)解:∵直线yx+4交x轴,y轴分别于点A,点B,
∴A(3,0),B(0,4),
∴OA=3,OB=4,
∵△AOB绕坐标原点逆时针旋转90°得到△COD,
∴△AOB≌△COD,
∴CO=OA=3,OD=OB=4,
∴C(0,3),D(﹣4,0),
设直线CD 的解析式为y=kx+b,
∴,解得,
∴直线CD 的解析式为yx+3,
故答案为:yx+3;
(2)证明:①由(1)知,△AOB≌△COD,
∴OB=OD,∠ABO=∠CDO,
∵OF⊥OE,∠COF+∠BOE=90°,
∵∠COE+∠DOF=90°,
∴∠BOE=∠DOF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴OE=OF,
∵∠EOF=90°,
∴△EOF是等腰直角三角形,
∴∠OEF=45°;
(3)解:如图1,
①∠DP'Q'=90°,
∵△P'Q'D≌△OCD,
∴DP'=OD=4,
∵CO=3,OD=4,
∴CD=Q'D=5,P'Q'=CO=3,
∴DQ' P'HP′Q' DP',
∴P'H,
作P'H⊥x轴,则DH,
∴OH=OD+DH,
∴点P'坐标(,);
②∠DQP=90°,
∵△PQD≌△COD,(SAS)
∴DQ=OD=4,PQ=3,
∴点P坐标(﹣8,﹣3);
③∠DP''Q''=90°,
∵△P''Q''D≌△OCD,(SAS)
∴DP''=OD=4,P''Q''=OC=3,
∴P''G,DG,
∴OG,
∴点P坐标(,);
即:△DPQ和△DOC全等时,点P的坐标为(,)或(﹣8,﹣3)或(,).
3.(2025春 黄陂区月考)如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足(b﹣2)2=0,直线y=x交AB于点M.
(1)求直线AB的解析式;
(2)如图1,直线x=m⊥x轴于C,分别交直线AB、直线y=x于D、E,若DE=3,求m值;
(3)如图2,在直线y=x上是否存在一点F,使得S△ABF=6?若存在,求出点F的坐标;若不存在,请说明理由.
【解答】解:(1)∵(b﹣2)2=0,
∴a﹣4=0,b﹣2=0,
∴a=4,b=2,
∴A(4,0),B(0,2),
设直线AB的解析式为y=kx+m,
∴,
∴,
∴直线AB的解析式为yx+2;
(2)设D(m,),E(m,m),
∵DE=3,
∴m﹣(m﹣2)=3,或,
解得m或m;
(3)存在点F,
∵F在y=x上,
∴设F(a,a) ①如图2,若F在AB的下方,
∵S△AOB=4,S△ABD=6,
∴F在MO的延长线上,
∴S△AOF+S△BOF+S△AOB=S△ABF,
∴(AO+BO)|a|+4=6,
∴6a=2,
解得:a,
∴F(,),
②若D在AB的上方同理求得F′(,),
即F(,)或(,).
4.(2025春 上海校级期末)如图,已知函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.
①点M在线段AO上,若△PQB的面积为2,求点P的坐标;
②点M在线段AC上运动的过程中,联结BM,若∠BMP=∠BAC,请直接写出点Q的坐标.
【解答】解:(1)在yx+3中,令x=0得y=3,令y=0得x=﹣6,
∴A(﹣6,0),B(0,3),
∵点C与点A关于y轴对称,
∴C(6,0),
设直线BC的函数解析式为y=kx+b,把B(0,3),C(6,0)代入得:
,
解得,
∴直线BC的函数解析式为yx+3;
(2)①设M(m,0),则P(m,m+3),Q(m,m+3),
∴PQm+3﹣(m+3)=﹣m,
∵△PQB的面积为2,
∴PQ |xM|=2,即(﹣m) (﹣m)=2,
解得m=2(此时M不在线段AO上,舍去)或m=﹣2,
∴P(﹣2,2);
②设Q(t,t+3),
当M在线段AO上时,过B作BH⊥PQ于H,如图:
∵∠BHM=∠HMO=∠MOB=90°,
∴四边形BOMH是矩形,
∴HM=OB=3,
∵∠BHM=90°=∠BOA,∠BMP=∠BAC,
∴△BHM∽△BOA,
∴,即,
解得t,
∴Q(,);
当P在线段OC上时,如图:
同理可得Q(,);
综上所述,Q的坐标为(,)或(,).
5.(2025春 衡阳期末)如图1,平面直角坐标系中,一次函数yx+2的图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C.
(1)直线BC的表达式为 y=﹣x+2 ,并直接写出点A的坐标 (﹣4,0) ,点C的坐标 (2,0) ;
(2)若点F为直线BC上的动点,当∠FAB=∠ABO时,请求出点F的坐标;
(3)如图2,已知点D(1,0),点F在直线BC上运动,连接DF,直线DF与直线AB交于点E,当△CDF与△BEF面积相等时,求出点E的坐标.
【解答】解:(1)在yx+2中,令x=0得y=2,
∴点B坐标为(0,2),
将点B坐标代入y=﹣x+b得:b=2,
∴直线BC的解析式为y=﹣x+2;
在yx+2中,令y=0得x=﹣4
∴点A坐标为(﹣4,0);
y=﹣x+2中,令y=0得x=2,
∴点C坐标为(2,0),
故答案为:y=﹣x+2,(﹣4,0),(2,0);
(2)当F在AB上方时,如图:
∵∠FAB=∠ABO,
∴AF∥y轴,
在y=﹣x+2中,令x=﹣4得y=6,
∴F(﹣4,6);
当F在AB下方时,设AF交y轴于K,如图:
设K(0,t),
∵∠FAB=∠ABO,
∴AK=BK,
∴16+t2=(2﹣t)2,
解得t=﹣3,
∴K(0,﹣3),
由A(﹣4,0),K(0,﹣3)得直线AF解析式为yx﹣3,
联立,
解得,
∴F(20,﹣18);
综上所述,F的坐标为(﹣4,6)或(20,﹣18);
(3)如图:
∵S△CDF=S△BEF,
∴S△CDF+S四边形ABFD=S△BEF+S四边形ABFD,即S△ABC=S△ADE,
∵A(﹣4,0),C(2,0),B(0,2),
∴S△ABCAC OB(2+4)×2=6,
设E(m,m+2),
∵D(1,0),
∴(1+4) (m+2)=6,
解得m,
∴点E的坐标为(,).
6.(2025春 垫江县月考)如图1,函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)如图1,若点P是直线AB上一动点,过点P作y轴的平行线,交直线BC于点Q.若△ABQ的面积为3,求点P的坐标;
(3)如图2,若点M是线段AC的一个动点,过点M作y轴的平行线,交直线AB于点N,连接BM,在点M的运动过程中是否存在∠BMN=∠BAC的情况,若存在,请求出点N坐标;若不存在,请说明理由.
【解答】解:(1)在yx+3中,令x=0得y=3,令y=0得x=﹣6,
∴A(﹣6,0),B(0,3),
∵点C与点A关于y轴对称,
∴C(6,0),
设直线BC解析式为y=kx+b,
把B(0,3),C(6,0)代入得:,
解得,
∴直线BC解析式为yx+3;
(2)设P(m,m+3),则Q(m,m+3),
∴PQ=|m+3﹣(m+3)|=|m|,
∵△ABQ的面积为3,
∴PQ |xA﹣xB|=3,即|m|×6=3,
解得m=1或m=﹣1,
∴P的坐标为(1,)或(﹣1,);
(3)在点M的运动过程中存在∠BMN=∠BAC的情况,理由如下:
设M(t,0),则N(t,t+3),
∵MN∥y轴,
∴∠BMN=∠MBO,
∵∠BMN=∠BAC,
∴∠MBO=∠BAC,
∵∠MOB=90°=∠BAO,
∴△MOB∽△BOA,
∴,即,
∴t或t,
∴N的坐标为(,)或(,).
7.(2025 新兴县一模)【模型建立】
如图1,三个直角三角形的直角顶点都在同一条直线上,这一模型叫作“一线三垂直”型.这种模型是证明三角形全等的常见模型,在数学解题中被广泛使用.如图,一次函数y=﹣x+10的图象与x轴、y轴分别交于B,A两点.
【模型探索】
(1)如图2,求证:△AOB是等腰直角三角形.
(2)如图3,M,N是直线y=kx上的两动点,连接BM,AN.若BM⊥MN,BM=6,求AN的长的最小值.
【模型应用】
(3)如图4,经过点B的直线与y轴交于点C,H为线段OB上的一点,作射线CH.若∠BCH=45°,求直线CH的函数解析式.
【解答】(1)证明:对于y=﹣x+10,当x=0时,y=10,当y=0时,x=10,
即点A、B的坐标分别为:(0,10)、(10,0),
则OA=OB,∠AOB为直角,
故△AOB是等腰直角三角形.
(2)解:当AN⊥MN时,AN最小,
由“一线三垂直”模型知,△ANO≌△OMB,
则AN=OM,
在Rt△BOM中,OB=10,BM=6,则OM=8=AN,
即AN的长的最小值为8.
(3)解:过点B作BT⊥CH于点T,则△BTC为等腰直角三角形,
过点T作MN⊥y轴交于点N,交过点B和y轴的平行线于点M,
则∠NTO=∠VTB=∠TMB=90°,BT=CT,
由“一线三垂直”模型知,△ONT≌△TMB,设点T(x,y),
则ON=TM,TN=BM,即10﹣x=y+5且x=y,
解得:x=y=2.5,即点T(2.5,2.5),
由点C(0,﹣5)和点T的坐标得,直线CH的表达式为:y=3x﹣5.
8.(2025春 福田区校级期末)如图,直线与坐标轴交于A、B两点,点C与点A关于y轴对称.CD⊥x轴与直线AB交于点D.
(1)求点A和点B的坐标;
(2)点P在直线CD上,且△ABP的面积为,
①求出点P的坐标;
②点Q为平面内一点,当点P在直线AB下方时,以点A、B、P、Q为顶点的四边形是平行四边形,请直接写出所有符合要求的点Q坐标.
【解答】解:(1)对于yx,令x=0,则y,令y=0,解得x=﹣2,
故点A、B的坐标分别为(﹣2,0)、(0,);
(2)①设直线AP交y轴于点H,
设直线AP的表达式为:y=k(x+2),
当x=0时,y=2k,当x=2时,y=4k,
即点H、P的坐标分别为(0,2k),(2,4k),
则△ABP的面积=S△HBP+S△HBAAC BH4(2k),
解得:k,
∴点P的坐标为(2,);
当点P在点D的上方时,根据对称性可知P(2,),
综上所述,点P的坐标为(2,)或(2,),
②由(1)(2)知,P(2,),A(﹣2,0),B(0,),设点Q(s,t),
∵点A、B、P、Q为顶点的四边形是平行四边形,
∴①Ⅰ、以AP为对角线,由中点坐标公式得,
∴,
∴点Q(0,﹣3),
Ⅱ、以AB为对角线,由中点坐标公式得,
∴,
∴点Q(﹣4,3);
Ⅲ、以AQ为对角线,由中点坐标公式得,
∴,
∴Q(4,0),
综上所述,以点A、B、P、Q为顶点的四边形是平行四边形,点Q坐标为(0,﹣3)或(﹣4,3)或(4,0).
9.(2025春 鲤城区校级期末)已知:如图,一次函数的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx﹣6的图象相交于点D,直线CD与y轴相交于点E.
(1)直线CD的函数表达式为: y=3x﹣6 ;点D的坐标为 (4,6) ;(直接写出结果)
(2)点Q为线段DE上的一个动点,连接BQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;
②点Q是否存在某个位置,将△BDE沿着直线BQ翻折,使得点D恰好落在直线AB下方的y轴上?若存在,请求出点Q的坐标;若不存在,请说明理由.
【解答】解:(1)把C(2,0)代入y=kx﹣6得,
0=2k﹣6,
∴k=3,
∴直线CD的解析式为y=3x﹣6.
解得,
∴D(4,6);
故答案为:y=3x﹣6,(4,6);
(2)①∵直线BQ将△BDE的面积分为1:2两部分,
∴S△BED或S△BEQS△BDE,
在yx+3中,当x=0时,y=3;当x=4时,y=6,
∴B(0,3),D(4,6),
在y=3x﹣6中,当x=0时,y=﹣6,
∴E(0,﹣6),
∴BE=9,
如图1中,过点D作DH⊥y轴于点H,则DH=4.
∴S△BDEBE DH9×4=18,
∴S△BEQ18=6或S△BED18=12,
设Q(t,3t﹣6),由题意知t>0.
过点Q作QM⊥y轴于点M,则QM=t.
∴或,
解得t或.
当t时,3t﹣6=﹣2;当t时3t﹣6=2.
∴Q的坐标为(,﹣2)或(,2);
②当点D落在y轴负半轴上(记为点D2)时,如图3中.
过点Q作QM⊥BD,QN⊥OB,垂足分别为点M、N.
由翻折得∠DBQ=∠D2BQ.
∴QM=QN.
由(2)知S△BDE=18,即S△BQD+S△BQE=18.
∴BD QMBE QN=18,
在Rt△BDH中,由勾股定理,得BD5,
∴,
解得QN,
∴点Q的横坐标为,
在y=3x﹣6中,当x18时,y,
∴Q().
10.(2025春 万州区期末)如图1,函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)如图1,若点P是直线AB上一动点,过点P作y轴的平行线,交直线BC于点Q.若△ABQ的面积为3,求点P的坐标;
(3)如图2,若点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点N,连接BM,在点M的运动过程中是否存在∠BMN=∠BAC的情况,若存在,请求出点N坐标;若不存在,请说明理由.
【解答】解:(1)对于yx+3,
当x=0时,y=3,
当y=0时,0x+3,
解得:x=﹣6,
∴点B(0,3),A(﹣6,0),
∵点C与点A关于y轴对称,
∴点C(6,0),
设直线BC的解析式为y=kx+b(k≠0),
∴,
解得,
∴直线BC的解析式为yx+3;
(2)如图1,①延长QP交x轴于点D,
设D(m,0),则点P(m,m+3),Q(m,m+3),
则PQ=|m+3﹣(m+3)=|m|,
∵△ABQ的面积为3,
∴PQ AO|m|×6=3,
解得:m=±1,
∴点P的坐标为(1,)或(﹣1,);
(3)如图2,当点M在y轴的左侧时,
∵点C与点A关于y轴对称,
∴AB=BC,
∴∠BAC=∠BCA,
∵∠BMN=∠BAC,
∴∠BMP=∠BCA,
∵∠BMN+∠BMC=90°,
∴∠BCA+∠BMC=90°,
∴∠MBC=180°﹣(∠BMC+∠BCA)=90°,
∴BM2+BC2=MC2,
设M(x,0),则N(x,x+3),
∴BM2=OM2+OB2=x2+9,MC2=(6﹣x)2,BC2=OC2+OB2=62+32=45,
∴x2+9+45=(6﹣x)2,
解得:x,
∴N(,),
当点M在y轴的右侧时,
同理可得N(,),
综上所述,点N的坐标为(,)或(,).
11.(2024秋 寿阳县期末)综合与探究
如图,在平面直角坐标系中,直线m:y=x﹣1与x轴、y轴分别交于点A,B,直线n:y=﹣2x+b经过点A,并与y轴交于点C.
(1)求A,B两点的坐标及b的值.
(2)若动点P在直线AC上运动,
①当时,求点P的坐标;
②当点P与点C重合时,在第一象限内是否存在一点Q,使△APQ为等腰直角三角形,若存在直接写出点Q的坐标;若不存在说明理由.
【解答】解:(1)直线m:y=x﹣1,令y=0,则x=1,
∴点A的坐标为(1,0),
令x=0,则y=﹣1,
∴点B的坐标为(0,﹣1),
将A(1,0)代入直线n:y=﹣2x+b,得0=﹣2+b,
解得b=2;
(2)①由(1)知,直线AC的表达式为y=﹣2x+2,
∴C(0,2),
∴S△ABCBC OA(1+2)×1,
设点P(t,﹣2t+2),
∵S△AOPS△ABC,
∴S△AOP1×|﹣2t+2|,
解得t或,
∴点P的坐标为(,)或(,);
②当点P与点C重合时,P(0,2),
在第一象限内存在一点Q,使△APQ为等腰直角三角形,分∠AQP=90°,AQ=PQ;∠QAP=90°,AQ=AP;∠APQ=90°,AP=QP三种情况,
当∠AQP=90°,AQ=PQ时,过点Q作y轴的平行线交x轴于点D,交过点P与x轴平行的直线于点E,
设点Q(m,n),而点A、P的坐标分别为:(1,0)、(0,2),
∵∠PQE+∠AQD=90°,∠QAD+∠AQD=90°,
∴∠QAD=∠PQE,
又∵∠ADQ=∠QEP=90°,AQ=QP,
∴△ADQ≌△QEP(AAS),
∴PE=QD,EQ=DA,
∴,解得,
∴点Q的坐标为(,);
当∠QAP=90°,AQ=AP时,过点Q作QD⊥x轴于点D,
设点Q(m,n),而点A、P的坐标分别为:(1,0)、(0,2),
同理得△ADQ≌△POA(AAS),
∴AD=PO=2,DQ=OA=1,
∴OD=3,
∴点Q的坐标为(3,1);
当∠APQ=90°,AP=QP时,过点Q作QD⊥y轴于点D,
设点Q(m,n),而点A、P的坐标分别为:(1,0)、(0,2),
同理得△QDP≌△POA(AAS),
∴QD=PO=2,DP=OA=1,
∴OD=3,
∴点Q的坐标为(2,3);
综上,点Q的坐标为(,)或(3,1)或(2,3).
12.(2025春 西山区校级期末)如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.
(1)若△APD为等腰直角三角形.
①求直线AP的函数解析式;
②在x轴上另有一点G的坐标为(2,0),请在直线AP上找一点M,使△GEM的周长最小,并求出此时点M的坐标和△GEM周长的最小值.
(2)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.
【解答】解:(1)①∵矩形OABC,OA=3,OC=2,
∴A(3,0),C(0,2),B(3,2),
∴AO∥BC,AO=BC=3,∠B=90°,CO=AB=2,
∵△APD为等腰直角三角形,
∴∠PAD=45°,
∵AO∥BC,
∴∠BPA=∠PAD=45°,
∵∠B=90°,
∴∠BAP=∠BPA=45°,
∴BP=AB=2,
∴P(1,2),
设直线AP解析式y=kx+b,
∴,
∴,
∴直线AP解析式y=﹣x+3;
②作点G关于直线AP对称点G'(3,1),
连接G'E交直线AP于M,此时△GEM周长的最小.
∵PB=AB=2,BC=OA=3,
∴PC=CE=1,
∴OE=OC﹣CE=1,
∴E(0,1),
∴EG′∥OA,
∴EG′=3,
∴△GEM周长的最小值=EG′+EG=33,
把y=1代入y=﹣x+3得,x=2,
∴M(2,1);
(2)如图:作PM⊥AD于M,
∵BC∥OA,
∴∠CPD=∠PDA且∠CPD=∠APB,
∴PD=PA,且PM⊥AD,
∴DM=AM,
∵四边形PAEF是平行四边形,
∴PD=DE,
又∵∠PMD=∠DOE,∠ODE=∠PDM,
∴△PMD≌△ODE(AAS),
∴OD=DM,OE=PM,
∴OD=DM=MA,
∵PM=2,OA=3,
∴OE=2,OM=2,
∴E(0,﹣2),P(2,2),
设直线PE的解析式y=mx+n,
则,
∴,
∴直线PE解析式y=2x﹣2.
13.(2025春 法库县期末)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与y轴交于点D,与正比例函数y=2x的图象相交于点C,点C的横坐标为1.
【基本问题】
(1)求k,b的值;
【问题探究】
(2)①M为射线CB(点C除外)上一点,过点M作y轴的平行线交y=2x于点N,设点M的横坐标为m,线段MN的长度为W,请求出W与m之间的函数关系式;
②当MN<2DO时,直接写出m的取值范围.
【问题拓展】
(3)在x轴上是否存在一点P,满足△APC是等腰三角形?若存在请直接写出点P的坐标,若不存在,请说明理由.
【解答】解:(1)在y=2x中,令x=1得y=2,
∴C(1,2),
把A(﹣2,6),C(1,2)代入y=kx+b得:
,
解得,
∴k的值是,b的值是;
(2)①∵M为射线CB(点C除外)上一点,设点M的横坐标为m,
∴,
∵MN∥y轴,
∴N(m,2m),
∴W=Ny﹣My=2m;
②由(1)知,直线AB的解析式为yx,
令x=0得y,
∴D(0,),
∴OD,
设M(m,m),则N(m,2m),
∵MN<2DO,
∴2m2,
解得m<3;
(3)设P(a,0),
∵A(﹣2,6),C(1,2),
∴AC5,AP,PC,
∵△APC是等腰三角形,
∴①当AC=AP时,即5,
此方程无解;故这种情况不存在;
②当AC=PC时,即5,
解得a=1±,
∴P(1,0)或(1,0);
③当PC=AP时,即,
解得a,
∴P(,0),
综上所述,存在点P,满足△APC是等腰三角形,点P的坐标(1,0)或(1,0)或(,0).
14.(2025春 金牛区校级期末)如图,直线y=x+2与坐标轴交于A,B两点,点C坐标为,将B点向右平移4个单位,再向下平移1个单位得到点D,直线CD交直线AB于点E.
(1)求直线CD的表达式;
(2)点F是直线AB上第一象限内一点,在△EFD中有一个内角是45°,求点F的坐标;
(3)在(2)的条件下,当点F的横坐标大于时,作点B关于x轴的对称点B′,点P为直线FD上的一个动点,连接AP,点Q为线段AP的中点,连接B'Q,当AP+2B'Q最小时,求点Q的坐标.
【解答】解:(1)在y=x+2中,当x=0时,y=0+2=2.
∴B(0,2),
将B(0,2)点向右平移4个单位,再向下平移1个单位得到点D,
∴D(4,1),
设直线CD的解析式为y=kx+b,
∴,
解得,
∴直线CD的解析式为yx;
(2)如图,∠EFD=45°时,
在y=x+2中,当y=0时,x=﹣2,
∴A(﹣2,0),
∴OA=OB=2,
∴∠OBA=45°,
∴∠OBA=∠EFD,
∴FD∥OB,
∴点F的横坐标为4,
∴F(4,6),
如图,当∠EDF=45°时,过点E作EH⊥ED,且EH=ED,过点E作GT∥y轴,分别过点H,D作GT的垂线,垂足别为G、T,
联立直线AB和CD:,
解得:,
∴E(1,3),
∴ET=2,DT=3,
∵EH⊥ED,∠EDH=45°,
∴△EDH是等腰直角三角形,
∴HE=ED,
∵∠G=∠T=90°,
∴∠GEH+∠TED=90°=∠TED+∠TDE,
∴∠GEH=∠TDE,
∴△GEH≌△TDE(AAS),
∴GE=DT=3,GH=ET=2,
∴H(3,6),
设直线DH的解析式为:y=mx+n,
∴,
解得:,
∴直线DH的解析式为:y=﹣5x+21,
联立直线AB与DH解析式:,
解得:,
∴点F(,),
综上所述,F的坐标为(4,6)或(,);
(3)∵点B′是点B关于x轴的对称点,
∴B(0,﹣2),
∵点F的横坐标大于,
∴F(4,6),
∴直线FD为直线x=4,
∵点P在直线x=4上运动,
∴点P的横坐标为4,
∵点Q为AP的中点,
∴点Q的横坐标为1,AQAP,
∴点Q在直线x=1上运动,
如图所示,作点B′关于直线x=1的对称点M,连接QM,
∴M(2,﹣2),
由轴对称的性质可得B′Q=QM,
∵AP+2B′Q=2(AP+B′Q)=2(AQ+B′Q)=2(AQ+MQ).
∴当A、Q、M三点共线时,AQ+MQ最小,即此时AP+2B′Q最小,
设直线AM的解析式为y=sx+t,
∴,
解得:,
∴直线AM的解析式为yx﹣1,
当x=1时,y,
∴Q(1,).
15.(2025春 东城区期末)在平面直角坐标系中,给出如下定义:P为图形M上任意一点,如果点P到直线EF的距离等于图形M上任意两点距离的最大值时,那么点P称为直线EF的“伴随点”.例如:如图①,已知点A(1,2),B(3,2),P(2,2)在线段AB上,则点P是直线EF:x轴的“伴随点”.
(1)如图②,已知点A(1,0),B(3,0),P是线段AB上一点,直线EF过点G(﹣1,0),且与x轴的夹角∠FGO=30°,当点P是直线EF的“伴随点”时,点P的坐标为 (3,0) ;
(2)如图③,x轴上方有一等边三角形ABC,BC⊥y轴,顶点A在y轴上且在BC上方,,点P是△ABC上一点,且点P是直线EF:x轴的“伴随点”,当点P到x轴的距离最小时,求等边三角形ABC的边长;
(3)如图④,以A(1,0),B(2,0),C(2,1)为顶点的正方形ABCD上始终存在点P,使得点P是直线EF:y=﹣x+b的“伴随点”,请直接写出b的取值范围.
【解答】解:(1)AB线段上任意两点距离的最大值为3﹣1=2,即P到EF的距离为2,
过P作PC⊥EF于点C,
∵∠FGO=30°,
∴GP4,
∵点G(﹣1,0),
∴OG=1,
∴P(3,0).
故答案为:(3,0),
(2)设等边三角形△ABC的边长为2a(0<a),则C(a,),
△ABC上任意两点距离的最大值即为2a,
当P在线段BC上时,P到x轴的距离最小,距离为,由题意知,
2a,
解得,a=1或﹣1(舍去),
所以此时等边三角形ABC的边长为2.
(3)由题意知,正方形ABCD的边长为1,
所以正方形ABCD上任意两点距离的最大值为,
即正方形ABCD上始终存在点P,P到EF的距离为.
则EF向上或者向下平移2个单位长度得到直线l1,l1与EF平行,且两直线间的距离为,
所以P既在l1上,又在正方形ABCD的边上,即l1与正方形ABCD有交点.
当b≤1时,l1为y=﹣x+b+2,
当l1过A时,b=﹣1,
当l1过C时,b=1,
即﹣1≤b≤1;
当b>1时,l1为y=﹣x+b﹣2,
当l1过A时,b=3,
当l1过C时,b=5,
即3≤b≤5;
综上所述,当﹣1≤b≤1或3≤b≤5时,正方形ABCD上始终存在点P,使得点P是直线EF:y=﹣x+b的“伴随点”.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【攻克压轴大题】2025年中考数学压轴题精选:一次函数
1.(2025春 重庆期末)如图1,在平面直角坐标系中,直线l1交y轴于点A,交x轴于点B,∠ABO=30°.直线l2:yx+6经过点A,交x轴于点C.
(1)求直线l1的解析式;
(2)如图2,点D是y轴负半轴上一动点,点E是x轴上一动点,若S△ACD=10,求DEBE的最小值;
(3)如图3,点P是直线l2上的一个动点,过点P作y轴的平行线交直线l1于点Q,平面内有一个动点M,若以C,P,Q,M为顶点的四边形是菱形,请直接写出点M的坐标.
2.(2025春 长安区期末)如图1,在平面直角坐标系中,直线yx+4分别与x轴、y轴交于点A、点B,将△AOB绕坐标原点逆时针旋转90°得到△COD,直线CD交直线AB于点E.
(1)直线CD的函数表达式为 ;
(2)如图2,连接OE,过点O作OF⊥OE交直线CD于点F,求证:∠OEF=45°;
(3)若点P是直线DC上一点,点Q是x轴上一点(点Q不与点O重合),当△DPQ与△DOC全等时,直接写出点P的坐标.
3.(2025春 黄陂区月考)如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足(b﹣2)2=0,直线y=x交AB于点M.
(1)求直线AB的解析式;
(2)如图1,直线x=m⊥x轴于C,分别交直线AB、直线y=x于D、E,若DE=3,求m值;
(3)如图2,在直线y=x上是否存在一点F,使得S△ABF=6?若存在,求出点F的坐标;若不存在,请说明理由.
4.(2025春 上海校级期末)如图,已知函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.
①点M在线段AO上,若△PQB的面积为2,求点P的坐标;
②点M在线段AC上运动的过程中,联结BM,若∠BMP=∠BAC,请直接写出点Q的坐标.
5.(2025春 衡阳期末)如图1,平面直角坐标系中,一次函数yx+2的图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C.
(1)直线BC的表达式为 ,并直接写出点A的坐标 ,点C的坐标 ;
(2)若点F为直线BC上的动点,当∠FAB=∠ABO时,请求出点F的坐标;
(3)如图2,已知点D(1,0),点F在直线BC上运动,连接DF,直线DF与直线AB交于点E,当△CDF与△BEF面积相等时,求出点E的坐标.
6.(2025春 垫江县月考)如图1,函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)如图1,若点P是直线AB上一动点,过点P作y轴的平行线,交直线BC于点Q.若△ABQ的面积为3,求点P的坐标;
(3)如图2,若点M是线段AC的一个动点,过点M作y轴的平行线,交直线AB于点N,连接BM,在点M的运动过程中是否存在∠BMN=∠BAC的情况,若存在,请求出点N坐标;若不存在,请说明理由.
7.(2025 新兴县一模)【模型建立】
如图1,三个直角三角形的直角顶点都在同一条直线上,这一模型叫作“一线三垂直”型.这种模型是证明三角形全等的常见模型,在数学解题中被广泛使用.如图,一次函数y=﹣x+10的图象与x轴、y轴分别交于B,A两点.
【模型探索】
(1)如图2,求证:△AOB是等腰直角三角形.
(2)如图3,M,N是直线y=kx上的两动点,连接BM,AN.若BM⊥MN,BM=6,求AN的长的最小值.
【模型应用】
(3)如图4,经过点B的直线与y轴交于点C,H为线段OB上的一点,作射线CH.若∠BCH=45°,求直线CH的函数解析式.
8.(2025春 福田区校级期末)如图,直线与坐标轴交于A、B两点,点C与点A关于y轴对称.CD⊥x轴与直线AB交于点D.
(1)求点A和点B的坐标;
(2)点P在直线CD上,且△ABP的面积为,
①求出点P的坐标;
②点Q为平面内一点,当点P在直线AB下方时,以点A、B、P、Q为顶点的四边形是平行四边形,请直接写出所有符合要求的点Q坐标.
9.(2025春 鲤城区校级期末)已知:如图,一次函数的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx﹣6的图象相交于点D,直线CD与y轴相交于点E.
(1)直线CD的函数表达式为: ;点D的坐标为 ;(直接写出结果)
(2)点Q为线段DE上的一个动点,连接BQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;
②点Q是否存在某个位置,将△BDE沿着直线BQ翻折,使得点D恰好落在直线AB下方的y轴上?若存在,请求出点Q的坐标;若不存在,请说明理由.
10.(2025春 万州区期末)如图1,函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)如图1,若点P是直线AB上一动点,过点P作y轴的平行线,交直线BC于点Q.若△ABQ的面积为3,求点P的坐标;
(3)如图2,若点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点N,连接BM,在点M的运动过程中是否存在∠BMN=∠BAC的情况,若存在,请求出点N坐标;若不存在,请说明理由.
11.(2024秋 寿阳县期末)综合与探究
如图,在平面直角坐标系中,直线m:y=x﹣1与x轴、y轴分别交于点A,B,直线n:y=﹣2x+b经过点A,并与y轴交于点C.
(1)求A,B两点的坐标及b的值.
(2)若动点P在直线AC上运动,
①当时,求点P的坐标;
②当点P与点C重合时,在第一象限内是否存在一点Q,使△APQ为等腰直角三角形,若存在直接写出点Q的坐标;若不存在说明理由.
12.(2025春 西山区校级期末)如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.
(1)若△APD为等腰直角三角形.
①求直线AP的函数解析式;
②在x轴上另有一点G的坐标为(2,0),请在直线AP上找一点M,使△GEM的周长最小,并求出此时点M的坐标和△GEM周长的最小值.
(2)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.
13.(2025春 法库县期末)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与y轴交于点D,与正比例函数y=2x的图象相交于点C,点C的横坐标为1.
【基本问题】
(1)求k,b的值;
【问题探究】
(2)①M为射线CB(点C除外)上一点,过点M作y轴的平行线交y=2x于点N,设点M的横坐标为m,线段MN的长度为W,请求出W与m之间的函数关系式;
②当MN<2DO时,直接写出m的取值范围.
【问题拓展】
(3)在x轴上是否存在一点P,满足△APC是等腰三角形?若存在请直接写出点P的坐标,若不存在,请说明理由.
14.(2025春 金牛区校级期末)如图,直线y=x+2与坐标轴交于A,B两点,点C坐标为,将B点向右平移4个单位,再向下平移1个单位得到点D,直线CD交直线AB于点E.
(1)求直线CD的表达式;
(2)点F是直线AB上第一象限内一点,在△EFD中有一个内角是45°,求点F的坐标;
(3)在(2)的条件下,当点F的横坐标大于时,作点B关于x轴的对称点B′,点P为直线FD上的一个动点,连接AP,点Q为线段AP的中点,连接B'Q,当AP+2B'Q最小时,求点Q的坐标.
15.(2025春 东城区期末)在平面直角坐标系中,给出如下定义:P为图形M上任意一点,如果点P到直线EF的距离等于图形M上任意两点距离的最大值时,那么点P称为直线EF的“伴随点”.例如:如图①,已知点A(1,2),B(3,2),P(2,2)在线段AB上,则点P是直线EF:x轴的“伴随点”.
(1)如图②,已知点A(1,0),B(3,0),P是线段AB上一点,直线EF过点G(﹣1,0),且与x轴的夹角∠FGO=30°,当点P是直线EF的“伴随点”时,点P的坐标为 ;
(2)如图③,x轴上方有一等边三角形ABC,BC⊥y轴,顶点A在y轴上且在BC上方,,点P是△ABC上一点,且点P是直线EF:x轴的“伴随点”,当点P到x轴的距离最小时,求等边三角形ABC的边长;
(3)如图④,以A(1,0),B(2,0),C(2,1)为顶点的正方形ABCD上始终存在点P,使得点P是直线EF:y=﹣x+b的“伴随点”,请直接写出b的取值范围.
【攻克压轴大题】2025年中考数学压轴题精选:一次函数
参考答案与试题解析
一.解答题(共15小题)
1.(2025春 重庆期末)如图1,在平面直角坐标系中,直线l1交y轴于点A,交x轴于点B,∠ABO=30°.直线l2:yx+6经过点A,交x轴于点C.
(1)求直线l1的解析式;
(2)如图2,点D是y轴负半轴上一动点,点E是x轴上一动点,若S△ACD=10,求DEBE的最小值;
(3)如图3,点P是直线l2上的一个动点,过点P作y轴的平行线交直线l1于点Q,平面内有一个动点M,若以C,P,Q,M为顶点的四边形是菱形,请直接写出点M的坐标.
【解答】解:(1)直线l2:yx+6经过点A,交x轴于点C,则点A、C的坐标分别为:(0,6)、(2,0),
在Rt△ABO中,OA=6,则AB=12,OB=6,即点B(﹣6,0),
设直线l1的解析式为:y=kx+6,
将点B的坐标代入上式得:0=﹣6k+6,则k,
则直线l1的解析式yx+6;
(2)S△ACD=10AD×COAD×2,
则AD=10,
过点D作DH⊥AB于点H,
∵∠ABC=30°,则HEBE,
此时DEBE=DE+HE=DH为最小,
在Rt△DHA中,∠BAO=60°,AD=10,
则AH=5,DH=5,
即DEBE的最小值为5;
(3)设点P(m,m+6),则点Q(m,m+6),点C(2,0),
则PQ=|m|,QC2=(m﹣2)2+(m+6)2,PC2=(m+6)2+(m﹣2)2,
当点P在AB的下方时,
则PQ=PC,即(|m|)2=(m+6)2+(m﹣2)2,
解得:m=12﹣6(不合题意的值已舍去),
则点P、Q的坐标分别为:(12﹣6,24﹣12)、(12﹣6,4),
由中点坐标公式得,点M(﹣2,1624);
当点P在AB的上方时,则PQ=CQ,
即(|m|)2=(m﹣2)2+(m+6)2,
解得:m=﹣2(不合题意的值已舍去),
则点P、Q的坐标分别为:(﹣2,12)、(﹣2,4),
由中点坐标公式得,点M(2,8);
综上,M(﹣2,1624)或(2,8).
2.(2025春 长安区期末)如图1,在平面直角坐标系中,直线yx+4分别与x轴、y轴交于点A、点B,将△AOB绕坐标原点逆时针旋转90°得到△COD,直线CD交直线AB于点E.
(1)直线CD的函数表达式为 yx+3 ;
(2)如图2,连接OE,过点O作OF⊥OE交直线CD于点F,求证:∠OEF=45°;
(3)若点P是直线DC上一点,点Q是x轴上一点(点Q不与点O重合),当△DPQ与△DOC全等时,直接写出点P的坐标.
【解答】(1)解:∵直线yx+4交x轴,y轴分别于点A,点B,
∴A(3,0),B(0,4),
∴OA=3,OB=4,
∵△AOB绕坐标原点逆时针旋转90°得到△COD,
∴△AOB≌△COD,
∴CO=OA=3,OD=OB=4,
∴C(0,3),D(﹣4,0),
设直线CD 的解析式为y=kx+b,
∴,解得,
∴直线CD 的解析式为yx+3,
故答案为:yx+3;
(2)证明:①由(1)知,△AOB≌△COD,
∴OB=OD,∠ABO=∠CDO,
∵OF⊥OE,∠COF+∠BOE=90°,
∵∠COE+∠DOF=90°,
∴∠BOE=∠DOF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴OE=OF,
∵∠EOF=90°,
∴△EOF是等腰直角三角形,
∴∠OEF=45°;
(3)解:如图1,
①∠DP'Q'=90°,
∵△P'Q'D≌△OCD,
∴DP'=OD=4,
∵CO=3,OD=4,
∴CD=Q'D=5,P'Q'=CO=3,
∴DQ' P'HP′Q' DP',
∴P'H,
作P'H⊥x轴,则DH,
∴OH=OD+DH,
∴点P'坐标(,);
②∠DQP=90°,
∵△PQD≌△COD,(SAS)
∴DQ=OD=4,PQ=3,
∴点P坐标(﹣8,﹣3);
③∠DP''Q''=90°,
∵△P''Q''D≌△OCD,(SAS)
∴DP''=OD=4,P''Q''=OC=3,
∴P''G,DG,
∴OG,
∴点P坐标(,);
即:△DPQ和△DOC全等时,点P的坐标为(,)或(﹣8,﹣3)或(,).
3.(2025春 黄陂区月考)如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足(b﹣2)2=0,直线y=x交AB于点M.
(1)求直线AB的解析式;
(2)如图1,直线x=m⊥x轴于C,分别交直线AB、直线y=x于D、E,若DE=3,求m值;
(3)如图2,在直线y=x上是否存在一点F,使得S△ABF=6?若存在,求出点F的坐标;若不存在,请说明理由.
【解答】解:(1)∵(b﹣2)2=0,
∴a﹣4=0,b﹣2=0,
∴a=4,b=2,
∴A(4,0),B(0,2),
设直线AB的解析式为y=kx+m,
∴,
∴,
∴直线AB的解析式为yx+2;
(2)设D(m,),E(m,m),
∵DE=3,
∴m﹣(m﹣2)=3,或,
解得m或m;
(3)存在点F,
∵F在y=x上,
∴设F(a,a) ①如图2,若F在AB的下方,
∵S△AOB=4,S△ABD=6,
∴F在MO的延长线上,
∴S△AOF+S△BOF+S△AOB=S△ABF,
∴(AO+BO)|a|+4=6,
∴6a=2,
解得:a,
∴F(,),
②若D在AB的上方同理求得F′(,),
即F(,)或(,).
4.(2025春 上海校级期末)如图,已知函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.
①点M在线段AO上,若△PQB的面积为2,求点P的坐标;
②点M在线段AC上运动的过程中,联结BM,若∠BMP=∠BAC,请直接写出点Q的坐标.
【解答】解:(1)在yx+3中,令x=0得y=3,令y=0得x=﹣6,
∴A(﹣6,0),B(0,3),
∵点C与点A关于y轴对称,
∴C(6,0),
设直线BC的函数解析式为y=kx+b,把B(0,3),C(6,0)代入得:
,
解得,
∴直线BC的函数解析式为yx+3;
(2)①设M(m,0),则P(m,m+3),Q(m,m+3),
∴PQm+3﹣(m+3)=﹣m,
∵△PQB的面积为2,
∴PQ |xM|=2,即(﹣m) (﹣m)=2,
解得m=2(此时M不在线段AO上,舍去)或m=﹣2,
∴P(﹣2,2);
②设Q(t,t+3),
当M在线段AO上时,过B作BH⊥PQ于H,如图:
∵∠BHM=∠HMO=∠MOB=90°,
∴四边形BOMH是矩形,
∴HM=OB=3,
∵∠BHM=90°=∠BOA,∠BMP=∠BAC,
∴△BHM∽△BOA,
∴,即,
解得t,
∴Q(,);
当P在线段OC上时,如图:
同理可得Q(,);
综上所述,Q的坐标为(,)或(,).
5.(2025春 衡阳期末)如图1,平面直角坐标系中,一次函数yx+2的图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C.
(1)直线BC的表达式为 y=﹣x+2 ,并直接写出点A的坐标 (﹣4,0) ,点C的坐标 (2,0) ;
(2)若点F为直线BC上的动点,当∠FAB=∠ABO时,请求出点F的坐标;
(3)如图2,已知点D(1,0),点F在直线BC上运动,连接DF,直线DF与直线AB交于点E,当△CDF与△BEF面积相等时,求出点E的坐标.
【解答】解:(1)在yx+2中,令x=0得y=2,
∴点B坐标为(0,2),
将点B坐标代入y=﹣x+b得:b=2,
∴直线BC的解析式为y=﹣x+2;
在yx+2中,令y=0得x=﹣4
∴点A坐标为(﹣4,0);
y=﹣x+2中,令y=0得x=2,
∴点C坐标为(2,0),
故答案为:y=﹣x+2,(﹣4,0),(2,0);
(2)当F在AB上方时,如图:
∵∠FAB=∠ABO,
∴AF∥y轴,
在y=﹣x+2中,令x=﹣4得y=6,
∴F(﹣4,6);
当F在AB下方时,设AF交y轴于K,如图:
设K(0,t),
∵∠FAB=∠ABO,
∴AK=BK,
∴16+t2=(2﹣t)2,
解得t=﹣3,
∴K(0,﹣3),
由A(﹣4,0),K(0,﹣3)得直线AF解析式为yx﹣3,
联立,
解得,
∴F(20,﹣18);
综上所述,F的坐标为(﹣4,6)或(20,﹣18);
(3)如图:
∵S△CDF=S△BEF,
∴S△CDF+S四边形ABFD=S△BEF+S四边形ABFD,即S△ABC=S△ADE,
∵A(﹣4,0),C(2,0),B(0,2),
∴S△ABCAC OB(2+4)×2=6,
设E(m,m+2),
∵D(1,0),
∴(1+4) (m+2)=6,
解得m,
∴点E的坐标为(,).
6.(2025春 垫江县月考)如图1,函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)如图1,若点P是直线AB上一动点,过点P作y轴的平行线,交直线BC于点Q.若△ABQ的面积为3,求点P的坐标;
(3)如图2,若点M是线段AC的一个动点,过点M作y轴的平行线,交直线AB于点N,连接BM,在点M的运动过程中是否存在∠BMN=∠BAC的情况,若存在,请求出点N坐标;若不存在,请说明理由.
【解答】解:(1)在yx+3中,令x=0得y=3,令y=0得x=﹣6,
∴A(﹣6,0),B(0,3),
∵点C与点A关于y轴对称,
∴C(6,0),
设直线BC解析式为y=kx+b,
把B(0,3),C(6,0)代入得:,
解得,
∴直线BC解析式为yx+3;
(2)设P(m,m+3),则Q(m,m+3),
∴PQ=|m+3﹣(m+3)|=|m|,
∵△ABQ的面积为3,
∴PQ |xA﹣xB|=3,即|m|×6=3,
解得m=1或m=﹣1,
∴P的坐标为(1,)或(﹣1,);
(3)在点M的运动过程中存在∠BMN=∠BAC的情况,理由如下:
设M(t,0),则N(t,t+3),
∵MN∥y轴,
∴∠BMN=∠MBO,
∵∠BMN=∠BAC,
∴∠MBO=∠BAC,
∵∠MOB=90°=∠BAO,
∴△MOB∽△BOA,
∴,即,
∴t或t,
∴N的坐标为(,)或(,).
7.(2025 新兴县一模)【模型建立】
如图1,三个直角三角形的直角顶点都在同一条直线上,这一模型叫作“一线三垂直”型.这种模型是证明三角形全等的常见模型,在数学解题中被广泛使用.如图,一次函数y=﹣x+10的图象与x轴、y轴分别交于B,A两点.
【模型探索】
(1)如图2,求证:△AOB是等腰直角三角形.
(2)如图3,M,N是直线y=kx上的两动点,连接BM,AN.若BM⊥MN,BM=6,求AN的长的最小值.
【模型应用】
(3)如图4,经过点B的直线与y轴交于点C,H为线段OB上的一点,作射线CH.若∠BCH=45°,求直线CH的函数解析式.
【解答】(1)证明:对于y=﹣x+10,当x=0时,y=10,当y=0时,x=10,
即点A、B的坐标分别为:(0,10)、(10,0),
则OA=OB,∠AOB为直角,
故△AOB是等腰直角三角形.
(2)解:当AN⊥MN时,AN最小,
由“一线三垂直”模型知,△ANO≌△OMB,
则AN=OM,
在Rt△BOM中,OB=10,BM=6,则OM=8=AN,
即AN的长的最小值为8.
(3)解:过点B作BT⊥CH于点T,则△BTC为等腰直角三角形,
过点T作MN⊥y轴交于点N,交过点B和y轴的平行线于点M,
则∠NTO=∠VTB=∠TMB=90°,BT=CT,
由“一线三垂直”模型知,△ONT≌△TMB,设点T(x,y),
则ON=TM,TN=BM,即10﹣x=y+5且x=y,
解得:x=y=2.5,即点T(2.5,2.5),
由点C(0,﹣5)和点T的坐标得,直线CH的表达式为:y=3x﹣5.
8.(2025春 福田区校级期末)如图,直线与坐标轴交于A、B两点,点C与点A关于y轴对称.CD⊥x轴与直线AB交于点D.
(1)求点A和点B的坐标;
(2)点P在直线CD上,且△ABP的面积为,
①求出点P的坐标;
②点Q为平面内一点,当点P在直线AB下方时,以点A、B、P、Q为顶点的四边形是平行四边形,请直接写出所有符合要求的点Q坐标.
【解答】解:(1)对于yx,令x=0,则y,令y=0,解得x=﹣2,
故点A、B的坐标分别为(﹣2,0)、(0,);
(2)①设直线AP交y轴于点H,
设直线AP的表达式为:y=k(x+2),
当x=0时,y=2k,当x=2时,y=4k,
即点H、P的坐标分别为(0,2k),(2,4k),
则△ABP的面积=S△HBP+S△HBAAC BH4(2k),
解得:k,
∴点P的坐标为(2,);
当点P在点D的上方时,根据对称性可知P(2,),
综上所述,点P的坐标为(2,)或(2,),
②由(1)(2)知,P(2,),A(﹣2,0),B(0,),设点Q(s,t),
∵点A、B、P、Q为顶点的四边形是平行四边形,
∴①Ⅰ、以AP为对角线,由中点坐标公式得,
∴,
∴点Q(0,﹣3),
Ⅱ、以AB为对角线,由中点坐标公式得,
∴,
∴点Q(﹣4,3);
Ⅲ、以AQ为对角线,由中点坐标公式得,
∴,
∴Q(4,0),
综上所述,以点A、B、P、Q为顶点的四边形是平行四边形,点Q坐标为(0,﹣3)或(﹣4,3)或(4,0).
9.(2025春 鲤城区校级期末)已知:如图,一次函数的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx﹣6的图象相交于点D,直线CD与y轴相交于点E.
(1)直线CD的函数表达式为: y=3x﹣6 ;点D的坐标为 (4,6) ;(直接写出结果)
(2)点Q为线段DE上的一个动点,连接BQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;
②点Q是否存在某个位置,将△BDE沿着直线BQ翻折,使得点D恰好落在直线AB下方的y轴上?若存在,请求出点Q的坐标;若不存在,请说明理由.
【解答】解:(1)把C(2,0)代入y=kx﹣6得,
0=2k﹣6,
∴k=3,
∴直线CD的解析式为y=3x﹣6.
解得,
∴D(4,6);
故答案为:y=3x﹣6,(4,6);
(2)①∵直线BQ将△BDE的面积分为1:2两部分,
∴S△BED或S△BEQS△BDE,
在yx+3中,当x=0时,y=3;当x=4时,y=6,
∴B(0,3),D(4,6),
在y=3x﹣6中,当x=0时,y=﹣6,
∴E(0,﹣6),
∴BE=9,
如图1中,过点D作DH⊥y轴于点H,则DH=4.
∴S△BDEBE DH9×4=18,
∴S△BEQ18=6或S△BED18=12,
设Q(t,3t﹣6),由题意知t>0.
过点Q作QM⊥y轴于点M,则QM=t.
∴或,
解得t或.
当t时,3t﹣6=﹣2;当t时3t﹣6=2.
∴Q的坐标为(,﹣2)或(,2);
②当点D落在y轴负半轴上(记为点D2)时,如图3中.
过点Q作QM⊥BD,QN⊥OB,垂足分别为点M、N.
由翻折得∠DBQ=∠D2BQ.
∴QM=QN.
由(2)知S△BDE=18,即S△BQD+S△BQE=18.
∴BD QMBE QN=18,
在Rt△BDH中,由勾股定理,得BD5,
∴,
解得QN,
∴点Q的横坐标为,
在y=3x﹣6中,当x18时,y,
∴Q().
10.(2025春 万州区期末)如图1,函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)如图1,若点P是直线AB上一动点,过点P作y轴的平行线,交直线BC于点Q.若△ABQ的面积为3,求点P的坐标;
(3)如图2,若点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点N,连接BM,在点M的运动过程中是否存在∠BMN=∠BAC的情况,若存在,请求出点N坐标;若不存在,请说明理由.
【解答】解:(1)对于yx+3,
当x=0时,y=3,
当y=0时,0x+3,
解得:x=﹣6,
∴点B(0,3),A(﹣6,0),
∵点C与点A关于y轴对称,
∴点C(6,0),
设直线BC的解析式为y=kx+b(k≠0),
∴,
解得,
∴直线BC的解析式为yx+3;
(2)如图1,①延长QP交x轴于点D,
设D(m,0),则点P(m,m+3),Q(m,m+3),
则PQ=|m+3﹣(m+3)=|m|,
∵△ABQ的面积为3,
∴PQ AO|m|×6=3,
解得:m=±1,
∴点P的坐标为(1,)或(﹣1,);
(3)如图2,当点M在y轴的左侧时,
∵点C与点A关于y轴对称,
∴AB=BC,
∴∠BAC=∠BCA,
∵∠BMN=∠BAC,
∴∠BMP=∠BCA,
∵∠BMN+∠BMC=90°,
∴∠BCA+∠BMC=90°,
∴∠MBC=180°﹣(∠BMC+∠BCA)=90°,
∴BM2+BC2=MC2,
设M(x,0),则N(x,x+3),
∴BM2=OM2+OB2=x2+9,MC2=(6﹣x)2,BC2=OC2+OB2=62+32=45,
∴x2+9+45=(6﹣x)2,
解得:x,
∴N(,),
当点M在y轴的右侧时,
同理可得N(,),
综上所述,点N的坐标为(,)或(,).
11.(2024秋 寿阳县期末)综合与探究
如图,在平面直角坐标系中,直线m:y=x﹣1与x轴、y轴分别交于点A,B,直线n:y=﹣2x+b经过点A,并与y轴交于点C.
(1)求A,B两点的坐标及b的值.
(2)若动点P在直线AC上运动,
①当时,求点P的坐标;
②当点P与点C重合时,在第一象限内是否存在一点Q,使△APQ为等腰直角三角形,若存在直接写出点Q的坐标;若不存在说明理由.
【解答】解:(1)直线m:y=x﹣1,令y=0,则x=1,
∴点A的坐标为(1,0),
令x=0,则y=﹣1,
∴点B的坐标为(0,﹣1),
将A(1,0)代入直线n:y=﹣2x+b,得0=﹣2+b,
解得b=2;
(2)①由(1)知,直线AC的表达式为y=﹣2x+2,
∴C(0,2),
∴S△ABCBC OA(1+2)×1,
设点P(t,﹣2t+2),
∵S△AOPS△ABC,
∴S△AOP1×|﹣2t+2|,
解得t或,
∴点P的坐标为(,)或(,);
②当点P与点C重合时,P(0,2),
在第一象限内存在一点Q,使△APQ为等腰直角三角形,分∠AQP=90°,AQ=PQ;∠QAP=90°,AQ=AP;∠APQ=90°,AP=QP三种情况,
当∠AQP=90°,AQ=PQ时,过点Q作y轴的平行线交x轴于点D,交过点P与x轴平行的直线于点E,
设点Q(m,n),而点A、P的坐标分别为:(1,0)、(0,2),
∵∠PQE+∠AQD=90°,∠QAD+∠AQD=90°,
∴∠QAD=∠PQE,
又∵∠ADQ=∠QEP=90°,AQ=QP,
∴△ADQ≌△QEP(AAS),
∴PE=QD,EQ=DA,
∴,解得,
∴点Q的坐标为(,);
当∠QAP=90°,AQ=AP时,过点Q作QD⊥x轴于点D,
设点Q(m,n),而点A、P的坐标分别为:(1,0)、(0,2),
同理得△ADQ≌△POA(AAS),
∴AD=PO=2,DQ=OA=1,
∴OD=3,
∴点Q的坐标为(3,1);
当∠APQ=90°,AP=QP时,过点Q作QD⊥y轴于点D,
设点Q(m,n),而点A、P的坐标分别为:(1,0)、(0,2),
同理得△QDP≌△POA(AAS),
∴QD=PO=2,DP=OA=1,
∴OD=3,
∴点Q的坐标为(2,3);
综上,点Q的坐标为(,)或(3,1)或(2,3).
12.(2025春 西山区校级期末)如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.
(1)若△APD为等腰直角三角形.
①求直线AP的函数解析式;
②在x轴上另有一点G的坐标为(2,0),请在直线AP上找一点M,使△GEM的周长最小,并求出此时点M的坐标和△GEM周长的最小值.
(2)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.
【解答】解:(1)①∵矩形OABC,OA=3,OC=2,
∴A(3,0),C(0,2),B(3,2),
∴AO∥BC,AO=BC=3,∠B=90°,CO=AB=2,
∵△APD为等腰直角三角形,
∴∠PAD=45°,
∵AO∥BC,
∴∠BPA=∠PAD=45°,
∵∠B=90°,
∴∠BAP=∠BPA=45°,
∴BP=AB=2,
∴P(1,2),
设直线AP解析式y=kx+b,
∴,
∴,
∴直线AP解析式y=﹣x+3;
②作点G关于直线AP对称点G'(3,1),
连接G'E交直线AP于M,此时△GEM周长的最小.
∵PB=AB=2,BC=OA=3,
∴PC=CE=1,
∴OE=OC﹣CE=1,
∴E(0,1),
∴EG′∥OA,
∴EG′=3,
∴△GEM周长的最小值=EG′+EG=33,
把y=1代入y=﹣x+3得,x=2,
∴M(2,1);
(2)如图:作PM⊥AD于M,
∵BC∥OA,
∴∠CPD=∠PDA且∠CPD=∠APB,
∴PD=PA,且PM⊥AD,
∴DM=AM,
∵四边形PAEF是平行四边形,
∴PD=DE,
又∵∠PMD=∠DOE,∠ODE=∠PDM,
∴△PMD≌△ODE(AAS),
∴OD=DM,OE=PM,
∴OD=DM=MA,
∵PM=2,OA=3,
∴OE=2,OM=2,
∴E(0,﹣2),P(2,2),
设直线PE的解析式y=mx+n,
则,
∴,
∴直线PE解析式y=2x﹣2.
13.(2025春 法库县期末)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与y轴交于点D,与正比例函数y=2x的图象相交于点C,点C的横坐标为1.
【基本问题】
(1)求k,b的值;
【问题探究】
(2)①M为射线CB(点C除外)上一点,过点M作y轴的平行线交y=2x于点N,设点M的横坐标为m,线段MN的长度为W,请求出W与m之间的函数关系式;
②当MN<2DO时,直接写出m的取值范围.
【问题拓展】
(3)在x轴上是否存在一点P,满足△APC是等腰三角形?若存在请直接写出点P的坐标,若不存在,请说明理由.
【解答】解:(1)在y=2x中,令x=1得y=2,
∴C(1,2),
把A(﹣2,6),C(1,2)代入y=kx+b得:
,
解得,
∴k的值是,b的值是;
(2)①∵M为射线CB(点C除外)上一点,设点M的横坐标为m,
∴,
∵MN∥y轴,
∴N(m,2m),
∴W=Ny﹣My=2m;
②由(1)知,直线AB的解析式为yx,
令x=0得y,
∴D(0,),
∴OD,
设M(m,m),则N(m,2m),
∵MN<2DO,
∴2m2,
解得m<3;
(3)设P(a,0),
∵A(﹣2,6),C(1,2),
∴AC5,AP,PC,
∵△APC是等腰三角形,
∴①当AC=AP时,即5,
此方程无解;故这种情况不存在;
②当AC=PC时,即5,
解得a=1±,
∴P(1,0)或(1,0);
③当PC=AP时,即,
解得a,
∴P(,0),
综上所述,存在点P,满足△APC是等腰三角形,点P的坐标(1,0)或(1,0)或(,0).
14.(2025春 金牛区校级期末)如图,直线y=x+2与坐标轴交于A,B两点,点C坐标为,将B点向右平移4个单位,再向下平移1个单位得到点D,直线CD交直线AB于点E.
(1)求直线CD的表达式;
(2)点F是直线AB上第一象限内一点,在△EFD中有一个内角是45°,求点F的坐标;
(3)在(2)的条件下,当点F的横坐标大于时,作点B关于x轴的对称点B′,点P为直线FD上的一个动点,连接AP,点Q为线段AP的中点,连接B'Q,当AP+2B'Q最小时,求点Q的坐标.
【解答】解:(1)在y=x+2中,当x=0时,y=0+2=2.
∴B(0,2),
将B(0,2)点向右平移4个单位,再向下平移1个单位得到点D,
∴D(4,1),
设直线CD的解析式为y=kx+b,
∴,
解得,
∴直线CD的解析式为yx;
(2)如图,∠EFD=45°时,
在y=x+2中,当y=0时,x=﹣2,
∴A(﹣2,0),
∴OA=OB=2,
∴∠OBA=45°,
∴∠OBA=∠EFD,
∴FD∥OB,
∴点F的横坐标为4,
∴F(4,6),
如图,当∠EDF=45°时,过点E作EH⊥ED,且EH=ED,过点E作GT∥y轴,分别过点H,D作GT的垂线,垂足别为G、T,
联立直线AB和CD:,
解得:,
∴E(1,3),
∴ET=2,DT=3,
∵EH⊥ED,∠EDH=45°,
∴△EDH是等腰直角三角形,
∴HE=ED,
∵∠G=∠T=90°,
∴∠GEH+∠TED=90°=∠TED+∠TDE,
∴∠GEH=∠TDE,
∴△GEH≌△TDE(AAS),
∴GE=DT=3,GH=ET=2,
∴H(3,6),
设直线DH的解析式为:y=mx+n,
∴,
解得:,
∴直线DH的解析式为:y=﹣5x+21,
联立直线AB与DH解析式:,
解得:,
∴点F(,),
综上所述,F的坐标为(4,6)或(,);
(3)∵点B′是点B关于x轴的对称点,
∴B(0,﹣2),
∵点F的横坐标大于,
∴F(4,6),
∴直线FD为直线x=4,
∵点P在直线x=4上运动,
∴点P的横坐标为4,
∵点Q为AP的中点,
∴点Q的横坐标为1,AQAP,
∴点Q在直线x=1上运动,
如图所示,作点B′关于直线x=1的对称点M,连接QM,
∴M(2,﹣2),
由轴对称的性质可得B′Q=QM,
∵AP+2B′Q=2(AP+B′Q)=2(AQ+B′Q)=2(AQ+MQ).
∴当A、Q、M三点共线时,AQ+MQ最小,即此时AP+2B′Q最小,
设直线AM的解析式为y=sx+t,
∴,
解得:,
∴直线AM的解析式为yx﹣1,
当x=1时,y,
∴Q(1,).
15.(2025春 东城区期末)在平面直角坐标系中,给出如下定义:P为图形M上任意一点,如果点P到直线EF的距离等于图形M上任意两点距离的最大值时,那么点P称为直线EF的“伴随点”.例如:如图①,已知点A(1,2),B(3,2),P(2,2)在线段AB上,则点P是直线EF:x轴的“伴随点”.
(1)如图②,已知点A(1,0),B(3,0),P是线段AB上一点,直线EF过点G(﹣1,0),且与x轴的夹角∠FGO=30°,当点P是直线EF的“伴随点”时,点P的坐标为 (3,0) ;
(2)如图③,x轴上方有一等边三角形ABC,BC⊥y轴,顶点A在y轴上且在BC上方,,点P是△ABC上一点,且点P是直线EF:x轴的“伴随点”,当点P到x轴的距离最小时,求等边三角形ABC的边长;
(3)如图④,以A(1,0),B(2,0),C(2,1)为顶点的正方形ABCD上始终存在点P,使得点P是直线EF:y=﹣x+b的“伴随点”,请直接写出b的取值范围.
【解答】解:(1)AB线段上任意两点距离的最大值为3﹣1=2,即P到EF的距离为2,
过P作PC⊥EF于点C,
∵∠FGO=30°,
∴GP4,
∵点G(﹣1,0),
∴OG=1,
∴P(3,0).
故答案为:(3,0),
(2)设等边三角形△ABC的边长为2a(0<a),则C(a,),
△ABC上任意两点距离的最大值即为2a,
当P在线段BC上时,P到x轴的距离最小,距离为,由题意知,
2a,
解得,a=1或﹣1(舍去),
所以此时等边三角形ABC的边长为2.
(3)由题意知,正方形ABCD的边长为1,
所以正方形ABCD上任意两点距离的最大值为,
即正方形ABCD上始终存在点P,P到EF的距离为.
则EF向上或者向下平移2个单位长度得到直线l1,l1与EF平行,且两直线间的距离为,
所以P既在l1上,又在正方形ABCD的边上,即l1与正方形ABCD有交点.
当b≤1时,l1为y=﹣x+b+2,
当l1过A时,b=﹣1,
当l1过C时,b=1,
即﹣1≤b≤1;
当b>1时,l1为y=﹣x+b﹣2,
当l1过A时,b=3,
当l1过C时,b=5,
即3≤b≤5;
综上所述,当﹣1≤b≤1或3≤b≤5时,正方形ABCD上始终存在点P,使得点P是直线EF:y=﹣x+b的“伴随点”.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
