【攻克压轴大题】2025年中考数学压轴题精选:圆(含解析)
文档属性
| 名称 | 【攻克压轴大题】2025年中考数学压轴题精选:圆(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
【攻克压轴大题】2025年中考数学压轴题精选:圆
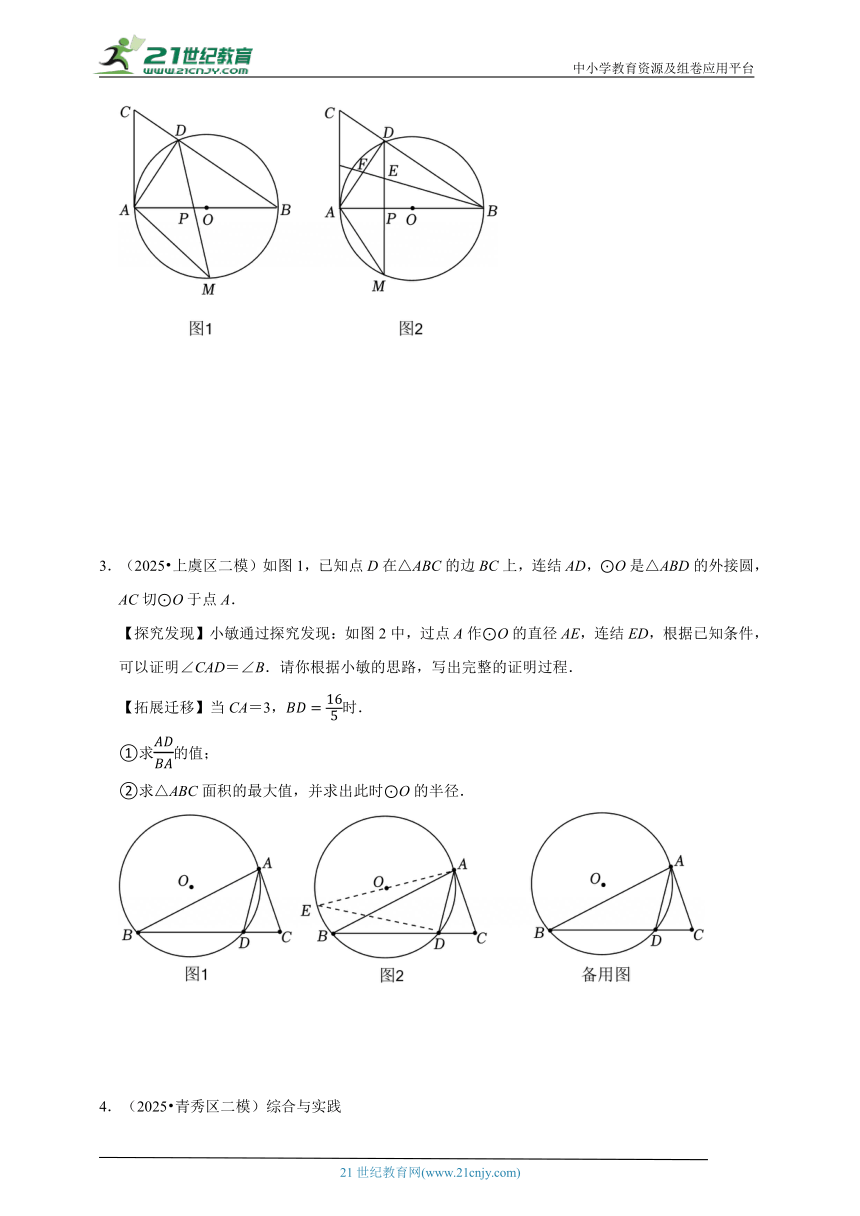
1.(2025 金华模拟)如图,在Rt△ABC中,AB=3,AC=5,以点C为圆心,为半径作圆.点D为边AB上的动点,DP,DQ分别切圆C于点P,点Q,连结PQ,分别交AC和BC于点E,F,取PQ的中点M.
(1)当∠PDQ=60°时,求劣弧PQ的度数;
(2)当CE=CF时,求AD的长;
(3)连接CM,BM.
①证明:ME CA=CM AD.
②在点D的运动过程中,BM是否存在最小值?若存在,直接写出BM的值;若不存在,请说明理由.
2.(2025 姑苏区校级二模)如图1,以AB为直径的⊙O与△ABC的边BC交于点D,∠CAD=∠ABC.点M是直径AB下方半圆上的一动点,连接AM,DM.DM交AB于点P.
(1)若AB=4,BC=2,求tan∠B的值;
(2)记△ACD的面积为S△ACD,△ABD的面积为S△ABD,若S△ACD:S△ABD,⊙O的半径为.求线段CD的长;
(3)如图2,当动点M运动到恰好使得P为DM的中点时,∠ABC的角平分线交DM于点E,交AD于点F,求的值.
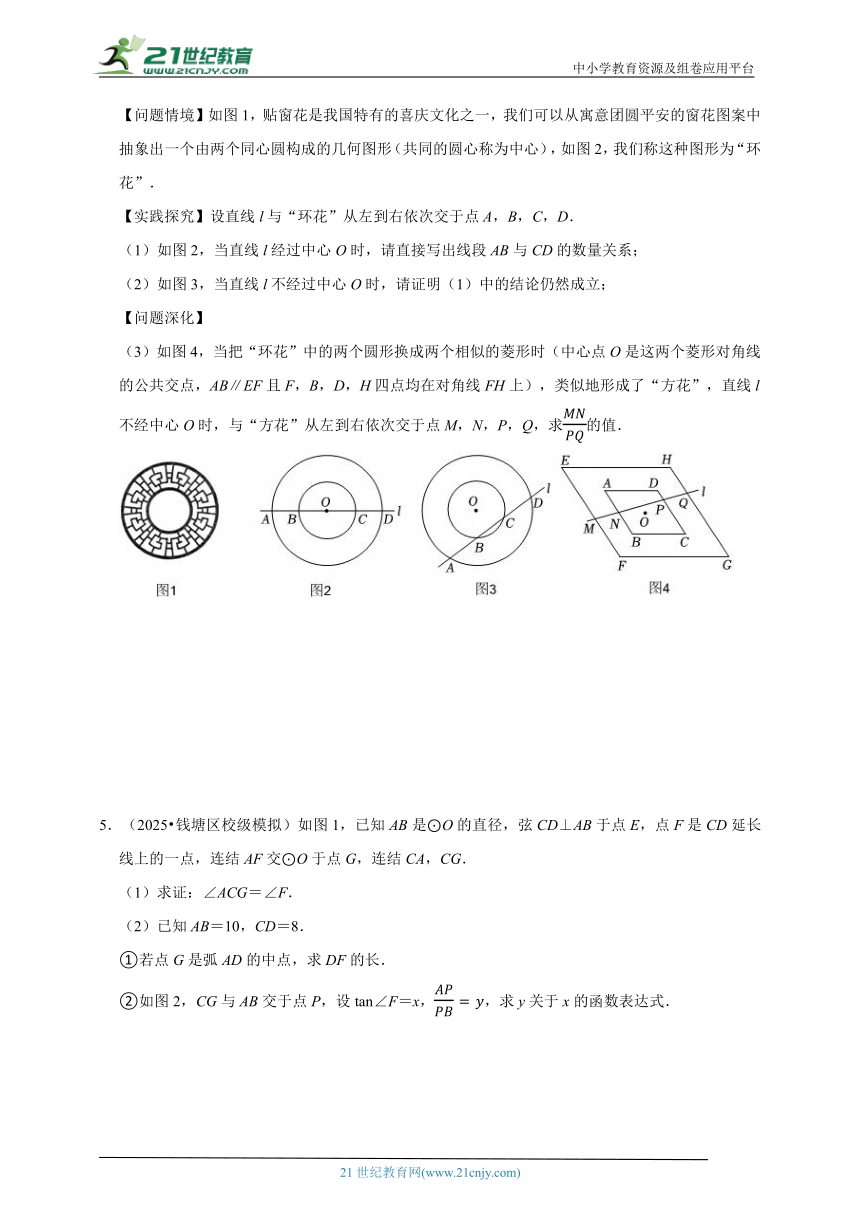
3.(2025 上虞区二模)如图1,已知点D在△ABC的边BC上,连结AD,⊙O是△ABD的外接圆,AC切⊙O于点A.
【探究发现】小敏通过探究发现:如图2中,过点A作⊙O的直径AE,连结ED,根据已知条件,可以证明∠CAD=∠B.请你根据小敏的思路,写出完整的证明过程.
【拓展迁移】当CA=3,时.
①求的值;
②求△ABC面积的最大值,并求出此时⊙O的半径.
4.(2025 青秀区二模)综合与实践
【问题情境】如图1,贴窗花是我国特有的喜庆文化之一,我们可以从寓意团圆平安的窗花图案中抽象出一个由两个同心圆构成的几何图形(共同的圆心称为中心),如图2,我们称这种图形为“环花”.
【实践探究】设直线l与“环花”从左到右依次交于点A,B,C,D.
(1)如图2,当直线l经过中心O时,请直接写出线段AB与CD的数量关系;
(2)如图3,当直线l不经过中心O时,请证明(1)中的结论仍然成立;
【问题深化】
(3)如图4,当把“环花”中的两个圆形换成两个相似的菱形时(中心点O是这两个菱形对角线的公共交点,AB∥EF且F,B,D,H四点均在对角线FH上),类似地形成了“方花”,直线l不经中心O时,与“方花”从左到右依次交于点M,N,P,Q,求的值.
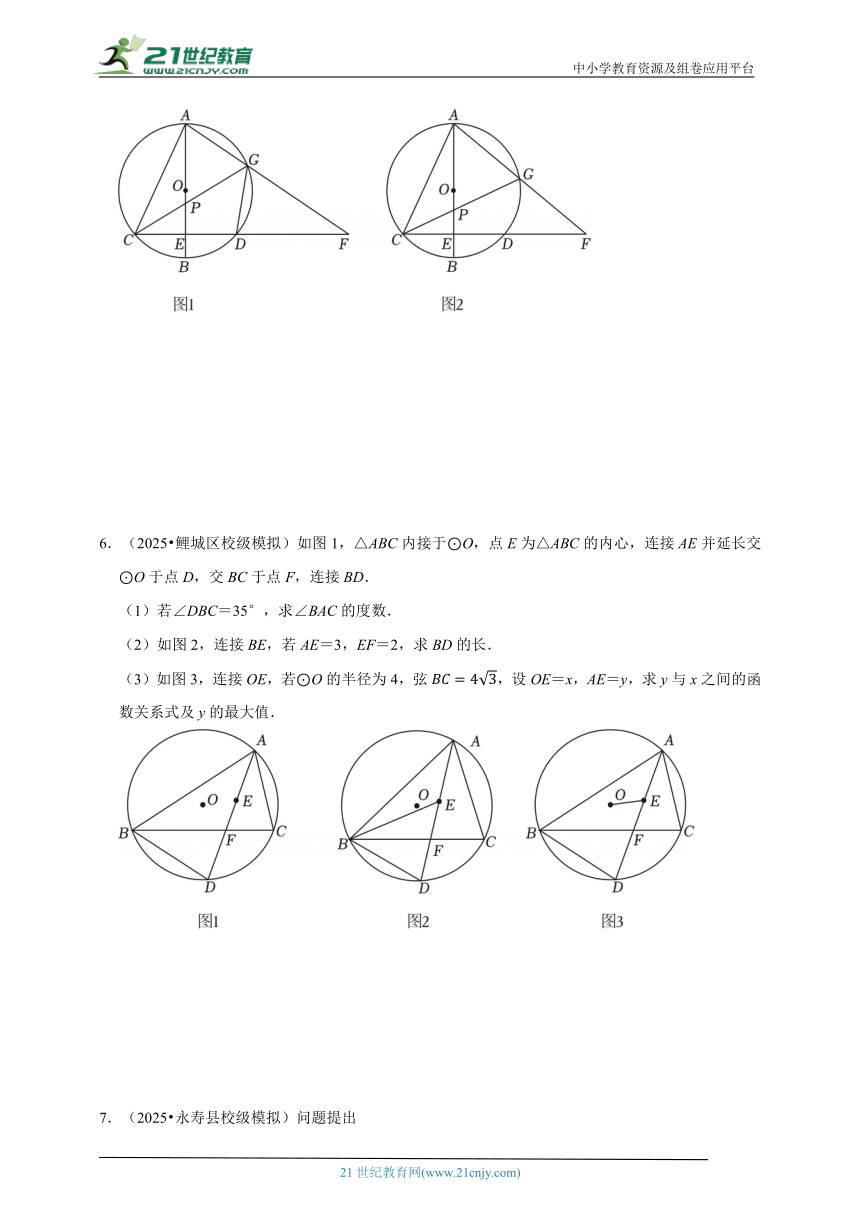
5.(2025 钱塘区校级模拟)如图1,已知AB是⊙O的直径,弦CD⊥AB于点E,点F是CD延长线上的一点,连结AF交⊙O于点G,连结CA,CG.
(1)求证:∠ACG=∠F.
(2)已知AB=10,CD=8.
①若点G是弧AD的中点,求DF的长.
②如图2,CG与AB交于点P,设tan∠F=x,,求y关于x的函数表达式.
6.(2025 鲤城区校级模拟)如图1,△ABC内接于⊙O,点E为△ABC的内心,连接AE并延长交⊙O于点D,交BC于点F,连接BD.
(1)若∠DBC=35°,求∠BAC的度数.
(2)如图2,连接BE,若AE=3,EF=2,求BD的长.
(3)如图3,连接OE,若⊙O的半径为4,弦,设OE=x,AE=y,求y与x之间的函数关系式及y的最大值.
7.(2025 永寿县校级模拟)问题提出
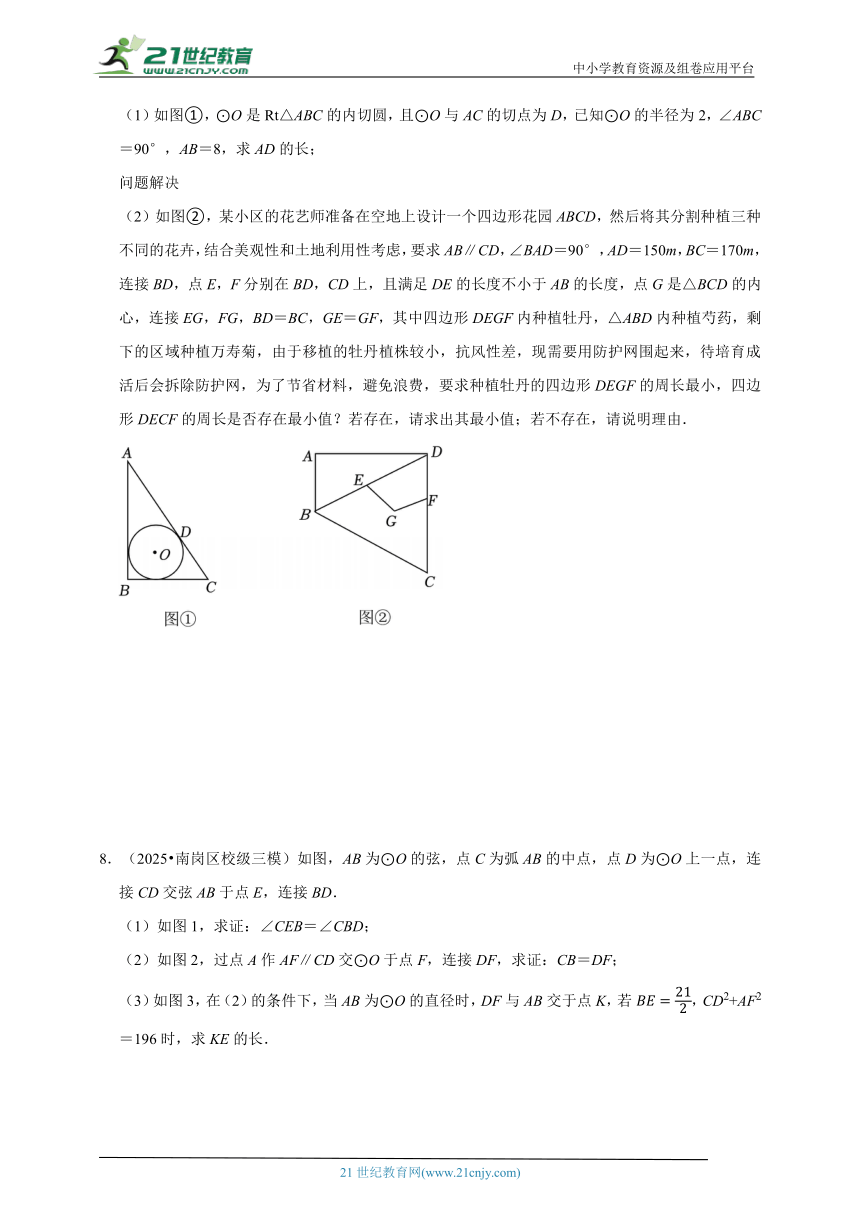
(1)如图①,⊙O是Rt△ABC的内切圆,且⊙O与AC的切点为D,已知⊙O的半径为2,∠ABC=90°,AB=8,求AD的长;
问题解决
(2)如图②,某小区的花艺师准备在空地上设计一个四边形花园ABCD,然后将其分割种植三种不同的花卉,结合美观性和土地利用性考虑,要求AB∥CD,∠BAD=90°,AD=150m,BC=170m,连接BD,点E,F分别在BD,CD上,且满足DE的长度不小于AB的长度,点G是△BCD的内心,连接EG,FG,BD=BC,GE=GF,其中四边形DEGF内种植牡丹,△ABD内种植芍药,剩下的区域种植万寿菊,由于移植的牡丹植株较小,抗风性差,现需要用防护网围起来,待培育成活后会拆除防护网,为了节省材料,避免浪费,要求种植牡丹的四边形DEGF的周长最小,四边形DECF的周长是否存在最小值?若存在,请求出其最小值;若不存在,请说明理由.
8.(2025 南岗区校级三模)如图,AB为⊙O的弦,点C为弧AB的中点,点D为⊙O上一点,连接CD交弦AB于点E,连接BD.
(1)如图1,求证:∠CEB=∠CBD;
(2)如图2,过点A作AF∥CD交⊙O于点F,连接DF,求证:CB=DF;
(3)如图3,在(2)的条件下,当AB为⊙O的直径时,DF与AB交于点K,若,CD2+AF2=196时,求KE的长.
9.(2025 平湖市二模)已知四边形ABCD内接于⊙O,对角线AC,BD交于点E,P为BD上一点,连结AP.
(1)如图1,若AB为⊙O的直径,且△ABC与△APD均为等腰直角三角形,求证:△ADC∽△APB.
(2)如图2,若△ABC与△APD均为等边三角形.
①求证:BP=CD.
②若AD=1,求的最小值.
10.(2025 广东模拟)综合与实践
【主题】圆形纸片与剪纸艺术
【素材】图1中半径为2的圆形纸片(⊙O)若干.
【实践操作】活动一:如图2,在该圆形纸片(⊙O)上剪出一个圆周角为90°的扇形.
活动二:如图3,在另一圆形纸片(⊙O)内剪出一个内接正六边形,设该正六边形ABCDEF的面积为S1,再连接AC,AE,剪出△ACE,设△ACE的面积为S2.
活动三:在活动二的基础上,装饰粘贴上六个弧形花瓣,中心为点O,所在圆的圆心C恰好是△ABO的内心.
【实践探索】
(1)根据剪纸要求,计算图2中的扇形ABC的面积.
(2)请直接写出的值: .
(3)求弧形花瓣总的周长(图4中实线部分的长度).(结果保留π)
11.(2025 缙云县二模)已知△PAB内接于⊙O,PH⊥AB于点H.
(1)如图1,当PH经过圆心O时,求证:PA=PB;
(2)如图2,当PH不经过圆心O时,过点A作AC⊥PB于点C,交PH于点D,交⊙O于点E,连结BD,BE,求证:∠PAC=∠PBD;
(3)如图3,在(2)的条件下,若AD=PD,AH:BH=5:2,,求⊙O的半径长.
12.(2025 石家庄二模)(1)图1是利用已知线段AB进行的尺规作图,请根据图1的作图填空:
①首先分别以A,B为圆心,以AB长为半径画弧,作了 △OAB;
②再以O为圆心,以 为半径作了圆O;
③最后在优弧ACB上作了 (选填“圆周角”或“圆心角”)∠ACB,算得∠ACB的度数为 .
(2)图2中四边形EFGH是矩形,其边EF=4,FG=6.已知点P在直线GH的左侧,且tan∠GPH.请按要求完成下列问题.
①通过尺规作图在图2中找到一个点P,使(保留作图痕迹,不写作图过程);
②使得的点P有多少个?说明理由;
③求点P到直线EF的最小距离.
13.(2025 德阳模拟)如图1,⊙O为△ABC的外接圆,点B为的中点,点F为劣弧AC上除弧中点外一动点,连接AF,∠AFB=60°,连接BF交AC于D点,过F点作⊙O的切线交直线AC于E点,连接BE.
(1)连接OA,OB,则∠AOB= °,若AB=3,则⊙O的面积= ;
(2)判断△DEF的形状,并进行证明;
(3)已知⊙O的半径为r,如图2,取AC延长线上一点G,连接BG,且BC平分∠GBF.
①求AF BG;(结果用r表示)
②是否为定值,若是请求出定值,若不是请说明理由.(结果用r表示)
14.(2025 黄岩区二模)如图1,AB是⊙O的直径,点C是圆上一点(A,B除外),点D,E在AB上,满足AD=AC,BE=BC,CD,CE的延长线分别交⊙O于点F,G.记∠CAB=α.
(1)若α=30°,求∠FCG的度数;
(2)连结FG,求证:;
(3)如图2,连结并延长BF,AG交于点H,若
①求的值;
②请直接写出cosα的值.
15.(2025 东莞市校级二模)综合与实践:根据以下素材,探索求圆半径的方法.
【背景素材】同学们用若干大小不一的透明圆形(或半圆形)纸片,及一张宽2cm且足够长的矩形纸带(如图1)设计了一系列任务,探索完成任务.
【任务一】若同学甲将一圆形纸片与矩形纸带摆放成如图2位置,使圆经过A,B,G.现测得AG=1cm,求出该圆的半径.
【任务二】按如图3摆放纸片,点A,P在圆上.在AD边上取点M使AM=2AB,作MN⊥BC于N,连结AN恰过圆心O,交圆于点Q,连结PN.量得∠1=∠2.
①判断直线PN与⊙O的位置关系,并说明理由;
②直接写出⊙O的半径为 cm.
【攻克压轴大题】2025年中考数学压轴题精选:圆
参考答案与试题解析
一.解答题(共15小题)
1.(2025 金华模拟)如图,在Rt△ABC中,AB=3,AC=5,以点C为圆心,为半径作圆.点D为边AB上的动点,DP,DQ分别切圆C于点P,点Q,连结PQ,分别交AC和BC于点E,F,取PQ的中点M.
(1)当∠PDQ=60°时,求劣弧PQ的度数;
(2)当CE=CF时,求AD的长;
(3)连接CM,BM.
①证明:ME CA=CM AD.
②在点D的运动过程中,BM是否存在最小值?若存在,直接写出BM的值;若不存在,请说明理由.
【解答】(1)解:连接CP,CQ,如图,
∵DP,DQ分别切圆C于点P,点Q,
∴CP⊥DP,CQ⊥DQ,
∴∠CPD=∠CQD=90°,
∵四边形DQCP的内角和为360°,
∴∠PDQ+∠PCQ=180°,
∵∠PDQ=60°,
∴∠PCQ=120°,
∴劣弧PQ的度数为120°;
(2)解:连接CP,CQ,CD,过点D作DG⊥BC于点G,如图,
∵DP,DQ分别切圆C于点P,点Q,
∴CP⊥DP,CQ⊥DQ,
在Rt△PCD和Rt△QCD中,
,
∴Rt△PCD≌Rt△QCD(HL),
∴∠PCD=∠QCD,
∵CP=CQ,
∴CD平分PQ,即CD经过点M,
∵CE=CF,M为PQ的中点,
∴CD平分∠ACB.
∵DA⊥AC,DG⊥BC,
∴DG=AD.
∵在Rt△ABC中,AB=3,AC=5,
∴BC.
∵,,
∴,
∴AD.
(3)①证明:连接CP,CQ,如图,
延长CM,由(2)知:CM经过点D,
∵M为PQ的中点,
∴CM⊥PQ,
∴∠CME=∠A=90°,
∵∠ECM=∠DCA,
∴△ECM∽△DCA,
∴,
∴ME CA=CM AD;
②解:在点D的运动过程中,BM存在最小值,BM的最小值为4,理由:
延长CM,由(2)知:CM经过点D,连接PC,如图,
∵M为PQ的中点,
∴CM⊥PQ,
∵DP切圆C于点P,
∴CP⊥DP,
∴∠CPD=90°,
∴△PCM∽△DCP,
∴,
∴PC2=CM CD,
由(3)①知:△ECM∽△DCA,
∴,
∴CM CD=CE CA,
∴PC2=CE CA,
∵PC,CA=5,
∴CE2.
∵∠CME=90°,
∴点M在以CE为直径的圆上运动,
取CE的中点O,如图,
则OC=OE=1,
∴AO=AC﹣OC=4,
∴BO5,
当点B,M,O三点在一条直线上时,BM取得最小值,
∴BM的最小值=BO﹣OM=5﹣1=4.
2.(2025 姑苏区校级二模)如图1,以AB为直径的⊙O与△ABC的边BC交于点D,∠CAD=∠ABC.点M是直径AB下方半圆上的一动点,连接AM,DM.DM交AB于点P.
(1)若AB=4,BC=2,求tan∠B的值;
(2)记△ACD的面积为S△ACD,△ABD的面积为S△ABD,若S△ACD:S△ABD,⊙O的半径为.求线段CD的长;
(3)如图2,当动点M运动到恰好使得P为DM的中点时,∠ABC的角平分线交DM于点E,交AD于点F,求的值.
【解答】解:(1)∵AB为圆的直径,
∴∠ADB=90°,
∴∠DAB+∠B=90°,
∵∠CAD=∠ABC,
∴∠DAB+∠CAD=90°,
∴∠CAB=90°,
∵AB=4,BC=2,
∴AC2,
∴tan∠B;
(2)∵∠ADB=90°,
∴AD⊥BC,
∴S△ACD,S△ABD,
∵S△ACD:S△ABD,
∴,
设CD=a,则BD=4a,
∵∠CAB=90°,AD⊥BC,
∴△ACD∽△BAD,
∴,
∴AD2=BD CD=4a2,
∴AD=2a.
∴ABa,
∵⊙O的半径为,
∴AB=22a,
∴a=1,
∴CD=a=1;
(3)过点F作FG⊥AB于点G,如图,
∵BF是∠ABC的角平分线,FG⊥AB,FD⊥BD,
∴FG=FD.
∵P为DM的中点,
∴DP=MP,
∵AB为圆的直径,
∴AB⊥MD,
∴△AFG∽△ADP,
∴,
∴.
∵AB为圆的直径,AB⊥MD,
∴,
∴∠MDB=∠BAD.
∵BF是∠ABC的角平分线,
∴∠DBF=∠ABF.
∵∠DEF=∠MDB+∠DBF,∠DFE=∠DAB+∠ABF,
∴∠DEF=∠DFE,
∴DF=DE,
∴,
∴1.
3.(2025 上虞区二模)如图1,已知点D在△ABC的边BC上,连结AD,⊙O是△ABD的外接圆,AC切⊙O于点A.
【探究发现】小敏通过探究发现:如图2中,过点A作⊙O的直径AE,连结ED,根据已知条件,可以证明∠CAD=∠B.请你根据小敏的思路,写出完整的证明过程.
【拓展迁移】当CA=3,时.
①求的值;
②求△ABC面积的最大值,并求出此时⊙O的半径.
【解答】【探究发现】证明:过点A作⊙O的直径AE,连结ED,如图,
∵AC切⊙O于点A,
∴OA⊥AC,
∴∠DAC+∠EAD=90°,
∵AE为⊙O的直径,
∴∠ADE=90°,
∴∠E+∠EAD=90°,
∴∠E=∠DAC,
∵∠E=∠B,
∴∠CAD=∠B;
【拓展迁移】解:①由【探究发现】知:∠CAD=∠B,
∵∠C=∠C,
∴△DAC∽△ABC,
∴,
∴,
∴DC或DC=﹣5(不合题意,舍去),
∵△DAC∽△ABC,
∴;
②由题意:当BA⊥AC时,△ABC面积最大,如图,
∵AC切⊙O于点A,BA⊥AC,
∴AB为圆的直径,
∴∠ADB=90°,
∴AD⊥BC,
由①知:DC,
∴AD,
∵,
∴BA=4.
∴此时⊙O的半径为2.
4.(2025 青秀区二模)综合与实践
【问题情境】如图1,贴窗花是我国特有的喜庆文化之一,我们可以从寓意团圆平安的窗花图案中抽象出一个由两个同心圆构成的几何图形(共同的圆心称为中心),如图2,我们称这种图形为“环花”.
【实践探究】设直线l与“环花”从左到右依次交于点A,B,C,D.
(1)如图2,当直线l经过中心O时,请直接写出线段AB与CD的数量关系;
(2)如图3,当直线l不经过中心O时,请证明(1)中的结论仍然成立;
【问题深化】
(3)如图4,当把“环花”中的两个圆形换成两个相似的菱形时(中心点O是这两个菱形对角线的公共交点,AB∥EF且F,B,D,H四点均在对角线FH上),类似地形成了“方花”,直线l不经中心O时,与“方花”从左到右依次交于点M,N,P,Q,求的值.
【解答】(1)①解:∵OA=OD,OB=OC,
∴OA﹣OB=OD﹣OC,
∴AB=CD;
②证明:如图,过点O作OE⊥l于点E,
∴AE=DE,BE=CE,
∴AB=CD.
(2)解:如图,连接FH,过点N作NR∥FH交EF于点R,过点P作PT∥FH交GH于点T,
∵AB∥EF,
∴四边形NRFB是平行四边形,
∴NR=FB,∠NRM=∠BFR,
同理得,PT=DH,∠DHT=∠PTQ,
∵四边形ABCD与四边形EFGH均为菱形,O为它们的中心,
∴OF=OH,OB=OD,GH∥EF,
∴FB=DH,∠PQT=∠NMR,∠DHT=∠BFR,
∴NR=PT,∠NRM=∠PTQ,
∴△MNR≌△PQT(AAS),
∴MN=PQ,
∴.
5.(2025 钱塘区校级模拟)如图1,已知AB是⊙O的直径,弦CD⊥AB于点E,点F是CD延长线上的一点,连结AF交⊙O于点G,连结CA,CG.
(1)求证:∠ACG=∠F.
(2)已知AB=10,CD=8.
①若点G是弧AD的中点,求DF的长.
②如图2,CG与AB交于点P,设tan∠F=x,,求y关于x的函数表达式.
【解答】(1)证明:∵AB是⊙O的直径,弦CD⊥AB,
∴,
∴∠ACD=∠AGC,
∵∠ACD=∠ACG+∠GCF,∠AGC=∠F+∠GCF,
∴∠ACG+∠GCF=∠F+∠GCF,
∴∠ACG=∠F.
(2)解:①连接OC,AD,如图,
∵AB是⊙O的直径,AB=10,
∴OC=OAAB=5,
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=DECD=4,
∴OE3,
∴AE=OA+OE=5+3=8,
∴AC4.
∵AB是⊙O的直径,弦CD⊥AB,
∴,
∴AC=AD=4.
∵点G是弧AD的中点,
∴,
∴∠ACG=∠DCG,
由(1)知:∠ACG=∠F,
∴∠F=∠DCG.
∵∠DCG=∠DAG,
∴∠F=∠DAG,
∴DF=AD=4;
②过点P作PH⊥AC于点H,连接BC,如图,
由(2)①知:AE=8,CE=4,AC=4,
∴BE=AB﹣AE=2,
∴BC2,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC⊥AC,
∵PH⊥AC,
∴PH∥BC,
∴△AHP∽△ACB,
∴2,
∴AH=2HP.
∵tan∠F=x,∠ACG=∠F,
∴tan∠ACG=x,
∵tan∠ACG,
∴x,
∴CH.
∵PH∥BC,
∴2x,
∵,
∴y关于x的函数表达式为y=2x.
6.(2025 鲤城区校级模拟)如图1,△ABC内接于⊙O,点E为△ABC的内心,连接AE并延长交⊙O于点D,交BC于点F,连接BD.
(1)若∠DBC=35°,求∠BAC的度数.
(2)如图2,连接BE,若AE=3,EF=2,求BD的长.
(3)如图3,连接OE,若⊙O的半径为4,弦,设OE=x,AE=y,求y与x之间的函数关系式及y的最大值.
【解答】解:(1)∵点E为△ABC的内心,
∴∠BAD=∠CAD,
∵,
∴∠CBD=∠CAD,
∴∠BAD=∠CAD=∠CBD=35°,
∴∠BAC=2∠BAD=70°.
(2)∵BE平分∠ABC,AE平分∠BAC,
设∠ABE=∠CBE=α,∠BAE=∠CAE=β,
∴∠CBD=β,
∴∠EBD=∠CBD+∠EBC=α+β,∠BED=∠ABE+∠BAE=α+β,
∴∠EBD=∠BED,
∴BD=ED,
设DF=x,
∵AE=3,EF=2,
∴BD=ED=DF+EF=x+2,
∴AD=AE+ED=x+5,
∵∠DBF=∠DAB,∠BDF=∠ADB,
∴△DBF∽△DAB,
∴,
∴DB2=DA DF,
∴(x+2)2=x(x+5),
∴x=4,
∴BD=ED=x+2=6.
(3)如图,连接OB,连接OD交BC于点M,
∵∠BAD=∠CAD,
∴BD=CD,
∴OD垂直平分BC,
∴BM=CMBC=2,
∵OB=4,
在Rt△OBM中,MO2,
∴DM=2,
∴.
由(2)得,当BE平分∠ABC,AE平分∠BAC时,
有BD=ED,
∴DE=BD=4
作OH⊥AD,连接OA,OE,
在Rt△OHA中,OH2=16﹣AH2,
在Rt△OHE中,OH2=x2﹣HE2,
∴x2=16﹣AH2+HE2,
∵AH=DH,DE=4,
∴x2=16﹣(AH2﹣HE2)=16﹣(AH+HE)(AH﹣HE)=16﹣(DH+HE)(AH﹣HE),
即x2=16﹣4y,
∴,
∵,
∴y的最大值是4,即AE的最大值为4.
7.(2025 永寿县校级模拟)问题提出
(1)如图①,⊙O是Rt△ABC的内切圆,且⊙O与AC的切点为D,已知⊙O的半径为2,∠ABC=90°,AB=8,求AD的长;
问题解决
(2)如图②,某小区的花艺师准备在空地上设计一个四边形花园ABCD,然后将其分割种植三种不同的花卉,结合美观性和土地利用性考虑,要求AB∥CD,∠BAD=90°,AD=150m,BC=170m,连接BD,点E,F分别在BD,CD上,且满足DE的长度不小于AB的长度,点G是△BCD的内心,连接EG,FG,BD=BC,GE=GF,其中四边形DEGF内种植牡丹,△ABD内种植芍药,剩下的区域种植万寿菊,由于移植的牡丹植株较小,抗风性差,现需要用防护网围起来,待培育成活后会拆除防护网,为了节省材料,避免浪费,要求种植牡丹的四边形DEGF的周长最小,四边形DECF的周长是否存在最小值?若存在,请求出其最小值;若不存在,请说明理由.
【解答】解:(1)连接OD,再记AB,BC分别与⊙O相切于点E,F,连接OE,OF,如图所示:
∵⊙O是Rt△ABC的内切圆,
∴AE=AD,∠OEB=∠OFB=90°,
∴∠ABC=90°,
∴四边形BFOE是矩形,
∵OF=OE,
∴四边形BFOE是正方形,
∴EB=OF=2,
∴AD=AE=AB﹣BE=8﹣2=6.
(2)四边形DEGF的周长存在最小值,且为256m,过程如下:
∵AB∥CD,∠BAD=90°,
∴∠ADC=90°∠BAD=90°,AD=150m,BC=170m,BD=BC,
∴BD=170m,
在Rt△ABD中,,
连接DG,过B作BW⊥CD,过G作GH⊥BD,如图所示:
则∠DWB=∠ADC=∠BAD=90°,
∴四边形ABWD是矩形,
∴DW=AB=80m,AD∥BW,
∵BD=BC,BW⊥CD,
∴DC=2DW=2×80m=160m,∠DBW=∠CBW,
∵点G是△BCD的内心,
∴点G在WB上,且DG是∠BDC的角平分线,
∵BW⊥CD,GH⊥BD,
∴HG=GW,∠EHG=∠FWG=90°,
∵GE=GF,
∴Rt△EHG≌Rt△FWG(HL),
∴EH=FW,
∴ED=EH+HD,DF=DW﹣FW,
∵∠DHG=∠DWG=90°,HG=GW,DG=DG,
∴Rt△DHG≌Rt△DWG(HL),
∴HD=DW=AB=80m,
∵四边形DEGF的周长=ED+EG+GF+DF,且GE=GF,
∴四边形DEGF的周长=EH+HD+2EG+GF+DW﹣FW=2HD+2EG,
即四边形DEGF的周长=2×80+2EG=160+2EG,
当EG⊥BD时,则四边形DEGF的周长有最小值,即EG=HG=GW,
则BW=AD=150m,BG+GW=BG+GH=150m,
∵AD∥BW,
∴∠GBH=∠ADW
故s,
∴,
∴,则,
解得BG=102m,
∴,
即四边形DEGF的周长=160+2×48=160+96=256(m),
∴四边形DEGF的周长存在最小值,且为256m.
8.(2025 南岗区校级三模)如图,AB为⊙O的弦,点C为弧AB的中点,点D为⊙O上一点,连接CD交弦AB于点E,连接BD.
(1)如图1,求证:∠CEB=∠CBD;
(2)如图2,过点A作AF∥CD交⊙O于点F,连接DF,求证:CB=DF;
(3)如图3,在(2)的条件下,当AB为⊙O的直径时,DF与AB交于点K,若,CD2+AF2=196时,求KE的长.
【解答】(1)证明:连接AC.
∵点C为弧AB的中点,
∴AC=BC,
∴∠CAB=∠CBA=∠CDB.
∵∠CEB是△ACE的外角,
∴∠CEB=∠CAB+∠ACD,
而∠CBD=∠CBA+∠ABD=∠CAB+∠ABD,
∵AD=AD,
∴∠ABD=∠ACD,
∴∠CEB=∠CBD.
(2)证明:∵AF∥CD,
∴∠AFD=∠CDF,
∴,
∴,
∴AC=DF,
∵点C为弧AB的中点,即AC=BC,
∴CB=DF.
(3)解:连接AD、AC,OC,
由(2),
∴,即,
∵DF=BC,
∴CD=BF,
∵AB是⊙O的直径,
∴∠ADB=∠AFB=90°,
∴AB2=AF2+BF2=AF2+CD2=196,
∴AB=14,
∴OB=OA=OCAB=7,
∵,
∴OE=BE﹣OB7,
∴AE=AB﹣BE=14,
∵点C为弧AB的中点,OC是半径,
∴OC⊥AB,AC=BC,∠CBE=∠CDB,
∴DF=AC=BC,CE,
∵∠CBE=∠CDB,∠DCB=∠BCE,
∴△BEC∽△DBC,
∴,
即,
,
即,
∴BD,BF=CD,
∴AF,
∵∠AFD=∠DBK,∠BDK=∠FAK,
∴△AFK∽△DBK,
∴,
∴BK,DK,
∵AB=AK+BK=14,
∴14﹣AK,
∴AK=2.
∴.
9.(2025 平湖市二模)已知四边形ABCD内接于⊙O,对角线AC,BD交于点E,P为BD上一点,连结AP.
(1)如图1,若AB为⊙O的直径,且△ABC与△APD均为等腰直角三角形,求证:△ADC∽△APB.
(2)如图2,若△ABC与△APD均为等边三角形.
①求证:BP=CD.
②若AD=1,求的最小值.
【解答】(1)证明:∵AB为⊙O的直径,
∴∠ADP=∠ACB=90°,
∵△ABC和△APD为等腰直角三角形,
∴,,∠DAP=∠CAB=45°,
∴,
∵∠DAP﹣∠CAP=∠CAB﹣∠CAP,
∴∠DAC=∠PAB,
∴△ADC∽△APB;
(2)证明:①∵△ADP和△ABC为等边三角形,
∴AD=AP,AC=AB,∠DAP=∠CAB=60°,
∴∠DAP﹣∠CAP=∠CAB﹣∠CAP,
∴∠DAC=∠PAB,
在△ACD和△ABP中,
,
∴△ACD≌△ABP(SAS),
∴CD=BP;
②解:∵△APD为等边三角形,
∴DP=AD=1,
设PE=x,则DE=1﹣x,
由①可知:CD=BP,∠BDC=∠APD=60°,
∴AP∥CD,
∴△APE∽△CDE,
∴,
∴,
∴,
∴BE=BP+PEx,BD=BP+PD.
∵∠DCA=∠CAP,∠DCA=∠EBA,
∴∠CAP=∠EBA.
∵∠AEP=∠BEA,
∴△AEP∽△BEA,
∴,
即,
∴AE2=x2﹣x+1,
∴AE,
∴,
∴,
∴,
∴当时,x2﹣x+1有最小值,
∴的最小值为.
10.(2025 广东模拟)综合与实践
【主题】圆形纸片与剪纸艺术
【素材】图1中半径为2的圆形纸片(⊙O)若干.
【实践操作】活动一:如图2,在该圆形纸片(⊙O)上剪出一个圆周角为90°的扇形.
活动二:如图3,在另一圆形纸片(⊙O)内剪出一个内接正六边形,设该正六边形ABCDEF的面积为S1,再连接AC,AE,剪出△ACE,设△ACE的面积为S2.
活动三:在活动二的基础上,装饰粘贴上六个弧形花瓣,中心为点O,所在圆的圆心C恰好是△ABO的内心.
【实践探索】
(1)根据剪纸要求,计算图2中的扇形ABC的面积.
(2)请直接写出的值: 2 .
(3)求弧形花瓣总的周长(图4中实线部分的长度).(结果保留π)
【解答】解:(1)如图,连接BC,
∵∠A=90°,
∴BC为⊙O的直径,即BC=4,
∵AB=AC,
∴,
∴扇形ABC的面积为;
(2)解:如图,连接OA,OC,OE,OF,
∵六边形ABCDEF为正六边形,
∴,,
∵OA=OF=OE,
∴△AOF,△FOE等边三角形,
∴OA=FA,OE=FE,∠AOF=∠FOE=60°,
∴∠AOE=∠AFE=120°,
∴△AOE≌△AFE(SAS),
同理可得△ABC≌△AOC,△COE≌△ADE,
∴,
故答案为:2;
(3)如图,过点C作CM⊥AB于点M,
∵六条等弧所对应的弦构成一个正六边形,中心为点O,
∴,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=2,
∴,
∵点O是△AOB的内心,
∴,∠ACB=2∠AOB=120°,
在Rt△ACM中,AM=1,∠CAM=30°,
∴,
∴,
∴花窗的周长为.
11.(2025 缙云县二模)已知△PAB内接于⊙O,PH⊥AB于点H.
(1)如图1,当PH经过圆心O时,求证:PA=PB;
(2)如图2,当PH不经过圆心O时,过点A作AC⊥PB于点C,交PH于点D,交⊙O于点E,连结BD,BE,求证:∠PAC=∠PBD;
(3)如图3,在(2)的条件下,若AD=PD,AH:BH=5:2,,求⊙O的半径长.
【解答】(1)证明:∵PH经过圆心O,PH⊥AB,
∴BH=AHAB,
∴PH垂直平分AB,
∴PA=PB;
(2)证明:连接PE,如图,
∵PH⊥AB,
∴∠BAE+∠ADH=90°,
∵∠ADH=∠PDC,
∴∠PDC+∠BAE=90°.
∵AC⊥PB,
∴∠PDC+∠CPD=90°,
∴∠CPD=∠BAE.
∵∠BAE=∠BPE,
∴∠BPE=∠DPC.
在△EPC和△DPC中,
,
∴△EPC≌△DPC(ASA),
∴EC=DC,
∵AC⊥PB,
∴PB是DE的垂直平分线,
∴BE=BD,
∴∠PBD=∠PBE.
∵∠PAC=∠PBE,
∴∠PAC=∠PBD;
(3)解:∵AH:BH=5:2,
∴设AH=5k,则BH=2k,
∴AB=AH+BH=7k.
在△PDC和△ADH中,
,
∴△PDC≌△ADH(AAS),
∴DC=DH,PC=AH=5k,
在Rt△BDC和Rt△BDH中,
,
∴Rt△BDC≌Rt△BDH(HL),
∴BC=BH=2k,
∴PC+BC=AH+BH,
∴PB=AB=7k,
∴PH2=PB2﹣BH2=(7k)2﹣(2k)2=45k2.
∵PA2=PH2+AH2,
∴,
∵k>0,
∴k.
∴AB=7k,
∵PD=AD,PB=AB,
∴BD在PA垂直平分线上,
延长BD,交PA于点G,连接OP,如图,
∵弦的垂直平分线经过圆心,
∴BG经过点O,PG=AG.
∴BG.
设⊙O的半径长为r,则OB=OP=r,OG=BG﹣OPr,
∵OG2+PG2=OP2,
∴,
∴r.
∴⊙O的半径长为.
12.(2025 石家庄二模)(1)图1是利用已知线段AB进行的尺规作图,请根据图1的作图填空:
①首先分别以A,B为圆心,以AB长为半径画弧,作了 等边 △OAB;
②再以O为圆心,以 OA 为半径作了圆O;
③最后在优弧ACB上作了 圆周角 (选填“圆周角”或“圆心角”)∠ACB,算得∠ACB的度数为 30° .
(2)图2中四边形EFGH是矩形,其边EF=4,FG=6.已知点P在直线GH的左侧,且tan∠GPH.请按要求完成下列问题.
①通过尺规作图在图2中找到一个点P,使(保留作图痕迹,不写作图过程);
②使得的点P有多少个?说明理由;
③求点P到直线EF的最小距离.
【解答】解:(1)①首先分别以A,B为圆心,以AB长为半径画弧,作了等边△OAB;
②再以O为圆心,以OA(答案不唯一,OA、AB、OB之一均可)为半径作了圆O;
③最后在优弧ACB上作了圆周角∠ACB,算得∠ACB的度数AOB30°.
故答案为:①等边;②OA(答案不唯一,OA、AB、OB之一均可);③圆周角,30°;
(2)①作出线段FG的垂直平分线MN,MN交FG于点P,如图,
点P即为所求;
②使得的点P有无数个.理由:
设FG的垂直平分线交EH于点Q,连接GQ交于PH点O,以点O为圆心,以OP为半径画圆,如图,
则圆O为矩形GHQP的外接圆,
∵同弧所对圆周角相等,
∴优弧上的点与G,H连线形成的圆周角都等于∠GPH,即优弧上的点都符合题意.
∴使得的点P有无数个;
③过点O作GH的中垂线MN,交EH于点M,交GH于点N,交劣弧于点W,如图,
∵PQ为FG的垂直平分线,
∴PG3,PQ⊥PG,
∵四边形EFGH为矩形,
∴∠E=∠F=∠EHG=∠HGF=90°,
∴四边形PQHG为矩形,
∵MN为GH的垂直平分线,
∴四边形EHNM是矩形,且N是GH的中点,
∴MN=EH=6,,
∵圆O的直径,
∴,
∴点P到直线EF最小距离等于WM=MN﹣ON﹣OW=2.
13.(2025 德阳模拟)如图1,⊙O为△ABC的外接圆,点B为的中点,点F为劣弧AC上除弧中点外一动点,连接AF,∠AFB=60°,连接BF交AC于D点,过F点作⊙O的切线交直线AC于E点,连接BE.
(1)连接OA,OB,则∠AOB= 120 °,若AB=3,则⊙O的面积= 3π ;
(2)判断△DEF的形状,并进行证明;
(3)已知⊙O的半径为r,如图2,取AC延长线上一点G,连接BG,且BC平分∠GBF.
①求AF BG;(结果用r表示)
②是否为定值,若是请求出定值,若不是请说明理由.(结果用r表示)
【解答】解:(1)连接OA,OB,过点O作OH⊥AB于点H,如图,
则∠AOB=2∠AFB=120°.
∵OA=OB,OH⊥AB,
∴∠AOH=∠BOH∠AOB=60°,AH=BHAB.
在Rt△AOH中,
∵sin∠AOH,
∴,
∴OA.
∴⊙O的面积=π OA2=3π.
故答案为:120;3π;
(2)△DEF的形状是等腰三角形,证明:
连接BO并延长交AC于点N,连接OC,OF,如图,
∵点B为的中点,
∴,
∴BN⊥AC,AB=BC.
∴∠BDN=90°﹣∠OBD.
∵EF为⊙O的切线,
∴OF⊥EF,
∴∠BFE=90°﹣∠OFB.
∵OB=OF,
∴∠OBD=∠OFB,
∴∠EFB=∠NDB.
∵∠NDB=∠FDE,
∴∠BFE=∠FDE,
∴EF=ED,
∴△DEF的形状是等腰三角形;
(3)①连接BO并延长交AC于点N,连接OC,OF,CF,如图,
∵点B为的中点,
∴,
∴BN⊥AC,AB=BC.
∵∠ACB=∠AFB=60°,
∴△ABC为等边三角形,
∴AB=BC=AC,∠BAC=∠ACB=∠ABC=60°.
由(1)知:ABOA.
∵⊙O的半径为r,
∴AB=BC=ACr.
∵BC平分∠GBF,
∴∠FBC=∠GBC.
∵∠G=∠ACB﹣∠GBC=60°﹣∠GBC,∠ABF=∠ABC﹣∠FBC=60°﹣∠FBC,
∴∠ABF=∠G.
∵∠AFB=∠BAC=60°,
∴△ABF∽△BGA,
∴,
∴AF BG=AB23r2.
②为定值,定值为,理由:
过点C作CH∥AB,交BG于点H,如图,
设CD=m,GC=n,
由①知:AB=BC=ACr,∠BAC=∠ACB=∠ABC=60°,
则AG=GC+AC=nr.
∵CH∥AB,
∴∠HCG=∠BAC=60°,
∴∠BCH=180°﹣∠ACB﹣∠HCG=60°=∠ACB.
在△BDC和△BHC中,
,
∴△BDC≌△BHC(ASA),
∴DC=HC=m.
∵CH∥AB,
∴△GHC∽△GBA,
∴,
∴,
∴mnmrnr,
∴r(n﹣m)=mn.
∴.
14.(2025 黄岩区二模)如图1,AB是⊙O的直径,点C是圆上一点(A,B除外),点D,E在AB上,满足AD=AC,BE=BC,CD,CE的延长线分别交⊙O于点F,G.记∠CAB=α.
(1)若α=30°,求∠FCG的度数;
(2)连结FG,求证:;
(3)如图2,连结并延长BF,AG交于点H,若
①求的值;
②请直接写出cosα的值.
【解答】(1)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵α=30°,
∴∠ABC=60°,
∵AD=AC,BE=BC,
∴∠ADC=75°,∠BEC=60°,
∴∠FCG=45°;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠CAB=α,
∴∠ABC=90°﹣α,
∵AD=AC,BE=BC,
∴,,
∴∠FCG=45°.
连结OF,OG,
则∠FOG=2∠FCG=90°,
∴FGOG,
∵AB=2OG,
∴;
(3)解:①∵四边形AGFB是圆内接四边形,
∴∠HFG=∠HAB,∠HGF=∠HBA,
∴△HFG∽△HAB,
∴,
∵,
∴设BF=a,FH=3a,则BH=4a,
∴,,
∴,
∴;
②连接BG、AF,过F作FH⊥AB于点H,
由①得BF=a,FH=3a,AGa,GH=2a,
∵∠FCG=45°,
∴∠CBF=∠FCG=45°,
∵∠BGH=90°,
∴△BGH是等腰直角三角形,
∴BG=GH=2a,
在Rt△BAG中,ABa,
∵AC=AD,
∴∠ACD=∠ADC,
∴∠BDF=∠ADC,
∵∠FBA=∠FCA,
∴△FBD∽△ACD,
∴FB=FD=a,
在Rt△ABF中,AF3a,
由等面积可得FHa,
∴BHa,
∴BD=2BHa,
∴AD=AB﹣BDa,
∴cosα.
15.(2025 东莞市校级二模)综合与实践:根据以下素材,探索求圆半径的方法.
【背景素材】同学们用若干大小不一的透明圆形(或半圆形)纸片,及一张宽2cm且足够长的矩形纸带(如图1)设计了一系列任务,探索完成任务.
【任务一】若同学甲将一圆形纸片与矩形纸带摆放成如图2位置,使圆经过A,B,G.现测得AG=1cm,求出该圆的半径.
【任务二】按如图3摆放纸片,点A,P在圆上.在AD边上取点M使AM=2AB,作MN⊥BC于N,连结AN恰过圆心O,交圆于点Q,连结PN.量得∠1=∠2.
①判断直线PN与⊙O的位置关系,并说明理由;
②直接写出⊙O的半径为 cm.
【解答】解:【任务一】∵四边形ABCD为矩形,
∴∠A=90°,
∴BG为经过A,B,G三点的圆的直径,
∵BG,
∴该圆的半径为BG;
【任务二】①直线PN与⊙O的位置关系为PN与⊙O相切,理由:
连接OP,如图,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠MAN=∠1,
∵∠1=∠2,
∴∠MAN=∠2,
∵∠NMA=∠PMN,
∴△NMA∽△PMN,
∴∠MNA=∠MPN,
∵MN⊥BC,
∴∠MAN+∠MNA=90°,
∴∠MPN+∠MAN=90°.
∵OA=OP,
∴∠MAN=∠OPA,
∴∠OPA+∠MPN=90°,
∴∠OPN=90°,
∴OP⊥NP,
∵OP为圆的半径,
∴PN与⊙O相切;
②∵AM=2AB,
∴AM=4cm.
∵四边形ABCD为矩形,
∴∠A=∠B=90°,MN⊥BC,
∴四边形ABNM为矩形,
∴MN=AB=2cm,BN=AM=4cm,
由①知:△NMA∽△PMN,
∴,
∴,
∴MP=1cm.
∴NPcm.
∵MN⊥BC,
∴AN2cm.
设⊙O的半径为x cm,则OA=OP=x cm,ON=AN﹣OA=(2x)cm,
∵OP⊥NP,
∴OP2+PN2=ON2,
∴,
∴x.
∴⊙O的半径为cm.
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【攻克压轴大题】2025年中考数学压轴题精选:圆
1.(2025 金华模拟)如图,在Rt△ABC中,AB=3,AC=5,以点C为圆心,为半径作圆.点D为边AB上的动点,DP,DQ分别切圆C于点P,点Q,连结PQ,分别交AC和BC于点E,F,取PQ的中点M.
(1)当∠PDQ=60°时,求劣弧PQ的度数;
(2)当CE=CF时,求AD的长;
(3)连接CM,BM.
①证明:ME CA=CM AD.
②在点D的运动过程中,BM是否存在最小值?若存在,直接写出BM的值;若不存在,请说明理由.
2.(2025 姑苏区校级二模)如图1,以AB为直径的⊙O与△ABC的边BC交于点D,∠CAD=∠ABC.点M是直径AB下方半圆上的一动点,连接AM,DM.DM交AB于点P.
(1)若AB=4,BC=2,求tan∠B的值;
(2)记△ACD的面积为S△ACD,△ABD的面积为S△ABD,若S△ACD:S△ABD,⊙O的半径为.求线段CD的长;
(3)如图2,当动点M运动到恰好使得P为DM的中点时,∠ABC的角平分线交DM于点E,交AD于点F,求的值.
3.(2025 上虞区二模)如图1,已知点D在△ABC的边BC上,连结AD,⊙O是△ABD的外接圆,AC切⊙O于点A.
【探究发现】小敏通过探究发现:如图2中,过点A作⊙O的直径AE,连结ED,根据已知条件,可以证明∠CAD=∠B.请你根据小敏的思路,写出完整的证明过程.
【拓展迁移】当CA=3,时.
①求的值;
②求△ABC面积的最大值,并求出此时⊙O的半径.
4.(2025 青秀区二模)综合与实践
【问题情境】如图1,贴窗花是我国特有的喜庆文化之一,我们可以从寓意团圆平安的窗花图案中抽象出一个由两个同心圆构成的几何图形(共同的圆心称为中心),如图2,我们称这种图形为“环花”.
【实践探究】设直线l与“环花”从左到右依次交于点A,B,C,D.
(1)如图2,当直线l经过中心O时,请直接写出线段AB与CD的数量关系;
(2)如图3,当直线l不经过中心O时,请证明(1)中的结论仍然成立;
【问题深化】
(3)如图4,当把“环花”中的两个圆形换成两个相似的菱形时(中心点O是这两个菱形对角线的公共交点,AB∥EF且F,B,D,H四点均在对角线FH上),类似地形成了“方花”,直线l不经中心O时,与“方花”从左到右依次交于点M,N,P,Q,求的值.
5.(2025 钱塘区校级模拟)如图1,已知AB是⊙O的直径,弦CD⊥AB于点E,点F是CD延长线上的一点,连结AF交⊙O于点G,连结CA,CG.
(1)求证:∠ACG=∠F.
(2)已知AB=10,CD=8.
①若点G是弧AD的中点,求DF的长.
②如图2,CG与AB交于点P,设tan∠F=x,,求y关于x的函数表达式.
6.(2025 鲤城区校级模拟)如图1,△ABC内接于⊙O,点E为△ABC的内心,连接AE并延长交⊙O于点D,交BC于点F,连接BD.
(1)若∠DBC=35°,求∠BAC的度数.
(2)如图2,连接BE,若AE=3,EF=2,求BD的长.
(3)如图3,连接OE,若⊙O的半径为4,弦,设OE=x,AE=y,求y与x之间的函数关系式及y的最大值.
7.(2025 永寿县校级模拟)问题提出
(1)如图①,⊙O是Rt△ABC的内切圆,且⊙O与AC的切点为D,已知⊙O的半径为2,∠ABC=90°,AB=8,求AD的长;
问题解决
(2)如图②,某小区的花艺师准备在空地上设计一个四边形花园ABCD,然后将其分割种植三种不同的花卉,结合美观性和土地利用性考虑,要求AB∥CD,∠BAD=90°,AD=150m,BC=170m,连接BD,点E,F分别在BD,CD上,且满足DE的长度不小于AB的长度,点G是△BCD的内心,连接EG,FG,BD=BC,GE=GF,其中四边形DEGF内种植牡丹,△ABD内种植芍药,剩下的区域种植万寿菊,由于移植的牡丹植株较小,抗风性差,现需要用防护网围起来,待培育成活后会拆除防护网,为了节省材料,避免浪费,要求种植牡丹的四边形DEGF的周长最小,四边形DECF的周长是否存在最小值?若存在,请求出其最小值;若不存在,请说明理由.
8.(2025 南岗区校级三模)如图,AB为⊙O的弦,点C为弧AB的中点,点D为⊙O上一点,连接CD交弦AB于点E,连接BD.
(1)如图1,求证:∠CEB=∠CBD;
(2)如图2,过点A作AF∥CD交⊙O于点F,连接DF,求证:CB=DF;
(3)如图3,在(2)的条件下,当AB为⊙O的直径时,DF与AB交于点K,若,CD2+AF2=196时,求KE的长.
9.(2025 平湖市二模)已知四边形ABCD内接于⊙O,对角线AC,BD交于点E,P为BD上一点,连结AP.
(1)如图1,若AB为⊙O的直径,且△ABC与△APD均为等腰直角三角形,求证:△ADC∽△APB.
(2)如图2,若△ABC与△APD均为等边三角形.
①求证:BP=CD.
②若AD=1,求的最小值.
10.(2025 广东模拟)综合与实践
【主题】圆形纸片与剪纸艺术
【素材】图1中半径为2的圆形纸片(⊙O)若干.
【实践操作】活动一:如图2,在该圆形纸片(⊙O)上剪出一个圆周角为90°的扇形.
活动二:如图3,在另一圆形纸片(⊙O)内剪出一个内接正六边形,设该正六边形ABCDEF的面积为S1,再连接AC,AE,剪出△ACE,设△ACE的面积为S2.
活动三:在活动二的基础上,装饰粘贴上六个弧形花瓣,中心为点O,所在圆的圆心C恰好是△ABO的内心.
【实践探索】
(1)根据剪纸要求,计算图2中的扇形ABC的面积.
(2)请直接写出的值: .
(3)求弧形花瓣总的周长(图4中实线部分的长度).(结果保留π)
11.(2025 缙云县二模)已知△PAB内接于⊙O,PH⊥AB于点H.
(1)如图1,当PH经过圆心O时,求证:PA=PB;
(2)如图2,当PH不经过圆心O时,过点A作AC⊥PB于点C,交PH于点D,交⊙O于点E,连结BD,BE,求证:∠PAC=∠PBD;
(3)如图3,在(2)的条件下,若AD=PD,AH:BH=5:2,,求⊙O的半径长.
12.(2025 石家庄二模)(1)图1是利用已知线段AB进行的尺规作图,请根据图1的作图填空:
①首先分别以A,B为圆心,以AB长为半径画弧,作了 △OAB;
②再以O为圆心,以 为半径作了圆O;
③最后在优弧ACB上作了 (选填“圆周角”或“圆心角”)∠ACB,算得∠ACB的度数为 .
(2)图2中四边形EFGH是矩形,其边EF=4,FG=6.已知点P在直线GH的左侧,且tan∠GPH.请按要求完成下列问题.
①通过尺规作图在图2中找到一个点P,使(保留作图痕迹,不写作图过程);
②使得的点P有多少个?说明理由;
③求点P到直线EF的最小距离.
13.(2025 德阳模拟)如图1,⊙O为△ABC的外接圆,点B为的中点,点F为劣弧AC上除弧中点外一动点,连接AF,∠AFB=60°,连接BF交AC于D点,过F点作⊙O的切线交直线AC于E点,连接BE.
(1)连接OA,OB,则∠AOB= °,若AB=3,则⊙O的面积= ;
(2)判断△DEF的形状,并进行证明;
(3)已知⊙O的半径为r,如图2,取AC延长线上一点G,连接BG,且BC平分∠GBF.
①求AF BG;(结果用r表示)
②是否为定值,若是请求出定值,若不是请说明理由.(结果用r表示)
14.(2025 黄岩区二模)如图1,AB是⊙O的直径,点C是圆上一点(A,B除外),点D,E在AB上,满足AD=AC,BE=BC,CD,CE的延长线分别交⊙O于点F,G.记∠CAB=α.
(1)若α=30°,求∠FCG的度数;
(2)连结FG,求证:;
(3)如图2,连结并延长BF,AG交于点H,若
①求的值;
②请直接写出cosα的值.
15.(2025 东莞市校级二模)综合与实践:根据以下素材,探索求圆半径的方法.
【背景素材】同学们用若干大小不一的透明圆形(或半圆形)纸片,及一张宽2cm且足够长的矩形纸带(如图1)设计了一系列任务,探索完成任务.
【任务一】若同学甲将一圆形纸片与矩形纸带摆放成如图2位置,使圆经过A,B,G.现测得AG=1cm,求出该圆的半径.
【任务二】按如图3摆放纸片,点A,P在圆上.在AD边上取点M使AM=2AB,作MN⊥BC于N,连结AN恰过圆心O,交圆于点Q,连结PN.量得∠1=∠2.
①判断直线PN与⊙O的位置关系,并说明理由;
②直接写出⊙O的半径为 cm.
【攻克压轴大题】2025年中考数学压轴题精选:圆
参考答案与试题解析
一.解答题(共15小题)
1.(2025 金华模拟)如图,在Rt△ABC中,AB=3,AC=5,以点C为圆心,为半径作圆.点D为边AB上的动点,DP,DQ分别切圆C于点P,点Q,连结PQ,分别交AC和BC于点E,F,取PQ的中点M.
(1)当∠PDQ=60°时,求劣弧PQ的度数;
(2)当CE=CF时,求AD的长;
(3)连接CM,BM.
①证明:ME CA=CM AD.
②在点D的运动过程中,BM是否存在最小值?若存在,直接写出BM的值;若不存在,请说明理由.
【解答】(1)解:连接CP,CQ,如图,
∵DP,DQ分别切圆C于点P,点Q,
∴CP⊥DP,CQ⊥DQ,
∴∠CPD=∠CQD=90°,
∵四边形DQCP的内角和为360°,
∴∠PDQ+∠PCQ=180°,
∵∠PDQ=60°,
∴∠PCQ=120°,
∴劣弧PQ的度数为120°;
(2)解:连接CP,CQ,CD,过点D作DG⊥BC于点G,如图,
∵DP,DQ分别切圆C于点P,点Q,
∴CP⊥DP,CQ⊥DQ,
在Rt△PCD和Rt△QCD中,
,
∴Rt△PCD≌Rt△QCD(HL),
∴∠PCD=∠QCD,
∵CP=CQ,
∴CD平分PQ,即CD经过点M,
∵CE=CF,M为PQ的中点,
∴CD平分∠ACB.
∵DA⊥AC,DG⊥BC,
∴DG=AD.
∵在Rt△ABC中,AB=3,AC=5,
∴BC.
∵,,
∴,
∴AD.
(3)①证明:连接CP,CQ,如图,
延长CM,由(2)知:CM经过点D,
∵M为PQ的中点,
∴CM⊥PQ,
∴∠CME=∠A=90°,
∵∠ECM=∠DCA,
∴△ECM∽△DCA,
∴,
∴ME CA=CM AD;
②解:在点D的运动过程中,BM存在最小值,BM的最小值为4,理由:
延长CM,由(2)知:CM经过点D,连接PC,如图,
∵M为PQ的中点,
∴CM⊥PQ,
∵DP切圆C于点P,
∴CP⊥DP,
∴∠CPD=90°,
∴△PCM∽△DCP,
∴,
∴PC2=CM CD,
由(3)①知:△ECM∽△DCA,
∴,
∴CM CD=CE CA,
∴PC2=CE CA,
∵PC,CA=5,
∴CE2.
∵∠CME=90°,
∴点M在以CE为直径的圆上运动,
取CE的中点O,如图,
则OC=OE=1,
∴AO=AC﹣OC=4,
∴BO5,
当点B,M,O三点在一条直线上时,BM取得最小值,
∴BM的最小值=BO﹣OM=5﹣1=4.
2.(2025 姑苏区校级二模)如图1,以AB为直径的⊙O与△ABC的边BC交于点D,∠CAD=∠ABC.点M是直径AB下方半圆上的一动点,连接AM,DM.DM交AB于点P.
(1)若AB=4,BC=2,求tan∠B的值;
(2)记△ACD的面积为S△ACD,△ABD的面积为S△ABD,若S△ACD:S△ABD,⊙O的半径为.求线段CD的长;
(3)如图2,当动点M运动到恰好使得P为DM的中点时,∠ABC的角平分线交DM于点E,交AD于点F,求的值.
【解答】解:(1)∵AB为圆的直径,
∴∠ADB=90°,
∴∠DAB+∠B=90°,
∵∠CAD=∠ABC,
∴∠DAB+∠CAD=90°,
∴∠CAB=90°,
∵AB=4,BC=2,
∴AC2,
∴tan∠B;
(2)∵∠ADB=90°,
∴AD⊥BC,
∴S△ACD,S△ABD,
∵S△ACD:S△ABD,
∴,
设CD=a,则BD=4a,
∵∠CAB=90°,AD⊥BC,
∴△ACD∽△BAD,
∴,
∴AD2=BD CD=4a2,
∴AD=2a.
∴ABa,
∵⊙O的半径为,
∴AB=22a,
∴a=1,
∴CD=a=1;
(3)过点F作FG⊥AB于点G,如图,
∵BF是∠ABC的角平分线,FG⊥AB,FD⊥BD,
∴FG=FD.
∵P为DM的中点,
∴DP=MP,
∵AB为圆的直径,
∴AB⊥MD,
∴△AFG∽△ADP,
∴,
∴.
∵AB为圆的直径,AB⊥MD,
∴,
∴∠MDB=∠BAD.
∵BF是∠ABC的角平分线,
∴∠DBF=∠ABF.
∵∠DEF=∠MDB+∠DBF,∠DFE=∠DAB+∠ABF,
∴∠DEF=∠DFE,
∴DF=DE,
∴,
∴1.
3.(2025 上虞区二模)如图1,已知点D在△ABC的边BC上,连结AD,⊙O是△ABD的外接圆,AC切⊙O于点A.
【探究发现】小敏通过探究发现:如图2中,过点A作⊙O的直径AE,连结ED,根据已知条件,可以证明∠CAD=∠B.请你根据小敏的思路,写出完整的证明过程.
【拓展迁移】当CA=3,时.
①求的值;
②求△ABC面积的最大值,并求出此时⊙O的半径.
【解答】【探究发现】证明:过点A作⊙O的直径AE,连结ED,如图,
∵AC切⊙O于点A,
∴OA⊥AC,
∴∠DAC+∠EAD=90°,
∵AE为⊙O的直径,
∴∠ADE=90°,
∴∠E+∠EAD=90°,
∴∠E=∠DAC,
∵∠E=∠B,
∴∠CAD=∠B;
【拓展迁移】解:①由【探究发现】知:∠CAD=∠B,
∵∠C=∠C,
∴△DAC∽△ABC,
∴,
∴,
∴DC或DC=﹣5(不合题意,舍去),
∵△DAC∽△ABC,
∴;
②由题意:当BA⊥AC时,△ABC面积最大,如图,
∵AC切⊙O于点A,BA⊥AC,
∴AB为圆的直径,
∴∠ADB=90°,
∴AD⊥BC,
由①知:DC,
∴AD,
∵,
∴BA=4.
∴此时⊙O的半径为2.
4.(2025 青秀区二模)综合与实践
【问题情境】如图1,贴窗花是我国特有的喜庆文化之一,我们可以从寓意团圆平安的窗花图案中抽象出一个由两个同心圆构成的几何图形(共同的圆心称为中心),如图2,我们称这种图形为“环花”.
【实践探究】设直线l与“环花”从左到右依次交于点A,B,C,D.
(1)如图2,当直线l经过中心O时,请直接写出线段AB与CD的数量关系;
(2)如图3,当直线l不经过中心O时,请证明(1)中的结论仍然成立;
【问题深化】
(3)如图4,当把“环花”中的两个圆形换成两个相似的菱形时(中心点O是这两个菱形对角线的公共交点,AB∥EF且F,B,D,H四点均在对角线FH上),类似地形成了“方花”,直线l不经中心O时,与“方花”从左到右依次交于点M,N,P,Q,求的值.
【解答】(1)①解:∵OA=OD,OB=OC,
∴OA﹣OB=OD﹣OC,
∴AB=CD;
②证明:如图,过点O作OE⊥l于点E,
∴AE=DE,BE=CE,
∴AB=CD.
(2)解:如图,连接FH,过点N作NR∥FH交EF于点R,过点P作PT∥FH交GH于点T,
∵AB∥EF,
∴四边形NRFB是平行四边形,
∴NR=FB,∠NRM=∠BFR,
同理得,PT=DH,∠DHT=∠PTQ,
∵四边形ABCD与四边形EFGH均为菱形,O为它们的中心,
∴OF=OH,OB=OD,GH∥EF,
∴FB=DH,∠PQT=∠NMR,∠DHT=∠BFR,
∴NR=PT,∠NRM=∠PTQ,
∴△MNR≌△PQT(AAS),
∴MN=PQ,
∴.
5.(2025 钱塘区校级模拟)如图1,已知AB是⊙O的直径,弦CD⊥AB于点E,点F是CD延长线上的一点,连结AF交⊙O于点G,连结CA,CG.
(1)求证:∠ACG=∠F.
(2)已知AB=10,CD=8.
①若点G是弧AD的中点,求DF的长.
②如图2,CG与AB交于点P,设tan∠F=x,,求y关于x的函数表达式.
【解答】(1)证明:∵AB是⊙O的直径,弦CD⊥AB,
∴,
∴∠ACD=∠AGC,
∵∠ACD=∠ACG+∠GCF,∠AGC=∠F+∠GCF,
∴∠ACG+∠GCF=∠F+∠GCF,
∴∠ACG=∠F.
(2)解:①连接OC,AD,如图,
∵AB是⊙O的直径,AB=10,
∴OC=OAAB=5,
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=DECD=4,
∴OE3,
∴AE=OA+OE=5+3=8,
∴AC4.
∵AB是⊙O的直径,弦CD⊥AB,
∴,
∴AC=AD=4.
∵点G是弧AD的中点,
∴,
∴∠ACG=∠DCG,
由(1)知:∠ACG=∠F,
∴∠F=∠DCG.
∵∠DCG=∠DAG,
∴∠F=∠DAG,
∴DF=AD=4;
②过点P作PH⊥AC于点H,连接BC,如图,
由(2)①知:AE=8,CE=4,AC=4,
∴BE=AB﹣AE=2,
∴BC2,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC⊥AC,
∵PH⊥AC,
∴PH∥BC,
∴△AHP∽△ACB,
∴2,
∴AH=2HP.
∵tan∠F=x,∠ACG=∠F,
∴tan∠ACG=x,
∵tan∠ACG,
∴x,
∴CH.
∵PH∥BC,
∴2x,
∵,
∴y关于x的函数表达式为y=2x.
6.(2025 鲤城区校级模拟)如图1,△ABC内接于⊙O,点E为△ABC的内心,连接AE并延长交⊙O于点D,交BC于点F,连接BD.
(1)若∠DBC=35°,求∠BAC的度数.
(2)如图2,连接BE,若AE=3,EF=2,求BD的长.
(3)如图3,连接OE,若⊙O的半径为4,弦,设OE=x,AE=y,求y与x之间的函数关系式及y的最大值.
【解答】解:(1)∵点E为△ABC的内心,
∴∠BAD=∠CAD,
∵,
∴∠CBD=∠CAD,
∴∠BAD=∠CAD=∠CBD=35°,
∴∠BAC=2∠BAD=70°.
(2)∵BE平分∠ABC,AE平分∠BAC,
设∠ABE=∠CBE=α,∠BAE=∠CAE=β,
∴∠CBD=β,
∴∠EBD=∠CBD+∠EBC=α+β,∠BED=∠ABE+∠BAE=α+β,
∴∠EBD=∠BED,
∴BD=ED,
设DF=x,
∵AE=3,EF=2,
∴BD=ED=DF+EF=x+2,
∴AD=AE+ED=x+5,
∵∠DBF=∠DAB,∠BDF=∠ADB,
∴△DBF∽△DAB,
∴,
∴DB2=DA DF,
∴(x+2)2=x(x+5),
∴x=4,
∴BD=ED=x+2=6.
(3)如图,连接OB,连接OD交BC于点M,
∵∠BAD=∠CAD,
∴BD=CD,
∴OD垂直平分BC,
∴BM=CMBC=2,
∵OB=4,
在Rt△OBM中,MO2,
∴DM=2,
∴.
由(2)得,当BE平分∠ABC,AE平分∠BAC时,
有BD=ED,
∴DE=BD=4
作OH⊥AD,连接OA,OE,
在Rt△OHA中,OH2=16﹣AH2,
在Rt△OHE中,OH2=x2﹣HE2,
∴x2=16﹣AH2+HE2,
∵AH=DH,DE=4,
∴x2=16﹣(AH2﹣HE2)=16﹣(AH+HE)(AH﹣HE)=16﹣(DH+HE)(AH﹣HE),
即x2=16﹣4y,
∴,
∵,
∴y的最大值是4,即AE的最大值为4.
7.(2025 永寿县校级模拟)问题提出
(1)如图①,⊙O是Rt△ABC的内切圆,且⊙O与AC的切点为D,已知⊙O的半径为2,∠ABC=90°,AB=8,求AD的长;
问题解决
(2)如图②,某小区的花艺师准备在空地上设计一个四边形花园ABCD,然后将其分割种植三种不同的花卉,结合美观性和土地利用性考虑,要求AB∥CD,∠BAD=90°,AD=150m,BC=170m,连接BD,点E,F分别在BD,CD上,且满足DE的长度不小于AB的长度,点G是△BCD的内心,连接EG,FG,BD=BC,GE=GF,其中四边形DEGF内种植牡丹,△ABD内种植芍药,剩下的区域种植万寿菊,由于移植的牡丹植株较小,抗风性差,现需要用防护网围起来,待培育成活后会拆除防护网,为了节省材料,避免浪费,要求种植牡丹的四边形DEGF的周长最小,四边形DECF的周长是否存在最小值?若存在,请求出其最小值;若不存在,请说明理由.
【解答】解:(1)连接OD,再记AB,BC分别与⊙O相切于点E,F,连接OE,OF,如图所示:
∵⊙O是Rt△ABC的内切圆,
∴AE=AD,∠OEB=∠OFB=90°,
∴∠ABC=90°,
∴四边形BFOE是矩形,
∵OF=OE,
∴四边形BFOE是正方形,
∴EB=OF=2,
∴AD=AE=AB﹣BE=8﹣2=6.
(2)四边形DEGF的周长存在最小值,且为256m,过程如下:
∵AB∥CD,∠BAD=90°,
∴∠ADC=90°∠BAD=90°,AD=150m,BC=170m,BD=BC,
∴BD=170m,
在Rt△ABD中,,
连接DG,过B作BW⊥CD,过G作GH⊥BD,如图所示:
则∠DWB=∠ADC=∠BAD=90°,
∴四边形ABWD是矩形,
∴DW=AB=80m,AD∥BW,
∵BD=BC,BW⊥CD,
∴DC=2DW=2×80m=160m,∠DBW=∠CBW,
∵点G是△BCD的内心,
∴点G在WB上,且DG是∠BDC的角平分线,
∵BW⊥CD,GH⊥BD,
∴HG=GW,∠EHG=∠FWG=90°,
∵GE=GF,
∴Rt△EHG≌Rt△FWG(HL),
∴EH=FW,
∴ED=EH+HD,DF=DW﹣FW,
∵∠DHG=∠DWG=90°,HG=GW,DG=DG,
∴Rt△DHG≌Rt△DWG(HL),
∴HD=DW=AB=80m,
∵四边形DEGF的周长=ED+EG+GF+DF,且GE=GF,
∴四边形DEGF的周长=EH+HD+2EG+GF+DW﹣FW=2HD+2EG,
即四边形DEGF的周长=2×80+2EG=160+2EG,
当EG⊥BD时,则四边形DEGF的周长有最小值,即EG=HG=GW,
则BW=AD=150m,BG+GW=BG+GH=150m,
∵AD∥BW,
∴∠GBH=∠ADW
故s,
∴,
∴,则,
解得BG=102m,
∴,
即四边形DEGF的周长=160+2×48=160+96=256(m),
∴四边形DEGF的周长存在最小值,且为256m.
8.(2025 南岗区校级三模)如图,AB为⊙O的弦,点C为弧AB的中点,点D为⊙O上一点,连接CD交弦AB于点E,连接BD.
(1)如图1,求证:∠CEB=∠CBD;
(2)如图2,过点A作AF∥CD交⊙O于点F,连接DF,求证:CB=DF;
(3)如图3,在(2)的条件下,当AB为⊙O的直径时,DF与AB交于点K,若,CD2+AF2=196时,求KE的长.
【解答】(1)证明:连接AC.
∵点C为弧AB的中点,
∴AC=BC,
∴∠CAB=∠CBA=∠CDB.
∵∠CEB是△ACE的外角,
∴∠CEB=∠CAB+∠ACD,
而∠CBD=∠CBA+∠ABD=∠CAB+∠ABD,
∵AD=AD,
∴∠ABD=∠ACD,
∴∠CEB=∠CBD.
(2)证明:∵AF∥CD,
∴∠AFD=∠CDF,
∴,
∴,
∴AC=DF,
∵点C为弧AB的中点,即AC=BC,
∴CB=DF.
(3)解:连接AD、AC,OC,
由(2),
∴,即,
∵DF=BC,
∴CD=BF,
∵AB是⊙O的直径,
∴∠ADB=∠AFB=90°,
∴AB2=AF2+BF2=AF2+CD2=196,
∴AB=14,
∴OB=OA=OCAB=7,
∵,
∴OE=BE﹣OB7,
∴AE=AB﹣BE=14,
∵点C为弧AB的中点,OC是半径,
∴OC⊥AB,AC=BC,∠CBE=∠CDB,
∴DF=AC=BC,CE,
∵∠CBE=∠CDB,∠DCB=∠BCE,
∴△BEC∽△DBC,
∴,
即,
,
即,
∴BD,BF=CD,
∴AF,
∵∠AFD=∠DBK,∠BDK=∠FAK,
∴△AFK∽△DBK,
∴,
∴BK,DK,
∵AB=AK+BK=14,
∴14﹣AK,
∴AK=2.
∴.
9.(2025 平湖市二模)已知四边形ABCD内接于⊙O,对角线AC,BD交于点E,P为BD上一点,连结AP.
(1)如图1,若AB为⊙O的直径,且△ABC与△APD均为等腰直角三角形,求证:△ADC∽△APB.
(2)如图2,若△ABC与△APD均为等边三角形.
①求证:BP=CD.
②若AD=1,求的最小值.
【解答】(1)证明:∵AB为⊙O的直径,
∴∠ADP=∠ACB=90°,
∵△ABC和△APD为等腰直角三角形,
∴,,∠DAP=∠CAB=45°,
∴,
∵∠DAP﹣∠CAP=∠CAB﹣∠CAP,
∴∠DAC=∠PAB,
∴△ADC∽△APB;
(2)证明:①∵△ADP和△ABC为等边三角形,
∴AD=AP,AC=AB,∠DAP=∠CAB=60°,
∴∠DAP﹣∠CAP=∠CAB﹣∠CAP,
∴∠DAC=∠PAB,
在△ACD和△ABP中,
,
∴△ACD≌△ABP(SAS),
∴CD=BP;
②解:∵△APD为等边三角形,
∴DP=AD=1,
设PE=x,则DE=1﹣x,
由①可知:CD=BP,∠BDC=∠APD=60°,
∴AP∥CD,
∴△APE∽△CDE,
∴,
∴,
∴,
∴BE=BP+PEx,BD=BP+PD.
∵∠DCA=∠CAP,∠DCA=∠EBA,
∴∠CAP=∠EBA.
∵∠AEP=∠BEA,
∴△AEP∽△BEA,
∴,
即,
∴AE2=x2﹣x+1,
∴AE,
∴,
∴,
∴,
∴当时,x2﹣x+1有最小值,
∴的最小值为.
10.(2025 广东模拟)综合与实践
【主题】圆形纸片与剪纸艺术
【素材】图1中半径为2的圆形纸片(⊙O)若干.
【实践操作】活动一:如图2,在该圆形纸片(⊙O)上剪出一个圆周角为90°的扇形.
活动二:如图3,在另一圆形纸片(⊙O)内剪出一个内接正六边形,设该正六边形ABCDEF的面积为S1,再连接AC,AE,剪出△ACE,设△ACE的面积为S2.
活动三:在活动二的基础上,装饰粘贴上六个弧形花瓣,中心为点O,所在圆的圆心C恰好是△ABO的内心.
【实践探索】
(1)根据剪纸要求,计算图2中的扇形ABC的面积.
(2)请直接写出的值: 2 .
(3)求弧形花瓣总的周长(图4中实线部分的长度).(结果保留π)
【解答】解:(1)如图,连接BC,
∵∠A=90°,
∴BC为⊙O的直径,即BC=4,
∵AB=AC,
∴,
∴扇形ABC的面积为;
(2)解:如图,连接OA,OC,OE,OF,
∵六边形ABCDEF为正六边形,
∴,,
∵OA=OF=OE,
∴△AOF,△FOE等边三角形,
∴OA=FA,OE=FE,∠AOF=∠FOE=60°,
∴∠AOE=∠AFE=120°,
∴△AOE≌△AFE(SAS),
同理可得△ABC≌△AOC,△COE≌△ADE,
∴,
故答案为:2;
(3)如图,过点C作CM⊥AB于点M,
∵六条等弧所对应的弦构成一个正六边形,中心为点O,
∴,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=2,
∴,
∵点O是△AOB的内心,
∴,∠ACB=2∠AOB=120°,
在Rt△ACM中,AM=1,∠CAM=30°,
∴,
∴,
∴花窗的周长为.
11.(2025 缙云县二模)已知△PAB内接于⊙O,PH⊥AB于点H.
(1)如图1,当PH经过圆心O时,求证:PA=PB;
(2)如图2,当PH不经过圆心O时,过点A作AC⊥PB于点C,交PH于点D,交⊙O于点E,连结BD,BE,求证:∠PAC=∠PBD;
(3)如图3,在(2)的条件下,若AD=PD,AH:BH=5:2,,求⊙O的半径长.
【解答】(1)证明:∵PH经过圆心O,PH⊥AB,
∴BH=AHAB,
∴PH垂直平分AB,
∴PA=PB;
(2)证明:连接PE,如图,
∵PH⊥AB,
∴∠BAE+∠ADH=90°,
∵∠ADH=∠PDC,
∴∠PDC+∠BAE=90°.
∵AC⊥PB,
∴∠PDC+∠CPD=90°,
∴∠CPD=∠BAE.
∵∠BAE=∠BPE,
∴∠BPE=∠DPC.
在△EPC和△DPC中,
,
∴△EPC≌△DPC(ASA),
∴EC=DC,
∵AC⊥PB,
∴PB是DE的垂直平分线,
∴BE=BD,
∴∠PBD=∠PBE.
∵∠PAC=∠PBE,
∴∠PAC=∠PBD;
(3)解:∵AH:BH=5:2,
∴设AH=5k,则BH=2k,
∴AB=AH+BH=7k.
在△PDC和△ADH中,
,
∴△PDC≌△ADH(AAS),
∴DC=DH,PC=AH=5k,
在Rt△BDC和Rt△BDH中,
,
∴Rt△BDC≌Rt△BDH(HL),
∴BC=BH=2k,
∴PC+BC=AH+BH,
∴PB=AB=7k,
∴PH2=PB2﹣BH2=(7k)2﹣(2k)2=45k2.
∵PA2=PH2+AH2,
∴,
∵k>0,
∴k.
∴AB=7k,
∵PD=AD,PB=AB,
∴BD在PA垂直平分线上,
延长BD,交PA于点G,连接OP,如图,
∵弦的垂直平分线经过圆心,
∴BG经过点O,PG=AG.
∴BG.
设⊙O的半径长为r,则OB=OP=r,OG=BG﹣OPr,
∵OG2+PG2=OP2,
∴,
∴r.
∴⊙O的半径长为.
12.(2025 石家庄二模)(1)图1是利用已知线段AB进行的尺规作图,请根据图1的作图填空:
①首先分别以A,B为圆心,以AB长为半径画弧,作了 等边 △OAB;
②再以O为圆心,以 OA 为半径作了圆O;
③最后在优弧ACB上作了 圆周角 (选填“圆周角”或“圆心角”)∠ACB,算得∠ACB的度数为 30° .
(2)图2中四边形EFGH是矩形,其边EF=4,FG=6.已知点P在直线GH的左侧,且tan∠GPH.请按要求完成下列问题.
①通过尺规作图在图2中找到一个点P,使(保留作图痕迹,不写作图过程);
②使得的点P有多少个?说明理由;
③求点P到直线EF的最小距离.
【解答】解:(1)①首先分别以A,B为圆心,以AB长为半径画弧,作了等边△OAB;
②再以O为圆心,以OA(答案不唯一,OA、AB、OB之一均可)为半径作了圆O;
③最后在优弧ACB上作了圆周角∠ACB,算得∠ACB的度数AOB30°.
故答案为:①等边;②OA(答案不唯一,OA、AB、OB之一均可);③圆周角,30°;
(2)①作出线段FG的垂直平分线MN,MN交FG于点P,如图,
点P即为所求;
②使得的点P有无数个.理由:
设FG的垂直平分线交EH于点Q,连接GQ交于PH点O,以点O为圆心,以OP为半径画圆,如图,
则圆O为矩形GHQP的外接圆,
∵同弧所对圆周角相等,
∴优弧上的点与G,H连线形成的圆周角都等于∠GPH,即优弧上的点都符合题意.
∴使得的点P有无数个;
③过点O作GH的中垂线MN,交EH于点M,交GH于点N,交劣弧于点W,如图,
∵PQ为FG的垂直平分线,
∴PG3,PQ⊥PG,
∵四边形EFGH为矩形,
∴∠E=∠F=∠EHG=∠HGF=90°,
∴四边形PQHG为矩形,
∵MN为GH的垂直平分线,
∴四边形EHNM是矩形,且N是GH的中点,
∴MN=EH=6,,
∵圆O的直径,
∴,
∴点P到直线EF最小距离等于WM=MN﹣ON﹣OW=2.
13.(2025 德阳模拟)如图1,⊙O为△ABC的外接圆,点B为的中点,点F为劣弧AC上除弧中点外一动点,连接AF,∠AFB=60°,连接BF交AC于D点,过F点作⊙O的切线交直线AC于E点,连接BE.
(1)连接OA,OB,则∠AOB= 120 °,若AB=3,则⊙O的面积= 3π ;
(2)判断△DEF的形状,并进行证明;
(3)已知⊙O的半径为r,如图2,取AC延长线上一点G,连接BG,且BC平分∠GBF.
①求AF BG;(结果用r表示)
②是否为定值,若是请求出定值,若不是请说明理由.(结果用r表示)
【解答】解:(1)连接OA,OB,过点O作OH⊥AB于点H,如图,
则∠AOB=2∠AFB=120°.
∵OA=OB,OH⊥AB,
∴∠AOH=∠BOH∠AOB=60°,AH=BHAB.
在Rt△AOH中,
∵sin∠AOH,
∴,
∴OA.
∴⊙O的面积=π OA2=3π.
故答案为:120;3π;
(2)△DEF的形状是等腰三角形,证明:
连接BO并延长交AC于点N,连接OC,OF,如图,
∵点B为的中点,
∴,
∴BN⊥AC,AB=BC.
∴∠BDN=90°﹣∠OBD.
∵EF为⊙O的切线,
∴OF⊥EF,
∴∠BFE=90°﹣∠OFB.
∵OB=OF,
∴∠OBD=∠OFB,
∴∠EFB=∠NDB.
∵∠NDB=∠FDE,
∴∠BFE=∠FDE,
∴EF=ED,
∴△DEF的形状是等腰三角形;
(3)①连接BO并延长交AC于点N,连接OC,OF,CF,如图,
∵点B为的中点,
∴,
∴BN⊥AC,AB=BC.
∵∠ACB=∠AFB=60°,
∴△ABC为等边三角形,
∴AB=BC=AC,∠BAC=∠ACB=∠ABC=60°.
由(1)知:ABOA.
∵⊙O的半径为r,
∴AB=BC=ACr.
∵BC平分∠GBF,
∴∠FBC=∠GBC.
∵∠G=∠ACB﹣∠GBC=60°﹣∠GBC,∠ABF=∠ABC﹣∠FBC=60°﹣∠FBC,
∴∠ABF=∠G.
∵∠AFB=∠BAC=60°,
∴△ABF∽△BGA,
∴,
∴AF BG=AB23r2.
②为定值,定值为,理由:
过点C作CH∥AB,交BG于点H,如图,
设CD=m,GC=n,
由①知:AB=BC=ACr,∠BAC=∠ACB=∠ABC=60°,
则AG=GC+AC=nr.
∵CH∥AB,
∴∠HCG=∠BAC=60°,
∴∠BCH=180°﹣∠ACB﹣∠HCG=60°=∠ACB.
在△BDC和△BHC中,
,
∴△BDC≌△BHC(ASA),
∴DC=HC=m.
∵CH∥AB,
∴△GHC∽△GBA,
∴,
∴,
∴mnmrnr,
∴r(n﹣m)=mn.
∴.
14.(2025 黄岩区二模)如图1,AB是⊙O的直径,点C是圆上一点(A,B除外),点D,E在AB上,满足AD=AC,BE=BC,CD,CE的延长线分别交⊙O于点F,G.记∠CAB=α.
(1)若α=30°,求∠FCG的度数;
(2)连结FG,求证:;
(3)如图2,连结并延长BF,AG交于点H,若
①求的值;
②请直接写出cosα的值.
【解答】(1)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵α=30°,
∴∠ABC=60°,
∵AD=AC,BE=BC,
∴∠ADC=75°,∠BEC=60°,
∴∠FCG=45°;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠CAB=α,
∴∠ABC=90°﹣α,
∵AD=AC,BE=BC,
∴,,
∴∠FCG=45°.
连结OF,OG,
则∠FOG=2∠FCG=90°,
∴FGOG,
∵AB=2OG,
∴;
(3)解:①∵四边形AGFB是圆内接四边形,
∴∠HFG=∠HAB,∠HGF=∠HBA,
∴△HFG∽△HAB,
∴,
∵,
∴设BF=a,FH=3a,则BH=4a,
∴,,
∴,
∴;
②连接BG、AF,过F作FH⊥AB于点H,
由①得BF=a,FH=3a,AGa,GH=2a,
∵∠FCG=45°,
∴∠CBF=∠FCG=45°,
∵∠BGH=90°,
∴△BGH是等腰直角三角形,
∴BG=GH=2a,
在Rt△BAG中,ABa,
∵AC=AD,
∴∠ACD=∠ADC,
∴∠BDF=∠ADC,
∵∠FBA=∠FCA,
∴△FBD∽△ACD,
∴FB=FD=a,
在Rt△ABF中,AF3a,
由等面积可得FHa,
∴BHa,
∴BD=2BHa,
∴AD=AB﹣BDa,
∴cosα.
15.(2025 东莞市校级二模)综合与实践:根据以下素材,探索求圆半径的方法.
【背景素材】同学们用若干大小不一的透明圆形(或半圆形)纸片,及一张宽2cm且足够长的矩形纸带(如图1)设计了一系列任务,探索完成任务.
【任务一】若同学甲将一圆形纸片与矩形纸带摆放成如图2位置,使圆经过A,B,G.现测得AG=1cm,求出该圆的半径.
【任务二】按如图3摆放纸片,点A,P在圆上.在AD边上取点M使AM=2AB,作MN⊥BC于N,连结AN恰过圆心O,交圆于点Q,连结PN.量得∠1=∠2.
①判断直线PN与⊙O的位置关系,并说明理由;
②直接写出⊙O的半径为 cm.
【解答】解:【任务一】∵四边形ABCD为矩形,
∴∠A=90°,
∴BG为经过A,B,G三点的圆的直径,
∵BG,
∴该圆的半径为BG;
【任务二】①直线PN与⊙O的位置关系为PN与⊙O相切,理由:
连接OP,如图,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠MAN=∠1,
∵∠1=∠2,
∴∠MAN=∠2,
∵∠NMA=∠PMN,
∴△NMA∽△PMN,
∴∠MNA=∠MPN,
∵MN⊥BC,
∴∠MAN+∠MNA=90°,
∴∠MPN+∠MAN=90°.
∵OA=OP,
∴∠MAN=∠OPA,
∴∠OPA+∠MPN=90°,
∴∠OPN=90°,
∴OP⊥NP,
∵OP为圆的半径,
∴PN与⊙O相切;
②∵AM=2AB,
∴AM=4cm.
∵四边形ABCD为矩形,
∴∠A=∠B=90°,MN⊥BC,
∴四边形ABNM为矩形,
∴MN=AB=2cm,BN=AM=4cm,
由①知:△NMA∽△PMN,
∴,
∴,
∴MP=1cm.
∴NPcm.
∵MN⊥BC,
∴AN2cm.
设⊙O的半径为x cm,则OA=OP=x cm,ON=AN﹣OA=(2x)cm,
∵OP⊥NP,
∴OP2+PN2=ON2,
∴,
∴x.
∴⊙O的半径为cm.
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
