【攻克压轴大题】2025年中考数学压轴题精选:二次函数习了平
文档属性
| 名称 | 【攻克压轴大题】2025年中考数学压轴题精选:二次函数习了平 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 21:02:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【攻克压轴大题】2025年中考数学压轴题精选:二次函数
1.(2025 石家庄二模)如图,抛物线L的顶点坐标为(4,36),与y轴交于点C(0,20),与x轴交于点A,B(点A在点B左侧).
(1)求抛物线L的解析式和A,B两点坐标;
(2)线段OB上的两个点D(m,0),E(m+1,0),分别过点D,E作x轴的垂线交抛物线L于点N,M,连接MN.
①线段ME的长度能否为线段DN长度的2倍,若能,求出m的值,若不能,请说明理由;
②当m为何值时MN的值最小,最小值是多少?
③当时,直接写出m的取值范围.
2.(2025 乾安县模拟)抛物线y=ax2﹣2x+c(b,c为常数)经过点A(0,﹣2),点N(3,1),点M在此抛物线上,点M的横坐标为m,点M不与A重合,抛物线上点M与点A之间的部分(包括端点)记为图象G.
(1)求此抛物线所对应的函数解析式;
(2)当图象G的最大值与最小值差为1时,直接写出m的取值范围;
(3)图象G与直线y=﹣2m+1有且只有一个交点时,求m的取值范围;
(4)连接AM,以AM为对角线构造矩形ABMC,AC∥BM∥x轴,CM∥y轴,矩形ABMC的边与抛物线的交点为点D(异于点A,M),点D关于CM的对称点是点E,当3DE=CM时,直接写出m的值.
3.(2025 康县四模)如图所示,在平面直角坐标系中,直线y=﹣x+3交坐标轴于B、C两点,抛物线y=ax2+bx+3经过B、C两点,且交x轴于另一点A(﹣1,0).点D为抛物线在第一象限内的一点,过点D作DQ∥CO,DQ交BC于点P,交x轴于点Q.
(1)求抛物线的解析式;
(2)设点P的横坐标为m,在点D的移动过程中,存在∠DCP=∠DPC,求出m值;
(3)在抛物线上取点E,在平面直角坐标系内取点F,问是否存在以C、B、E、F为顶点且以CB为边的矩形?如果存在,请求出点F的坐标;如果不存在,请说明理由.
4.(2025 西陵区模拟)如图1,抛物线y=x2+mx+n交x轴于A(﹣1,0),B(3,0),交y轴于点C.
(1)求m和n的值;
(2)点P为抛物线上第一象限内一点,且△POC的面积等于6,求点P的坐标;
(3)如图2,将图1抛物线位于x轴下方的部分沿x轴翻折到x轴上方,保留其原本位于x轴上方的部分,得到如图2所示的新函数图象,记此新函数为G(x).
①若直线l:y=kx﹣k+6(k≠0)与函数G(x)的图象有且仅有3个交点,求k的值;
②在①的条件下,设|k|的最大值为p,若直线y=px+t与函数G(x)的图象围成的封闭图形内部(不包括边界)恰有4个横、纵坐标均为整数的点,直接写出t的取值范围.
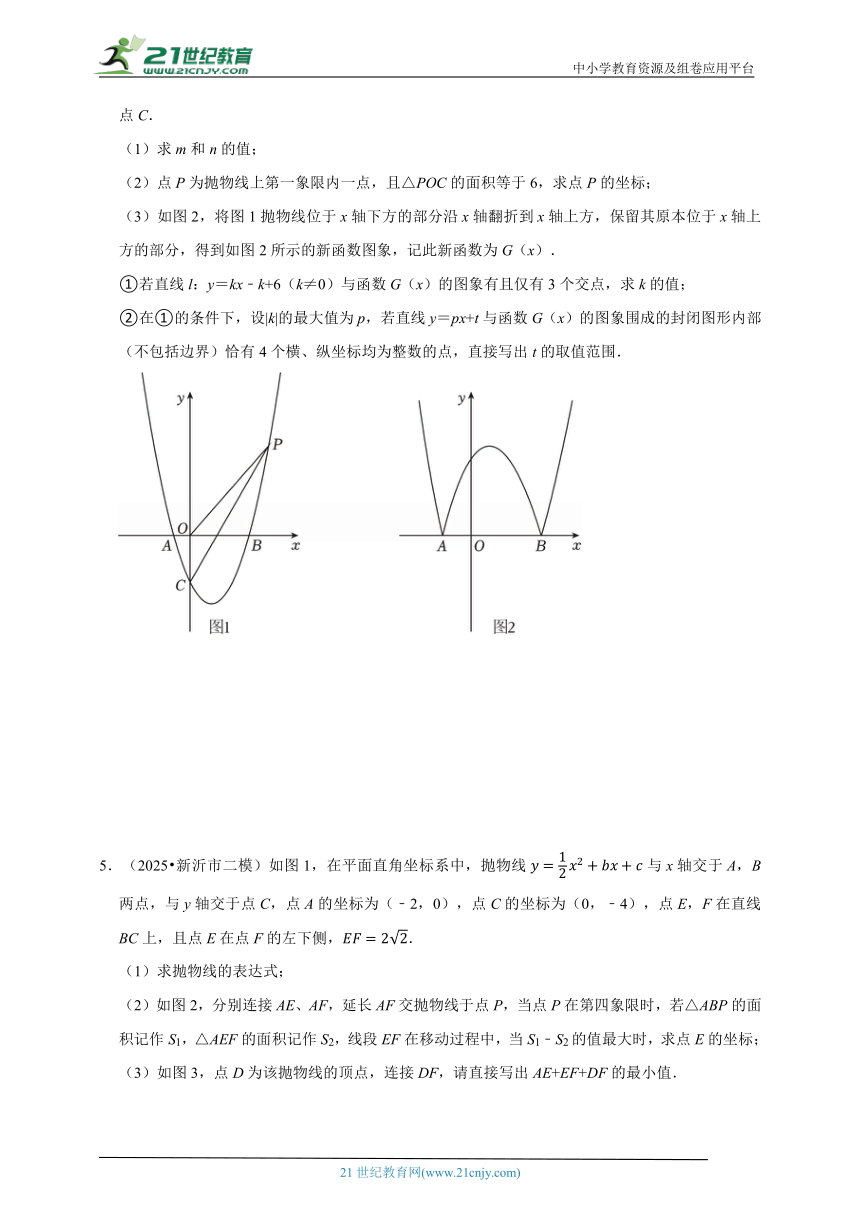
5.(2025 新沂市二模)如图1,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,点A的坐标为(﹣2,0),点C的坐标为(0,﹣4),点E,F在直线BC上,且点E在点F的左下侧,.
(1)求抛物线的表达式;
(2)如图2,分别连接AE、AF,延长AF交抛物线于点P,当点P在第四象限时,若△ABP的面积记作S1,△AEF的面积记作S2,线段EF在移动过程中,当S1﹣S2的值最大时,求点E的坐标;
(3)如图3,点D为该抛物线的顶点,连接DF,请直接写出AE+EF+DF的最小值.
6.(2025 裕华区校级二模)在平面直角坐标系中,抛物线y=x2+bx+c与x轴分别交于点A(﹣3,0)与点B(1,0).已知点P是该抛物线上一动点(不与点B重合).
(1)求抛物线的解析式和顶点坐标.
(2)将抛物线上P、B两点之间的部分(包括端点)记作图象W,当图象W上最高点与最低点的纵坐标的差是5时,求点P的坐标.
(3)若动点P的横坐标是n,另有坐标系中一动点Q,其坐标是(﹣3n,n).如图2,在坐标系中构造一个各边均与坐标轴垂直的矩形,使PQ为矩形的对角线.当抛物线在矩形内部的部分对应的函数值y随x的增大而增大,直接写出n的取值范围.
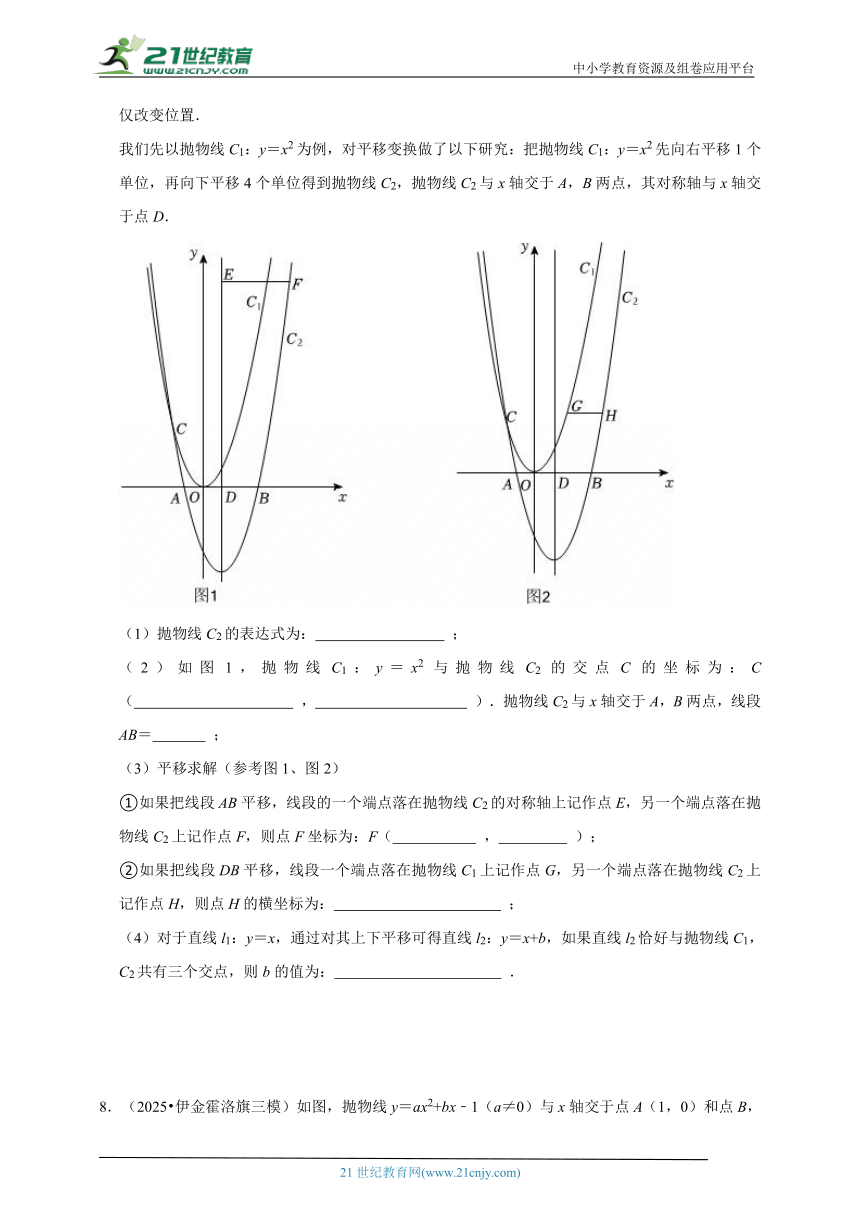
7.(2025 福田区模拟)平移是初中数学中的重要图形变换之一,其特点是保持图形形状、大小不变,仅改变位置.
我们先以抛物线C1:y=x2为例,对平移变换做了以下研究:把抛物线C1:y=x2先向右平移1个单位,再向下平移4个单位得到抛物线C2,抛物线C2与x轴交于A,B两点,其对称轴与x轴交于点D.
(1)抛物线C2的表达式为: ;
(2)如图1,抛物线C1:y=x2与抛物线C2的交点C的坐标为:C( , ).抛物线C2与x轴交于A,B两点,线段AB= ;
(3)平移求解(参考图1、图2)
①如果把线段AB平移,线段的一个端点落在抛物线C2的对称轴上记作点E,另一个端点落在抛物线C2上记作点F,则点F坐标为:F( , );
②如果把线段DB平移,线段一个端点落在抛物线C1上记作点G,另一个端点落在抛物线C2上记作点H,则点H的横坐标为: ;
(4)对于直线l1:y=x,通过对其上下平移可得直线l2:y=x+b,如果直线l2恰好与抛物线C1,C2共有三个交点,则b的值为: .
8.(2025 伊金霍洛旗三模)如图,抛物线y=ax2+bx﹣1(a≠0)与x轴交于点A(1,0)和点B,与y轴交于点C,抛物线的对称轴交x轴于点D(3,0),过点B作直线l⊥x轴,过点D作DE⊥CD,交直线l于点E.
(1)求抛物线的解析式;
(2)连接AC,求证:∠ACD+∠BED=45°;
(3)如图,点P为第三象限内抛物线上的点,连接CE和BP交于点Q,当时,求点P的坐标.
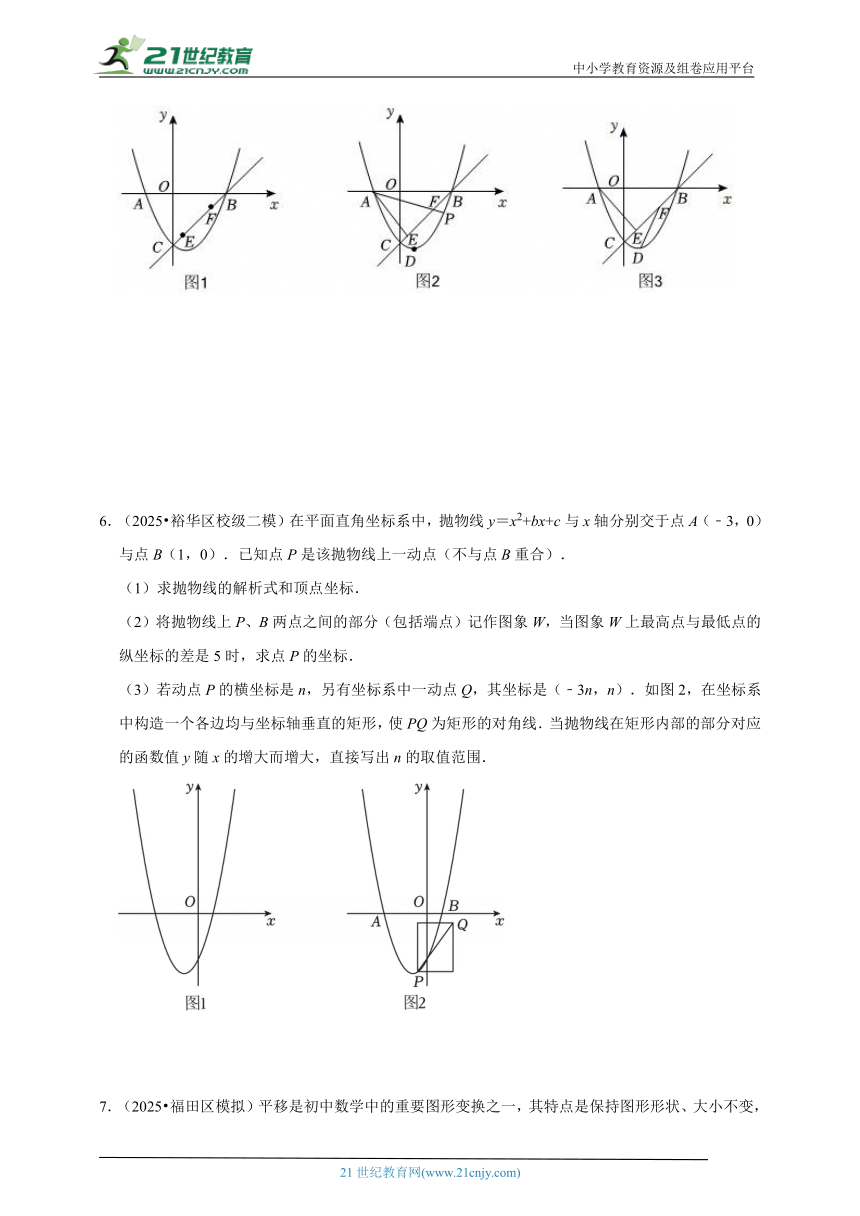
9.(2025 天桥区三模)已知抛物线y=x2+mx+n与x轴交于A(﹣1,0),B两点,与y轴交于点C(0,﹣4).
(1)求抛物线的解析式;
(2)如图1,已知点E为第四象限抛物线上的点,连接AC、BE、AE、BC,且AE和BC相交于点F,设△ACF的面积为S1,△BEF的面积为S2,当S1﹣S2=5时,求点E的坐标.
(3)如图2,设点P(x1,y1),Q(x2,y2)是直线BC下方抛物线上的两动点,且x2=x1+1,过点P作PM∥y轴,交BC于点M,过点Q作QN⊥BC,交BC于点N.求的最大值.
10.(2025 江阳区模拟)如图(1),抛物线交x轴于A,B两点(点A在左边),交y轴于点C.
(1)直接写出A,B,C三点的坐标;
(2)D是抛物线第四象限上的一点,连接AD分别交BC,OC于E,F两点,若∠FEC=∠FCE,求直线AD的解析式;
(3)平移抛物线使它的顶点为(0,1),如图(2).R是y轴上一个定点,以点R为直角顶点作Rt△RST,使顶点S,T分别在x轴和抛物线上.若Rt△RST在变化的过程中,直线ST与抛物线始终有唯一公共点,求点R的坐标.
11.(2025 祁阳市校级一模)如图,直线y=﹣x+3与x轴的正半轴、y轴的正半轴分别相交于点A和点C,点B是点A关于原点O的对称点,四边形ABCD是平行四边形,抛物线y=ax2+bx﹣10经过点B和点D.
(1)求平行四边形ABCD的面积;
(2)求抛物线的解析式;
(3)动点P从点C出发,以每秒1个单位的速度匀速运动到点D;同时动点Q从点A出发,以每秒1个单位的速度匀速运动到点C,设运动的时间为t.
①当CP=CQ时,求t的值;
②请你猜想,在P,Q两点的运动过程中,是否存在某一时刻t,使得四边形ADPQ的面积最小?若存在,求出t的值,并求出这个最小值;若不存在,请说明理由.
12.(2025 河源二模)如图所示,已知二次函数图象与直线y=﹣x+m相交于点A(5,0).直线交y轴于B,点P为抛物线上一点,将点P绕着原点O逆时针旋转90°得到对应点Q,连接PQ.
(1)求抛物线和直线AB的函数解析式.
(2)当点P坐标为(6,2)时,求证:点P,Q,B三点在同一直线上.
(3)当△OPQ有一顶点在直线AB上时,
①求PQ长;
②在①的条件下,当点P在第四象限时,在PQ上取点C,在OP上取点D,使QC=PD,连接OC,DQ,求OC+DQ的最小值.
13.(2025 同安区一模)如图,抛物线y=﹣x2+bx+c与x轴,y轴分别交于A,B,C三点(点A在点B的左侧),其中点A(﹣3,0).对称轴.
(1)求抛物线的解析式;
(2)如图1,点D(1,4)在抛物线上,过点D作DF⊥x轴于点F,过点A的直线交y轴于点E(0,2),点P是直线AE上方抛物线上的一动点,过点P作PM⊥AE于点M,PN⊥DF于点N,求的最大值,以及此时点P的坐标;
(3)如图2,在(2)的条件下,将抛物线y=﹣x2+bx+c先向下平移2个单位长度,再向左平移2个单位长度,得到新抛物线y1,点R是新抛物线y1上一个动点且在AD上方,当∠RAD+∠BDF=45°时,请求出符合条件的点R的坐标.
14.(2025 洪山区模拟)如图,抛物线y=﹣x2+bx+c交x轴于A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)如图1,抛物线顶点N,AN与y轴交于点C,若x轴上存在一点M使∠NBA=∠CMG,MG交NB于点G,当,求点G坐标;
(3)如图2,点D为x轴上方抛物线上一点,点R(6,0),若Q为线段DR上一点,过Q作PQ∥AD交x轴于点P,求△PQD面积最大值.
15.(2025 宝安区模拟)我校九年级学生去游乐园进行春游,在过山车项目排队时,小明发现过山车的轨道可近似看出多个函数图象的组合.活动结束后,数学老师给同学们提出如下问题:如图是水上过山车的示意图.
如图1,AB段为直滑道,BC段、EF段为平行滑道,C、F分别为冲刺顶点,CDE段为抛物线y=ax2+bx+227的一部分,D为抛物线顶点,FG段为双曲线y的一部分,其中冲刺顶点C离地距离27m,冲刺顶点F离地距离18m,水面高度为1m,G为抛物线和水面的接触点,B(8,27),D(15,2),E(m,18),BC=EF=2m.
(1)求抛物线CDE解析式和点E坐标.
(2)出于安全需求,游乐园在抛物线轨道和双曲线轨道离地高12米处添加纵向加固杆进行加固,请求出每条加固杆离出发点的水平距离(3.16,结果保留一位小数).
(3)过山车冲入水面时,水花会向四周飞溅,为确保游客安全,游乐园计划将冲刺顶点FC向下调整至F′,使仰角∠FGF′降低至37°,∠EFF′=90°.如图2所示,请求出∠FEF′的正切值.(sin37°,cos37,tan37)
【攻克压轴大题】2025年中考数学压轴题精选:二次函数
参考答案与试题解析
一.解答题(共15小题)
1.(2025 石家庄二模)如图,抛物线L的顶点坐标为(4,36),与y轴交于点C(0,20),与x轴交于点A,B(点A在点B左侧).
(1)求抛物线L的解析式和A,B两点坐标;
(2)线段OB上的两个点D(m,0),E(m+1,0),分别过点D,E作x轴的垂线交抛物线L于点N,M,连接MN.
①线段ME的长度能否为线段DN长度的2倍,若能,求出m的值,若不能,请说明理由;
②当m为何值时MN的值最小,最小值是多少?
③当时,直接写出m的取值范围.
【解答】解:(1)设抛物线L的解析式为y=a(x﹣4)2+36,将点C(0,20)代入,
得16a+36=20,
∴a=﹣1,
∴抛物线L的解析式y=﹣(x﹣4)2+36=﹣x2+8x+20,
当 y=0 时,﹣(x﹣4)2+36=0,
解得x1=﹣2,x2=10,
∴点A(﹣2,0),点B(10,0);
(2)①不能,理由如下:
当 x=m+1时,ME=y=﹣(m+1)2+8(m+1)+20=﹣m2+6m+27,
当 x=m时,DN=y=﹣m2+8m+20,
若 ME=2DN,则﹣m2+6m+27=2(﹣m2+8m+20),
整理,得m2﹣10m﹣13=0,
解得:,,
∴,
∵0≤m≤9,
∴和都不符合题意,
∴不存在m的值使ME=2DN;
②过点N作NG⊥ME,则 NG=DE=1,如图所示,
随着m的值的变化,MN≥NG,
当yM=yN,MN最小=NG=DE=1,
此时由对称性可知,
解得m=3.5,
∴当m=3.5时,MN的值最小,最小值为 1;
③2.5≤m≤3或4≤m≤4.5;
若yM>yN时,yM﹣yN=(﹣m2+6m+27)﹣(﹣m2+8m+20)=﹣2m+7,
当﹣2m+7=1 时,,此时 m=3,
当﹣2m+7=2 时,,此时m=2.5,
∴当时,2.5≤m≤3;
若yM<yN时,yM﹣yN=2m﹣7,
当2m﹣7=1时,,此时 m=4,
当2m﹣7=2 时,,此时 m=4.5,
∴当时,4≤m≤4.5;
综上可得:m的取值范围为2.5≤m≤3或4≤m≤4.5.
2.(2025 乾安县模拟)抛物线y=ax2﹣2x+c(b,c为常数)经过点A(0,﹣2),点N(3,1),点M在此抛物线上,点M的横坐标为m,点M不与A重合,抛物线上点M与点A之间的部分(包括端点)记为图象G.
(1)求此抛物线所对应的函数解析式;
(2)当图象G的最大值与最小值差为1时,直接写出m的取值范围;
(3)图象G与直线y=﹣2m+1有且只有一个交点时,求m的取值范围;
(4)连接AM,以AM为对角线构造矩形ABMC,AC∥BM∥x轴,CM∥y轴,矩形ABMC的边与抛物线的交点为点D(异于点A,M),点D关于CM的对称点是点E,当3DE=CM时,直接写出m的值.
【解答】解:(1)∵抛物线y=ax2﹣2x+c(b,c为常数)经过点A(0,﹣2),点N(3,1),
∴
解得
∴y=x2﹣2x﹣2;
(2)∵y=x2﹣2x﹣2=(x﹣1)2﹣3,
∴当x=1时,y取得最小值:﹣3;
当x<1时,y随值的增大而减小;当x<1时,y随x值的增大而减小;
①m<0时,
当x=m时,函数有最大值m2﹣2m﹣2,
当x=0时,函数有最小值:﹣2.
∴m2﹣2m﹣2﹣(﹣2)=1.
解得,(舍去).
②0<m≤1时,
x=m时,函数有最小值m2﹣2m﹣2,x=0时,函数有最大值﹣2.
∴(﹣2)﹣m2+2m+2=1.
解得m=1.
③m>1时,x=1时,函数有最小值﹣3.
由题意,得函数的最大值﹣3+1=﹣2.
∵A(0,﹣2),
∴A关于对称轴的对称点为(2,﹣2).
1<m≤2时,满足图G的最大值与最小值差为1.
综上所述,1≤m≤2或.
(3)当图G与直y=﹣2m+1有且只有一个交点时,
I.如图①,m<0时,
则﹣2≤﹣2m+1≤m2﹣2m﹣2,
解得.
II.如图②,0<m<2时,
则m2﹣2m﹣2<﹣2m+1≤﹣2,
解得.
III.如图③,m>2时,
则﹣2m+1<﹣3,
∴直线与图象G没有交点,不符合题意.
IV.m=2时,直线过图象G顶点.
综上所述,或或m=2.
(4)第一种情况:m>0且M在A上方时,如图④所示,
∵A(0,﹣2),M(m,m2﹣2m﹣2),AC//BM//x轴,CM//y轴,ABMC的边与抛物线的交点为D,
∴C(m,﹣2),D(2,﹣2),
∴CD=m﹣2,CM=m2﹣2m﹣2+2=m2﹣2m,
∵D,E关CM对称,
∴DE=2CD=2m﹣4.
∵3DE=CM,
∴3(2m﹣4)=m2﹣2m.
解得m=6,m=2(不合题意,舍去).
第二种情况:m>0且M在A下方时,如图⑤所示.
∵A(0,﹣2),M(m,m2﹣2m﹣2),AC//BM//x轴,CM//y轴,
∴C(m,﹣2),
由图可知D,M关于抛物线的对称轴对称,
∴D(2﹣m,m2﹣2m﹣2),
∴MD=m﹣(2﹣m)=2m﹣2,
CM=2﹣m2+2m+2=﹣m2+2m,
∵D,E关CM对称,
∴DE=2MD=4m﹣4.
∵3DE=CM,
∴3(4m﹣4)=﹣m2+2m,
解得.
第三种情况:m<0时,M在A上方,如图⑥所示,
此时,矩形的边与抛物线没有A,M之外的交点,不符合题意;
综上所述,符合条件m的值为6或.
3.(2025 康县四模)如图所示,在平面直角坐标系中,直线y=﹣x+3交坐标轴于B、C两点,抛物线y=ax2+bx+3经过B、C两点,且交x轴于另一点A(﹣1,0).点D为抛物线在第一象限内的一点,过点D作DQ∥CO,DQ交BC于点P,交x轴于点Q.
(1)求抛物线的解析式;
(2)设点P的横坐标为m,在点D的移动过程中,存在∠DCP=∠DPC,求出m值;
(3)在抛物线上取点E,在平面直角坐标系内取点F,问是否存在以C、B、E、F为顶点且以CB为边的矩形?如果存在,请求出点F的坐标;如果不存在,请说明理由.
【解答】解:(1)∵直线y=﹣x+3交坐标轴与B、C两点,
∴点B(3,0),点C(0,3),
∵抛物线y=ax2+bx+3经过B、C两点,且交x轴于另一点A(﹣1,0),
,
∴,
∴抛物线解析式为:y=﹣x2+2x+3;
(2)解:∵B(3,0),C(0,3),
∴OB=OC=3,
∴∠OCB=∠OBC=∠BPQ=∠DPC=45°,
∵∠DCP=∠DPC(已知),
∴∠DCO=∠DCP+∠OCB=90°,
∵∠AOC=90°,
∴CD∥AB(内错角相等,两直线平行),
∴点D的纵坐标与点C的纵坐标相同,即为3,
当y=3时,﹣x2+2x+3=3,
解得x=2或x=0(舍去),
则m=2;
(3)存在,求解如下:
设点F的坐标为F(s,t),
①当四边形BCEF是矩形时,则CE⊥BC,
∵直线BC的解析式为y=﹣x+3,
∴设直线CE的解析式为y=x+c,
把点C(0,3)代入得:c=3,
∴直线CE的解析式为:y=x+3,
联立,
解得:或(即为点C,舍去),
∴E(1,4),
∵四边形BCEF是矩形,且B(3,0),C(0,3),E(1,4),
∴,
解得,
则此时点F的坐标为F(4,1);
②当四边形BCFE是矩形时,则BE⊥BC,
设直线BE的解析式为y=x+n,
将点B(3,0)代入得:3+n=0,
解得:n=﹣3,
则直线BE的解析式为y=x﹣3,
联立,
解得:或(即为点B,舍去),
∴E(﹣2,﹣5),
∵四边形BCFE是矩形,且B(3,0),C(0,3),E(﹣2,﹣5),
∴,
解得:,
则此时点F的坐标为F(﹣5,﹣2),
综上,存在以C、B、E、F为顶点且以CB为边的矩形,此时点F的坐标为(4,1)或(﹣5,﹣2).
4.(2025 西陵区模拟)如图1,抛物线y=x2+mx+n交x轴于A(﹣1,0),B(3,0),交y轴于点C.
(1)求m和n的值;
(2)点P为抛物线上第一象限内一点,且△POC的面积等于6,求点P的坐标;
(3)如图2,将图1抛物线位于x轴下方的部分沿x轴翻折到x轴上方,保留其原本位于x轴上方的部分,得到如图2所示的新函数图象,记此新函数为G(x).
①若直线l:y=kx﹣k+6(k≠0)与函数G(x)的图象有且仅有3个交点,求k的值;
②在①的条件下,设|k|的最大值为p,若直线y=px+t与函数G(x)的图象围成的封闭图形内部(不包括边界)恰有4个横、纵坐标均为整数的点,直接写出t的取值范围.
【解答】解:(1)把A(﹣1,0),B(3,0)代入抛物线y=x2+mx+n中,
得,解得,
故m=﹣2,n=﹣3;
(2)由(1)知抛物线解析式为y=x2﹣2x﹣3,OC=3,
故△POC的面积6,
∴xP=4,
从而P(4,5);
(3)①∵y=kx﹣k+6(k≠0)恒过定点(1,6),
由题意可知函数G(x)在﹣1≤x≤3内的函数表达式为y=﹣x2+2x+3,
当k>0时,联立y=﹣x2+2x+3和y=kx﹣k+6,可得x2+(k﹣2)x+3﹣k=0,
令Δ=0,即(k﹣2)2﹣4(3﹣k)=0,
解得k(负值舍去);
当k<0时,同理可得k;
或当直线l:y=kx﹣k+6经过A(﹣1,0)或B(3,0)时,可得k=3或﹣3,
以上情况皆满足直线l:y=kx﹣k+6(k≠0)与函数G(x)的图象有且仅有3个交点,
综上,k的值为或±3;
②由①可知|k|的最大值为p=3,即y=3x+t,
若y=3x+t过(3,4),则t=﹣5,即y=3x﹣5,
当x=4时,y=7>6,则(4,6),在直线y=3x+t与函数G(x)的图象围成的封闭图形内部(不包括边界),共有(3,1)、(3,2)、(3,3)、(4,6)4个整点;
若y=3x+t过(3,3)时,则t=﹣6,即y=3x﹣6,
当x=4时,y=12﹣6=6,则直线y=3x+t过(4,6),此时在直线y=3x+t与函数G(x)的图象围成的封闭图形内部(不包括边界),只有(3,1)、(3,2)两个整点,
综上,t的取值范围为﹣6<t≤﹣5.
5.(2025 新沂市二模)如图1,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,点A的坐标为(﹣2,0),点C的坐标为(0,﹣4),点E,F在直线BC上,且点E在点F的左下侧,.
(1)求抛物线的表达式;
(2)如图2,分别连接AE、AF,延长AF交抛物线于点P,当点P在第四象限时,若△ABP的面积记作S1,△AEF的面积记作S2,线段EF在移动过程中,当S1﹣S2的值最大时,求点E的坐标;
(3)如图3,点D为该抛物线的顶点,连接DF,请直接写出AE+EF+DF的最小值.
【解答】解:(1)由题意得:,
解得:,
则抛物线的表达式为:yx2﹣x﹣4;
(2)∵EF为常数,点A到BC的距离也为常数,故S2为常数,
故当S1﹣S2的值最大时,即S2取得最大值即可,而S2AB×|yP|,
故当yP取得最大值时,符合题意,即点P、D重合,
由抛物线的表达式知,点D(1,),即P(1,);
由点A、P的坐标得,直线AP的表达式为:y(x+2),
由点B(4,0)、C的坐标得,直线BC的表达式为:y=x﹣4,
联立上述两个函数表达式得:x﹣4(x+2),则x,则点F(,),
∵点E、F在直线y=x﹣4上,则点F向左向下各2个单位得到点E,即点E(,);
(3)将点A向右向上各平移2个单位得到点Q(0,2),则AQ=2EF,AQ∥EF,
连接DQ交BC于点F,将点F沿BC向下平移2个单位得到点F,则此时AE+EF+DF的最小,
理由:AQ=2EF,AQ∥EF,则四边形AQFE为平行四边形,则QF=AE,
则AE+EF+DE=QF+DF+2DQ+222为最小.
6.(2025 裕华区校级二模)在平面直角坐标系中,抛物线y=x2+bx+c与x轴分别交于点A(﹣3,0)与点B(1,0).已知点P是该抛物线上一动点(不与点B重合).
(1)求抛物线的解析式和顶点坐标.
(2)将抛物线上P、B两点之间的部分(包括端点)记作图象W,当图象W上最高点与最低点的纵坐标的差是5时,求点P的坐标.
(3)若动点P的横坐标是n,另有坐标系中一动点Q,其坐标是(﹣3n,n).如图2,在坐标系中构造一个各边均与坐标轴垂直的矩形,使PQ为矩形的对角线.当抛物线在矩形内部的部分对应的函数值y随x的增大而增大,直接写出n的取值范围.
【解答】解:(1)∵抛物线y=x2+bx+c与x轴分别交于点A(﹣3,0)与点B(1,0),
∴,
解得:,
∴抛物线的解析式为y=x2+2x﹣3,
∵y=x2+2x﹣3=(x+1)2﹣4,
∴顶点坐标为(﹣1,﹣4).
(2)设点P(m,m2+2m﹣3),
当m<1时,m2+2m﹣3﹣(﹣4)=5,
解得:m1=﹣1,m2=﹣1(舍去),
∴P(﹣1,1);
当m>1时,m2+2m﹣3=5,
解得:m1=2,m2=﹣4(舍去),
∴P(2,5);
综上,点P的坐标为(﹣1,1)或(2,5).
(3)∵y=x2+2x﹣3=(x+1)2﹣4,
∴抛物线的对称轴为直线x=﹣1,
∵抛物线在矩形内部的部分对应的函数值y随x的增大而增大,
∴抛物线在矩形内部的部分位于直线x=﹣1的右侧,
当n>0时,﹣3n≥﹣1,
解得:n,
∴0<n;
当n<0时,n≥﹣1,
∴﹣1≤n<0;
综上,n的取值范围为﹣1≤n<0或0<n.
7.(2025 福田区模拟)平移是初中数学中的重要图形变换之一,其特点是保持图形形状、大小不变,仅改变位置.
我们先以抛物线C1:y=x2为例,对平移变换做了以下研究:把抛物线C1:y=x2先向右平移1个单位,再向下平移4个单位得到抛物线C2,抛物线C2与x轴交于A,B两点,其对称轴与x轴交于点D.
(1)抛物线C2的表达式为: y=(x﹣1)2﹣4 ;
(2)如图1,抛物线C1:y=x2与抛物线C2的交点C的坐标为:C( , ).抛物线C2与x轴交于A,B两点,线段AB= 4 ;
(3)平移求解(参考图1、图2)
①如果把线段AB平移,线段的一个端点落在抛物线C2的对称轴上记作点E,另一个端点落在抛物线C2上记作点F,则点F坐标为:F( 5或﹣3 , 12 );
②如果把线段DB平移,线段一个端点落在抛物线C1上记作点G,另一个端点落在抛物线C2上记作点H,则点H的横坐标为: 或 ;
(4)对于直线l1:y=x,通过对其上下平移可得直线l2:y=x+b,如果直线l2恰好与抛物线C1,C2共有三个交点,则b的值为: 或 .
【解答】解:(1)根据平移法则可知,抛物线C2的表达式为y=(x﹣1)2﹣4;
故答案为:y=(x﹣1)2﹣4;
(2)令x2=(x﹣1)2﹣4,
解得x,此时y=x2,
∴C(,);
令y=(x﹣1)2﹣4=0,
解得x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),
∴AB=4;
故答案为:(,),4;
(3)①∵抛物线C2的表达式为y=(x﹣1)2﹣4,
∴对称轴为直线x=1,
当点F在E点右侧时,
∵AB=EF=4,且点E在直线x=1上,
∴xF=5,此时y=(5﹣1)2﹣4=12,
∴F(5,12);
当点F在E点左侧时,
∵AB=EF=4,且点E在直线x=1上,
∴xF=﹣3,此时y=(﹣3﹣1)2﹣4=12,
∴F(﹣3,12);
故答案为:(5,12)或(﹣3,12);
②由题可知D(1,0),B(3,0),
∴DB=2,
设H(t,t2﹣2t﹣3),
当点G在点H左侧时,则G(t﹣2,t2﹣2t﹣3),
∵点G在抛物线C1上,
∴(t﹣2)2=t2﹣2t﹣3,
解得t;
当点G在点H右侧时,则G(t+2,t2﹣2t﹣3),
∵点G在抛物线C1上,
∴(t+2)2=t2﹣2t﹣3,
解得t;
综上,点H的横坐标为或;
故答案为:或;
(4)如图,
由图象可知,当直线l2:y=x+b经过点C或者与抛物线C1相切时,直线l2恰好与抛物线C1,C2共有三个交点;
①当直线l2:y=x+b经过点C时,
即b,
解得b;
②当直线l2:y=x+b与抛物线C1相切时,
令x+b=x2,即x2﹣x﹣b=0,
∴Δ=1+4b=0,
解得b;
综上,b的值为或.
故答案为:或.
8.(2025 伊金霍洛旗三模)如图,抛物线y=ax2+bx﹣1(a≠0)与x轴交于点A(1,0)和点B,与y轴交于点C,抛物线的对称轴交x轴于点D(3,0),过点B作直线l⊥x轴,过点D作DE⊥CD,交直线l于点E.
(1)求抛物线的解析式;
(2)连接AC,求证:∠ACD+∠BED=45°;
(3)如图,点P为第三象限内抛物线上的点,连接CE和BP交于点Q,当时,求点P的坐标.
【解答】(1)解:由题意得:B(5,0),
设抛物线的解析式为:y=a(x﹣1)(x﹣5),
将点C(0,﹣1)代入得,﹣1=a (﹣1)×(﹣5),
∴,
∴;
(2)证明:∵OA=OC=1,
∴∠OAC=45°,
∵∠COD=∠DBE=90°,
∴∠ADC=∠BED=90°﹣∠BDE,
∴∠ACD+∠BED=∠ACD+∠ADC,
∵∠OAC=∠ACD+∠ADC=45°,
∠ACD+∠BED=45°;
(3)解:如图1,
∵直线l⊥x轴,DE⊥CD,
∴∠COD=∠CDE=∠EBD=90°,
∴∠ODC+∠OCD=90°,∠ODC+∠BDE=90°,
∴∠OCD=∠BDE,
∴△OCD∽△BDE,
∴,
∵OC=1,OD=3,BD=OB﹣OD=5﹣3=2,
∴,
∴BE=6,
∴E(5,﹣6),
设CE的解析式为:y=kx+n,
∴,
∴,
∴y=﹣x﹣1,
作PT⊥x轴,交直线CE于点T,
设,
∴T(m,﹣m﹣1),PT∥BE,
∴,△PQT∽△BQE,
∴,
∴,
∴m1=﹣3,m2=14(舍去),
当m=﹣3时,,
∴.
9.(2025 天桥区三模)已知抛物线y=x2+mx+n与x轴交于A(﹣1,0),B两点,与y轴交于点C(0,﹣4).
(1)求抛物线的解析式;
(2)如图1,已知点E为第四象限抛物线上的点,连接AC、BE、AE、BC,且AE和BC相交于点F,设△ACF的面积为S1,△BEF的面积为S2,当S1﹣S2=5时,求点E的坐标.
(3)如图2,设点P(x1,y1),Q(x2,y2)是直线BC下方抛物线上的两动点,且x2=x1+1,过点P作PM∥y轴,交BC于点M,过点Q作QN⊥BC,交BC于点N.求的最大值.
【解答】解:(1)把点A(﹣1,0)和C(0,﹣4)代入抛物线y=x2+mx+n中,
得:,
解得:,
∴抛物线的解析式为:y=x2﹣3x﹣4;
(2)当y=0时,x2﹣3x﹣4=0,
解得:x1=﹣1,x2=4,
∴B(4,0),
∵S1﹣S2=5
∴(S1+S△ABF)﹣(S2+S△ABF)=5,
∴S△ABC﹣S△ABE=5,
∴,
∴,
∴|yE|=2,
∵点E在第四象限,
∴yE=﹣2,
令y=x2﹣3x﹣4=﹣2得,,
∵点E在第四象限,
∴点E的坐标为;
(3)设BC的解析式为:y=kx+b,分别代入B(4,0),C(0,﹣4),
∴,
解得:,
∴BC的解析式为:y=x﹣4,
∵OB=OC=4,∠BOC=90°,
∴∠OCB=45°,
如图,过点Q作QK∥y轴交BC于K,
∴∠NKQ=∠OCB=45°,
∵QN⊥BC,
∴∠BNQ=90°,
∴△KNQ是等腰直角三角形,
∴,
∵点P(x1,y1),Q(x2,y2)是直线BC下方抛物线上的两动点,且x2=x1+1,
∴点M(x1,x1﹣4),Q(x1+1,,K(x1+1,x1﹣3),
∴,,
∴,
∵﹣2<0,
∴当时,有最大值,其最大值是.
10.(2025 江阳区模拟)如图(1),抛物线交x轴于A,B两点(点A在左边),交y轴于点C.
(1)直接写出A,B,C三点的坐标;
(2)D是抛物线第四象限上的一点,连接AD分别交BC,OC于E,F两点,若∠FEC=∠FCE,求直线AD的解析式;
(3)平移抛物线使它的顶点为(0,1),如图(2).R是y轴上一个定点,以点R为直角顶点作Rt△RST,使顶点S,T分别在x轴和抛物线上.若Rt△RST在变化的过程中,直线ST与抛物线始终有唯一公共点,求点R的坐标.
【解答】解:(1)令中y为0,
则,解得x=6或﹣2,
故A(﹣2,0),B(6,0),
由解析式可知C(0,﹣3).
(2)作OG∥AD交抛物线于点G,交BC于点P,如图(1)所示,
∴∠FEC=∠OPC,
∵∠FEC=∠FCE,
∴∠OPC=∠FCE.
∴OP=OC=3.
由待定系数法可得直线BC的表达式为y,
设P(m,),则OC2=OP2,
即,解得m或0,
故P(,),故kOP.
∵OG∥AD,
∴kAD,
∴直线AD的表达式为y(x+2).
(3)由平移可得新抛物线的表达式为,
设T(t,),
由于直线ST与抛物线有且只有一个交点,亦可看成有两个重合的交点,
故可由待定系数法得直线ST的表达式为y,
再令y=0,解得xS.
作TQ⊥y轴于点Q,如图(2)所示,
∴∠TQR+∠QRT=90°,
∵∠TRS=90°,
∴∠QRT+∠ORS=90°,
∴∠TQR=∠ORS,
又∵∠TQR=∠ROS=90°,
∴△TQR∽△ROS,
∴,设R(0,r),
即,整理可得t2(2﹣r)=4r﹣4r2+8,
∵当T点运动时,上式中r的值与点T的位置无关,
∴2﹣r=0,即r=2,
故点R的坐标为(0,2).
11.(2025 祁阳市校级一模)如图,直线y=﹣x+3与x轴的正半轴、y轴的正半轴分别相交于点A和点C,点B是点A关于原点O的对称点,四边形ABCD是平行四边形,抛物线y=ax2+bx﹣10经过点B和点D.
(1)求平行四边形ABCD的面积;
(2)求抛物线的解析式;
(3)动点P从点C出发,以每秒1个单位的速度匀速运动到点D;同时动点Q从点A出发,以每秒1个单位的速度匀速运动到点C,设运动的时间为t.
①当CP=CQ时,求t的值;
②请你猜想,在P,Q两点的运动过程中,是否存在某一时刻t,使得四边形ADPQ的面积最小?若存在,求出t的值,并求出这个最小值;若不存在,请说明理由.
【解答】解:(1)当x=0时,y=3,
∴C(0,3),
当y=0时,x=3,
∴A(3,0),
∵点B是点A关于原点O的对称点,
∴B(﹣3,0),
∴AB=6,
∴平行四边形ABCD的面积=AB CO=6×3=18;
(2)∵四边形ABCD是平行四边形,AB=6,
∴D(6,3),
将B点、D点代入y=ax2+bx﹣10,
∴,
解得,
∴抛物线的解析式为yx2x﹣10;
(3)①∵A(3,0),C(0,3),
∴AC=3,
∵CP=CQ,
∴t=3t,
解得t;
②存在t,使得四边形ABCD的面积最小,理由如下:
当t=3时,点Q、CC重合,此时四边形ADPQ为三角形,且面积不为最小值,
故只研究0≤t≤3运动的情况,
t秒时,点Q的纵坐标为t,
则四边形ADPQ的面积=S△ADC﹣S△CPQCD×OCCP×(yC﹣yQ)
t×(3t)t2t+9(t)2,
即t时,四边形ADPQ的面积的最小值为:.
12.(2025 河源二模)如图所示,已知二次函数图象与直线y=﹣x+m相交于点A(5,0).直线交y轴于B,点P为抛物线上一点,将点P绕着原点O逆时针旋转90°得到对应点Q,连接PQ.
(1)求抛物线和直线AB的函数解析式.
(2)当点P坐标为(6,2)时,求证:点P,Q,B三点在同一直线上.
(3)当△OPQ有一顶点在直线AB上时,
①求PQ长;
②在①的条件下,当点P在第四象限时,在PQ上取点C,在OP上取点D,使QC=PD,连接OC,DQ,求OC+DQ的最小值.
【解答】解:(1)∵二次函数和直线的交点为A(5,0),
∴0=52a﹣5,则a;0=﹣5+m,则m=5.
故抛物线解析式为yx2x;直线AB解析式为y=﹣x+5.
(2)证明:设PQ与y轴交于点E,过点P、Q向x轴作垂线,垂足分别为F、G.
根据题意易得△POQ为等腰直角三角形.
∴OP=OQ,∠QOE+∠POE=90°,
∵∠POE+∠POF=90°,
∴∠QOE=∠POF,
∵GQ⊥x轴,
∴GQ∥y轴,
∴∠QOE=∠GQO=∠POF.
在△GQO和△FOP中,∠QOE=∠GQO,∠QOE=∠GQO,OQ=OP,
∴△GQO≌△FOP(AAS),
∴GQ=OF,GO=PF.
∴点Q的坐标为(﹣2,6).
设直线PQ解析式为y=kx+b,则有:
,解得,
∴直线PQ解析式为yx+5.
令x=0,y=5,即OE=5,
对于直线y=﹣x+5,令x=0,y=5,即OB=5,
∴BE两点重合,
∴点P,Q,B三点在同一直线上.
(3)△OPQ有一顶点在直线AB上分为两种情况:
点P在直线AB上;点Q在直线AB上.
①当点P在直线AB上,设点P坐标为(p,p2p),
∴p2p=﹣p+5,解得p=5或﹣3,
当p=5时,点P坐标为(5,0),A、P两点重合,B、Q两点重合,不符合△OPQ有一顶点在直线AB上,舍去.
当p=﹣3时,点P坐标为(﹣3,8),OP绕点O逆时针旋转90°,点Q显然不在AB上,符合题意.
根据△OPQ为等腰直角三角形,PQOP.
当点Q在直线AB上,由(2)可知点Q坐标为(﹣yP,xP),即Q(p2p,p).
∵点Q在AB上,
∴p=﹣(p2p)+5,解得p=5或3,p=5不合题意舍去.
当p=3时,点P坐标为(3,﹣2),OP,PQOP.
故PQ的长度为或.
②如图,当点P在第四象限时,点P坐标为(3,﹣2),作EQ⊥OQ,QE=PQ.连接CE,OE.
根据题意△POQ为等腰直角三角形.
∵∠OQC+∠EQC=90°,
∴∠EQC=∠QPD=45°,
又∵QC=DP,QE=PQ,
∴△EQC≌△QPD(SAS),
∴CE=DQ,
由OC+CE≥OE可得OC+DQ的最小值为OE.
在Rt△OQE中,OE.
故OC+DQ的最小值为.
13.(2025 同安区一模)如图,抛物线y=﹣x2+bx+c与x轴,y轴分别交于A,B,C三点(点A在点B的左侧),其中点A(﹣3,0).对称轴.
(1)求抛物线的解析式;
(2)如图1,点D(1,4)在抛物线上,过点D作DF⊥x轴于点F,过点A的直线交y轴于点E(0,2),点P是直线AE上方抛物线上的一动点,过点P作PM⊥AE于点M,PN⊥DF于点N,求的最大值,以及此时点P的坐标;
(3)如图2,在(2)的条件下,将抛物线y=﹣x2+bx+c先向下平移2个单位长度,再向左平移2个单位长度,得到新抛物线y1,点R是新抛物线y1上一个动点且在AD上方,当∠RAD+∠BDF=45°时,请求出符合条件的点R的坐标.
【解答】解:(1)点A(﹣3.0),抛物线的对称轴,则点B(2,0),
则抛物线的表达式为:y=﹣(x+3)(x﹣2)=﹣x2﹣x+6;
(2)过点P作y轴的平行线交AE于点H,
由点A、E的坐标得,直线AE的表达式为:yx+2,则tan∠EAOtanα,则cosα,
设点P(x,﹣x2﹣x+6),则点H(x,x+2)
则PM=PH,而PN=1﹣x,
则(﹣x2﹣x+6)﹣(x+2)+1﹣x=﹣(x)2,
即的最大值为,
此时点P(,);
(3)新抛物线的表达式由y1=﹣(x+2)2﹣(x+2)﹣2+6=﹣x2﹣5x﹣2,
由点A、D的坐标,直线∠DAB=45°,作∠DAH=∠DAR,
∵∠RAD+∠BDF=45°,∠DAH+∠HAB=45°,
则∠HAB=∠BDF,
由点B、D、F的坐标知,tan∠BDFtan∠HAB,
则直线AH的表达式为:y(x+3),
根据图像的对称性,直线AR的表达式为:y=4(x+3),
联立上式和新抛物线的表达式得:﹣x2﹣5x﹣2=4(x+3),
解得:x=﹣7(舍去)或﹣2,
即点R(﹣2,4).
14.(2025 洪山区模拟)如图,抛物线y=﹣x2+bx+c交x轴于A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)如图1,抛物线顶点N,AN与y轴交于点C,若x轴上存在一点M使∠NBA=∠CMG,MG交NB于点G,当,求点G坐标;
(3)如图2,点D为x轴上方抛物线上一点,点R(6,0),若Q为线段DR上一点,过Q作PQ∥AD交x轴于点P,求△PQD面积最大值.
【解答】解:(1)∵抛物线y=﹣x2+bx+c交x轴于A(﹣1,0),B(3,0),
∴,
∴,
∴y=﹣x2+2x+3;
(2)如图,
由(1)可知,抛物线解析式为y=﹣x2+2x+3,顶点N(1,4),
∵N(1,4),A(﹣1,0),
设AN:y=mx+n,
∴,解得,
∴直线AN:y=2x+2,
∴C(0,2),
∴OC=2,
∵A(﹣1,0),
∴OA=1,
∴,
∵∠NBA=∠CMG,∠NBA+∠MGB=∠CMG+∠CMA,
∴∠MGB=∠CMA,
由抛物线的轴对称性质可知∠GBM=∠MAC,
∴△MGB∽△CMA,
∴,∠GMB=∠MCA,
∴BM=3,
∵AB=4,
∴AM=1,
∴M(0,0),即点M在原点,
如图,过G作GD⊥AB于D,
∴∠CMB=∠CMG+∠MBG=∠NBA+∠BMG=90°,
∴∠MGB=∠CMA=90°,
∵GD⊥AB,
∴,
∴设BD=x,DG=2x,MD=4x,
∴MB=5x=3,
∴,
∴,
∴;
(3)设P(t,0)(﹣1≤t≤6),
则AP=t+1,AR=7,
∵PQ∥AD,
∴,
∴,
∴,
当t,yQ=yN=4时,
.
15.(2025 宝安区模拟)我校九年级学生去游乐园进行春游,在过山车项目排队时,小明发现过山车的轨道可近似看出多个函数图象的组合.活动结束后,数学老师给同学们提出如下问题:如图是水上过山车的示意图.
如图1,AB段为直滑道,BC段、EF段为平行滑道,C、F分别为冲刺顶点,CDE段为抛物线y=ax2+bx+227的一部分,D为抛物线顶点,FG段为双曲线y的一部分,其中冲刺顶点C离地距离27m,冲刺顶点F离地距离18m,水面高度为1m,G为抛物线和水面的接触点,B(8,27),D(15,2),E(m,18),BC=EF=2m.
(1)求抛物线CDE解析式和点E坐标.
(2)出于安全需求,游乐园在抛物线轨道和双曲线轨道离地高12米处添加纵向加固杆进行加固,请求出每条加固杆离出发点的水平距离(3.16,结果保留一位小数).
(3)过山车冲入水面时,水花会向四周飞溅,为确保游客安全,游乐园计划将冲刺顶点FC向下调整至F′,使仰角∠FGF′降低至37°,∠EFF′=90°.如图2所示,请求出∠FEF′的正切值.(sin37°,cos37,tan37)
【解答】解:(1)∵B(8,27),BC=2,
∴C(10,27),
∵抛物线顶点坐标D(15,2),
设抛物线解析式y=a(x﹣15)2+2,且过D(15,2),
由题意得27=a(10﹣15)2+2,
解得a=1,
∴y=(x﹣15)2+2=x2﹣30x+227,
把y=18代入y=x2﹣30x+227,
得18=x2﹣30x+227,
解得x1=19,x2=11,
∵E在抛物线右侧,
∴E(19,18);
(2)把y=12代入y=x2﹣30x+227,
得x2﹣30x+227=12,
解得,
即x1≈18.2,x2≈11.8,
把y=12代入,
得x=21.5,
∴加固杆离出发点的水平距离分别是18.2m,11.8m,21.5m;
(3)把y=1代入,
得1,
解得x=38,
经检验,x=38是原方程的解,
∴G(38,1),
∵,
∴设,且过G(38,1),
由题意得,
解得,
∴,
联立,
解得,,
∴F'(,),
∴tan∠FEF′.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【攻克压轴大题】2025年中考数学压轴题精选:二次函数
1.(2025 石家庄二模)如图,抛物线L的顶点坐标为(4,36),与y轴交于点C(0,20),与x轴交于点A,B(点A在点B左侧).
(1)求抛物线L的解析式和A,B两点坐标;
(2)线段OB上的两个点D(m,0),E(m+1,0),分别过点D,E作x轴的垂线交抛物线L于点N,M,连接MN.
①线段ME的长度能否为线段DN长度的2倍,若能,求出m的值,若不能,请说明理由;
②当m为何值时MN的值最小,最小值是多少?
③当时,直接写出m的取值范围.
2.(2025 乾安县模拟)抛物线y=ax2﹣2x+c(b,c为常数)经过点A(0,﹣2),点N(3,1),点M在此抛物线上,点M的横坐标为m,点M不与A重合,抛物线上点M与点A之间的部分(包括端点)记为图象G.
(1)求此抛物线所对应的函数解析式;
(2)当图象G的最大值与最小值差为1时,直接写出m的取值范围;
(3)图象G与直线y=﹣2m+1有且只有一个交点时,求m的取值范围;
(4)连接AM,以AM为对角线构造矩形ABMC,AC∥BM∥x轴,CM∥y轴,矩形ABMC的边与抛物线的交点为点D(异于点A,M),点D关于CM的对称点是点E,当3DE=CM时,直接写出m的值.
3.(2025 康县四模)如图所示,在平面直角坐标系中,直线y=﹣x+3交坐标轴于B、C两点,抛物线y=ax2+bx+3经过B、C两点,且交x轴于另一点A(﹣1,0).点D为抛物线在第一象限内的一点,过点D作DQ∥CO,DQ交BC于点P,交x轴于点Q.
(1)求抛物线的解析式;
(2)设点P的横坐标为m,在点D的移动过程中,存在∠DCP=∠DPC,求出m值;
(3)在抛物线上取点E,在平面直角坐标系内取点F,问是否存在以C、B、E、F为顶点且以CB为边的矩形?如果存在,请求出点F的坐标;如果不存在,请说明理由.
4.(2025 西陵区模拟)如图1,抛物线y=x2+mx+n交x轴于A(﹣1,0),B(3,0),交y轴于点C.
(1)求m和n的值;
(2)点P为抛物线上第一象限内一点,且△POC的面积等于6,求点P的坐标;
(3)如图2,将图1抛物线位于x轴下方的部分沿x轴翻折到x轴上方,保留其原本位于x轴上方的部分,得到如图2所示的新函数图象,记此新函数为G(x).
①若直线l:y=kx﹣k+6(k≠0)与函数G(x)的图象有且仅有3个交点,求k的值;
②在①的条件下,设|k|的最大值为p,若直线y=px+t与函数G(x)的图象围成的封闭图形内部(不包括边界)恰有4个横、纵坐标均为整数的点,直接写出t的取值范围.
5.(2025 新沂市二模)如图1,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,点A的坐标为(﹣2,0),点C的坐标为(0,﹣4),点E,F在直线BC上,且点E在点F的左下侧,.
(1)求抛物线的表达式;
(2)如图2,分别连接AE、AF,延长AF交抛物线于点P,当点P在第四象限时,若△ABP的面积记作S1,△AEF的面积记作S2,线段EF在移动过程中,当S1﹣S2的值最大时,求点E的坐标;
(3)如图3,点D为该抛物线的顶点,连接DF,请直接写出AE+EF+DF的最小值.
6.(2025 裕华区校级二模)在平面直角坐标系中,抛物线y=x2+bx+c与x轴分别交于点A(﹣3,0)与点B(1,0).已知点P是该抛物线上一动点(不与点B重合).
(1)求抛物线的解析式和顶点坐标.
(2)将抛物线上P、B两点之间的部分(包括端点)记作图象W,当图象W上最高点与最低点的纵坐标的差是5时,求点P的坐标.
(3)若动点P的横坐标是n,另有坐标系中一动点Q,其坐标是(﹣3n,n).如图2,在坐标系中构造一个各边均与坐标轴垂直的矩形,使PQ为矩形的对角线.当抛物线在矩形内部的部分对应的函数值y随x的增大而增大,直接写出n的取值范围.
7.(2025 福田区模拟)平移是初中数学中的重要图形变换之一,其特点是保持图形形状、大小不变,仅改变位置.
我们先以抛物线C1:y=x2为例,对平移变换做了以下研究:把抛物线C1:y=x2先向右平移1个单位,再向下平移4个单位得到抛物线C2,抛物线C2与x轴交于A,B两点,其对称轴与x轴交于点D.
(1)抛物线C2的表达式为: ;
(2)如图1,抛物线C1:y=x2与抛物线C2的交点C的坐标为:C( , ).抛物线C2与x轴交于A,B两点,线段AB= ;
(3)平移求解(参考图1、图2)
①如果把线段AB平移,线段的一个端点落在抛物线C2的对称轴上记作点E,另一个端点落在抛物线C2上记作点F,则点F坐标为:F( , );
②如果把线段DB平移,线段一个端点落在抛物线C1上记作点G,另一个端点落在抛物线C2上记作点H,则点H的横坐标为: ;
(4)对于直线l1:y=x,通过对其上下平移可得直线l2:y=x+b,如果直线l2恰好与抛物线C1,C2共有三个交点,则b的值为: .
8.(2025 伊金霍洛旗三模)如图,抛物线y=ax2+bx﹣1(a≠0)与x轴交于点A(1,0)和点B,与y轴交于点C,抛物线的对称轴交x轴于点D(3,0),过点B作直线l⊥x轴,过点D作DE⊥CD,交直线l于点E.
(1)求抛物线的解析式;
(2)连接AC,求证:∠ACD+∠BED=45°;
(3)如图,点P为第三象限内抛物线上的点,连接CE和BP交于点Q,当时,求点P的坐标.
9.(2025 天桥区三模)已知抛物线y=x2+mx+n与x轴交于A(﹣1,0),B两点,与y轴交于点C(0,﹣4).
(1)求抛物线的解析式;
(2)如图1,已知点E为第四象限抛物线上的点,连接AC、BE、AE、BC,且AE和BC相交于点F,设△ACF的面积为S1,△BEF的面积为S2,当S1﹣S2=5时,求点E的坐标.
(3)如图2,设点P(x1,y1),Q(x2,y2)是直线BC下方抛物线上的两动点,且x2=x1+1,过点P作PM∥y轴,交BC于点M,过点Q作QN⊥BC,交BC于点N.求的最大值.
10.(2025 江阳区模拟)如图(1),抛物线交x轴于A,B两点(点A在左边),交y轴于点C.
(1)直接写出A,B,C三点的坐标;
(2)D是抛物线第四象限上的一点,连接AD分别交BC,OC于E,F两点,若∠FEC=∠FCE,求直线AD的解析式;
(3)平移抛物线使它的顶点为(0,1),如图(2).R是y轴上一个定点,以点R为直角顶点作Rt△RST,使顶点S,T分别在x轴和抛物线上.若Rt△RST在变化的过程中,直线ST与抛物线始终有唯一公共点,求点R的坐标.
11.(2025 祁阳市校级一模)如图,直线y=﹣x+3与x轴的正半轴、y轴的正半轴分别相交于点A和点C,点B是点A关于原点O的对称点,四边形ABCD是平行四边形,抛物线y=ax2+bx﹣10经过点B和点D.
(1)求平行四边形ABCD的面积;
(2)求抛物线的解析式;
(3)动点P从点C出发,以每秒1个单位的速度匀速运动到点D;同时动点Q从点A出发,以每秒1个单位的速度匀速运动到点C,设运动的时间为t.
①当CP=CQ时,求t的值;
②请你猜想,在P,Q两点的运动过程中,是否存在某一时刻t,使得四边形ADPQ的面积最小?若存在,求出t的值,并求出这个最小值;若不存在,请说明理由.
12.(2025 河源二模)如图所示,已知二次函数图象与直线y=﹣x+m相交于点A(5,0).直线交y轴于B,点P为抛物线上一点,将点P绕着原点O逆时针旋转90°得到对应点Q,连接PQ.
(1)求抛物线和直线AB的函数解析式.
(2)当点P坐标为(6,2)时,求证:点P,Q,B三点在同一直线上.
(3)当△OPQ有一顶点在直线AB上时,
①求PQ长;
②在①的条件下,当点P在第四象限时,在PQ上取点C,在OP上取点D,使QC=PD,连接OC,DQ,求OC+DQ的最小值.
13.(2025 同安区一模)如图,抛物线y=﹣x2+bx+c与x轴,y轴分别交于A,B,C三点(点A在点B的左侧),其中点A(﹣3,0).对称轴.
(1)求抛物线的解析式;
(2)如图1,点D(1,4)在抛物线上,过点D作DF⊥x轴于点F,过点A的直线交y轴于点E(0,2),点P是直线AE上方抛物线上的一动点,过点P作PM⊥AE于点M,PN⊥DF于点N,求的最大值,以及此时点P的坐标;
(3)如图2,在(2)的条件下,将抛物线y=﹣x2+bx+c先向下平移2个单位长度,再向左平移2个单位长度,得到新抛物线y1,点R是新抛物线y1上一个动点且在AD上方,当∠RAD+∠BDF=45°时,请求出符合条件的点R的坐标.
14.(2025 洪山区模拟)如图,抛物线y=﹣x2+bx+c交x轴于A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)如图1,抛物线顶点N,AN与y轴交于点C,若x轴上存在一点M使∠NBA=∠CMG,MG交NB于点G,当,求点G坐标;
(3)如图2,点D为x轴上方抛物线上一点,点R(6,0),若Q为线段DR上一点,过Q作PQ∥AD交x轴于点P,求△PQD面积最大值.
15.(2025 宝安区模拟)我校九年级学生去游乐园进行春游,在过山车项目排队时,小明发现过山车的轨道可近似看出多个函数图象的组合.活动结束后,数学老师给同学们提出如下问题:如图是水上过山车的示意图.
如图1,AB段为直滑道,BC段、EF段为平行滑道,C、F分别为冲刺顶点,CDE段为抛物线y=ax2+bx+227的一部分,D为抛物线顶点,FG段为双曲线y的一部分,其中冲刺顶点C离地距离27m,冲刺顶点F离地距离18m,水面高度为1m,G为抛物线和水面的接触点,B(8,27),D(15,2),E(m,18),BC=EF=2m.
(1)求抛物线CDE解析式和点E坐标.
(2)出于安全需求,游乐园在抛物线轨道和双曲线轨道离地高12米处添加纵向加固杆进行加固,请求出每条加固杆离出发点的水平距离(3.16,结果保留一位小数).
(3)过山车冲入水面时,水花会向四周飞溅,为确保游客安全,游乐园计划将冲刺顶点FC向下调整至F′,使仰角∠FGF′降低至37°,∠EFF′=90°.如图2所示,请求出∠FEF′的正切值.(sin37°,cos37,tan37)
【攻克压轴大题】2025年中考数学压轴题精选:二次函数
参考答案与试题解析
一.解答题(共15小题)
1.(2025 石家庄二模)如图,抛物线L的顶点坐标为(4,36),与y轴交于点C(0,20),与x轴交于点A,B(点A在点B左侧).
(1)求抛物线L的解析式和A,B两点坐标;
(2)线段OB上的两个点D(m,0),E(m+1,0),分别过点D,E作x轴的垂线交抛物线L于点N,M,连接MN.
①线段ME的长度能否为线段DN长度的2倍,若能,求出m的值,若不能,请说明理由;
②当m为何值时MN的值最小,最小值是多少?
③当时,直接写出m的取值范围.
【解答】解:(1)设抛物线L的解析式为y=a(x﹣4)2+36,将点C(0,20)代入,
得16a+36=20,
∴a=﹣1,
∴抛物线L的解析式y=﹣(x﹣4)2+36=﹣x2+8x+20,
当 y=0 时,﹣(x﹣4)2+36=0,
解得x1=﹣2,x2=10,
∴点A(﹣2,0),点B(10,0);
(2)①不能,理由如下:
当 x=m+1时,ME=y=﹣(m+1)2+8(m+1)+20=﹣m2+6m+27,
当 x=m时,DN=y=﹣m2+8m+20,
若 ME=2DN,则﹣m2+6m+27=2(﹣m2+8m+20),
整理,得m2﹣10m﹣13=0,
解得:,,
∴,
∵0≤m≤9,
∴和都不符合题意,
∴不存在m的值使ME=2DN;
②过点N作NG⊥ME,则 NG=DE=1,如图所示,
随着m的值的变化,MN≥NG,
当yM=yN,MN最小=NG=DE=1,
此时由对称性可知,
解得m=3.5,
∴当m=3.5时,MN的值最小,最小值为 1;
③2.5≤m≤3或4≤m≤4.5;
若yM>yN时,yM﹣yN=(﹣m2+6m+27)﹣(﹣m2+8m+20)=﹣2m+7,
当﹣2m+7=1 时,,此时 m=3,
当﹣2m+7=2 时,,此时m=2.5,
∴当时,2.5≤m≤3;
若yM<yN时,yM﹣yN=2m﹣7,
当2m﹣7=1时,,此时 m=4,
当2m﹣7=2 时,,此时 m=4.5,
∴当时,4≤m≤4.5;
综上可得:m的取值范围为2.5≤m≤3或4≤m≤4.5.
2.(2025 乾安县模拟)抛物线y=ax2﹣2x+c(b,c为常数)经过点A(0,﹣2),点N(3,1),点M在此抛物线上,点M的横坐标为m,点M不与A重合,抛物线上点M与点A之间的部分(包括端点)记为图象G.
(1)求此抛物线所对应的函数解析式;
(2)当图象G的最大值与最小值差为1时,直接写出m的取值范围;
(3)图象G与直线y=﹣2m+1有且只有一个交点时,求m的取值范围;
(4)连接AM,以AM为对角线构造矩形ABMC,AC∥BM∥x轴,CM∥y轴,矩形ABMC的边与抛物线的交点为点D(异于点A,M),点D关于CM的对称点是点E,当3DE=CM时,直接写出m的值.
【解答】解:(1)∵抛物线y=ax2﹣2x+c(b,c为常数)经过点A(0,﹣2),点N(3,1),
∴
解得
∴y=x2﹣2x﹣2;
(2)∵y=x2﹣2x﹣2=(x﹣1)2﹣3,
∴当x=1时,y取得最小值:﹣3;
当x<1时,y随值的增大而减小;当x<1时,y随x值的增大而减小;
①m<0时,
当x=m时,函数有最大值m2﹣2m﹣2,
当x=0时,函数有最小值:﹣2.
∴m2﹣2m﹣2﹣(﹣2)=1.
解得,(舍去).
②0<m≤1时,
x=m时,函数有最小值m2﹣2m﹣2,x=0时,函数有最大值﹣2.
∴(﹣2)﹣m2+2m+2=1.
解得m=1.
③m>1时,x=1时,函数有最小值﹣3.
由题意,得函数的最大值﹣3+1=﹣2.
∵A(0,﹣2),
∴A关于对称轴的对称点为(2,﹣2).
1<m≤2时,满足图G的最大值与最小值差为1.
综上所述,1≤m≤2或.
(3)当图G与直y=﹣2m+1有且只有一个交点时,
I.如图①,m<0时,
则﹣2≤﹣2m+1≤m2﹣2m﹣2,
解得.
II.如图②,0<m<2时,
则m2﹣2m﹣2<﹣2m+1≤﹣2,
解得.
III.如图③,m>2时,
则﹣2m+1<﹣3,
∴直线与图象G没有交点,不符合题意.
IV.m=2时,直线过图象G顶点.
综上所述,或或m=2.
(4)第一种情况:m>0且M在A上方时,如图④所示,
∵A(0,﹣2),M(m,m2﹣2m﹣2),AC//BM//x轴,CM//y轴,ABMC的边与抛物线的交点为D,
∴C(m,﹣2),D(2,﹣2),
∴CD=m﹣2,CM=m2﹣2m﹣2+2=m2﹣2m,
∵D,E关CM对称,
∴DE=2CD=2m﹣4.
∵3DE=CM,
∴3(2m﹣4)=m2﹣2m.
解得m=6,m=2(不合题意,舍去).
第二种情况:m>0且M在A下方时,如图⑤所示.
∵A(0,﹣2),M(m,m2﹣2m﹣2),AC//BM//x轴,CM//y轴,
∴C(m,﹣2),
由图可知D,M关于抛物线的对称轴对称,
∴D(2﹣m,m2﹣2m﹣2),
∴MD=m﹣(2﹣m)=2m﹣2,
CM=2﹣m2+2m+2=﹣m2+2m,
∵D,E关CM对称,
∴DE=2MD=4m﹣4.
∵3DE=CM,
∴3(4m﹣4)=﹣m2+2m,
解得.
第三种情况:m<0时,M在A上方,如图⑥所示,
此时,矩形的边与抛物线没有A,M之外的交点,不符合题意;
综上所述,符合条件m的值为6或.
3.(2025 康县四模)如图所示,在平面直角坐标系中,直线y=﹣x+3交坐标轴于B、C两点,抛物线y=ax2+bx+3经过B、C两点,且交x轴于另一点A(﹣1,0).点D为抛物线在第一象限内的一点,过点D作DQ∥CO,DQ交BC于点P,交x轴于点Q.
(1)求抛物线的解析式;
(2)设点P的横坐标为m,在点D的移动过程中,存在∠DCP=∠DPC,求出m值;
(3)在抛物线上取点E,在平面直角坐标系内取点F,问是否存在以C、B、E、F为顶点且以CB为边的矩形?如果存在,请求出点F的坐标;如果不存在,请说明理由.
【解答】解:(1)∵直线y=﹣x+3交坐标轴与B、C两点,
∴点B(3,0),点C(0,3),
∵抛物线y=ax2+bx+3经过B、C两点,且交x轴于另一点A(﹣1,0),
,
∴,
∴抛物线解析式为:y=﹣x2+2x+3;
(2)解:∵B(3,0),C(0,3),
∴OB=OC=3,
∴∠OCB=∠OBC=∠BPQ=∠DPC=45°,
∵∠DCP=∠DPC(已知),
∴∠DCO=∠DCP+∠OCB=90°,
∵∠AOC=90°,
∴CD∥AB(内错角相等,两直线平行),
∴点D的纵坐标与点C的纵坐标相同,即为3,
当y=3时,﹣x2+2x+3=3,
解得x=2或x=0(舍去),
则m=2;
(3)存在,求解如下:
设点F的坐标为F(s,t),
①当四边形BCEF是矩形时,则CE⊥BC,
∵直线BC的解析式为y=﹣x+3,
∴设直线CE的解析式为y=x+c,
把点C(0,3)代入得:c=3,
∴直线CE的解析式为:y=x+3,
联立,
解得:或(即为点C,舍去),
∴E(1,4),
∵四边形BCEF是矩形,且B(3,0),C(0,3),E(1,4),
∴,
解得,
则此时点F的坐标为F(4,1);
②当四边形BCFE是矩形时,则BE⊥BC,
设直线BE的解析式为y=x+n,
将点B(3,0)代入得:3+n=0,
解得:n=﹣3,
则直线BE的解析式为y=x﹣3,
联立,
解得:或(即为点B,舍去),
∴E(﹣2,﹣5),
∵四边形BCFE是矩形,且B(3,0),C(0,3),E(﹣2,﹣5),
∴,
解得:,
则此时点F的坐标为F(﹣5,﹣2),
综上,存在以C、B、E、F为顶点且以CB为边的矩形,此时点F的坐标为(4,1)或(﹣5,﹣2).
4.(2025 西陵区模拟)如图1,抛物线y=x2+mx+n交x轴于A(﹣1,0),B(3,0),交y轴于点C.
(1)求m和n的值;
(2)点P为抛物线上第一象限内一点,且△POC的面积等于6,求点P的坐标;
(3)如图2,将图1抛物线位于x轴下方的部分沿x轴翻折到x轴上方,保留其原本位于x轴上方的部分,得到如图2所示的新函数图象,记此新函数为G(x).
①若直线l:y=kx﹣k+6(k≠0)与函数G(x)的图象有且仅有3个交点,求k的值;
②在①的条件下,设|k|的最大值为p,若直线y=px+t与函数G(x)的图象围成的封闭图形内部(不包括边界)恰有4个横、纵坐标均为整数的点,直接写出t的取值范围.
【解答】解:(1)把A(﹣1,0),B(3,0)代入抛物线y=x2+mx+n中,
得,解得,
故m=﹣2,n=﹣3;
(2)由(1)知抛物线解析式为y=x2﹣2x﹣3,OC=3,
故△POC的面积6,
∴xP=4,
从而P(4,5);
(3)①∵y=kx﹣k+6(k≠0)恒过定点(1,6),
由题意可知函数G(x)在﹣1≤x≤3内的函数表达式为y=﹣x2+2x+3,
当k>0时,联立y=﹣x2+2x+3和y=kx﹣k+6,可得x2+(k﹣2)x+3﹣k=0,
令Δ=0,即(k﹣2)2﹣4(3﹣k)=0,
解得k(负值舍去);
当k<0时,同理可得k;
或当直线l:y=kx﹣k+6经过A(﹣1,0)或B(3,0)时,可得k=3或﹣3,
以上情况皆满足直线l:y=kx﹣k+6(k≠0)与函数G(x)的图象有且仅有3个交点,
综上,k的值为或±3;
②由①可知|k|的最大值为p=3,即y=3x+t,
若y=3x+t过(3,4),则t=﹣5,即y=3x﹣5,
当x=4时,y=7>6,则(4,6),在直线y=3x+t与函数G(x)的图象围成的封闭图形内部(不包括边界),共有(3,1)、(3,2)、(3,3)、(4,6)4个整点;
若y=3x+t过(3,3)时,则t=﹣6,即y=3x﹣6,
当x=4时,y=12﹣6=6,则直线y=3x+t过(4,6),此时在直线y=3x+t与函数G(x)的图象围成的封闭图形内部(不包括边界),只有(3,1)、(3,2)两个整点,
综上,t的取值范围为﹣6<t≤﹣5.
5.(2025 新沂市二模)如图1,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,点A的坐标为(﹣2,0),点C的坐标为(0,﹣4),点E,F在直线BC上,且点E在点F的左下侧,.
(1)求抛物线的表达式;
(2)如图2,分别连接AE、AF,延长AF交抛物线于点P,当点P在第四象限时,若△ABP的面积记作S1,△AEF的面积记作S2,线段EF在移动过程中,当S1﹣S2的值最大时,求点E的坐标;
(3)如图3,点D为该抛物线的顶点,连接DF,请直接写出AE+EF+DF的最小值.
【解答】解:(1)由题意得:,
解得:,
则抛物线的表达式为:yx2﹣x﹣4;
(2)∵EF为常数,点A到BC的距离也为常数,故S2为常数,
故当S1﹣S2的值最大时,即S2取得最大值即可,而S2AB×|yP|,
故当yP取得最大值时,符合题意,即点P、D重合,
由抛物线的表达式知,点D(1,),即P(1,);
由点A、P的坐标得,直线AP的表达式为:y(x+2),
由点B(4,0)、C的坐标得,直线BC的表达式为:y=x﹣4,
联立上述两个函数表达式得:x﹣4(x+2),则x,则点F(,),
∵点E、F在直线y=x﹣4上,则点F向左向下各2个单位得到点E,即点E(,);
(3)将点A向右向上各平移2个单位得到点Q(0,2),则AQ=2EF,AQ∥EF,
连接DQ交BC于点F,将点F沿BC向下平移2个单位得到点F,则此时AE+EF+DF的最小,
理由:AQ=2EF,AQ∥EF,则四边形AQFE为平行四边形,则QF=AE,
则AE+EF+DE=QF+DF+2DQ+222为最小.
6.(2025 裕华区校级二模)在平面直角坐标系中,抛物线y=x2+bx+c与x轴分别交于点A(﹣3,0)与点B(1,0).已知点P是该抛物线上一动点(不与点B重合).
(1)求抛物线的解析式和顶点坐标.
(2)将抛物线上P、B两点之间的部分(包括端点)记作图象W,当图象W上最高点与最低点的纵坐标的差是5时,求点P的坐标.
(3)若动点P的横坐标是n,另有坐标系中一动点Q,其坐标是(﹣3n,n).如图2,在坐标系中构造一个各边均与坐标轴垂直的矩形,使PQ为矩形的对角线.当抛物线在矩形内部的部分对应的函数值y随x的增大而增大,直接写出n的取值范围.
【解答】解:(1)∵抛物线y=x2+bx+c与x轴分别交于点A(﹣3,0)与点B(1,0),
∴,
解得:,
∴抛物线的解析式为y=x2+2x﹣3,
∵y=x2+2x﹣3=(x+1)2﹣4,
∴顶点坐标为(﹣1,﹣4).
(2)设点P(m,m2+2m﹣3),
当m<1时,m2+2m﹣3﹣(﹣4)=5,
解得:m1=﹣1,m2=﹣1(舍去),
∴P(﹣1,1);
当m>1时,m2+2m﹣3=5,
解得:m1=2,m2=﹣4(舍去),
∴P(2,5);
综上,点P的坐标为(﹣1,1)或(2,5).
(3)∵y=x2+2x﹣3=(x+1)2﹣4,
∴抛物线的对称轴为直线x=﹣1,
∵抛物线在矩形内部的部分对应的函数值y随x的增大而增大,
∴抛物线在矩形内部的部分位于直线x=﹣1的右侧,
当n>0时,﹣3n≥﹣1,
解得:n,
∴0<n;
当n<0时,n≥﹣1,
∴﹣1≤n<0;
综上,n的取值范围为﹣1≤n<0或0<n.
7.(2025 福田区模拟)平移是初中数学中的重要图形变换之一,其特点是保持图形形状、大小不变,仅改变位置.
我们先以抛物线C1:y=x2为例,对平移变换做了以下研究:把抛物线C1:y=x2先向右平移1个单位,再向下平移4个单位得到抛物线C2,抛物线C2与x轴交于A,B两点,其对称轴与x轴交于点D.
(1)抛物线C2的表达式为: y=(x﹣1)2﹣4 ;
(2)如图1,抛物线C1:y=x2与抛物线C2的交点C的坐标为:C( , ).抛物线C2与x轴交于A,B两点,线段AB= 4 ;
(3)平移求解(参考图1、图2)
①如果把线段AB平移,线段的一个端点落在抛物线C2的对称轴上记作点E,另一个端点落在抛物线C2上记作点F,则点F坐标为:F( 5或﹣3 , 12 );
②如果把线段DB平移,线段一个端点落在抛物线C1上记作点G,另一个端点落在抛物线C2上记作点H,则点H的横坐标为: 或 ;
(4)对于直线l1:y=x,通过对其上下平移可得直线l2:y=x+b,如果直线l2恰好与抛物线C1,C2共有三个交点,则b的值为: 或 .
【解答】解:(1)根据平移法则可知,抛物线C2的表达式为y=(x﹣1)2﹣4;
故答案为:y=(x﹣1)2﹣4;
(2)令x2=(x﹣1)2﹣4,
解得x,此时y=x2,
∴C(,);
令y=(x﹣1)2﹣4=0,
解得x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),
∴AB=4;
故答案为:(,),4;
(3)①∵抛物线C2的表达式为y=(x﹣1)2﹣4,
∴对称轴为直线x=1,
当点F在E点右侧时,
∵AB=EF=4,且点E在直线x=1上,
∴xF=5,此时y=(5﹣1)2﹣4=12,
∴F(5,12);
当点F在E点左侧时,
∵AB=EF=4,且点E在直线x=1上,
∴xF=﹣3,此时y=(﹣3﹣1)2﹣4=12,
∴F(﹣3,12);
故答案为:(5,12)或(﹣3,12);
②由题可知D(1,0),B(3,0),
∴DB=2,
设H(t,t2﹣2t﹣3),
当点G在点H左侧时,则G(t﹣2,t2﹣2t﹣3),
∵点G在抛物线C1上,
∴(t﹣2)2=t2﹣2t﹣3,
解得t;
当点G在点H右侧时,则G(t+2,t2﹣2t﹣3),
∵点G在抛物线C1上,
∴(t+2)2=t2﹣2t﹣3,
解得t;
综上,点H的横坐标为或;
故答案为:或;
(4)如图,
由图象可知,当直线l2:y=x+b经过点C或者与抛物线C1相切时,直线l2恰好与抛物线C1,C2共有三个交点;
①当直线l2:y=x+b经过点C时,
即b,
解得b;
②当直线l2:y=x+b与抛物线C1相切时,
令x+b=x2,即x2﹣x﹣b=0,
∴Δ=1+4b=0,
解得b;
综上,b的值为或.
故答案为:或.
8.(2025 伊金霍洛旗三模)如图,抛物线y=ax2+bx﹣1(a≠0)与x轴交于点A(1,0)和点B,与y轴交于点C,抛物线的对称轴交x轴于点D(3,0),过点B作直线l⊥x轴,过点D作DE⊥CD,交直线l于点E.
(1)求抛物线的解析式;
(2)连接AC,求证:∠ACD+∠BED=45°;
(3)如图,点P为第三象限内抛物线上的点,连接CE和BP交于点Q,当时,求点P的坐标.
【解答】(1)解:由题意得:B(5,0),
设抛物线的解析式为:y=a(x﹣1)(x﹣5),
将点C(0,﹣1)代入得,﹣1=a (﹣1)×(﹣5),
∴,
∴;
(2)证明:∵OA=OC=1,
∴∠OAC=45°,
∵∠COD=∠DBE=90°,
∴∠ADC=∠BED=90°﹣∠BDE,
∴∠ACD+∠BED=∠ACD+∠ADC,
∵∠OAC=∠ACD+∠ADC=45°,
∠ACD+∠BED=45°;
(3)解:如图1,
∵直线l⊥x轴,DE⊥CD,
∴∠COD=∠CDE=∠EBD=90°,
∴∠ODC+∠OCD=90°,∠ODC+∠BDE=90°,
∴∠OCD=∠BDE,
∴△OCD∽△BDE,
∴,
∵OC=1,OD=3,BD=OB﹣OD=5﹣3=2,
∴,
∴BE=6,
∴E(5,﹣6),
设CE的解析式为:y=kx+n,
∴,
∴,
∴y=﹣x﹣1,
作PT⊥x轴,交直线CE于点T,
设,
∴T(m,﹣m﹣1),PT∥BE,
∴,△PQT∽△BQE,
∴,
∴,
∴m1=﹣3,m2=14(舍去),
当m=﹣3时,,
∴.
9.(2025 天桥区三模)已知抛物线y=x2+mx+n与x轴交于A(﹣1,0),B两点,与y轴交于点C(0,﹣4).
(1)求抛物线的解析式;
(2)如图1,已知点E为第四象限抛物线上的点,连接AC、BE、AE、BC,且AE和BC相交于点F,设△ACF的面积为S1,△BEF的面积为S2,当S1﹣S2=5时,求点E的坐标.
(3)如图2,设点P(x1,y1),Q(x2,y2)是直线BC下方抛物线上的两动点,且x2=x1+1,过点P作PM∥y轴,交BC于点M,过点Q作QN⊥BC,交BC于点N.求的最大值.
【解答】解:(1)把点A(﹣1,0)和C(0,﹣4)代入抛物线y=x2+mx+n中,
得:,
解得:,
∴抛物线的解析式为:y=x2﹣3x﹣4;
(2)当y=0时,x2﹣3x﹣4=0,
解得:x1=﹣1,x2=4,
∴B(4,0),
∵S1﹣S2=5
∴(S1+S△ABF)﹣(S2+S△ABF)=5,
∴S△ABC﹣S△ABE=5,
∴,
∴,
∴|yE|=2,
∵点E在第四象限,
∴yE=﹣2,
令y=x2﹣3x﹣4=﹣2得,,
∵点E在第四象限,
∴点E的坐标为;
(3)设BC的解析式为:y=kx+b,分别代入B(4,0),C(0,﹣4),
∴,
解得:,
∴BC的解析式为:y=x﹣4,
∵OB=OC=4,∠BOC=90°,
∴∠OCB=45°,
如图,过点Q作QK∥y轴交BC于K,
∴∠NKQ=∠OCB=45°,
∵QN⊥BC,
∴∠BNQ=90°,
∴△KNQ是等腰直角三角形,
∴,
∵点P(x1,y1),Q(x2,y2)是直线BC下方抛物线上的两动点,且x2=x1+1,
∴点M(x1,x1﹣4),Q(x1+1,,K(x1+1,x1﹣3),
∴,,
∴,
∵﹣2<0,
∴当时,有最大值,其最大值是.
10.(2025 江阳区模拟)如图(1),抛物线交x轴于A,B两点(点A在左边),交y轴于点C.
(1)直接写出A,B,C三点的坐标;
(2)D是抛物线第四象限上的一点,连接AD分别交BC,OC于E,F两点,若∠FEC=∠FCE,求直线AD的解析式;
(3)平移抛物线使它的顶点为(0,1),如图(2).R是y轴上一个定点,以点R为直角顶点作Rt△RST,使顶点S,T分别在x轴和抛物线上.若Rt△RST在变化的过程中,直线ST与抛物线始终有唯一公共点,求点R的坐标.
【解答】解:(1)令中y为0,
则,解得x=6或﹣2,
故A(﹣2,0),B(6,0),
由解析式可知C(0,﹣3).
(2)作OG∥AD交抛物线于点G,交BC于点P,如图(1)所示,
∴∠FEC=∠OPC,
∵∠FEC=∠FCE,
∴∠OPC=∠FCE.
∴OP=OC=3.
由待定系数法可得直线BC的表达式为y,
设P(m,),则OC2=OP2,
即,解得m或0,
故P(,),故kOP.
∵OG∥AD,
∴kAD,
∴直线AD的表达式为y(x+2).
(3)由平移可得新抛物线的表达式为,
设T(t,),
由于直线ST与抛物线有且只有一个交点,亦可看成有两个重合的交点,
故可由待定系数法得直线ST的表达式为y,
再令y=0,解得xS.
作TQ⊥y轴于点Q,如图(2)所示,
∴∠TQR+∠QRT=90°,
∵∠TRS=90°,
∴∠QRT+∠ORS=90°,
∴∠TQR=∠ORS,
又∵∠TQR=∠ROS=90°,
∴△TQR∽△ROS,
∴,设R(0,r),
即,整理可得t2(2﹣r)=4r﹣4r2+8,
∵当T点运动时,上式中r的值与点T的位置无关,
∴2﹣r=0,即r=2,
故点R的坐标为(0,2).
11.(2025 祁阳市校级一模)如图,直线y=﹣x+3与x轴的正半轴、y轴的正半轴分别相交于点A和点C,点B是点A关于原点O的对称点,四边形ABCD是平行四边形,抛物线y=ax2+bx﹣10经过点B和点D.
(1)求平行四边形ABCD的面积;
(2)求抛物线的解析式;
(3)动点P从点C出发,以每秒1个单位的速度匀速运动到点D;同时动点Q从点A出发,以每秒1个单位的速度匀速运动到点C,设运动的时间为t.
①当CP=CQ时,求t的值;
②请你猜想,在P,Q两点的运动过程中,是否存在某一时刻t,使得四边形ADPQ的面积最小?若存在,求出t的值,并求出这个最小值;若不存在,请说明理由.
【解答】解:(1)当x=0时,y=3,
∴C(0,3),
当y=0时,x=3,
∴A(3,0),
∵点B是点A关于原点O的对称点,
∴B(﹣3,0),
∴AB=6,
∴平行四边形ABCD的面积=AB CO=6×3=18;
(2)∵四边形ABCD是平行四边形,AB=6,
∴D(6,3),
将B点、D点代入y=ax2+bx﹣10,
∴,
解得,
∴抛物线的解析式为yx2x﹣10;
(3)①∵A(3,0),C(0,3),
∴AC=3,
∵CP=CQ,
∴t=3t,
解得t;
②存在t,使得四边形ABCD的面积最小,理由如下:
当t=3时,点Q、CC重合,此时四边形ADPQ为三角形,且面积不为最小值,
故只研究0≤t≤3运动的情况,
t秒时,点Q的纵坐标为t,
则四边形ADPQ的面积=S△ADC﹣S△CPQCD×OCCP×(yC﹣yQ)
t×(3t)t2t+9(t)2,
即t时,四边形ADPQ的面积的最小值为:.
12.(2025 河源二模)如图所示,已知二次函数图象与直线y=﹣x+m相交于点A(5,0).直线交y轴于B,点P为抛物线上一点,将点P绕着原点O逆时针旋转90°得到对应点Q,连接PQ.
(1)求抛物线和直线AB的函数解析式.
(2)当点P坐标为(6,2)时,求证:点P,Q,B三点在同一直线上.
(3)当△OPQ有一顶点在直线AB上时,
①求PQ长;
②在①的条件下,当点P在第四象限时,在PQ上取点C,在OP上取点D,使QC=PD,连接OC,DQ,求OC+DQ的最小值.
【解答】解:(1)∵二次函数和直线的交点为A(5,0),
∴0=52a﹣5,则a;0=﹣5+m,则m=5.
故抛物线解析式为yx2x;直线AB解析式为y=﹣x+5.
(2)证明:设PQ与y轴交于点E,过点P、Q向x轴作垂线,垂足分别为F、G.
根据题意易得△POQ为等腰直角三角形.
∴OP=OQ,∠QOE+∠POE=90°,
∵∠POE+∠POF=90°,
∴∠QOE=∠POF,
∵GQ⊥x轴,
∴GQ∥y轴,
∴∠QOE=∠GQO=∠POF.
在△GQO和△FOP中,∠QOE=∠GQO,∠QOE=∠GQO,OQ=OP,
∴△GQO≌△FOP(AAS),
∴GQ=OF,GO=PF.
∴点Q的坐标为(﹣2,6).
设直线PQ解析式为y=kx+b,则有:
,解得,
∴直线PQ解析式为yx+5.
令x=0,y=5,即OE=5,
对于直线y=﹣x+5,令x=0,y=5,即OB=5,
∴BE两点重合,
∴点P,Q,B三点在同一直线上.
(3)△OPQ有一顶点在直线AB上分为两种情况:
点P在直线AB上;点Q在直线AB上.
①当点P在直线AB上,设点P坐标为(p,p2p),
∴p2p=﹣p+5,解得p=5或﹣3,
当p=5时,点P坐标为(5,0),A、P两点重合,B、Q两点重合,不符合△OPQ有一顶点在直线AB上,舍去.
当p=﹣3时,点P坐标为(﹣3,8),OP绕点O逆时针旋转90°,点Q显然不在AB上,符合题意.
根据△OPQ为等腰直角三角形,PQOP.
当点Q在直线AB上,由(2)可知点Q坐标为(﹣yP,xP),即Q(p2p,p).
∵点Q在AB上,
∴p=﹣(p2p)+5,解得p=5或3,p=5不合题意舍去.
当p=3时,点P坐标为(3,﹣2),OP,PQOP.
故PQ的长度为或.
②如图,当点P在第四象限时,点P坐标为(3,﹣2),作EQ⊥OQ,QE=PQ.连接CE,OE.
根据题意△POQ为等腰直角三角形.
∵∠OQC+∠EQC=90°,
∴∠EQC=∠QPD=45°,
又∵QC=DP,QE=PQ,
∴△EQC≌△QPD(SAS),
∴CE=DQ,
由OC+CE≥OE可得OC+DQ的最小值为OE.
在Rt△OQE中,OE.
故OC+DQ的最小值为.
13.(2025 同安区一模)如图,抛物线y=﹣x2+bx+c与x轴,y轴分别交于A,B,C三点(点A在点B的左侧),其中点A(﹣3,0).对称轴.
(1)求抛物线的解析式;
(2)如图1,点D(1,4)在抛物线上,过点D作DF⊥x轴于点F,过点A的直线交y轴于点E(0,2),点P是直线AE上方抛物线上的一动点,过点P作PM⊥AE于点M,PN⊥DF于点N,求的最大值,以及此时点P的坐标;
(3)如图2,在(2)的条件下,将抛物线y=﹣x2+bx+c先向下平移2个单位长度,再向左平移2个单位长度,得到新抛物线y1,点R是新抛物线y1上一个动点且在AD上方,当∠RAD+∠BDF=45°时,请求出符合条件的点R的坐标.
【解答】解:(1)点A(﹣3.0),抛物线的对称轴,则点B(2,0),
则抛物线的表达式为:y=﹣(x+3)(x﹣2)=﹣x2﹣x+6;
(2)过点P作y轴的平行线交AE于点H,
由点A、E的坐标得,直线AE的表达式为:yx+2,则tan∠EAOtanα,则cosα,
设点P(x,﹣x2﹣x+6),则点H(x,x+2)
则PM=PH,而PN=1﹣x,
则(﹣x2﹣x+6)﹣(x+2)+1﹣x=﹣(x)2,
即的最大值为,
此时点P(,);
(3)新抛物线的表达式由y1=﹣(x+2)2﹣(x+2)﹣2+6=﹣x2﹣5x﹣2,
由点A、D的坐标,直线∠DAB=45°,作∠DAH=∠DAR,
∵∠RAD+∠BDF=45°,∠DAH+∠HAB=45°,
则∠HAB=∠BDF,
由点B、D、F的坐标知,tan∠BDFtan∠HAB,
则直线AH的表达式为:y(x+3),
根据图像的对称性,直线AR的表达式为:y=4(x+3),
联立上式和新抛物线的表达式得:﹣x2﹣5x﹣2=4(x+3),
解得:x=﹣7(舍去)或﹣2,
即点R(﹣2,4).
14.(2025 洪山区模拟)如图,抛物线y=﹣x2+bx+c交x轴于A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)如图1,抛物线顶点N,AN与y轴交于点C,若x轴上存在一点M使∠NBA=∠CMG,MG交NB于点G,当,求点G坐标;
(3)如图2,点D为x轴上方抛物线上一点,点R(6,0),若Q为线段DR上一点,过Q作PQ∥AD交x轴于点P,求△PQD面积最大值.
【解答】解:(1)∵抛物线y=﹣x2+bx+c交x轴于A(﹣1,0),B(3,0),
∴,
∴,
∴y=﹣x2+2x+3;
(2)如图,
由(1)可知,抛物线解析式为y=﹣x2+2x+3,顶点N(1,4),
∵N(1,4),A(﹣1,0),
设AN:y=mx+n,
∴,解得,
∴直线AN:y=2x+2,
∴C(0,2),
∴OC=2,
∵A(﹣1,0),
∴OA=1,
∴,
∵∠NBA=∠CMG,∠NBA+∠MGB=∠CMG+∠CMA,
∴∠MGB=∠CMA,
由抛物线的轴对称性质可知∠GBM=∠MAC,
∴△MGB∽△CMA,
∴,∠GMB=∠MCA,
∴BM=3,
∵AB=4,
∴AM=1,
∴M(0,0),即点M在原点,
如图,过G作GD⊥AB于D,
∴∠CMB=∠CMG+∠MBG=∠NBA+∠BMG=90°,
∴∠MGB=∠CMA=90°,
∵GD⊥AB,
∴,
∴设BD=x,DG=2x,MD=4x,
∴MB=5x=3,
∴,
∴,
∴;
(3)设P(t,0)(﹣1≤t≤6),
则AP=t+1,AR=7,
∵PQ∥AD,
∴,
∴,
∴,
当t,yQ=yN=4时,
.
15.(2025 宝安区模拟)我校九年级学生去游乐园进行春游,在过山车项目排队时,小明发现过山车的轨道可近似看出多个函数图象的组合.活动结束后,数学老师给同学们提出如下问题:如图是水上过山车的示意图.
如图1,AB段为直滑道,BC段、EF段为平行滑道,C、F分别为冲刺顶点,CDE段为抛物线y=ax2+bx+227的一部分,D为抛物线顶点,FG段为双曲线y的一部分,其中冲刺顶点C离地距离27m,冲刺顶点F离地距离18m,水面高度为1m,G为抛物线和水面的接触点,B(8,27),D(15,2),E(m,18),BC=EF=2m.
(1)求抛物线CDE解析式和点E坐标.
(2)出于安全需求,游乐园在抛物线轨道和双曲线轨道离地高12米处添加纵向加固杆进行加固,请求出每条加固杆离出发点的水平距离(3.16,结果保留一位小数).
(3)过山车冲入水面时,水花会向四周飞溅,为确保游客安全,游乐园计划将冲刺顶点FC向下调整至F′,使仰角∠FGF′降低至37°,∠EFF′=90°.如图2所示,请求出∠FEF′的正切值.(sin37°,cos37,tan37)
【解答】解:(1)∵B(8,27),BC=2,
∴C(10,27),
∵抛物线顶点坐标D(15,2),
设抛物线解析式y=a(x﹣15)2+2,且过D(15,2),
由题意得27=a(10﹣15)2+2,
解得a=1,
∴y=(x﹣15)2+2=x2﹣30x+227,
把y=18代入y=x2﹣30x+227,
得18=x2﹣30x+227,
解得x1=19,x2=11,
∵E在抛物线右侧,
∴E(19,18);
(2)把y=12代入y=x2﹣30x+227,
得x2﹣30x+227=12,
解得,
即x1≈18.2,x2≈11.8,
把y=12代入,
得x=21.5,
∴加固杆离出发点的水平距离分别是18.2m,11.8m,21.5m;
(3)把y=1代入,
得1,
解得x=38,
经检验,x=38是原方程的解,
∴G(38,1),
∵,
∴设,且过G(38,1),
由题意得,
解得,
∴,
联立,
解得,,
∴F'(,),
∴tan∠FEF′.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
