【攻克压轴大题】2025年中考数学压轴题精选:反比例函数
文档属性
| 名称 | 【攻克压轴大题】2025年中考数学压轴题精选:反比例函数 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 21:02:40 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【攻克压轴大题】2025年中考数学压轴题精选:反比例函数
1.(2025 姑苏区校级二模)一次函数与x轴交于C点,与y轴交于B点,点A(2,a)在直线BC上,过点A作反比例函数的图象.
(1)求出a,k的值;
(2)在x轴上是否存在点D,使得∠BOA=∠OAD,若不存在,请说明理由;若存在,求出点D的坐标.
2.(2025 锦江区校级模拟)如图,一次函数y=kx+b与反比例函数的图象相交于点A(3,4)、B(6,m)两点.
(1)求一次函数与反比例函数的解析式;
(2)若点C为线段AB上一点,且,连接AO、CO,求S△AOC;
(3)如果一个矩形的长宽之比为2:1,我们把该矩形称为“倍边矩形”.请探究,在平面内是否存在P、Q两点(点P在直线AB上方),使得四边形APBQ为倍边矩形,若存在,请求P、Q两点的坐标;若不存在,请说明理由.
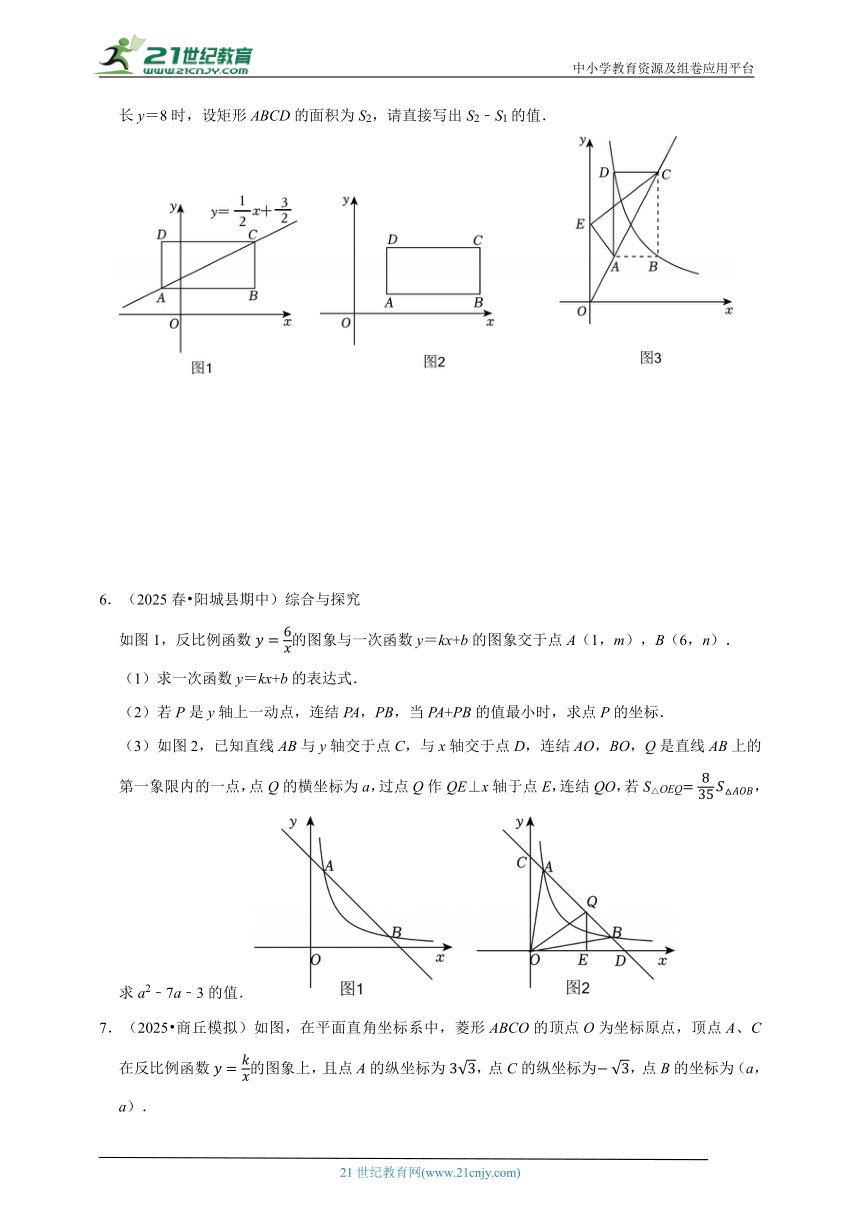
3.(2025 天桥区三模)如图,一次函数y=kx+b的图象与反比例函数的图象相交于点A(2,3),B(6,n)两点,与x轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)点P是y轴上一动点,连接AP,BP,当△ABP面积为10时,请求出点P的坐标;
(3)将线段AB绕点B顺时针旋转90°,得到线段BD,连接CD,在反比例函数上,是否存在一点Q,使得∠CDB+∠QCO=90°?若存在,请求出点Q的坐标;若不存在,请说明理由.
4.(2025 沁阳市二模)如图,在平面直角坐标系xOy中,一次函数y1=ax+3的图象与反比例函数的图象交于点A,B,与x轴、y轴分别交于点C(﹣6,0)、D,点E在第一象限,点F是x轴正半轴上一点,菱形CDEF的边DE与反比例函数的图象交于点G,且.
(1)利用无刻度的直尺,在反比例函数的图象上作出点Q,使S△OCB=S△OCQ(不写作法,保留作图痕迹).
(2)求a的值和反比例函数的表达式;
(3)将菱形CDEF向下平移,当点C落在这个反比例函数的图象上时,平移的距离为 .
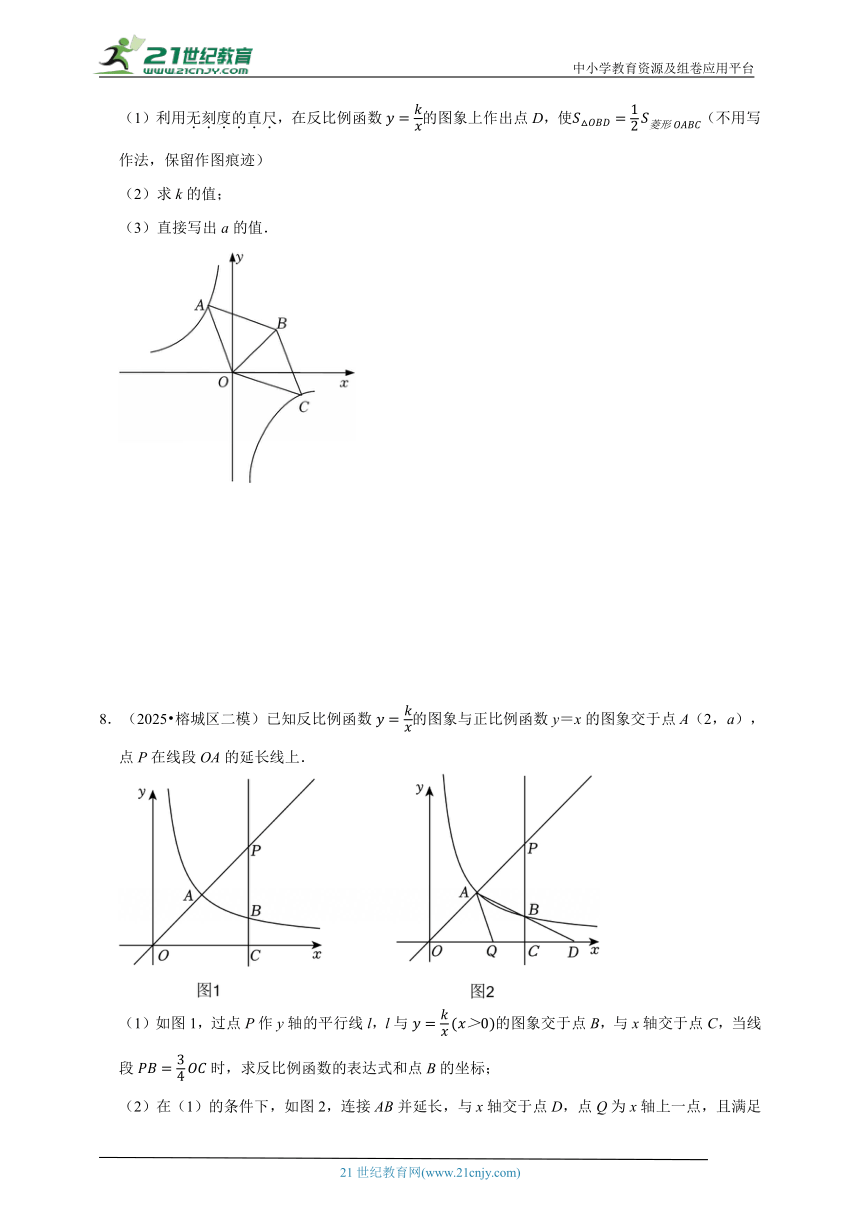
5.(2025 广东模拟)在平面直角坐标系中,若某函数的图象经过矩形ABCD对角线的两个端点,则定义该函数为矩形ABCD 的“友好函数”.例如:如图1,矩形ABCD,经过点A(﹣1,1)和点C(3,3)的一次函数y是矩形ABCD的“友好函数”.
(1)如图2,矩形ABCD的顶点坐标分别为A(2,1),B(6,1),C(6,3),D(2,3),反比例函数y(x>0)经过点B,求反比例函数y(x>0)的函数表达式,并判断该函数是否为矩形ABCD的“友好函数”;
(2)矩形ABCD在第一象限,AB∥x轴,AD∥y轴,且点A的坐标为(1,2),正比例函数y1=ax经过点A,且是矩形ABCD的“友好函数”,反比例函数y2(x>0)经过点B,且是矩形ABCD的“友好函数”.
①如图3,当OC>OA时,将矩形ABCD沿AC折叠,点B的对应点为E,若点E落在y轴上,求k的值;
②设矩形ABCD的周长为y,求y关于k的函数表达式;
③在②的条件下,当矩形ABCD的周长y=4时,设矩形ABCD的面积为S1;当矩形ABCD的周长y=8时,设矩形ABCD的面积为S2,请直接写出S2﹣S1的值.
6.(2025春 阳城县期中)综合与探究
如图1,反比例函数的图象与一次函数y=kx+b的图象交于点A(1,m),B(6,n).
(1)求一次函数y=kx+b的表达式.
(2)若P是y轴上一动点,连结PA,PB,当PA+PB的值最小时,求点P的坐标.
(3)如图2,已知直线AB与y轴交于点C,与x轴交于点D,连结AO,BO,Q是直线AB上的第一象限内的一点,点Q的横坐标为a,过点Q作QE⊥x轴于点E,连结QO,若S△OEQ,求a2﹣7a﹣3的值.
7.(2025 商丘模拟)如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,顶点A、C在反比例函数的图象上,且点A的纵坐标为,点C的纵坐标为,点B的坐标为(a,a).
(1)利用无刻度的直尺,在反比例函数的图象上作出点D,使(不用写作法,保留作图痕迹)
(2)求k的值;
(3)直接写出a的值.
8.(2025 榕城区二模)已知反比例函数的图象与正比例函数y=x的图象交于点A(2,a),点P在线段OA的延长线上.
(1)如图1,过点P作y轴的平行线l,l与的图象交于点B,与x轴交于点C,当线段时,求反比例函数的表达式和点B的坐标;
(2)在(1)的条件下,如图2,连接AB并延长,与x轴交于点D,点Q为x轴上一点,且满足∠AQO=∠ADO+∠OPC,求点Q的坐标.
9.(2025 翠屏区二模)如图,在平面直角坐标系中,反比例函数与一次函数y=kx+b相交于点A(a,1)和点B(1,4),AO的延长线交反比例函数的图象于点C.
(1)求反比例函数和一次函数的解析式;
(2)直接写出不等式的解集;
(3)点D是线段AB上一点.连结CD,交反比例函数在第一象限的图象于点E,连结OE、AE.当的值最小时,求的值.
10.(2025 莱芜区三模)在平面直角坐标系xOy中,一次函数y=kx﹣2的图象与反比例函数的图象交于点A(1,﹣4),B(﹣2,n)两点.
(1)求反比例函数的关系式和一次函数的关系式;
(2)如图1,点C是第二象限内反比例函数图象上一点,且点C位于点B右侧,若△ABC的面积为6,求点C的坐标;
(3)在(2)的条件下,点M是坐标轴上的点,点N是平面内一点,是否存在点M,N,使得四边形BCMN是矩形?若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.
11.(2025春 梁溪区校级月考)在图中,A,B两点在反比例函数的图象上,AB过点O,△ABC是等边三角形,请仅用无刻度的直尺完成以下作图(保留作图痕迹).
(1)图1中,作AE⊥BC,垂足为点E;
(2)图2中,点D为AC的中点,在x轴上作出点F,使四边形ADBF为矩形;
(3)图3中,在第二象限内作出点G,使四边形ACBG为菱形.
12.(2025春 宜宾期中)如图,一次函数y=kx﹣4k(k≠0)的图象与反比例函数1≠0)的图象交于点C,与x轴交于点A,过点C作CB⊥y轴,垂足为B,连接OC,AB.已知四边形ABCO是平行四边形,且其面积是12.
(1)求点A的坐标及m和k的值;
(2)若两函数图象另一个交点坐标D的纵坐标为,请结合图象,直接写出不等式的解集;
(3)若直线y=x+t与 ABCO有交点时,求t的取值范围.
13.(2025春 玄武区校级月考)如图,在平面直角坐标系中,矩形ABOC的顶点C在y轴上,B在x轴上,把矩形ABOC沿对角线BC所在的直线翻折,点A恰好落在反比例函数的图象上点D处,BD与y轴交于点E,延长CD交x轴于点F,点D刚好是CF的中点.已知B的坐标为(﹣2,0).
(1)求∠DBF的度数;
(2)求反比例函数的函数表达式;
(3)若Q是反比例函数图象上的一点,P点在x轴上,若以P,Q,B,E为顶点的四边形是平行四边形,请直接写出P点的坐标 .
14.(2025春 常熟市月考)如图,已知直线与反比例函数的图象交于点A,B,点A的横坐标为﹣4,点B的横坐标为2.
(1)求k和b的值;
(2)若点C在反比例函数第一象限内的图象上,直线OC与直线AB交于点M,且BM=4AM,求点C的坐标;
(3)是否存在点C在反比例函数第一象限内的图象上,点D是平面直角坐标系内的一点,使得以点A,B,C,D为顶点的四边形是矩形,若存在,直接写出C的坐标;若不存在,请说明理由.
15.(2025 山东模拟)如图①,点A的坐标为(3,0),把点A先向左平移2个单位长度,再向上平移3个单位长度,可以平移到点D的位置.
(1)①请直接写出点D的坐标为( , );
②若反比例函数y(x>0)的图象与线段AD有且只有一个交点时,请确定k的取值范围并说明理由;
(2)如图②,当k=12时,以AD为一边的平行四边形ABCD的另外两个顶点B与C均在反比例函数y(x>0)的图象上.请求出△ABC的面积.
【攻克压轴大题】2025年中考数学压轴题精选:反比例函数
参考答案与试题解析
一.解答题(共15小题)
1.(2025 姑苏区校级二模)一次函数与x轴交于C点,与y轴交于B点,点A(2,a)在直线BC上,过点A作反比例函数的图象.
(1)求出a,k的值;
(2)在x轴上是否存在点D,使得∠BOA=∠OAD,若不存在,请说明理由;若存在,求出点D的坐标.
【解答】解:(1)∵点A(2,a)在直线BC:yx+2上,
∴a2+2=3,
∴A(2,3),
∵反比例函数y经过点A(2,3),
∴3,
解得:k=6;
(2)在x轴上存在点D,使得∠BOA=∠OAD.
当点D在x轴正半轴上时,如图,过点A作AD1∥y轴交x轴于点D1,
则∠BOA=∠OAD1,
此时点D1(2,0);
当点D2在x轴负半轴上时,如图,设AD2与y轴交于点E(0,n),
∵∠BOA=∠OAD2,
∴AE=OE,
∴(2﹣0)2+(3﹣n)2=n2,
解得:n,
∴E(0,),
设直线AE的解析式为y=sx+t,
则,
解得,
∴直线AE的解析式为yx,
令y=0,得x0,
解得:x,
∴D2(,0);
综上所述,点D的坐标为(2,0)或(,0).
2.(2025 锦江区校级模拟)如图,一次函数y=kx+b与反比例函数的图象相交于点A(3,4)、B(6,m)两点.
(1)求一次函数与反比例函数的解析式;
(2)若点C为线段AB上一点,且,连接AO、CO,求S△AOC;
(3)如果一个矩形的长宽之比为2:1,我们把该矩形称为“倍边矩形”.请探究,在平面内是否存在P、Q两点(点P在直线AB上方),使得四边形APBQ为倍边矩形,若存在,请求P、Q两点的坐标;若不存在,请说明理由.
【解答】解:(1)由题意得:n=3×4=12,
则反比例函数的表达式为:y,
将点B的坐标代入上式得:m2,
即点B(6,2),
由点A、B的坐标得,直线AB的表达式为:yx+6;
(2)连接OA、OB,
由一次函数的表达式知,点E(9,0),
则S△AOB=S△OEA﹣S△OEBOE×(yA﹣yB)9×(4﹣2)=9,
∵,
则S△AOCS△AOB=3;
(3)存在,理由:
由题意得,∠APB=90°,AP:BP=2,
过点P作x轴的平行线分别交过点A、B和y轴的平行线于点M、N,
则△AMP和△PNB的相似比为1:2或2:1,
当△AMP和△PNB的相似比为1:2时,
设PN=m,BN=n,
则AMm,MPn,
则MNn+m=xB﹣xA=3且BN﹣AMm=yA﹣yB=2,
解得:m,n,
则点P(,),
由中点坐标公式得:点Q(,);
即P(,)、点(,);
当△AMP和△PNB的相似比为2:1时,
同理可得:2m+n=2且2n﹣m=3,
解得:m,n,
则P(,)、点Q(,).
综上,P(,)、点Q(,)或P(,)Q(,).
3.(2025 天桥区三模)如图,一次函数y=kx+b的图象与反比例函数的图象相交于点A(2,3),B(6,n)两点,与x轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)点P是y轴上一动点,连接AP,BP,当△ABP面积为10时,请求出点P的坐标;
(3)将线段AB绕点B顺时针旋转90°,得到线段BD,连接CD,在反比例函数上,是否存在一点Q,使得∠CDB+∠QCO=90°?若存在,请求出点Q的坐标;若不存在,请说明理由.
【解答】解:(1)∵反比例函数经过点A(2,3),
∴3,
∴m=2×3=6,
∴反比例函数的解析式为y.
将点B(6,n)代入y得,n1,
∴B(6,1),
把A(2,3)和B(6,1)分别代入y=kx+b,得,
解得
∴一次函数的解析式为yx+4;
(2)设直线交y轴于点G,如图,
令x=0 得,y=4,
则G(0,4),
设P(0,y),则 PG=|y﹣4|,
∵S△ABPPG (xB﹣xA)=10,
∴|y﹣4|×(6﹣2)=10,
解得:y=﹣1 或9,
∴点P的坐标为(0,﹣1)或(0,9);
(3)存在,如图2,设CQ交y轴于点M,
∵直线AB与x轴交于点C,
∴y=﹣x+4=0,
解得 x=8,
∴C(8,0),
∵A(2,3),B(6,1),
∴BC,AB2,
∵线段AB绕点B顺时针旋转90°,得到线段BD,
∴BD=AB=2,∠ABD=∠CBD=90°,
∵∠COM=90°,
∴∠CBD=∠COM,
∴∠CDB+∠DCB=90°,∠CDB+∠QCO=90°,
∴∠DCB=∠QCO,
∴△CMO∽△CDB,
∴,
∴,
∴OM=16,
∴M(0,16),
∴直线CQ的解析式为 y=﹣2x+16,
∴,
解得:,.
∴点Q的坐标为(4,8+2)或(4,8﹣2).
4.(2025 沁阳市二模)如图,在平面直角坐标系xOy中,一次函数y1=ax+3的图象与反比例函数的图象交于点A,B,与x轴、y轴分别交于点C(﹣6,0)、D,点E在第一象限,点F是x轴正半轴上一点,菱形CDEF的边DE与反比例函数的图象交于点G,且.
(1)利用无刻度的直尺,在反比例函数的图象上作出点Q,使S△OCB=S△OCQ(不写作法,保留作图痕迹).
(2)求a的值和反比例函数的表达式;
(3)将菱形CDEF向下平移,当点C落在这个反比例函数的图象上时,平移的距离为 .
【解答】解:(1)如图,点Q为所求解;
(2)∵点C(﹣6,0)在一次函数y=ax+3 的图象上,
∴﹣6a+3=0,
∴a,
∴一次函数的表达式为:y1x+3,
∵一次函数y1x+3与x轴、y轴分别交于点C(﹣6,0)、D,
∴D(0,3),
∴,
∵四边形OCDE是菱形,
∴,
∵DE∥x轴,,
∴DG=2,点G的纵坐标为3,
∴点G(2,3),
∴,
∴反比例函数的表达式为y2;
(3)设平移的距离为h,
∵点C(﹣6,0),将菱形CDEF向下平移,
∴点C平移后的对应点的坐标为(﹣6,﹣h),
∵点C落在这个反比例函数的图象上,
∴﹣h,
∴h,
故答案为:.
5.(2025 广东模拟)在平面直角坐标系中,若某函数的图象经过矩形ABCD对角线的两个端点,则定义该函数为矩形ABCD 的“友好函数”.例如:如图1,矩形ABCD,经过点A(﹣1,1)和点C(3,3)的一次函数y是矩形ABCD的“友好函数”.
(1)如图2,矩形ABCD的顶点坐标分别为A(2,1),B(6,1),C(6,3),D(2,3),反比例函数y(x>0)经过点B,求反比例函数y(x>0)的函数表达式,并判断该函数是否为矩形ABCD的“友好函数”;
(2)矩形ABCD在第一象限,AB∥x轴,AD∥y轴,且点A的坐标为(1,2),正比例函数y1=ax经过点A,且是矩形ABCD的“友好函数”,反比例函数y2(x>0)经过点B,且是矩形ABCD的“友好函数”.
①如图3,当OC>OA时,将矩形ABCD沿AC折叠,点B的对应点为E,若点E落在y轴上,求k的值;
②设矩形ABCD的周长为y,求y关于k的函数表达式;
③在②的条件下,当矩形ABCD的周长y=4时,设矩形ABCD的面积为S1;当矩形ABCD的周长y=8时,设矩形ABCD的面积为S2,请直接写出S2﹣S1的值.
【解答】解:(1)将点B的坐标代入反比例函数表达式得:k=1×6=6,
则反比例函数的表达式为:y,
当x=2时,y=3,即点D在反比例函数表达式上,
故该函数是否为矩形ABCD的“友好函数”;
(2)将点A的坐标代入正比例函数表达式得:2=k,
则正比例函数表达式为:y=2x,
∵正比例函数是矩形ABCD的“友好函数”,
即点C在直线y=2x上,故设点C(m,2m),
①当OC>OA时,
当点B、D的坐标分别为:(m,2)、(1,2m),
则AB=m﹣1,BC=2m﹣2;
∵将矩形ABCD沿AC折叠,点B的对应点为E,若点E落在y轴上,
则∠EAC=∠BAC=∠CAE,
即OE=EC,
故OE=EC=BC,设点E(0,y),
则y2m﹣2,
解得:m,y,
即点E(0,),
则k=2m;
②当OC>OA时,
将点B(m,2)的坐标代入反比例函数表达式得:k=2m,
∵AB=m﹣1,BC=2m﹣2;
则y=2(AB+BC)=6m﹣6=3k﹣6;
当OC<OA时,
此时,点A、B、C、D的坐标分别为:(1,2)、(1,2m)、(m,2m)、(m,2),
将点B(1,2m)的坐标代入反比例函数表达式得:k=2m,
∵AB=2﹣2m,BC=1﹣m;
则y=2(AB+BC)=6﹣6m=6﹣3k,
综上,y=|6﹣3k|;
③当OC>OA时,
当y=4时,即3k﹣6=4,
则k,则m,
则S1=AB×BC=(m﹣1)(2m﹣2)=2(m﹣1)2;
当y=8时,即3k﹣6=8,
则k,则m,
则S2=AB×BC=(m﹣1)(2m﹣2)=2(m﹣1)2;
则S2﹣S1;
当OC<OA时,
当y=4时,即6﹣3k=4,
则k,则m,
则S1=AB×BC=(2﹣2m)(1﹣m)=2(m﹣1)2;
当y=8时,即6﹣3k=8,
则k,不合题意,舍去;
综上,S2﹣S1.
6.(2025春 阳城县期中)综合与探究
如图1,反比例函数的图象与一次函数y=kx+b的图象交于点A(1,m),B(6,n).
(1)求一次函数y=kx+b的表达式.
(2)若P是y轴上一动点,连结PA,PB,当PA+PB的值最小时,求点P的坐标.
(3)如图2,已知直线AB与y轴交于点C,与x轴交于点D,连结AO,BO,Q是直线AB上的第一象限内的一点,点Q的横坐标为a,过点Q作QE⊥x轴于点E,连结QO,若S△OEQ,求a2﹣7a﹣3的值.
【解答】解:(1)∵反比例函数的图象与一次函数y=kx+b的图象交于点A(1,m),B(6,n).
∴m6,n1,
∴点A(1,6),B(6,1),
把点A(1,6),B(6,1)代入y=kx+b得,
∴,
∴一次函数y=kx+b的表达式为y=﹣x+7;
(2)作点A关于y轴的对称点A′,连接A′B交y轴于P,
则此时,PA+PB的值最小,
∵A(1,6),
∴A′(﹣1,6),
∵设直线A′B的解析式为y=mx+n,
∴,
∴,
∴直线A′B的解析式为yx,
当x=0时,y,
∴P(0,);
(3)如图,过A作AM⊥x轴于M,BN⊥x于n,
∵点A(1,6),B(6,1),
∴S△AOM=S△OBN,AM=ON=6,OM=BN=1,
∴S△AOB=S四边形AMNB,
S△AOB(6﹣1)(6+1),
设Q(a,﹣a+7),
∵QE⊥x轴于点E,
∴E(a,0),
∴S△OEQa(﹣a+7)(a2﹣7a),
∵S△OEQ,
∴(a2﹣7a)(6﹣1)(6+1)4,
∴a2﹣7a=﹣8,
∴a2﹣7a﹣3=﹣11.
7.(2025 商丘模拟)如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,顶点A、C在反比例函数的图象上,且点A的纵坐标为,点C的纵坐标为,点B的坐标为(a,a).
(1)利用无刻度的直尺,在反比例函数的图象上作出点D,使(不用写作法,保留作图痕迹)
(2)求k的值;
(3)直接写出a的值.
【解答】解:(1)如图(1),点D即为所求;
理由如下:
根据反比例函数的图象,直线AD均是关于点O的中心对称图形,
∴点D,A关于点O对称,
∴OD=OA,
∵四边形OABC为菱形,
∴OA∥BC,
∴;
(2)如图(2),过点C作CE⊥x轴于点E,过点A作AF⊥y轴于点F,
则,
∵四边形OABC是菱形,
∴∠AOB=∠COB,OA=OC,
∵B(a,a),
∴点B在∠FOE的平分线上,
∴∠FOB=∠EOB,
∴∠AOB﹣∠FOB=∠COB﹣∠EOB,即∠AOF=∠COE,
在△OAF和△OCE中,
,
∴△OAF≌△OCE(AAS),
∴
∴,
将代入,得:
3,
解得:k=﹣9;
(3).理由如下:
如图(2),连接AC交OB于点P,则PO=PB,PA=PC,
∵点A的纵坐标为,
∴,
由(2)可知,△OAF≌△OCE,
∴,
∴,
∴xA+xC=2xP=xO+xB,即,
∴.
8.(2025 榕城区二模)已知反比例函数的图象与正比例函数y=x的图象交于点A(2,a),点P在线段OA的延长线上.
(1)如图1,过点P作y轴的平行线l,l与的图象交于点B,与x轴交于点C,当线段时,求反比例函数的表达式和点B的坐标;
(2)在(1)的条件下,如图2,连接AB并延长,与x轴交于点D,点Q为x轴上一点,且满足∠AQO=∠ADO+∠OPC,求点Q的坐标.
【解答】解:(1)已知反比例函数的图象与正比例函数y=x的图象交于点A(2,a),将点A的坐标代入y=x得:a=2,
∴A(2,2),
将点A的坐标代入反比例函数得:
2,
解得:k=4,
∴反比例函数的解析式为;
设点B的坐标为,则P(m,m),C(m,0),
∴OC=m,,
∵,
∴,
整理得:m2=16,
∴m=4或﹣4(不合题意,舍去),
∴点B的坐标为(4,1);
(2)∵点P在直线y=x图象上,PC∥y轴,由(1)可知P(4,4),
∴△POC是等腰直角三角形,
∴∠OPC=45°,
∵∠AQO=∠ADO+∠OPC,∠AQO=∠ADO+∠QAD,
∴∠QAD=∠OPC=45°,
设直线AB的解析式为y=kx+b,将点A,点B的坐标分别代入得:
,
解得,
∴直线AB的解析式为,
当y=0时,x=6,
∴D(6,0),
∴,
∵∠AOD=∠QAD=45°,∠ADQ=∠ODA,
∴△ADQ∽△ODA,
∴,即,
∴,
∴,
∴点Q的坐标为.
9.(2025 翠屏区二模)如图,在平面直角坐标系中,反比例函数与一次函数y=kx+b相交于点A(a,1)和点B(1,4),AO的延长线交反比例函数的图象于点C.
(1)求反比例函数和一次函数的解析式;
(2)直接写出不等式的解集;
(3)点D是线段AB上一点.连结CD,交反比例函数在第一象限的图象于点E,连结OE、AE.当的值最小时,求的值.
【解答】解:(1)把B(1,4)代入,
得,
∴m=4,
∴反比例函数的解析式为,
把A(a,1)代入,
得,
∴a=4,
∴A(4,1),
把 A(4,1),B(1,4)代入y=nx+b得,
,
解得,
∴一次函数的解析式为y=﹣x+5;
(2)由函数图象可得,当0<x<1或x>4时,反比例函数图象位于一次函数图象上方,
∴不等式的解集为0<x<1或x>4;
(3)如图,过D,E分别作y轴的平行线,交过C与x轴的平行线交于K,H,EH,AO的交点为N,DK,AE的交点为Q,
∴EH∥DK,
∴,
∵AO的延长线交反比例函数的图象于点C,A(4,1),
∴C(﹣4,﹣1),
设直线CD为y=k(x+4)﹣1=kx+4k﹣1,
∴,
∴,
即kx2+(4k﹣1)x﹣4=0,
∴,
解得,
同理,
解得,
∴
,
∵D在线段AB上,当D,B重合时,同理可得;
当D,A重合时,同理可得,
∴;
当最小,最小,
∵,
∴,
∴此时,
解得,舍去),
∴E(2,2),,
同理可得,直线OA为,
∴,
∴,
同理可得直线AE为,
∴,
∴,
∴.
10.(2025 莱芜区三模)在平面直角坐标系xOy中,一次函数y=kx﹣2的图象与反比例函数的图象交于点A(1,﹣4),B(﹣2,n)两点.
(1)求反比例函数的关系式和一次函数的关系式;
(2)如图1,点C是第二象限内反比例函数图象上一点,且点C位于点B右侧,若△ABC的面积为6,求点C的坐标;
(3)在(2)的条件下,点M是坐标轴上的点,点N是平面内一点,是否存在点M,N,使得四边形BCMN是矩形?若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.
【解答】解:(1)把 A(1,﹣4)代入y=kx﹣2 得,k=﹣2,
∴一次函数的表达式为 y=﹣2x﹣2,
把A(1,﹣4)代入得,m=﹣4,
∴反比例函数的表达式为;
(2)过C点作CD⊥x轴,交AB于D点,
设,则D(t,﹣2t﹣2)
∴,
将B(﹣2,n)代入得 n=2,
∴B(﹣2,2),
∵S△ABC=6
∴S△BCD+S△ACD=6,
∴,
∴,
∴t1=﹣1,t2=2(舍去),
∴C(﹣1,4);
(3)存在,
理由:设直线BC的表达式为 y=kx+b,将 B(﹣2,2),C(﹣1,4)代入上式,得,
解得,
∴y=2x+6,
当四边形BCMN是矩形时,∠BCM=90°,
∴kBC kCM=﹣1,
∴kCM,
设直线CM的解析式为yx,
∴当x=0时,y,
∴M(0,),
当y=0时,x=7,
∴M(7,0),
∵把C(﹣1,4)平移到B(﹣2,2),
∴同理N(﹣1,)或(6,﹣2).
11.(2025春 梁溪区校级月考)在图中,A,B两点在反比例函数的图象上,AB过点O,△ABC是等边三角形,请仅用无刻度的直尺完成以下作图(保留作图痕迹).
(1)图1中,作AE⊥BC,垂足为点E;
(2)图2中,点D为AC的中点,在x轴上作出点F,使四边形ADBF为矩形;
(3)图3中,在第二象限内作出点G,使四边形ACBG为菱形.
【解答】解:(1)如图:
连接OC、BD交于H,连接AH并延长交BC于E,点E即为所求;
(2)如图:
连接并延长BD交反比例函数y的图象于G,连接并延长GO交反比例函数y的图象于M,连接AM交x轴于F,则点F即为所求;
(3)如图:
与(2)一样方法得到点G,则CO和GF的延长线相交于点G,则四边形ACBG为菱形.
12.(2025春 宜宾期中)如图,一次函数y=kx﹣4k(k≠0)的图象与反比例函数1≠0)的图象交于点C,与x轴交于点A,过点C作CB⊥y轴,垂足为B,连接OC,AB.已知四边形ABCO是平行四边形,且其面积是12.
(1)求点A的坐标及m和k的值;
(2)若两函数图象另一个交点坐标D的纵坐标为,请结合图象,直接写出不等式的解集;
(3)若直线y=x+t与 ABCO有交点时,求t的取值范围.
【解答】解:(1)令y=0,则kx﹣4k=0,
∴x=4,
∴A(4,0),
∴OA=4,
∵四边形ABCO为平行四边形,
∴BC=OA=4,
∵CB⊥y轴,
∴设C(﹣4,b),
∵平行四边形ABCO的面积是12,
∴4b=12,
∴b=3,
∴C(﹣4,3),m﹣1=﹣4×3=﹣12,
∴m=﹣11,
∵点C在直线y=kx﹣4k上,
∴3=﹣4k﹣4k,
∴k,
即A(4,0),m=﹣11,k;
(2)由(1)知,k,
∴直线AC的解析式为y=﹣x+1①,
由(1)知,m=﹣5,
∴反比例函数的解析式为y=﹣②,
联立①②解得,(点C的坐标)或,
∴一次函数图象与反比例函数图象的另一个交点坐标为(6,﹣1);
由图可得,当﹣3<x<0或x>6时,反比例函数 的图象在一次函数=kx﹣3k(k≠0)的图象上方,
∴不等式的解集为:﹣3<x<0或x>6;
(3)如图所示,当直线y=x+t经过点C时,t 取最大值,当直线y=x+t经过点A时,t取最小值,
将点C(﹣3,2)代入y=x+t,得2=﹣3+t,
解得t=5;
将点A(3,0)代入y=x+t,得0=3+t,
解得t=﹣3,
∴若直线y=x+t与四边形ABCO有交点时,t的取值范围为﹣3<t<5.
13.(2025春 玄武区校级月考)如图,在平面直角坐标系中,矩形ABOC的顶点C在y轴上,B在x轴上,把矩形ABOC沿对角线BC所在的直线翻折,点A恰好落在反比例函数的图象上点D处,BD与y轴交于点E,延长CD交x轴于点F,点D刚好是CF的中点.已知B的坐标为(﹣2,0).
(1)求∠DBF的度数;
(2)求反比例函数的函数表达式;
(3)若Q是反比例函数图象上的一点,P点在x轴上,若以P,Q,B,E为顶点的四边形是平行四边形,请直接写出P点的坐标 或或 .
【解答】解:(1)∵把矩形ABOC沿对角线BC所在的直线翻折,
∴∠ABC=∠DBC,∠CDB=∠A=90°,
又∵D是CF中点,
∴BD垂直平分CF,
∴BF=BC,∠DBC=∠DBF,
∴∠ABC=∠DBC=∠DBF=30°;
(2)由折叠∠ABC=∠DBC=30°,
∵AB∥OC,
∴∠OCB=∠ABC,
∴∠EBC=∠ECB=30°,
∴BE=CE,
∴OE=DE,
∵B的坐标为(﹣2,0).
∴OB=2,又∠DBF=30°,
∴,,
∴,
∴BH=3,
∴,
∵点D在反比例函数的图象上,
∴,
∴反比例函数的解析式;
(3)如图2中,作EQ∥x轴交,
∵OB=2,
∴,
∴,
∴以DQ为边构造平行四边形可得;
如图3,取E关于x的对称点E'(0,,作E′Q∥x轴,交,连接EQ,交x轴于M,
,
∴,
∴,
∴,
∴,
综上,P点的坐标为或或,
故答案为:或或.
14.(2025春 常熟市月考)如图,已知直线与反比例函数的图象交于点A,B,点A的横坐标为﹣4,点B的横坐标为2.
(1)求k和b的值;
(2)若点C在反比例函数第一象限内的图象上,直线OC与直线AB交于点M,且BM=4AM,求点C的坐标;
(3)是否存在点C在反比例函数第一象限内的图象上,点D是平面直角坐标系内的一点,使得以点A,B,C,D为顶点的四边形是矩形,若存在,直接写出C的坐标;若不存在,请说明理由.
【解答】解:(1)设点A的坐标为(﹣4,t),代入反比例函数的表达式得k=﹣4t,
∴点B的坐标为 (2,﹣2t),
将点A,B的坐标分别代入得,
解得
∴k=﹣4t=12;
(2)解:由(1),得 A(﹣4,﹣3),B(2,6),
∴直线AB的函数表达式为,
∵直线OC与直线AB交于点M,
∴点M在直线AB上,
设,
①如图1,当点M在线段AB上时,分别过点A、B作x轴和y轴的平行线,交于一点N,过点M作MD⊥AN于点D,如图,
∴MD∥BN,AD=m+4,AN=6,
∴△AMD∽△ABN,
∵BM=4AM,
∴,
∵△AMD∽△ABN,
∴,
解得,
∴点M的坐标为,
设直线CM的函数表达式为 y=kx,
∴,
解得:,
∴直线CM的函数表达式为,
由得(负值舍去),
∴点C的坐标为;
②如图2,当点M在线段BA的延长线上时,
∵BM=4AM,
∴,
同理①,得,
解得 m=﹣6,
∴点M的坐标为 (﹣6,﹣6),
同理可得:直线CM的解析式为y=x,
由得负值舍去),
∴点C的坐标为,
③由BM=4AM,知 BM>AM,则点M不在线段AB的延长线上,
综上所述,点C的坐标为或;
(3)解:设点C的坐标为,且n>0,
①如图3,当AB为矩形的边时,过点B作x轴的平行线,
分别过点A,C作这条平行线的垂线,垂足分别为M,N,
∴∠AMB=∠BNC=∠ABC=90°,
∴∠ABM+∠NBC=∠ABM+∠MAB=90°,
∴∠MAB=∠NBC,
∴△ABM﹣△BCN,
∴;
即;
化简,得n2﹣11n+18=0,
解得n1=9,n2=2(与点B重合,舍去),
∴点;
②如图4,当AB为矩形的对角线时,过点C作y轴的平行线,分别过点A,B作这条平行线的垂线,垂足分别为P,Q,
同理①可得:△APC﹣△CQB,
∴,
∴,
化简,得(n2+2n﹣8)(n2﹣18)=0,
解得,(负值舍去),n3=﹣4(负值舍去),n4=2与点B重合,舍去;
∴点C的坐标为,
综上所述,点C的坐标为或.
15.(2025 山东模拟)如图①,点A的坐标为(3,0),把点A先向左平移2个单位长度,再向上平移3个单位长度,可以平移到点D的位置.
(1)①请直接写出点D的坐标为( 1 , 3 );
②若反比例函数y(x>0)的图象与线段AD有且只有一个交点时,请确定k的取值范围并说明理由;
(2)如图②,当k=12时,以AD为一边的平行四边形ABCD的另外两个顶点B与C均在反比例函数y(x>0)的图象上.请求出△ABC的面积.
【解答】解:(1)①∵3﹣2=1,0+3=3,
∴D(1,3),
故答案为:1,3;
②如图1,
0<k≤3,理由如下:
作DE⊥x轴,交反比例函数y(x>0)的图象于E,
则xE=1,0<yE≤3,
∴k=xy≤3,
∴0<k≤3;
(2)如图2,
连接BD,
设B(x,),则C(x﹣2,),
∴(x﹣2) ,
∴x1=4,x2=﹣2(舍去),
∴B(4,3)C(2,6),
∵D(1,3),
∴BD∥x轴,
∴S△BCDBD (yC﹣yD),
∵四边形ABCD是平行四边形,
∴S△ABC=S△BCD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【攻克压轴大题】2025年中考数学压轴题精选:反比例函数
1.(2025 姑苏区校级二模)一次函数与x轴交于C点,与y轴交于B点,点A(2,a)在直线BC上,过点A作反比例函数的图象.
(1)求出a,k的值;
(2)在x轴上是否存在点D,使得∠BOA=∠OAD,若不存在,请说明理由;若存在,求出点D的坐标.
2.(2025 锦江区校级模拟)如图,一次函数y=kx+b与反比例函数的图象相交于点A(3,4)、B(6,m)两点.
(1)求一次函数与反比例函数的解析式;
(2)若点C为线段AB上一点,且,连接AO、CO,求S△AOC;
(3)如果一个矩形的长宽之比为2:1,我们把该矩形称为“倍边矩形”.请探究,在平面内是否存在P、Q两点(点P在直线AB上方),使得四边形APBQ为倍边矩形,若存在,请求P、Q两点的坐标;若不存在,请说明理由.
3.(2025 天桥区三模)如图,一次函数y=kx+b的图象与反比例函数的图象相交于点A(2,3),B(6,n)两点,与x轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)点P是y轴上一动点,连接AP,BP,当△ABP面积为10时,请求出点P的坐标;
(3)将线段AB绕点B顺时针旋转90°,得到线段BD,连接CD,在反比例函数上,是否存在一点Q,使得∠CDB+∠QCO=90°?若存在,请求出点Q的坐标;若不存在,请说明理由.
4.(2025 沁阳市二模)如图,在平面直角坐标系xOy中,一次函数y1=ax+3的图象与反比例函数的图象交于点A,B,与x轴、y轴分别交于点C(﹣6,0)、D,点E在第一象限,点F是x轴正半轴上一点,菱形CDEF的边DE与反比例函数的图象交于点G,且.
(1)利用无刻度的直尺,在反比例函数的图象上作出点Q,使S△OCB=S△OCQ(不写作法,保留作图痕迹).
(2)求a的值和反比例函数的表达式;
(3)将菱形CDEF向下平移,当点C落在这个反比例函数的图象上时,平移的距离为 .
5.(2025 广东模拟)在平面直角坐标系中,若某函数的图象经过矩形ABCD对角线的两个端点,则定义该函数为矩形ABCD 的“友好函数”.例如:如图1,矩形ABCD,经过点A(﹣1,1)和点C(3,3)的一次函数y是矩形ABCD的“友好函数”.
(1)如图2,矩形ABCD的顶点坐标分别为A(2,1),B(6,1),C(6,3),D(2,3),反比例函数y(x>0)经过点B,求反比例函数y(x>0)的函数表达式,并判断该函数是否为矩形ABCD的“友好函数”;
(2)矩形ABCD在第一象限,AB∥x轴,AD∥y轴,且点A的坐标为(1,2),正比例函数y1=ax经过点A,且是矩形ABCD的“友好函数”,反比例函数y2(x>0)经过点B,且是矩形ABCD的“友好函数”.
①如图3,当OC>OA时,将矩形ABCD沿AC折叠,点B的对应点为E,若点E落在y轴上,求k的值;
②设矩形ABCD的周长为y,求y关于k的函数表达式;
③在②的条件下,当矩形ABCD的周长y=4时,设矩形ABCD的面积为S1;当矩形ABCD的周长y=8时,设矩形ABCD的面积为S2,请直接写出S2﹣S1的值.
6.(2025春 阳城县期中)综合与探究
如图1,反比例函数的图象与一次函数y=kx+b的图象交于点A(1,m),B(6,n).
(1)求一次函数y=kx+b的表达式.
(2)若P是y轴上一动点,连结PA,PB,当PA+PB的值最小时,求点P的坐标.
(3)如图2,已知直线AB与y轴交于点C,与x轴交于点D,连结AO,BO,Q是直线AB上的第一象限内的一点,点Q的横坐标为a,过点Q作QE⊥x轴于点E,连结QO,若S△OEQ,求a2﹣7a﹣3的值.
7.(2025 商丘模拟)如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,顶点A、C在反比例函数的图象上,且点A的纵坐标为,点C的纵坐标为,点B的坐标为(a,a).
(1)利用无刻度的直尺,在反比例函数的图象上作出点D,使(不用写作法,保留作图痕迹)
(2)求k的值;
(3)直接写出a的值.
8.(2025 榕城区二模)已知反比例函数的图象与正比例函数y=x的图象交于点A(2,a),点P在线段OA的延长线上.
(1)如图1,过点P作y轴的平行线l,l与的图象交于点B,与x轴交于点C,当线段时,求反比例函数的表达式和点B的坐标;
(2)在(1)的条件下,如图2,连接AB并延长,与x轴交于点D,点Q为x轴上一点,且满足∠AQO=∠ADO+∠OPC,求点Q的坐标.
9.(2025 翠屏区二模)如图,在平面直角坐标系中,反比例函数与一次函数y=kx+b相交于点A(a,1)和点B(1,4),AO的延长线交反比例函数的图象于点C.
(1)求反比例函数和一次函数的解析式;
(2)直接写出不等式的解集;
(3)点D是线段AB上一点.连结CD,交反比例函数在第一象限的图象于点E,连结OE、AE.当的值最小时,求的值.
10.(2025 莱芜区三模)在平面直角坐标系xOy中,一次函数y=kx﹣2的图象与反比例函数的图象交于点A(1,﹣4),B(﹣2,n)两点.
(1)求反比例函数的关系式和一次函数的关系式;
(2)如图1,点C是第二象限内反比例函数图象上一点,且点C位于点B右侧,若△ABC的面积为6,求点C的坐标;
(3)在(2)的条件下,点M是坐标轴上的点,点N是平面内一点,是否存在点M,N,使得四边形BCMN是矩形?若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.
11.(2025春 梁溪区校级月考)在图中,A,B两点在反比例函数的图象上,AB过点O,△ABC是等边三角形,请仅用无刻度的直尺完成以下作图(保留作图痕迹).
(1)图1中,作AE⊥BC,垂足为点E;
(2)图2中,点D为AC的中点,在x轴上作出点F,使四边形ADBF为矩形;
(3)图3中,在第二象限内作出点G,使四边形ACBG为菱形.
12.(2025春 宜宾期中)如图,一次函数y=kx﹣4k(k≠0)的图象与反比例函数1≠0)的图象交于点C,与x轴交于点A,过点C作CB⊥y轴,垂足为B,连接OC,AB.已知四边形ABCO是平行四边形,且其面积是12.
(1)求点A的坐标及m和k的值;
(2)若两函数图象另一个交点坐标D的纵坐标为,请结合图象,直接写出不等式的解集;
(3)若直线y=x+t与 ABCO有交点时,求t的取值范围.
13.(2025春 玄武区校级月考)如图,在平面直角坐标系中,矩形ABOC的顶点C在y轴上,B在x轴上,把矩形ABOC沿对角线BC所在的直线翻折,点A恰好落在反比例函数的图象上点D处,BD与y轴交于点E,延长CD交x轴于点F,点D刚好是CF的中点.已知B的坐标为(﹣2,0).
(1)求∠DBF的度数;
(2)求反比例函数的函数表达式;
(3)若Q是反比例函数图象上的一点,P点在x轴上,若以P,Q,B,E为顶点的四边形是平行四边形,请直接写出P点的坐标 .
14.(2025春 常熟市月考)如图,已知直线与反比例函数的图象交于点A,B,点A的横坐标为﹣4,点B的横坐标为2.
(1)求k和b的值;
(2)若点C在反比例函数第一象限内的图象上,直线OC与直线AB交于点M,且BM=4AM,求点C的坐标;
(3)是否存在点C在反比例函数第一象限内的图象上,点D是平面直角坐标系内的一点,使得以点A,B,C,D为顶点的四边形是矩形,若存在,直接写出C的坐标;若不存在,请说明理由.
15.(2025 山东模拟)如图①,点A的坐标为(3,0),把点A先向左平移2个单位长度,再向上平移3个单位长度,可以平移到点D的位置.
(1)①请直接写出点D的坐标为( , );
②若反比例函数y(x>0)的图象与线段AD有且只有一个交点时,请确定k的取值范围并说明理由;
(2)如图②,当k=12时,以AD为一边的平行四边形ABCD的另外两个顶点B与C均在反比例函数y(x>0)的图象上.请求出△ABC的面积.
【攻克压轴大题】2025年中考数学压轴题精选:反比例函数
参考答案与试题解析
一.解答题(共15小题)
1.(2025 姑苏区校级二模)一次函数与x轴交于C点,与y轴交于B点,点A(2,a)在直线BC上,过点A作反比例函数的图象.
(1)求出a,k的值;
(2)在x轴上是否存在点D,使得∠BOA=∠OAD,若不存在,请说明理由;若存在,求出点D的坐标.
【解答】解:(1)∵点A(2,a)在直线BC:yx+2上,
∴a2+2=3,
∴A(2,3),
∵反比例函数y经过点A(2,3),
∴3,
解得:k=6;
(2)在x轴上存在点D,使得∠BOA=∠OAD.
当点D在x轴正半轴上时,如图,过点A作AD1∥y轴交x轴于点D1,
则∠BOA=∠OAD1,
此时点D1(2,0);
当点D2在x轴负半轴上时,如图,设AD2与y轴交于点E(0,n),
∵∠BOA=∠OAD2,
∴AE=OE,
∴(2﹣0)2+(3﹣n)2=n2,
解得:n,
∴E(0,),
设直线AE的解析式为y=sx+t,
则,
解得,
∴直线AE的解析式为yx,
令y=0,得x0,
解得:x,
∴D2(,0);
综上所述,点D的坐标为(2,0)或(,0).
2.(2025 锦江区校级模拟)如图,一次函数y=kx+b与反比例函数的图象相交于点A(3,4)、B(6,m)两点.
(1)求一次函数与反比例函数的解析式;
(2)若点C为线段AB上一点,且,连接AO、CO,求S△AOC;
(3)如果一个矩形的长宽之比为2:1,我们把该矩形称为“倍边矩形”.请探究,在平面内是否存在P、Q两点(点P在直线AB上方),使得四边形APBQ为倍边矩形,若存在,请求P、Q两点的坐标;若不存在,请说明理由.
【解答】解:(1)由题意得:n=3×4=12,
则反比例函数的表达式为:y,
将点B的坐标代入上式得:m2,
即点B(6,2),
由点A、B的坐标得,直线AB的表达式为:yx+6;
(2)连接OA、OB,
由一次函数的表达式知,点E(9,0),
则S△AOB=S△OEA﹣S△OEBOE×(yA﹣yB)9×(4﹣2)=9,
∵,
则S△AOCS△AOB=3;
(3)存在,理由:
由题意得,∠APB=90°,AP:BP=2,
过点P作x轴的平行线分别交过点A、B和y轴的平行线于点M、N,
则△AMP和△PNB的相似比为1:2或2:1,
当△AMP和△PNB的相似比为1:2时,
设PN=m,BN=n,
则AMm,MPn,
则MNn+m=xB﹣xA=3且BN﹣AMm=yA﹣yB=2,
解得:m,n,
则点P(,),
由中点坐标公式得:点Q(,);
即P(,)、点(,);
当△AMP和△PNB的相似比为2:1时,
同理可得:2m+n=2且2n﹣m=3,
解得:m,n,
则P(,)、点Q(,).
综上,P(,)、点Q(,)或P(,)Q(,).
3.(2025 天桥区三模)如图,一次函数y=kx+b的图象与反比例函数的图象相交于点A(2,3),B(6,n)两点,与x轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)点P是y轴上一动点,连接AP,BP,当△ABP面积为10时,请求出点P的坐标;
(3)将线段AB绕点B顺时针旋转90°,得到线段BD,连接CD,在反比例函数上,是否存在一点Q,使得∠CDB+∠QCO=90°?若存在,请求出点Q的坐标;若不存在,请说明理由.
【解答】解:(1)∵反比例函数经过点A(2,3),
∴3,
∴m=2×3=6,
∴反比例函数的解析式为y.
将点B(6,n)代入y得,n1,
∴B(6,1),
把A(2,3)和B(6,1)分别代入y=kx+b,得,
解得
∴一次函数的解析式为yx+4;
(2)设直线交y轴于点G,如图,
令x=0 得,y=4,
则G(0,4),
设P(0,y),则 PG=|y﹣4|,
∵S△ABPPG (xB﹣xA)=10,
∴|y﹣4|×(6﹣2)=10,
解得:y=﹣1 或9,
∴点P的坐标为(0,﹣1)或(0,9);
(3)存在,如图2,设CQ交y轴于点M,
∵直线AB与x轴交于点C,
∴y=﹣x+4=0,
解得 x=8,
∴C(8,0),
∵A(2,3),B(6,1),
∴BC,AB2,
∵线段AB绕点B顺时针旋转90°,得到线段BD,
∴BD=AB=2,∠ABD=∠CBD=90°,
∵∠COM=90°,
∴∠CBD=∠COM,
∴∠CDB+∠DCB=90°,∠CDB+∠QCO=90°,
∴∠DCB=∠QCO,
∴△CMO∽△CDB,
∴,
∴,
∴OM=16,
∴M(0,16),
∴直线CQ的解析式为 y=﹣2x+16,
∴,
解得:,.
∴点Q的坐标为(4,8+2)或(4,8﹣2).
4.(2025 沁阳市二模)如图,在平面直角坐标系xOy中,一次函数y1=ax+3的图象与反比例函数的图象交于点A,B,与x轴、y轴分别交于点C(﹣6,0)、D,点E在第一象限,点F是x轴正半轴上一点,菱形CDEF的边DE与反比例函数的图象交于点G,且.
(1)利用无刻度的直尺,在反比例函数的图象上作出点Q,使S△OCB=S△OCQ(不写作法,保留作图痕迹).
(2)求a的值和反比例函数的表达式;
(3)将菱形CDEF向下平移,当点C落在这个反比例函数的图象上时,平移的距离为 .
【解答】解:(1)如图,点Q为所求解;
(2)∵点C(﹣6,0)在一次函数y=ax+3 的图象上,
∴﹣6a+3=0,
∴a,
∴一次函数的表达式为:y1x+3,
∵一次函数y1x+3与x轴、y轴分别交于点C(﹣6,0)、D,
∴D(0,3),
∴,
∵四边形OCDE是菱形,
∴,
∵DE∥x轴,,
∴DG=2,点G的纵坐标为3,
∴点G(2,3),
∴,
∴反比例函数的表达式为y2;
(3)设平移的距离为h,
∵点C(﹣6,0),将菱形CDEF向下平移,
∴点C平移后的对应点的坐标为(﹣6,﹣h),
∵点C落在这个反比例函数的图象上,
∴﹣h,
∴h,
故答案为:.
5.(2025 广东模拟)在平面直角坐标系中,若某函数的图象经过矩形ABCD对角线的两个端点,则定义该函数为矩形ABCD 的“友好函数”.例如:如图1,矩形ABCD,经过点A(﹣1,1)和点C(3,3)的一次函数y是矩形ABCD的“友好函数”.
(1)如图2,矩形ABCD的顶点坐标分别为A(2,1),B(6,1),C(6,3),D(2,3),反比例函数y(x>0)经过点B,求反比例函数y(x>0)的函数表达式,并判断该函数是否为矩形ABCD的“友好函数”;
(2)矩形ABCD在第一象限,AB∥x轴,AD∥y轴,且点A的坐标为(1,2),正比例函数y1=ax经过点A,且是矩形ABCD的“友好函数”,反比例函数y2(x>0)经过点B,且是矩形ABCD的“友好函数”.
①如图3,当OC>OA时,将矩形ABCD沿AC折叠,点B的对应点为E,若点E落在y轴上,求k的值;
②设矩形ABCD的周长为y,求y关于k的函数表达式;
③在②的条件下,当矩形ABCD的周长y=4时,设矩形ABCD的面积为S1;当矩形ABCD的周长y=8时,设矩形ABCD的面积为S2,请直接写出S2﹣S1的值.
【解答】解:(1)将点B的坐标代入反比例函数表达式得:k=1×6=6,
则反比例函数的表达式为:y,
当x=2时,y=3,即点D在反比例函数表达式上,
故该函数是否为矩形ABCD的“友好函数”;
(2)将点A的坐标代入正比例函数表达式得:2=k,
则正比例函数表达式为:y=2x,
∵正比例函数是矩形ABCD的“友好函数”,
即点C在直线y=2x上,故设点C(m,2m),
①当OC>OA时,
当点B、D的坐标分别为:(m,2)、(1,2m),
则AB=m﹣1,BC=2m﹣2;
∵将矩形ABCD沿AC折叠,点B的对应点为E,若点E落在y轴上,
则∠EAC=∠BAC=∠CAE,
即OE=EC,
故OE=EC=BC,设点E(0,y),
则y2m﹣2,
解得:m,y,
即点E(0,),
则k=2m;
②当OC>OA时,
将点B(m,2)的坐标代入反比例函数表达式得:k=2m,
∵AB=m﹣1,BC=2m﹣2;
则y=2(AB+BC)=6m﹣6=3k﹣6;
当OC<OA时,
此时,点A、B、C、D的坐标分别为:(1,2)、(1,2m)、(m,2m)、(m,2),
将点B(1,2m)的坐标代入反比例函数表达式得:k=2m,
∵AB=2﹣2m,BC=1﹣m;
则y=2(AB+BC)=6﹣6m=6﹣3k,
综上,y=|6﹣3k|;
③当OC>OA时,
当y=4时,即3k﹣6=4,
则k,则m,
则S1=AB×BC=(m﹣1)(2m﹣2)=2(m﹣1)2;
当y=8时,即3k﹣6=8,
则k,则m,
则S2=AB×BC=(m﹣1)(2m﹣2)=2(m﹣1)2;
则S2﹣S1;
当OC<OA时,
当y=4时,即6﹣3k=4,
则k,则m,
则S1=AB×BC=(2﹣2m)(1﹣m)=2(m﹣1)2;
当y=8时,即6﹣3k=8,
则k,不合题意,舍去;
综上,S2﹣S1.
6.(2025春 阳城县期中)综合与探究
如图1,反比例函数的图象与一次函数y=kx+b的图象交于点A(1,m),B(6,n).
(1)求一次函数y=kx+b的表达式.
(2)若P是y轴上一动点,连结PA,PB,当PA+PB的值最小时,求点P的坐标.
(3)如图2,已知直线AB与y轴交于点C,与x轴交于点D,连结AO,BO,Q是直线AB上的第一象限内的一点,点Q的横坐标为a,过点Q作QE⊥x轴于点E,连结QO,若S△OEQ,求a2﹣7a﹣3的值.
【解答】解:(1)∵反比例函数的图象与一次函数y=kx+b的图象交于点A(1,m),B(6,n).
∴m6,n1,
∴点A(1,6),B(6,1),
把点A(1,6),B(6,1)代入y=kx+b得,
∴,
∴一次函数y=kx+b的表达式为y=﹣x+7;
(2)作点A关于y轴的对称点A′,连接A′B交y轴于P,
则此时,PA+PB的值最小,
∵A(1,6),
∴A′(﹣1,6),
∵设直线A′B的解析式为y=mx+n,
∴,
∴,
∴直线A′B的解析式为yx,
当x=0时,y,
∴P(0,);
(3)如图,过A作AM⊥x轴于M,BN⊥x于n,
∵点A(1,6),B(6,1),
∴S△AOM=S△OBN,AM=ON=6,OM=BN=1,
∴S△AOB=S四边形AMNB,
S△AOB(6﹣1)(6+1),
设Q(a,﹣a+7),
∵QE⊥x轴于点E,
∴E(a,0),
∴S△OEQa(﹣a+7)(a2﹣7a),
∵S△OEQ,
∴(a2﹣7a)(6﹣1)(6+1)4,
∴a2﹣7a=﹣8,
∴a2﹣7a﹣3=﹣11.
7.(2025 商丘模拟)如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,顶点A、C在反比例函数的图象上,且点A的纵坐标为,点C的纵坐标为,点B的坐标为(a,a).
(1)利用无刻度的直尺,在反比例函数的图象上作出点D,使(不用写作法,保留作图痕迹)
(2)求k的值;
(3)直接写出a的值.
【解答】解:(1)如图(1),点D即为所求;
理由如下:
根据反比例函数的图象,直线AD均是关于点O的中心对称图形,
∴点D,A关于点O对称,
∴OD=OA,
∵四边形OABC为菱形,
∴OA∥BC,
∴;
(2)如图(2),过点C作CE⊥x轴于点E,过点A作AF⊥y轴于点F,
则,
∵四边形OABC是菱形,
∴∠AOB=∠COB,OA=OC,
∵B(a,a),
∴点B在∠FOE的平分线上,
∴∠FOB=∠EOB,
∴∠AOB﹣∠FOB=∠COB﹣∠EOB,即∠AOF=∠COE,
在△OAF和△OCE中,
,
∴△OAF≌△OCE(AAS),
∴
∴,
将代入,得:
3,
解得:k=﹣9;
(3).理由如下:
如图(2),连接AC交OB于点P,则PO=PB,PA=PC,
∵点A的纵坐标为,
∴,
由(2)可知,△OAF≌△OCE,
∴,
∴,
∴xA+xC=2xP=xO+xB,即,
∴.
8.(2025 榕城区二模)已知反比例函数的图象与正比例函数y=x的图象交于点A(2,a),点P在线段OA的延长线上.
(1)如图1,过点P作y轴的平行线l,l与的图象交于点B,与x轴交于点C,当线段时,求反比例函数的表达式和点B的坐标;
(2)在(1)的条件下,如图2,连接AB并延长,与x轴交于点D,点Q为x轴上一点,且满足∠AQO=∠ADO+∠OPC,求点Q的坐标.
【解答】解:(1)已知反比例函数的图象与正比例函数y=x的图象交于点A(2,a),将点A的坐标代入y=x得:a=2,
∴A(2,2),
将点A的坐标代入反比例函数得:
2,
解得:k=4,
∴反比例函数的解析式为;
设点B的坐标为,则P(m,m),C(m,0),
∴OC=m,,
∵,
∴,
整理得:m2=16,
∴m=4或﹣4(不合题意,舍去),
∴点B的坐标为(4,1);
(2)∵点P在直线y=x图象上,PC∥y轴,由(1)可知P(4,4),
∴△POC是等腰直角三角形,
∴∠OPC=45°,
∵∠AQO=∠ADO+∠OPC,∠AQO=∠ADO+∠QAD,
∴∠QAD=∠OPC=45°,
设直线AB的解析式为y=kx+b,将点A,点B的坐标分别代入得:
,
解得,
∴直线AB的解析式为,
当y=0时,x=6,
∴D(6,0),
∴,
∵∠AOD=∠QAD=45°,∠ADQ=∠ODA,
∴△ADQ∽△ODA,
∴,即,
∴,
∴,
∴点Q的坐标为.
9.(2025 翠屏区二模)如图,在平面直角坐标系中,反比例函数与一次函数y=kx+b相交于点A(a,1)和点B(1,4),AO的延长线交反比例函数的图象于点C.
(1)求反比例函数和一次函数的解析式;
(2)直接写出不等式的解集;
(3)点D是线段AB上一点.连结CD,交反比例函数在第一象限的图象于点E,连结OE、AE.当的值最小时,求的值.
【解答】解:(1)把B(1,4)代入,
得,
∴m=4,
∴反比例函数的解析式为,
把A(a,1)代入,
得,
∴a=4,
∴A(4,1),
把 A(4,1),B(1,4)代入y=nx+b得,
,
解得,
∴一次函数的解析式为y=﹣x+5;
(2)由函数图象可得,当0<x<1或x>4时,反比例函数图象位于一次函数图象上方,
∴不等式的解集为0<x<1或x>4;
(3)如图,过D,E分别作y轴的平行线,交过C与x轴的平行线交于K,H,EH,AO的交点为N,DK,AE的交点为Q,
∴EH∥DK,
∴,
∵AO的延长线交反比例函数的图象于点C,A(4,1),
∴C(﹣4,﹣1),
设直线CD为y=k(x+4)﹣1=kx+4k﹣1,
∴,
∴,
即kx2+(4k﹣1)x﹣4=0,
∴,
解得,
同理,
解得,
∴
,
∵D在线段AB上,当D,B重合时,同理可得;
当D,A重合时,同理可得,
∴;
当最小,最小,
∵,
∴,
∴此时,
解得,舍去),
∴E(2,2),,
同理可得,直线OA为,
∴,
∴,
同理可得直线AE为,
∴,
∴,
∴.
10.(2025 莱芜区三模)在平面直角坐标系xOy中,一次函数y=kx﹣2的图象与反比例函数的图象交于点A(1,﹣4),B(﹣2,n)两点.
(1)求反比例函数的关系式和一次函数的关系式;
(2)如图1,点C是第二象限内反比例函数图象上一点,且点C位于点B右侧,若△ABC的面积为6,求点C的坐标;
(3)在(2)的条件下,点M是坐标轴上的点,点N是平面内一点,是否存在点M,N,使得四边形BCMN是矩形?若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.
【解答】解:(1)把 A(1,﹣4)代入y=kx﹣2 得,k=﹣2,
∴一次函数的表达式为 y=﹣2x﹣2,
把A(1,﹣4)代入得,m=﹣4,
∴反比例函数的表达式为;
(2)过C点作CD⊥x轴,交AB于D点,
设,则D(t,﹣2t﹣2)
∴,
将B(﹣2,n)代入得 n=2,
∴B(﹣2,2),
∵S△ABC=6
∴S△BCD+S△ACD=6,
∴,
∴,
∴t1=﹣1,t2=2(舍去),
∴C(﹣1,4);
(3)存在,
理由:设直线BC的表达式为 y=kx+b,将 B(﹣2,2),C(﹣1,4)代入上式,得,
解得,
∴y=2x+6,
当四边形BCMN是矩形时,∠BCM=90°,
∴kBC kCM=﹣1,
∴kCM,
设直线CM的解析式为yx,
∴当x=0时,y,
∴M(0,),
当y=0时,x=7,
∴M(7,0),
∵把C(﹣1,4)平移到B(﹣2,2),
∴同理N(﹣1,)或(6,﹣2).
11.(2025春 梁溪区校级月考)在图中,A,B两点在反比例函数的图象上,AB过点O,△ABC是等边三角形,请仅用无刻度的直尺完成以下作图(保留作图痕迹).
(1)图1中,作AE⊥BC,垂足为点E;
(2)图2中,点D为AC的中点,在x轴上作出点F,使四边形ADBF为矩形;
(3)图3中,在第二象限内作出点G,使四边形ACBG为菱形.
【解答】解:(1)如图:
连接OC、BD交于H,连接AH并延长交BC于E,点E即为所求;
(2)如图:
连接并延长BD交反比例函数y的图象于G,连接并延长GO交反比例函数y的图象于M,连接AM交x轴于F,则点F即为所求;
(3)如图:
与(2)一样方法得到点G,则CO和GF的延长线相交于点G,则四边形ACBG为菱形.
12.(2025春 宜宾期中)如图,一次函数y=kx﹣4k(k≠0)的图象与反比例函数1≠0)的图象交于点C,与x轴交于点A,过点C作CB⊥y轴,垂足为B,连接OC,AB.已知四边形ABCO是平行四边形,且其面积是12.
(1)求点A的坐标及m和k的值;
(2)若两函数图象另一个交点坐标D的纵坐标为,请结合图象,直接写出不等式的解集;
(3)若直线y=x+t与 ABCO有交点时,求t的取值范围.
【解答】解:(1)令y=0,则kx﹣4k=0,
∴x=4,
∴A(4,0),
∴OA=4,
∵四边形ABCO为平行四边形,
∴BC=OA=4,
∵CB⊥y轴,
∴设C(﹣4,b),
∵平行四边形ABCO的面积是12,
∴4b=12,
∴b=3,
∴C(﹣4,3),m﹣1=﹣4×3=﹣12,
∴m=﹣11,
∵点C在直线y=kx﹣4k上,
∴3=﹣4k﹣4k,
∴k,
即A(4,0),m=﹣11,k;
(2)由(1)知,k,
∴直线AC的解析式为y=﹣x+1①,
由(1)知,m=﹣5,
∴反比例函数的解析式为y=﹣②,
联立①②解得,(点C的坐标)或,
∴一次函数图象与反比例函数图象的另一个交点坐标为(6,﹣1);
由图可得,当﹣3<x<0或x>6时,反比例函数 的图象在一次函数=kx﹣3k(k≠0)的图象上方,
∴不等式的解集为:﹣3<x<0或x>6;
(3)如图所示,当直线y=x+t经过点C时,t 取最大值,当直线y=x+t经过点A时,t取最小值,
将点C(﹣3,2)代入y=x+t,得2=﹣3+t,
解得t=5;
将点A(3,0)代入y=x+t,得0=3+t,
解得t=﹣3,
∴若直线y=x+t与四边形ABCO有交点时,t的取值范围为﹣3<t<5.
13.(2025春 玄武区校级月考)如图,在平面直角坐标系中,矩形ABOC的顶点C在y轴上,B在x轴上,把矩形ABOC沿对角线BC所在的直线翻折,点A恰好落在反比例函数的图象上点D处,BD与y轴交于点E,延长CD交x轴于点F,点D刚好是CF的中点.已知B的坐标为(﹣2,0).
(1)求∠DBF的度数;
(2)求反比例函数的函数表达式;
(3)若Q是反比例函数图象上的一点,P点在x轴上,若以P,Q,B,E为顶点的四边形是平行四边形,请直接写出P点的坐标 或或 .
【解答】解:(1)∵把矩形ABOC沿对角线BC所在的直线翻折,
∴∠ABC=∠DBC,∠CDB=∠A=90°,
又∵D是CF中点,
∴BD垂直平分CF,
∴BF=BC,∠DBC=∠DBF,
∴∠ABC=∠DBC=∠DBF=30°;
(2)由折叠∠ABC=∠DBC=30°,
∵AB∥OC,
∴∠OCB=∠ABC,
∴∠EBC=∠ECB=30°,
∴BE=CE,
∴OE=DE,
∵B的坐标为(﹣2,0).
∴OB=2,又∠DBF=30°,
∴,,
∴,
∴BH=3,
∴,
∵点D在反比例函数的图象上,
∴,
∴反比例函数的解析式;
(3)如图2中,作EQ∥x轴交,
∵OB=2,
∴,
∴,
∴以DQ为边构造平行四边形可得;
如图3,取E关于x的对称点E'(0,,作E′Q∥x轴,交,连接EQ,交x轴于M,
,
∴,
∴,
∴,
∴,
综上,P点的坐标为或或,
故答案为:或或.
14.(2025春 常熟市月考)如图,已知直线与反比例函数的图象交于点A,B,点A的横坐标为﹣4,点B的横坐标为2.
(1)求k和b的值;
(2)若点C在反比例函数第一象限内的图象上,直线OC与直线AB交于点M,且BM=4AM,求点C的坐标;
(3)是否存在点C在反比例函数第一象限内的图象上,点D是平面直角坐标系内的一点,使得以点A,B,C,D为顶点的四边形是矩形,若存在,直接写出C的坐标;若不存在,请说明理由.
【解答】解:(1)设点A的坐标为(﹣4,t),代入反比例函数的表达式得k=﹣4t,
∴点B的坐标为 (2,﹣2t),
将点A,B的坐标分别代入得,
解得
∴k=﹣4t=12;
(2)解:由(1),得 A(﹣4,﹣3),B(2,6),
∴直线AB的函数表达式为,
∵直线OC与直线AB交于点M,
∴点M在直线AB上,
设,
①如图1,当点M在线段AB上时,分别过点A、B作x轴和y轴的平行线,交于一点N,过点M作MD⊥AN于点D,如图,
∴MD∥BN,AD=m+4,AN=6,
∴△AMD∽△ABN,
∵BM=4AM,
∴,
∵△AMD∽△ABN,
∴,
解得,
∴点M的坐标为,
设直线CM的函数表达式为 y=kx,
∴,
解得:,
∴直线CM的函数表达式为,
由得(负值舍去),
∴点C的坐标为;
②如图2,当点M在线段BA的延长线上时,
∵BM=4AM,
∴,
同理①,得,
解得 m=﹣6,
∴点M的坐标为 (﹣6,﹣6),
同理可得:直线CM的解析式为y=x,
由得负值舍去),
∴点C的坐标为,
③由BM=4AM,知 BM>AM,则点M不在线段AB的延长线上,
综上所述,点C的坐标为或;
(3)解:设点C的坐标为,且n>0,
①如图3,当AB为矩形的边时,过点B作x轴的平行线,
分别过点A,C作这条平行线的垂线,垂足分别为M,N,
∴∠AMB=∠BNC=∠ABC=90°,
∴∠ABM+∠NBC=∠ABM+∠MAB=90°,
∴∠MAB=∠NBC,
∴△ABM﹣△BCN,
∴;
即;
化简,得n2﹣11n+18=0,
解得n1=9,n2=2(与点B重合,舍去),
∴点;
②如图4,当AB为矩形的对角线时,过点C作y轴的平行线,分别过点A,B作这条平行线的垂线,垂足分别为P,Q,
同理①可得:△APC﹣△CQB,
∴,
∴,
化简,得(n2+2n﹣8)(n2﹣18)=0,
解得,(负值舍去),n3=﹣4(负值舍去),n4=2与点B重合,舍去;
∴点C的坐标为,
综上所述,点C的坐标为或.
15.(2025 山东模拟)如图①,点A的坐标为(3,0),把点A先向左平移2个单位长度,再向上平移3个单位长度,可以平移到点D的位置.
(1)①请直接写出点D的坐标为( 1 , 3 );
②若反比例函数y(x>0)的图象与线段AD有且只有一个交点时,请确定k的取值范围并说明理由;
(2)如图②,当k=12时,以AD为一边的平行四边形ABCD的另外两个顶点B与C均在反比例函数y(x>0)的图象上.请求出△ABC的面积.
【解答】解:(1)①∵3﹣2=1,0+3=3,
∴D(1,3),
故答案为:1,3;
②如图1,
0<k≤3,理由如下:
作DE⊥x轴,交反比例函数y(x>0)的图象于E,
则xE=1,0<yE≤3,
∴k=xy≤3,
∴0<k≤3;
(2)如图2,
连接BD,
设B(x,),则C(x﹣2,),
∴(x﹣2) ,
∴x1=4,x2=﹣2(舍去),
∴B(4,3)C(2,6),
∵D(1,3),
∴BD∥x轴,
∴S△BCDBD (yC﹣yD),
∵四边形ABCD是平行四边形,
∴S△ABC=S△BCD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
