【攻克压轴大题】2025年中考数学压轴题精选:三角形和四边形(含解析)
文档属性
| 名称 | 【攻克压轴大题】2025年中考数学压轴题精选:三角形和四边形(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 21:06:16 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【攻克压轴大题】2025年中考数学压轴题精选:三角形和四边形
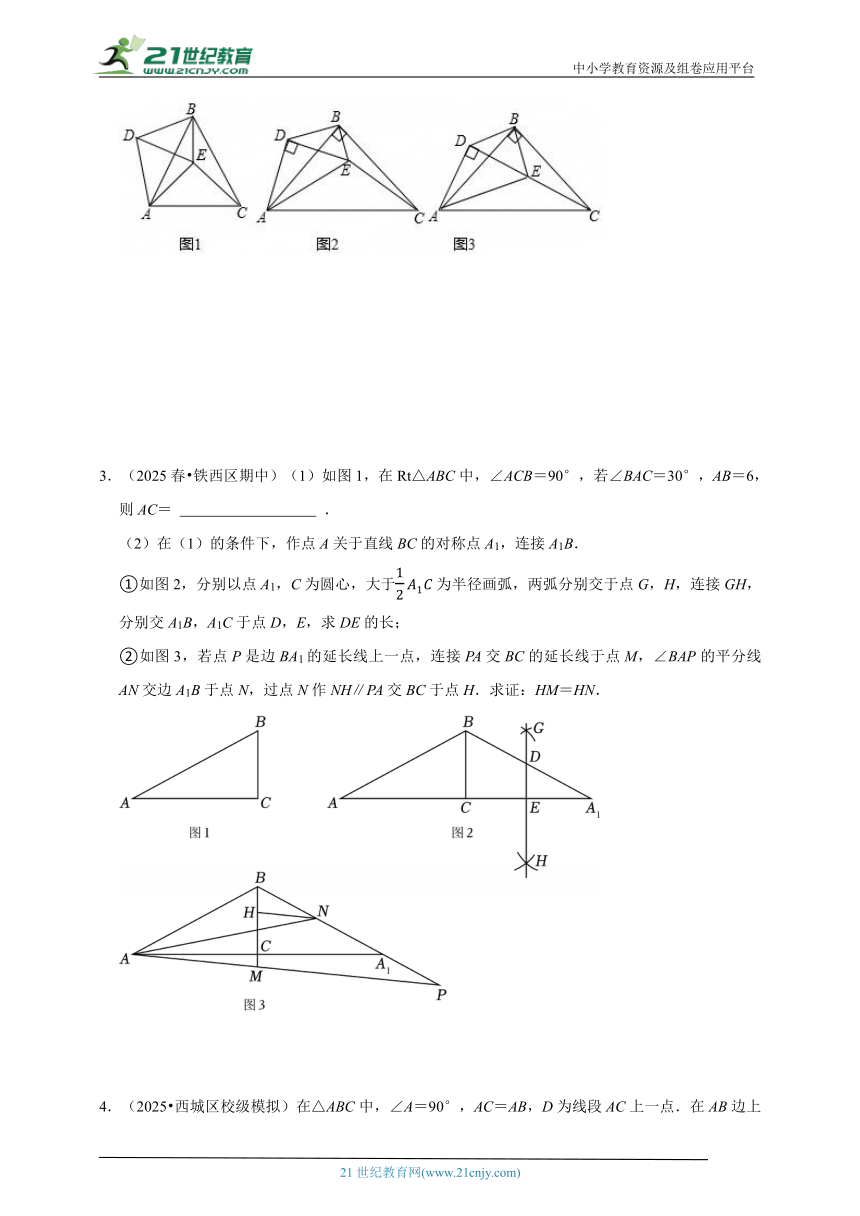
1.(2025 乾安县模拟)【探究思考】
(1)通过添加辅助线构造“全等三角形”证明线段相等或角相等,是我们常用的方法.已知,如图①,△ABC是等边三角形,CE是△ABC的外角∠ACF的平分线,点D为射线BC上一点,且∠ADE=∠ABC,DE与CE相交于点E.我们可以过点D作AC的平行线,交AB于点G,构造得到 (填两个全等三角形),来证明AD=DE;
【问题解决】
(2)如图②,在△ABC中,AB=BC,在边BC上取一点D,以D为顶点,AD为一条边在AD的右侧作∠ADE=∠ABC,点F在BC延长线上,∠ECF=∠ACB.
①求证:AD=DE;
②如图③所示,当点D在BC的延长线上时,若∠CAD=∠B,CD=1,AB=4,直接写出DE的长.
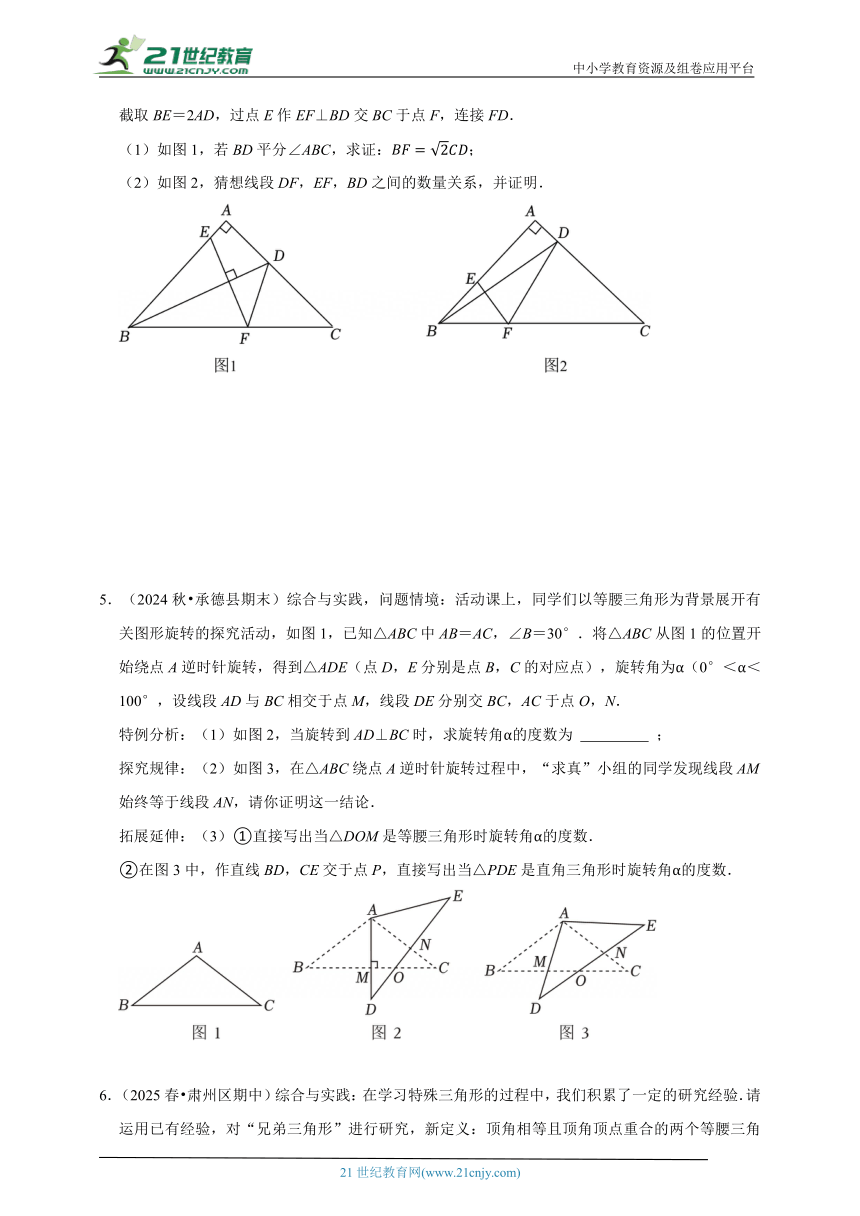
2.(2025 港北区三模)在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE,点E在△ABC的内部,连接EC,EB和BD,设EC=k BD(k≠0).
(1)当∠ABC=∠ADE=60°时,如图1,请求出k值,并给予证明;
(2)当∠ABC=∠ADE=90°时:
①如图2,(1)中的k值是否发生变化,如无变化,请给予证明;如有变化,请求出k值并说明理由;
②如图3,当D,E,C三点共线,且E为DC中点时,请求出tan∠EAC的值.
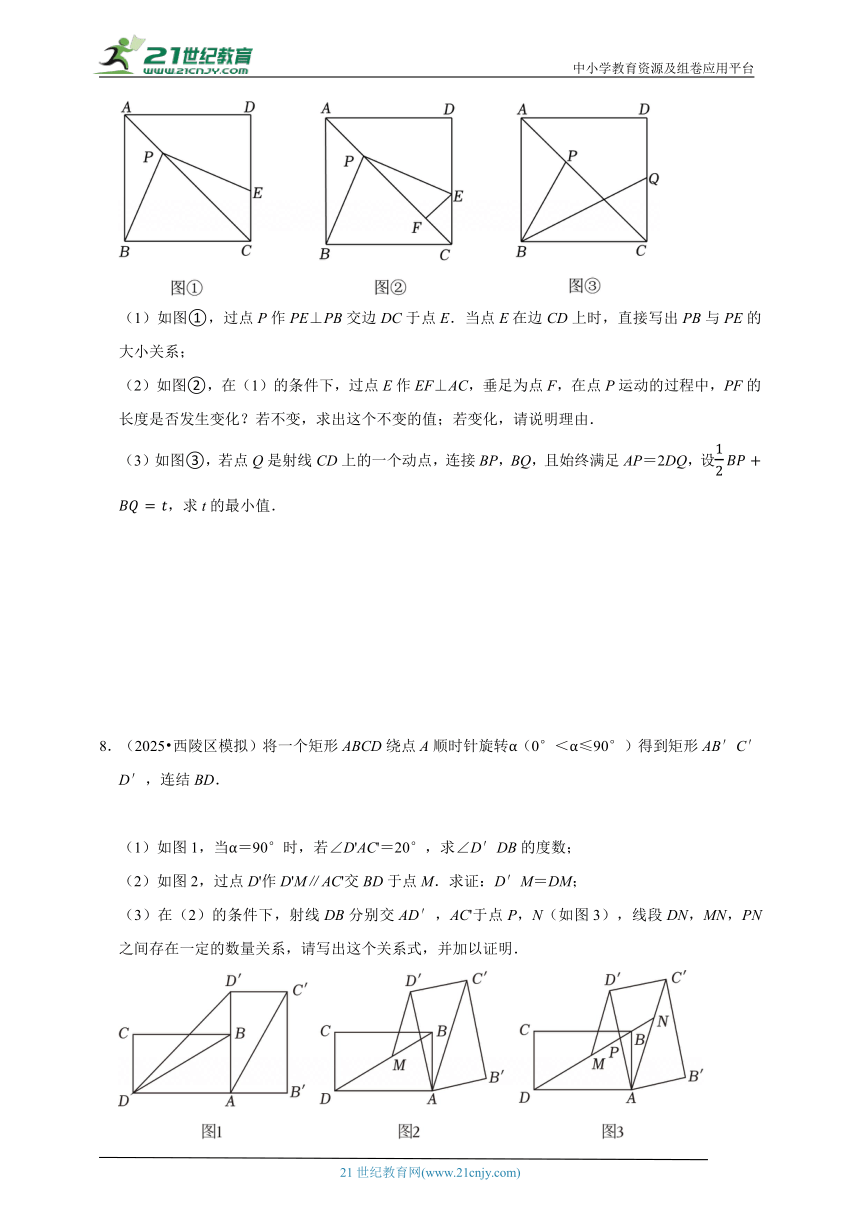
3.(2025春 铁西区期中)(1)如图1,在Rt△ABC中,∠ACB=90°,若∠BAC=30°,AB=6,则AC= .
(2)在(1)的条件下,作点A关于直线BC的对称点A1,连接A1B.
①如图2,分别以点A1,C为圆心,大于为半径画弧,两弧分别交于点G,H,连接GH,分别交A1B,A1C于点D,E,求DE的长;
②如图3,若点P是边BA1的延长线上一点,连接PA交BC的延长线于点M,∠BAP的平分线AN交边A1B于点N,过点N作NH∥PA交BC于点H.求证:HM=HN.
4.(2025 西城区校级模拟)在△ABC中,∠A=90°,AC=AB,D为线段AC上一点.在AB边上截取BE=2AD,过点E作EF⊥BD交BC于点F,连接FD.
(1)如图1,若BD平分∠ABC,求证:;
(2)如图2,猜想线段DF,EF,BD之间的数量关系,并证明.
5.(2024秋 承德县期末)综合与实践,问题情境:活动课上,同学们以等腰三角形为背景展开有关图形旋转的探究活动,如图1,已知△ABC中AB=AC,∠B=30°.将△ABC从图1的位置开始绕点A逆时针旋转,得到△ADE(点D,E分别是点B,C的对应点),旋转角为α(0°<α<100°,设线段AD与BC相交于点M,线段DE分别交BC,AC于点O,N.
特例分析:(1)如图2,当旋转到AD⊥BC时,求旋转角α的度数为 ;
探究规律:(2)如图3,在△ABC绕点A逆时针旋转过程中,“求真”小组的同学发现线段AM始终等于线段AN,请你证明这一结论.
拓展延伸:(3)①直接写出当△DOM是等腰三角形时旋转角α的度数.
②在图3中,作直线BD,CE交于点P,直接写出当△PDE是直角三角形时旋转角α的度数.
6.(2025春 肃州区期中)综合与实践:在学习特殊三角形的过程中,我们积累了一定的研究经验.请运用已有经验,对“兄弟三角形”进行研究,新定义:顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.
操作判断:
(1)如图1,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点.请直接写出线段BD与CE之间的数量关系: .
性质探究:
(2)如图2,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点,D,E均在△ABC外,连结BD、CE,试说明(1)中BD和CE之间的数量关系是否还成立?若成立,给出证明过程.
拓展应用:
(3)如图3,△ABC和△CDE互为“兄弟三角形”,点C为重合的顶角顶点,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CN为△CDE的高,连结BE,请直接写出线段CN,AE,BE之间的数量关系: .
7.(2025 海珠区校级二模)如图,在正方形ABCD中,AB=4,点P为正方形ABCD的对角线AC上一动点.
(1)如图①,过点P作PE⊥PB交边DC于点E.当点E在边CD上时,直接写出PB与PE的大小关系;
(2)如图②,在(1)的条件下,过点E作EF⊥AC,垂足为点F,在点P运动的过程中,PF的长度是否发生变化?若不变,求出这个不变的值;若变化,请说明理由.
(3)如图③,若点Q是射线CD上的一个动点,连接BP,BQ,且始终满足AP=2DQ,设,求t的最小值.
8.(2025 西陵区模拟)将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°)得到矩形AB′C′D′,连结BD.
(1)如图1,当α=90°时,若∠D'AC'=20°,求∠D′DB的度数;
(2)如图2,过点D'作D'M∥AC'交BD于点M.求证:D′M=DM;
(3)在(2)的条件下,射线DB分别交AD′,AC'于点P,N(如图3),线段DN,MN,PN之间存在一定的数量关系,请写出这个关系式,并加以证明.
9.(2025 翔安区二模)在一次数学活动课中,小明对“折纸中的数学问题”进行探究.
【活动1】折叠矩形纸片:
第一步:如图1,把矩形纸片ABCD对折,使AD与BC重合,折痕为EF,把纸片展平;
第二步:点M在AD上,再次沿BM折叠纸片,使点A落在EF上的点N处.
【活动2】折叠正方形纸片:
第一步:如图2,把正方形纸片ABCD对折,使AD与BC重合,折痕为EF,把纸片展平;
第二步:点M在AD上(不与点A,D重合),再次沿BM折叠纸片,使点A落在EF下方的点N处,延长MN交CF于点P.
(1)在活动1中,求证:∠NBC=30°;
(2)在活动2中,若正方形ABCD的边长为8,PF=3,求AM的长.
10.(2025 铁岭县二模)【问题初探】
(1)如图①,在△ABC中,∠ACB=90°,AC=BC,点E在BC上(且不与点B,C重合),在△ABC的外部作△BED,使∠BED=90°,BE=DE,连接CD,过点A作CD的平行线交DE的延长线于点F,连接CF.根据以上操作,判断:四边形ACDF是 , .
【变换探究】
(2)如图②,将图①中的△BED绕点B逆时针旋转,使点E落在AB边上,过点A作CD的平行线,过点D作AC的平行线,它们相交于点F,连接CE,CF,若CE=4,求CF的长.
勤奋小组通过第(1)问的解题经验,尝试连接EF,猜想△CEF为特殊的三角形;
创思小组在勤奋小组的提示下,成功地证明出一对三角形全等,进而求得CF的长度.
请结合两个小组的解题思路,写出解题过程.
【迁移拓展】
(3)如图③博文小组在第(2)问的基础上进行了如下创新,将图①中的△BED绕点B顺时针旋转,使点D在BC的右侧,过点A作CD的平行线,过点D作AC的平行线,它们相交于点F,连接CF,并尝试连接CE,EF.他们发现:若BE=1,BC=3,当四边形ACDF为菱形时,可求得CF的长度.请完成以下问题:
①求CF的长;
②当点D在BC左侧时,请直接写出CF的长.
11.(2025 南海区校级三模)综合与实践
如果从一个平行四边形的一个顶点向不过该顶点的对角线作垂线,垂线交平行四边形的边于另一点,且该点为所在边的三等分点,那么这个平行四边形叫做“垂对三等分平行四边形”,垂足叫做“垂三等分点”.
(1)理解应用
如图1,在 ABCD中,AE⊥BD于点P,交CD于点E,若E为CD的三等分点,则 ABCD是垂对三等分平行四边形,P是垂三等分点.若DE,BP=6,则DP= ;AD= .
(2)问题探究
如图2,在垂对三等分平行四边形ABCD中,P是垂三等分点,且满足AEAB,若CE=CB,试猜想BD与BC的数量关系,并说明理由.
(3)拓展延伸
已知四边形ABCD是矩形,过点A作AE⊥BD于点P,交CD于点E,AB=9,当四边形ABCD是垂对三等分平行四边形时,直接写出AD的长度.
12.(2025春 离石区期中)综合与实践
【问题情境】综合与实践课上,王老师提出了一个有关正方形中“十字型”的问题:
如图1,在正方形ABCD中,边长为6,E,F分别是边CD,AD上的点,AE⊥BF.
【独立思考】
(1)试判断AE与BF的数量关系,并说明理由.
【问题解决】
(2)阳光小组在王老师的问题上继续思考.如图2,记AE与BF的交点为G,若阴影部分的面积之和为24,求△ABG的面积.
【实践探究】
(3)缤纷小组进一步探究,如图5,连接EF并延长,交BA的延长线于点P.已知DF=2,,请直接写出PE的长.
13.(2025春 杭州月考)在矩形ABCD中,AB=4,BC=3,点P在线段BC上运动,作△ACD关于直线AP的对称△AC1D1(点C,D的对称点分别为C1,D1).
(1)如图1,当点C1在AB的延长线上时,求CC1的长.
(2)如图2,当点P与点C重合时,连结DD1,CD1、DD1交AB分别于点E、F.求证:BD1⊥DD1.
(3)当直线C1D1经过点B时,求CP的长.
14.(2025 雁塔区校级模拟)问题发现:
(1)如图①,在△ABC中,AB=AC=6,∠BAC=120°,若AD将△ABC分成面积相等的两部分,则AD= ;
(2)如图②,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2,若直线l经过点E,且将该菱形的面积平分,并与边BC交于点F,求线段EF的长.
问题解决:
(3)某市为保护生态环境,方便市民观光游览,准备在秦岭北麓兴建一处“和谐观光园”,其形状为四边形ABCD,如图③所示.在四边形ABCD中,∠B=∠D=90°,实际长度AD=5公里,AB=9公里,BC=13公里,CD=15公里,点P在CD上且PD=5公里,根据用地需求,需在BC上确定点E,将五边形ABEPD作为特色植物繁育展示区,使其面积为四边形ABCD总面积的一半,并在AB上确定点F,在△PEF中修建游客休息区,剩余部分作为花卉展示区,为方便游客游览,要求修建PE、PF、EF三条观光道路的总长度最小.请问这样的△PEF是否存在?若存在,请求出点E到点B的距离及△PEF周长的最小值;若不存在,请说明理由.
【攻克压轴大题】2025年中考数学压轴题精选:三角形和四边形
参考答案与试题解析
一.解答题(共14小题)
1.(2025 乾安县模拟)【探究思考】
(1)通过添加辅助线构造“全等三角形”证明线段相等或角相等,是我们常用的方法.已知,如图①,△ABC是等边三角形,CE是△ABC的外角∠ACF的平分线,点D为射线BC上一点,且∠ADE=∠ABC,DE与CE相交于点E.我们可以过点D作AC的平行线,交AB于点G,构造得到 △DCE≌△AGD (填两个全等三角形),来证明AD=DE;
【问题解决】
(2)如图②,在△ABC中,AB=BC,在边BC上取一点D,以D为顶点,AD为一条边在AD的右侧作∠ADE=∠ABC,点F在BC延长线上,∠ECF=∠ACB.
①求证:AD=DE;
②如图③所示,当点D在BC的延长线上时,若∠CAD=∠B,CD=1,AB=4,直接写出DE的长.
【解答】(1)解:过点D作AC的平行线,交AB于点G,构造得到△DCE≌△AGD,来证明AD=DE,如图1,
证明:∵△ABC为等边三角形,
∴∠ABC=∠ACB=∠CAB=60°,
∴∠BGD=∠BDG=60°,
∴BD=BG,
∴BC﹣BD=AB﹣BG,
∴AG=CD,
∵∠BAD+∠ABC=∠EDC+∠ADE,
又∵∠ADE=∠ABC,
∴∠BAD=∠EDC,
∵∠BGD=60°,
∴∠AGD=120°,
∵CE是△ABC的外角∠ACF的平分线,
又∵ACB=60°,
∴∠ACE=60°,∠DCE=60°+60°=120°,
∴∠AGD=∠DCE,
在△DCE与△AGD中,
,
∴△DCE≌△AGD(ASA),
∴AD=DE,
故答案为:△DCE≌△AGD;
(2)①证明:如图②,过点D作AC的平行线,交AB于点G′,
∴∠BDG′=∠ACB,∠BG′D=∠BAC,
∵AB=BC,
∴∠BAC=∠ACB,
∴∠BG′D=∠BDG′,
∴BD=BG′,
∴BC﹣BD=AB﹣BG′,
∴AG′=CD,
∵∠BAD+∠ABC=∠EDC+∠ADE,
又∵∠ADE=∠ABC,
∴∠BAD=∠EDC,
∴∠ECF=∠ACB=∠BG′D,
∴∠AG′D=∠DCE.
在△DCE与△AG′D中,
,
∴△DCE≌△AG′D(ASA),
∴AD=DE;
②解:如图3,过点D作AC的平行线,交AB于点G″,
∴∠BDG″=∠ACB,∠BG″D=∠BAC,
∵AB=BC,
∴∠CAB=∠ACB,
∴∠BG″D=∠BDG″,
∴BD=BG'',
∴BD﹣BC=BG″﹣AB,
∴AG''=CD,
∵∠BAD﹣∠ABC=∠EDC﹣∠ADE,
又∵∠ADE=∠ABC,
∴∠BAD=∠EDC,
∴∠ECF=∠ACB=∠BG″D,
∴∠AG″D=∠DCE,
在△DCE与△AGD中,
,
∴△DCE≌△AGD(ASA),
∴AD=DE,
∵∠ADB=∠CDA,∠CAD=∠B,
∴△ABD∽△CAD,
∴,
∴AD2=BD CD,
∵CD=1,AB=BC=4,
∴AD,
∴DE=AD.
2.(2025 港北区三模)在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE,点E在△ABC的内部,连接EC,EB和BD,设EC=k BD(k≠0).
(1)当∠ABC=∠ADE=60°时,如图1,请求出k值,并给予证明;
(2)当∠ABC=∠ADE=90°时:
①如图2,(1)中的k值是否发生变化,如无变化,请给予证明;如有变化,请求出k值并说明理由;
②如图3,当D,E,C三点共线,且E为DC中点时,请求出tan∠EAC的值.
【解答】解:(1)k=1,
理由如下:如图1,∵∠ABC=∠ADE=60°,BA=BC,DA=DE,
∴△ABC和△ADE都是等边三角形,
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,
∴∠DAB=∠EAC,
在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS)
∴EC=DB,即k=1;
(2)①k值发生变化,k,
∵∠ABC=∠ADE=90°,BA=BC,DA=DE,
∴△ABC和△ADE都是等腰直角三角形,
∴,,∠DAE=∠BAC=45°,
∴,∠DAB=∠EAC,
∴△EAC∽△DAB,
∴,即ECBD,
∴k;
②作EF⊥AC于F,
设AD=DE=a,则AEa,
∵点E为DC中点,
∴CD=2a,
由勾股定理得,ACa,
∵∠CFE=∠CDA=90°,∠FCE=∠DCA,
∴△CFE∽△CAD,
∴,即,
解得,EFa,
∴AFa,
则tan∠EAC.
3.(2025春 铁西区期中)(1)如图1,在Rt△ABC中,∠ACB=90°,若∠BAC=30°,AB=6,则AC= 3 .
(2)在(1)的条件下,作点A关于直线BC的对称点A1,连接A1B.
①如图2,分别以点A1,C为圆心,大于为半径画弧,两弧分别交于点G,H,连接GH,分别交A1B,A1C于点D,E,求DE的长;
②如图3,若点P是边BA1的延长线上一点,连接PA交BC的延长线于点M,∠BAP的平分线AN交边A1B于点N,过点N作NH∥PA交BC于点H.求证:HM=HN.
【解答】(1)解:∵∠BAC=30°,AB=6,∠ACB=90°,
∴BC=3,
∴AC3,
故答案为:3;
(2)①解∵点A关于直线BC的对称点A1,
∴AC=A1C=3,∠A=∠A1=30°,
由作图可知:DE是A1C的垂直平分线,
∴CE=A1C,DE⊥A1C,
∴A1D=2DE,
∵A1D2=DE2+A1E2,
∴DE;
②证明:如图,连接MN,过N作NG⊥AP于点G,作NK⊥AB交延长线于点K,作NL⊥MB于点L,
∵AN平分∠BAP,
∴NK=NG,
∵∠ABC=∠MBP=60°,
∴∠KBP=60°=∠MBP,即BP平分∠MBK,
∴NK=NL,
∴NL=NG,
∴MN平分∠BMP,
∴∠HMN=∠PMN,
∵HN∥AP,
∴∠HNM=∠PMN,
∴∠HMN=∠HNM,
∴HM=HN.
4.(2025 西城区校级模拟)在△ABC中,∠A=90°,AC=AB,D为线段AC上一点.在AB边上截取BE=2AD,过点E作EF⊥BD交BC于点F,连接FD.
(1)如图1,若BD平分∠ABC,求证:;
(2)如图2,猜想线段DF,EF,BD之间的数量关系,并证明.
【解答】(1)证明:如图,过点D作DM⊥BC于M,设EF,AD交于O,
∵BD平分∠ABC,∠A=90°,DM⊥BC,
∴DM=AD,∠EBO=∠FBO,
设AD=DM=a,则BE=2AD=2a,
∵∠A=90°,AC=AB,
∴∠C=∠ABC=45°,
∴△DMC是等腰直角三角形,
∴CM=DM=a,
∴;
∵EF⊥BD,∠BOE=∠BOF=90°,
又∵OB=OB,
∴△BOE≌△BOF(ASA),
∴BF=BE=2a,
∴;
(2)解:BD=EF+DF,证明如下:
如图,作正方形ABHC,取BE中点G,连接HG交BD于T,延长EF交CH于M,
由正方形的性质可得AB=BH,∠A=∠ABH=90°,AB∥CH,
∵G是BE中点,BE=2AD,
∴BG=AD,
∴△BGH≌△ADB(SAS),
∴GH=BD,∠ABD=∠BHG,
∵∠BHG+∠BGH=90°,
∴∠ABD+∠BGH=90°,
∴∠BTG=90°,
∴GH⊥BD,
∵EF⊥BD,
∴GH∥EM,
又∵AB∥CH,
∴四边形GHME是平行四边形,
∴BD=GH=EM,,
∴AC﹣AD=CH﹣HM,
即CD=CM,
∵CF=CF,∠DCF=∠MCF=45°,
∴△DCF≌△MCF(SAS),
∴DF=MF,
∵EM=EF+MF,
∴BD=EF+DF.
5.(2024秋 承德县期末)综合与实践,问题情境:活动课上,同学们以等腰三角形为背景展开有关图形旋转的探究活动,如图1,已知△ABC中AB=AC,∠B=30°.将△ABC从图1的位置开始绕点A逆时针旋转,得到△ADE(点D,E分别是点B,C的对应点),旋转角为α(0°<α<100°,设线段AD与BC相交于点M,线段DE分别交BC,AC于点O,N.
特例分析:(1)如图2,当旋转到AD⊥BC时,求旋转角α的度数为 60 ;
探究规律:(2)如图3,在△ABC绕点A逆时针旋转过程中,“求真”小组的同学发现线段AM始终等于线段AN,请你证明这一结论.
拓展延伸:(3)①直接写出当△DOM是等腰三角形时旋转角α的度数.
②在图3中,作直线BD,CE交于点P,直接写出当△PDE是直角三角形时旋转角α的度数.
【解答】(1)解:∵AB=AC,AD⊥BC,
∴∠C=∠B=30°,∠BAD∠BAC,
∴∠BAD60,
∴α=60°,
故答案为:60°;
(2)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠MAN=∠DAE﹣∠MAN,
即:∠BAM=∠EAN,
在△BAM和△EAN中,
,
∴△BAM≌△EAN(ASA),
∴AM=AN;
(3)解:①如图1,
当DM=OM时,∠MOD=∠D=30°,
∵∠B=∠D,∠AMB=∠DMO,
∴∠BAD=∠MOD=30°,
∴α=30°,
如图2,
当DM=DO时,∠DMO=∠DOM75°,
∴α=∠DOM=75°,
如图3,
当OM=OD时,∠OMD=∠D=30°,
∴α=∠DOM=120°,
此时AD和AC重合,这种情形不存在.
综上所述:α=30°或75°.
②如图:
当∠EDP=90°时,
∵∠ABC=ADE=30°,
∴∠ADB=90°﹣30°=60°,
∴∠BAD=180°﹣60°﹣60°=60°,
∵0°<α<100°,
∴旋转角α为60°.
6.(2025春 肃州区期中)综合与实践:在学习特殊三角形的过程中,我们积累了一定的研究经验.请运用已有经验,对“兄弟三角形”进行研究,新定义:顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.
操作判断:
(1)如图1,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点.请直接写出线段BD与CE之间的数量关系: BD=CE .
性质探究:
(2)如图2,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点,D,E均在△ABC外,连结BD、CE,试说明(1)中BD和CE之间的数量关系是否还成立?若成立,给出证明过程.
拓展应用:
(3)如图3,△ABC和△CDE互为“兄弟三角形”,点C为重合的顶角顶点,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CN为△CDE的高,连结BE,请直接写出线段CN,AE,BE之间的数量关系: CN(AE﹣BE) .
【解答】解:(1)∵△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点,
∴AB=AC,AD=AE,∠BAC=∠DAE,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,
故答案为:BD=CE.
(2)BD和CE之间的数量关系仍然成立,理由如下:
∵△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点,
∴AB=AC,AD=AE,∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(3)CN(AE﹣BE),
理由:∵△ABC和△CDE互为“兄弟三角形”,点C为重合的顶角顶点,∠ACB=∠DCE=90°,
∴AC=BC,DC=EC,∠ACD=∠BCE=90°﹣∠BCD,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∵点A,D,E在同一条直线上,
∴DE=AE﹣AD=AE﹣BE,
∵CN为△DCE的高,
∴CN⊥DE,
∵DC=EC,
∴DN=EN,
∵∠DCE=90°,
∴CNDE,
∴CN(AE﹣BE).
故答案为:CN(AE﹣BE).
7.(2025 海珠区校级二模)如图,在正方形ABCD中,AB=4,点P为正方形ABCD的对角线AC上一动点.
(1)如图①,过点P作PE⊥PB交边DC于点E.当点E在边CD上时,直接写出PB与PE的大小关系;
(2)如图②,在(1)的条件下,过点E作EF⊥AC,垂足为点F,在点P运动的过程中,PF的长度是否发生变化?若不变,求出这个不变的值;若变化,请说明理由.
(3)如图③,若点Q是射线CD上的一个动点,连接BP,BQ,且始终满足AP=2DQ,设,求t的最小值.
【解答】解:(1)连接PD,如图1所示:
由条件可知CB=CD,∠PCB=∠PCD=45°,
在△PCB和△PCD中,
,
∴△PCB≌△PCD(SAS),
∴PB=PD,∠CBP=∠CDP,
∵PE⊥PB,
∴∠BPE=∠BCE=90°,
∴∠CBP+∠CEP=180°,
∵∠CEP+∠PED=180°,
∴∠PED=∠CBP,
∴∠PED=∠CDP,
∴PE=PD,
∴PB=PE;
(2)点P在运动过程中,PF的长度不变,值为.理由如下:
连接BD,与AC相交于点O,如图2.
由条件可知∠BOP=90°,
∵PE⊥PB,即∠BPE=90°,
∴∠PBO=90°﹣∠BPO=∠EPF,
∵EF⊥PC,即∠PFE=90°,
∴∠BOP=∠PFE,
在△BOP和△PFE中,
,
∴△BOP≌△PFE(AAS),
∴BO=PF,
∵四边形ABCD是正方形,
∴OB=OA,∠AOB=90°,
∴AB2=2OB2,
∵AB=4,
∴,(负值不合题意,已经舍去),
∴,
∴点P在运动过程中,PF的长度不变,值为;
(3)如图3所示:过点D在正方形外作∠FDC=45°,使FD=AB=4,在CQ上取点E,使QE=DQ,连接EF,
由条件可知∠ACB=∠ACD=∠BAP=45°,
∴∠BAP=∠FDE=45°,
∵AP=2DQ,DQ=QE,
∴AP=DE,
∴△ABP≌△DFE(SAS),
∴BP=FE,
如图3所示:在FD上取点G,使DG=FG,连接QG、BG,
又∵DQ=QE,
∴,
∴,
即:当B、Q、G三点共线时,t最小,最小值为t=BG,
如图3所示:过点G作GH⊥AB,垂足为H,交CD于K,
由条件可知四边形ADKH是矩形,
∴AH=DK,AD=HK=4,∠DKG=90°,
∵∠FDE=45°,
∴△DKG是等腰直角三角形,
∵,
∴,
∴,
,
在Rt△BHG中,,
∴t的最小值为6.
8.(2025 西陵区模拟)将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°)得到矩形AB′C′D′,连结BD.
(1)如图1,当α=90°时,若∠D'AC'=20°,求∠D′DB的度数;
(2)如图2,过点D'作D'M∥AC'交BD于点M.求证:D′M=DM;
(3)在(2)的条件下,射线DB分别交AD′,AC'于点P,N(如图3),线段DN,MN,PN之间存在一定的数量关系,请写出这个关系式,并加以证明.
【解答】解:(1)∵矩形ABCD绕点A顺时针旋转90°得到矩形AB′C′D′,
∴点A,B,D′在同一直线上,
∴∠DAD′=90°,AD=AD′.∠D′AC′=∠ADB=20°,
∴∠ADD′=∠AD′D=45°,
∴∠D′DB=∠ADD′﹣∠ADB=25°,
(2):D'M=DM.
证明:如图2,连接DD',
∵D'M∥AC',
∴∠AD'M=∠D'AC',
∵AD'=AD,∠AD'C'=∠DAB=90°,D'C'=AB,
∴△AC'D'≌△DAB(SAS),
∴∠ADB=∠D'AC',
∴∠AD'M=∠ADB,
∵AD=AD',
∴∠AD'D=∠ADD',
∴∠MD'D=∠MDD',
∴D'M=DM;
(3)关系式为MN2=PN DN.
证明:如图3,连接AM,
∵D'M=DM,AD'=AD,AM=AM,
∴△AD'M≌△ADM(SSS),
∴∠MAD=∠MAD',
∵∠AMN=∠MAD+∠NDA,
∠NAM=∠MAD'+∠NAP,
∴∠NAM=∠AMN,
∴MN=AN,
在△NAP和△NDA中,∠ANP=∠DNA,∠NAP=∠NDA,
∴△NPA∽△NAD,
∴,
∴AN2=PN DN,
∴MN2=PN DN.
9.(2025 翔安区二模)在一次数学活动课中,小明对“折纸中的数学问题”进行探究.
【活动1】折叠矩形纸片:
第一步:如图1,把矩形纸片ABCD对折,使AD与BC重合,折痕为EF,把纸片展平;
第二步:点M在AD上,再次沿BM折叠纸片,使点A落在EF上的点N处.
【活动2】折叠正方形纸片:
第一步:如图2,把正方形纸片ABCD对折,使AD与BC重合,折痕为EF,把纸片展平;
第二步:点M在AD上(不与点A,D重合),再次沿BM折叠纸片,使点A落在EF下方的点N处,延长MN交CF于点P.
(1)在活动1中,求证:∠NBC=30°;
(2)在活动2中,若正方形ABCD的边长为8,PF=3,求AM的长.
【解答】解:(1))∵AE=BEAB,AB=BN,
∴BEBN,
∵∠BEN=90°,sin∠BNE,
∴∠BNE=30°,
∴∠NBE=60°,
∵∠ABM=∠NBM,
∴∠ABM=∠NBM=∠NBC=30°;
(2)连接BP,
∵BN=BC,BP=BP,
∴Rt△BNP≌Rt△BCP(HL),
∴NP=CP,
∵PF=3,DF=CFCD=4,
∵DP=DF+FP=3+4=7,
∵NP=PC=CF﹣PF=1,
设AM=NM=x,MD=8﹣x,
∴MD2+DP2=PM2,
即(8﹣x)2+72=(x+1)2,
解得:x,
∴AM.
10.(2025 铁岭县二模)【问题初探】
(1)如图①,在△ABC中,∠ACB=90°,AC=BC,点E在BC上(且不与点B,C重合),在△ABC的外部作△BED,使∠BED=90°,BE=DE,连接CD,过点A作CD的平行线交DE的延长线于点F,连接CF.根据以上操作,判断:四边形ACDF是 平行四边形 , .
【变换探究】
(2)如图②,将图①中的△BED绕点B逆时针旋转,使点E落在AB边上,过点A作CD的平行线,过点D作AC的平行线,它们相交于点F,连接CE,CF,若CE=4,求CF的长.
勤奋小组通过第(1)问的解题经验,尝试连接EF,猜想△CEF为特殊的三角形;
创思小组在勤奋小组的提示下,成功地证明出一对三角形全等,进而求得CF的长度.
请结合两个小组的解题思路,写出解题过程.
【迁移拓展】
(3)如图③博文小组在第(2)问的基础上进行了如下创新,将图①中的△BED绕点B顺时针旋转,使点D在BC的右侧,过点A作CD的平行线,过点D作AC的平行线,它们相交于点F,连接CF,并尝试连接CE,EF.他们发现:若BE=1,BC=3,当四边形ACDF为菱形时,可求得CF的长度.请完成以下问题:
①求CF的长;
②当点D在BC左侧时,请直接写出CF的长.
【解答】解:(1)∵∠ACB=90°,∠BED=90°,
∴DF∥AC,
∵AF∥CD,
∴四边形ACDF是平行四边形,
∴DF=AC=BC,
∴DE+EF=BE+CE,
∵BE=DE,
∴EF=CE,
∵∠BED=90°,
∴∠CEF=90°,
由勾股定理得:,.
故答案为:平行四边形,;
(2)如图①,连接EF.
∴四边形ACDF是平行四边形,∠ACD=90°,
∴四边形ACDF是矩形,
∴DF=AC=BC,∠CDF=90°,
∴∠BDF=90°.
∵∠BED=90°,BE=DE,
∴∠EDB=∠B=45°,
∴∠FDE=∠BDF﹣∠EDB=45°=∠B.
∵DF=BC,∠FDE=∠B,DE=BE,
∴△FDE≌△CBE(SAS),
∴EF=EC=4,∠FED=∠CEB,
∴∠FED﹣∠CED=∠CEB﹣∠CED,
即∠FEC=∠DEB=90°,
∴由勾股定理,得,
即CF的长为;
(3)①∵四边形ACDF为菱形,
∴CD=DF=AC=BC,
∴∠CBD=∠CDB.
∵BC=CD,BE=DE,CE=CE,
∴△BCE≌△DCE(SSS),
∴∠BCE=∠DCE,∠CBE=∠CDE.
设∠BCE=∠DCE=α,则∠CBD=∠CDB=90°﹣α,∠ACD=90°+2α,∠FCD∠ACD=45°+α,∠FCE=∠FCD﹣∠DCE=45°.
∴∠CDE=∠CDB﹣∠EDB=90°﹣α﹣45°=45°﹣α,
∵DF∥AC,
∴∠CDF=180°﹣∠ACD=90°﹣2α,
∴∠FDE=∠CDF﹣∠CDE=45°﹣α=∠CDE.
∵DF=CD,∠FDE=∠CDE,DE=DE,
∴△FDE≌△CDE(SAS),
∴EF=EC,
∴∠EFC=∠FCE=45°,
∴∠CEF=90°,
∴CFCE,
如图②,延长CE交BD于点G.
∵BC=CD,∠BCE=∠DCE,
∴CG⊥BD,
∴,.
∴在Rt△BCG中,由勾股定理,得CG,
∴CE=CG﹣EG,
∴CFCE1;
②当点D在BC左侧时,如图4,连接AD,记AD,CF的交点为O,
∵四边形ACDF为菱形,
∴CD=DF=AD=AC,OC=OF,∠DOC=∠DOF=90°,
∴∠CBD=∠CDB,
同理①:△BCE≌△DCE(SSS),
∴∠BCE=∠DCE,,
设∠BCE=∠DCE=α,则∠ACD=90°﹣2α,
∴,∠CED+∠DCE=45°+α=∠CDA,
∴∠CDA为△CDE的外角,即A、D、E三点共线,
∵OC=OF,∠EOC=∠EOF,EO=EO,
∴△EOC≌△EOF(SAS),
∴CE=EF,∠OEF=∠OEC=45°,
∴∠CEF=90°,
∴,
如图4,记CE、BD的交点为H,
∵BC=CD,∠BCE=∠DCE,
∴CE⊥BD,BH,EH=BE sin 45°,
由勾股定理得:CH,
∴CE=CH+EH,
∴CFCE1.
11.(2025 南海区校级三模)综合与实践
如果从一个平行四边形的一个顶点向不过该顶点的对角线作垂线,垂线交平行四边形的边于另一点,且该点为所在边的三等分点,那么这个平行四边形叫做“垂对三等分平行四边形”,垂足叫做“垂三等分点”.
(1)理解应用
如图1,在 ABCD中,AE⊥BD于点P,交CD于点E,若E为CD的三等分点,则 ABCD是垂对三等分平行四边形,P是垂三等分点.若DE,BP=6,则DP= 2 ;AD= .
(2)问题探究
如图2,在垂对三等分平行四边形ABCD中,P是垂三等分点,且满足AEAB,若CE=CB,试猜想BD与BC的数量关系,并说明理由.
(3)拓展延伸
已知四边形ABCD是矩形,过点A作AE⊥BD于点P,交CD于点E,AB=9,当四边形ABCD是垂对三等分平行四边形时,直接写出AD的长度.
【解答】解:(1)∵,,
∴CD=3DE,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△DEP∽△BAP,
∴,即,
∴DP=2.
∵AE⊥BD,
∴在Rt△ABP中,AP,
在Rt△ADP中,AD.
故答案为:2;;
(2)BD=2BC,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,,
∴,
∵AB∥CD,
∴△BEP∽△DCP,
∴,
∴设EP=2a,则CP=3a,CE=CP+EP=5a,
∴BC=CE=5a,
∵CE⊥BD,
∴在Rt△BCP中,,
∴,
∴,
∴BD=DP+BP=10a,
∵BC=5a,
∴BD=2BC;
(3)分两种情况讨论:①如图,若,
∵在矩形ABCD中,CD∥AB,
∴△DEP∽△BAP,
∴,
设EP=a,则AP=3EP=3a,AE=AP+EP=4a,
∵AE⊥BD,
∴∠DPE=90°,
∵在矩形ABCD中,∠ADC=90°,
∴∠DPE=∠ADE,
∵∠DEP=∠AED,
∴△DEP∽△AED,
∴,即,
解得a=1或a=﹣1(舍去),
∴AE=4,
∴在Rt△ADE中,.
②如图,若,
∵在矩形ABCD中,CD∥AB,
∴△DEP∽△BAP,
∴,
设EP=2b,则,AE=AP+EP=5b,
∵AE⊥BD,
∴∠DPE=90°,
∵在矩形ABCD中,∠ADC=90°,
∴∠DPE=∠ADE,
∵∠DEP=∠AED,
∴△DEP∽△AED,
∴,即,
解得或(舍去),
∴,
∴在Rt△ADE中,.
综上所述,AD的长为或.
12.(2025春 离石区期中)综合与实践
【问题情境】综合与实践课上,王老师提出了一个有关正方形中“十字型”的问题:
如图1,在正方形ABCD中,边长为6,E,F分别是边CD,AD上的点,AE⊥BF.
【独立思考】
(1)试判断AE与BF的数量关系,并说明理由.
【问题解决】
(2)阳光小组在王老师的问题上继续思考.如图2,记AE与BF的交点为G,若阴影部分的面积之和为24,求△ABG的面积.
【实践探究】
(3)缤纷小组进一步探究,如图5,连接EF并延长,交BA的延长线于点P.已知DF=2,,请直接写出PE的长.
【解答】解:(1)AB=BF,理由如下:
∵四边形ABCD是正方形,
∴∠BAD=∠D=90°,AD=AB,
∴∠DAE+∠BAE=90°,
∵AE⊥BF,
∴∠ABF+∠BAE=90°,
∴∠DAE=∠ABF,
∴△ADE≌△BAF(ASA),
∴AE=BF;
(2)由(1)知,△ADE≌△BAF,
∴S△ADE=S△BAF,
∴S△ADE﹣S△AFG=S△BAF﹣S△AFG,
∴S四边形DEGF=S△ABG,
∵S正方形=AB2=62=36,S阴影=24,
∴S△ABG+S四边形DEGF=36﹣24=12,
∴S△ABG;
(3)如图,
连接PD,作PH⊥CD,交CD的延长线于H,
∴∠H=90°,
设S△DEF=S,
∵DF=2,AD=6,
∴S△ADE=3S,
∴S△AEF=S△ADE﹣S△DEF=2S,
∵四边形ABCD是正方形,
∴AB∥CD,
∴S△PDE=S△ADE=3S,
∴S△PDF=S△PDE﹣S△DEF=2S,
∴S△APF=2S△PDF=4S,
∴S△APD=S△APF+S△PDF=6S,
∴,
∴,
设AE=13a,则AP=4a,
∴DE=2a,
在Rt△ADE中,由勾股定理得,AE2﹣DE2=AD2,
∴,
∴a或a(舍去),
∴AP=48,DE=4,
∵四边形ABCD是正方形,
∴∠PAD=∠DAB=∠ADH=∠ADC=90°,
∴四边形APHD是矩形,
∴PH=AD=6,DH=AP=8,
∴EH=DH+DE=12,
∴PE6.
13.(2025春 杭州月考)在矩形ABCD中,AB=4,BC=3,点P在线段BC上运动,作△ACD关于直线AP的对称△AC1D1(点C,D的对称点分别为C1,D1).
(1)如图1,当点C1在AB的延长线上时,求CC1的长.
(2)如图2,当点P与点C重合时,连结DD1,CD1、DD1交AB分别于点E、F.求证:BD1⊥DD1.
(3)当直线C1D1经过点B时,求CP的长.
【解答】(1)解:在矩形ABCD中,AB=4,BC=3,
∴,
∵△ACD、△ACD关于直线AP对称,
∴AC1=AC=5,
∴BC=AC﹣AB=1,
在Rt△BCC1中,由勾股定理得,
,
∴CC1的长为;
(2)证明:连结BD交AC于点O,
∵ABCD为矩形,
∴OB=OD
∵D,D1关于AC对称,
∴AC垂直平分DD1,
∴H为DD1的中点,
∴OH为△BDD1的中位线,
∴OH∥BD1,
∵AC⊥DD1,
∴∠DHO=90°,
∵OH∥BD,
∴∠BD1D=∠DHO=90°,
∴DD⊥BD1;
(3)解:连接PC1,
∵△ACD、△AC1D1关于直线AP对称,
∴AD=AD,CD=CD,∠ACD=∠AC1B∠ACP=∠AC1PPC=PC1,∠ADC=∠AC1C=90°,
∵∠ACD+∠ACP=90°
∴∠AC1B+∠AC1P=90°,
即∠BC1P=90°,
当直线C1D1经过点B时,
在Rt△AD1B中,BD1,
∴BC1=C1D1﹣BD1=4,
在Rt△BC1P中,,
∴,,
∴.
14.(2025 雁塔区校级模拟)问题发现:
(1)如图①,在△ABC中,AB=AC=6,∠BAC=120°,若AD将△ABC分成面积相等的两部分,则AD= 3 ;
(2)如图②,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2,若直线l经过点E,且将该菱形的面积平分,并与边BC交于点F,求线段EF的长.
问题解决:
(3)某市为保护生态环境,方便市民观光游览,准备在秦岭北麓兴建一处“和谐观光园”,其形状为四边形ABCD,如图③所示.在四边形ABCD中,∠B=∠D=90°,实际长度AD=5公里,AB=9公里,BC=13公里,CD=15公里,点P在CD上且PD=5公里,根据用地需求,需在BC上确定点E,将五边形ABEPD作为特色植物繁育展示区,使其面积为四边形ABCD总面积的一半,并在AB上确定点F,在△PEF中修建游客休息区,剩余部分作为花卉展示区,为方便游客游览,要求修建PE、PF、EF三条观光道路的总长度最小.请问这样的△PEF是否存在?若存在,请求出点E到点B的距离及△PEF周长的最小值;若不存在,请说明理由.
【解答】解:(1)如图①中,取BC的中点D,连接AD,线段AD即为所求.
∵AB=AC=6,BD=DC,
∴AD⊥BC,∠B=∠C(180°﹣120°)=30°,
∴ADAB=3,
故答案为:3;
(2)解:如图,过点A和点E作AG⊥BC,EH⊥BC于点G和H,得矩形AGHE,
∴GH=AE=2,
∵在菱形ABCD中,AB=6,∠B=60°,
∴BG=3,AG=3EH,
∴HC=BC﹣BG﹣GH=6﹣3﹣2=1,
∵EF平分菱形面积,EF经过菱形对角线交点,
∴FC=AE=2,
∴FH=FC﹣HC=2﹣1=1,
在Rt△EFH中,根据勾股定理,得
EF2;
(3)存在这样的这样的△PEF,
如图③,作DH⊥BC于点H,DG⊥BA交BA的延长线于点G,连接BD,
∵∠DHB=∠HBG=∠G=90°,
∴四边形DGBH是矩形,
∴DG=BH,∠GDH=∠ADC=90°,
∴∠ADG=∠CDH=90°﹣∠ADH,
∵∠G=∠DHC=90°,AD=5公里,CD=15公里,
∴△ADG∽△CDH,
∴,
∴DH=3DG=3BH,
∵S△ABD+S△CBD=S△ABC+S△ADC=S四边形ABCD,AB=9公里,BC=13公里,
∴9BH13×3BH9×135×15,
解得BH=4,
∴DH=12公里,CH=13﹣4=9(公里),
∵CD=15公里,PD=5公里,
∴PC=15﹣5=10(公里),
作DK⊥BC于点K,则∠PKE=90°,BK∥DH,
∴△PCK∽△DCH,
∴,
∴CKCH9=6(公里),PKDH12=8(公里),
∵S五边形ABEPDS四边形ABCD,
∴S△PCES四边形ABCD,
∴8CE(9×135×15),
解得CE=12,
∴BE=13﹣12=1(公里),EK=12﹣6=6(公里),
∴PE10(公里),
延长CB到点L,使BL=BE=1公里,连接PL、FL,则LK=6+1+1=8(公里),
∴PL8(公里),
∵AB垂直平分EL,
∴LF=EF,
∵PF+LF≥PL,
∴PE+PF+EF≥PL+PE,
∴PE+PF+EF≥810,
∴当点F落在PL上时,PE+PF+EF取得最小值,最小值为(810)公里,
∴存在这样的这样的△PEF,点E到点B的距离为1公里,△PEF周长的最小值为(810)公里.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【攻克压轴大题】2025年中考数学压轴题精选:三角形和四边形
1.(2025 乾安县模拟)【探究思考】
(1)通过添加辅助线构造“全等三角形”证明线段相等或角相等,是我们常用的方法.已知,如图①,△ABC是等边三角形,CE是△ABC的外角∠ACF的平分线,点D为射线BC上一点,且∠ADE=∠ABC,DE与CE相交于点E.我们可以过点D作AC的平行线,交AB于点G,构造得到 (填两个全等三角形),来证明AD=DE;
【问题解决】
(2)如图②,在△ABC中,AB=BC,在边BC上取一点D,以D为顶点,AD为一条边在AD的右侧作∠ADE=∠ABC,点F在BC延长线上,∠ECF=∠ACB.
①求证:AD=DE;
②如图③所示,当点D在BC的延长线上时,若∠CAD=∠B,CD=1,AB=4,直接写出DE的长.
2.(2025 港北区三模)在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE,点E在△ABC的内部,连接EC,EB和BD,设EC=k BD(k≠0).
(1)当∠ABC=∠ADE=60°时,如图1,请求出k值,并给予证明;
(2)当∠ABC=∠ADE=90°时:
①如图2,(1)中的k值是否发生变化,如无变化,请给予证明;如有变化,请求出k值并说明理由;
②如图3,当D,E,C三点共线,且E为DC中点时,请求出tan∠EAC的值.
3.(2025春 铁西区期中)(1)如图1,在Rt△ABC中,∠ACB=90°,若∠BAC=30°,AB=6,则AC= .
(2)在(1)的条件下,作点A关于直线BC的对称点A1,连接A1B.
①如图2,分别以点A1,C为圆心,大于为半径画弧,两弧分别交于点G,H,连接GH,分别交A1B,A1C于点D,E,求DE的长;
②如图3,若点P是边BA1的延长线上一点,连接PA交BC的延长线于点M,∠BAP的平分线AN交边A1B于点N,过点N作NH∥PA交BC于点H.求证:HM=HN.
4.(2025 西城区校级模拟)在△ABC中,∠A=90°,AC=AB,D为线段AC上一点.在AB边上截取BE=2AD,过点E作EF⊥BD交BC于点F,连接FD.
(1)如图1,若BD平分∠ABC,求证:;
(2)如图2,猜想线段DF,EF,BD之间的数量关系,并证明.
5.(2024秋 承德县期末)综合与实践,问题情境:活动课上,同学们以等腰三角形为背景展开有关图形旋转的探究活动,如图1,已知△ABC中AB=AC,∠B=30°.将△ABC从图1的位置开始绕点A逆时针旋转,得到△ADE(点D,E分别是点B,C的对应点),旋转角为α(0°<α<100°,设线段AD与BC相交于点M,线段DE分别交BC,AC于点O,N.
特例分析:(1)如图2,当旋转到AD⊥BC时,求旋转角α的度数为 ;
探究规律:(2)如图3,在△ABC绕点A逆时针旋转过程中,“求真”小组的同学发现线段AM始终等于线段AN,请你证明这一结论.
拓展延伸:(3)①直接写出当△DOM是等腰三角形时旋转角α的度数.
②在图3中,作直线BD,CE交于点P,直接写出当△PDE是直角三角形时旋转角α的度数.
6.(2025春 肃州区期中)综合与实践:在学习特殊三角形的过程中,我们积累了一定的研究经验.请运用已有经验,对“兄弟三角形”进行研究,新定义:顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.
操作判断:
(1)如图1,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点.请直接写出线段BD与CE之间的数量关系: .
性质探究:
(2)如图2,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点,D,E均在△ABC外,连结BD、CE,试说明(1)中BD和CE之间的数量关系是否还成立?若成立,给出证明过程.
拓展应用:
(3)如图3,△ABC和△CDE互为“兄弟三角形”,点C为重合的顶角顶点,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CN为△CDE的高,连结BE,请直接写出线段CN,AE,BE之间的数量关系: .
7.(2025 海珠区校级二模)如图,在正方形ABCD中,AB=4,点P为正方形ABCD的对角线AC上一动点.
(1)如图①,过点P作PE⊥PB交边DC于点E.当点E在边CD上时,直接写出PB与PE的大小关系;
(2)如图②,在(1)的条件下,过点E作EF⊥AC,垂足为点F,在点P运动的过程中,PF的长度是否发生变化?若不变,求出这个不变的值;若变化,请说明理由.
(3)如图③,若点Q是射线CD上的一个动点,连接BP,BQ,且始终满足AP=2DQ,设,求t的最小值.
8.(2025 西陵区模拟)将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°)得到矩形AB′C′D′,连结BD.
(1)如图1,当α=90°时,若∠D'AC'=20°,求∠D′DB的度数;
(2)如图2,过点D'作D'M∥AC'交BD于点M.求证:D′M=DM;
(3)在(2)的条件下,射线DB分别交AD′,AC'于点P,N(如图3),线段DN,MN,PN之间存在一定的数量关系,请写出这个关系式,并加以证明.
9.(2025 翔安区二模)在一次数学活动课中,小明对“折纸中的数学问题”进行探究.
【活动1】折叠矩形纸片:
第一步:如图1,把矩形纸片ABCD对折,使AD与BC重合,折痕为EF,把纸片展平;
第二步:点M在AD上,再次沿BM折叠纸片,使点A落在EF上的点N处.
【活动2】折叠正方形纸片:
第一步:如图2,把正方形纸片ABCD对折,使AD与BC重合,折痕为EF,把纸片展平;
第二步:点M在AD上(不与点A,D重合),再次沿BM折叠纸片,使点A落在EF下方的点N处,延长MN交CF于点P.
(1)在活动1中,求证:∠NBC=30°;
(2)在活动2中,若正方形ABCD的边长为8,PF=3,求AM的长.
10.(2025 铁岭县二模)【问题初探】
(1)如图①,在△ABC中,∠ACB=90°,AC=BC,点E在BC上(且不与点B,C重合),在△ABC的外部作△BED,使∠BED=90°,BE=DE,连接CD,过点A作CD的平行线交DE的延长线于点F,连接CF.根据以上操作,判断:四边形ACDF是 , .
【变换探究】
(2)如图②,将图①中的△BED绕点B逆时针旋转,使点E落在AB边上,过点A作CD的平行线,过点D作AC的平行线,它们相交于点F,连接CE,CF,若CE=4,求CF的长.
勤奋小组通过第(1)问的解题经验,尝试连接EF,猜想△CEF为特殊的三角形;
创思小组在勤奋小组的提示下,成功地证明出一对三角形全等,进而求得CF的长度.
请结合两个小组的解题思路,写出解题过程.
【迁移拓展】
(3)如图③博文小组在第(2)问的基础上进行了如下创新,将图①中的△BED绕点B顺时针旋转,使点D在BC的右侧,过点A作CD的平行线,过点D作AC的平行线,它们相交于点F,连接CF,并尝试连接CE,EF.他们发现:若BE=1,BC=3,当四边形ACDF为菱形时,可求得CF的长度.请完成以下问题:
①求CF的长;
②当点D在BC左侧时,请直接写出CF的长.
11.(2025 南海区校级三模)综合与实践
如果从一个平行四边形的一个顶点向不过该顶点的对角线作垂线,垂线交平行四边形的边于另一点,且该点为所在边的三等分点,那么这个平行四边形叫做“垂对三等分平行四边形”,垂足叫做“垂三等分点”.
(1)理解应用
如图1,在 ABCD中,AE⊥BD于点P,交CD于点E,若E为CD的三等分点,则 ABCD是垂对三等分平行四边形,P是垂三等分点.若DE,BP=6,则DP= ;AD= .
(2)问题探究
如图2,在垂对三等分平行四边形ABCD中,P是垂三等分点,且满足AEAB,若CE=CB,试猜想BD与BC的数量关系,并说明理由.
(3)拓展延伸
已知四边形ABCD是矩形,过点A作AE⊥BD于点P,交CD于点E,AB=9,当四边形ABCD是垂对三等分平行四边形时,直接写出AD的长度.
12.(2025春 离石区期中)综合与实践
【问题情境】综合与实践课上,王老师提出了一个有关正方形中“十字型”的问题:
如图1,在正方形ABCD中,边长为6,E,F分别是边CD,AD上的点,AE⊥BF.
【独立思考】
(1)试判断AE与BF的数量关系,并说明理由.
【问题解决】
(2)阳光小组在王老师的问题上继续思考.如图2,记AE与BF的交点为G,若阴影部分的面积之和为24,求△ABG的面积.
【实践探究】
(3)缤纷小组进一步探究,如图5,连接EF并延长,交BA的延长线于点P.已知DF=2,,请直接写出PE的长.
13.(2025春 杭州月考)在矩形ABCD中,AB=4,BC=3,点P在线段BC上运动,作△ACD关于直线AP的对称△AC1D1(点C,D的对称点分别为C1,D1).
(1)如图1,当点C1在AB的延长线上时,求CC1的长.
(2)如图2,当点P与点C重合时,连结DD1,CD1、DD1交AB分别于点E、F.求证:BD1⊥DD1.
(3)当直线C1D1经过点B时,求CP的长.
14.(2025 雁塔区校级模拟)问题发现:
(1)如图①,在△ABC中,AB=AC=6,∠BAC=120°,若AD将△ABC分成面积相等的两部分,则AD= ;
(2)如图②,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2,若直线l经过点E,且将该菱形的面积平分,并与边BC交于点F,求线段EF的长.
问题解决:
(3)某市为保护生态环境,方便市民观光游览,准备在秦岭北麓兴建一处“和谐观光园”,其形状为四边形ABCD,如图③所示.在四边形ABCD中,∠B=∠D=90°,实际长度AD=5公里,AB=9公里,BC=13公里,CD=15公里,点P在CD上且PD=5公里,根据用地需求,需在BC上确定点E,将五边形ABEPD作为特色植物繁育展示区,使其面积为四边形ABCD总面积的一半,并在AB上确定点F,在△PEF中修建游客休息区,剩余部分作为花卉展示区,为方便游客游览,要求修建PE、PF、EF三条观光道路的总长度最小.请问这样的△PEF是否存在?若存在,请求出点E到点B的距离及△PEF周长的最小值;若不存在,请说明理由.
【攻克压轴大题】2025年中考数学压轴题精选:三角形和四边形
参考答案与试题解析
一.解答题(共14小题)
1.(2025 乾安县模拟)【探究思考】
(1)通过添加辅助线构造“全等三角形”证明线段相等或角相等,是我们常用的方法.已知,如图①,△ABC是等边三角形,CE是△ABC的外角∠ACF的平分线,点D为射线BC上一点,且∠ADE=∠ABC,DE与CE相交于点E.我们可以过点D作AC的平行线,交AB于点G,构造得到 △DCE≌△AGD (填两个全等三角形),来证明AD=DE;
【问题解决】
(2)如图②,在△ABC中,AB=BC,在边BC上取一点D,以D为顶点,AD为一条边在AD的右侧作∠ADE=∠ABC,点F在BC延长线上,∠ECF=∠ACB.
①求证:AD=DE;
②如图③所示,当点D在BC的延长线上时,若∠CAD=∠B,CD=1,AB=4,直接写出DE的长.
【解答】(1)解:过点D作AC的平行线,交AB于点G,构造得到△DCE≌△AGD,来证明AD=DE,如图1,
证明:∵△ABC为等边三角形,
∴∠ABC=∠ACB=∠CAB=60°,
∴∠BGD=∠BDG=60°,
∴BD=BG,
∴BC﹣BD=AB﹣BG,
∴AG=CD,
∵∠BAD+∠ABC=∠EDC+∠ADE,
又∵∠ADE=∠ABC,
∴∠BAD=∠EDC,
∵∠BGD=60°,
∴∠AGD=120°,
∵CE是△ABC的外角∠ACF的平分线,
又∵ACB=60°,
∴∠ACE=60°,∠DCE=60°+60°=120°,
∴∠AGD=∠DCE,
在△DCE与△AGD中,
,
∴△DCE≌△AGD(ASA),
∴AD=DE,
故答案为:△DCE≌△AGD;
(2)①证明:如图②,过点D作AC的平行线,交AB于点G′,
∴∠BDG′=∠ACB,∠BG′D=∠BAC,
∵AB=BC,
∴∠BAC=∠ACB,
∴∠BG′D=∠BDG′,
∴BD=BG′,
∴BC﹣BD=AB﹣BG′,
∴AG′=CD,
∵∠BAD+∠ABC=∠EDC+∠ADE,
又∵∠ADE=∠ABC,
∴∠BAD=∠EDC,
∴∠ECF=∠ACB=∠BG′D,
∴∠AG′D=∠DCE.
在△DCE与△AG′D中,
,
∴△DCE≌△AG′D(ASA),
∴AD=DE;
②解:如图3,过点D作AC的平行线,交AB于点G″,
∴∠BDG″=∠ACB,∠BG″D=∠BAC,
∵AB=BC,
∴∠CAB=∠ACB,
∴∠BG″D=∠BDG″,
∴BD=BG'',
∴BD﹣BC=BG″﹣AB,
∴AG''=CD,
∵∠BAD﹣∠ABC=∠EDC﹣∠ADE,
又∵∠ADE=∠ABC,
∴∠BAD=∠EDC,
∴∠ECF=∠ACB=∠BG″D,
∴∠AG″D=∠DCE,
在△DCE与△AGD中,
,
∴△DCE≌△AGD(ASA),
∴AD=DE,
∵∠ADB=∠CDA,∠CAD=∠B,
∴△ABD∽△CAD,
∴,
∴AD2=BD CD,
∵CD=1,AB=BC=4,
∴AD,
∴DE=AD.
2.(2025 港北区三模)在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE,点E在△ABC的内部,连接EC,EB和BD,设EC=k BD(k≠0).
(1)当∠ABC=∠ADE=60°时,如图1,请求出k值,并给予证明;
(2)当∠ABC=∠ADE=90°时:
①如图2,(1)中的k值是否发生变化,如无变化,请给予证明;如有变化,请求出k值并说明理由;
②如图3,当D,E,C三点共线,且E为DC中点时,请求出tan∠EAC的值.
【解答】解:(1)k=1,
理由如下:如图1,∵∠ABC=∠ADE=60°,BA=BC,DA=DE,
∴△ABC和△ADE都是等边三角形,
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,
∴∠DAB=∠EAC,
在△DAB和△EAC中,
,
∴△DAB≌△EAC(SAS)
∴EC=DB,即k=1;
(2)①k值发生变化,k,
∵∠ABC=∠ADE=90°,BA=BC,DA=DE,
∴△ABC和△ADE都是等腰直角三角形,
∴,,∠DAE=∠BAC=45°,
∴,∠DAB=∠EAC,
∴△EAC∽△DAB,
∴,即ECBD,
∴k;
②作EF⊥AC于F,
设AD=DE=a,则AEa,
∵点E为DC中点,
∴CD=2a,
由勾股定理得,ACa,
∵∠CFE=∠CDA=90°,∠FCE=∠DCA,
∴△CFE∽△CAD,
∴,即,
解得,EFa,
∴AFa,
则tan∠EAC.
3.(2025春 铁西区期中)(1)如图1,在Rt△ABC中,∠ACB=90°,若∠BAC=30°,AB=6,则AC= 3 .
(2)在(1)的条件下,作点A关于直线BC的对称点A1,连接A1B.
①如图2,分别以点A1,C为圆心,大于为半径画弧,两弧分别交于点G,H,连接GH,分别交A1B,A1C于点D,E,求DE的长;
②如图3,若点P是边BA1的延长线上一点,连接PA交BC的延长线于点M,∠BAP的平分线AN交边A1B于点N,过点N作NH∥PA交BC于点H.求证:HM=HN.
【解答】(1)解:∵∠BAC=30°,AB=6,∠ACB=90°,
∴BC=3,
∴AC3,
故答案为:3;
(2)①解∵点A关于直线BC的对称点A1,
∴AC=A1C=3,∠A=∠A1=30°,
由作图可知:DE是A1C的垂直平分线,
∴CE=A1C,DE⊥A1C,
∴A1D=2DE,
∵A1D2=DE2+A1E2,
∴DE;
②证明:如图,连接MN,过N作NG⊥AP于点G,作NK⊥AB交延长线于点K,作NL⊥MB于点L,
∵AN平分∠BAP,
∴NK=NG,
∵∠ABC=∠MBP=60°,
∴∠KBP=60°=∠MBP,即BP平分∠MBK,
∴NK=NL,
∴NL=NG,
∴MN平分∠BMP,
∴∠HMN=∠PMN,
∵HN∥AP,
∴∠HNM=∠PMN,
∴∠HMN=∠HNM,
∴HM=HN.
4.(2025 西城区校级模拟)在△ABC中,∠A=90°,AC=AB,D为线段AC上一点.在AB边上截取BE=2AD,过点E作EF⊥BD交BC于点F,连接FD.
(1)如图1,若BD平分∠ABC,求证:;
(2)如图2,猜想线段DF,EF,BD之间的数量关系,并证明.
【解答】(1)证明:如图,过点D作DM⊥BC于M,设EF,AD交于O,
∵BD平分∠ABC,∠A=90°,DM⊥BC,
∴DM=AD,∠EBO=∠FBO,
设AD=DM=a,则BE=2AD=2a,
∵∠A=90°,AC=AB,
∴∠C=∠ABC=45°,
∴△DMC是等腰直角三角形,
∴CM=DM=a,
∴;
∵EF⊥BD,∠BOE=∠BOF=90°,
又∵OB=OB,
∴△BOE≌△BOF(ASA),
∴BF=BE=2a,
∴;
(2)解:BD=EF+DF,证明如下:
如图,作正方形ABHC,取BE中点G,连接HG交BD于T,延长EF交CH于M,
由正方形的性质可得AB=BH,∠A=∠ABH=90°,AB∥CH,
∵G是BE中点,BE=2AD,
∴BG=AD,
∴△BGH≌△ADB(SAS),
∴GH=BD,∠ABD=∠BHG,
∵∠BHG+∠BGH=90°,
∴∠ABD+∠BGH=90°,
∴∠BTG=90°,
∴GH⊥BD,
∵EF⊥BD,
∴GH∥EM,
又∵AB∥CH,
∴四边形GHME是平行四边形,
∴BD=GH=EM,,
∴AC﹣AD=CH﹣HM,
即CD=CM,
∵CF=CF,∠DCF=∠MCF=45°,
∴△DCF≌△MCF(SAS),
∴DF=MF,
∵EM=EF+MF,
∴BD=EF+DF.
5.(2024秋 承德县期末)综合与实践,问题情境:活动课上,同学们以等腰三角形为背景展开有关图形旋转的探究活动,如图1,已知△ABC中AB=AC,∠B=30°.将△ABC从图1的位置开始绕点A逆时针旋转,得到△ADE(点D,E分别是点B,C的对应点),旋转角为α(0°<α<100°,设线段AD与BC相交于点M,线段DE分别交BC,AC于点O,N.
特例分析:(1)如图2,当旋转到AD⊥BC时,求旋转角α的度数为 60 ;
探究规律:(2)如图3,在△ABC绕点A逆时针旋转过程中,“求真”小组的同学发现线段AM始终等于线段AN,请你证明这一结论.
拓展延伸:(3)①直接写出当△DOM是等腰三角形时旋转角α的度数.
②在图3中,作直线BD,CE交于点P,直接写出当△PDE是直角三角形时旋转角α的度数.
【解答】(1)解:∵AB=AC,AD⊥BC,
∴∠C=∠B=30°,∠BAD∠BAC,
∴∠BAD60,
∴α=60°,
故答案为:60°;
(2)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠MAN=∠DAE﹣∠MAN,
即:∠BAM=∠EAN,
在△BAM和△EAN中,
,
∴△BAM≌△EAN(ASA),
∴AM=AN;
(3)解:①如图1,
当DM=OM时,∠MOD=∠D=30°,
∵∠B=∠D,∠AMB=∠DMO,
∴∠BAD=∠MOD=30°,
∴α=30°,
如图2,
当DM=DO时,∠DMO=∠DOM75°,
∴α=∠DOM=75°,
如图3,
当OM=OD时,∠OMD=∠D=30°,
∴α=∠DOM=120°,
此时AD和AC重合,这种情形不存在.
综上所述:α=30°或75°.
②如图:
当∠EDP=90°时,
∵∠ABC=ADE=30°,
∴∠ADB=90°﹣30°=60°,
∴∠BAD=180°﹣60°﹣60°=60°,
∵0°<α<100°,
∴旋转角α为60°.
6.(2025春 肃州区期中)综合与实践:在学习特殊三角形的过程中,我们积累了一定的研究经验.请运用已有经验,对“兄弟三角形”进行研究,新定义:顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.
操作判断:
(1)如图1,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点.请直接写出线段BD与CE之间的数量关系: BD=CE .
性质探究:
(2)如图2,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点,D,E均在△ABC外,连结BD、CE,试说明(1)中BD和CE之间的数量关系是否还成立?若成立,给出证明过程.
拓展应用:
(3)如图3,△ABC和△CDE互为“兄弟三角形”,点C为重合的顶角顶点,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CN为△CDE的高,连结BE,请直接写出线段CN,AE,BE之间的数量关系: CN(AE﹣BE) .
【解答】解:(1)∵△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点,
∴AB=AC,AD=AE,∠BAC=∠DAE,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,
故答案为:BD=CE.
(2)BD和CE之间的数量关系仍然成立,理由如下:
∵△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点,
∴AB=AC,AD=AE,∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(3)CN(AE﹣BE),
理由:∵△ABC和△CDE互为“兄弟三角形”,点C为重合的顶角顶点,∠ACB=∠DCE=90°,
∴AC=BC,DC=EC,∠ACD=∠BCE=90°﹣∠BCD,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∵点A,D,E在同一条直线上,
∴DE=AE﹣AD=AE﹣BE,
∵CN为△DCE的高,
∴CN⊥DE,
∵DC=EC,
∴DN=EN,
∵∠DCE=90°,
∴CNDE,
∴CN(AE﹣BE).
故答案为:CN(AE﹣BE).
7.(2025 海珠区校级二模)如图,在正方形ABCD中,AB=4,点P为正方形ABCD的对角线AC上一动点.
(1)如图①,过点P作PE⊥PB交边DC于点E.当点E在边CD上时,直接写出PB与PE的大小关系;
(2)如图②,在(1)的条件下,过点E作EF⊥AC,垂足为点F,在点P运动的过程中,PF的长度是否发生变化?若不变,求出这个不变的值;若变化,请说明理由.
(3)如图③,若点Q是射线CD上的一个动点,连接BP,BQ,且始终满足AP=2DQ,设,求t的最小值.
【解答】解:(1)连接PD,如图1所示:
由条件可知CB=CD,∠PCB=∠PCD=45°,
在△PCB和△PCD中,
,
∴△PCB≌△PCD(SAS),
∴PB=PD,∠CBP=∠CDP,
∵PE⊥PB,
∴∠BPE=∠BCE=90°,
∴∠CBP+∠CEP=180°,
∵∠CEP+∠PED=180°,
∴∠PED=∠CBP,
∴∠PED=∠CDP,
∴PE=PD,
∴PB=PE;
(2)点P在运动过程中,PF的长度不变,值为.理由如下:
连接BD,与AC相交于点O,如图2.
由条件可知∠BOP=90°,
∵PE⊥PB,即∠BPE=90°,
∴∠PBO=90°﹣∠BPO=∠EPF,
∵EF⊥PC,即∠PFE=90°,
∴∠BOP=∠PFE,
在△BOP和△PFE中,
,
∴△BOP≌△PFE(AAS),
∴BO=PF,
∵四边形ABCD是正方形,
∴OB=OA,∠AOB=90°,
∴AB2=2OB2,
∵AB=4,
∴,(负值不合题意,已经舍去),
∴,
∴点P在运动过程中,PF的长度不变,值为;
(3)如图3所示:过点D在正方形外作∠FDC=45°,使FD=AB=4,在CQ上取点E,使QE=DQ,连接EF,
由条件可知∠ACB=∠ACD=∠BAP=45°,
∴∠BAP=∠FDE=45°,
∵AP=2DQ,DQ=QE,
∴AP=DE,
∴△ABP≌△DFE(SAS),
∴BP=FE,
如图3所示:在FD上取点G,使DG=FG,连接QG、BG,
又∵DQ=QE,
∴,
∴,
即:当B、Q、G三点共线时,t最小,最小值为t=BG,
如图3所示:过点G作GH⊥AB,垂足为H,交CD于K,
由条件可知四边形ADKH是矩形,
∴AH=DK,AD=HK=4,∠DKG=90°,
∵∠FDE=45°,
∴△DKG是等腰直角三角形,
∵,
∴,
∴,
,
在Rt△BHG中,,
∴t的最小值为6.
8.(2025 西陵区模拟)将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°)得到矩形AB′C′D′,连结BD.
(1)如图1,当α=90°时,若∠D'AC'=20°,求∠D′DB的度数;
(2)如图2,过点D'作D'M∥AC'交BD于点M.求证:D′M=DM;
(3)在(2)的条件下,射线DB分别交AD′,AC'于点P,N(如图3),线段DN,MN,PN之间存在一定的数量关系,请写出这个关系式,并加以证明.
【解答】解:(1)∵矩形ABCD绕点A顺时针旋转90°得到矩形AB′C′D′,
∴点A,B,D′在同一直线上,
∴∠DAD′=90°,AD=AD′.∠D′AC′=∠ADB=20°,
∴∠ADD′=∠AD′D=45°,
∴∠D′DB=∠ADD′﹣∠ADB=25°,
(2):D'M=DM.
证明:如图2,连接DD',
∵D'M∥AC',
∴∠AD'M=∠D'AC',
∵AD'=AD,∠AD'C'=∠DAB=90°,D'C'=AB,
∴△AC'D'≌△DAB(SAS),
∴∠ADB=∠D'AC',
∴∠AD'M=∠ADB,
∵AD=AD',
∴∠AD'D=∠ADD',
∴∠MD'D=∠MDD',
∴D'M=DM;
(3)关系式为MN2=PN DN.
证明:如图3,连接AM,
∵D'M=DM,AD'=AD,AM=AM,
∴△AD'M≌△ADM(SSS),
∴∠MAD=∠MAD',
∵∠AMN=∠MAD+∠NDA,
∠NAM=∠MAD'+∠NAP,
∴∠NAM=∠AMN,
∴MN=AN,
在△NAP和△NDA中,∠ANP=∠DNA,∠NAP=∠NDA,
∴△NPA∽△NAD,
∴,
∴AN2=PN DN,
∴MN2=PN DN.
9.(2025 翔安区二模)在一次数学活动课中,小明对“折纸中的数学问题”进行探究.
【活动1】折叠矩形纸片:
第一步:如图1,把矩形纸片ABCD对折,使AD与BC重合,折痕为EF,把纸片展平;
第二步:点M在AD上,再次沿BM折叠纸片,使点A落在EF上的点N处.
【活动2】折叠正方形纸片:
第一步:如图2,把正方形纸片ABCD对折,使AD与BC重合,折痕为EF,把纸片展平;
第二步:点M在AD上(不与点A,D重合),再次沿BM折叠纸片,使点A落在EF下方的点N处,延长MN交CF于点P.
(1)在活动1中,求证:∠NBC=30°;
(2)在活动2中,若正方形ABCD的边长为8,PF=3,求AM的长.
【解答】解:(1))∵AE=BEAB,AB=BN,
∴BEBN,
∵∠BEN=90°,sin∠BNE,
∴∠BNE=30°,
∴∠NBE=60°,
∵∠ABM=∠NBM,
∴∠ABM=∠NBM=∠NBC=30°;
(2)连接BP,
∵BN=BC,BP=BP,
∴Rt△BNP≌Rt△BCP(HL),
∴NP=CP,
∵PF=3,DF=CFCD=4,
∵DP=DF+FP=3+4=7,
∵NP=PC=CF﹣PF=1,
设AM=NM=x,MD=8﹣x,
∴MD2+DP2=PM2,
即(8﹣x)2+72=(x+1)2,
解得:x,
∴AM.
10.(2025 铁岭县二模)【问题初探】
(1)如图①,在△ABC中,∠ACB=90°,AC=BC,点E在BC上(且不与点B,C重合),在△ABC的外部作△BED,使∠BED=90°,BE=DE,连接CD,过点A作CD的平行线交DE的延长线于点F,连接CF.根据以上操作,判断:四边形ACDF是 平行四边形 , .
【变换探究】
(2)如图②,将图①中的△BED绕点B逆时针旋转,使点E落在AB边上,过点A作CD的平行线,过点D作AC的平行线,它们相交于点F,连接CE,CF,若CE=4,求CF的长.
勤奋小组通过第(1)问的解题经验,尝试连接EF,猜想△CEF为特殊的三角形;
创思小组在勤奋小组的提示下,成功地证明出一对三角形全等,进而求得CF的长度.
请结合两个小组的解题思路,写出解题过程.
【迁移拓展】
(3)如图③博文小组在第(2)问的基础上进行了如下创新,将图①中的△BED绕点B顺时针旋转,使点D在BC的右侧,过点A作CD的平行线,过点D作AC的平行线,它们相交于点F,连接CF,并尝试连接CE,EF.他们发现:若BE=1,BC=3,当四边形ACDF为菱形时,可求得CF的长度.请完成以下问题:
①求CF的长;
②当点D在BC左侧时,请直接写出CF的长.
【解答】解:(1)∵∠ACB=90°,∠BED=90°,
∴DF∥AC,
∵AF∥CD,
∴四边形ACDF是平行四边形,
∴DF=AC=BC,
∴DE+EF=BE+CE,
∵BE=DE,
∴EF=CE,
∵∠BED=90°,
∴∠CEF=90°,
由勾股定理得:,.
故答案为:平行四边形,;
(2)如图①,连接EF.
∴四边形ACDF是平行四边形,∠ACD=90°,
∴四边形ACDF是矩形,
∴DF=AC=BC,∠CDF=90°,
∴∠BDF=90°.
∵∠BED=90°,BE=DE,
∴∠EDB=∠B=45°,
∴∠FDE=∠BDF﹣∠EDB=45°=∠B.
∵DF=BC,∠FDE=∠B,DE=BE,
∴△FDE≌△CBE(SAS),
∴EF=EC=4,∠FED=∠CEB,
∴∠FED﹣∠CED=∠CEB﹣∠CED,
即∠FEC=∠DEB=90°,
∴由勾股定理,得,
即CF的长为;
(3)①∵四边形ACDF为菱形,
∴CD=DF=AC=BC,
∴∠CBD=∠CDB.
∵BC=CD,BE=DE,CE=CE,
∴△BCE≌△DCE(SSS),
∴∠BCE=∠DCE,∠CBE=∠CDE.
设∠BCE=∠DCE=α,则∠CBD=∠CDB=90°﹣α,∠ACD=90°+2α,∠FCD∠ACD=45°+α,∠FCE=∠FCD﹣∠DCE=45°.
∴∠CDE=∠CDB﹣∠EDB=90°﹣α﹣45°=45°﹣α,
∵DF∥AC,
∴∠CDF=180°﹣∠ACD=90°﹣2α,
∴∠FDE=∠CDF﹣∠CDE=45°﹣α=∠CDE.
∵DF=CD,∠FDE=∠CDE,DE=DE,
∴△FDE≌△CDE(SAS),
∴EF=EC,
∴∠EFC=∠FCE=45°,
∴∠CEF=90°,
∴CFCE,
如图②,延长CE交BD于点G.
∵BC=CD,∠BCE=∠DCE,
∴CG⊥BD,
∴,.
∴在Rt△BCG中,由勾股定理,得CG,
∴CE=CG﹣EG,
∴CFCE1;
②当点D在BC左侧时,如图4,连接AD,记AD,CF的交点为O,
∵四边形ACDF为菱形,
∴CD=DF=AD=AC,OC=OF,∠DOC=∠DOF=90°,
∴∠CBD=∠CDB,
同理①:△BCE≌△DCE(SSS),
∴∠BCE=∠DCE,,
设∠BCE=∠DCE=α,则∠ACD=90°﹣2α,
∴,∠CED+∠DCE=45°+α=∠CDA,
∴∠CDA为△CDE的外角,即A、D、E三点共线,
∵OC=OF,∠EOC=∠EOF,EO=EO,
∴△EOC≌△EOF(SAS),
∴CE=EF,∠OEF=∠OEC=45°,
∴∠CEF=90°,
∴,
如图4,记CE、BD的交点为H,
∵BC=CD,∠BCE=∠DCE,
∴CE⊥BD,BH,EH=BE sin 45°,
由勾股定理得:CH,
∴CE=CH+EH,
∴CFCE1.
11.(2025 南海区校级三模)综合与实践
如果从一个平行四边形的一个顶点向不过该顶点的对角线作垂线,垂线交平行四边形的边于另一点,且该点为所在边的三等分点,那么这个平行四边形叫做“垂对三等分平行四边形”,垂足叫做“垂三等分点”.
(1)理解应用
如图1,在 ABCD中,AE⊥BD于点P,交CD于点E,若E为CD的三等分点,则 ABCD是垂对三等分平行四边形,P是垂三等分点.若DE,BP=6,则DP= 2 ;AD= .
(2)问题探究
如图2,在垂对三等分平行四边形ABCD中,P是垂三等分点,且满足AEAB,若CE=CB,试猜想BD与BC的数量关系,并说明理由.
(3)拓展延伸
已知四边形ABCD是矩形,过点A作AE⊥BD于点P,交CD于点E,AB=9,当四边形ABCD是垂对三等分平行四边形时,直接写出AD的长度.
【解答】解:(1)∵,,
∴CD=3DE,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△DEP∽△BAP,
∴,即,
∴DP=2.
∵AE⊥BD,
∴在Rt△ABP中,AP,
在Rt△ADP中,AD.
故答案为:2;;
(2)BD=2BC,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,,
∴,
∵AB∥CD,
∴△BEP∽△DCP,
∴,
∴设EP=2a,则CP=3a,CE=CP+EP=5a,
∴BC=CE=5a,
∵CE⊥BD,
∴在Rt△BCP中,,
∴,
∴,
∴BD=DP+BP=10a,
∵BC=5a,
∴BD=2BC;
(3)分两种情况讨论:①如图,若,
∵在矩形ABCD中,CD∥AB,
∴△DEP∽△BAP,
∴,
设EP=a,则AP=3EP=3a,AE=AP+EP=4a,
∵AE⊥BD,
∴∠DPE=90°,
∵在矩形ABCD中,∠ADC=90°,
∴∠DPE=∠ADE,
∵∠DEP=∠AED,
∴△DEP∽△AED,
∴,即,
解得a=1或a=﹣1(舍去),
∴AE=4,
∴在Rt△ADE中,.
②如图,若,
∵在矩形ABCD中,CD∥AB,
∴△DEP∽△BAP,
∴,
设EP=2b,则,AE=AP+EP=5b,
∵AE⊥BD,
∴∠DPE=90°,
∵在矩形ABCD中,∠ADC=90°,
∴∠DPE=∠ADE,
∵∠DEP=∠AED,
∴△DEP∽△AED,
∴,即,
解得或(舍去),
∴,
∴在Rt△ADE中,.
综上所述,AD的长为或.
12.(2025春 离石区期中)综合与实践
【问题情境】综合与实践课上,王老师提出了一个有关正方形中“十字型”的问题:
如图1,在正方形ABCD中,边长为6,E,F分别是边CD,AD上的点,AE⊥BF.
【独立思考】
(1)试判断AE与BF的数量关系,并说明理由.
【问题解决】
(2)阳光小组在王老师的问题上继续思考.如图2,记AE与BF的交点为G,若阴影部分的面积之和为24,求△ABG的面积.
【实践探究】
(3)缤纷小组进一步探究,如图5,连接EF并延长,交BA的延长线于点P.已知DF=2,,请直接写出PE的长.
【解答】解:(1)AB=BF,理由如下:
∵四边形ABCD是正方形,
∴∠BAD=∠D=90°,AD=AB,
∴∠DAE+∠BAE=90°,
∵AE⊥BF,
∴∠ABF+∠BAE=90°,
∴∠DAE=∠ABF,
∴△ADE≌△BAF(ASA),
∴AE=BF;
(2)由(1)知,△ADE≌△BAF,
∴S△ADE=S△BAF,
∴S△ADE﹣S△AFG=S△BAF﹣S△AFG,
∴S四边形DEGF=S△ABG,
∵S正方形=AB2=62=36,S阴影=24,
∴S△ABG+S四边形DEGF=36﹣24=12,
∴S△ABG;
(3)如图,
连接PD,作PH⊥CD,交CD的延长线于H,
∴∠H=90°,
设S△DEF=S,
∵DF=2,AD=6,
∴S△ADE=3S,
∴S△AEF=S△ADE﹣S△DEF=2S,
∵四边形ABCD是正方形,
∴AB∥CD,
∴S△PDE=S△ADE=3S,
∴S△PDF=S△PDE﹣S△DEF=2S,
∴S△APF=2S△PDF=4S,
∴S△APD=S△APF+S△PDF=6S,
∴,
∴,
设AE=13a,则AP=4a,
∴DE=2a,
在Rt△ADE中,由勾股定理得,AE2﹣DE2=AD2,
∴,
∴a或a(舍去),
∴AP=48,DE=4,
∵四边形ABCD是正方形,
∴∠PAD=∠DAB=∠ADH=∠ADC=90°,
∴四边形APHD是矩形,
∴PH=AD=6,DH=AP=8,
∴EH=DH+DE=12,
∴PE6.
13.(2025春 杭州月考)在矩形ABCD中,AB=4,BC=3,点P在线段BC上运动,作△ACD关于直线AP的对称△AC1D1(点C,D的对称点分别为C1,D1).
(1)如图1,当点C1在AB的延长线上时,求CC1的长.
(2)如图2,当点P与点C重合时,连结DD1,CD1、DD1交AB分别于点E、F.求证:BD1⊥DD1.
(3)当直线C1D1经过点B时,求CP的长.
【解答】(1)解:在矩形ABCD中,AB=4,BC=3,
∴,
∵△ACD、△ACD关于直线AP对称,
∴AC1=AC=5,
∴BC=AC﹣AB=1,
在Rt△BCC1中,由勾股定理得,
,
∴CC1的长为;
(2)证明:连结BD交AC于点O,
∵ABCD为矩形,
∴OB=OD
∵D,D1关于AC对称,
∴AC垂直平分DD1,
∴H为DD1的中点,
∴OH为△BDD1的中位线,
∴OH∥BD1,
∵AC⊥DD1,
∴∠DHO=90°,
∵OH∥BD,
∴∠BD1D=∠DHO=90°,
∴DD⊥BD1;
(3)解:连接PC1,
∵△ACD、△AC1D1关于直线AP对称,
∴AD=AD,CD=CD,∠ACD=∠AC1B∠ACP=∠AC1PPC=PC1,∠ADC=∠AC1C=90°,
∵∠ACD+∠ACP=90°
∴∠AC1B+∠AC1P=90°,
即∠BC1P=90°,
当直线C1D1经过点B时,
在Rt△AD1B中,BD1,
∴BC1=C1D1﹣BD1=4,
在Rt△BC1P中,,
∴,,
∴.
14.(2025 雁塔区校级模拟)问题发现:
(1)如图①,在△ABC中,AB=AC=6,∠BAC=120°,若AD将△ABC分成面积相等的两部分,则AD= 3 ;
(2)如图②,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2,若直线l经过点E,且将该菱形的面积平分,并与边BC交于点F,求线段EF的长.
问题解决:
(3)某市为保护生态环境,方便市民观光游览,准备在秦岭北麓兴建一处“和谐观光园”,其形状为四边形ABCD,如图③所示.在四边形ABCD中,∠B=∠D=90°,实际长度AD=5公里,AB=9公里,BC=13公里,CD=15公里,点P在CD上且PD=5公里,根据用地需求,需在BC上确定点E,将五边形ABEPD作为特色植物繁育展示区,使其面积为四边形ABCD总面积的一半,并在AB上确定点F,在△PEF中修建游客休息区,剩余部分作为花卉展示区,为方便游客游览,要求修建PE、PF、EF三条观光道路的总长度最小.请问这样的△PEF是否存在?若存在,请求出点E到点B的距离及△PEF周长的最小值;若不存在,请说明理由.
【解答】解:(1)如图①中,取BC的中点D,连接AD,线段AD即为所求.
∵AB=AC=6,BD=DC,
∴AD⊥BC,∠B=∠C(180°﹣120°)=30°,
∴ADAB=3,
故答案为:3;
(2)解:如图,过点A和点E作AG⊥BC,EH⊥BC于点G和H,得矩形AGHE,
∴GH=AE=2,
∵在菱形ABCD中,AB=6,∠B=60°,
∴BG=3,AG=3EH,
∴HC=BC﹣BG﹣GH=6﹣3﹣2=1,
∵EF平分菱形面积,EF经过菱形对角线交点,
∴FC=AE=2,
∴FH=FC﹣HC=2﹣1=1,
在Rt△EFH中,根据勾股定理,得
EF2;
(3)存在这样的这样的△PEF,
如图③,作DH⊥BC于点H,DG⊥BA交BA的延长线于点G,连接BD,
∵∠DHB=∠HBG=∠G=90°,
∴四边形DGBH是矩形,
∴DG=BH,∠GDH=∠ADC=90°,
∴∠ADG=∠CDH=90°﹣∠ADH,
∵∠G=∠DHC=90°,AD=5公里,CD=15公里,
∴△ADG∽△CDH,
∴,
∴DH=3DG=3BH,
∵S△ABD+S△CBD=S△ABC+S△ADC=S四边形ABCD,AB=9公里,BC=13公里,
∴9BH13×3BH9×135×15,
解得BH=4,
∴DH=12公里,CH=13﹣4=9(公里),
∵CD=15公里,PD=5公里,
∴PC=15﹣5=10(公里),
作DK⊥BC于点K,则∠PKE=90°,BK∥DH,
∴△PCK∽△DCH,
∴,
∴CKCH9=6(公里),PKDH12=8(公里),
∵S五边形ABEPDS四边形ABCD,
∴S△PCES四边形ABCD,
∴8CE(9×135×15),
解得CE=12,
∴BE=13﹣12=1(公里),EK=12﹣6=6(公里),
∴PE10(公里),
延长CB到点L,使BL=BE=1公里,连接PL、FL,则LK=6+1+1=8(公里),
∴PL8(公里),
∵AB垂直平分EL,
∴LF=EF,
∵PF+LF≥PL,
∴PE+PF+EF≥PL+PE,
∴PE+PF+EF≥810,
∴当点F落在PL上时,PE+PF+EF取得最小值,最小值为(810)公里,
∴存在这样的这样的△PEF,点E到点B的距离为1公里,△PEF周长的最小值为(810)公里.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
