【期末专项押题卷】解答题-2024-2025学年高一数学下学期人教A版(2019)必修第二册(含解析)
文档属性
| 名称 | 【期末专项押题卷】解答题-2024-2025学年高一数学下学期人教A版(2019)必修第二册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 11:06:25 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【期末专项押题卷】解答题-2024-2025学年高一数学下学期人教A版(2019)必修第二册
1.(2025春 河南期末)已知复数z1=﹣1+2i,z2=﹣2﹣6i.
(1)若,求|z|;
(2)在复平面内,复数z1z2对应的向量分别是,,其中O是坐标原点,求∠AOB的大小.
2.(2025春 贵州期末)已知复数z1=1+i,z2=a﹣2i(a∈R).
(1)若z1z2是纯虚数,求a的值;
(2)若复数z1z2在复平面内所对应的点位于第四象限内,求a的取值范围.
3.(2025春 邢台校级期末)已知复数z=m﹣i(m∈R),且为纯虚数(是z的共轭复数).
(1)求实数m的值;
(2)设复数,求|z1|;
(3)复数在复平面内对应的点在第一象限,求实数a的取值范围.
4.(2025春 浙江期末)已知复数z=1+mi(m∈R),且(3+i)为纯虚数.
(1)求实数m及|z|;
(2)若z是关于x的方程x2+px+q=0(p,q∈R)的一个根,求2p+q的值.
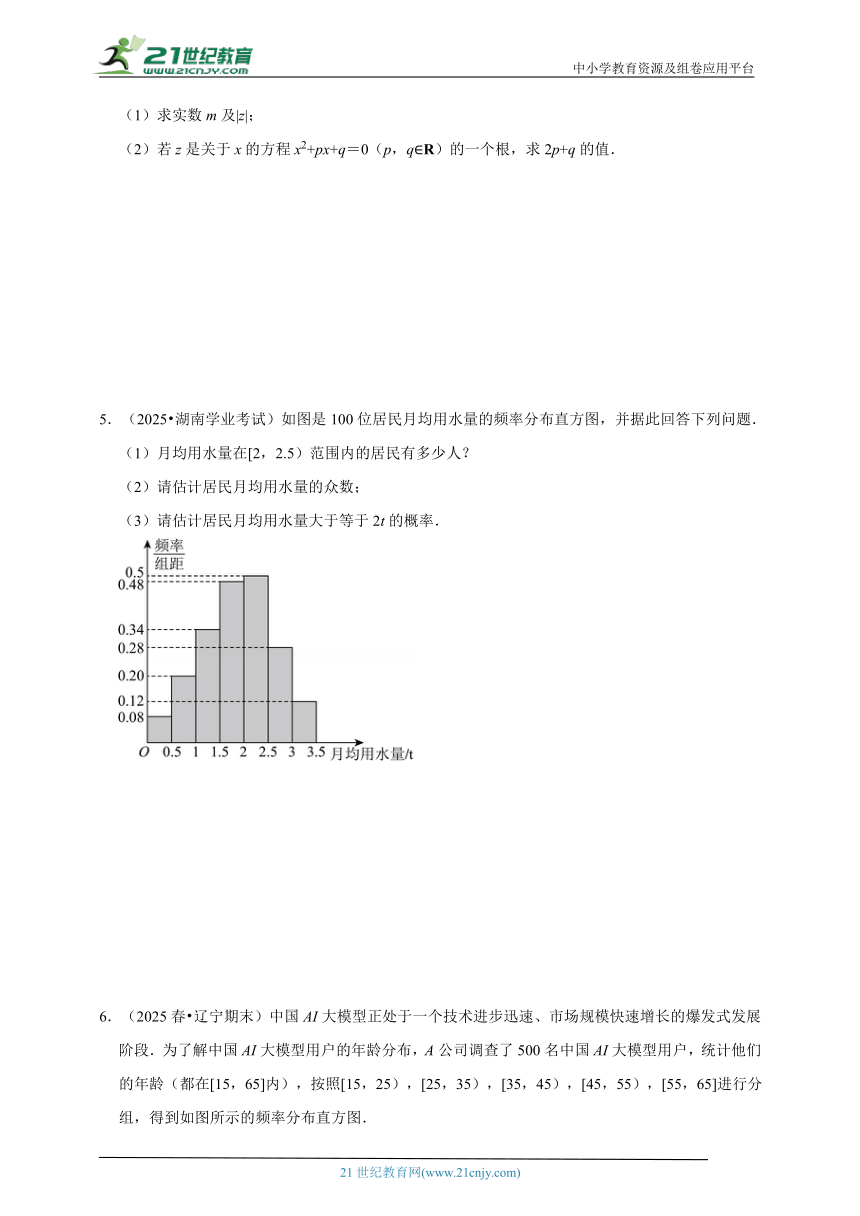
5.(2025 湖南学业考试)如图是100位居民月均用水量的频率分布直方图,并据此回答下列问题.
(1)月均用水量在[2,2.5)范围内的居民有多少人?
(2)请估计居民月均用水量的众数;
(3)请估计居民月均用水量大于等于2t的概率.
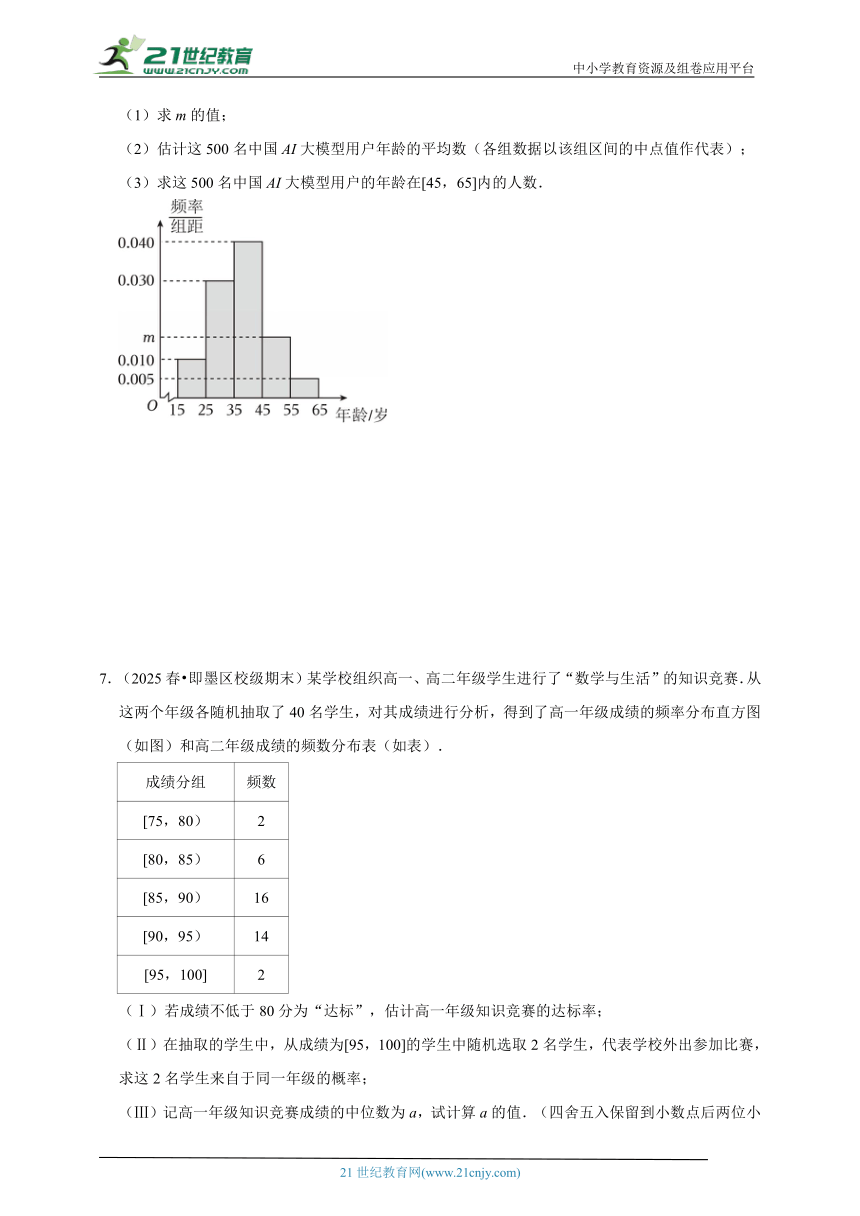
6.(2025春 辽宁期末)中国AI大模型正处于一个技术进步迅速、市场规模快速增长的爆发式发展阶段.为了解中国AI大模型用户的年龄分布,A公司调查了500名中国AI大模型用户,统计他们的年龄(都在[15,65]内),按照[15,25),[25,35),[35,45),[45,55),[55,65]进行分组,得到如图所示的频率分布直方图.
(1)求m的值;
(2)估计这500名中国AI大模型用户年龄的平均数(各组数据以该组区间的中点值作代表);
(3)求这500名中国AI大模型用户的年龄在[45,65]内的人数.
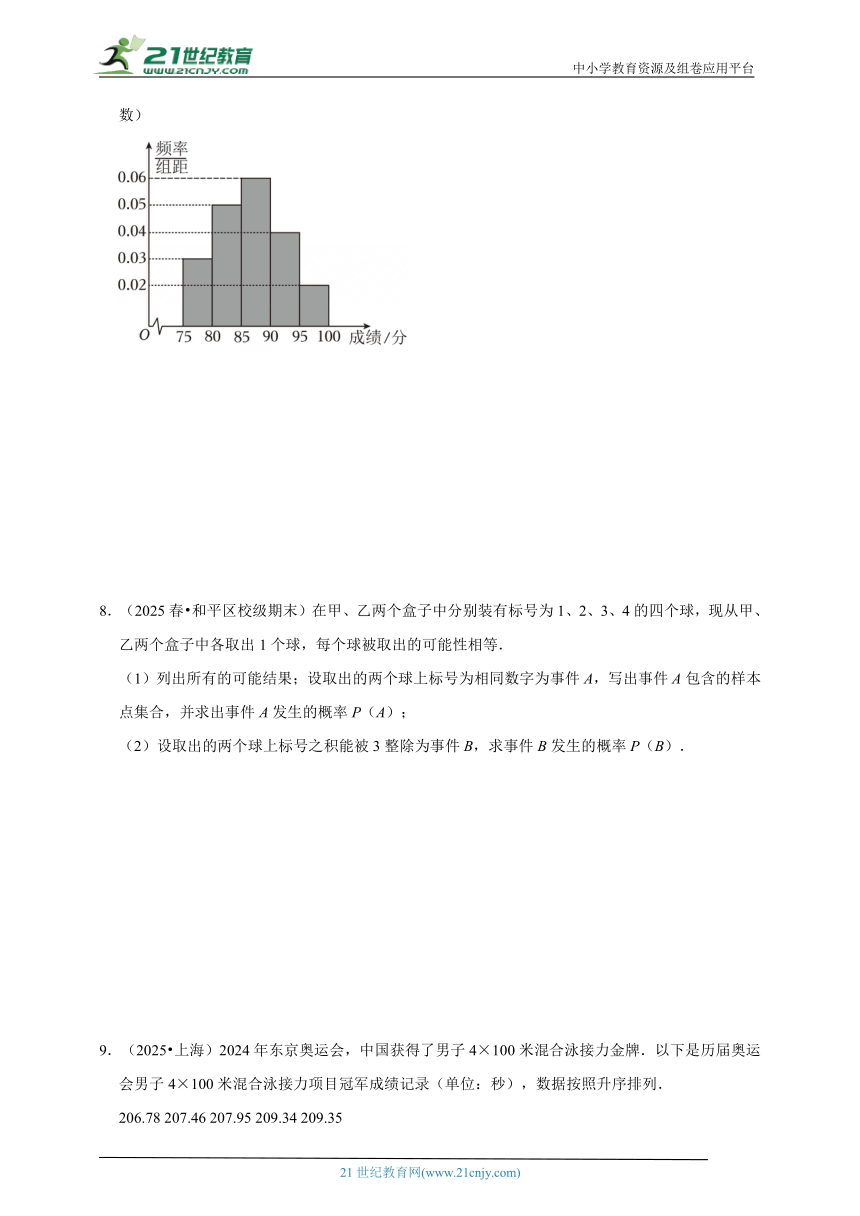
7.(2025春 即墨区校级期末)某学校组织高一、高二年级学生进行了“数学与生活”的知识竞赛.从这两个年级各随机抽取了40名学生,对其成绩进行分析,得到了高一年级成绩的频率分布直方图(如图)和高二年级成绩的频数分布表(如表).
成绩分组 频数
[75,80) 2
[80,85) 6
[85,90) 16
[90,95) 14
[95,100] 2
(Ⅰ)若成绩不低于80分为“达标”,估计高一年级知识竞赛的达标率;
(Ⅱ)在抽取的学生中,从成绩为[95,100]的学生中随机选取2名学生,代表学校外出参加比赛,求这2名学生来自于同一年级的概率;
(Ⅲ)记高一年级知识竞赛成绩的中位数为a,试计算a的值.(四舍五入保留到小数点后两位小数)
8.(2025春 和平区校级期末)在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)列出所有的可能结果;设取出的两个球上标号为相同数字为事件A,写出事件A包含的样本点集合,并求出事件A发生的概率P(A);
(2)设取出的两个球上标号之积能被3整除为事件B,求事件B发生的概率P(B).
9.(2025 上海)2024年东京奥运会,中国获得了男子4×100米混合泳接力金牌.以下是历届奥运会男子4×100米混合泳接力项目冠军成绩记录(单位:秒),数据按照升序排列.
206.78 207.46 207.95 209.34 209.35
210.68 213.73 214.84 216.93 216.93
(1)求这组数据的极差与中位数;
(2)从这10个数据中任选3个,求恰有2个数据在211以上的概率;
(3)若比赛成绩y关于年份x的回归方程为y=﹣0.311x,年份x的平均数为2006,预测2028年冠军队的成绩(精确到0.01秒).
10.(2025春 驻马店期末)已知一个古典概型试验中,事件A发生的概率为,事件B发生的概率为,且事件A和事件B的并集发生的概率为.
(1)求事件A和事件B同时发生的概率P(A∩B).
(2)若事件C是事件A的对立事件,求事件C和事件B同时发生的概率P(C∩B).
(3)若事件D是事件A和事件B的交集的对立事件,求事件D发生的概率P(D).
11.(2025 重庆校级模拟)已知△ABC内角A,B,C所对的边分别为a,b,c,△ABC的面积为.
(1)求角A的大小;
(2)D为BC边上一点,DA⊥BA,且BD=3DC,求cosC.
12.(2025 武昌区校级模拟)已知a,b,c分别为锐角△ABC三个内角A,B,C的对边,且.
(1)求A;
(2)若a=3,求△ABC周长的取值范围.
13.(2025 山西模拟)设△ABC的内角A,B,C的对边分别为a,b,c,且满足.
(1)证明:tanA=2tanB;
(2)已知,求tanAtanBtanC取得最小值时tanB的值.
14.(2025春 墨玉县期末)某景区为打造景区风景亮点,欲在一不规则湖面区域(阴影部分)上A,B两点之间建一条观光通道,如图所示.在湖面所在的平面(不考虑湖面离地平面的距离,视湖面与地平面为同一平面)内距离点B50米的点C处建一凉亭,距离点B70米的点D处再建一凉亭,测得∠ACB=∠ACD,cos∠ACB.
(1)求sin∠BDC的值;
(2)测得AC=AD,观光通道每米的造价为2000元,若景区准备预算资金8万元建观光通道,问:预算资金够用吗?
15.(2025春 和平区校级期末)已知向量满足.
(1)若,且,求的坐标;
(2)求;
(3)若向量与向量的夹角为锐角,求实数m的范围.
16.(2025春 青浦区校级期末)空间四边形ABCD中,E,F,G,H分别在AB,BC,CD,AD上,且满足AE:EB=CF:FB=2:1,CG:GD=AH:HD=3:1.
(1)判断四边形EFGH的形状?并说明理由.
(2)求证:EH,FG,BD三线共点.
17.(2025春 和平区校级期末)如图所示的多面体中,已知菱形ABCD和直角梯形ACEF所在的平面互相垂直,其中∠FAC为直角,∠ABC=60°,EF∥AC,EF.
(1)求证:CE∥平面BDF;
(2)求证:CE⊥BD;
(3)求多面体ABCDEF的体积.
(此题不能利用空间建系方法)
18.(2025春 和平区校级期末)如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD为菱形,∠ADC=120°,E,F分别为AB,PD的中点.已知,二面角E﹣FC﹣D的大小为60°.
(1)求PB和AD所成角的余弦值;
(2)求直线AC与平面EFC所成角的正弦值;
(3)求点B到面EFC的距离.
19.(2025春 信都区校级期末)一正三棱台木块ABC﹣A1B1C1如图所示,已知2AC=3A1C1=6,AA1=2,点O在平面ABC内且为△ABC的重心.
(1)证明:BB1∥平面OA1C1;
(2)设平面OA1C1∩平面ABC=l,试判断直线AC与l的位置关系,并给出证明;
(3)在棱台的底面A1B1C1上(包括边界)是否存在点M,使得直线OM∥平面ACC1A1?若存在,说明点M的轨迹,并进行证明;若不存在,说明理由.
20.(2025春 海安市校级期末)如图,在直三棱柱ABC﹣A1B1C1中,点D在BC上,AD⊥DC1.
(1)证明:AD⊥平面BB1C1C;
(2)若,AB⊥AC,二面角C﹣AC1﹣D的大小为.
①求AC与平面ADC1所成角的大小;
②点E在侧面ABB1A1内,且三棱锥E﹣ADC1的体积为,求E的轨迹长度.
【期末专项押题卷】解答题-2024-2025学年高一数学下学期人教A版(2019)必修第二册
参考答案与试题解析
一.解答题(共20小题)
1.(2025春 河南期末)已知复数z1=﹣1+2i,z2=﹣2﹣6i.
(1)若,求|z|;
(2)在复平面内,复数z1z2对应的向量分别是,,其中O是坐标原点,求∠AOB的大小.
【解答】解:(1)复数z1=﹣1+2i,z2=﹣2﹣6i,
则,
故|z|;
(2)复数z1z2对应的向量分别是,,其中O是坐标原点,
则,
,,
因为∠AOB∈[0,π],
所以cos∠AOB,
故∠AOB.
2.(2025春 贵州期末)已知复数z1=1+i,z2=a﹣2i(a∈R).
(1)若z1z2是纯虚数,求a的值;
(2)若复数z1z2在复平面内所对应的点位于第四象限内,求a的取值范围.
【解答】解:(1)复数z1=1+i,z2=a﹣2i,
则.
因为z1z2是纯虚数,
所以,解得a=﹣2;
(2)复数z1z2在复平面内所对应的点位于第四象限内,
则,解得﹣2<a<2,即a的取值范围为(﹣2,2).
3.(2025春 邢台校级期末)已知复数z=m﹣i(m∈R),且为纯虚数(是z的共轭复数).
(1)求实数m的值;
(2)设复数,求|z1|;
(3)复数在复平面内对应的点在第一象限,求实数a的取值范围.
【解答】解:(1)因为z=m﹣i,则,
所以,又为纯虚数,
所以m=3;
(2),
所以;
(3)因为i2025=i506×4+1=i,
所以,
因为复数在复平面内对应的点在第一象限,则,
解得,所以实数a的取值范围为.
4.(2025春 浙江期末)已知复数z=1+mi(m∈R),且(3+i)为纯虚数.
(1)求实数m及|z|;
(2)若z是关于x的方程x2+px+q=0(p,q∈R)的一个根,求2p+q的值.
【解答】解:(1)复数z=1+mi(m∈R),
则,
则
因是纯虚数,
则,得m=﹣3,
则z=1﹣3i,得.
(2)由题意可知,(1﹣3i)2+p(1﹣3i)+q=0,
则﹣8+p+q+(﹣6﹣3p)i=0,
则﹣8+p+q=0且﹣6﹣3p=0,
得p=﹣2,q=10,故2p+q=6.
5.(2025 湖南学业考试)如图是100位居民月均用水量的频率分布直方图,并据此回答下列问题.
(1)月均用水量在[2,2.5)范围内的居民有多少人?
(2)请估计居民月均用水量的众数;
(3)请估计居民月均用水量大于等于2t的概率.
【解答】解:(1)根据题意可得所求人数为100×(2.5﹣2)×0.5=25(人);
(2)估计居民月均用水量的众数为;
(3)由频率分布直方图可知,居民月均用水量大于等于2t的概率为:
(0.5+0.28+0.12)×0.5=0.45.
6.(2025春 辽宁期末)中国AI大模型正处于一个技术进步迅速、市场规模快速增长的爆发式发展阶段.为了解中国AI大模型用户的年龄分布,A公司调查了500名中国AI大模型用户,统计他们的年龄(都在[15,65]内),按照[15,25),[25,35),[35,45),[45,55),[55,65]进行分组,得到如图所示的频率分布直方图.
(1)求m的值;
(2)估计这500名中国AI大模型用户年龄的平均数(各组数据以该组区间的中点值作代表);
(3)求这500名中国AI大模型用户的年龄在[45,65]内的人数.
【解答】解:(1)由频率分布直方图得:
(0.01+0.03+0.04+m+0.005)×10=1,
解得m=0.015.
(2)由频率分布直方图得:
(20×0.01+30×0.03+40×0.04+50×0.015+60×0.005)×10=37.5,
∴估计这500名中国AI大模型用户年龄的平均数(各组数据以该组区间的中点值作代表)为37.5岁;
(3)由频率分布直方图可知中国AI大模型用户的年龄在[45,65]内的频率为:
0.15+0.05=0.2,
则这500名中国AI大模型用户的年龄在[45,65]内的人数为500×0.2=100.
7.(2025春 即墨区校级期末)某学校组织高一、高二年级学生进行了“数学与生活”的知识竞赛.从这两个年级各随机抽取了40名学生,对其成绩进行分析,得到了高一年级成绩的频率分布直方图(如图)和高二年级成绩的频数分布表(如表).
成绩分组 频数
[75,80) 2
[80,85) 6
[85,90) 16
[90,95) 14
[95,100] 2
(Ⅰ)若成绩不低于80分为“达标”,估计高一年级知识竞赛的达标率;
(Ⅱ)在抽取的学生中,从成绩为[95,100]的学生中随机选取2名学生,代表学校外出参加比赛,求这2名学生来自于同一年级的概率;
(Ⅲ)记高一年级知识竞赛成绩的中位数为a,试计算a的值.(四舍五入保留到小数点后两位小数)
【解答】解:(Ⅰ)因为高一样本中各组的频率依次为0.15,0.25,0.3,0.2,0.1,
又成绩不低于80分为“达标”,
所以计高一年级知识竞赛的达标率为1﹣0.15=0.85;
(Ⅱ)因为样本中高一成绩在[95,100]中的学生数为40×0.1=4,
样本中高二成绩在[95,100]中的学生数为2,
所以从成绩为[95,100]的6名学生中随机选取2名学生,这2名学生来自于同一年级的概率为;
(Ⅲ)因为高一样本中各组的频率依次为0.15,0.25,0.3,0.2,0.1,
所以高一年级知识竞赛成绩的中位数a∈(85,90),
所以a86.67分.
8.(2025春 和平区校级期末)在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)列出所有的可能结果;设取出的两个球上标号为相同数字为事件A,写出事件A包含的样本点集合,并求出事件A发生的概率P(A);
(2)设取出的两个球上标号之积能被3整除为事件B,求事件B发生的概率P(B).
【解答】解:由题意,设从甲、乙两个盒子中各取1个球,其数字分别为x、y,用(x,y)表示抽取结果,
可得(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),
则所有可能的结果有16种,
(1)设“取出的两个球上的标号相同”为事件A,
则A={(1,1),(2,2),(3,3),(4,4)},共4种,
故取出的两个球上的标号为相同数字的概率P(A);
(2)设“取出的两个球上标号的数字之积能被3整除”为事件B,
则B={(1,3),(3,1),(2,3),(3,2),(3,3),(3,4),(4,3)},共7种,
故取出的两个球上标号之积能被3整除的概率P(B).
9.(2025 上海)2024年东京奥运会,中国获得了男子4×100米混合泳接力金牌.以下是历届奥运会男子4×100米混合泳接力项目冠军成绩记录(单位:秒),数据按照升序排列.
206.78 207.46 207.95 209.34 209.35
210.68 213.73 214.84 216.93 216.93
(1)求这组数据的极差与中位数;
(2)从这10个数据中任选3个,求恰有2个数据在211以上的概率;
(3)若比赛成绩y关于年份x的回归方程为y=﹣0.311x,年份x的平均数为2006,预测2028年冠军队的成绩(精确到0.01秒).
【解答】解:(1)数据从小到大排列为:206.78,207.46,207.95,209.34,209.35,210.68,213.73,214.84,216.93,216.93,
所以这10个数据的极差为216.93﹣206.78=10.15,中位数为210.015.
(2)由题意知,10个数据中在211以上有4个,
从这10个数据中任选3个,求恰有2个数据在211以上的概率P.
(3)由题意知,(206.78+207.46+207.95+209.34+209.35+210.68+213.73+214.84+216.93+216.93)=211.399,
则0.311211.399+0.311×2006=835.265,
所以y=﹣0.311x+835.265,
令x=2028,得y=204.557≈204.56.
故预测2028年冠军队的成绩为204.56.
10.(2025春 驻马店期末)已知一个古典概型试验中,事件A发生的概率为,事件B发生的概率为,且事件A和事件B的并集发生的概率为.
(1)求事件A和事件B同时发生的概率P(A∩B).
(2)若事件C是事件A的对立事件,求事件C和事件B同时发生的概率P(C∩B).
(3)若事件D是事件A和事件B的交集的对立事件,求事件D发生的概率P(D).
【解答】解:(1)根据题意,,,且.
则.
(2)根据题意,因事件C是事件A的对立事件,则B=(A∩B)∪(C∩B),
依题意,事件A∩B与事件C∩B互斥,则P(B)=P(A∩B)+P(C∩B),
即,解得.
(3)根据题意,因事件D是事件A和事件B的交集的对立事件,
则.
11.(2025 重庆校级模拟)已知△ABC内角A,B,C所对的边分别为a,b,c,△ABC的面积为.
(1)求角A的大小;
(2)D为BC边上一点,DA⊥BA,且BD=3DC,求cosC.
【解答】解:(1)根据余弦定理a2=b2+c2﹣2bccosA,则a2﹣b2﹣c2=﹣2bccosA,
根据题意可知,,
故,即,所以A∈(0,π),所以;
(2)如图,过C作CE⊥AB交BA延长线于E,
因为,所以,,
因为DA⊥BA,且BD=3DC,∴AD∥EC,,
在△ABC中,,
即,,
故cosC的值为.
12.(2025 武昌区校级模拟)已知a,b,c分别为锐角△ABC三个内角A,B,C的对边,且.
(1)求A;
(2)若a=3,求△ABC周长的取值范围.
【解答】解:(1)因为,
所以由正弦定理得:,
在△ABC中,因为sinB=sin(A+C)=sinAcosC+cosAsinC,
代入上式化简得:sinC=0,
因为sinC≠0,所以,即,
因为A为锐角,所以;
(2)由正弦定理得:,
所以,,
所以
,
因为△ABC是锐角三角形,所以,
解得,所以,
即,所以,
所以,
所以△ABC周长的取值范围为.
13.(2025 山西模拟)设△ABC的内角A,B,C的对边分别为a,b,c,且满足.
(1)证明:tanA=2tanB;
(2)已知,求tanAtanBtanC取得最小值时tanB的值.
【解答】解:(1)证明:由,有,有3sinAcosB﹣3sinBcosA=sin(A+B),
有3sinAcosB﹣3sinBcosA=sinAcosB+cosAsinB,
有2sinAcosB=4sinBcosA,有tanA=2tanB;
(2),
故,令tanB=x(x≥1),
设,,
令f'(x)>0,解得,f(x)单调递增,令f'(x)<0,解得,f(x)单调递减,
综上所述,f(x)取得最小值时,,即tanAtanBtanC取得最小值时,tanB为.
14.(2025春 墨玉县期末)某景区为打造景区风景亮点,欲在一不规则湖面区域(阴影部分)上A,B两点之间建一条观光通道,如图所示.在湖面所在的平面(不考虑湖面离地平面的距离,视湖面与地平面为同一平面)内距离点B50米的点C处建一凉亭,距离点B70米的点D处再建一凉亭,测得∠ACB=∠ACD,cos∠ACB.
(1)求sin∠BDC的值;
(2)测得AC=AD,观光通道每米的造价为2000元,若景区准备预算资金8万元建观光通道,问:预算资金够用吗?
【解答】解:(1)设∠ACB=∠ACD=θ,则∠BCD=2θ∈(0°,180°),所以θ∈(0°,90°),
因为cosθ,所以,
所以,在△BCD中,由正弦定理:,
所以;
(2)由(1)知,sin,cos,sin,cos,
所以sin∠CBD=sin[π﹣(∠BCD+∠BDC)]=sin(∠BCD+∠BDC)=sin∠BCDcos∠BDC+cos∠BCDsin∠BDC,
在△BCD中,由正弦定理得:,
所以,
设AC=AD=y,在△ACD中,由余弦定理有:AD2=AC2+CD2﹣2AC CD cos∠ACD,
即,解得,
在△ABC中,由余弦定理:AB2=AC2+BC2﹣2AC BC cos∠ACD=10001500,
所以AB,
所以总造价为2000×10,所以预算资金够用.
15.(2025春 和平区校级期末)已知向量满足.
(1)若,且,求的坐标;
(2)求;
(3)若向量与向量的夹角为锐角,求实数m的范围.
【解答】解:(1)因为,,
所以,则,
所以(3,1)﹣(2,3)=(1,﹣2),
由,可设,又,则有,
解得,则或;
(2)因为,
所以;
(3)因为,,
所以,
m(2,3)+(1,﹣2)=(2m+1,3m﹣2),
因为与的夹角为锐角,则有,
即(2+m)(2m+1)+(3﹣2m)(3m﹣2)>0,
化简得2m2﹣9m+2<0,解得,
由与共线,
可得(3﹣2m)(2m+1)=(2+m)(3m﹣2),解得m=1或m=﹣1,
当m=1时,,,则,
此时与方向相同,夹角为0,不符题意,故m≠1,
综上,实数m的取值范围是.
16.(2025春 青浦区校级期末)空间四边形ABCD中,E,F,G,H分别在AB,BC,CD,AD上,且满足AE:EB=CF:FB=2:1,CG:GD=AH:HD=3:1.
(1)判断四边形EFGH的形状?并说明理由.
(2)求证:EH,FG,BD三线共点.
【解答】(1)解:四边形EFGH是梯形理由如下:在△ABC中,因为AE:EB=CF:FB=2:1,
根据平行线分线段成比例定理,可得EF∥AC.且.在△ADC中,
由于CG:GD=AH:HD=3:1,
同样依据平行线分线段成比例定理,可知GH∥AC且,
因为EF∥AC且GH∥AC,根据平行公理(平行于同一条直线的两条直线互相平行),
所以EF∥GH,EF≠GH,所以四边形EFGH是梯形.
(2)证明:由(1)知四边形EFGH是梯形,所以EH与FG相交,
设EH∩FG =P.因为面EH 平面ABD(E、H分别在AB、AD上),
P∈EH,所以P∈平面 ABD.又因为FG 平面BCD(F、G分别在BC、CD上),
P∈FG,所以P∈平面 BCD.平面ABD∩平面BCD=BD,
因为P∈平面ABD且P∈平面BCD,所以P∈BD,
即EH,FG,BD三线共点.
17.(2025春 和平区校级期末)如图所示的多面体中,已知菱形ABCD和直角梯形ACEF所在的平面互相垂直,其中∠FAC为直角,∠ABC=60°,EF∥AC,EF.
(1)求证:CE∥平面BDF;
(2)求证:CE⊥BD;
(3)求多面体ABCDEF的体积.
(此题不能利用空间建系方法)
【解答】(1)证明:连接OE,
因为四边形ABCD为菱形,且∠ABC=60°,
所以△ABC为等边三角形,即AC=AB,
又因为EF∥AC,EFABAC,
所以四边形EFCO为平行四边形,所以CE∥FO,
而CE 平面BDF,OF 平面BDF,
所以CE∥平面BDF;
(2)证明:因为平面ABCD⊥平面ACEF,∠FAC为直角,
又因为平面ABCD∩平面ACEF=AC,AF 平面ACEF,
所以AF⊥平面ABCD,
又因为BD 平面ABCD,所以BD⊥AF,
在菱形ABCD中,可得AC⊥BD,
又因为AC∩FA=A,AC,FA 平面ACEF,
所以BD⊥平面ACEF,而CE 平面ACEF,
所以CE⊥BD;
(3)由(2)可得BD⊥平面ACEF,且S梯形ACEF(EF+AC) FA(1+2) ,
菱形ABCD中,BD=2 ABsin∠2×22,
所以VABCDEF=VB﹣ACEF+VD﹣ACEFS梯形ACEF BD23.
18.(2025春 和平区校级期末)如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD为菱形,∠ADC=120°,E,F分别为AB,PD的中点.已知,二面角E﹣FC﹣D的大小为60°.
(1)求PB和AD所成角的余弦值;
(2)求直线AC与平面EFC所成角的正弦值;
(3)求点B到面EFC的距离.
【解答】解:(1)如图,连接BD,PE,由PD⊥平面ABCD,AD,CD 平面ABCD,
得PD⊥AD,PD⊥CD,
∵四边形ABCD为菱形,∴∠DAB=60°,
AB∥∥CD,故△ABD为等边三角形,
∵E为AB的中点,
∴AB⊥DE,
故DE⊥CD,DE⊥CD,PD⊥CD,DE∩PD=D,DE,PD 平面PDE,
∴CD⊥平面PDE,
∵DE 平面PDE,
得DE⊥CD,
故以D为原点,DE,DC,DP所在的直线分别为x,y,z轴,建立空间直角坐标系,
∵△ADB为正三角形,且,∴DE=3,
设PD=2a(a>0),则F(0,0,a),E(3,0,0),,P(0,0,2a),,,
∴,,
由题意得,平面FCD的一个法向量为,
设平面EFC的法向量为,
则
取x=2a,可得,
,
解得a=2,∴,,
∴,
即PB和AD所成角的余弦值为;
(2)设直线AC与平面EFC所成的角为θ,
由(1)知,平面EFC的法向量为,,
∴,
即直线AC与平面EFC所成角的正弦值为;
(3)∵,
由(2)知平面EFC为,
故点B到面EFC的距离.
19.(2025春 信都区校级期末)一正三棱台木块ABC﹣A1B1C1如图所示,已知2AC=3A1C1=6,AA1=2,点O在平面ABC内且为△ABC的重心.
(1)证明:BB1∥平面OA1C1;
(2)设平面OA1C1∩平面ABC=l,试判断直线AC与l的位置关系,并给出证明;
(3)在棱台的底面A1B1C1上(包括边界)是否存在点M,使得直线OM∥平面ACC1A1?若存在,说明点M的轨迹,并进行证明;若不存在,说明理由.
【解答】解:(1)证明,如图所示:
设A1C1,AC的中点分别为F、G,
易得B1F∥BG,又2AC=3A1C1=6,
所以,,
又点O为△ABC的重心,
所以,
所以B1F与BO平行且相等,
从而可得BB1∥OF,又BB1 平面OA1C1,OF 平面OA1C1,
所以BB1∥平面OA1C1;
(2)证明:直线AC与l平行,证明如下:
因为AC∥A1C1,AC 平面OA1C1,A1C1 平面OA1C1,
所以AC∥平面OA1C1,又AC 平面ABC,平面ABC∩平面OA1C1=l,
所以AC∥l;
(3)分别取B1C1、A1B1的中点K、L,则当点M∈KL时,有OM∥平面ACC1A1,
证明如下:
因为K、L分别为B1C1、A1B1的中点,所以KL∥A1C1,
过点O作AC的平行线交BC、BA于D、E两点,
因为DE∥AC,A1C1∥AC,所以KL∥DE,所以D、E、K、L四点共面,
又2AC=3A1C1,点O为重心,
所以,
又由正三棱台ABC﹣A1B1C1性质CE∥C1K,
所以四边形CEMC1为平行四边形,所以EK∥CC1,
又EK 平面ACC1A1、CC1 平面ACC1A1,
所以EK∥平面ACC1A1,同理DE∥平面ACC1A1,
又DE∩EK=E,DE、EK 平面DEKL,
所以平面DEKL∥平面ACC1A1,当点M∈KL时,OM 平面DEKL,
所以OM∥平面ACC1A1.
20.(2025春 海安市校级期末)如图,在直三棱柱ABC﹣A1B1C1中,点D在BC上,AD⊥DC1.
(1)证明:AD⊥平面BB1C1C;
(2)若,AB⊥AC,二面角C﹣AC1﹣D的大小为.
①求AC与平面ADC1所成角的大小;
②点E在侧面ABB1A1内,且三棱锥E﹣ADC1的体积为,求E的轨迹长度.
【解答】解:(1)证明:在直三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,
因为AD 平面ABC,所以CC1⊥AD.
又因为AD⊥DC1,CC1∩DC1=C1,CC1,DC 平面BB1C1C,
所以AD⊥平面BB1C1C.
(2)①作CG⊥DC1于G,作GH⊥AC1于H,连接CH,
由(1)知AD⊥平面BB1CC1,
因为AD 平面ADC1,所以平面ADC1⊥平面BB1CC1,
因为平面ADC1∩平面BB1CC1=DC1,CG 平面BB1CC1,CG⊥DC1,
所以CG⊥平面ADC1,
所以AC与平面ADC1所成角正弦值为cos∠ACG,
因为AC1 平面ADC1,所以CG⊥AC1,
因为GH⊥AC1,GHOCG=G,GH,CH 平面CGH,
所以AC1⊥平面CGH,因为CH 平面CGH,
所以AC1⊥CH,
所以平面ADC1与平面DAC1所成二面角即∠CHG,
设CC1为x,因为,AB⊥AC,所以△ABC为等腰直角三角形,
因为AD⊥DC,所以BD=CD=2,
因为,所以,
同理,
在Rt△HGC中,,
解得x=2,所以,
设AC与平面ADC1所成角为θ,
在Rt△ACG中,.
因为,所以;
②设E到平面ADC1距离为d,
因为,
所以,
取B1C1中点E,连接B1D,BE,AE,
因为C1E,BD平行且相等,
所以四边形C1EBD为平行四边形,
因为BE∥DC1,BE 平面ADC1,DC1 平面ADC1,
所以BE∥平面ADC1,
同理AE∥平面ADC1,
因为BE∩AE=E,BE、AE 平面ABE,
所以平面ADC1∥平面ABE,
所以平面ADC1与平面ABE间距离为E到平面ADC1距离,
因为B1BDE为正方形,所以B1D⊥BE,因为BE∥DC1,所以B1D⊥DC1,
因为AD⊥平面BB1CC1,B1D 平面BB1CC1,
所以AD⊥B1D,
因为AD∩DC1=D,DC1,AD 平面ADC1,
所以B1D⊥平面ADC1,因为E为B1C1中点,
所以E到平面ADC1距离为.
所以E点轨迹长度即线段A1B长度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【期末专项押题卷】解答题-2024-2025学年高一数学下学期人教A版(2019)必修第二册
1.(2025春 河南期末)已知复数z1=﹣1+2i,z2=﹣2﹣6i.
(1)若,求|z|;
(2)在复平面内,复数z1z2对应的向量分别是,,其中O是坐标原点,求∠AOB的大小.
2.(2025春 贵州期末)已知复数z1=1+i,z2=a﹣2i(a∈R).
(1)若z1z2是纯虚数,求a的值;
(2)若复数z1z2在复平面内所对应的点位于第四象限内,求a的取值范围.
3.(2025春 邢台校级期末)已知复数z=m﹣i(m∈R),且为纯虚数(是z的共轭复数).
(1)求实数m的值;
(2)设复数,求|z1|;
(3)复数在复平面内对应的点在第一象限,求实数a的取值范围.
4.(2025春 浙江期末)已知复数z=1+mi(m∈R),且(3+i)为纯虚数.
(1)求实数m及|z|;
(2)若z是关于x的方程x2+px+q=0(p,q∈R)的一个根,求2p+q的值.
5.(2025 湖南学业考试)如图是100位居民月均用水量的频率分布直方图,并据此回答下列问题.
(1)月均用水量在[2,2.5)范围内的居民有多少人?
(2)请估计居民月均用水量的众数;
(3)请估计居民月均用水量大于等于2t的概率.
6.(2025春 辽宁期末)中国AI大模型正处于一个技术进步迅速、市场规模快速增长的爆发式发展阶段.为了解中国AI大模型用户的年龄分布,A公司调查了500名中国AI大模型用户,统计他们的年龄(都在[15,65]内),按照[15,25),[25,35),[35,45),[45,55),[55,65]进行分组,得到如图所示的频率分布直方图.
(1)求m的值;
(2)估计这500名中国AI大模型用户年龄的平均数(各组数据以该组区间的中点值作代表);
(3)求这500名中国AI大模型用户的年龄在[45,65]内的人数.
7.(2025春 即墨区校级期末)某学校组织高一、高二年级学生进行了“数学与生活”的知识竞赛.从这两个年级各随机抽取了40名学生,对其成绩进行分析,得到了高一年级成绩的频率分布直方图(如图)和高二年级成绩的频数分布表(如表).
成绩分组 频数
[75,80) 2
[80,85) 6
[85,90) 16
[90,95) 14
[95,100] 2
(Ⅰ)若成绩不低于80分为“达标”,估计高一年级知识竞赛的达标率;
(Ⅱ)在抽取的学生中,从成绩为[95,100]的学生中随机选取2名学生,代表学校外出参加比赛,求这2名学生来自于同一年级的概率;
(Ⅲ)记高一年级知识竞赛成绩的中位数为a,试计算a的值.(四舍五入保留到小数点后两位小数)
8.(2025春 和平区校级期末)在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)列出所有的可能结果;设取出的两个球上标号为相同数字为事件A,写出事件A包含的样本点集合,并求出事件A发生的概率P(A);
(2)设取出的两个球上标号之积能被3整除为事件B,求事件B发生的概率P(B).
9.(2025 上海)2024年东京奥运会,中国获得了男子4×100米混合泳接力金牌.以下是历届奥运会男子4×100米混合泳接力项目冠军成绩记录(单位:秒),数据按照升序排列.
206.78 207.46 207.95 209.34 209.35
210.68 213.73 214.84 216.93 216.93
(1)求这组数据的极差与中位数;
(2)从这10个数据中任选3个,求恰有2个数据在211以上的概率;
(3)若比赛成绩y关于年份x的回归方程为y=﹣0.311x,年份x的平均数为2006,预测2028年冠军队的成绩(精确到0.01秒).
10.(2025春 驻马店期末)已知一个古典概型试验中,事件A发生的概率为,事件B发生的概率为,且事件A和事件B的并集发生的概率为.
(1)求事件A和事件B同时发生的概率P(A∩B).
(2)若事件C是事件A的对立事件,求事件C和事件B同时发生的概率P(C∩B).
(3)若事件D是事件A和事件B的交集的对立事件,求事件D发生的概率P(D).
11.(2025 重庆校级模拟)已知△ABC内角A,B,C所对的边分别为a,b,c,△ABC的面积为.
(1)求角A的大小;
(2)D为BC边上一点,DA⊥BA,且BD=3DC,求cosC.
12.(2025 武昌区校级模拟)已知a,b,c分别为锐角△ABC三个内角A,B,C的对边,且.
(1)求A;
(2)若a=3,求△ABC周长的取值范围.
13.(2025 山西模拟)设△ABC的内角A,B,C的对边分别为a,b,c,且满足.
(1)证明:tanA=2tanB;
(2)已知,求tanAtanBtanC取得最小值时tanB的值.
14.(2025春 墨玉县期末)某景区为打造景区风景亮点,欲在一不规则湖面区域(阴影部分)上A,B两点之间建一条观光通道,如图所示.在湖面所在的平面(不考虑湖面离地平面的距离,视湖面与地平面为同一平面)内距离点B50米的点C处建一凉亭,距离点B70米的点D处再建一凉亭,测得∠ACB=∠ACD,cos∠ACB.
(1)求sin∠BDC的值;
(2)测得AC=AD,观光通道每米的造价为2000元,若景区准备预算资金8万元建观光通道,问:预算资金够用吗?
15.(2025春 和平区校级期末)已知向量满足.
(1)若,且,求的坐标;
(2)求;
(3)若向量与向量的夹角为锐角,求实数m的范围.
16.(2025春 青浦区校级期末)空间四边形ABCD中,E,F,G,H分别在AB,BC,CD,AD上,且满足AE:EB=CF:FB=2:1,CG:GD=AH:HD=3:1.
(1)判断四边形EFGH的形状?并说明理由.
(2)求证:EH,FG,BD三线共点.
17.(2025春 和平区校级期末)如图所示的多面体中,已知菱形ABCD和直角梯形ACEF所在的平面互相垂直,其中∠FAC为直角,∠ABC=60°,EF∥AC,EF.
(1)求证:CE∥平面BDF;
(2)求证:CE⊥BD;
(3)求多面体ABCDEF的体积.
(此题不能利用空间建系方法)
18.(2025春 和平区校级期末)如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD为菱形,∠ADC=120°,E,F分别为AB,PD的中点.已知,二面角E﹣FC﹣D的大小为60°.
(1)求PB和AD所成角的余弦值;
(2)求直线AC与平面EFC所成角的正弦值;
(3)求点B到面EFC的距离.
19.(2025春 信都区校级期末)一正三棱台木块ABC﹣A1B1C1如图所示,已知2AC=3A1C1=6,AA1=2,点O在平面ABC内且为△ABC的重心.
(1)证明:BB1∥平面OA1C1;
(2)设平面OA1C1∩平面ABC=l,试判断直线AC与l的位置关系,并给出证明;
(3)在棱台的底面A1B1C1上(包括边界)是否存在点M,使得直线OM∥平面ACC1A1?若存在,说明点M的轨迹,并进行证明;若不存在,说明理由.
20.(2025春 海安市校级期末)如图,在直三棱柱ABC﹣A1B1C1中,点D在BC上,AD⊥DC1.
(1)证明:AD⊥平面BB1C1C;
(2)若,AB⊥AC,二面角C﹣AC1﹣D的大小为.
①求AC与平面ADC1所成角的大小;
②点E在侧面ABB1A1内,且三棱锥E﹣ADC1的体积为,求E的轨迹长度.
【期末专项押题卷】解答题-2024-2025学年高一数学下学期人教A版(2019)必修第二册
参考答案与试题解析
一.解答题(共20小题)
1.(2025春 河南期末)已知复数z1=﹣1+2i,z2=﹣2﹣6i.
(1)若,求|z|;
(2)在复平面内,复数z1z2对应的向量分别是,,其中O是坐标原点,求∠AOB的大小.
【解答】解:(1)复数z1=﹣1+2i,z2=﹣2﹣6i,
则,
故|z|;
(2)复数z1z2对应的向量分别是,,其中O是坐标原点,
则,
,,
因为∠AOB∈[0,π],
所以cos∠AOB,
故∠AOB.
2.(2025春 贵州期末)已知复数z1=1+i,z2=a﹣2i(a∈R).
(1)若z1z2是纯虚数,求a的值;
(2)若复数z1z2在复平面内所对应的点位于第四象限内,求a的取值范围.
【解答】解:(1)复数z1=1+i,z2=a﹣2i,
则.
因为z1z2是纯虚数,
所以,解得a=﹣2;
(2)复数z1z2在复平面内所对应的点位于第四象限内,
则,解得﹣2<a<2,即a的取值范围为(﹣2,2).
3.(2025春 邢台校级期末)已知复数z=m﹣i(m∈R),且为纯虚数(是z的共轭复数).
(1)求实数m的值;
(2)设复数,求|z1|;
(3)复数在复平面内对应的点在第一象限,求实数a的取值范围.
【解答】解:(1)因为z=m﹣i,则,
所以,又为纯虚数,
所以m=3;
(2),
所以;
(3)因为i2025=i506×4+1=i,
所以,
因为复数在复平面内对应的点在第一象限,则,
解得,所以实数a的取值范围为.
4.(2025春 浙江期末)已知复数z=1+mi(m∈R),且(3+i)为纯虚数.
(1)求实数m及|z|;
(2)若z是关于x的方程x2+px+q=0(p,q∈R)的一个根,求2p+q的值.
【解答】解:(1)复数z=1+mi(m∈R),
则,
则
因是纯虚数,
则,得m=﹣3,
则z=1﹣3i,得.
(2)由题意可知,(1﹣3i)2+p(1﹣3i)+q=0,
则﹣8+p+q+(﹣6﹣3p)i=0,
则﹣8+p+q=0且﹣6﹣3p=0,
得p=﹣2,q=10,故2p+q=6.
5.(2025 湖南学业考试)如图是100位居民月均用水量的频率分布直方图,并据此回答下列问题.
(1)月均用水量在[2,2.5)范围内的居民有多少人?
(2)请估计居民月均用水量的众数;
(3)请估计居民月均用水量大于等于2t的概率.
【解答】解:(1)根据题意可得所求人数为100×(2.5﹣2)×0.5=25(人);
(2)估计居民月均用水量的众数为;
(3)由频率分布直方图可知,居民月均用水量大于等于2t的概率为:
(0.5+0.28+0.12)×0.5=0.45.
6.(2025春 辽宁期末)中国AI大模型正处于一个技术进步迅速、市场规模快速增长的爆发式发展阶段.为了解中国AI大模型用户的年龄分布,A公司调查了500名中国AI大模型用户,统计他们的年龄(都在[15,65]内),按照[15,25),[25,35),[35,45),[45,55),[55,65]进行分组,得到如图所示的频率分布直方图.
(1)求m的值;
(2)估计这500名中国AI大模型用户年龄的平均数(各组数据以该组区间的中点值作代表);
(3)求这500名中国AI大模型用户的年龄在[45,65]内的人数.
【解答】解:(1)由频率分布直方图得:
(0.01+0.03+0.04+m+0.005)×10=1,
解得m=0.015.
(2)由频率分布直方图得:
(20×0.01+30×0.03+40×0.04+50×0.015+60×0.005)×10=37.5,
∴估计这500名中国AI大模型用户年龄的平均数(各组数据以该组区间的中点值作代表)为37.5岁;
(3)由频率分布直方图可知中国AI大模型用户的年龄在[45,65]内的频率为:
0.15+0.05=0.2,
则这500名中国AI大模型用户的年龄在[45,65]内的人数为500×0.2=100.
7.(2025春 即墨区校级期末)某学校组织高一、高二年级学生进行了“数学与生活”的知识竞赛.从这两个年级各随机抽取了40名学生,对其成绩进行分析,得到了高一年级成绩的频率分布直方图(如图)和高二年级成绩的频数分布表(如表).
成绩分组 频数
[75,80) 2
[80,85) 6
[85,90) 16
[90,95) 14
[95,100] 2
(Ⅰ)若成绩不低于80分为“达标”,估计高一年级知识竞赛的达标率;
(Ⅱ)在抽取的学生中,从成绩为[95,100]的学生中随机选取2名学生,代表学校外出参加比赛,求这2名学生来自于同一年级的概率;
(Ⅲ)记高一年级知识竞赛成绩的中位数为a,试计算a的值.(四舍五入保留到小数点后两位小数)
【解答】解:(Ⅰ)因为高一样本中各组的频率依次为0.15,0.25,0.3,0.2,0.1,
又成绩不低于80分为“达标”,
所以计高一年级知识竞赛的达标率为1﹣0.15=0.85;
(Ⅱ)因为样本中高一成绩在[95,100]中的学生数为40×0.1=4,
样本中高二成绩在[95,100]中的学生数为2,
所以从成绩为[95,100]的6名学生中随机选取2名学生,这2名学生来自于同一年级的概率为;
(Ⅲ)因为高一样本中各组的频率依次为0.15,0.25,0.3,0.2,0.1,
所以高一年级知识竞赛成绩的中位数a∈(85,90),
所以a86.67分.
8.(2025春 和平区校级期末)在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)列出所有的可能结果;设取出的两个球上标号为相同数字为事件A,写出事件A包含的样本点集合,并求出事件A发生的概率P(A);
(2)设取出的两个球上标号之积能被3整除为事件B,求事件B发生的概率P(B).
【解答】解:由题意,设从甲、乙两个盒子中各取1个球,其数字分别为x、y,用(x,y)表示抽取结果,
可得(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),
则所有可能的结果有16种,
(1)设“取出的两个球上的标号相同”为事件A,
则A={(1,1),(2,2),(3,3),(4,4)},共4种,
故取出的两个球上的标号为相同数字的概率P(A);
(2)设“取出的两个球上标号的数字之积能被3整除”为事件B,
则B={(1,3),(3,1),(2,3),(3,2),(3,3),(3,4),(4,3)},共7种,
故取出的两个球上标号之积能被3整除的概率P(B).
9.(2025 上海)2024年东京奥运会,中国获得了男子4×100米混合泳接力金牌.以下是历届奥运会男子4×100米混合泳接力项目冠军成绩记录(单位:秒),数据按照升序排列.
206.78 207.46 207.95 209.34 209.35
210.68 213.73 214.84 216.93 216.93
(1)求这组数据的极差与中位数;
(2)从这10个数据中任选3个,求恰有2个数据在211以上的概率;
(3)若比赛成绩y关于年份x的回归方程为y=﹣0.311x,年份x的平均数为2006,预测2028年冠军队的成绩(精确到0.01秒).
【解答】解:(1)数据从小到大排列为:206.78,207.46,207.95,209.34,209.35,210.68,213.73,214.84,216.93,216.93,
所以这10个数据的极差为216.93﹣206.78=10.15,中位数为210.015.
(2)由题意知,10个数据中在211以上有4个,
从这10个数据中任选3个,求恰有2个数据在211以上的概率P.
(3)由题意知,(206.78+207.46+207.95+209.34+209.35+210.68+213.73+214.84+216.93+216.93)=211.399,
则0.311211.399+0.311×2006=835.265,
所以y=﹣0.311x+835.265,
令x=2028,得y=204.557≈204.56.
故预测2028年冠军队的成绩为204.56.
10.(2025春 驻马店期末)已知一个古典概型试验中,事件A发生的概率为,事件B发生的概率为,且事件A和事件B的并集发生的概率为.
(1)求事件A和事件B同时发生的概率P(A∩B).
(2)若事件C是事件A的对立事件,求事件C和事件B同时发生的概率P(C∩B).
(3)若事件D是事件A和事件B的交集的对立事件,求事件D发生的概率P(D).
【解答】解:(1)根据题意,,,且.
则.
(2)根据题意,因事件C是事件A的对立事件,则B=(A∩B)∪(C∩B),
依题意,事件A∩B与事件C∩B互斥,则P(B)=P(A∩B)+P(C∩B),
即,解得.
(3)根据题意,因事件D是事件A和事件B的交集的对立事件,
则.
11.(2025 重庆校级模拟)已知△ABC内角A,B,C所对的边分别为a,b,c,△ABC的面积为.
(1)求角A的大小;
(2)D为BC边上一点,DA⊥BA,且BD=3DC,求cosC.
【解答】解:(1)根据余弦定理a2=b2+c2﹣2bccosA,则a2﹣b2﹣c2=﹣2bccosA,
根据题意可知,,
故,即,所以A∈(0,π),所以;
(2)如图,过C作CE⊥AB交BA延长线于E,
因为,所以,,
因为DA⊥BA,且BD=3DC,∴AD∥EC,,
在△ABC中,,
即,,
故cosC的值为.
12.(2025 武昌区校级模拟)已知a,b,c分别为锐角△ABC三个内角A,B,C的对边,且.
(1)求A;
(2)若a=3,求△ABC周长的取值范围.
【解答】解:(1)因为,
所以由正弦定理得:,
在△ABC中,因为sinB=sin(A+C)=sinAcosC+cosAsinC,
代入上式化简得:sinC=0,
因为sinC≠0,所以,即,
因为A为锐角,所以;
(2)由正弦定理得:,
所以,,
所以
,
因为△ABC是锐角三角形,所以,
解得,所以,
即,所以,
所以,
所以△ABC周长的取值范围为.
13.(2025 山西模拟)设△ABC的内角A,B,C的对边分别为a,b,c,且满足.
(1)证明:tanA=2tanB;
(2)已知,求tanAtanBtanC取得最小值时tanB的值.
【解答】解:(1)证明:由,有,有3sinAcosB﹣3sinBcosA=sin(A+B),
有3sinAcosB﹣3sinBcosA=sinAcosB+cosAsinB,
有2sinAcosB=4sinBcosA,有tanA=2tanB;
(2),
故,令tanB=x(x≥1),
设,,
令f'(x)>0,解得,f(x)单调递增,令f'(x)<0,解得,f(x)单调递减,
综上所述,f(x)取得最小值时,,即tanAtanBtanC取得最小值时,tanB为.
14.(2025春 墨玉县期末)某景区为打造景区风景亮点,欲在一不规则湖面区域(阴影部分)上A,B两点之间建一条观光通道,如图所示.在湖面所在的平面(不考虑湖面离地平面的距离,视湖面与地平面为同一平面)内距离点B50米的点C处建一凉亭,距离点B70米的点D处再建一凉亭,测得∠ACB=∠ACD,cos∠ACB.
(1)求sin∠BDC的值;
(2)测得AC=AD,观光通道每米的造价为2000元,若景区准备预算资金8万元建观光通道,问:预算资金够用吗?
【解答】解:(1)设∠ACB=∠ACD=θ,则∠BCD=2θ∈(0°,180°),所以θ∈(0°,90°),
因为cosθ,所以,
所以,在△BCD中,由正弦定理:,
所以;
(2)由(1)知,sin,cos,sin,cos,
所以sin∠CBD=sin[π﹣(∠BCD+∠BDC)]=sin(∠BCD+∠BDC)=sin∠BCDcos∠BDC+cos∠BCDsin∠BDC,
在△BCD中,由正弦定理得:,
所以,
设AC=AD=y,在△ACD中,由余弦定理有:AD2=AC2+CD2﹣2AC CD cos∠ACD,
即,解得,
在△ABC中,由余弦定理:AB2=AC2+BC2﹣2AC BC cos∠ACD=10001500,
所以AB,
所以总造价为2000×10,所以预算资金够用.
15.(2025春 和平区校级期末)已知向量满足.
(1)若,且,求的坐标;
(2)求;
(3)若向量与向量的夹角为锐角,求实数m的范围.
【解答】解:(1)因为,,
所以,则,
所以(3,1)﹣(2,3)=(1,﹣2),
由,可设,又,则有,
解得,则或;
(2)因为,
所以;
(3)因为,,
所以,
m(2,3)+(1,﹣2)=(2m+1,3m﹣2),
因为与的夹角为锐角,则有,
即(2+m)(2m+1)+(3﹣2m)(3m﹣2)>0,
化简得2m2﹣9m+2<0,解得,
由与共线,
可得(3﹣2m)(2m+1)=(2+m)(3m﹣2),解得m=1或m=﹣1,
当m=1时,,,则,
此时与方向相同,夹角为0,不符题意,故m≠1,
综上,实数m的取值范围是.
16.(2025春 青浦区校级期末)空间四边形ABCD中,E,F,G,H分别在AB,BC,CD,AD上,且满足AE:EB=CF:FB=2:1,CG:GD=AH:HD=3:1.
(1)判断四边形EFGH的形状?并说明理由.
(2)求证:EH,FG,BD三线共点.
【解答】(1)解:四边形EFGH是梯形理由如下:在△ABC中,因为AE:EB=CF:FB=2:1,
根据平行线分线段成比例定理,可得EF∥AC.且.在△ADC中,
由于CG:GD=AH:HD=3:1,
同样依据平行线分线段成比例定理,可知GH∥AC且,
因为EF∥AC且GH∥AC,根据平行公理(平行于同一条直线的两条直线互相平行),
所以EF∥GH,EF≠GH,所以四边形EFGH是梯形.
(2)证明:由(1)知四边形EFGH是梯形,所以EH与FG相交,
设EH∩FG =P.因为面EH 平面ABD(E、H分别在AB、AD上),
P∈EH,所以P∈平面 ABD.又因为FG 平面BCD(F、G分别在BC、CD上),
P∈FG,所以P∈平面 BCD.平面ABD∩平面BCD=BD,
因为P∈平面ABD且P∈平面BCD,所以P∈BD,
即EH,FG,BD三线共点.
17.(2025春 和平区校级期末)如图所示的多面体中,已知菱形ABCD和直角梯形ACEF所在的平面互相垂直,其中∠FAC为直角,∠ABC=60°,EF∥AC,EF.
(1)求证:CE∥平面BDF;
(2)求证:CE⊥BD;
(3)求多面体ABCDEF的体积.
(此题不能利用空间建系方法)
【解答】(1)证明:连接OE,
因为四边形ABCD为菱形,且∠ABC=60°,
所以△ABC为等边三角形,即AC=AB,
又因为EF∥AC,EFABAC,
所以四边形EFCO为平行四边形,所以CE∥FO,
而CE 平面BDF,OF 平面BDF,
所以CE∥平面BDF;
(2)证明:因为平面ABCD⊥平面ACEF,∠FAC为直角,
又因为平面ABCD∩平面ACEF=AC,AF 平面ACEF,
所以AF⊥平面ABCD,
又因为BD 平面ABCD,所以BD⊥AF,
在菱形ABCD中,可得AC⊥BD,
又因为AC∩FA=A,AC,FA 平面ACEF,
所以BD⊥平面ACEF,而CE 平面ACEF,
所以CE⊥BD;
(3)由(2)可得BD⊥平面ACEF,且S梯形ACEF(EF+AC) FA(1+2) ,
菱形ABCD中,BD=2 ABsin∠2×22,
所以VABCDEF=VB﹣ACEF+VD﹣ACEFS梯形ACEF BD23.
18.(2025春 和平区校级期末)如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD为菱形,∠ADC=120°,E,F分别为AB,PD的中点.已知,二面角E﹣FC﹣D的大小为60°.
(1)求PB和AD所成角的余弦值;
(2)求直线AC与平面EFC所成角的正弦值;
(3)求点B到面EFC的距离.
【解答】解:(1)如图,连接BD,PE,由PD⊥平面ABCD,AD,CD 平面ABCD,
得PD⊥AD,PD⊥CD,
∵四边形ABCD为菱形,∴∠DAB=60°,
AB∥∥CD,故△ABD为等边三角形,
∵E为AB的中点,
∴AB⊥DE,
故DE⊥CD,DE⊥CD,PD⊥CD,DE∩PD=D,DE,PD 平面PDE,
∴CD⊥平面PDE,
∵DE 平面PDE,
得DE⊥CD,
故以D为原点,DE,DC,DP所在的直线分别为x,y,z轴,建立空间直角坐标系,
∵△ADB为正三角形,且,∴DE=3,
设PD=2a(a>0),则F(0,0,a),E(3,0,0),,P(0,0,2a),,,
∴,,
由题意得,平面FCD的一个法向量为,
设平面EFC的法向量为,
则
取x=2a,可得,
,
解得a=2,∴,,
∴,
即PB和AD所成角的余弦值为;
(2)设直线AC与平面EFC所成的角为θ,
由(1)知,平面EFC的法向量为,,
∴,
即直线AC与平面EFC所成角的正弦值为;
(3)∵,
由(2)知平面EFC为,
故点B到面EFC的距离.
19.(2025春 信都区校级期末)一正三棱台木块ABC﹣A1B1C1如图所示,已知2AC=3A1C1=6,AA1=2,点O在平面ABC内且为△ABC的重心.
(1)证明:BB1∥平面OA1C1;
(2)设平面OA1C1∩平面ABC=l,试判断直线AC与l的位置关系,并给出证明;
(3)在棱台的底面A1B1C1上(包括边界)是否存在点M,使得直线OM∥平面ACC1A1?若存在,说明点M的轨迹,并进行证明;若不存在,说明理由.
【解答】解:(1)证明,如图所示:
设A1C1,AC的中点分别为F、G,
易得B1F∥BG,又2AC=3A1C1=6,
所以,,
又点O为△ABC的重心,
所以,
所以B1F与BO平行且相等,
从而可得BB1∥OF,又BB1 平面OA1C1,OF 平面OA1C1,
所以BB1∥平面OA1C1;
(2)证明:直线AC与l平行,证明如下:
因为AC∥A1C1,AC 平面OA1C1,A1C1 平面OA1C1,
所以AC∥平面OA1C1,又AC 平面ABC,平面ABC∩平面OA1C1=l,
所以AC∥l;
(3)分别取B1C1、A1B1的中点K、L,则当点M∈KL时,有OM∥平面ACC1A1,
证明如下:
因为K、L分别为B1C1、A1B1的中点,所以KL∥A1C1,
过点O作AC的平行线交BC、BA于D、E两点,
因为DE∥AC,A1C1∥AC,所以KL∥DE,所以D、E、K、L四点共面,
又2AC=3A1C1,点O为重心,
所以,
又由正三棱台ABC﹣A1B1C1性质CE∥C1K,
所以四边形CEMC1为平行四边形,所以EK∥CC1,
又EK 平面ACC1A1、CC1 平面ACC1A1,
所以EK∥平面ACC1A1,同理DE∥平面ACC1A1,
又DE∩EK=E,DE、EK 平面DEKL,
所以平面DEKL∥平面ACC1A1,当点M∈KL时,OM 平面DEKL,
所以OM∥平面ACC1A1.
20.(2025春 海安市校级期末)如图,在直三棱柱ABC﹣A1B1C1中,点D在BC上,AD⊥DC1.
(1)证明:AD⊥平面BB1C1C;
(2)若,AB⊥AC,二面角C﹣AC1﹣D的大小为.
①求AC与平面ADC1所成角的大小;
②点E在侧面ABB1A1内,且三棱锥E﹣ADC1的体积为,求E的轨迹长度.
【解答】解:(1)证明:在直三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,
因为AD 平面ABC,所以CC1⊥AD.
又因为AD⊥DC1,CC1∩DC1=C1,CC1,DC 平面BB1C1C,
所以AD⊥平面BB1C1C.
(2)①作CG⊥DC1于G,作GH⊥AC1于H,连接CH,
由(1)知AD⊥平面BB1CC1,
因为AD 平面ADC1,所以平面ADC1⊥平面BB1CC1,
因为平面ADC1∩平面BB1CC1=DC1,CG 平面BB1CC1,CG⊥DC1,
所以CG⊥平面ADC1,
所以AC与平面ADC1所成角正弦值为cos∠ACG,
因为AC1 平面ADC1,所以CG⊥AC1,
因为GH⊥AC1,GHOCG=G,GH,CH 平面CGH,
所以AC1⊥平面CGH,因为CH 平面CGH,
所以AC1⊥CH,
所以平面ADC1与平面DAC1所成二面角即∠CHG,
设CC1为x,因为,AB⊥AC,所以△ABC为等腰直角三角形,
因为AD⊥DC,所以BD=CD=2,
因为,所以,
同理,
在Rt△HGC中,,
解得x=2,所以,
设AC与平面ADC1所成角为θ,
在Rt△ACG中,.
因为,所以;
②设E到平面ADC1距离为d,
因为,
所以,
取B1C1中点E,连接B1D,BE,AE,
因为C1E,BD平行且相等,
所以四边形C1EBD为平行四边形,
因为BE∥DC1,BE 平面ADC1,DC1 平面ADC1,
所以BE∥平面ADC1,
同理AE∥平面ADC1,
因为BE∩AE=E,BE、AE 平面ABE,
所以平面ADC1∥平面ABE,
所以平面ADC1与平面ABE间距离为E到平面ADC1距离,
因为B1BDE为正方形,所以B1D⊥BE,因为BE∥DC1,所以B1D⊥DC1,
因为AD⊥平面BB1CC1,B1D 平面BB1CC1,
所以AD⊥B1D,
因为AD∩DC1=D,DC1,AD 平面ADC1,
所以B1D⊥平面ADC1,因为E为B1C1中点,
所以E到平面ADC1距离为.
所以E点轨迹长度即线段A1B长度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
