【期末专项押题卷】填空题-2024-2025学年高一数学下学期人教A版(2019)必修第二册(含解析)
文档属性
| 名称 | 【期末专项押题卷】填空题-2024-2025学年高一数学下学期人教A版(2019)必修第二册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 463.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 11:06:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【期末专项押题卷】填空题-2024-2025学年高一数学下学期人教A版(2019)必修第二册
1.(2025 天津)已知i是虚数单位,则||= .
2.(2025 上海)已知复数z满足z2=()2,|z|≤1,则|z﹣2﹣3i|的最小值是 .
3.(2025 金凤区校级模拟)已知复数z=(1﹣a2)+(a+1)i(i∈R)为纯虚数,则a= .
4.(2025春 和平区校级月考)设m∈R,复数z=(m2﹣2m﹣3)+(2m2+m﹣1)i,若z为纯虚数,则m= .
5.(2025春 广东月考)已知复数,则|z|的最小值为 .
6.(2025 信阳二模)已知从小到大排列的一组数据:1,5,a,10,11,13,15,21,42,57,若这组数据的极差是其第30百分位数的7倍,则a的值为 .
7.(2025 上海模拟)现有如下10个数据:296,301,305,293,293,305,302,303,306,294,则这批数据的第25百分位数为 .
8.(2025春 七里河区校级期中)已知某地区有小学生12000人,初中生11000人,高中生9000人,现在要了解该地区学生的近视情况,准备抽取320人进行调查,则应该抽取小学生、初中生、高中生的人数分别是 .
9.(2025春 滨海新区校级期中)某校学生高一年级有880人,高二年级有800人,高三年级有720人,现用分层随机抽样方法共选取n名学生进行竞赛答题,已知高三年级选出9名选手,则n= ;选出的高三年级9名选手分别答对题目数量为:2,3,7,5,1,6,8,3,8,则这组数据的第60百分位数为 .
10.(2025春 保定月考)若数据x1,x2, ,x10的平均数为3,方差为4,则数据4x1+1,4x2+1, ,4x10+1的平均数为 方差为 .
11.(2025 重庆校级模拟)盒子中有8个除颜色外均相同的小球,其中红球和黑球各有2个,白球有4个.现从中不放回的每次抽出一个,则前两次均抽出红球的概率为 ;若一直抽取直到小球全部抽完为止,则红球最先被抽完的概率为 .
12.(2025春 长沙月考)在平面直角坐标系中,一个质点在随机外力的作用下,从原点O出发,每隔1秒等可能地向上、下、左、右四个方向移动1个单位.若第5秒时该质点在(1,0)处,则在此前的运动过程中,质点经过(0,1)处的概率为 .
13.(2025春 朝阳月考)已知事件A,B相互独立,且P(A)=p,,则当p= 时,P(AB)取得最大值,最大值为 .
14.(2025 赤峰模拟)小张连续9天去快递店拿快递的个数依次为3,1,5,2,3,4,1,4,6.若从这组数据中随机删除1个数后,得到一组新数据,则这组新数据的中位数与原数据的中位数相等的概率为 .
15.(2025 天宁区校级三模)10名象棋选手进行单循环赛(即每两名选手比赛一场).规定两人对局胜者得2分,平局各得1分,负者得0分,并按总得分由高到低进行排序.比赛结束后,10名选手的得分各不相同,且第二名的得分是最后五名选手得分之和的.则第二名选手的得分是 .
16.(2025 和平区校级二模)已知一批零件是由甲、乙、丙三名工人生产的,三人的产品分别占总产量的20%,40%,40%.若已知三人的次品率分别为各自产品的5%,4%,3%.现任取一个零件,则它是次品的概率为 .
17.(2025 浦东新区校级模拟)向量、满足,,且与夹角的余弦值为,则 .
18.(2025 新余校级模拟)已知平面向量,是非零向量,(2)⊥(2),向量在向量方向上的投影向量为,则 ;向量,的夹角为 .
19.(2025春 青浦区校级月考)如图所示,△ABC中,AB=3,AC=2,BC=4,点M为线段AB中点,P为线段CM的中点,延长AP交BC于点N,则 .
20.(2025春 徐汇区校级月考)已知非零向量、、互不相等,且,,若,则的最大值为 .
21.(2025 青浦区校级模拟)若向量与不共线也不垂直,且,则向量夹角 .
22.(2025春 青羊区校级月考)在△ABC中,角A,B,C的对边分别为a,b,c,若,则A= .
23.(2025 息县二模)设锐角△ABC三个内角A,B,C所对应的边分别为a,b,c,若a=2,bsinA,c=3,则b= .
24.(2025 长沙模拟)在△ABC中,记角A,B,C所对的边分别为a,b,c,已知,且a+c=4,则△ABC面积的最大值为 .
25.(2025春 青羊区校级月考)半径为5的球内有一个高为8的内接正四棱锥,则该球与该内接正四棱锥体积之比为 .
26.(2025 山东模拟)已知底面半径均为R的圆锥和圆台,它们的内切球半径也均为r(内切球分别与圆锥和圆台的底面以及侧面均相切),若R=2r,则圆锥和圆台的体积比为 .
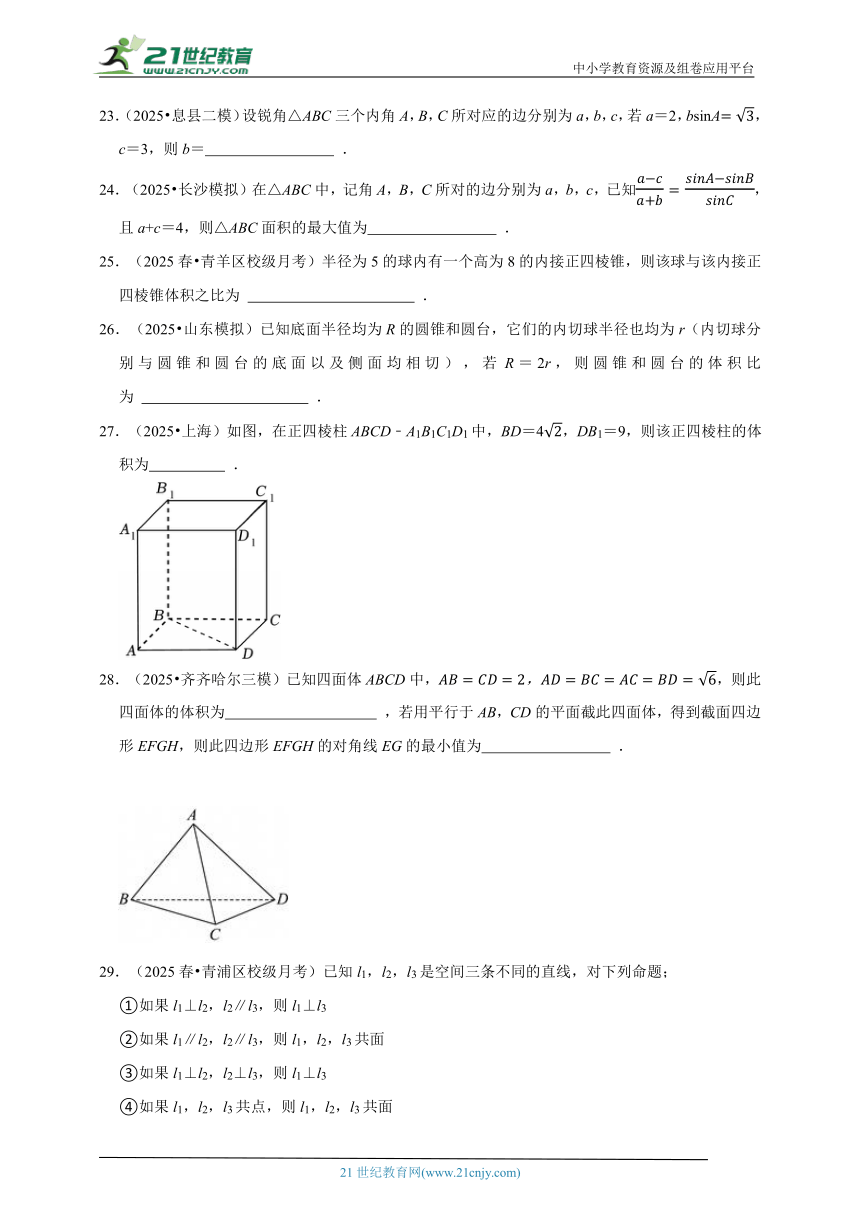
27.(2025 上海)如图,在正四棱柱ABCD﹣A1B1C1D1中,BD=4,DB1=9,则该正四棱柱的体积为 .
28.(2025 齐齐哈尔三模)已知四面体ABCD中,,则此四面体的体积为 ,若用平行于AB,CD的平面截此四面体,得到截面四边形EFGH,则此四边形EFGH的对角线EG的最小值为 .
29.(2025春 青浦区校级月考)已知l1,l2,l3是空间三条不同的直线,对下列命题;
①如果l1⊥l2,l2∥l3,则l1⊥l3
②如果l1∥l2,l2∥l3,则l1,l2,l3共面
③如果l1⊥l2,l2⊥l3,则l1⊥l3
④如果l1,l2,l3共点,则l1,l2,l3共面
其中正确的命题是 (填序号).
30.(2025春 信都区校级月考)如图,正方体ABCD﹣A1B1C1D1中,P、Q、R、S、T分别为线段AA1、AB、BC、BD、BB1的中点,联结A1S、D1T对空间任意两点M、N,若线段MN与线段A1S不相交或与线段D1T不相交,则称M、N两点可视.则此正方体中的点A、P、Q、R中与点C1可视的点有 .(答案从“点A、点P、点Q、点R”中选择)
【期末专项押题卷】填空题-2024-2025学年高一数学下学期人教A版(2019)必修第二册
参考答案与试题解析
一.填空题(共30小题)
1.(2025 天津)已知i是虚数单位,则||= .
【解答】解:因为1﹣3i,
所以||=|1﹣3i|.
故答案为:.
2.(2025 上海)已知复数z满足z2=()2,|z|≤1,则|z﹣2﹣3i|的最小值是 2 .
【解答】解:设z=a+bi(a,b∈R),则z2=a2﹣b2+2abi,()2=a2﹣b2﹣2abi,
因为z2=()2,所以abi=0,即ab=0,
又|z|≤1,所以z在复平面内对应的点的轨迹为或,
|z﹣2﹣3i|表示点(a,b)到点(2,3)的距离,
由点(a,b)的轨迹可知,当a=0,b=1时,|z﹣2﹣3i|有最小值,最小值为2.
故答案为:2.
3.(2025 金凤区校级模拟)已知复数z=(1﹣a2)+(a+1)i(i∈R)为纯虚数,则a= 1 .
【解答】解:由复数z=(1﹣a2)+(a+1)i(i∈R)为纯虚数,得,即a=1.
故答案为:1.
4.(2025春 和平区校级月考)设m∈R,复数z=(m2﹣2m﹣3)+(2m2+m﹣1)i,若z为纯虚数,则m= 3 .
【解答】解:由复数z=(m2﹣2m﹣3)+(2m2+m﹣1)i,若z为纯虚数,得,即m=3.
故答案为:3.
5.(2025春 广东月考)已知复数,则|z|的最小值为 2 .
【解答】解:,
故|z|,
因为a2≥0,所以|z|2.
故答案为:2.
6.(2025 信阳二模)已知从小到大排列的一组数据:1,5,a,10,11,13,15,21,42,57,若这组数据的极差是其第30百分位数的7倍,则a的值为 6 .
【解答】解:由题意知这组数据的极差是57﹣1=56,
由于10×30%=3,故第30百分位数为,
故,∴a=6.
故答案为:6.
7.(2025 上海模拟)现有如下10个数据:296,301,305,293,293,305,302,303,306,294,则这批数据的第25百分位数为 294 .
【解答】解:10个数据:296,301,305,293,293,305,302,303,306,294,
将10个数据从小到大排序为:293,293,294,296,301,302,303,305,305,306,
∵10×25%=2.5,
∴这批数据的第25百分位数为排序后的第3个数,即294.
故答案为:294.
8.(2025春 七里河区校级期中)已知某地区有小学生12000人,初中生11000人,高中生9000人,现在要了解该地区学生的近视情况,准备抽取320人进行调查,则应该抽取小学生、初中生、高中生的人数分别是 120,110,90 .
【解答】解:某地区有小学生12000人,初中生11000人,高中生9000人
所占的人数的比例分别为12000:11000:9000=12:11:9,
故抽取的小学生,初中生,高中生的人数分别.
故答案为:120,110,90.
9.(2025春 滨海新区校级期中)某校学生高一年级有880人,高二年级有800人,高三年级有720人,现用分层随机抽样方法共选取n名学生进行竞赛答题,已知高三年级选出9名选手,则n= 30 ;选出的高三年级9名选手分别答对题目数量为:2,3,7,5,1,6,8,3,8,则这组数据的第60百分位数为 6 .
【解答】解:由题意可知,,
解得n=30,
数据从小到大排列为:1,2,3,3,5,6,7,8,8,
因为9×60%=5.4,
所以这组数据的第60百分位数为6.
故答案为:30;6.
10.(2025春 保定月考)若数据x1,x2, ,x10的平均数为3,方差为4,则数据4x1+1,4x2+1, ,4x10+1的平均数为 13 方差为 64 .
【解答】解:设yi=4xi+1,设xi,i=1,2, ,n的平均数为,方差为s2,
yi,i=1,2, ,n的平均数为,方差为,则,s2=4,
则,42s2=16×4=64.
故答案为:13;64.
11.(2025 重庆校级模拟)盒子中有8个除颜色外均相同的小球,其中红球和黑球各有2个,白球有4个.现从中不放回的每次抽出一个,则前两次均抽出红球的概率为 ;若一直抽取直到小球全部抽完为止,则红球最先被抽完的概率为 .
【解答】解:根据题意,盒子中有红球和黑球各有2个,白球有4个.
则第一次抽红球的概率为,在次条件下,第二次抽红球的概率为,
故前两次均抽出红球的概率为;
设A表示“红球最先被抽完”,B表示“最后一次抽到白球”,C表示“最后一次抽到黑球”,
所以,
故答案为:;.
12.(2025春 长沙月考)在平面直角坐标系中,一个质点在随机外力的作用下,从原点O出发,每隔1秒等可能地向上、下、左、右四个方向移动1个单位.若第5秒时该质点在(1,0)处,则在此前的运动过程中,质点经过(0,1)处的概率为 .
【解答】解:根据题意,若第5秒时该质点在(1,0)处,
分3种情况讨论:
①左2次右3次,共有种情况;
②上下各1次,左1次右2次,共有种情况;
③上下各2次,右1次,共有种情况;
若在此前的运动过程中,质点经过(0,1)处,
情况②中:上下各1次,左1次右2次,要经过(0,1)处的情况是向上的一次在向下的一次前面移动,
则第一步向上平移有:上下左右右,上下右右左,上下右左右,上右下左右,上右下右左,上右右下左,上右右左下,上右左右下,上右左下右,
上左右右下,上左右下右,上左下右右,12种情况;
第一步向左平移有左上右下右,左上右右下,左右上下右,左右上右下,4种情况;
第一步向右平移有右左上下右,右左上右下,右上左下右,右上左右下,4种情况;
满足条件的种数为12+4+4=20种;
情况③中:上下各2次,右1次,要经过(0,1)处,
则第一步向上平移有:上上下下右,上上右下下,上上下右下,上下下上右,上下下右上,
上下上下右,上下上右下,上下右下上,上下右上下,上右上下下,上右下下上,上右下上下,12种情况;
第一步向下平移有下上上下右,下上上右下2种情况;
第一步向右平移不合题意;所以经过(0,1)处的情况的种数为12+2=14种;
共有14+20=34种情况经过(0,1)且第5秒时该质点在(1,0)处;
故要求概率P.
故答案为:.
13.(2025春 朝阳月考)已知事件A,B相互独立,且P(A)=p,,则当p= 时,P(AB)取得最大值,最大值为 .
【解答】解:根据题意,P(A)=p,,
则,解可得0≤p,
事件A,B相互独立,则P(AB)=p(p),
又由0≤p,则P(AB)=p(p)≤()2,当且仅当p时,等号成立,
故当p,P(AB)取得最大值,最大值为.
故答案为:;.
14.(2025 赤峰模拟)小张连续9天去快递店拿快递的个数依次为3,1,5,2,3,4,1,4,6.若从这组数据中随机删除1个数后,得到一组新数据,则这组新数据的中位数与原数据的中位数相等的概率为 .
【解答】解:将这组数据按照从小到大的顺序排列为1,1,2,3,3,4,4,5,6,则这组数据的中位数为3,
若删除的数字是4或5或6,所得一组新数据的中位数也是3,
若删除的数字是1或2或3,所得一组新数据的中位数是3.5,
故所求概率为P.
故答案为:.
15.(2025 天宁区校级三模)10名象棋选手进行单循环赛(即每两名选手比赛一场).规定两人对局胜者得2分,平局各得1分,负者得0分,并按总得分由高到低进行排序.比赛结束后,10名选手的得分各不相同,且第二名的得分是最后五名选手得分之和的.则第二名选手的得分是 16 .
【解答】解:每个选手需要进行9场比赛,则全胜的选手得:9×2=18(分),
而最后五名之间赛10场,至少共得:10×2=20(分),
所以第二名的选手得分至少为2016(分).
故答案是:16
16.(2025 和平区校级二模)已知一批零件是由甲、乙、丙三名工人生产的,三人的产品分别占总产量的20%,40%,40%.若已知三人的次品率分别为各自产品的5%,4%,3%.现任取一个零件,则它是次品的概率为 0.038 .
【解答】解:由题意利用全概率公式得所求概率为:0.2×0.05+0.4×0.04+0.4×0.03=0.038.
故答案为:0.038.
17.(2025 浦东新区校级模拟)向量、满足,,且与夹角的余弦值为,则 .
【解答】解:由题意,,,且与夹角的余弦值为,
则.
故答案为:.
18.(2025 新余校级模拟)已知平面向量,是非零向量,(2)⊥(2),向量在向量方向上的投影向量为,则 ﹣1 ;向量,的夹角为 .
【解答】解:因为向量在向量方向上的投影向量为,
所以,即;
因为平面向量,是非零向量,(2)⊥(2),
所以,即,
设向量,的夹角为θ,
所以,
所以,
因为θ∈[0,π],所以.
故答案为:﹣1;.
19.(2025春 青浦区校级月考)如图所示,△ABC中,AB=3,AC=2,BC=4,点M为线段AB中点,P为线段CM的中点,延长AP交BC于点N,则 .
【解答】解:在△ABC中,AB=3,AC=2,BC=4,
由余弦定理可得cosA,
因为点M为线段AB中点,P为线段CM的中点,
所以2,两边平方可得4222 AB2+AC2+AB ACcosA9+4+2×3×(),
可得||,
设μμμ,
又因为B,D,C三点共线,所以x(1﹣x),
可得,两式相加可得μ,
所以||||.
故答案为:.
20.(2025春 徐汇区校级月考)已知非零向量、、互不相等,且,,若,则的最大值为 .
【解答】解:已知非零向量、、互不相等,且,
则,
又,
则,
即,
又,
则,
又,
则,当且仅当时取等号,
即的最大值为.
故答案为:.
21.(2025 青浦区校级模拟)若向量与不共线也不垂直,且,则向量夹角 .
【解答】解:∵,
∴,
则,即向量夹角.
故答案为:.
22.(2025春 青羊区校级月考)在△ABC中,角A,B,C的对边分别为a,b,c,若,则A= .
【解答】解:因为,
所以,即b2+c2﹣a2=bc,
由余弦定理得,
所以.
故答案为:.
23.(2025 息县二模)设锐角△ABC三个内角A,B,C所对应的边分别为a,b,c,若a=2,bsinA,c=3,则b= .
【解答】解:法一:因为a=2,bsinA,
所以sinA,
由余弦定理得,cosA,
由题意知A为锐角,且1,
整理得,b4﹣26b2+133=0,
所以b或b,
当b时,a=2,c=3,此时a2+c2<b2,B为钝角,与已知矛盾,
故b.
法二:由正弦定理得,asinB=bsinA,
又a=2,
所以sinB,
由B为锐角得,B,
由余弦定理得,b2=a2+c2﹣2accosB=4+9﹣27,
所以b.
故答案为:.
24.(2025 长沙模拟)在△ABC中,记角A,B,C所对的边分别为a,b,c,已知,且a+c=4,则△ABC面积的最大值为 .
【解答】解:因为,
所以由正弦定理得:,
化简得:a2+c2﹣b2=ac,
由余弦定理得:,
因为B∈(0,π),所以B=60°,
因为a+c=4,所以,当a=c=2时取等号,
所以S△ABC的最大值为.
故答案为:.
25.(2025春 青羊区校级月考)半径为5的球内有一个高为8的内接正四棱锥,则该球与该内接正四棱锥体积之比为 125π: .
【解答】解:根据题意可得球心到正四棱锥的底面的距离为8﹣5=3,
所以底面正三角形的外接圆的半径为4,
所以底面正三角形的边长为2×4×sin60°,
所以该球与该内接正四棱锥体积之比为125π:.
故答案为:125π:.
26.(2025 山东模拟)已知底面半径均为R的圆锥和圆台,它们的内切球半径也均为r(内切球分别与圆锥和圆台的底面以及侧面均相切),若R=2r,则圆锥和圆台的体积比为 .
【解答】解:设圆锥的高为h,圆台的上底面圆的半径为a,
则根据相似比可得:,又R=2r,
化简可得h,
又(2r)2+(R﹣a)2=(R+a)2,化简可得a,
所以圆锥和圆台的体积比为:
.
故答案为:.
27.(2025 上海)如图,在正四棱柱ABCD﹣A1B1C1D1中,BD=4,DB1=9,则该正四棱柱的体积为 112 .
【解答】解:由题知,底面ABCD为正方形,所以2AB2=BD2=32,所以AB=4,
因为四棱柱ABCD﹣A1B1C1D1为正四棱柱,
所以BB1⊥底面ABCD,因为BD 底面ABCD,
所以BB1⊥BD,所以,
所以,
所以该正四棱柱的体积为4×4×7=112.
故答案为:112.
28.(2025 齐齐哈尔三模)已知四面体ABCD中,,则此四面体的体积为 ,若用平行于AB,CD的平面截此四面体,得到截面四边形EFGH,则此四边形EFGH的对角线EG的最小值为 .
【解答】解:(1)将四面体ABCD补成长方体,设长方体的长、宽、高分别为a,b,c,如图所示:
根据长方体面对角线的性质,得.
三式相加得2(a2+b2+c2)=4+6+6=16,则a2+b2+c2=8.
分别求解可得c2=4,b2=2,a2=2,解得a,b,c=2.
因为四面体ABCD的体积V等于长方体体积减去四个等体积的三棱锥体积.
长方体体积为V=abc2=4.
一个三棱锥的体积为V1abc2.
四个三棱锥体积为4V1=4.
所以四面体ABCD的体积为V=V﹣4V1=4.
(2)因为平面EFGH∥AB,平面EFGH∥CD,平面ABC∩平面EFGH=EF,平面ABC∩AB=AB,
根据面面平行的性质知EF∥AB,同理HG∥AB,EH∥CD,FG∥CD,所以四边形EFGH是平行四边形.
设x(0<x<1),则1﹣x.
由△AEH~△ACD,可得x,因为CD=2,所以EH=2x.
由△CEF~△CAB,可得1﹣x,因为AB=2,所以EF=2(1﹣x).
因为a,b,补成的长方体上下底面为正方形,可得AB⊥CD,
所以∠HEF=90°,则EG2=EH2+HG2=EH2+EF2.
将EH=2x,EF=2(1﹣x)代入可得EG2=(2x)2+[2(1﹣x)]2=4x2+4(1﹣2x+x2)=8x2﹣8x+4.
令y=8x2﹣8x+4,0<x<1,这是一个二次函数,图象开口向上,对称轴为x.
当x时,y取得最小值,ymin=884=2,所以EGmin.
故答案为:;.
29.(2025春 青浦区校级月考)已知l1,l2,l3是空间三条不同的直线,对下列命题;
①如果l1⊥l2,l2∥l3,则l1⊥l3
②如果l1∥l2,l2∥l3,则l1,l2,l3共面
③如果l1⊥l2,l2⊥l3,则l1⊥l3
④如果l1,l2,l3共点,则l1,l2,l3共面
其中正确的命题是 ① (填序号).
【解答】解:因为l1,l2,l3是空间三条不同的直线,
若l1⊥l2,l2∥l3,则l1⊥l3,所以①正确;
若l1∥l2,l2∥l3,则l1∥l3,但l1,l2,l3不一定共面,所以②错误;
若l1⊥l2,l2⊥l3,则l1与l3可以成任意角,所以③错误;
若l1,l2,l3共点,则l1,l2,l3共面不一定成立,所以④错误.
故答案为:①.
30.(2025春 信都区校级月考)如图,正方体ABCD﹣A1B1C1D1中,P、Q、R、S、T分别为线段AA1、AB、BC、BD、BB1的中点,联结A1S、D1T对空间任意两点M、N,若线段MN与线段A1S不相交或与线段D1T不相交,则称M、N两点可视.则此正方体中的点A、P、Q、R中与点C1可视的点有 点A,点Q,点R .(答案从“点A、点P、点Q、点R”中选择)
【解答】解:对于点A,连接AD1,BC1,AC1,因为D1、A、C1∈平面D1C1BA,T 平面D1C1BA,且D1 AC1,
所以直线D1T与AC1是异面直线,
所以点C1与点A可视;
对于点P,如图,连接A1C1,PC1,BD,AC,得A1S、PC1 平面A1C1CA,且A1S与PC1相交,
连接D1P,PT,TC1,因为D1C1∥PT,D1C1=PT,
所以四边形D1C1TP是平行四边形,得D1T与PC1相交,所以点C1与点P不可视,
对于点Q,如图,连接A1C1,AC,C1Q,
因为A1、S、C1∈平面A1C1CA,Q 平面A1C1CA,且C1 A1S,
所以直线A1S.与QC1是异面直线,所以点C1与点Q可视;
对于点R,如图,连接RC1,TC1,TD1,
因为C1、T、D1∈平面D1C1T,R 平面D1C1T,且C1 D1T,
所以直线D1T与RC1是异面直线,所以点C1与点R可视,故D错误.
故答案为:点A、点Q、点R.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【期末专项押题卷】填空题-2024-2025学年高一数学下学期人教A版(2019)必修第二册
1.(2025 天津)已知i是虚数单位,则||= .
2.(2025 上海)已知复数z满足z2=()2,|z|≤1,则|z﹣2﹣3i|的最小值是 .
3.(2025 金凤区校级模拟)已知复数z=(1﹣a2)+(a+1)i(i∈R)为纯虚数,则a= .
4.(2025春 和平区校级月考)设m∈R,复数z=(m2﹣2m﹣3)+(2m2+m﹣1)i,若z为纯虚数,则m= .
5.(2025春 广东月考)已知复数,则|z|的最小值为 .
6.(2025 信阳二模)已知从小到大排列的一组数据:1,5,a,10,11,13,15,21,42,57,若这组数据的极差是其第30百分位数的7倍,则a的值为 .
7.(2025 上海模拟)现有如下10个数据:296,301,305,293,293,305,302,303,306,294,则这批数据的第25百分位数为 .
8.(2025春 七里河区校级期中)已知某地区有小学生12000人,初中生11000人,高中生9000人,现在要了解该地区学生的近视情况,准备抽取320人进行调查,则应该抽取小学生、初中生、高中生的人数分别是 .
9.(2025春 滨海新区校级期中)某校学生高一年级有880人,高二年级有800人,高三年级有720人,现用分层随机抽样方法共选取n名学生进行竞赛答题,已知高三年级选出9名选手,则n= ;选出的高三年级9名选手分别答对题目数量为:2,3,7,5,1,6,8,3,8,则这组数据的第60百分位数为 .
10.(2025春 保定月考)若数据x1,x2, ,x10的平均数为3,方差为4,则数据4x1+1,4x2+1, ,4x10+1的平均数为 方差为 .
11.(2025 重庆校级模拟)盒子中有8个除颜色外均相同的小球,其中红球和黑球各有2个,白球有4个.现从中不放回的每次抽出一个,则前两次均抽出红球的概率为 ;若一直抽取直到小球全部抽完为止,则红球最先被抽完的概率为 .
12.(2025春 长沙月考)在平面直角坐标系中,一个质点在随机外力的作用下,从原点O出发,每隔1秒等可能地向上、下、左、右四个方向移动1个单位.若第5秒时该质点在(1,0)处,则在此前的运动过程中,质点经过(0,1)处的概率为 .
13.(2025春 朝阳月考)已知事件A,B相互独立,且P(A)=p,,则当p= 时,P(AB)取得最大值,最大值为 .
14.(2025 赤峰模拟)小张连续9天去快递店拿快递的个数依次为3,1,5,2,3,4,1,4,6.若从这组数据中随机删除1个数后,得到一组新数据,则这组新数据的中位数与原数据的中位数相等的概率为 .
15.(2025 天宁区校级三模)10名象棋选手进行单循环赛(即每两名选手比赛一场).规定两人对局胜者得2分,平局各得1分,负者得0分,并按总得分由高到低进行排序.比赛结束后,10名选手的得分各不相同,且第二名的得分是最后五名选手得分之和的.则第二名选手的得分是 .
16.(2025 和平区校级二模)已知一批零件是由甲、乙、丙三名工人生产的,三人的产品分别占总产量的20%,40%,40%.若已知三人的次品率分别为各自产品的5%,4%,3%.现任取一个零件,则它是次品的概率为 .
17.(2025 浦东新区校级模拟)向量、满足,,且与夹角的余弦值为,则 .
18.(2025 新余校级模拟)已知平面向量,是非零向量,(2)⊥(2),向量在向量方向上的投影向量为,则 ;向量,的夹角为 .
19.(2025春 青浦区校级月考)如图所示,△ABC中,AB=3,AC=2,BC=4,点M为线段AB中点,P为线段CM的中点,延长AP交BC于点N,则 .
20.(2025春 徐汇区校级月考)已知非零向量、、互不相等,且,,若,则的最大值为 .
21.(2025 青浦区校级模拟)若向量与不共线也不垂直,且,则向量夹角 .
22.(2025春 青羊区校级月考)在△ABC中,角A,B,C的对边分别为a,b,c,若,则A= .
23.(2025 息县二模)设锐角△ABC三个内角A,B,C所对应的边分别为a,b,c,若a=2,bsinA,c=3,则b= .
24.(2025 长沙模拟)在△ABC中,记角A,B,C所对的边分别为a,b,c,已知,且a+c=4,则△ABC面积的最大值为 .
25.(2025春 青羊区校级月考)半径为5的球内有一个高为8的内接正四棱锥,则该球与该内接正四棱锥体积之比为 .
26.(2025 山东模拟)已知底面半径均为R的圆锥和圆台,它们的内切球半径也均为r(内切球分别与圆锥和圆台的底面以及侧面均相切),若R=2r,则圆锥和圆台的体积比为 .
27.(2025 上海)如图,在正四棱柱ABCD﹣A1B1C1D1中,BD=4,DB1=9,则该正四棱柱的体积为 .
28.(2025 齐齐哈尔三模)已知四面体ABCD中,,则此四面体的体积为 ,若用平行于AB,CD的平面截此四面体,得到截面四边形EFGH,则此四边形EFGH的对角线EG的最小值为 .
29.(2025春 青浦区校级月考)已知l1,l2,l3是空间三条不同的直线,对下列命题;
①如果l1⊥l2,l2∥l3,则l1⊥l3
②如果l1∥l2,l2∥l3,则l1,l2,l3共面
③如果l1⊥l2,l2⊥l3,则l1⊥l3
④如果l1,l2,l3共点,则l1,l2,l3共面
其中正确的命题是 (填序号).
30.(2025春 信都区校级月考)如图,正方体ABCD﹣A1B1C1D1中,P、Q、R、S、T分别为线段AA1、AB、BC、BD、BB1的中点,联结A1S、D1T对空间任意两点M、N,若线段MN与线段A1S不相交或与线段D1T不相交,则称M、N两点可视.则此正方体中的点A、P、Q、R中与点C1可视的点有 .(答案从“点A、点P、点Q、点R”中选择)
【期末专项押题卷】填空题-2024-2025学年高一数学下学期人教A版(2019)必修第二册
参考答案与试题解析
一.填空题(共30小题)
1.(2025 天津)已知i是虚数单位,则||= .
【解答】解:因为1﹣3i,
所以||=|1﹣3i|.
故答案为:.
2.(2025 上海)已知复数z满足z2=()2,|z|≤1,则|z﹣2﹣3i|的最小值是 2 .
【解答】解:设z=a+bi(a,b∈R),则z2=a2﹣b2+2abi,()2=a2﹣b2﹣2abi,
因为z2=()2,所以abi=0,即ab=0,
又|z|≤1,所以z在复平面内对应的点的轨迹为或,
|z﹣2﹣3i|表示点(a,b)到点(2,3)的距离,
由点(a,b)的轨迹可知,当a=0,b=1时,|z﹣2﹣3i|有最小值,最小值为2.
故答案为:2.
3.(2025 金凤区校级模拟)已知复数z=(1﹣a2)+(a+1)i(i∈R)为纯虚数,则a= 1 .
【解答】解:由复数z=(1﹣a2)+(a+1)i(i∈R)为纯虚数,得,即a=1.
故答案为:1.
4.(2025春 和平区校级月考)设m∈R,复数z=(m2﹣2m﹣3)+(2m2+m﹣1)i,若z为纯虚数,则m= 3 .
【解答】解:由复数z=(m2﹣2m﹣3)+(2m2+m﹣1)i,若z为纯虚数,得,即m=3.
故答案为:3.
5.(2025春 广东月考)已知复数,则|z|的最小值为 2 .
【解答】解:,
故|z|,
因为a2≥0,所以|z|2.
故答案为:2.
6.(2025 信阳二模)已知从小到大排列的一组数据:1,5,a,10,11,13,15,21,42,57,若这组数据的极差是其第30百分位数的7倍,则a的值为 6 .
【解答】解:由题意知这组数据的极差是57﹣1=56,
由于10×30%=3,故第30百分位数为,
故,∴a=6.
故答案为:6.
7.(2025 上海模拟)现有如下10个数据:296,301,305,293,293,305,302,303,306,294,则这批数据的第25百分位数为 294 .
【解答】解:10个数据:296,301,305,293,293,305,302,303,306,294,
将10个数据从小到大排序为:293,293,294,296,301,302,303,305,305,306,
∵10×25%=2.5,
∴这批数据的第25百分位数为排序后的第3个数,即294.
故答案为:294.
8.(2025春 七里河区校级期中)已知某地区有小学生12000人,初中生11000人,高中生9000人,现在要了解该地区学生的近视情况,准备抽取320人进行调查,则应该抽取小学生、初中生、高中生的人数分别是 120,110,90 .
【解答】解:某地区有小学生12000人,初中生11000人,高中生9000人
所占的人数的比例分别为12000:11000:9000=12:11:9,
故抽取的小学生,初中生,高中生的人数分别.
故答案为:120,110,90.
9.(2025春 滨海新区校级期中)某校学生高一年级有880人,高二年级有800人,高三年级有720人,现用分层随机抽样方法共选取n名学生进行竞赛答题,已知高三年级选出9名选手,则n= 30 ;选出的高三年级9名选手分别答对题目数量为:2,3,7,5,1,6,8,3,8,则这组数据的第60百分位数为 6 .
【解答】解:由题意可知,,
解得n=30,
数据从小到大排列为:1,2,3,3,5,6,7,8,8,
因为9×60%=5.4,
所以这组数据的第60百分位数为6.
故答案为:30;6.
10.(2025春 保定月考)若数据x1,x2, ,x10的平均数为3,方差为4,则数据4x1+1,4x2+1, ,4x10+1的平均数为 13 方差为 64 .
【解答】解:设yi=4xi+1,设xi,i=1,2, ,n的平均数为,方差为s2,
yi,i=1,2, ,n的平均数为,方差为,则,s2=4,
则,42s2=16×4=64.
故答案为:13;64.
11.(2025 重庆校级模拟)盒子中有8个除颜色外均相同的小球,其中红球和黑球各有2个,白球有4个.现从中不放回的每次抽出一个,则前两次均抽出红球的概率为 ;若一直抽取直到小球全部抽完为止,则红球最先被抽完的概率为 .
【解答】解:根据题意,盒子中有红球和黑球各有2个,白球有4个.
则第一次抽红球的概率为,在次条件下,第二次抽红球的概率为,
故前两次均抽出红球的概率为;
设A表示“红球最先被抽完”,B表示“最后一次抽到白球”,C表示“最后一次抽到黑球”,
所以,
故答案为:;.
12.(2025春 长沙月考)在平面直角坐标系中,一个质点在随机外力的作用下,从原点O出发,每隔1秒等可能地向上、下、左、右四个方向移动1个单位.若第5秒时该质点在(1,0)处,则在此前的运动过程中,质点经过(0,1)处的概率为 .
【解答】解:根据题意,若第5秒时该质点在(1,0)处,
分3种情况讨论:
①左2次右3次,共有种情况;
②上下各1次,左1次右2次,共有种情况;
③上下各2次,右1次,共有种情况;
若在此前的运动过程中,质点经过(0,1)处,
情况②中:上下各1次,左1次右2次,要经过(0,1)处的情况是向上的一次在向下的一次前面移动,
则第一步向上平移有:上下左右右,上下右右左,上下右左右,上右下左右,上右下右左,上右右下左,上右右左下,上右左右下,上右左下右,
上左右右下,上左右下右,上左下右右,12种情况;
第一步向左平移有左上右下右,左上右右下,左右上下右,左右上右下,4种情况;
第一步向右平移有右左上下右,右左上右下,右上左下右,右上左右下,4种情况;
满足条件的种数为12+4+4=20种;
情况③中:上下各2次,右1次,要经过(0,1)处,
则第一步向上平移有:上上下下右,上上右下下,上上下右下,上下下上右,上下下右上,
上下上下右,上下上右下,上下右下上,上下右上下,上右上下下,上右下下上,上右下上下,12种情况;
第一步向下平移有下上上下右,下上上右下2种情况;
第一步向右平移不合题意;所以经过(0,1)处的情况的种数为12+2=14种;
共有14+20=34种情况经过(0,1)且第5秒时该质点在(1,0)处;
故要求概率P.
故答案为:.
13.(2025春 朝阳月考)已知事件A,B相互独立,且P(A)=p,,则当p= 时,P(AB)取得最大值,最大值为 .
【解答】解:根据题意,P(A)=p,,
则,解可得0≤p,
事件A,B相互独立,则P(AB)=p(p),
又由0≤p,则P(AB)=p(p)≤()2,当且仅当p时,等号成立,
故当p,P(AB)取得最大值,最大值为.
故答案为:;.
14.(2025 赤峰模拟)小张连续9天去快递店拿快递的个数依次为3,1,5,2,3,4,1,4,6.若从这组数据中随机删除1个数后,得到一组新数据,则这组新数据的中位数与原数据的中位数相等的概率为 .
【解答】解:将这组数据按照从小到大的顺序排列为1,1,2,3,3,4,4,5,6,则这组数据的中位数为3,
若删除的数字是4或5或6,所得一组新数据的中位数也是3,
若删除的数字是1或2或3,所得一组新数据的中位数是3.5,
故所求概率为P.
故答案为:.
15.(2025 天宁区校级三模)10名象棋选手进行单循环赛(即每两名选手比赛一场).规定两人对局胜者得2分,平局各得1分,负者得0分,并按总得分由高到低进行排序.比赛结束后,10名选手的得分各不相同,且第二名的得分是最后五名选手得分之和的.则第二名选手的得分是 16 .
【解答】解:每个选手需要进行9场比赛,则全胜的选手得:9×2=18(分),
而最后五名之间赛10场,至少共得:10×2=20(分),
所以第二名的选手得分至少为2016(分).
故答案是:16
16.(2025 和平区校级二模)已知一批零件是由甲、乙、丙三名工人生产的,三人的产品分别占总产量的20%,40%,40%.若已知三人的次品率分别为各自产品的5%,4%,3%.现任取一个零件,则它是次品的概率为 0.038 .
【解答】解:由题意利用全概率公式得所求概率为:0.2×0.05+0.4×0.04+0.4×0.03=0.038.
故答案为:0.038.
17.(2025 浦东新区校级模拟)向量、满足,,且与夹角的余弦值为,则 .
【解答】解:由题意,,,且与夹角的余弦值为,
则.
故答案为:.
18.(2025 新余校级模拟)已知平面向量,是非零向量,(2)⊥(2),向量在向量方向上的投影向量为,则 ﹣1 ;向量,的夹角为 .
【解答】解:因为向量在向量方向上的投影向量为,
所以,即;
因为平面向量,是非零向量,(2)⊥(2),
所以,即,
设向量,的夹角为θ,
所以,
所以,
因为θ∈[0,π],所以.
故答案为:﹣1;.
19.(2025春 青浦区校级月考)如图所示,△ABC中,AB=3,AC=2,BC=4,点M为线段AB中点,P为线段CM的中点,延长AP交BC于点N,则 .
【解答】解:在△ABC中,AB=3,AC=2,BC=4,
由余弦定理可得cosA,
因为点M为线段AB中点,P为线段CM的中点,
所以2,两边平方可得4222 AB2+AC2+AB ACcosA9+4+2×3×(),
可得||,
设μμμ,
又因为B,D,C三点共线,所以x(1﹣x),
可得,两式相加可得μ,
所以||||.
故答案为:.
20.(2025春 徐汇区校级月考)已知非零向量、、互不相等,且,,若,则的最大值为 .
【解答】解:已知非零向量、、互不相等,且,
则,
又,
则,
即,
又,
则,
又,
则,当且仅当时取等号,
即的最大值为.
故答案为:.
21.(2025 青浦区校级模拟)若向量与不共线也不垂直,且,则向量夹角 .
【解答】解:∵,
∴,
则,即向量夹角.
故答案为:.
22.(2025春 青羊区校级月考)在△ABC中,角A,B,C的对边分别为a,b,c,若,则A= .
【解答】解:因为,
所以,即b2+c2﹣a2=bc,
由余弦定理得,
所以.
故答案为:.
23.(2025 息县二模)设锐角△ABC三个内角A,B,C所对应的边分别为a,b,c,若a=2,bsinA,c=3,则b= .
【解答】解:法一:因为a=2,bsinA,
所以sinA,
由余弦定理得,cosA,
由题意知A为锐角,且1,
整理得,b4﹣26b2+133=0,
所以b或b,
当b时,a=2,c=3,此时a2+c2<b2,B为钝角,与已知矛盾,
故b.
法二:由正弦定理得,asinB=bsinA,
又a=2,
所以sinB,
由B为锐角得,B,
由余弦定理得,b2=a2+c2﹣2accosB=4+9﹣27,
所以b.
故答案为:.
24.(2025 长沙模拟)在△ABC中,记角A,B,C所对的边分别为a,b,c,已知,且a+c=4,则△ABC面积的最大值为 .
【解答】解:因为,
所以由正弦定理得:,
化简得:a2+c2﹣b2=ac,
由余弦定理得:,
因为B∈(0,π),所以B=60°,
因为a+c=4,所以,当a=c=2时取等号,
所以S△ABC的最大值为.
故答案为:.
25.(2025春 青羊区校级月考)半径为5的球内有一个高为8的内接正四棱锥,则该球与该内接正四棱锥体积之比为 125π: .
【解答】解:根据题意可得球心到正四棱锥的底面的距离为8﹣5=3,
所以底面正三角形的外接圆的半径为4,
所以底面正三角形的边长为2×4×sin60°,
所以该球与该内接正四棱锥体积之比为125π:.
故答案为:125π:.
26.(2025 山东模拟)已知底面半径均为R的圆锥和圆台,它们的内切球半径也均为r(内切球分别与圆锥和圆台的底面以及侧面均相切),若R=2r,则圆锥和圆台的体积比为 .
【解答】解:设圆锥的高为h,圆台的上底面圆的半径为a,
则根据相似比可得:,又R=2r,
化简可得h,
又(2r)2+(R﹣a)2=(R+a)2,化简可得a,
所以圆锥和圆台的体积比为:
.
故答案为:.
27.(2025 上海)如图,在正四棱柱ABCD﹣A1B1C1D1中,BD=4,DB1=9,则该正四棱柱的体积为 112 .
【解答】解:由题知,底面ABCD为正方形,所以2AB2=BD2=32,所以AB=4,
因为四棱柱ABCD﹣A1B1C1D1为正四棱柱,
所以BB1⊥底面ABCD,因为BD 底面ABCD,
所以BB1⊥BD,所以,
所以,
所以该正四棱柱的体积为4×4×7=112.
故答案为:112.
28.(2025 齐齐哈尔三模)已知四面体ABCD中,,则此四面体的体积为 ,若用平行于AB,CD的平面截此四面体,得到截面四边形EFGH,则此四边形EFGH的对角线EG的最小值为 .
【解答】解:(1)将四面体ABCD补成长方体,设长方体的长、宽、高分别为a,b,c,如图所示:
根据长方体面对角线的性质,得.
三式相加得2(a2+b2+c2)=4+6+6=16,则a2+b2+c2=8.
分别求解可得c2=4,b2=2,a2=2,解得a,b,c=2.
因为四面体ABCD的体积V等于长方体体积减去四个等体积的三棱锥体积.
长方体体积为V=abc2=4.
一个三棱锥的体积为V1abc2.
四个三棱锥体积为4V1=4.
所以四面体ABCD的体积为V=V﹣4V1=4.
(2)因为平面EFGH∥AB,平面EFGH∥CD,平面ABC∩平面EFGH=EF,平面ABC∩AB=AB,
根据面面平行的性质知EF∥AB,同理HG∥AB,EH∥CD,FG∥CD,所以四边形EFGH是平行四边形.
设x(0<x<1),则1﹣x.
由△AEH~△ACD,可得x,因为CD=2,所以EH=2x.
由△CEF~△CAB,可得1﹣x,因为AB=2,所以EF=2(1﹣x).
因为a,b,补成的长方体上下底面为正方形,可得AB⊥CD,
所以∠HEF=90°,则EG2=EH2+HG2=EH2+EF2.
将EH=2x,EF=2(1﹣x)代入可得EG2=(2x)2+[2(1﹣x)]2=4x2+4(1﹣2x+x2)=8x2﹣8x+4.
令y=8x2﹣8x+4,0<x<1,这是一个二次函数,图象开口向上,对称轴为x.
当x时,y取得最小值,ymin=884=2,所以EGmin.
故答案为:;.
29.(2025春 青浦区校级月考)已知l1,l2,l3是空间三条不同的直线,对下列命题;
①如果l1⊥l2,l2∥l3,则l1⊥l3
②如果l1∥l2,l2∥l3,则l1,l2,l3共面
③如果l1⊥l2,l2⊥l3,则l1⊥l3
④如果l1,l2,l3共点,则l1,l2,l3共面
其中正确的命题是 ① (填序号).
【解答】解:因为l1,l2,l3是空间三条不同的直线,
若l1⊥l2,l2∥l3,则l1⊥l3,所以①正确;
若l1∥l2,l2∥l3,则l1∥l3,但l1,l2,l3不一定共面,所以②错误;
若l1⊥l2,l2⊥l3,则l1与l3可以成任意角,所以③错误;
若l1,l2,l3共点,则l1,l2,l3共面不一定成立,所以④错误.
故答案为:①.
30.(2025春 信都区校级月考)如图,正方体ABCD﹣A1B1C1D1中,P、Q、R、S、T分别为线段AA1、AB、BC、BD、BB1的中点,联结A1S、D1T对空间任意两点M、N,若线段MN与线段A1S不相交或与线段D1T不相交,则称M、N两点可视.则此正方体中的点A、P、Q、R中与点C1可视的点有 点A,点Q,点R .(答案从“点A、点P、点Q、点R”中选择)
【解答】解:对于点A,连接AD1,BC1,AC1,因为D1、A、C1∈平面D1C1BA,T 平面D1C1BA,且D1 AC1,
所以直线D1T与AC1是异面直线,
所以点C1与点A可视;
对于点P,如图,连接A1C1,PC1,BD,AC,得A1S、PC1 平面A1C1CA,且A1S与PC1相交,
连接D1P,PT,TC1,因为D1C1∥PT,D1C1=PT,
所以四边形D1C1TP是平行四边形,得D1T与PC1相交,所以点C1与点P不可视,
对于点Q,如图,连接A1C1,AC,C1Q,
因为A1、S、C1∈平面A1C1CA,Q 平面A1C1CA,且C1 A1S,
所以直线A1S.与QC1是异面直线,所以点C1与点Q可视;
对于点R,如图,连接RC1,TC1,TD1,
因为C1、T、D1∈平面D1C1T,R 平面D1C1T,且C1 D1T,
所以直线D1T与RC1是异面直线,所以点C1与点R可视,故D错误.
故答案为:点A、点Q、点R.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
