【期末专项押题卷】单选题-2024-2025学年高一数学下学期人教A版(2019)必修第二册(含解析)
文档属性
| 名称 | 【期末专项押题卷】单选题-2024-2025学年高一数学下学期人教A版(2019)必修第二册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 552.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 11:06:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【期末专项押题卷】单选题-2024-2025学年高一数学下学期人教A版(2019)必修第二册
1.(2025 齐齐哈尔三模)已知复数z=i(1+i),则z在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2025 泰安模拟)已知复数z满足,则( )
A.1﹣i B.1+i C.2﹣2i D.2+2i
3.(2024秋 耒阳市校级期末)已知z1=a﹣i,z2=1+bi(a,b∈R,i为虚数单位),若z1 z2是实数,则( )
A.ab﹣1=0 B.ab+1=0 C.a﹣b=0 D.a+b=0
4.(2025 新余校级模拟)已知复数z满足|z|=1,则|z﹣3﹣2i|的最小值为( )
A. B. C. D.
5.(2025 肥城市模拟)已知复数(i为虚数单位),则为( )
A.5 B. C.7 D.
6.(2025 陕西校级模拟)已知a,b∈R,a﹣2i=(b+i)i(i为虚数单位),则( )
A.a=1,b=﹣2 B.a=﹣1,b=2 C.a=﹣1,b=﹣2 D.a=1,b=2
7.(2025 安徽模拟)已知a,b,c的平均数与方差均为4,则a2,b2,c2的平均数为( )
A.16 B.18 C.20 D.24
8.(2025春 长沙月考)若样本平均数为,总体平均数为,则( )
A. B.
C.是的估计值 D.是的估计值
9.(2025 新余校级模拟)一个样本容量为4的样本的平均数为18,现样本加入新数8,此时样本数据的和为( )
A.26 B.60 C.72 D.80
10.(2025春 渝北区校级月考)下列说法正确的是( )
A.数据1,3,3,5,6的第60百分位数是5.5
B.若一组样本数据4,6,7,8,9,a的平均数为7,则a=7
C.用分层随机抽样时,个体数最多的层里的个体被抽到的概率最大
D.若x1,x2, ,x10的标准差为4,则﹣2x1+3,﹣2x2+3, ,﹣2x10+3的标准差是8
11.(2025 信阳二模)四名同学各掷骰子5次,分别记录每次骰子出现的点数.根据四名同学的统计结果,可以判断出一定没有出现点数6的是( )
A.平均数为2,方差为2.4
B.中位数为3,方差为2.8
C.平均数为3,中位数为2
D.中位数为3,众数为2
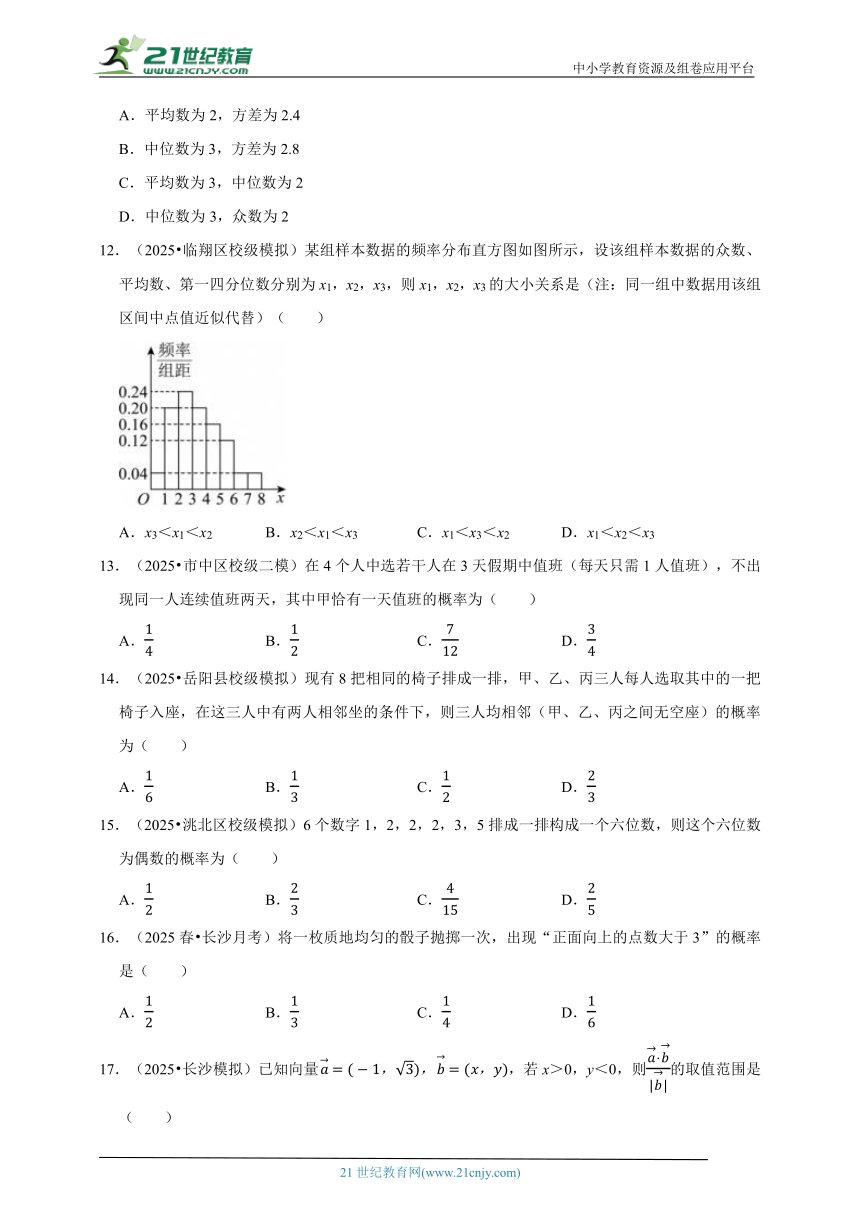
12.(2025 临翔区校级模拟)某组样本数据的频率分布直方图如图所示,设该组样本数据的众数、平均数、第一四分位数分别为x1,x2,x3,则x1,x2,x3的大小关系是(注:同一组中数据用该组区间中点值近似代替)( )
A.x3<x1<x2 B.x2<x1<x3 C.x1<x3<x2 D.x1<x2<x3
13.(2025 市中区校级二模)在4个人中选若干人在3天假期中值班(每天只需1人值班),不出现同一人连续值班两天,其中甲恰有一天值班的概率为( )
A. B. C. D.
14.(2025 岳阳县校级模拟)现有8把相同的椅子排成一排,甲、乙、丙三人每人选取其中的一把椅子入座,在这三人中有两人相邻坐的条件下,则三人均相邻(甲、乙、丙之间无空座)的概率为( )
A. B. C. D.
15.(2025 洮北区校级模拟)6个数字1,2,2,2,3,5排成一排构成一个六位数,则这个六位数为偶数的概率为( )
A. B. C. D.
16.(2025春 长沙月考)将一枚质地均匀的骰子抛掷一次,出现“正面向上的点数大于3”的概率是( )
A. B. C. D.
17.(2025 长沙模拟)已知向量,若x>0,y<0,则的取值范围是( )
A.[﹣2,﹣1) B. C. D.
18.(2025 泉州校级模拟)已知向量和的夹角为60°,且,,则( )
A.3 B.﹣1 C. D.13
19.(2025春 青羊区校级月考)一船以15nmile/h的速度向东航行,船在点A处看到一个灯塔B在北偏东60°,行驶4h后,船到达点C处,看到这个灯塔在北偏东15°,这时船与灯塔的距离为( )
A.nmile B.nmile C.nmile D.nmile
20.(2025春 江阴市月考)△ABC的内角A,B,C的对边分别为a,b,c,已知c2=2a2﹣2b2,则A﹣B的最大值为( )
A. B. C. D.
21.(2025 金凤区校级模拟)已知△ABC的三个内角A,B,C所对的边分别为a,b,c,且,B=30°,,则b=( )
A. B. C. D.
22.(2025 乐山模拟)某数学兴趣小组成员为测量某建筑的高度OP,选取了在同一水平面上的A,B,C三处,如图.已知在A,B,C处测得该建筑顶部P的仰角分别为30°,45°,60°,,AB=10米,则该建筑的高度OP=( )
A.米 B.米 C.米 D.米
23.(2025 汉川市校级模拟)点P在边长为1的正三角形ABC的外接圆上,则的最大值为( )
A. B. C. D.
24.(2025 天津)若m为直线,α,β为两个平面,则下列结论中正确的是( )
A.若m∥α,n α,则m∥n B.若m⊥α,m⊥β,则α⊥β
C.若m∥α,m⊥β,则α⊥β D.若m α,α⊥β,则m⊥β
25.(2025 山西模拟)已知母线长为2的圆锥的侧面积是底面积的2倍,则圆锥的体积为( )
A. B. C. D.2π
26.(2025 宁远县模拟)将上下底分别为2,4,高为1的直角梯形绕其最短的底边旋转一周得到的几何体的体积为( )
A.8π B. C. D.
27.(2025 内江三模)已知点M为正三棱柱ABC﹣A1B1C1表面上一个异于点A1的动点,若,BB1=1,且满足,则动点M的轨迹的长度为( )
A.2π B. C. D.
28.(2025 青浦区校级模拟)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段EB的中点,则( )
A.DM≠EN,且直线DM、EN是异面直线
B.DM=EN,且直线DM、EN是异面直线
C.DM≠EN,且直线DM、EN是相交直线
D.DM=EN,且直线DM、EN是相交直线
29.(2025春 信都区校级月考)如图,四棱柱ABCD﹣A1B1C1D1中,四边形ABCD为平行四边形,E,F分别在线段DB,DD1上,且,G在CC1上且平面AEF∥平面BD1G,则( )
A. B. C. D.
30.(2025春 定海区校级期中)石墩是常见的维护交通秩序的道路设施.某路口放置的石墩(如图),其上部是原球半径为15cm的球缺,下部可看作是上、下底面半径分别为9cm、16cm的圆台,球缺的截面圆与圆台的上底面完全吻合,整个石墩的高为33cm,则石墩的体积为( )
(注:球体被平面所截,截得的部分叫球缺,球缺表面上的点到截面的最大距离为球缺的高,球缺的体积,其中R为原球半径,h为球缺的高.)
A.4374πcm3 B.5048πcm3 C.5336πcm3 D.7260πcm3
【期末专项押题卷】单选题-2024-2025学年高一数学下学期人教A版(2019)必修第二册
参考答案与试题解析
一.选择题(共30小题)
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B B A C B C C D D D A
题号 12 13 14 15 16 17 18 19 20 21 22
答案 A C A A A A A B A B B
题号 23 24 25 26 27 28 29 30
答案 A C C D C D B C
一.选择题(共30小题)
1.(2025 齐齐哈尔三模)已知复数z=i(1+i),则z在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:∵z=i(1+i)=﹣1+i,
∴复数z在复平面内对应的点的坐标为(﹣1,1),位于第二象限.
故选:B.
2.(2025 泰安模拟)已知复数z满足,则( )
A.1﹣i B.1+i C.2﹣2i D.2+2i
【解答】解:2,
则z,
故.
故选:B.
3.(2024秋 耒阳市校级期末)已知z1=a﹣i,z2=1+bi(a,b∈R,i为虚数单位),若z1 z2是实数,则( )
A.ab﹣1=0 B.ab+1=0 C.a﹣b=0 D.a+b=0
【解答】解:z1 z2=(a﹣i)(1+bi)=a+b+(ab﹣1)i为实数,
则ab﹣1=0.
故选:A.
4.(2025 新余校级模拟)已知复数z满足|z|=1,则|z﹣3﹣2i|的最小值为( )
A. B. C. D.
【解答】解:设z=a+bi(a,b∈R),由|z|=1,可得a2+b2=1;
而,
故|z﹣3﹣2i|的最小值为.
故选:C.
5.(2025 肥城市模拟)已知复数(i为虚数单位),则为( )
A.5 B. C.7 D.
【解答】解:因为,
所以,
故.
故选:B.
6.(2025 陕西校级模拟)已知a,b∈R,a﹣2i=(b+i)i(i为虚数单位),则( )
A.a=1,b=﹣2 B.a=﹣1,b=2 C.a=﹣1,b=﹣2 D.a=1,b=2
【解答】解:a﹣2i=(b+i)i=﹣1+bi,
则a=﹣1,b=﹣2.
故选:C.
7.(2025 安徽模拟)已知a,b,c的平均数与方差均为4,则a2,b2,c2的平均数为( )
A.16 B.18 C.20 D.24
【解答】解:a,b,c的平均数与方差均为4,
∴由题意得,,
∴a+b+c=12,
,故,
解得,
∴a2,b2,c2的平均数为20.
故选:C.
8.(2025春 长沙月考)若样本平均数为,总体平均数为,则( )
A. B.
C.是的估计值 D.是的估计值
【解答】解:样本平均数为,总体平均数为,
在统计学中,可以利用样本数据估计总体数据,
∴样本平均数是总体平均数的估计值,
综上,是的估计值.
故选:D.
9.(2025 新余校级模拟)一个样本容量为4的样本的平均数为18,现样本加入新数8,此时样本数据的和为( )
A.26 B.60 C.72 D.80
【解答】解:一个样本容量为4的样本的平均数为18,
设这个样本容量为4的样本数据分别为x1,x2,x3,x4,
则,
∴x1+x2+x3+x4=72,
样本加入新数8,此时样本数据的和为72+8=80.
故选:D.
10.(2025春 渝北区校级月考)下列说法正确的是( )
A.数据1,3,3,5,6的第60百分位数是5.5
B.若一组样本数据4,6,7,8,9,a的平均数为7,则a=7
C.用分层随机抽样时,个体数最多的层里的个体被抽到的概率最大
D.若x1,x2, ,x10的标准差为4,则﹣2x1+3,﹣2x2+3, ,﹣2x10+3的标准差是8
【解答】解:对于A,因为5×60%=3,
所以数据1,3,3,5,6的第60百分位数是4,故A错误;
对于B,若一组样本数据4,6,7,8,9,a的平均数为7,则7,
解得a=8,故B错误;
对于C,用分层随机抽样时,每个个体被抽到的概率都相等,故C错误;
对于D,若x1,x2, ,x10的标准差为4,则﹣2x1+3,﹣2x2+3, ,﹣2x10+3的标准差是8,故D正确.
故选:D.
11.(2025 信阳二模)四名同学各掷骰子5次,分别记录每次骰子出现的点数.根据四名同学的统计结果,可以判断出一定没有出现点数6的是( )
A.平均数为2,方差为2.4
B.中位数为3,方差为2.8
C.平均数为3,中位数为2
D.中位数为3,众数为2
【解答】解:根据题意,依次分析选项:
对于A,若平均数为2,且出现6点,则方差S2(6﹣2)2=3.2>2.4,反之若平均数为2,方差为2.4时,一定没有出现点数6;
对于B,当投掷骰子出现结果为1,2,3,3,6时,满足中位数为3,方差为2.8,不符合题意;
对于C,当投掷骰子出现结果为1,1,2,5,6时,满足平均数为3,中位数为2,不符合题意;
对于D,当投掷骰子出现结果为2,2,3,4,6时,满足中位数为3,众数为2,不符合题意;
故选:A.
12.(2025 临翔区校级模拟)某组样本数据的频率分布直方图如图所示,设该组样本数据的众数、平均数、第一四分位数分别为x1,x2,x3,则x1,x2,x3的大小关系是(注:同一组中数据用该组区间中点值近似代替)( )
A.x3<x1<x2 B.x2<x1<x3 C.x1<x3<x2 D.x1<x2<x3
【解答】解:由频率分布直方图可知众数为,即x1=2.5,
平均数x2=0.2×1.5+0.24×2.5+0.2×3.5+0.16×4.5+0.12×5.5+0.04×6.5+0.04×7.5=3.54,
显然第一四分位数位于[2,3)之间,则0.2+(x3﹣2)×0.24=0.25,
解得x3≈2.208,
所以x3<x1<x2.
故选:A.
13.(2025 市中区校级二模)在4个人中选若干人在3天假期中值班(每天只需1人值班),不出现同一人连续值班两天,其中甲恰有一天值班的概率为( )
A. B. C. D.
【解答】解:根据题意,在4个人中选若干人在3天假期中值班,
分2种情况讨论:
在4个人中选3人在3天假期中值班,有24种选法,
在4个人中选2人在3天假期中值班,有12种选法,
则共有24+12=36种选法,
若甲恰有一天值班,有21种选法,
则甲恰有一天值班的概率P.
故选:C.
14.(2025 岳阳县校级模拟)现有8把相同的椅子排成一排,甲、乙、丙三人每人选取其中的一把椅子入座,在这三人中有两人相邻坐的条件下,则三人均相邻(甲、乙、丙之间无空座)的概率为( )
A. B. C. D.
【解答】解:根据题意,现有8把相同的椅子排成一排,
甲、乙、丙三人每人选取其中的一把椅子入座,有种情况,
其中,甲乙丙互不相邻的排法有种,
则这三人中有两人相邻坐情况有216种,
而甲、乙、丙均相邻的情况有636种,
则要求概率P.
故选:A.
15.(2025 洮北区校级模拟)6个数字1,2,2,2,3,5排成一排构成一个六位数,则这个六位数为偶数的概率为( )
A. B. C. D.
【解答】解:根据题意,6个数字1,2,2,2,3,5排成一排构成一个六位数,有120种取法,
若这个六位数为偶数,即2在个位,有60种取法,
则这个六位数为偶数的概率P.
故选:A.
16.(2025春 长沙月考)将一枚质地均匀的骰子抛掷一次,出现“正面向上的点数大于3”的概率是( )
A. B. C. D.
【解答】解:根据题意,将一枚质地均匀的骰子抛掷一次,有6种结果,分别为1,2,3,4,5,6,
其中大于3的结果有4,5,6.
所以“正面向上的点数大于3”的概率.
故选:A.
17.(2025 长沙模拟)已知向量,若x>0,y<0,则的取值范围是( )
A.[﹣2,﹣1) B. C. D.
【解答】解:设向量的夹角为θ,
设的起点在原点,与x轴正方向的夹角为α,
由可得与x轴正方向的夹角为120°,
由x>0,y<0可得的终点在第四象限,当两向量反向共线时,夹角最大,
当的终点趋于x正方向时,夹角趋近于120°,
所以120°<θ≤180°,
,
则,所以.
故选:A.
18.(2025 泉州校级模拟)已知向量和的夹角为60°,且,,则( )
A.3 B.﹣1 C. D.13
【解答】解:由和的夹角为60°,,,
可得
=8﹣5=3.
故选:A.
19.(2025春 青羊区校级月考)一船以15nmile/h的速度向东航行,船在点A处看到一个灯塔B在北偏东60°,行驶4h后,船到达点C处,看到这个灯塔在北偏东15°,这时船与灯塔的距离为( )
A.nmile B.nmile C.nmile D.nmile
【解答】解:根据题意,可得AC=15×4=60(km),
∠BAC=90°﹣60°=30°,∠ACB=90°+15°=105°,所以∠ABC=180°﹣∠BAC﹣∠ACB=45°.
由正弦定理,可得BCkm,即船与灯塔的距离为.
故选:B.
20.(2025春 江阴市月考)△ABC的内角A,B,C的对边分别为a,b,c,已知c2=2a2﹣2b2,则A﹣B的最大值为( )
A. B. C. D.
【解答】解:已知c2=2a2﹣2b2,根据正弦定理,则sin2C=2sin2A﹣2sin2B,
利用平方差公式,和差化积公式,sinC=sin(A+B),
左边等于sin2C=sin2(A+B),
右边等于2sin2A﹣2sin2B=2(sin2A﹣sin2B)=2(sinA+sinB)(sinA﹣sinB),
则sin2(A+B)=2(sinA+sinB)(sinA﹣sinB),
sin(A+B) 2 sincos2 2 sincos 2 cossin,
因为sin,cos0,
则sin(A+B)=4cossin,
则sin(A+B)=2sin(A﹣B),
则sinAcosB+cosAsinB=2(sinAcosB﹣cosAsinB),整理得,sinAcosB=3cosAsinB,
因为cosA,cosB≠0,否则角度为,与等式矛盾,两边除以cosAcosB,得tanA=3tanB,
设tanB=t,t>0,因B为锐角,否则tanB≤0导致A为钝角或直角,矛盾,则tanA=3t,
利用差角公式:,
根据基本不等式,当且仅当3t2=1,即t时取等号,
故:,
当时,,综上,A﹣B的最大值为.
故选:A.
21.(2025 金凤区校级模拟)已知△ABC的三个内角A,B,C所对的边分别为a,b,c,且,B=30°,,则b=( )
A. B. C. D.
【解答】解:因为,B=30°,,
所以S△ABC,解得c=4,
所以由余弦定理得:b2=a2+c2﹣2accosB7,
所以.
故选:B.
22.(2025 乐山模拟)某数学兴趣小组成员为测量某建筑的高度OP,选取了在同一水平面上的A,B,C三处,如图.已知在A,B,C处测得该建筑顶部P的仰角分别为30°,45°,60°,,AB=10米,则该建筑的高度OP=( )
A.米 B.米 C.米 D.米
【解答】解:设OP=x,则可得,OB=x,,
由,可得B是AC的中点,
所以AB=BC=10,
而∠OBA+∠OBC=π,则cos∠OBA+cos∠OBC=0,
在△ABO,△CBO中,由余弦定理可得:
,解得.
故选:B.
23.(2025 汉川市校级模拟)点P在边长为1的正三角形ABC的外接圆上,则的最大值为( )
A. B. C. D.
【解答】解:已知点P在边长为1的正三角形ABC的外接圆上,
设外接圆圆心为O,
则,,
则
,即,
又当时,
有,
故P在△ABC的外接圆上,
此时
,
综上可得:的最大值是.
故选:A.
24.(2025 天津)若m为直线,α,β为两个平面,则下列结论中正确的是( )
A.若m∥α,n α,则m∥n B.若m⊥α,m⊥β,则α⊥β
C.若m∥α,m⊥β,则α⊥β D.若m α,α⊥β,则m⊥β
【解答】解:对于A,若m∥α,n α,则m与n可能平行也可能异面,故A错误;
对于B,若m⊥α,m⊥β,则α∥β,故B错误;
对于C,若m∥α,m⊥β,则α⊥β,C正确;
对于D,若m α,α⊥β,则m可能平行于β,也可能与β斜交,也可能垂直于β,故D错误.
故选:C.
25.(2025 山西模拟)已知母线长为2的圆锥的侧面积是底面积的2倍,则圆锥的体积为( )
A. B. C. D.2π
【解答】解:设圆锥的底面半径为r,
由侧面积是底面积的2倍,
可得2πr=2πr2,解得r=1.
∴圆锥的高为h.
∴圆锥的体积为V.
故选:C.
26.(2025 宁远县模拟)将上下底分别为2,4,高为1的直角梯形绕其最短的底边旋转一周得到的几何体的体积为( )
A.8π B. C. D.
【解答】解:根据题意可得所求几何体为圆柱减去圆锥的体积,
所以所求为.
故选:D.
27.(2025 内江三模)已知点M为正三棱柱ABC﹣A1B1C1表面上一个异于点A1的动点,若,BB1=1,且满足,则动点M的轨迹的长度为( )
A.2π B. C. D.
【解答】解:
由题意可知,动点M在矩形ABB1A1与矩形ACC1A1的轨迹是以A1为圆心,
半径为的圆弧,此时弧长为,
动点M在△ABC的轨迹是以A为圆心,半径为1的圆弧.
此时弧长,动点M在ΔA1B1C1没有轨迹,
动点M在矩形BCC1B1的轨迹是以B1C1的中点为圆心,半径为的圆弧.
此时的弧长为,综上所述动点M的轨迹长度为.
故选:C.
28.(2025 青浦区校级模拟)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段EB的中点,则( )
A.DM≠EN,且直线DM、EN是异面直线
B.DM=EN,且直线DM、EN是异面直线
C.DM≠EN,且直线DM、EN是相交直线
D.DM=EN,且直线DM、EN是相交直线
【解答】解:取CD的中点O,连接OB、OE,连接BD、BO,
设CD=2a,则OE,OB,
∵平面ECD⊥平面ABCD,且平面ECD∩平面ABCD=CD,
OE⊥CD,则OE⊥平面ABCD,可得OE⊥OB,
∴BE,
在正方形ABCD中,BD=2,
在等腰三角形BED中,BD=BE,
又∵M是线段EB的中点,N是BD的中点,
∴△EBN≌△DBM,可得DM=EN,即DM=EN,且直线DM、EN是相交直线.
故选:D.
29.(2025春 信都区校级月考)如图,四棱柱ABCD﹣A1B1C1D1中,四边形ABCD为平行四边形,E,F分别在线段DB,DD1上,且,G在CC1上且平面AEF∥平面BD1G,则( )
A. B. C. D.
【解答】解:在四棱柱ABCD﹣A1B1C1D1中,连接B1D1,FG,如图,
因为平面AEF∥平面BD1G,平面AEF∩平面BB1D1D=EF,
平面BD1G∩平面BB1D1D=BD1,则EF∥BD1,于是,
平面ADD1A1∥平面BCC1B1,而BG 平面BCC1B1,则BG∥平面ADD1A1,
在平面ADD1A1内存在与AF不重合的直线l∥BG,又平面AEF∥平面BD1G,BG 平面BD1G,
则BG∥平面AEF,在平面AEF内存在与AF不重合直线m∥BG,从而m∥l,m 平面AEF,
l 平面AEF,则l∥平面AEF,又l 平面ADD1A1,平面AEF∩平面ADD1A1=AF,
因此AF∥l∥BG,BG,AF可确定平面ABGF,因为平面ABB1A1∥平面CDD1C1,
平面ABGF∩平面ABB1A1=AB,平面ABGF∩平面CDD1C1=FG,于是AB∥FG,即有CD∥FG,
所以.
故选:B.
30.(2025春 定海区校级期中)石墩是常见的维护交通秩序的道路设施.某路口放置的石墩(如图),其上部是原球半径为15cm的球缺,下部可看作是上、下底面半径分别为9cm、16cm的圆台,球缺的截面圆与圆台的上底面完全吻合,整个石墩的高为33cm,则石墩的体积为( )
(注:球体被平面所截,截得的部分叫球缺,球缺表面上的点到截面的最大距离为球缺的高,球缺的体积,其中R为原球半径,h为球缺的高.)
A.4374πcm3 B.5048πcm3 C.5336πcm3 D.7260πcm3
【解答】解:作出示意图如下:
因为石墩上部是原球半径为15cm的球缺,
又下部是上、下底面半径分别为9cm、16cm的圆台,
且球缺的截面圆与圆台的上底面完全吻合,整个石墩的高为33cm,
设FC为整个几何体的高度,设A为球心,B,C分别为圆台上下底面圆心,
所以FC=33cm,r1=BD=9cm,r2=EC=16cm,R=AD=15cm,
所以,则球缺的高h=FB=R+AB=27cm,
则圆台的高h′=BC=FC﹣FB=6cm,
故石墩的体积为
.
故选:C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【期末专项押题卷】单选题-2024-2025学年高一数学下学期人教A版(2019)必修第二册
1.(2025 齐齐哈尔三模)已知复数z=i(1+i),则z在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2025 泰安模拟)已知复数z满足,则( )
A.1﹣i B.1+i C.2﹣2i D.2+2i
3.(2024秋 耒阳市校级期末)已知z1=a﹣i,z2=1+bi(a,b∈R,i为虚数单位),若z1 z2是实数,则( )
A.ab﹣1=0 B.ab+1=0 C.a﹣b=0 D.a+b=0
4.(2025 新余校级模拟)已知复数z满足|z|=1,则|z﹣3﹣2i|的最小值为( )
A. B. C. D.
5.(2025 肥城市模拟)已知复数(i为虚数单位),则为( )
A.5 B. C.7 D.
6.(2025 陕西校级模拟)已知a,b∈R,a﹣2i=(b+i)i(i为虚数单位),则( )
A.a=1,b=﹣2 B.a=﹣1,b=2 C.a=﹣1,b=﹣2 D.a=1,b=2
7.(2025 安徽模拟)已知a,b,c的平均数与方差均为4,则a2,b2,c2的平均数为( )
A.16 B.18 C.20 D.24
8.(2025春 长沙月考)若样本平均数为,总体平均数为,则( )
A. B.
C.是的估计值 D.是的估计值
9.(2025 新余校级模拟)一个样本容量为4的样本的平均数为18,现样本加入新数8,此时样本数据的和为( )
A.26 B.60 C.72 D.80
10.(2025春 渝北区校级月考)下列说法正确的是( )
A.数据1,3,3,5,6的第60百分位数是5.5
B.若一组样本数据4,6,7,8,9,a的平均数为7,则a=7
C.用分层随机抽样时,个体数最多的层里的个体被抽到的概率最大
D.若x1,x2, ,x10的标准差为4,则﹣2x1+3,﹣2x2+3, ,﹣2x10+3的标准差是8
11.(2025 信阳二模)四名同学各掷骰子5次,分别记录每次骰子出现的点数.根据四名同学的统计结果,可以判断出一定没有出现点数6的是( )
A.平均数为2,方差为2.4
B.中位数为3,方差为2.8
C.平均数为3,中位数为2
D.中位数为3,众数为2
12.(2025 临翔区校级模拟)某组样本数据的频率分布直方图如图所示,设该组样本数据的众数、平均数、第一四分位数分别为x1,x2,x3,则x1,x2,x3的大小关系是(注:同一组中数据用该组区间中点值近似代替)( )
A.x3<x1<x2 B.x2<x1<x3 C.x1<x3<x2 D.x1<x2<x3
13.(2025 市中区校级二模)在4个人中选若干人在3天假期中值班(每天只需1人值班),不出现同一人连续值班两天,其中甲恰有一天值班的概率为( )
A. B. C. D.
14.(2025 岳阳县校级模拟)现有8把相同的椅子排成一排,甲、乙、丙三人每人选取其中的一把椅子入座,在这三人中有两人相邻坐的条件下,则三人均相邻(甲、乙、丙之间无空座)的概率为( )
A. B. C. D.
15.(2025 洮北区校级模拟)6个数字1,2,2,2,3,5排成一排构成一个六位数,则这个六位数为偶数的概率为( )
A. B. C. D.
16.(2025春 长沙月考)将一枚质地均匀的骰子抛掷一次,出现“正面向上的点数大于3”的概率是( )
A. B. C. D.
17.(2025 长沙模拟)已知向量,若x>0,y<0,则的取值范围是( )
A.[﹣2,﹣1) B. C. D.
18.(2025 泉州校级模拟)已知向量和的夹角为60°,且,,则( )
A.3 B.﹣1 C. D.13
19.(2025春 青羊区校级月考)一船以15nmile/h的速度向东航行,船在点A处看到一个灯塔B在北偏东60°,行驶4h后,船到达点C处,看到这个灯塔在北偏东15°,这时船与灯塔的距离为( )
A.nmile B.nmile C.nmile D.nmile
20.(2025春 江阴市月考)△ABC的内角A,B,C的对边分别为a,b,c,已知c2=2a2﹣2b2,则A﹣B的最大值为( )
A. B. C. D.
21.(2025 金凤区校级模拟)已知△ABC的三个内角A,B,C所对的边分别为a,b,c,且,B=30°,,则b=( )
A. B. C. D.
22.(2025 乐山模拟)某数学兴趣小组成员为测量某建筑的高度OP,选取了在同一水平面上的A,B,C三处,如图.已知在A,B,C处测得该建筑顶部P的仰角分别为30°,45°,60°,,AB=10米,则该建筑的高度OP=( )
A.米 B.米 C.米 D.米
23.(2025 汉川市校级模拟)点P在边长为1的正三角形ABC的外接圆上,则的最大值为( )
A. B. C. D.
24.(2025 天津)若m为直线,α,β为两个平面,则下列结论中正确的是( )
A.若m∥α,n α,则m∥n B.若m⊥α,m⊥β,则α⊥β
C.若m∥α,m⊥β,则α⊥β D.若m α,α⊥β,则m⊥β
25.(2025 山西模拟)已知母线长为2的圆锥的侧面积是底面积的2倍,则圆锥的体积为( )
A. B. C. D.2π
26.(2025 宁远县模拟)将上下底分别为2,4,高为1的直角梯形绕其最短的底边旋转一周得到的几何体的体积为( )
A.8π B. C. D.
27.(2025 内江三模)已知点M为正三棱柱ABC﹣A1B1C1表面上一个异于点A1的动点,若,BB1=1,且满足,则动点M的轨迹的长度为( )
A.2π B. C. D.
28.(2025 青浦区校级模拟)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段EB的中点,则( )
A.DM≠EN,且直线DM、EN是异面直线
B.DM=EN,且直线DM、EN是异面直线
C.DM≠EN,且直线DM、EN是相交直线
D.DM=EN,且直线DM、EN是相交直线
29.(2025春 信都区校级月考)如图,四棱柱ABCD﹣A1B1C1D1中,四边形ABCD为平行四边形,E,F分别在线段DB,DD1上,且,G在CC1上且平面AEF∥平面BD1G,则( )
A. B. C. D.
30.(2025春 定海区校级期中)石墩是常见的维护交通秩序的道路设施.某路口放置的石墩(如图),其上部是原球半径为15cm的球缺,下部可看作是上、下底面半径分别为9cm、16cm的圆台,球缺的截面圆与圆台的上底面完全吻合,整个石墩的高为33cm,则石墩的体积为( )
(注:球体被平面所截,截得的部分叫球缺,球缺表面上的点到截面的最大距离为球缺的高,球缺的体积,其中R为原球半径,h为球缺的高.)
A.4374πcm3 B.5048πcm3 C.5336πcm3 D.7260πcm3
【期末专项押题卷】单选题-2024-2025学年高一数学下学期人教A版(2019)必修第二册
参考答案与试题解析
一.选择题(共30小题)
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B B A C B C C D D D A
题号 12 13 14 15 16 17 18 19 20 21 22
答案 A C A A A A A B A B B
题号 23 24 25 26 27 28 29 30
答案 A C C D C D B C
一.选择题(共30小题)
1.(2025 齐齐哈尔三模)已知复数z=i(1+i),则z在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:∵z=i(1+i)=﹣1+i,
∴复数z在复平面内对应的点的坐标为(﹣1,1),位于第二象限.
故选:B.
2.(2025 泰安模拟)已知复数z满足,则( )
A.1﹣i B.1+i C.2﹣2i D.2+2i
【解答】解:2,
则z,
故.
故选:B.
3.(2024秋 耒阳市校级期末)已知z1=a﹣i,z2=1+bi(a,b∈R,i为虚数单位),若z1 z2是实数,则( )
A.ab﹣1=0 B.ab+1=0 C.a﹣b=0 D.a+b=0
【解答】解:z1 z2=(a﹣i)(1+bi)=a+b+(ab﹣1)i为实数,
则ab﹣1=0.
故选:A.
4.(2025 新余校级模拟)已知复数z满足|z|=1,则|z﹣3﹣2i|的最小值为( )
A. B. C. D.
【解答】解:设z=a+bi(a,b∈R),由|z|=1,可得a2+b2=1;
而,
故|z﹣3﹣2i|的最小值为.
故选:C.
5.(2025 肥城市模拟)已知复数(i为虚数单位),则为( )
A.5 B. C.7 D.
【解答】解:因为,
所以,
故.
故选:B.
6.(2025 陕西校级模拟)已知a,b∈R,a﹣2i=(b+i)i(i为虚数单位),则( )
A.a=1,b=﹣2 B.a=﹣1,b=2 C.a=﹣1,b=﹣2 D.a=1,b=2
【解答】解:a﹣2i=(b+i)i=﹣1+bi,
则a=﹣1,b=﹣2.
故选:C.
7.(2025 安徽模拟)已知a,b,c的平均数与方差均为4,则a2,b2,c2的平均数为( )
A.16 B.18 C.20 D.24
【解答】解:a,b,c的平均数与方差均为4,
∴由题意得,,
∴a+b+c=12,
,故,
解得,
∴a2,b2,c2的平均数为20.
故选:C.
8.(2025春 长沙月考)若样本平均数为,总体平均数为,则( )
A. B.
C.是的估计值 D.是的估计值
【解答】解:样本平均数为,总体平均数为,
在统计学中,可以利用样本数据估计总体数据,
∴样本平均数是总体平均数的估计值,
综上,是的估计值.
故选:D.
9.(2025 新余校级模拟)一个样本容量为4的样本的平均数为18,现样本加入新数8,此时样本数据的和为( )
A.26 B.60 C.72 D.80
【解答】解:一个样本容量为4的样本的平均数为18,
设这个样本容量为4的样本数据分别为x1,x2,x3,x4,
则,
∴x1+x2+x3+x4=72,
样本加入新数8,此时样本数据的和为72+8=80.
故选:D.
10.(2025春 渝北区校级月考)下列说法正确的是( )
A.数据1,3,3,5,6的第60百分位数是5.5
B.若一组样本数据4,6,7,8,9,a的平均数为7,则a=7
C.用分层随机抽样时,个体数最多的层里的个体被抽到的概率最大
D.若x1,x2, ,x10的标准差为4,则﹣2x1+3,﹣2x2+3, ,﹣2x10+3的标准差是8
【解答】解:对于A,因为5×60%=3,
所以数据1,3,3,5,6的第60百分位数是4,故A错误;
对于B,若一组样本数据4,6,7,8,9,a的平均数为7,则7,
解得a=8,故B错误;
对于C,用分层随机抽样时,每个个体被抽到的概率都相等,故C错误;
对于D,若x1,x2, ,x10的标准差为4,则﹣2x1+3,﹣2x2+3, ,﹣2x10+3的标准差是8,故D正确.
故选:D.
11.(2025 信阳二模)四名同学各掷骰子5次,分别记录每次骰子出现的点数.根据四名同学的统计结果,可以判断出一定没有出现点数6的是( )
A.平均数为2,方差为2.4
B.中位数为3,方差为2.8
C.平均数为3,中位数为2
D.中位数为3,众数为2
【解答】解:根据题意,依次分析选项:
对于A,若平均数为2,且出现6点,则方差S2(6﹣2)2=3.2>2.4,反之若平均数为2,方差为2.4时,一定没有出现点数6;
对于B,当投掷骰子出现结果为1,2,3,3,6时,满足中位数为3,方差为2.8,不符合题意;
对于C,当投掷骰子出现结果为1,1,2,5,6时,满足平均数为3,中位数为2,不符合题意;
对于D,当投掷骰子出现结果为2,2,3,4,6时,满足中位数为3,众数为2,不符合题意;
故选:A.
12.(2025 临翔区校级模拟)某组样本数据的频率分布直方图如图所示,设该组样本数据的众数、平均数、第一四分位数分别为x1,x2,x3,则x1,x2,x3的大小关系是(注:同一组中数据用该组区间中点值近似代替)( )
A.x3<x1<x2 B.x2<x1<x3 C.x1<x3<x2 D.x1<x2<x3
【解答】解:由频率分布直方图可知众数为,即x1=2.5,
平均数x2=0.2×1.5+0.24×2.5+0.2×3.5+0.16×4.5+0.12×5.5+0.04×6.5+0.04×7.5=3.54,
显然第一四分位数位于[2,3)之间,则0.2+(x3﹣2)×0.24=0.25,
解得x3≈2.208,
所以x3<x1<x2.
故选:A.
13.(2025 市中区校级二模)在4个人中选若干人在3天假期中值班(每天只需1人值班),不出现同一人连续值班两天,其中甲恰有一天值班的概率为( )
A. B. C. D.
【解答】解:根据题意,在4个人中选若干人在3天假期中值班,
分2种情况讨论:
在4个人中选3人在3天假期中值班,有24种选法,
在4个人中选2人在3天假期中值班,有12种选法,
则共有24+12=36种选法,
若甲恰有一天值班,有21种选法,
则甲恰有一天值班的概率P.
故选:C.
14.(2025 岳阳县校级模拟)现有8把相同的椅子排成一排,甲、乙、丙三人每人选取其中的一把椅子入座,在这三人中有两人相邻坐的条件下,则三人均相邻(甲、乙、丙之间无空座)的概率为( )
A. B. C. D.
【解答】解:根据题意,现有8把相同的椅子排成一排,
甲、乙、丙三人每人选取其中的一把椅子入座,有种情况,
其中,甲乙丙互不相邻的排法有种,
则这三人中有两人相邻坐情况有216种,
而甲、乙、丙均相邻的情况有636种,
则要求概率P.
故选:A.
15.(2025 洮北区校级模拟)6个数字1,2,2,2,3,5排成一排构成一个六位数,则这个六位数为偶数的概率为( )
A. B. C. D.
【解答】解:根据题意,6个数字1,2,2,2,3,5排成一排构成一个六位数,有120种取法,
若这个六位数为偶数,即2在个位,有60种取法,
则这个六位数为偶数的概率P.
故选:A.
16.(2025春 长沙月考)将一枚质地均匀的骰子抛掷一次,出现“正面向上的点数大于3”的概率是( )
A. B. C. D.
【解答】解:根据题意,将一枚质地均匀的骰子抛掷一次,有6种结果,分别为1,2,3,4,5,6,
其中大于3的结果有4,5,6.
所以“正面向上的点数大于3”的概率.
故选:A.
17.(2025 长沙模拟)已知向量,若x>0,y<0,则的取值范围是( )
A.[﹣2,﹣1) B. C. D.
【解答】解:设向量的夹角为θ,
设的起点在原点,与x轴正方向的夹角为α,
由可得与x轴正方向的夹角为120°,
由x>0,y<0可得的终点在第四象限,当两向量反向共线时,夹角最大,
当的终点趋于x正方向时,夹角趋近于120°,
所以120°<θ≤180°,
,
则,所以.
故选:A.
18.(2025 泉州校级模拟)已知向量和的夹角为60°,且,,则( )
A.3 B.﹣1 C. D.13
【解答】解:由和的夹角为60°,,,
可得
=8﹣5=3.
故选:A.
19.(2025春 青羊区校级月考)一船以15nmile/h的速度向东航行,船在点A处看到一个灯塔B在北偏东60°,行驶4h后,船到达点C处,看到这个灯塔在北偏东15°,这时船与灯塔的距离为( )
A.nmile B.nmile C.nmile D.nmile
【解答】解:根据题意,可得AC=15×4=60(km),
∠BAC=90°﹣60°=30°,∠ACB=90°+15°=105°,所以∠ABC=180°﹣∠BAC﹣∠ACB=45°.
由正弦定理,可得BCkm,即船与灯塔的距离为.
故选:B.
20.(2025春 江阴市月考)△ABC的内角A,B,C的对边分别为a,b,c,已知c2=2a2﹣2b2,则A﹣B的最大值为( )
A. B. C. D.
【解答】解:已知c2=2a2﹣2b2,根据正弦定理,则sin2C=2sin2A﹣2sin2B,
利用平方差公式,和差化积公式,sinC=sin(A+B),
左边等于sin2C=sin2(A+B),
右边等于2sin2A﹣2sin2B=2(sin2A﹣sin2B)=2(sinA+sinB)(sinA﹣sinB),
则sin2(A+B)=2(sinA+sinB)(sinA﹣sinB),
sin(A+B) 2 sincos2 2 sincos 2 cossin,
因为sin,cos0,
则sin(A+B)=4cossin,
则sin(A+B)=2sin(A﹣B),
则sinAcosB+cosAsinB=2(sinAcosB﹣cosAsinB),整理得,sinAcosB=3cosAsinB,
因为cosA,cosB≠0,否则角度为,与等式矛盾,两边除以cosAcosB,得tanA=3tanB,
设tanB=t,t>0,因B为锐角,否则tanB≤0导致A为钝角或直角,矛盾,则tanA=3t,
利用差角公式:,
根据基本不等式,当且仅当3t2=1,即t时取等号,
故:,
当时,,综上,A﹣B的最大值为.
故选:A.
21.(2025 金凤区校级模拟)已知△ABC的三个内角A,B,C所对的边分别为a,b,c,且,B=30°,,则b=( )
A. B. C. D.
【解答】解:因为,B=30°,,
所以S△ABC,解得c=4,
所以由余弦定理得:b2=a2+c2﹣2accosB7,
所以.
故选:B.
22.(2025 乐山模拟)某数学兴趣小组成员为测量某建筑的高度OP,选取了在同一水平面上的A,B,C三处,如图.已知在A,B,C处测得该建筑顶部P的仰角分别为30°,45°,60°,,AB=10米,则该建筑的高度OP=( )
A.米 B.米 C.米 D.米
【解答】解:设OP=x,则可得,OB=x,,
由,可得B是AC的中点,
所以AB=BC=10,
而∠OBA+∠OBC=π,则cos∠OBA+cos∠OBC=0,
在△ABO,△CBO中,由余弦定理可得:
,解得.
故选:B.
23.(2025 汉川市校级模拟)点P在边长为1的正三角形ABC的外接圆上,则的最大值为( )
A. B. C. D.
【解答】解:已知点P在边长为1的正三角形ABC的外接圆上,
设外接圆圆心为O,
则,,
则
,即,
又当时,
有,
故P在△ABC的外接圆上,
此时
,
综上可得:的最大值是.
故选:A.
24.(2025 天津)若m为直线,α,β为两个平面,则下列结论中正确的是( )
A.若m∥α,n α,则m∥n B.若m⊥α,m⊥β,则α⊥β
C.若m∥α,m⊥β,则α⊥β D.若m α,α⊥β,则m⊥β
【解答】解:对于A,若m∥α,n α,则m与n可能平行也可能异面,故A错误;
对于B,若m⊥α,m⊥β,则α∥β,故B错误;
对于C,若m∥α,m⊥β,则α⊥β,C正确;
对于D,若m α,α⊥β,则m可能平行于β,也可能与β斜交,也可能垂直于β,故D错误.
故选:C.
25.(2025 山西模拟)已知母线长为2的圆锥的侧面积是底面积的2倍,则圆锥的体积为( )
A. B. C. D.2π
【解答】解:设圆锥的底面半径为r,
由侧面积是底面积的2倍,
可得2πr=2πr2,解得r=1.
∴圆锥的高为h.
∴圆锥的体积为V.
故选:C.
26.(2025 宁远县模拟)将上下底分别为2,4,高为1的直角梯形绕其最短的底边旋转一周得到的几何体的体积为( )
A.8π B. C. D.
【解答】解:根据题意可得所求几何体为圆柱减去圆锥的体积,
所以所求为.
故选:D.
27.(2025 内江三模)已知点M为正三棱柱ABC﹣A1B1C1表面上一个异于点A1的动点,若,BB1=1,且满足,则动点M的轨迹的长度为( )
A.2π B. C. D.
【解答】解:
由题意可知,动点M在矩形ABB1A1与矩形ACC1A1的轨迹是以A1为圆心,
半径为的圆弧,此时弧长为,
动点M在△ABC的轨迹是以A为圆心,半径为1的圆弧.
此时弧长,动点M在ΔA1B1C1没有轨迹,
动点M在矩形BCC1B1的轨迹是以B1C1的中点为圆心,半径为的圆弧.
此时的弧长为,综上所述动点M的轨迹长度为.
故选:C.
28.(2025 青浦区校级模拟)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段EB的中点,则( )
A.DM≠EN,且直线DM、EN是异面直线
B.DM=EN,且直线DM、EN是异面直线
C.DM≠EN,且直线DM、EN是相交直线
D.DM=EN,且直线DM、EN是相交直线
【解答】解:取CD的中点O,连接OB、OE,连接BD、BO,
设CD=2a,则OE,OB,
∵平面ECD⊥平面ABCD,且平面ECD∩平面ABCD=CD,
OE⊥CD,则OE⊥平面ABCD,可得OE⊥OB,
∴BE,
在正方形ABCD中,BD=2,
在等腰三角形BED中,BD=BE,
又∵M是线段EB的中点,N是BD的中点,
∴△EBN≌△DBM,可得DM=EN,即DM=EN,且直线DM、EN是相交直线.
故选:D.
29.(2025春 信都区校级月考)如图,四棱柱ABCD﹣A1B1C1D1中,四边形ABCD为平行四边形,E,F分别在线段DB,DD1上,且,G在CC1上且平面AEF∥平面BD1G,则( )
A. B. C. D.
【解答】解:在四棱柱ABCD﹣A1B1C1D1中,连接B1D1,FG,如图,
因为平面AEF∥平面BD1G,平面AEF∩平面BB1D1D=EF,
平面BD1G∩平面BB1D1D=BD1,则EF∥BD1,于是,
平面ADD1A1∥平面BCC1B1,而BG 平面BCC1B1,则BG∥平面ADD1A1,
在平面ADD1A1内存在与AF不重合的直线l∥BG,又平面AEF∥平面BD1G,BG 平面BD1G,
则BG∥平面AEF,在平面AEF内存在与AF不重合直线m∥BG,从而m∥l,m 平面AEF,
l 平面AEF,则l∥平面AEF,又l 平面ADD1A1,平面AEF∩平面ADD1A1=AF,
因此AF∥l∥BG,BG,AF可确定平面ABGF,因为平面ABB1A1∥平面CDD1C1,
平面ABGF∩平面ABB1A1=AB,平面ABGF∩平面CDD1C1=FG,于是AB∥FG,即有CD∥FG,
所以.
故选:B.
30.(2025春 定海区校级期中)石墩是常见的维护交通秩序的道路设施.某路口放置的石墩(如图),其上部是原球半径为15cm的球缺,下部可看作是上、下底面半径分别为9cm、16cm的圆台,球缺的截面圆与圆台的上底面完全吻合,整个石墩的高为33cm,则石墩的体积为( )
(注:球体被平面所截,截得的部分叫球缺,球缺表面上的点到截面的最大距离为球缺的高,球缺的体积,其中R为原球半径,h为球缺的高.)
A.4374πcm3 B.5048πcm3 C.5336πcm3 D.7260πcm3
【解答】解:作出示意图如下:
因为石墩上部是原球半径为15cm的球缺,
又下部是上、下底面半径分别为9cm、16cm的圆台,
且球缺的截面圆与圆台的上底面完全吻合,整个石墩的高为33cm,
设FC为整个几何体的高度,设A为球心,B,C分别为圆台上下底面圆心,
所以FC=33cm,r1=BD=9cm,r2=EC=16cm,R=AD=15cm,
所以,则球缺的高h=FB=R+AB=27cm,
则圆台的高h′=BC=FC﹣FB=6cm,
故石墩的体积为
.
故选:C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
