【专项押题卷】临考题型分类专项押题:解答题-2024年中考数学(含解析)
文档属性
| 名称 | 【专项押题卷】临考题型分类专项押题:解答题-2024年中考数学(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 21:03:29 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【专项押题卷】临考题型分类专项押题:解答题-2024年中考数学
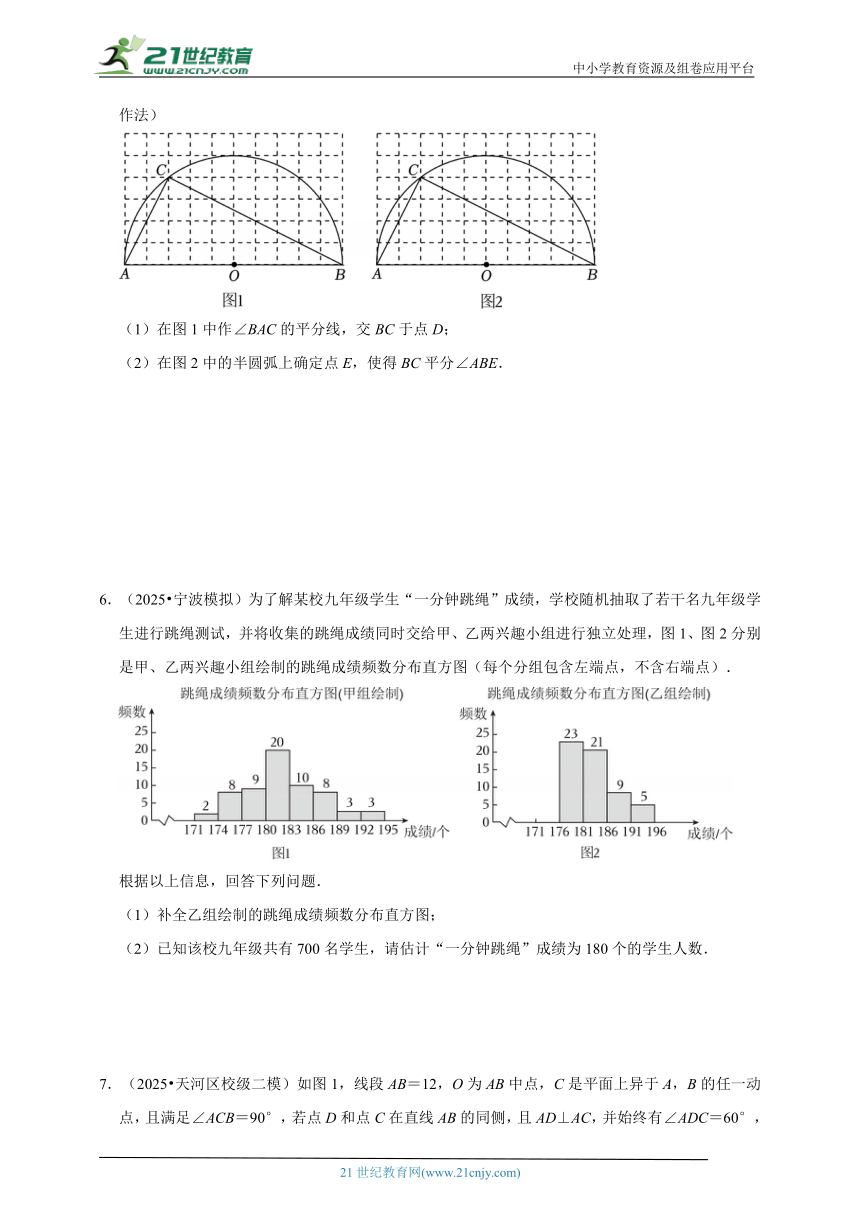
1.(2025 合肥模拟)在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系xOy,已知格点(网格线的交点)△ABC.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)在所给的网格图中确定格点D,使得点A,C1,D组成以AC1为直角边的直角三角形,并写出所有点D的坐标.
2.(2025 辽宁模拟)如图,点I在反比例函数G:(x>0,m≠0)的图象上,G过点(2,2),过点I作G的切线l:y=kx+b(k≠0)交y、x轴于A、B,连接OI.
(1)求m的值;
(2)求证:△AOB的面积为常数.
3.(2025 广东模拟)如图,已知在Rt△ABC中∠BAC=90°.
(1)实践与操作:用尺规作图法在边BC上找一点P,连接AP,使得△APC∽△BAC;(保留作图痕迹,不写作法,不用证明)
(2)应用与求解:若AD为BC边上的中线,且AB=6,AC=7,△ABD的周长为16,求△ACD的周长.
4.(2025 合肥模拟)小明在探究杠杆平衡条件的实验中,使用了一个长度为6米的杠杆,支点位于中点.杠杆左侧有A,B,C三个挂钩点,距离支点分别为1米,2米,3米;右侧有D,E,F三个挂钩点,距离支点同样为1米,2米,3米.实验中,小明在挂钩点放置物体后,杠杆可能在支点保持平衡.请回答以下问题.(杠杆定理公式:动力×动力臂=阻力×阻力臂)
(1)小明在左侧随机选择一个挂钩点挂3N的物体,在右侧也随机选择一个挂钩点挂3N的物体.请用树状图或列表法求此时杠杆恰好平衡的概率;
(2)小明改为在左侧随机选择一个挂钩点挂两个3N的物体(总重力6N),右侧随机选择一个挂钩点挂重力为G的物体.若此时杠杆平衡的概率为,请求出G的值.
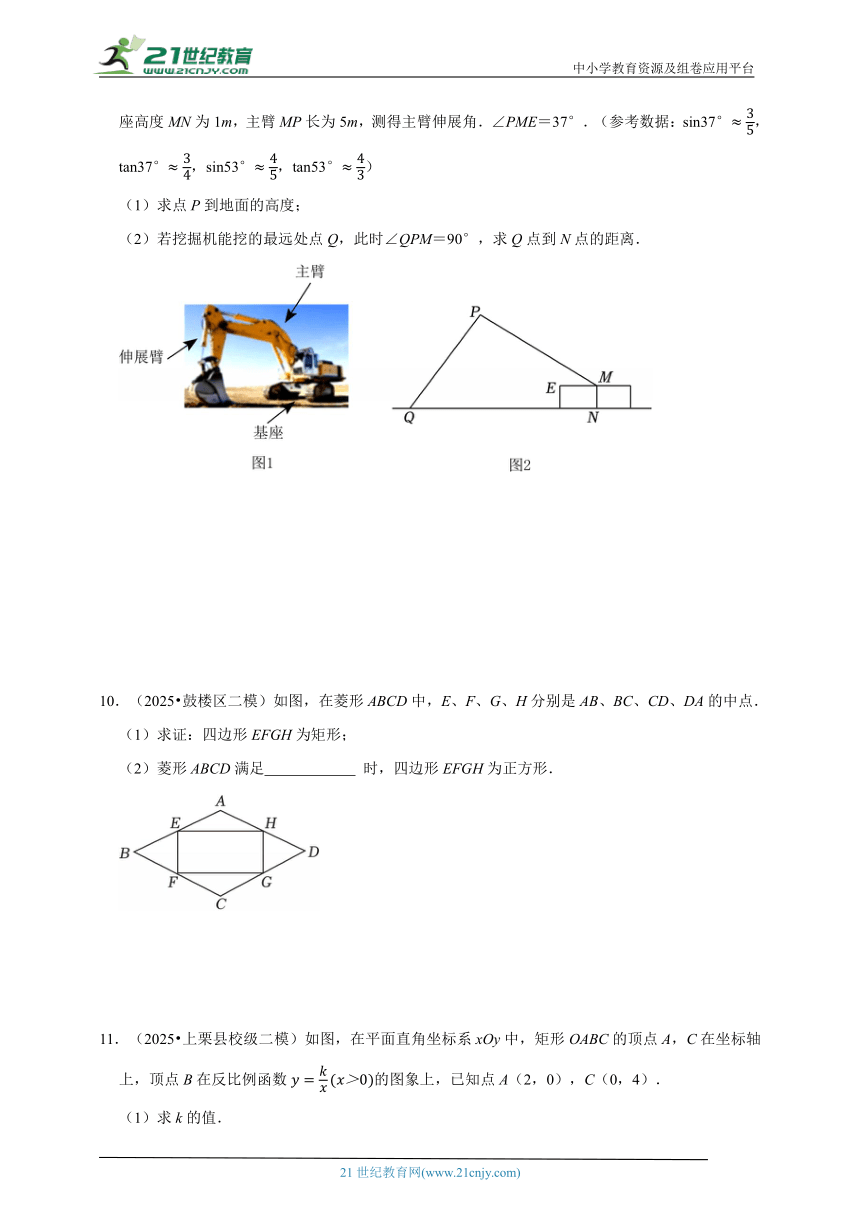
5.(2025 泰州二模)如图,是由边长为1的小正方形组成的10×6的网格,点A,B均在格点上,以AB为直径画半圆O,格点C在半圆O上.请仅用无刻度的直尺画图.(保留作图痕迹,不写作法)
(1)在图1中作∠BAC的平分线,交BC于点D;
(2)在图2中的半圆弧上确定点E,使得BC平分∠ABE.
6.(2025 宁波模拟)为了解某校九年级学生“一分钟跳绳”成绩,学校随机抽取了若干名九年级学生进行跳绳测试,并将收集的跳绳成绩同时交给甲、乙两兴趣小组进行独立处理,图1、图2分别是甲、乙两兴趣小组绘制的跳绳成绩频数分布直方图(每个分组包含左端点,不含右端点).
根据以上信息,回答下列问题.
(1)补全乙组绘制的跳绳成绩频数分布直方图;
(2)已知该校九年级共有700名学生,请估计“一分钟跳绳”成绩为180个的学生人数.
7.(2025 天河区校级二模)如图1,线段AB=12,O为AB中点,C是平面上异于A,B的任一动点,且满足∠ACB=90°,若点D和点C在直线AB的同侧,且AD⊥AC,并始终有∠ADC=60°,连接OD,CD.
(1)如图2,若∠B=∠ADC,求线段AD的长;
(2)若AC将线段OD三等分,求线段AD的长;
(3)直接写出线段OD长度的取值范围.
8.(2025 余姚市三模)如图,菱形ABCD中,以A为圆心,AD为半径画弧,以B为圆心,BD为半径画弧,两弧交于点E.
(1)求证:DE⊥AB;
(2)连结AC,若,求cos∠C的值.
9.(2025 广东模拟)图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂,EM∥QN).已知基座高度MN为1m,主臂MP长为5m,测得主臂伸展角.∠PME=37°.(参考数据:sin37°,tan37°,sin53°,tan53°)
(1)求点P到地面的高度;
(2)若挖掘机能挖的最远处点Q,此时∠QPM=90°,求Q点到N点的距离.
10.(2025 鼓楼区二模)如图,在菱形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)求证:四边形EFGH为矩形;
(2)菱形ABCD满足 时,四边形EFGH为正方形.
11.(2025 上栗县校级二模)如图,在平面直角坐标系xOy中,矩形OABC的顶点A,C在坐标轴上,顶点B在反比例函数的图象上,已知点A(2,0),C(0,4).
(1)求k的值.
(2)连接AC,BO交于点D,将矩形OABC向右平移m个单位长度得到矩形O'A'B'C'平移后点D的对应点D'在反比例函数的图象上,求m的值.
12.(2025 清丰县校级一模)周末,小轩和家人们去爬张家山锻炼身体,刚开始小轩精力充沛,爬山的速度比较快,爬了30分钟后,开始体力不支,于是减速爬到山顶.他距山脚出发地的路程s(米)与登山时间t(分钟)之间的函数关系如图所示.
(1)小轩减速前的速度为 米/分钟;
(2)求小轩减速后s与t之间的函数关系式;
(3)当小轩爬了1小时时,他距离山脚出发地的路程是多少米?
13.(2025 柯桥区二模)如图,已知菱形ABCD,∠DAB=120°,延长AC至点F,连接DF,∠FDA=90°,延长BC交DF于点E.
(1)求证:BD=DF;
(2)若AD=1,求△BDE的面积.
14.(2025 庐阳区校级三模)有一张菱形纸片,其一个内角为60°,取菱形纸片的四边和短对角线的中点,按“8”字形顺次连接各点,形成两个小三角形,这两个小三角形组成的图形简称“沙漏形”,如图(1),将“沙漏形”挖去,对剩下纸片中的菱形纸片重复上述操作,得到如图(2)所示的图形…设图(n)中的沙漏形”的个数为fn(n为正整数).
观察以上图形,解答下列问题:
(1)填空:f5= ,fn= (用含n的式子表示);
(2)当n的值为多少时,fn﹣fn﹣1的值开始大于2025.
15.(2025 高密市三模)定义:在四边形中,若有一个角是直角,且从这个直角顶点引出的对角线把对角分成的两个角中,有一个是直角,我们称这样的四边形为“双垂四边形”.
(1)如图1,在“双垂四边形ABCD”中,若∠A=65°,则∠CBD= ;
(2)如图2,在“双垂四边形ABCD”中,∠ADB=∠ABC=90°,∠A=45°,E为线段AB上一点,CD=5,且CD⊥DE,求DE的长.
16.(2025 乾安县模拟)山西某中学为提升学生的劳动能力,开辟一块菜地供学生实践使用,为保护菜地,需要利用护栏将菜地圈起来,李老师以招募工人和发放劳动报酬的方式来完成该项工作.小组的同学把“劳动基地菜地护栏建设”作为一项课题活动,利用课余时间完成了实践调查,并形成了活动报告.请根据活动报告计算支付给工人的总费用.
课题 劳动基地菜地护栏建设
调查方式 走访调研、实地查看测量
测量过程及计算 调研内容及图示
相关数据及说明: ①护栏安装工作包括安装横杠和安装竖杠两部分,且要求所有的安装工作在一天内完成,安装横杠的工人每人当天费用为200元,安装竖杠的工人每人当天费用为240元. ②共招募6名工人,每名工人在相同的时间内安装横杠2根或竖杠3根,且每名工人只完成一项工作,要求两项安装任务同时开始,并在当天同时完成.
计算结果 …
17.(2025 伊川县模拟)新年前夕,国家主席习近平通过中央广播电视总台和互联网,发表二〇二五年新年贺词,其中提到:“我们因地制宜培育新质生产力,新产业新业态新模式竞相涌现,新能源汽车年产量首次突破1000万辆,集成电路、人工智能、量子通信等领域取得新成果.”随着新能源汽车的发展,某市计划引进一批新能源公交车投入运营.新能源公交车有A,B两种车型,若购买A型公交车30辆,B型公交车10辆,共需2600万元;若购买A型公交车20辆,B型公交车30辆,共需3600万元.
(1)求购买A型和B型新能源公交车每辆分别需要多少万元.
(2)交通管理部门调研发现:A型新能源公交车适合支线道路运营,B型新能源公交车适合主干道运营.若本批次计划购买A,B两种新能源公交车共80辆,且支线道路运营车辆不超过主干道运营车辆为,请问分别购买多少辆A,B两种新能源公交车可使得政府投入的费用最少?并求出最少费用.
18.(2025 鼓楼区校级模拟)如图,在⊙O中,直径AB垂直弦CD于点E,连接AC,AD,BC,作CF⊥AD于点F,交线段OB于点G(不与点O,B重合),连接OF.
(1)若BE=1,求GE的长.
(2)求证:BC2=BG BO.
(3)若FO=FG,猜想∠CAD的度数,并证明你的结论.
19.(2025 余姚市三模)已知二次函数y=ax2+bx+1(a,b是常数).
(1)求二次函数图象经过的定点的坐标;
(2)已知函数图象过(2,1).
①若函数图象与直线y=﹣1只有一个公共点,求a的值;
②求证:当0≤x<t,且1<t≤2时,函数最大值与最小值的差为|a|.
20.(2025 通许县一模)射水鱼以陆生昆虫为食物,它在捕食时,能从口中射出一股水流,准确击中2m以内的昆虫.如果不考虑空气阻力,那么射水鱼射出的水流可以看成一条抛物线的一部分(如图).在一次捕食时,射水鱼射出的水流向上运动的高度y(单位:cm)与向前运动的水平距离x(单位:cm)的关系可以近似地表示为y=﹣0.2x2+6x.
(1)如果这次射出的水流没有遇到障碍物,它运动的高度逐步上升时,水流向前运动的水平距离x的范围是 ,它运动的高度逐步下降时,水流向前运动的水平距离x的范围是 ;
(2)假设要捕食的昆虫位于射水鱼正前方水平距离10cm,高度50cm处,那么这次射出的水流能否击中这只昆虫?
(3)假设捕食的昆虫位于射水鱼正前方25cm高度,并沿水平直线飞行,那么这次射出的水流要击中这只昆虫,可能在射水鱼正前方多远处?
21.(2025 辽宁模拟)如图1,在Rt△ABC中,AB≠AC,∠CAB=90°,点D为AC中点,连接BD,点E为BD中点,连接AE,过E作EF⊥AE交AC于F.
(1)若AB=k EF(1<k<2),求tanC的值(用含有k的代数式表示);
(2)如图2,若∠GFA=∠FAE﹣∠EAB,∠G=90°,求的值.
22.(2025 庐阳区校级二模)已知二次函数y=﹣x2+bx+c的图象经过点A(1,0).
(1)如图,当二次函数y=﹣x2+bx+c的图象与x轴另一交点为C(C点在A点右侧),交y轴于D点,直线x=2交抛物线、x轴于B、E两点,设B点坐标为(2,a).
①用含a的代数式表示b= ,c= .
②当DC=2BC时,求二次函数解析式.
(2)二次函数y=﹣x2+bx+c图象的对称轴为直线x=m,m取值范围为0≤m≤3时,求该二次函数最大值n取值范围.
23.(2025 新民市三模)已知△ABC是⊙O的内接三角形,CA=CB,∠ACB=40°,点D是⊙O上一点,连接AD,BD,CD.
(1)如图1,若BD为⊙O的直径,求∠CBD的度数;
(2)如图2,若AD∥BC,过点D作⊙O的切线交OA的延长线于点E,若DE=5,求的长.
24.(2025 顺庆区二模)在平面直角坐标系中,二次函数的图象与x轴交于A和B(1,0)两点,与y轴相交于C,且顶点D(﹣1,4),P是抛物线上一动点.
(1)求二次函数的解析式;
(2)如图1,连接BC,若∠PBC=45°,求P的坐标;
(3)如图2,过P作PQ∥AC交抛物线于Q,以P、Q、D为顶点的三角形是否存在直角三角形,若存在,求出P的坐标;若不存在,通过计算说明.
【专项押题卷】临考题型分类专项押题:解答题-2024年中考数学
参考答案与试题解析
一.解答题(共24小题)
1.(2025 合肥模拟)在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系xOy,已知格点(网格线的交点)△ABC.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)在所给的网格图中确定格点D,使得点A,C1,D组成以AC1为直角边的直角三角形,并写出所有点D的坐标.
【解答】解:(1)如图,所作△A1B1C1即为所求;
(2)如图,点D的坐标为(﹣5,5)或(3,﹣1).
理由:∵,,
,
∴,,
∴∠D2AC1=90°=∠D1AC1.
2.(2025 辽宁模拟)如图,点I在反比例函数G:(x>0,m≠0)的图象上,G过点(2,2),过点I作G的切线l:y=kx+b(k≠0)交y、x轴于A、B,连接OI.
(1)求m的值;
(2)求证:△AOB的面积为常数.
【解答】解:(1)由条件可得,
解得:m=4;
(2)设AB:y=kx+b(k≠0),
联立,
得到:,
∵x>0,
∴上式化简为:kx2+bx﹣4=0,
∵双曲线与直线的位置关系是相切,
∴Δ=b2+16k=0①,
设,将①式代入可知:,
过I作IK⊥x轴于点K,即IK∥y轴,2IK=OA,
∴△IKB∽△AOB,即I为AB中点,
∴OI=AI=IB,即∠IOK=∠IKB,
根据双曲线的性质得S△IOK=2,
∴S△IKB=2,
∵,
∴S△AOB=8,即知S△AOB的面积为常数.
3.(2025 广东模拟)如图,已知在Rt△ABC中∠BAC=90°.
(1)实践与操作:用尺规作图法在边BC上找一点P,连接AP,使得△APC∽△BAC;(保留作图痕迹,不写作法,不用证明)
(2)应用与求解:若AD为BC边上的中线,且AB=6,AC=7,△ABD的周长为16,求△ACD的周长.
【解答】解:(1)如图所示,作∠PAC=∠B,则点P即为所求.(作法不唯一);
(2)由条件可知BD=CD.
∵△ABD的周长为16,AB=6,
∴AD+BD=10,
∴AD+CD=10,
∴AD+CD+AC=17,
∴△ACD的周长为17.
4.(2025 合肥模拟)小明在探究杠杆平衡条件的实验中,使用了一个长度为6米的杠杆,支点位于中点.杠杆左侧有A,B,C三个挂钩点,距离支点分别为1米,2米,3米;右侧有D,E,F三个挂钩点,距离支点同样为1米,2米,3米.实验中,小明在挂钩点放置物体后,杠杆可能在支点保持平衡.请回答以下问题.(杠杆定理公式:动力×动力臂=阻力×阻力臂)
(1)小明在左侧随机选择一个挂钩点挂3N的物体,在右侧也随机选择一个挂钩点挂3N的物体.请用树状图或列表法求此时杠杆恰好平衡的概率;
(2)小明改为在左侧随机选择一个挂钩点挂两个3N的物体(总重力6N),右侧随机选择一个挂钩点挂重力为G的物体.若此时杠杆平衡的概率为,请求出G的值.
【解答】解:(1)画树状图如下,
从树状图中可以看到,总共有9种等可能的结果.
当左右两侧力都为3N时,只有左右两侧力臂相等,杠杆才能平衡.
所以杠杆平衡的情况有:左侧A点,右侧D点;左侧B点,右侧E点;左侧C点,右侧F点,共3种,
∴此时杠杆恰好平衡的概率;
(2)左侧随机选一个挂钩点挂6N物体,右侧随机选一个挂钩点挂重力为G的物体,同样有9种等可能的结果,
设左侧力臂为L1,取值为1米,2米,3米;右侧力臂为L2,取值为1米,2米,3米,根据杠杆定理公式可得6×L1=G×L2,即.
已知杠杆平衡的概率为,由概率公式可知平衡的情况数为种,
分情况讨论求出G的值:
当L1=1米,L2=1米时,;
当L1=1米,L2=2米时,;
当L1=1米,L2=3米时,;
当L1=2米,L2=1米时,;
当L1=2米,L2=2米时,;
当L1=2米,L2=3米时,;
当L1=3米,L2=1米时,;
当L1=3米,L2=2米时,;
当L1=3米,L2=3米时,.
要使平衡情况有3种,G的值为6N.
5.(2025 泰州二模)如图,是由边长为1的小正方形组成的10×6的网格,点A,B均在格点上,以AB为直径画半圆O,格点C在半圆O上.请仅用无刻度的直尺画图.(保留作图痕迹,不写作法)
(1)在图1中作∠BAC的平分线,交BC于点D;
(2)在图2中的半圆弧上确定点E,使得BC平分∠ABE.
【解答】解:(1)如图1,取格点G,连接OG并延长交⊙O于F,连接AF交BC于D,点D即为所求;
∵OF∥AC,
∴∠CAF=∠OFA,
∴∠OAF=∠OFA,
∴∠OAF=∠CAF;
(2)如图2,取格点H,连接AH并延长交⊙O于E,则点E即为所求;
∵,
∴∠CAE=∠ABC,
∵∠CBE=∠CAE
∴∠CBE=∠ABC.
6.(2025 宁波模拟)为了解某校九年级学生“一分钟跳绳”成绩,学校随机抽取了若干名九年级学生进行跳绳测试,并将收集的跳绳成绩同时交给甲、乙两兴趣小组进行独立处理,图1、图2分别是甲、乙两兴趣小组绘制的跳绳成绩频数分布直方图(每个分组包含左端点,不含右端点).
根据以上信息,回答下列问题.
(1)补全乙组绘制的跳绳成绩频数分布直方图;
(2)已知该校九年级共有700名学生,请估计“一分钟跳绳”成绩为180个的学生人数.
【解答】解:(1)根据题意计算出总人数为2+8+9+20+10+8+3+3=63,
∴171个≤跳绳成绩<176个的频数为63﹣23﹣21﹣9﹣5=5,
如图补全图形如下:
(2)由甲频数分布直方图得:跳绳成绩小于180个的频数为2+8+9=19,
由乙频数分布直方图得:跳绳成绩小于181个的频数为23+5=28,
所以样本中跳绳成绩等于180个的频数为28﹣19=9,
(人),
答:九年级学生中约有100人“一分钟跳绳”成绩为180个.
7.(2025 天河区校级二模)如图1,线段AB=12,O为AB中点,C是平面上异于A,B的任一动点,且满足∠ACB=90°,若点D和点C在直线AB的同侧,且AD⊥AC,并始终有∠ADC=60°,连接OD,CD.
(1)如图2,若∠B=∠ADC,求线段AD的长;
(2)若AC将线段OD三等分,求线段AD的长;
(3)直接写出线段OD长度的取值范围.
【解答】解:(1)∵∠ADC=60°,∠B=∠ADC,
∴∠B=60°,
∵∠ACB=90°,
∴,
∵AD⊥AC,
∴∠DAC=90°,
∴;
(2)取AC中点T,连接OT,设OD,AC交于R,
由题意可得:OT是△ABC的中位线,
∴,
∴∠OTA=∠BCA=90°,
∵AD⊥AC,
∴∠DAC=90°,
∴∠DAR=∠OTR=90°,
又∵∠DRA=∠ORT,
∴△DRA∽△ORT,
∴;
由题意可得:当点R是靠近点D的三等分点时,则,
∴OT=2AD,
∴BC=4AD,
在Rt△ADC中,,
在Rt△ABC中,由勾股定理得AB2=AC2+BC2,
∴,
解得或(舍去),
当点R是靠近点O的三等分点时,则,
∴,
∴BC=AD,
∴,
∴AB2=AC2+BC2,
∴,
解得AD=6或AD=﹣6(舍去);
∴AD的长为或6;
(3)过点A作AF⊥AB,使∠AOF=60°,连接OC,CF.
则∠OAF=90°,
∴∠OFA=30°,
∴OF=2OA=12,
∴,
∵,
∴,
∵∠DAC=∠OAF=90°,
∴∠DAC+∠CAO=∠OAF+∠CAO,
即∠DAO=∠CAF,
∴△CAF∽△DAO,
∴,
∴.
∵∠ACB=90°,O为AB的中点,
∴,
∵点D和点C在直线AB的同侧,
∴AF<CF,
∵AF<CF≤OF+OC,
∴,
∴.
8.(2025 余姚市三模)如图,菱形ABCD中,以A为圆心,AD为半径画弧,以B为圆心,BD为半径画弧,两弧交于点E.
(1)求证:DE⊥AB;
(2)连结AC,若,求cos∠C的值.
【解答】(1)证明:连接BD,如图1,
∵以A为圆心,AD为半径画弧,以B为圆心,BD为半径画弧,两弧交于点E,
∴BD=BE,AD=AE,
∴AB为DE的中垂线,
∴DE⊥AB;
(2)解:如图2,连接AC,BD,
∵AB为DE的中垂线,
∴∠ABD=∠ABE,
∵四边形ABCD是菱形,
∴AB=BC,∠ABD=∠CBD,
∴∠ABC=∠DBE,
∵,
∴△ABC∽△EBD,
∴,
设AF=x,AD=5a=AB,则BD=4a,BF=5a﹣x,
则(5a)2﹣x2=(4a)2﹣(5a﹣x)2,
解得x=3.4a,
∴.
9.(2025 广东模拟)图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂,EM∥QN).已知基座高度MN为1m,主臂MP长为5m,测得主臂伸展角.∠PME=37°.(参考数据:sin37°,tan37°,sin53°,tan53°)
(1)求点P到地面的高度;
(2)若挖掘机能挖的最远处点Q,此时∠QPM=90°,求Q点到N点的距离.
【解答】解:(1)作PB⊥QN于点B,延长ME交PB于点A.
∴∠PBQ=∠PBN=90°.
∵EM∥QN,
∴∠BAE=∠PAE=90°.
由题意得:MN⊥BN,
∴∠MNB=90°.
∴四边形ABNM是矩形.
∴AB=MN=1(m),AM=BN.
∵PM=5m,∠PME=37°,
∴PA=PM sin∠PME≈53(m).
∴PB=PA+AB=3+1=4(m).
答:点P到地面的高度约为4m;
(2)∵PA=3m,PM=5m,∠PAM=90°,
∴AM=4(m),∠APM+∠PME=90°.
∴BN=4(m).
∵∠QPM=90°,
∴∠QPB+∠APM=90°.
∴∠QPB=∠PME=37°.
∴QB=PB tan∠QPB≈43(m).
∴QN=QB+BN=7(m).
答:Q点到N点的距离约为7m.
10.(2025 鼓楼区二模)如图,在菱形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)求证:四边形EFGH为矩形;
(2)菱形ABCD满足 AC=BD 时,四边形EFGH为正方形.
【解答】(1)证明:如图,连接FH,EG,AC,BD,
∵四边形ABCD是菱形,E、F、G、H分别是AB、BC、CD、DA的中点,
∴AB=AD,AE∥GD,AE=GD,EF,且EF∥AC∥GH,
∴四边形EGDA是平行四边形,四边形EFGH是平行四边形,
∴EG=AD,
同理可证FH=AB,
∴EG=FH,
∴四边形EFGH为矩形;
(2)解:菱形ABCD满足AC=BD时,四边形EFGH为正方形,
∵AC=BD,
∴EF,
又∵四边形EFGH为矩形,
∴四边形EFGH为正方形.
故答案为:AC=BD.
11.(2025 上栗县校级二模)如图,在平面直角坐标系xOy中,矩形OABC的顶点A,C在坐标轴上,顶点B在反比例函数的图象上,已知点A(2,0),C(0,4).
(1)求k的值.
(2)连接AC,BO交于点D,将矩形OABC向右平移m个单位长度得到矩形O'A'B'C'平移后点D的对应点D'在反比例函数的图象上,求m的值.
【解答】解:(1)∵四边形OABC是矩形,
∴AB=OC,AO=BC,
∵A(2,0),C(0,4),
∴OA=2,OC=4,
∴点B的坐标为(2,4),
∵点B(2,4)在反比例函数的图象上,
∴k=2×4=8;
(2)∵点A的坐标为(2,0),点C的坐标为(0,4),D是AC的中点,
∴点D的坐标为(1,2),
∵将矩形OABC向右平移m个单位长度得到矩形O'A'B'C'平移后点D的对应点D'在反比例函数y的图象上,
∴D′(1+m,2),
∴2(1+m)=8,
∴m=4﹣1=3.
12.(2025 清丰县校级一模)周末,小轩和家人们去爬张家山锻炼身体,刚开始小轩精力充沛,爬山的速度比较快,爬了30分钟后,开始体力不支,于是减速爬到山顶.他距山脚出发地的路程s(米)与登山时间t(分钟)之间的函数关系如图所示.
(1)小轩减速前的速度为 20 米/分钟;
(2)求小轩减速后s与t之间的函数关系式;
(3)当小轩爬了1小时时,他距离山脚出发地的路程是多少米?
【解答】解:(1)由图象可知:小轩减速前爬山600米,用时30分钟,则小轩减速前的速度为600÷30=20米/分钟.
故答案为:20.
(2)设小轩减速后s与t之间的函数表达式为s=kt+b,
由题意可得:
,
.
∴s=8t+360;
(3)1小时=60分钟,
当t=60时,s=8×60+360=840,
答:当小轩爬了1小时时,他距离山脚出发地的路程是840米.
13.(2025 柯桥区二模)如图,已知菱形ABCD,∠DAB=120°,延长AC至点F,连接DF,∠FDA=90°,延长BC交DF于点E.
(1)求证:BD=DF;
(2)若AD=1,求△BDE的面积.
【解答】(1)证明:在菱形ABCD中,∠DAB=120°,BD平分∠CDA,AD=CD,
∴∠CDA=60°,∠DCB=∠DAB=120°,
∵∠FDA=90°,
∴∠CDB=∠ADB=∠FDC=30°,
∵∠CDA=60°,AD=CD,
∴△DCA为等边三角形.
∴∠DCA=60°,
∴∠DCF=120°,
在△DCF与△DCB中,
,
∴△DCF≌△DCB(ASA),
∴DF=BD,
即BD=DF;
(2)解:由(1)得,∠BDE=∠CDB+∠FDC=60°,∠DBE=30°.
∴∠DEB=90°,
∵AD=1,
∵四边形ABCD是菱形,△DCA为等边三角形,
∴AC⊥BD,AC=1,
∴.
∴,
∴S△BDEBE ED.
14.(2025 庐阳区校级三模)有一张菱形纸片,其一个内角为60°,取菱形纸片的四边和短对角线的中点,按“8”字形顺次连接各点,形成两个小三角形,这两个小三角形组成的图形简称“沙漏形”,如图(1),将“沙漏形”挖去,对剩下纸片中的菱形纸片重复上述操作,得到如图(2)所示的图形…设图(n)中的沙漏形”的个数为fn(n为正整数).
观察以上图形,解答下列问题:
(1)填空:f5= 31 ,fn= 2n﹣1 (用含n的式子表示);
(2)当n的值为多少时,fn﹣fn﹣1的值开始大于2025.
【解答】解:(1)第一个图形有1个“沙漏型”,
第二个图形有1+2=3 个“沙漏型”,
第三个图形有1+2+4=7个“沙漏型”,
….
由此可得到规律,第n个图形有个1+2+4+ +2n﹣1=2n﹣1图形,即,
∴fs=1+2+4+8+16=31,
故答案为:31,2n﹣1;
(2)∵,
∴
=2×2n﹣1﹣2n﹣1+1
=2n﹣1(2﹣1)+1
=2n﹣1+1,
∴2n﹣1+1>2025,
则当 n=12成立,212﹣1+1=2024+1=2025,
∴n=12.
15.(2025 高密市三模)定义:在四边形中,若有一个角是直角,且从这个直角顶点引出的对角线把对角分成的两个角中,有一个是直角,我们称这样的四边形为“双垂四边形”.
(1)如图1,在“双垂四边形ABCD”中,若∠A=65°,则∠CBD= 65° ;
(2)如图2,在“双垂四边形ABCD”中,∠ADB=∠ABC=90°,∠A=45°,E为线段AB上一点,CD=5,且CD⊥DE,求DE的长.
【解答】解:(1)∵∠ABC=∠ADB=90°,
∴∠A+∠ABD=∠CBD+∠ABD=90°,
∴∠CBD=∠A=65°,
故答案为:65°;
(2)∵同理(1)可得,∠CBD=∠A,
∵∠ADB=90°,∠A=45°,
∴∠ABD=∠DAB=45°,
∴DB=DA,
又∵∠ADB=∠CDE=90°,
∴∠CDB=∠ADE,
∴△CDB≌△EDA(ASA),
∴DE=CD=5.
16.(2025 乾安县模拟)山西某中学为提升学生的劳动能力,开辟一块菜地供学生实践使用,为保护菜地,需要利用护栏将菜地圈起来,李老师以招募工人和发放劳动报酬的方式来完成该项工作.小组的同学把“劳动基地菜地护栏建设”作为一项课题活动,利用课余时间完成了实践调查,并形成了活动报告.请根据活动报告计算支付给工人的总费用.
课题 劳动基地菜地护栏建设
调查方式 走访调研、实地查看测量
测量过程及计算 调研内容及图示
相关数据及说明: ①护栏安装工作包括安装横杠和安装竖杠两部分,且要求所有的安装工作在一天内完成,安装横杠的工人每人当天费用为200元,安装竖杠的工人每人当天费用为240元. ②共招募6名工人,每名工人在相同的时间内安装横杠2根或竖杠3根,且每名工人只完成一项工作,要求两项安装任务同时开始,并在当天同时完成.
计算结果 …
【解答】解:设招募安装横杠的工人x名,则安装竖杠的工人(6﹣x) 名.
由题意,得,
解得 x=2,
经检验,x=2 是原方程的解,
则 6﹣x=4,
支付给工人师傅的总费用为:2×200+4×240=1360(元).
答:支付给工人师傅的总费用为1360元.
17.(2025 伊川县模拟)新年前夕,国家主席习近平通过中央广播电视总台和互联网,发表二〇二五年新年贺词,其中提到:“我们因地制宜培育新质生产力,新产业新业态新模式竞相涌现,新能源汽车年产量首次突破1000万辆,集成电路、人工智能、量子通信等领域取得新成果.”随着新能源汽车的发展,某市计划引进一批新能源公交车投入运营.新能源公交车有A,B两种车型,若购买A型公交车30辆,B型公交车10辆,共需2600万元;若购买A型公交车20辆,B型公交车30辆,共需3600万元.
(1)求购买A型和B型新能源公交车每辆分别需要多少万元.
(2)交通管理部门调研发现:A型新能源公交车适合支线道路运营,B型新能源公交车适合主干道运营.若本批次计划购买A,B两种新能源公交车共80辆,且支线道路运营车辆不超过主干道运营车辆为,请问分别购买多少辆A,B两种新能源公交车可使得政府投入的费用最少?并求出最少费用.
【解答】解:(1)设购买A型新能源公交车每辆需要a元,购买B型新能源公交车每辆需要b元.
,
∴,
答:购买A型每辆需要60元,购买B型每辆需要80元;
(2)设购买A型m辆,则购买B型(80﹣m)辆,
∴,
解得m≤16,
设投入的费用为w元,则w=60m+80(80﹣m)=﹣20m+6400,
∵﹣20<0,
∴w随m的增大而减小,
∵m≤16,
∴当m=16时w的值最小,w最小=﹣20×16+6400=6080,
80﹣16=64(辆).
答:购买A型新能源公交车16辆、B型新能源公交车64辆可使得政府投入的费用最少,最少费用为6080万元.
18.(2025 鼓楼区校级模拟)如图,在⊙O中,直径AB垂直弦CD于点E,连接AC,AD,BC,作CF⊥AD于点F,交线段OB于点G(不与点O,B重合),连接OF.
(1)若BE=1,求GE的长.
(2)求证:BC2=BG BO.
(3)若FO=FG,猜想∠CAD的度数,并证明你的结论.
【解答】(1)解:∵直径AB垂直弦CD,
∴∠AED=90°,
∴∠DAE+∠D=90°,
∵CF⊥AD,
∴∠FCD+∠D=90°,
∴∠DAE=∠FCD,
由圆周角定理得∠DAE=∠BCD,
∴∠BCD=∠FCD,
在△BCE和△GCE中,
,
,∴△BCE≌△GCE(ASA),
∴GE=BE=1;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
在△ACB和△CEB中,
,
,∴△ACB∽△CEB,
∴,
∴BC2=BA BE,
由(1)知GE=BE,
∴,
又∵AB=2BO,
∴;
(3)解:∠CAD=45°,证明如下:
如图,连接OC,
∵FO=FG,
∴∠FOG=∠FGO,
∵直径AB垂直弦CD,
∴CE=DE,∠AED=∠AEC=90°,
又∵AE=AE,
∴△ACE≌△ADE(SAS),
∴∠DAE=∠CAE,
设∠DAE=∠CAE=α,∠FOG=∠FGO=β,
则∠FCD=∠BCD=∠DAE=α,
∵OA=OC,
∴∠OCA=∠OAC=α,
又∵∠ACB=90°,
∴∠OCF=∠ACB﹣∠OCA﹣∠FCD﹣∠BCD=90°﹣3α,
∵∠CGE=∠OGF=β,∠GCE=α,∠CGE+∠GCE=90°,
∴β+α=90°,
∴α=90°﹣β,
∵∠COG=∠OAC+∠OCA=α+α=2α,
∴∠COF=∠COG+∠GOF=2α+β=2(90°﹣β)+β=180°﹣β,
∴∠COF=∠AOF,
在△COF和△AOF中,
,
∴△COF≌△AOF(SAS),
∴∠OCF=∠OAF,
即90°﹣3α=α,
∴α=22.5°,
∴∠CAD=2α=45°.
19.(2025 余姚市三模)已知二次函数y=ax2+bx+1(a,b是常数).
(1)求二次函数图象经过的定点的坐标;
(2)已知函数图象过(2,1).
①若函数图象与直线y=﹣1只有一个公共点,求a的值;
②求证:当0≤x<t,且1<t≤2时,函数最大值与最小值的差为|a|.
【解答】解:(1)令x=0,则y=1,
∴函数图象过定点(0,1);
(2)①由题意可得:
∴函数图象对称轴为直线x=1,即顶点坐标为(1,﹣1),
∴,
∴a=2,
②证明:函数图象顶点为(1,﹣a+1),
若a>0,当x=0时,y取最大值为1,x=1时,y取最小值为﹣a+1,
∴1﹣(﹣a+1)=a=|a|.
若a<0,x=1时,y取最大值为﹣a+1,x=0时,y取最小值为1,
∴(﹣a+1)﹣1=﹣a=|a|,
∴函数最大值与最小值的差为|a|.
20.(2025 通许县一模)射水鱼以陆生昆虫为食物,它在捕食时,能从口中射出一股水流,准确击中2m以内的昆虫.如果不考虑空气阻力,那么射水鱼射出的水流可以看成一条抛物线的一部分(如图).在一次捕食时,射水鱼射出的水流向上运动的高度y(单位:cm)与向前运动的水平距离x(单位:cm)的关系可以近似地表示为y=﹣0.2x2+6x.
(1)如果这次射出的水流没有遇到障碍物,它运动的高度逐步上升时,水流向前运动的水平距离x的范围是 0<x<15 ,它运动的高度逐步下降时,水流向前运动的水平距离x的范围是 15<x<30 ;
(2)假设要捕食的昆虫位于射水鱼正前方水平距离10cm,高度50cm处,那么这次射出的水流能否击中这只昆虫?
(3)假设捕食的昆虫位于射水鱼正前方25cm高度,并沿水平直线飞行,那么这次射出的水流要击中这只昆虫,可能在射水鱼正前方多远处?
【解答】解:(1)当y=0时,
﹣0.2x2+6x=0,
∴x1=0,x2=30,
抛物线的顶点横坐标为:
,
∴它运动的高度逐步上升时,水流向前运动的水平距离x的范围是0<x<15,它运动的高度逐步下降时,水流向前运动的水平距离x的范围是15<x<30;
故答案为:0<x<15,15<x<30;
(2)当x=10时,
y=﹣0.2×102+6×10=40<50,
∴不能击中这只昆虫;
(3)当y=25时,
25=﹣0.2x2+6x,
∴x1=5,x2=25,
∴可能在射水鱼正前方5cm或25cm处.
21.(2025 辽宁模拟)如图1,在Rt△ABC中,AB≠AC,∠CAB=90°,点D为AC中点,连接BD,点E为BD中点,连接AE,过E作EF⊥AE交AC于F.
(1)若AB=k EF(1<k<2),求tanC的值(用含有k的代数式表示);
(2)如图2,若∠GFA=∠FAE﹣∠EAB,∠G=90°,求的值.
【解答】解:(1)由题意可得:AE=BE,
∴∠EAB=∠ABE.
∵∠EFA+∠FAE=∠EAB+∠DAE=90°,
∴∠ABD=∠AFE,
∵∠ABD=∠AFE,∠AEF=∠DAB=90°,
∴△AEF∽△ABD,
∴,
设AE=DE=BE=a,BD=2a,AD=ka,
∵,
∴;
(2)延长FE至H,使得FE=EH,连接BH、AH,如图1,
∵DE=CE,FE=EH,∠DEF=∠CEH,
∴△DFE≌△BEH(SAS),
∴∠FDE=∠HBE,
∴∠ABH=∠EBH﹣∠ABD=∠FDE﹣∠ABD=∠DAB=90°=∠G.
∴AF=AH,
∴∠EAH=∠FAE,
又∵∠GFA=∠FAE﹣∠EAB=∠EAH﹣∠BAE=∠BAH,
∴△GAF≌△BHA(AAS),
∴DF=BH=AG.
∴.
22.(2025 庐阳区校级二模)已知二次函数y=﹣x2+bx+c的图象经过点A(1,0).
(1)如图,当二次函数y=﹣x2+bx+c的图象与x轴另一交点为C(C点在A点右侧),交y轴于D点,直线x=2交抛物线、x轴于B、E两点,设B点坐标为(2,a).
①用含a的代数式表示b= a+3 ,c= ﹣a﹣2 .
②当DC=2BC时,求二次函数解析式.
(2)二次函数y=﹣x2+bx+c图象的对称轴为直线x=m,m取值范围为0≤m≤3时,求该二次函数最大值n取值范围.
【解答】解:(1)①把A(1,0),B(2,a)代入y=﹣x2+bx+c,得:,
解得:,
故答案为:a+3,﹣a﹣2;
②由①知:y=﹣x2+(a+3)x﹣a﹣2,
当x=0时,y=﹣a﹣2,当y=﹣x2+(a+3)x﹣a﹣2=0时,x1=1,x2=a+2,
∴C(a+2,0),D(0,﹣a﹣2),a+2>1,
∴a>﹣1;
∵DC=2BC,B(2,a),
∴(a+2)2+(a+2)2=4[(a+2﹣2)2+a2],
解得:或a=2,
∴或y=﹣x2+(2+3)x﹣2﹣2=﹣x2+5x﹣4,
综上:或y=﹣x2+5x﹣4;
(2)把A(1,0),代入y=﹣x2+bx+c,得:﹣1+b+c=0,
∴c=1﹣b,
∴y=﹣x2+bx+1﹣b,
∵对称轴为直线,
∴b=2m,
∴y=﹣x2+2mx+1﹣2m,
∴当x=m时,函数有最大值为:n=﹣m2+2m2+1﹣2m=(m﹣1)2,
对于n=﹣m2+2m2+1﹣2m=(m﹣1)2,
抛物线的开口向上,对称轴为直线m=1,抛物线上的点离对称轴越远,函数值越大,
∵0≤m≤3,
∴当m=1时,函数有最小值为:(1﹣1)2=0,当m=3时,函数有最大值为:(3﹣1)2=4,
∴0≤n≤4.
23.(2025 新民市三模)已知△ABC是⊙O的内接三角形,CA=CB,∠ACB=40°,点D是⊙O上一点,连接AD,BD,CD.
(1)如图1,若BD为⊙O的直径,求∠CBD的度数;
(2)如图2,若AD∥BC,过点D作⊙O的切线交OA的延长线于点E,若DE=5,求的长.
【解答】解:(1)∵CA=CB,∠ACB=40°,
∴,
若BD为⊙O的直径,
∴∠BCD=90°,
∴∠ACD=∠BCD﹣∠ACB=90°﹣40°=50°,
∵,
∴∠ACD=∠ABD=50°,
∴∠CBD=∠CBA﹣∠ABD=70°﹣50°=20°;
(2)∵,
∴∠BAC=∠BDC=70°,
∵,
∴∠ACB=∠ADB=40°,
∴∠ADC=∠ADB+∠BDC=40°+70°=110°,
∵AD∥BC,
∴∠BCD=180°﹣∠ADC=70°,
∴∠ACD=∠BCD﹣∠ACB=70°﹣40°=30°,
如图所示,连接OD,
∵所对圆心角是∠AOD,所对圆周角是∠ACD,
∴∠AOD=2∠ACD=60°,
∵DE是⊙O的切线,
∴∠ODE=90°,
在Rt△ODE中,∠E=30°,
∴OE=2OD,
∴OE2=OD2+DE2,即可(2OD)2=OD2+52,
解得,(负值舍去),
∴长.
24.(2025 顺庆区二模)在平面直角坐标系中,二次函数的图象与x轴交于A和B(1,0)两点,与y轴相交于C,且顶点D(﹣1,4),P是抛物线上一动点.
(1)求二次函数的解析式;
(2)如图1,连接BC,若∠PBC=45°,求P的坐标;
(3)如图2,过P作PQ∥AC交抛物线于Q,以P、Q、D为顶点的三角形是否存在直角三角形,若存在,求出P的坐标;若不存在,通过计算说明.
【解答】解:(1)∵二次函数的图象顶点为点D(﹣1,4),
故设抛物线解析式为y=a(x+1)2+4(a≠0)),
∵抛物线图象经过B(1,0),
∴a(1+1)2+4=0,
解得:a=﹣1,
∴抛物线解析式为y=﹣(x+1)2+4,即y=﹣x2﹣2x+3;
(2)将CB以C为旋转中心顺时针旋转90°,B对应点B',连接BB'交抛物线于P,过C作MN∥x轴,且BN⊥MN,B'M⊥MN,
∴∠PBC=45°,
令﹣x2﹣2x+3=0,解得:x1=﹣3,x2=1,
∴A(﹣3,0),B(1,0),
∵当x=0时,y=3,
∴C(0,3),
∵∠MCB'=∠CBN=90°﹣∠NCB,
∴在△MB'C和△NCB中,
,
∴△MB'C≌△NCB(AAS),
∴NB=MC=yc﹣yb=3,CN=B'M=xB﹣xC=1,
∴B'(﹣3,2),
设BB'的直线解析式为y=kx+b(k≠0),
∴,
解得:,,
∴BB'的直线解析式为,
∴,
整理得2x2+3x﹣5=0,
解得:,x2=1,
当时,,
∴;
(3)①当∠PDQ=90°时,设PD的直线方程为y=k1(x+1)+4,
设QD的直线方程为y=k2(x+1)+4,
∴,
整理得x2+(k1+2)x+k1+1=0,
∴xP+xD=﹣k1﹣2,xP xD=k1+1,
∴xP﹣1=﹣k1﹣2,
∴k1=﹣xP﹣1,
∴,
整理得x2+(k2+2)x+k2+1=0,
∴xD+xQ=﹣k2﹣2,xD xQ=k2+1,
∴xQ﹣1=﹣k2﹣2,
∴k2=﹣xQ﹣1,
∵∠PDQ=90°,
∴直线PD与x轴夹角的正切值=直线DQ与x轴夹角的正切值的倒数,
∴,即,
∴k1 k2=﹣1,
∴(﹣xP﹣1)(﹣xQ﹣1)=﹣1,
即xP xQ+xP+xQ+2=0,
∵PQ∥AC,
设PQ的直线解析式为y=x+b,
,
整理得:x2+3x+b﹣3=0,
∴xP+xQ=﹣3,xP xQ=b﹣3,
∴b﹣3+(﹣3)+2=0,
解得:b=4,
∴PQ的直线解析式为y=x+4,
∴,
整理得x2+3x+1=0,
解得:,,
∵当P在Q的左侧时,
∴,
∴,
∴,
∵当P在Q的右侧时,
,,
∴;
②由(1)知,顶点D(﹣1,4),C(0,3),A(﹣3,0),
DC2=(﹣1﹣0)2+(4﹣3)2=2,
AC2=32+32=18,
AD2=(﹣1+3)2+(4﹣0)2=20,
∴AD2=AC2+CD2,
∴此时△ACD为直角三角形,即∠ACD=90°,
若∠PQD=90°,此时PQ与AC重合,与题意不合,应舍去.
综上,或时,以P,Q,D为顶点的三角形是直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【专项押题卷】临考题型分类专项押题:解答题-2024年中考数学
1.(2025 合肥模拟)在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系xOy,已知格点(网格线的交点)△ABC.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)在所给的网格图中确定格点D,使得点A,C1,D组成以AC1为直角边的直角三角形,并写出所有点D的坐标.
2.(2025 辽宁模拟)如图,点I在反比例函数G:(x>0,m≠0)的图象上,G过点(2,2),过点I作G的切线l:y=kx+b(k≠0)交y、x轴于A、B,连接OI.
(1)求m的值;
(2)求证:△AOB的面积为常数.
3.(2025 广东模拟)如图,已知在Rt△ABC中∠BAC=90°.
(1)实践与操作:用尺规作图法在边BC上找一点P,连接AP,使得△APC∽△BAC;(保留作图痕迹,不写作法,不用证明)
(2)应用与求解:若AD为BC边上的中线,且AB=6,AC=7,△ABD的周长为16,求△ACD的周长.
4.(2025 合肥模拟)小明在探究杠杆平衡条件的实验中,使用了一个长度为6米的杠杆,支点位于中点.杠杆左侧有A,B,C三个挂钩点,距离支点分别为1米,2米,3米;右侧有D,E,F三个挂钩点,距离支点同样为1米,2米,3米.实验中,小明在挂钩点放置物体后,杠杆可能在支点保持平衡.请回答以下问题.(杠杆定理公式:动力×动力臂=阻力×阻力臂)
(1)小明在左侧随机选择一个挂钩点挂3N的物体,在右侧也随机选择一个挂钩点挂3N的物体.请用树状图或列表法求此时杠杆恰好平衡的概率;
(2)小明改为在左侧随机选择一个挂钩点挂两个3N的物体(总重力6N),右侧随机选择一个挂钩点挂重力为G的物体.若此时杠杆平衡的概率为,请求出G的值.
5.(2025 泰州二模)如图,是由边长为1的小正方形组成的10×6的网格,点A,B均在格点上,以AB为直径画半圆O,格点C在半圆O上.请仅用无刻度的直尺画图.(保留作图痕迹,不写作法)
(1)在图1中作∠BAC的平分线,交BC于点D;
(2)在图2中的半圆弧上确定点E,使得BC平分∠ABE.
6.(2025 宁波模拟)为了解某校九年级学生“一分钟跳绳”成绩,学校随机抽取了若干名九年级学生进行跳绳测试,并将收集的跳绳成绩同时交给甲、乙两兴趣小组进行独立处理,图1、图2分别是甲、乙两兴趣小组绘制的跳绳成绩频数分布直方图(每个分组包含左端点,不含右端点).
根据以上信息,回答下列问题.
(1)补全乙组绘制的跳绳成绩频数分布直方图;
(2)已知该校九年级共有700名学生,请估计“一分钟跳绳”成绩为180个的学生人数.
7.(2025 天河区校级二模)如图1,线段AB=12,O为AB中点,C是平面上异于A,B的任一动点,且满足∠ACB=90°,若点D和点C在直线AB的同侧,且AD⊥AC,并始终有∠ADC=60°,连接OD,CD.
(1)如图2,若∠B=∠ADC,求线段AD的长;
(2)若AC将线段OD三等分,求线段AD的长;
(3)直接写出线段OD长度的取值范围.
8.(2025 余姚市三模)如图,菱形ABCD中,以A为圆心,AD为半径画弧,以B为圆心,BD为半径画弧,两弧交于点E.
(1)求证:DE⊥AB;
(2)连结AC,若,求cos∠C的值.
9.(2025 广东模拟)图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂,EM∥QN).已知基座高度MN为1m,主臂MP长为5m,测得主臂伸展角.∠PME=37°.(参考数据:sin37°,tan37°,sin53°,tan53°)
(1)求点P到地面的高度;
(2)若挖掘机能挖的最远处点Q,此时∠QPM=90°,求Q点到N点的距离.
10.(2025 鼓楼区二模)如图,在菱形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)求证:四边形EFGH为矩形;
(2)菱形ABCD满足 时,四边形EFGH为正方形.
11.(2025 上栗县校级二模)如图,在平面直角坐标系xOy中,矩形OABC的顶点A,C在坐标轴上,顶点B在反比例函数的图象上,已知点A(2,0),C(0,4).
(1)求k的值.
(2)连接AC,BO交于点D,将矩形OABC向右平移m个单位长度得到矩形O'A'B'C'平移后点D的对应点D'在反比例函数的图象上,求m的值.
12.(2025 清丰县校级一模)周末,小轩和家人们去爬张家山锻炼身体,刚开始小轩精力充沛,爬山的速度比较快,爬了30分钟后,开始体力不支,于是减速爬到山顶.他距山脚出发地的路程s(米)与登山时间t(分钟)之间的函数关系如图所示.
(1)小轩减速前的速度为 米/分钟;
(2)求小轩减速后s与t之间的函数关系式;
(3)当小轩爬了1小时时,他距离山脚出发地的路程是多少米?
13.(2025 柯桥区二模)如图,已知菱形ABCD,∠DAB=120°,延长AC至点F,连接DF,∠FDA=90°,延长BC交DF于点E.
(1)求证:BD=DF;
(2)若AD=1,求△BDE的面积.
14.(2025 庐阳区校级三模)有一张菱形纸片,其一个内角为60°,取菱形纸片的四边和短对角线的中点,按“8”字形顺次连接各点,形成两个小三角形,这两个小三角形组成的图形简称“沙漏形”,如图(1),将“沙漏形”挖去,对剩下纸片中的菱形纸片重复上述操作,得到如图(2)所示的图形…设图(n)中的沙漏形”的个数为fn(n为正整数).
观察以上图形,解答下列问题:
(1)填空:f5= ,fn= (用含n的式子表示);
(2)当n的值为多少时,fn﹣fn﹣1的值开始大于2025.
15.(2025 高密市三模)定义:在四边形中,若有一个角是直角,且从这个直角顶点引出的对角线把对角分成的两个角中,有一个是直角,我们称这样的四边形为“双垂四边形”.
(1)如图1,在“双垂四边形ABCD”中,若∠A=65°,则∠CBD= ;
(2)如图2,在“双垂四边形ABCD”中,∠ADB=∠ABC=90°,∠A=45°,E为线段AB上一点,CD=5,且CD⊥DE,求DE的长.
16.(2025 乾安县模拟)山西某中学为提升学生的劳动能力,开辟一块菜地供学生实践使用,为保护菜地,需要利用护栏将菜地圈起来,李老师以招募工人和发放劳动报酬的方式来完成该项工作.小组的同学把“劳动基地菜地护栏建设”作为一项课题活动,利用课余时间完成了实践调查,并形成了活动报告.请根据活动报告计算支付给工人的总费用.
课题 劳动基地菜地护栏建设
调查方式 走访调研、实地查看测量
测量过程及计算 调研内容及图示
相关数据及说明: ①护栏安装工作包括安装横杠和安装竖杠两部分,且要求所有的安装工作在一天内完成,安装横杠的工人每人当天费用为200元,安装竖杠的工人每人当天费用为240元. ②共招募6名工人,每名工人在相同的时间内安装横杠2根或竖杠3根,且每名工人只完成一项工作,要求两项安装任务同时开始,并在当天同时完成.
计算结果 …
17.(2025 伊川县模拟)新年前夕,国家主席习近平通过中央广播电视总台和互联网,发表二〇二五年新年贺词,其中提到:“我们因地制宜培育新质生产力,新产业新业态新模式竞相涌现,新能源汽车年产量首次突破1000万辆,集成电路、人工智能、量子通信等领域取得新成果.”随着新能源汽车的发展,某市计划引进一批新能源公交车投入运营.新能源公交车有A,B两种车型,若购买A型公交车30辆,B型公交车10辆,共需2600万元;若购买A型公交车20辆,B型公交车30辆,共需3600万元.
(1)求购买A型和B型新能源公交车每辆分别需要多少万元.
(2)交通管理部门调研发现:A型新能源公交车适合支线道路运营,B型新能源公交车适合主干道运营.若本批次计划购买A,B两种新能源公交车共80辆,且支线道路运营车辆不超过主干道运营车辆为,请问分别购买多少辆A,B两种新能源公交车可使得政府投入的费用最少?并求出最少费用.
18.(2025 鼓楼区校级模拟)如图,在⊙O中,直径AB垂直弦CD于点E,连接AC,AD,BC,作CF⊥AD于点F,交线段OB于点G(不与点O,B重合),连接OF.
(1)若BE=1,求GE的长.
(2)求证:BC2=BG BO.
(3)若FO=FG,猜想∠CAD的度数,并证明你的结论.
19.(2025 余姚市三模)已知二次函数y=ax2+bx+1(a,b是常数).
(1)求二次函数图象经过的定点的坐标;
(2)已知函数图象过(2,1).
①若函数图象与直线y=﹣1只有一个公共点,求a的值;
②求证:当0≤x<t,且1<t≤2时,函数最大值与最小值的差为|a|.
20.(2025 通许县一模)射水鱼以陆生昆虫为食物,它在捕食时,能从口中射出一股水流,准确击中2m以内的昆虫.如果不考虑空气阻力,那么射水鱼射出的水流可以看成一条抛物线的一部分(如图).在一次捕食时,射水鱼射出的水流向上运动的高度y(单位:cm)与向前运动的水平距离x(单位:cm)的关系可以近似地表示为y=﹣0.2x2+6x.
(1)如果这次射出的水流没有遇到障碍物,它运动的高度逐步上升时,水流向前运动的水平距离x的范围是 ,它运动的高度逐步下降时,水流向前运动的水平距离x的范围是 ;
(2)假设要捕食的昆虫位于射水鱼正前方水平距离10cm,高度50cm处,那么这次射出的水流能否击中这只昆虫?
(3)假设捕食的昆虫位于射水鱼正前方25cm高度,并沿水平直线飞行,那么这次射出的水流要击中这只昆虫,可能在射水鱼正前方多远处?
21.(2025 辽宁模拟)如图1,在Rt△ABC中,AB≠AC,∠CAB=90°,点D为AC中点,连接BD,点E为BD中点,连接AE,过E作EF⊥AE交AC于F.
(1)若AB=k EF(1<k<2),求tanC的值(用含有k的代数式表示);
(2)如图2,若∠GFA=∠FAE﹣∠EAB,∠G=90°,求的值.
22.(2025 庐阳区校级二模)已知二次函数y=﹣x2+bx+c的图象经过点A(1,0).
(1)如图,当二次函数y=﹣x2+bx+c的图象与x轴另一交点为C(C点在A点右侧),交y轴于D点,直线x=2交抛物线、x轴于B、E两点,设B点坐标为(2,a).
①用含a的代数式表示b= ,c= .
②当DC=2BC时,求二次函数解析式.
(2)二次函数y=﹣x2+bx+c图象的对称轴为直线x=m,m取值范围为0≤m≤3时,求该二次函数最大值n取值范围.
23.(2025 新民市三模)已知△ABC是⊙O的内接三角形,CA=CB,∠ACB=40°,点D是⊙O上一点,连接AD,BD,CD.
(1)如图1,若BD为⊙O的直径,求∠CBD的度数;
(2)如图2,若AD∥BC,过点D作⊙O的切线交OA的延长线于点E,若DE=5,求的长.
24.(2025 顺庆区二模)在平面直角坐标系中,二次函数的图象与x轴交于A和B(1,0)两点,与y轴相交于C,且顶点D(﹣1,4),P是抛物线上一动点.
(1)求二次函数的解析式;
(2)如图1,连接BC,若∠PBC=45°,求P的坐标;
(3)如图2,过P作PQ∥AC交抛物线于Q,以P、Q、D为顶点的三角形是否存在直角三角形,若存在,求出P的坐标;若不存在,通过计算说明.
【专项押题卷】临考题型分类专项押题:解答题-2024年中考数学
参考答案与试题解析
一.解答题(共24小题)
1.(2025 合肥模拟)在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系xOy,已知格点(网格线的交点)△ABC.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)在所给的网格图中确定格点D,使得点A,C1,D组成以AC1为直角边的直角三角形,并写出所有点D的坐标.
【解答】解:(1)如图,所作△A1B1C1即为所求;
(2)如图,点D的坐标为(﹣5,5)或(3,﹣1).
理由:∵,,
,
∴,,
∴∠D2AC1=90°=∠D1AC1.
2.(2025 辽宁模拟)如图,点I在反比例函数G:(x>0,m≠0)的图象上,G过点(2,2),过点I作G的切线l:y=kx+b(k≠0)交y、x轴于A、B,连接OI.
(1)求m的值;
(2)求证:△AOB的面积为常数.
【解答】解:(1)由条件可得,
解得:m=4;
(2)设AB:y=kx+b(k≠0),
联立,
得到:,
∵x>0,
∴上式化简为:kx2+bx﹣4=0,
∵双曲线与直线的位置关系是相切,
∴Δ=b2+16k=0①,
设,将①式代入可知:,
过I作IK⊥x轴于点K,即IK∥y轴,2IK=OA,
∴△IKB∽△AOB,即I为AB中点,
∴OI=AI=IB,即∠IOK=∠IKB,
根据双曲线的性质得S△IOK=2,
∴S△IKB=2,
∵,
∴S△AOB=8,即知S△AOB的面积为常数.
3.(2025 广东模拟)如图,已知在Rt△ABC中∠BAC=90°.
(1)实践与操作:用尺规作图法在边BC上找一点P,连接AP,使得△APC∽△BAC;(保留作图痕迹,不写作法,不用证明)
(2)应用与求解:若AD为BC边上的中线,且AB=6,AC=7,△ABD的周长为16,求△ACD的周长.
【解答】解:(1)如图所示,作∠PAC=∠B,则点P即为所求.(作法不唯一);
(2)由条件可知BD=CD.
∵△ABD的周长为16,AB=6,
∴AD+BD=10,
∴AD+CD=10,
∴AD+CD+AC=17,
∴△ACD的周长为17.
4.(2025 合肥模拟)小明在探究杠杆平衡条件的实验中,使用了一个长度为6米的杠杆,支点位于中点.杠杆左侧有A,B,C三个挂钩点,距离支点分别为1米,2米,3米;右侧有D,E,F三个挂钩点,距离支点同样为1米,2米,3米.实验中,小明在挂钩点放置物体后,杠杆可能在支点保持平衡.请回答以下问题.(杠杆定理公式:动力×动力臂=阻力×阻力臂)
(1)小明在左侧随机选择一个挂钩点挂3N的物体,在右侧也随机选择一个挂钩点挂3N的物体.请用树状图或列表法求此时杠杆恰好平衡的概率;
(2)小明改为在左侧随机选择一个挂钩点挂两个3N的物体(总重力6N),右侧随机选择一个挂钩点挂重力为G的物体.若此时杠杆平衡的概率为,请求出G的值.
【解答】解:(1)画树状图如下,
从树状图中可以看到,总共有9种等可能的结果.
当左右两侧力都为3N时,只有左右两侧力臂相等,杠杆才能平衡.
所以杠杆平衡的情况有:左侧A点,右侧D点;左侧B点,右侧E点;左侧C点,右侧F点,共3种,
∴此时杠杆恰好平衡的概率;
(2)左侧随机选一个挂钩点挂6N物体,右侧随机选一个挂钩点挂重力为G的物体,同样有9种等可能的结果,
设左侧力臂为L1,取值为1米,2米,3米;右侧力臂为L2,取值为1米,2米,3米,根据杠杆定理公式可得6×L1=G×L2,即.
已知杠杆平衡的概率为,由概率公式可知平衡的情况数为种,
分情况讨论求出G的值:
当L1=1米,L2=1米时,;
当L1=1米,L2=2米时,;
当L1=1米,L2=3米时,;
当L1=2米,L2=1米时,;
当L1=2米,L2=2米时,;
当L1=2米,L2=3米时,;
当L1=3米,L2=1米时,;
当L1=3米,L2=2米时,;
当L1=3米,L2=3米时,.
要使平衡情况有3种,G的值为6N.
5.(2025 泰州二模)如图,是由边长为1的小正方形组成的10×6的网格,点A,B均在格点上,以AB为直径画半圆O,格点C在半圆O上.请仅用无刻度的直尺画图.(保留作图痕迹,不写作法)
(1)在图1中作∠BAC的平分线,交BC于点D;
(2)在图2中的半圆弧上确定点E,使得BC平分∠ABE.
【解答】解:(1)如图1,取格点G,连接OG并延长交⊙O于F,连接AF交BC于D,点D即为所求;
∵OF∥AC,
∴∠CAF=∠OFA,
∴∠OAF=∠OFA,
∴∠OAF=∠CAF;
(2)如图2,取格点H,连接AH并延长交⊙O于E,则点E即为所求;
∵,
∴∠CAE=∠ABC,
∵∠CBE=∠CAE
∴∠CBE=∠ABC.
6.(2025 宁波模拟)为了解某校九年级学生“一分钟跳绳”成绩,学校随机抽取了若干名九年级学生进行跳绳测试,并将收集的跳绳成绩同时交给甲、乙两兴趣小组进行独立处理,图1、图2分别是甲、乙两兴趣小组绘制的跳绳成绩频数分布直方图(每个分组包含左端点,不含右端点).
根据以上信息,回答下列问题.
(1)补全乙组绘制的跳绳成绩频数分布直方图;
(2)已知该校九年级共有700名学生,请估计“一分钟跳绳”成绩为180个的学生人数.
【解答】解:(1)根据题意计算出总人数为2+8+9+20+10+8+3+3=63,
∴171个≤跳绳成绩<176个的频数为63﹣23﹣21﹣9﹣5=5,
如图补全图形如下:
(2)由甲频数分布直方图得:跳绳成绩小于180个的频数为2+8+9=19,
由乙频数分布直方图得:跳绳成绩小于181个的频数为23+5=28,
所以样本中跳绳成绩等于180个的频数为28﹣19=9,
(人),
答:九年级学生中约有100人“一分钟跳绳”成绩为180个.
7.(2025 天河区校级二模)如图1,线段AB=12,O为AB中点,C是平面上异于A,B的任一动点,且满足∠ACB=90°,若点D和点C在直线AB的同侧,且AD⊥AC,并始终有∠ADC=60°,连接OD,CD.
(1)如图2,若∠B=∠ADC,求线段AD的长;
(2)若AC将线段OD三等分,求线段AD的长;
(3)直接写出线段OD长度的取值范围.
【解答】解:(1)∵∠ADC=60°,∠B=∠ADC,
∴∠B=60°,
∵∠ACB=90°,
∴,
∵AD⊥AC,
∴∠DAC=90°,
∴;
(2)取AC中点T,连接OT,设OD,AC交于R,
由题意可得:OT是△ABC的中位线,
∴,
∴∠OTA=∠BCA=90°,
∵AD⊥AC,
∴∠DAC=90°,
∴∠DAR=∠OTR=90°,
又∵∠DRA=∠ORT,
∴△DRA∽△ORT,
∴;
由题意可得:当点R是靠近点D的三等分点时,则,
∴OT=2AD,
∴BC=4AD,
在Rt△ADC中,,
在Rt△ABC中,由勾股定理得AB2=AC2+BC2,
∴,
解得或(舍去),
当点R是靠近点O的三等分点时,则,
∴,
∴BC=AD,
∴,
∴AB2=AC2+BC2,
∴,
解得AD=6或AD=﹣6(舍去);
∴AD的长为或6;
(3)过点A作AF⊥AB,使∠AOF=60°,连接OC,CF.
则∠OAF=90°,
∴∠OFA=30°,
∴OF=2OA=12,
∴,
∵,
∴,
∵∠DAC=∠OAF=90°,
∴∠DAC+∠CAO=∠OAF+∠CAO,
即∠DAO=∠CAF,
∴△CAF∽△DAO,
∴,
∴.
∵∠ACB=90°,O为AB的中点,
∴,
∵点D和点C在直线AB的同侧,
∴AF<CF,
∵AF<CF≤OF+OC,
∴,
∴.
8.(2025 余姚市三模)如图,菱形ABCD中,以A为圆心,AD为半径画弧,以B为圆心,BD为半径画弧,两弧交于点E.
(1)求证:DE⊥AB;
(2)连结AC,若,求cos∠C的值.
【解答】(1)证明:连接BD,如图1,
∵以A为圆心,AD为半径画弧,以B为圆心,BD为半径画弧,两弧交于点E,
∴BD=BE,AD=AE,
∴AB为DE的中垂线,
∴DE⊥AB;
(2)解:如图2,连接AC,BD,
∵AB为DE的中垂线,
∴∠ABD=∠ABE,
∵四边形ABCD是菱形,
∴AB=BC,∠ABD=∠CBD,
∴∠ABC=∠DBE,
∵,
∴△ABC∽△EBD,
∴,
设AF=x,AD=5a=AB,则BD=4a,BF=5a﹣x,
则(5a)2﹣x2=(4a)2﹣(5a﹣x)2,
解得x=3.4a,
∴.
9.(2025 广东模拟)图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂,EM∥QN).已知基座高度MN为1m,主臂MP长为5m,测得主臂伸展角.∠PME=37°.(参考数据:sin37°,tan37°,sin53°,tan53°)
(1)求点P到地面的高度;
(2)若挖掘机能挖的最远处点Q,此时∠QPM=90°,求Q点到N点的距离.
【解答】解:(1)作PB⊥QN于点B,延长ME交PB于点A.
∴∠PBQ=∠PBN=90°.
∵EM∥QN,
∴∠BAE=∠PAE=90°.
由题意得:MN⊥BN,
∴∠MNB=90°.
∴四边形ABNM是矩形.
∴AB=MN=1(m),AM=BN.
∵PM=5m,∠PME=37°,
∴PA=PM sin∠PME≈53(m).
∴PB=PA+AB=3+1=4(m).
答:点P到地面的高度约为4m;
(2)∵PA=3m,PM=5m,∠PAM=90°,
∴AM=4(m),∠APM+∠PME=90°.
∴BN=4(m).
∵∠QPM=90°,
∴∠QPB+∠APM=90°.
∴∠QPB=∠PME=37°.
∴QB=PB tan∠QPB≈43(m).
∴QN=QB+BN=7(m).
答:Q点到N点的距离约为7m.
10.(2025 鼓楼区二模)如图,在菱形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)求证:四边形EFGH为矩形;
(2)菱形ABCD满足 AC=BD 时,四边形EFGH为正方形.
【解答】(1)证明:如图,连接FH,EG,AC,BD,
∵四边形ABCD是菱形,E、F、G、H分别是AB、BC、CD、DA的中点,
∴AB=AD,AE∥GD,AE=GD,EF,且EF∥AC∥GH,
∴四边形EGDA是平行四边形,四边形EFGH是平行四边形,
∴EG=AD,
同理可证FH=AB,
∴EG=FH,
∴四边形EFGH为矩形;
(2)解:菱形ABCD满足AC=BD时,四边形EFGH为正方形,
∵AC=BD,
∴EF,
又∵四边形EFGH为矩形,
∴四边形EFGH为正方形.
故答案为:AC=BD.
11.(2025 上栗县校级二模)如图,在平面直角坐标系xOy中,矩形OABC的顶点A,C在坐标轴上,顶点B在反比例函数的图象上,已知点A(2,0),C(0,4).
(1)求k的值.
(2)连接AC,BO交于点D,将矩形OABC向右平移m个单位长度得到矩形O'A'B'C'平移后点D的对应点D'在反比例函数的图象上,求m的值.
【解答】解:(1)∵四边形OABC是矩形,
∴AB=OC,AO=BC,
∵A(2,0),C(0,4),
∴OA=2,OC=4,
∴点B的坐标为(2,4),
∵点B(2,4)在反比例函数的图象上,
∴k=2×4=8;
(2)∵点A的坐标为(2,0),点C的坐标为(0,4),D是AC的中点,
∴点D的坐标为(1,2),
∵将矩形OABC向右平移m个单位长度得到矩形O'A'B'C'平移后点D的对应点D'在反比例函数y的图象上,
∴D′(1+m,2),
∴2(1+m)=8,
∴m=4﹣1=3.
12.(2025 清丰县校级一模)周末,小轩和家人们去爬张家山锻炼身体,刚开始小轩精力充沛,爬山的速度比较快,爬了30分钟后,开始体力不支,于是减速爬到山顶.他距山脚出发地的路程s(米)与登山时间t(分钟)之间的函数关系如图所示.
(1)小轩减速前的速度为 20 米/分钟;
(2)求小轩减速后s与t之间的函数关系式;
(3)当小轩爬了1小时时,他距离山脚出发地的路程是多少米?
【解答】解:(1)由图象可知:小轩减速前爬山600米,用时30分钟,则小轩减速前的速度为600÷30=20米/分钟.
故答案为:20.
(2)设小轩减速后s与t之间的函数表达式为s=kt+b,
由题意可得:
,
.
∴s=8t+360;
(3)1小时=60分钟,
当t=60时,s=8×60+360=840,
答:当小轩爬了1小时时,他距离山脚出发地的路程是840米.
13.(2025 柯桥区二模)如图,已知菱形ABCD,∠DAB=120°,延长AC至点F,连接DF,∠FDA=90°,延长BC交DF于点E.
(1)求证:BD=DF;
(2)若AD=1,求△BDE的面积.
【解答】(1)证明:在菱形ABCD中,∠DAB=120°,BD平分∠CDA,AD=CD,
∴∠CDA=60°,∠DCB=∠DAB=120°,
∵∠FDA=90°,
∴∠CDB=∠ADB=∠FDC=30°,
∵∠CDA=60°,AD=CD,
∴△DCA为等边三角形.
∴∠DCA=60°,
∴∠DCF=120°,
在△DCF与△DCB中,
,
∴△DCF≌△DCB(ASA),
∴DF=BD,
即BD=DF;
(2)解:由(1)得,∠BDE=∠CDB+∠FDC=60°,∠DBE=30°.
∴∠DEB=90°,
∵AD=1,
∵四边形ABCD是菱形,△DCA为等边三角形,
∴AC⊥BD,AC=1,
∴.
∴,
∴S△BDEBE ED.
14.(2025 庐阳区校级三模)有一张菱形纸片,其一个内角为60°,取菱形纸片的四边和短对角线的中点,按“8”字形顺次连接各点,形成两个小三角形,这两个小三角形组成的图形简称“沙漏形”,如图(1),将“沙漏形”挖去,对剩下纸片中的菱形纸片重复上述操作,得到如图(2)所示的图形…设图(n)中的沙漏形”的个数为fn(n为正整数).
观察以上图形,解答下列问题:
(1)填空:f5= 31 ,fn= 2n﹣1 (用含n的式子表示);
(2)当n的值为多少时,fn﹣fn﹣1的值开始大于2025.
【解答】解:(1)第一个图形有1个“沙漏型”,
第二个图形有1+2=3 个“沙漏型”,
第三个图形有1+2+4=7个“沙漏型”,
….
由此可得到规律,第n个图形有个1+2+4+ +2n﹣1=2n﹣1图形,即,
∴fs=1+2+4+8+16=31,
故答案为:31,2n﹣1;
(2)∵,
∴
=2×2n﹣1﹣2n﹣1+1
=2n﹣1(2﹣1)+1
=2n﹣1+1,
∴2n﹣1+1>2025,
则当 n=12成立,212﹣1+1=2024+1=2025,
∴n=12.
15.(2025 高密市三模)定义:在四边形中,若有一个角是直角,且从这个直角顶点引出的对角线把对角分成的两个角中,有一个是直角,我们称这样的四边形为“双垂四边形”.
(1)如图1,在“双垂四边形ABCD”中,若∠A=65°,则∠CBD= 65° ;
(2)如图2,在“双垂四边形ABCD”中,∠ADB=∠ABC=90°,∠A=45°,E为线段AB上一点,CD=5,且CD⊥DE,求DE的长.
【解答】解:(1)∵∠ABC=∠ADB=90°,
∴∠A+∠ABD=∠CBD+∠ABD=90°,
∴∠CBD=∠A=65°,
故答案为:65°;
(2)∵同理(1)可得,∠CBD=∠A,
∵∠ADB=90°,∠A=45°,
∴∠ABD=∠DAB=45°,
∴DB=DA,
又∵∠ADB=∠CDE=90°,
∴∠CDB=∠ADE,
∴△CDB≌△EDA(ASA),
∴DE=CD=5.
16.(2025 乾安县模拟)山西某中学为提升学生的劳动能力,开辟一块菜地供学生实践使用,为保护菜地,需要利用护栏将菜地圈起来,李老师以招募工人和发放劳动报酬的方式来完成该项工作.小组的同学把“劳动基地菜地护栏建设”作为一项课题活动,利用课余时间完成了实践调查,并形成了活动报告.请根据活动报告计算支付给工人的总费用.
课题 劳动基地菜地护栏建设
调查方式 走访调研、实地查看测量
测量过程及计算 调研内容及图示
相关数据及说明: ①护栏安装工作包括安装横杠和安装竖杠两部分,且要求所有的安装工作在一天内完成,安装横杠的工人每人当天费用为200元,安装竖杠的工人每人当天费用为240元. ②共招募6名工人,每名工人在相同的时间内安装横杠2根或竖杠3根,且每名工人只完成一项工作,要求两项安装任务同时开始,并在当天同时完成.
计算结果 …
【解答】解:设招募安装横杠的工人x名,则安装竖杠的工人(6﹣x) 名.
由题意,得,
解得 x=2,
经检验,x=2 是原方程的解,
则 6﹣x=4,
支付给工人师傅的总费用为:2×200+4×240=1360(元).
答:支付给工人师傅的总费用为1360元.
17.(2025 伊川县模拟)新年前夕,国家主席习近平通过中央广播电视总台和互联网,发表二〇二五年新年贺词,其中提到:“我们因地制宜培育新质生产力,新产业新业态新模式竞相涌现,新能源汽车年产量首次突破1000万辆,集成电路、人工智能、量子通信等领域取得新成果.”随着新能源汽车的发展,某市计划引进一批新能源公交车投入运营.新能源公交车有A,B两种车型,若购买A型公交车30辆,B型公交车10辆,共需2600万元;若购买A型公交车20辆,B型公交车30辆,共需3600万元.
(1)求购买A型和B型新能源公交车每辆分别需要多少万元.
(2)交通管理部门调研发现:A型新能源公交车适合支线道路运营,B型新能源公交车适合主干道运营.若本批次计划购买A,B两种新能源公交车共80辆,且支线道路运营车辆不超过主干道运营车辆为,请问分别购买多少辆A,B两种新能源公交车可使得政府投入的费用最少?并求出最少费用.
【解答】解:(1)设购买A型新能源公交车每辆需要a元,购买B型新能源公交车每辆需要b元.
,
∴,
答:购买A型每辆需要60元,购买B型每辆需要80元;
(2)设购买A型m辆,则购买B型(80﹣m)辆,
∴,
解得m≤16,
设投入的费用为w元,则w=60m+80(80﹣m)=﹣20m+6400,
∵﹣20<0,
∴w随m的增大而减小,
∵m≤16,
∴当m=16时w的值最小,w最小=﹣20×16+6400=6080,
80﹣16=64(辆).
答:购买A型新能源公交车16辆、B型新能源公交车64辆可使得政府投入的费用最少,最少费用为6080万元.
18.(2025 鼓楼区校级模拟)如图,在⊙O中,直径AB垂直弦CD于点E,连接AC,AD,BC,作CF⊥AD于点F,交线段OB于点G(不与点O,B重合),连接OF.
(1)若BE=1,求GE的长.
(2)求证:BC2=BG BO.
(3)若FO=FG,猜想∠CAD的度数,并证明你的结论.
【解答】(1)解:∵直径AB垂直弦CD,
∴∠AED=90°,
∴∠DAE+∠D=90°,
∵CF⊥AD,
∴∠FCD+∠D=90°,
∴∠DAE=∠FCD,
由圆周角定理得∠DAE=∠BCD,
∴∠BCD=∠FCD,
在△BCE和△GCE中,
,
,∴△BCE≌△GCE(ASA),
∴GE=BE=1;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
在△ACB和△CEB中,
,
,∴△ACB∽△CEB,
∴,
∴BC2=BA BE,
由(1)知GE=BE,
∴,
又∵AB=2BO,
∴;
(3)解:∠CAD=45°,证明如下:
如图,连接OC,
∵FO=FG,
∴∠FOG=∠FGO,
∵直径AB垂直弦CD,
∴CE=DE,∠AED=∠AEC=90°,
又∵AE=AE,
∴△ACE≌△ADE(SAS),
∴∠DAE=∠CAE,
设∠DAE=∠CAE=α,∠FOG=∠FGO=β,
则∠FCD=∠BCD=∠DAE=α,
∵OA=OC,
∴∠OCA=∠OAC=α,
又∵∠ACB=90°,
∴∠OCF=∠ACB﹣∠OCA﹣∠FCD﹣∠BCD=90°﹣3α,
∵∠CGE=∠OGF=β,∠GCE=α,∠CGE+∠GCE=90°,
∴β+α=90°,
∴α=90°﹣β,
∵∠COG=∠OAC+∠OCA=α+α=2α,
∴∠COF=∠COG+∠GOF=2α+β=2(90°﹣β)+β=180°﹣β,
∴∠COF=∠AOF,
在△COF和△AOF中,
,
∴△COF≌△AOF(SAS),
∴∠OCF=∠OAF,
即90°﹣3α=α,
∴α=22.5°,
∴∠CAD=2α=45°.
19.(2025 余姚市三模)已知二次函数y=ax2+bx+1(a,b是常数).
(1)求二次函数图象经过的定点的坐标;
(2)已知函数图象过(2,1).
①若函数图象与直线y=﹣1只有一个公共点,求a的值;
②求证:当0≤x<t,且1<t≤2时,函数最大值与最小值的差为|a|.
【解答】解:(1)令x=0,则y=1,
∴函数图象过定点(0,1);
(2)①由题意可得:
∴函数图象对称轴为直线x=1,即顶点坐标为(1,﹣1),
∴,
∴a=2,
②证明:函数图象顶点为(1,﹣a+1),
若a>0,当x=0时,y取最大值为1,x=1时,y取最小值为﹣a+1,
∴1﹣(﹣a+1)=a=|a|.
若a<0,x=1时,y取最大值为﹣a+1,x=0时,y取最小值为1,
∴(﹣a+1)﹣1=﹣a=|a|,
∴函数最大值与最小值的差为|a|.
20.(2025 通许县一模)射水鱼以陆生昆虫为食物,它在捕食时,能从口中射出一股水流,准确击中2m以内的昆虫.如果不考虑空气阻力,那么射水鱼射出的水流可以看成一条抛物线的一部分(如图).在一次捕食时,射水鱼射出的水流向上运动的高度y(单位:cm)与向前运动的水平距离x(单位:cm)的关系可以近似地表示为y=﹣0.2x2+6x.
(1)如果这次射出的水流没有遇到障碍物,它运动的高度逐步上升时,水流向前运动的水平距离x的范围是 0<x<15 ,它运动的高度逐步下降时,水流向前运动的水平距离x的范围是 15<x<30 ;
(2)假设要捕食的昆虫位于射水鱼正前方水平距离10cm,高度50cm处,那么这次射出的水流能否击中这只昆虫?
(3)假设捕食的昆虫位于射水鱼正前方25cm高度,并沿水平直线飞行,那么这次射出的水流要击中这只昆虫,可能在射水鱼正前方多远处?
【解答】解:(1)当y=0时,
﹣0.2x2+6x=0,
∴x1=0,x2=30,
抛物线的顶点横坐标为:
,
∴它运动的高度逐步上升时,水流向前运动的水平距离x的范围是0<x<15,它运动的高度逐步下降时,水流向前运动的水平距离x的范围是15<x<30;
故答案为:0<x<15,15<x<30;
(2)当x=10时,
y=﹣0.2×102+6×10=40<50,
∴不能击中这只昆虫;
(3)当y=25时,
25=﹣0.2x2+6x,
∴x1=5,x2=25,
∴可能在射水鱼正前方5cm或25cm处.
21.(2025 辽宁模拟)如图1,在Rt△ABC中,AB≠AC,∠CAB=90°,点D为AC中点,连接BD,点E为BD中点,连接AE,过E作EF⊥AE交AC于F.
(1)若AB=k EF(1<k<2),求tanC的值(用含有k的代数式表示);
(2)如图2,若∠GFA=∠FAE﹣∠EAB,∠G=90°,求的值.
【解答】解:(1)由题意可得:AE=BE,
∴∠EAB=∠ABE.
∵∠EFA+∠FAE=∠EAB+∠DAE=90°,
∴∠ABD=∠AFE,
∵∠ABD=∠AFE,∠AEF=∠DAB=90°,
∴△AEF∽△ABD,
∴,
设AE=DE=BE=a,BD=2a,AD=ka,
∵,
∴;
(2)延长FE至H,使得FE=EH,连接BH、AH,如图1,
∵DE=CE,FE=EH,∠DEF=∠CEH,
∴△DFE≌△BEH(SAS),
∴∠FDE=∠HBE,
∴∠ABH=∠EBH﹣∠ABD=∠FDE﹣∠ABD=∠DAB=90°=∠G.
∴AF=AH,
∴∠EAH=∠FAE,
又∵∠GFA=∠FAE﹣∠EAB=∠EAH﹣∠BAE=∠BAH,
∴△GAF≌△BHA(AAS),
∴DF=BH=AG.
∴.
22.(2025 庐阳区校级二模)已知二次函数y=﹣x2+bx+c的图象经过点A(1,0).
(1)如图,当二次函数y=﹣x2+bx+c的图象与x轴另一交点为C(C点在A点右侧),交y轴于D点,直线x=2交抛物线、x轴于B、E两点,设B点坐标为(2,a).
①用含a的代数式表示b= a+3 ,c= ﹣a﹣2 .
②当DC=2BC时,求二次函数解析式.
(2)二次函数y=﹣x2+bx+c图象的对称轴为直线x=m,m取值范围为0≤m≤3时,求该二次函数最大值n取值范围.
【解答】解:(1)①把A(1,0),B(2,a)代入y=﹣x2+bx+c,得:,
解得:,
故答案为:a+3,﹣a﹣2;
②由①知:y=﹣x2+(a+3)x﹣a﹣2,
当x=0时,y=﹣a﹣2,当y=﹣x2+(a+3)x﹣a﹣2=0时,x1=1,x2=a+2,
∴C(a+2,0),D(0,﹣a﹣2),a+2>1,
∴a>﹣1;
∵DC=2BC,B(2,a),
∴(a+2)2+(a+2)2=4[(a+2﹣2)2+a2],
解得:或a=2,
∴或y=﹣x2+(2+3)x﹣2﹣2=﹣x2+5x﹣4,
综上:或y=﹣x2+5x﹣4;
(2)把A(1,0),代入y=﹣x2+bx+c,得:﹣1+b+c=0,
∴c=1﹣b,
∴y=﹣x2+bx+1﹣b,
∵对称轴为直线,
∴b=2m,
∴y=﹣x2+2mx+1﹣2m,
∴当x=m时,函数有最大值为:n=﹣m2+2m2+1﹣2m=(m﹣1)2,
对于n=﹣m2+2m2+1﹣2m=(m﹣1)2,
抛物线的开口向上,对称轴为直线m=1,抛物线上的点离对称轴越远,函数值越大,
∵0≤m≤3,
∴当m=1时,函数有最小值为:(1﹣1)2=0,当m=3时,函数有最大值为:(3﹣1)2=4,
∴0≤n≤4.
23.(2025 新民市三模)已知△ABC是⊙O的内接三角形,CA=CB,∠ACB=40°,点D是⊙O上一点,连接AD,BD,CD.
(1)如图1,若BD为⊙O的直径,求∠CBD的度数;
(2)如图2,若AD∥BC,过点D作⊙O的切线交OA的延长线于点E,若DE=5,求的长.
【解答】解:(1)∵CA=CB,∠ACB=40°,
∴,
若BD为⊙O的直径,
∴∠BCD=90°,
∴∠ACD=∠BCD﹣∠ACB=90°﹣40°=50°,
∵,
∴∠ACD=∠ABD=50°,
∴∠CBD=∠CBA﹣∠ABD=70°﹣50°=20°;
(2)∵,
∴∠BAC=∠BDC=70°,
∵,
∴∠ACB=∠ADB=40°,
∴∠ADC=∠ADB+∠BDC=40°+70°=110°,
∵AD∥BC,
∴∠BCD=180°﹣∠ADC=70°,
∴∠ACD=∠BCD﹣∠ACB=70°﹣40°=30°,
如图所示,连接OD,
∵所对圆心角是∠AOD,所对圆周角是∠ACD,
∴∠AOD=2∠ACD=60°,
∵DE是⊙O的切线,
∴∠ODE=90°,
在Rt△ODE中,∠E=30°,
∴OE=2OD,
∴OE2=OD2+DE2,即可(2OD)2=OD2+52,
解得,(负值舍去),
∴长.
24.(2025 顺庆区二模)在平面直角坐标系中,二次函数的图象与x轴交于A和B(1,0)两点,与y轴相交于C,且顶点D(﹣1,4),P是抛物线上一动点.
(1)求二次函数的解析式;
(2)如图1,连接BC,若∠PBC=45°,求P的坐标;
(3)如图2,过P作PQ∥AC交抛物线于Q,以P、Q、D为顶点的三角形是否存在直角三角形,若存在,求出P的坐标;若不存在,通过计算说明.
【解答】解:(1)∵二次函数的图象顶点为点D(﹣1,4),
故设抛物线解析式为y=a(x+1)2+4(a≠0)),
∵抛物线图象经过B(1,0),
∴a(1+1)2+4=0,
解得:a=﹣1,
∴抛物线解析式为y=﹣(x+1)2+4,即y=﹣x2﹣2x+3;
(2)将CB以C为旋转中心顺时针旋转90°,B对应点B',连接BB'交抛物线于P,过C作MN∥x轴,且BN⊥MN,B'M⊥MN,
∴∠PBC=45°,
令﹣x2﹣2x+3=0,解得:x1=﹣3,x2=1,
∴A(﹣3,0),B(1,0),
∵当x=0时,y=3,
∴C(0,3),
∵∠MCB'=∠CBN=90°﹣∠NCB,
∴在△MB'C和△NCB中,
,
∴△MB'C≌△NCB(AAS),
∴NB=MC=yc﹣yb=3,CN=B'M=xB﹣xC=1,
∴B'(﹣3,2),
设BB'的直线解析式为y=kx+b(k≠0),
∴,
解得:,,
∴BB'的直线解析式为,
∴,
整理得2x2+3x﹣5=0,
解得:,x2=1,
当时,,
∴;
(3)①当∠PDQ=90°时,设PD的直线方程为y=k1(x+1)+4,
设QD的直线方程为y=k2(x+1)+4,
∴,
整理得x2+(k1+2)x+k1+1=0,
∴xP+xD=﹣k1﹣2,xP xD=k1+1,
∴xP﹣1=﹣k1﹣2,
∴k1=﹣xP﹣1,
∴,
整理得x2+(k2+2)x+k2+1=0,
∴xD+xQ=﹣k2﹣2,xD xQ=k2+1,
∴xQ﹣1=﹣k2﹣2,
∴k2=﹣xQ﹣1,
∵∠PDQ=90°,
∴直线PD与x轴夹角的正切值=直线DQ与x轴夹角的正切值的倒数,
∴,即,
∴k1 k2=﹣1,
∴(﹣xP﹣1)(﹣xQ﹣1)=﹣1,
即xP xQ+xP+xQ+2=0,
∵PQ∥AC,
设PQ的直线解析式为y=x+b,
,
整理得:x2+3x+b﹣3=0,
∴xP+xQ=﹣3,xP xQ=b﹣3,
∴b﹣3+(﹣3)+2=0,
解得:b=4,
∴PQ的直线解析式为y=x+4,
∴,
整理得x2+3x+1=0,
解得:,,
∵当P在Q的左侧时,
∴,
∴,
∴,
∵当P在Q的右侧时,
,,
∴;
②由(1)知,顶点D(﹣1,4),C(0,3),A(﹣3,0),
DC2=(﹣1﹣0)2+(4﹣3)2=2,
AC2=32+32=18,
AD2=(﹣1+3)2+(4﹣0)2=20,
∴AD2=AC2+CD2,
∴此时△ACD为直角三角形,即∠ACD=90°,
若∠PQD=90°,此时PQ与AC重合,与题意不合,应舍去.
综上,或时,以P,Q,D为顶点的三角形是直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
