【专项押题卷】临考题型分类专项押题:填空题-2024年中考数学(含解析)
文档属性
| 名称 | 【专项押题卷】临考题型分类专项押题:填空题-2024年中考数学(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 21:05:32 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【专项押题卷】临考题型分类专项押题:填空题-2024年中考数学
1.(2025 祁阳市校级一模)将﹣8360000用科学记数法表示为 .
2.(2025 重庆校级模拟)为了丰富学生的课外活动,某中学开设了多种兴趣小组.其中,两名学生想从摄影、舞蹈、编程、书法中选报一个兴趣小组.两名学生恰好选报同一个兴趣小组的概率为 .
3.(2025 武威一模)已知函数,其中m为常数.若该函数的图象显示y随着x的增大而增大,则m的取值范围为 .
4.(2025 广东模拟)进行心肺复苏急救措施时,一般胸外心脏按压速度x(单位:次/min)的范围如图所示,则x的取值范围可表示为 .
5.(2025 巢湖市模拟)如图,四边形ABCD是半径为3的⊙O的内接四边形,CD∥AB,连接AC,AB=AC,若,则的长为 .
6.(2025 重庆校级模拟)如图,⊙O的直径CD=10,弦AB=8,且CD⊥AB于点E,连接AC,以AC,AB为边作平行四边形ABFC,连接AF,BC交于点K,则AK= .
7.(2025 哈尔滨模拟)双曲线经过点(﹣2,4),则k= .
8.(2025 通许县一模)通常情况下酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色.化学实验室中有四瓶标签被污染无法识别的无色溶液,分别是A:盐酸(呈酸性),B:硝酸钾溶液(呈中性),C:氢氧化钠溶液(呈碱性),D:氢氧化钾溶液(呈碱性).小周同学在这四瓶溶液中取样,用酚酞检测其碱性.若小周将酚酞随机滴入两种样本溶液中,两种样本溶液恰好都变红色的概率是 .
9.(2025 无锡校级二模)两个半径相等的半圆按如图所示放置,半圆O′的圆心落在半圆O的圆弧上,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为1,则阴影部分的面积是 .
10.(2025 洛宁县模拟)如图,点A,B,C在⊙O上,OA⊥BC,若∠ABC=35°,则∠BCO的度数为 .
11.(2025 辽宁模拟)如图,在△ABC中,∠C=60°,∠A=45°,BC=2,分别以B、A为圆心,大于的长为半径作弧,连接弧的两个交点;分别以A、C为圆心,大于的长为半径作弧,连接弧的两个交点,取所作两条直线的交点,以该交点为圆心,该交点到A的距离为半径作弧交于B,则弧AB的长为 .
12.(2025 南关区二模)如图,将△ABC折叠,使点B与点A重合,折痕为DE.若AC=4,BC=7,则△ACD的周长为 .
13.(2025 柯桥区二模)一副三角板ABC和CDE按如图方式摆放,其中∠BAC=∠DCE=90°,∠D=30°,∠B=45°,点A恰好落在DE上,且BC∥DE,则∠ACE的度数为 .
14.(2025 南关区二模)《九章算术》中记载了一道数学问题,其译文为:有人合伙购物,每人出8钱,多余3钱;每人出7钱,还缺4钱,问合伙人数是多少?为解决此问题,设合伙人数为x人,根据题意,可列方程为 .
15.(2025 江阳区校级模拟)在平面直角坐标系中,若点P(n,1)与点Q(﹣2,m)关于原点对称,则m+n的值是 .
16.(2025 辽宁模拟)一次函数y=2x+5与抛物线y=2x2﹣4x+3的交点个数为 个.
17.(2025 台江区模拟)如图,一个正五边形纸片可裁成五个全等的等腰三角形和一个五边形,则图中∠α的度数是 °.
18.(2025 台江区模拟)如图,在平面直角坐标系中,△ABO与△A′B′O是以原点O为位似中心的位似图形.点B(﹣6,3)的对应点为B′(2,﹣1),若AA′=12,则A的坐标为 .
19.(2025 成华区校级三模)如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2,分别以AB,BC为直径画半圆,则图中阴影部分的面积为 .
20.(2025 开州区模拟)如图,△OAB是等边三角形,点B的坐标是(2,0),若反比例函数图象的一支经过点A,则k的值是 .
21.(2025 天河区校级二模)一个几何体的三视图如图所示,根据图示的数据计算该几何体的侧面积为
(结果保留π).
22.(2025 包河区三模)如图,△ABC中,∠BAC=90°,BC=5,D为AB边的中点,将线段BD以B点中心逆时针旋转90°得到线段BD’,连接CD’.
(1)若AC=3,则BD′长为 ;
(2)CD′长最大为 .
23.(2025 青羊区校级模拟)在平面直角坐标系xOy中,已知抛物线y=ax2+2a(a﹣3)x(a≠0),设抛物线的对称轴为x=t.点(x1,y1),(x2,y2)是抛物线上两个点,当﹣1<x1<2时,对x1的每一个值,总存在x2,使得﹣1<x2<2,x2>x1,且y2>y1成立,则t的取值范围为 .
24.(2025 宝应县一模)如图,把R1、R2、R3三个电阻串联起来,线路AB上的电流为I,电压为U,则U=IR1+IR2+IR3,当R1=19.2,R2=35.4,R3=45.4,I=2.2时,U的值为 .
25.(2025 重庆模拟)若关于x的不等式组所有整数解的和为14,且关于y的分式方程的解为非负整数,则所有满足条件的整数a的值之和为 .
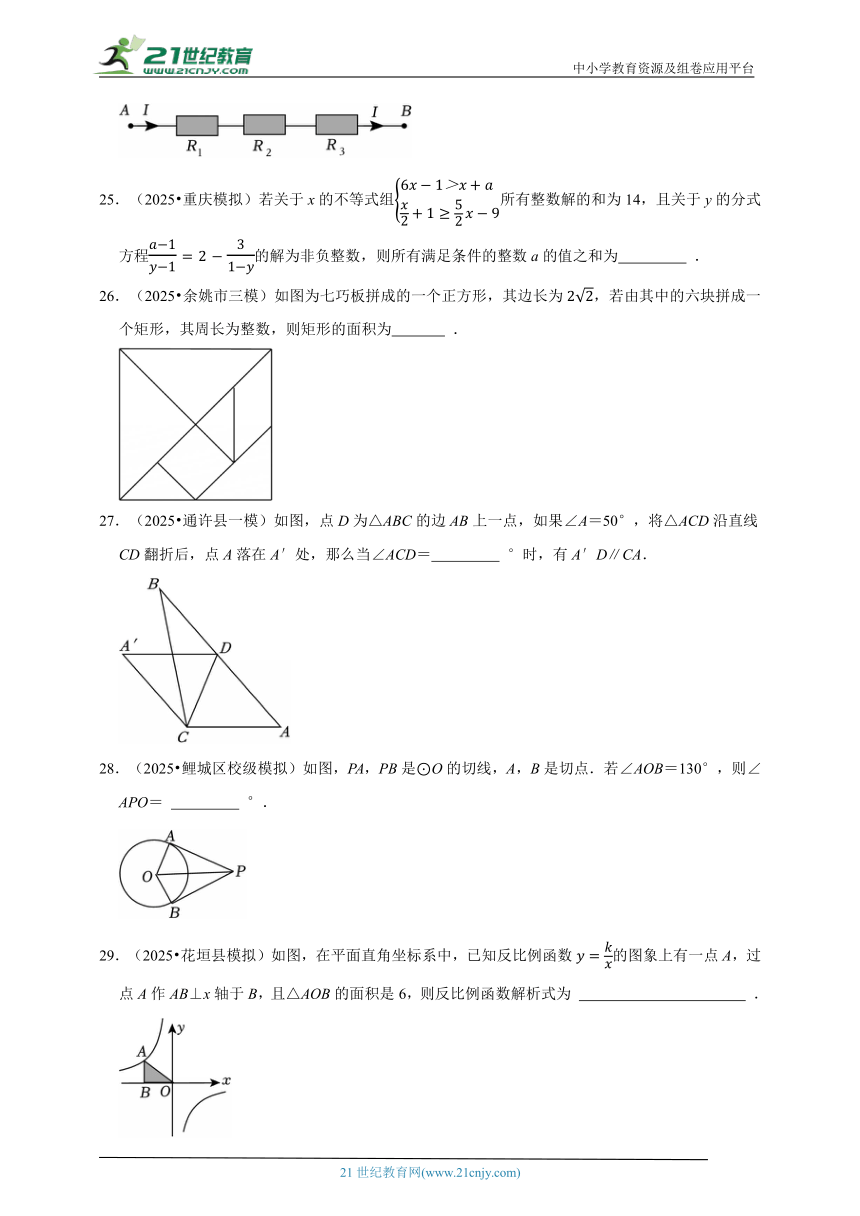
26.(2025 余姚市三模)如图为七巧板拼成的一个正方形,其边长为,若由其中的六块拼成一个矩形,其周长为整数,则矩形的面积为 .
27.(2025 通许县一模)如图,点D为△ABC的边AB上一点,如果∠A=50°,将△ACD沿直线CD翻折后,点A落在A′处,那么当∠ACD= °时,有A′D∥CA.
28.(2025 鲤城区校级模拟)如图,PA,PB是⊙O的切线,A,B是切点.若∠AOB=130°,则∠APO= °.
29.(2025 花垣县模拟)如图,在平面直角坐标系中,已知反比例函数的图象上有一点A,过点A作AB⊥x轴于B,且△AOB的面积是6,则反比例函数解析式为 .
30.(2025 海珠区校级二模)定义一种新运算“m n”,规定当m≥n时,m n=3n+1;当m<n时,m n=2m+4.例如:3 1=3×1+1=4,(﹣2) 1=2×(﹣2)+4=0.如果(2x﹣3) (﹣2x﹣1)=﹣6,那么x的值为 .
【专项押题卷】临考题型分类专项押题:填空题-2024年中考数学
参考答案与试题解析
一.填空题(共30小题)
1.(2025 祁阳市校级一模)将﹣8360000用科学记数法表示为 ﹣8.36×106 .
【解答】解:﹣8360000=﹣8.36×106.
故答案为:﹣8.36×106.
2.(2025 重庆校级模拟)为了丰富学生的课外活动,某中学开设了多种兴趣小组.其中,两名学生想从摄影、舞蹈、编程、书法中选报一个兴趣小组.两名学生恰好选报同一个兴趣小组的概率为 .
【解答】解:分别记摄影、舞蹈、编程、书法为A、B、C、D,
根据题意列表如下:
同学1 同学2 A B C D
A A,A A,B A,C A,D
B B,A B,B B,C B,D
C C,A C,B C,C C,D
D D,A D,B D,C D,D
由列表可知:两名学生恰好选报同一个兴趣小组的概率为.
故答案为:.
3.(2025 武威一模)已知函数,其中m为常数.若该函数的图象显示y随着x的增大而增大,则m的取值范围为 .
【解答】解:左段函数为y=﹣2x2+8x+5(x<m),
该函数开口向下,对称轴为直线x=2,
要使该函数的图象显示y随着x的增大而增大,
则m≤2,
右段函数为y=x2+mx+3m2﹣1(x≥m),
该函数开口向上,对称轴为直线,
要使该函数的图象显示y随着x的增大而增大,
则,解得m≥0,
当x=m时,左段函数值要小于等于右段函数,
即﹣2m2+8m+5≤m2+m2+3m2﹣1,
整理可得7m2﹣8m﹣6≥0,
令7m2﹣8m﹣6=0,
解得,,
根据二次函数的图象可得7m2﹣8m﹣6≥0的解集为或(舍去),
综上,,
故答案为:.
4.(2025 广东模拟)进行心肺复苏急救措施时,一般胸外心脏按压速度x(单位:次/min)的范围如图所示,则x的取值范围可表示为 100≤x≤120 .
【解答】解:通过观察数轴端点情况可得:100≤x≤120,
故答案为:100≤x≤120.
5.(2025 巢湖市模拟)如图,四边形ABCD是半径为3的⊙O的内接四边形,CD∥AB,连接AC,AB=AC,若,则的长为 .
【解答】解:由条件可知∠ABC=∠ACB,∠ABC+∠D=180°,
∵,
∴,
∴,
∴,
∴∠ACD=∠BAC=45°,
连接AO,DO,
∴∠AOD=2∠ACD=90°,
则的长,
故答案为:.
6.(2025 重庆校级模拟)如图,⊙O的直径CD=10,弦AB=8,且CD⊥AB于点E,连接AC,以AC,AB为边作平行四边形ABFC,连接AF,BC交于点K,则AK= .
【解答】解:过点A作AM⊥AB于点A,交FC的延长线于点M,连接OB,
由条件可知BE=AE=4,OB=OC=OD=5,
∴,
∴CE=OE+OC=8,
由条件可知CF=AB=8,CF∥AB,
∵AM⊥AB,CD⊥AB,
∴AM∥CD,
∴四边形MCEA是平行四边形,
∵AM⊥AB,
∴四边形MCEA是矩形,
∴MC=AE=4,∠M=90°,MF=MC+CF=12,
∴,
∵CF∥AB,
∴△AEK∽△FCK,
∴,
∴.
7.(2025 哈尔滨模拟)双曲线经过点(﹣2,4),则k= ﹣8 .
【解答】解:由条件可知k=﹣2×4=﹣8.
故答案为:﹣8.
8.(2025 通许县一模)通常情况下酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色.化学实验室中有四瓶标签被污染无法识别的无色溶液,分别是A:盐酸(呈酸性),B:硝酸钾溶液(呈中性),C:氢氧化钠溶液(呈碱性),D:氢氧化钾溶液(呈碱性).小周同学在这四瓶溶液中取样,用酚酞检测其碱性.若小周将酚酞随机滴入两种样本溶液中,两种样本溶液恰好都变红色的概率是 .
【解答】解:画树状图如下,
由树状图可知:两种样本溶液恰好都变红色的概率是,
故答案为:.
9.(2025 无锡校级二模)两个半径相等的半圆按如图所示放置,半圆O′的圆心落在半圆O的圆弧上,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为1,则阴影部分的面积是 .
【解答】解:如图,连接OA,OA′,过点A作AB⊥OO′于点B,
由题意可知,△OO′A是等边三角形,
∴∠AOO′=∠AO′O=60°,,
∴,
∴S阴影=S扇形AOO′+S扇形AO′O﹣S△OO′A
,
故答案为:.
10.(2025 洛宁县模拟)如图,点A,B,C在⊙O上,OA⊥BC,若∠ABC=35°,则∠BCO的度数为 20° .
【解答】解:如下图所示,连接OB,
∵OA⊥BC,
根据垂径定理可得:,
由条件可知∠AOC=2∠ABC=70°,
∴∠BOC=2∠AOC=140°,
又∵OC=OB,
∴.
故答案为:20°.
11.(2025 辽宁模拟)如图,在△ABC中,∠C=60°,∠A=45°,BC=2,分别以B、A为圆心,大于的长为半径作弧,连接弧的两个交点;分别以A、C为圆心,大于的长为半径作弧,连接弧的两个交点,取所作两条直线的交点,以该交点为圆心,该交点到A的距离为半径作弧交于B,则弧AB的长为 .
【解答】解:如图,由作图可知,点O为△ABC的外接圆圆心,连接OB,OC,
由条件可知∠AOB=2∠ACB=120°,∠BOC=2∠BAC=90°,
∴,
∴,
∴弧AB的长为,
故答案为:.
12.(2025 南关区二模)如图,将△ABC折叠,使点B与点A重合,折痕为DE.若AC=4,BC=7,则△ACD的周长为 11 .
【解答】解:根据折叠的性质得:BD=AD,
∴AD+DC=BC=7.
∴△ACD的周长=CD+AD+AC=BC+AC=7+4=11,
故答案为:11.
13.(2025 柯桥区二模)一副三角板ABC和CDE按如图方式摆放,其中∠BAC=∠DCE=90°,∠D=30°,∠B=45°,点A恰好落在DE上,且BC∥DE,则∠ACE的度数为 75° .
【解答】解:∵∠B=45°,∠BAC=90°,
∴∠ACB=90°﹣45°=45°,
∵BC∥DE,
∴∠CAE=∠ACB=45°,
∵∠D=30°,∠DCE=90°,
∴∠E=90°﹣30°=60°,
∴∠ACE=180°﹣60°﹣45°=75°.
故答案为:75°.
14.(2025 南关区二模)《九章算术》中记载了一道数学问题,其译文为:有人合伙购物,每人出8钱,多余3钱;每人出7钱,还缺4钱,问合伙人数是多少?为解决此问题,设合伙人数为x人,根据题意,可列方程为 8x﹣3=7x+4 .
【解答】解:∵每人出8钱,会多出3钱;每人出7钱,又差4钱,设人数为x,
∴8x﹣3=7x+4,
故答案为:8x﹣3=7x+4.
15.(2025 江阳区校级模拟)在平面直角坐标系中,若点P(n,1)与点Q(﹣2,m)关于原点对称,则m+n的值是 1 .
【解答】解:∵点P(n,1)与点Q(﹣2,m)关于原点对称,
∴m=﹣1,n=2,
∴m+n=﹣1+2=1.
故答案为:1.
16.(2025 辽宁模拟)一次函数y=2x+5与抛物线y=2x2﹣4x+3的交点个数为 2 个.
【解答】解:联立方程组,
整理得x2﹣3x﹣1=0,
∴Δ=(﹣3)2﹣4×(﹣1)=13>0,
∴函数y=2x+5与抛物线y=2x2﹣4x+3的交点个数为2个,
故答案为:2.
17.(2025 台江区模拟)如图,一个正五边形纸片可裁成五个全等的等腰三角形和一个五边形,则图中∠α的度数是 36 °.
【解答】解:∵等腰三角形的底角72°,
∴∠α=180°﹣72°﹣72°=36°.
故答案为:36.
18.(2025 台江区模拟)如图,在平面直角坐标系中,△ABO与△A′B′O是以原点O为位似中心的位似图形.点B(﹣6,3)的对应点为B′(2,﹣1),若AA′=12,则A的坐标为 (﹣9,0) .
【解答】解:∵△ABO与△A′B′O是以原点O为位似中心的位似图形,点B(﹣6,3)的对应点为B′(2,﹣1),
∴△ABO与△A′B′O的位似比为3,
∴OA:OA′=3:1,
∵AA′为12,
∴OA=9,
∴点A的坐标为(﹣9,0).
故答案为:(﹣9,0).
19.(2025 成华区校级三模)如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2,分别以AB,BC为直径画半圆,则图中阴影部分的面积为 4 .
【解答】解:连接BD,如图所示,
由图可得,∠ADB=∠BDC=90°,
∵AB=4,BC=2,
∴图中阴影部分的面积为:S半圆ADB﹣S△ABD+S半圆BCD﹣S△BDC
=S半圆ADB+S半圆BCD﹣S△ABC
=π×()2π×()2
4,
故答案为:4.
20.(2025 开州区模拟)如图,△OAB是等边三角形,点B的坐标是(2,0),若反比例函数图象的一支经过点A,则k的值是 .
【解答】解:如图,过点A作AD⊥OB于点D,
∵△OAB是等边三角形,点B的坐标是(2,0),
∴OB=OA=2,
∴ODOB=1,
∴AD,
∴A(1,),
∵反比例函数图象的一支经过点A,
∴k=1.
故答案为:.
21.(2025 天河区校级二模)一个几何体的三视图如图所示,根据图示的数据计算该几何体的侧面积为 65π (结果保留π).
【解答】解:由图示可知,圆锥的高为12,底面圆的直径为10,
∴圆锥的母线为:,
∴圆锥的侧面积为:πrl=π×5×13=65π,
故答案为:65π.
22.(2025 包河区三模)如图,△ABC中,∠BAC=90°,BC=5,D为AB边的中点,将线段BD以B点中心逆时针旋转90°得到线段BD’,连接CD’.
(1)若AC=3,则BD′长为 2 ;
(2)CD′长最大为 .
【解答】解:(1)由勾股定理得,
∵D为AB边的中点,
∴,
故答案为:2;
(2)如图,以BC为直径画⊙O,则点A在⊙O上,
过点B作BH⊥BC,使,
以线段BH的中点I为圆心,BI长为半径画⊙I,
连接CI并延长,交⊙I于点D',此时CD'长最大,
∴,
∴,
由勾股定理得,
∴,
故答案为:.
23.(2025 青羊区校级模拟)在平面直角坐标系xOy中,已知抛物线y=ax2+2a(a﹣3)x(a≠0),设抛物线的对称轴为x=t.点(x1,y1),(x2,y2)是抛物线上两个点,当﹣1<x1<2时,对x1的每一个值,总存在x2,使得﹣1<x2<2,x2>x1,且y2>y1成立,则t的取值范围为 t的取值范围是或t>3 .
【解答】解:抛物线的对称轴为x=t,且t=3﹣a,
当﹣1<x1<2时,对于x1的每一个值,总存在x2,使得﹣1<x2<2x2>x1,且y2>y1成立,
①若a>0,此时t<3,
则当x≥t时,y随x的增大而增大;当x≤t时,y随x的增大而减小,
(i)当t≤﹣1时,
∵t<x1<x2,
∴y2>y1成立,
(ii)当﹣1<t<2时,
∵点(﹣1,m)关于对称轴直线x=t的对称点为(2t+1,m),
∴2t+1≤2,
∴,
∴当时,y2>y1成立,
(ii)当t≥2时,不合题意,舍去,
②若a<0,此时t>3,
则当x≥t时,y随x的增大而减小;当x≤t时,y随x的增大而增大,
∴t>3满足题意,
综上所述,t的取值范围是.
24.(2025 宝应县一模)如图,把R1、R2、R3三个电阻串联起来,线路AB上的电流为I,电压为U,则U=IR1+IR2+IR3,当R1=19.2,R2=35.4,R3=45.4,I=2.2时,U的值为 220 .
【解答】解:当R1=19.2,R2=35.4,R3=45.4,I=2.2时,
U=IR1+IR2+IR3
=I(R1+R2+R3)
=2.2×(19.2+35.4+45.4)
=2.2×100
=220,
故答案为:220.
25.(2025 重庆模拟)若关于x的不等式组所有整数解的和为14,且关于y的分式方程的解为非负整数,则所有满足条件的整数a的值之和为 14 .
【解答】解:,
解不等式①,得,
解不等式②,得x≤5,
∴不等式组的解集为:,
∵不等式组所有整数解的和为14,
∴不等式组的整数解为5,4,3,2或5,4,3,2,1,0,﹣1,
∴或,
解得:4≤a<9或﹣11≤a<﹣6;
,
解得:,
∵解为非负整数,
∴﹣11≤a<﹣6这种情况应舍去,
∴,即a≥2且a为偶数,
由题意得,当a=8时,;
当a=6时,;
当a=4时,(不合题意,舍去);
∴所有满足条件的整数a的值为8、6,
即8+6=14.
故答案为:14.
26.(2025 余姚市三模)如图为七巧板拼成的一个正方形,其边长为,若由其中的六块拼成一个矩形,其周长为整数,则矩形的面积为 6 .
【解答】解:由条件可知正方形的面积为,
结合七巧板,各图形的面积由大到小分别为2,2,1,1,1,,,
∴或或,
则六块拼成的矩形的面积为或7或6,
∵其周长为整数,
∴面积为6,
如图所示:
故答案为:6.
27.(2025 通许县一模)如图,点D为△ABC的边AB上一点,如果∠A=50°,将△ACD沿直线CD翻折后,点A落在A′处,那么当∠ACD= 65 °时,有A′D∥CA.
【解答】解:将△ACD沿直线CD翻折后,点A落在A′处,如果∠A=50°,
∴∠ADC=∠A′DC,
当A′D∥CA,
∴∠A′DC=∠ACD,
∴∠ADC=∠ACD,
∴,
故答案为:65.
28.(2025 鲤城区校级模拟)如图,PA,PB是⊙O的切线,A,B是切点.若∠AOB=130°,则∠APO= 25 °.
【解答】解:由题意可得:∠OAP=∠OBP=90°.
∵OP=OP.AO=BO,
∴Rt△AOP≌Rt△BOP,
∴∠AOP=∠BOP.
∵∠AOB=130°,
∴,
∴∠APO=90°﹣65°=25°.
故答案为:25.
29.(2025 花垣县模拟)如图,在平面直角坐标系中,已知反比例函数的图象上有一点A,过点A作AB⊥x轴于B,且△AOB的面积是6,则反比例函数解析式为 y .
【解答】解:∵反比例函数y的图象的一支在第二象限,
∴k<0,
∵AB⊥x轴,垂足为B,△ABO的面积为6,
∴|k|=2×6=12,
∴k=﹣12,
∴反比例函数的解析式为:y.
故答案为:y.
30.(2025 海珠区校级二模)定义一种新运算“m n”,规定当m≥n时,m n=3n+1;当m<n时,m n=2m+4.例如:3 1=3×1+1=4,(﹣2) 1=2×(﹣2)+4=0.如果(2x﹣3) (﹣2x﹣1)=﹣6,那么x的值为 ﹣1或 .
【解答】解:当2x﹣3≥﹣2x﹣1时,即时,
原式=3×(﹣2x﹣1)+1=﹣6,
解得:,
当2x﹣3<﹣2x﹣1时,即时,
原式=2×(2x﹣3)+4=﹣6,
解得:x=﹣1,
故x的值为﹣1或.
故答案为:﹣1或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【专项押题卷】临考题型分类专项押题:填空题-2024年中考数学
1.(2025 祁阳市校级一模)将﹣8360000用科学记数法表示为 .
2.(2025 重庆校级模拟)为了丰富学生的课外活动,某中学开设了多种兴趣小组.其中,两名学生想从摄影、舞蹈、编程、书法中选报一个兴趣小组.两名学生恰好选报同一个兴趣小组的概率为 .
3.(2025 武威一模)已知函数,其中m为常数.若该函数的图象显示y随着x的增大而增大,则m的取值范围为 .
4.(2025 广东模拟)进行心肺复苏急救措施时,一般胸外心脏按压速度x(单位:次/min)的范围如图所示,则x的取值范围可表示为 .
5.(2025 巢湖市模拟)如图,四边形ABCD是半径为3的⊙O的内接四边形,CD∥AB,连接AC,AB=AC,若,则的长为 .
6.(2025 重庆校级模拟)如图,⊙O的直径CD=10,弦AB=8,且CD⊥AB于点E,连接AC,以AC,AB为边作平行四边形ABFC,连接AF,BC交于点K,则AK= .
7.(2025 哈尔滨模拟)双曲线经过点(﹣2,4),则k= .
8.(2025 通许县一模)通常情况下酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色.化学实验室中有四瓶标签被污染无法识别的无色溶液,分别是A:盐酸(呈酸性),B:硝酸钾溶液(呈中性),C:氢氧化钠溶液(呈碱性),D:氢氧化钾溶液(呈碱性).小周同学在这四瓶溶液中取样,用酚酞检测其碱性.若小周将酚酞随机滴入两种样本溶液中,两种样本溶液恰好都变红色的概率是 .
9.(2025 无锡校级二模)两个半径相等的半圆按如图所示放置,半圆O′的圆心落在半圆O的圆弧上,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为1,则阴影部分的面积是 .
10.(2025 洛宁县模拟)如图,点A,B,C在⊙O上,OA⊥BC,若∠ABC=35°,则∠BCO的度数为 .
11.(2025 辽宁模拟)如图,在△ABC中,∠C=60°,∠A=45°,BC=2,分别以B、A为圆心,大于的长为半径作弧,连接弧的两个交点;分别以A、C为圆心,大于的长为半径作弧,连接弧的两个交点,取所作两条直线的交点,以该交点为圆心,该交点到A的距离为半径作弧交于B,则弧AB的长为 .
12.(2025 南关区二模)如图,将△ABC折叠,使点B与点A重合,折痕为DE.若AC=4,BC=7,则△ACD的周长为 .
13.(2025 柯桥区二模)一副三角板ABC和CDE按如图方式摆放,其中∠BAC=∠DCE=90°,∠D=30°,∠B=45°,点A恰好落在DE上,且BC∥DE,则∠ACE的度数为 .
14.(2025 南关区二模)《九章算术》中记载了一道数学问题,其译文为:有人合伙购物,每人出8钱,多余3钱;每人出7钱,还缺4钱,问合伙人数是多少?为解决此问题,设合伙人数为x人,根据题意,可列方程为 .
15.(2025 江阳区校级模拟)在平面直角坐标系中,若点P(n,1)与点Q(﹣2,m)关于原点对称,则m+n的值是 .
16.(2025 辽宁模拟)一次函数y=2x+5与抛物线y=2x2﹣4x+3的交点个数为 个.
17.(2025 台江区模拟)如图,一个正五边形纸片可裁成五个全等的等腰三角形和一个五边形,则图中∠α的度数是 °.
18.(2025 台江区模拟)如图,在平面直角坐标系中,△ABO与△A′B′O是以原点O为位似中心的位似图形.点B(﹣6,3)的对应点为B′(2,﹣1),若AA′=12,则A的坐标为 .
19.(2025 成华区校级三模)如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2,分别以AB,BC为直径画半圆,则图中阴影部分的面积为 .
20.(2025 开州区模拟)如图,△OAB是等边三角形,点B的坐标是(2,0),若反比例函数图象的一支经过点A,则k的值是 .
21.(2025 天河区校级二模)一个几何体的三视图如图所示,根据图示的数据计算该几何体的侧面积为
(结果保留π).
22.(2025 包河区三模)如图,△ABC中,∠BAC=90°,BC=5,D为AB边的中点,将线段BD以B点中心逆时针旋转90°得到线段BD’,连接CD’.
(1)若AC=3,则BD′长为 ;
(2)CD′长最大为 .
23.(2025 青羊区校级模拟)在平面直角坐标系xOy中,已知抛物线y=ax2+2a(a﹣3)x(a≠0),设抛物线的对称轴为x=t.点(x1,y1),(x2,y2)是抛物线上两个点,当﹣1<x1<2时,对x1的每一个值,总存在x2,使得﹣1<x2<2,x2>x1,且y2>y1成立,则t的取值范围为 .
24.(2025 宝应县一模)如图,把R1、R2、R3三个电阻串联起来,线路AB上的电流为I,电压为U,则U=IR1+IR2+IR3,当R1=19.2,R2=35.4,R3=45.4,I=2.2时,U的值为 .
25.(2025 重庆模拟)若关于x的不等式组所有整数解的和为14,且关于y的分式方程的解为非负整数,则所有满足条件的整数a的值之和为 .
26.(2025 余姚市三模)如图为七巧板拼成的一个正方形,其边长为,若由其中的六块拼成一个矩形,其周长为整数,则矩形的面积为 .
27.(2025 通许县一模)如图,点D为△ABC的边AB上一点,如果∠A=50°,将△ACD沿直线CD翻折后,点A落在A′处,那么当∠ACD= °时,有A′D∥CA.
28.(2025 鲤城区校级模拟)如图,PA,PB是⊙O的切线,A,B是切点.若∠AOB=130°,则∠APO= °.
29.(2025 花垣县模拟)如图,在平面直角坐标系中,已知反比例函数的图象上有一点A,过点A作AB⊥x轴于B,且△AOB的面积是6,则反比例函数解析式为 .
30.(2025 海珠区校级二模)定义一种新运算“m n”,规定当m≥n时,m n=3n+1;当m<n时,m n=2m+4.例如:3 1=3×1+1=4,(﹣2) 1=2×(﹣2)+4=0.如果(2x﹣3) (﹣2x﹣1)=﹣6,那么x的值为 .
【专项押题卷】临考题型分类专项押题:填空题-2024年中考数学
参考答案与试题解析
一.填空题(共30小题)
1.(2025 祁阳市校级一模)将﹣8360000用科学记数法表示为 ﹣8.36×106 .
【解答】解:﹣8360000=﹣8.36×106.
故答案为:﹣8.36×106.
2.(2025 重庆校级模拟)为了丰富学生的课外活动,某中学开设了多种兴趣小组.其中,两名学生想从摄影、舞蹈、编程、书法中选报一个兴趣小组.两名学生恰好选报同一个兴趣小组的概率为 .
【解答】解:分别记摄影、舞蹈、编程、书法为A、B、C、D,
根据题意列表如下:
同学1 同学2 A B C D
A A,A A,B A,C A,D
B B,A B,B B,C B,D
C C,A C,B C,C C,D
D D,A D,B D,C D,D
由列表可知:两名学生恰好选报同一个兴趣小组的概率为.
故答案为:.
3.(2025 武威一模)已知函数,其中m为常数.若该函数的图象显示y随着x的增大而增大,则m的取值范围为 .
【解答】解:左段函数为y=﹣2x2+8x+5(x<m),
该函数开口向下,对称轴为直线x=2,
要使该函数的图象显示y随着x的增大而增大,
则m≤2,
右段函数为y=x2+mx+3m2﹣1(x≥m),
该函数开口向上,对称轴为直线,
要使该函数的图象显示y随着x的增大而增大,
则,解得m≥0,
当x=m时,左段函数值要小于等于右段函数,
即﹣2m2+8m+5≤m2+m2+3m2﹣1,
整理可得7m2﹣8m﹣6≥0,
令7m2﹣8m﹣6=0,
解得,,
根据二次函数的图象可得7m2﹣8m﹣6≥0的解集为或(舍去),
综上,,
故答案为:.
4.(2025 广东模拟)进行心肺复苏急救措施时,一般胸外心脏按压速度x(单位:次/min)的范围如图所示,则x的取值范围可表示为 100≤x≤120 .
【解答】解:通过观察数轴端点情况可得:100≤x≤120,
故答案为:100≤x≤120.
5.(2025 巢湖市模拟)如图,四边形ABCD是半径为3的⊙O的内接四边形,CD∥AB,连接AC,AB=AC,若,则的长为 .
【解答】解:由条件可知∠ABC=∠ACB,∠ABC+∠D=180°,
∵,
∴,
∴,
∴,
∴∠ACD=∠BAC=45°,
连接AO,DO,
∴∠AOD=2∠ACD=90°,
则的长,
故答案为:.
6.(2025 重庆校级模拟)如图,⊙O的直径CD=10,弦AB=8,且CD⊥AB于点E,连接AC,以AC,AB为边作平行四边形ABFC,连接AF,BC交于点K,则AK= .
【解答】解:过点A作AM⊥AB于点A,交FC的延长线于点M,连接OB,
由条件可知BE=AE=4,OB=OC=OD=5,
∴,
∴CE=OE+OC=8,
由条件可知CF=AB=8,CF∥AB,
∵AM⊥AB,CD⊥AB,
∴AM∥CD,
∴四边形MCEA是平行四边形,
∵AM⊥AB,
∴四边形MCEA是矩形,
∴MC=AE=4,∠M=90°,MF=MC+CF=12,
∴,
∵CF∥AB,
∴△AEK∽△FCK,
∴,
∴.
7.(2025 哈尔滨模拟)双曲线经过点(﹣2,4),则k= ﹣8 .
【解答】解:由条件可知k=﹣2×4=﹣8.
故答案为:﹣8.
8.(2025 通许县一模)通常情况下酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色.化学实验室中有四瓶标签被污染无法识别的无色溶液,分别是A:盐酸(呈酸性),B:硝酸钾溶液(呈中性),C:氢氧化钠溶液(呈碱性),D:氢氧化钾溶液(呈碱性).小周同学在这四瓶溶液中取样,用酚酞检测其碱性.若小周将酚酞随机滴入两种样本溶液中,两种样本溶液恰好都变红色的概率是 .
【解答】解:画树状图如下,
由树状图可知:两种样本溶液恰好都变红色的概率是,
故答案为:.
9.(2025 无锡校级二模)两个半径相等的半圆按如图所示放置,半圆O′的圆心落在半圆O的圆弧上,半圆O′的一个直径端点与半圆O的圆心重合,若半圆的半径为1,则阴影部分的面积是 .
【解答】解:如图,连接OA,OA′,过点A作AB⊥OO′于点B,
由题意可知,△OO′A是等边三角形,
∴∠AOO′=∠AO′O=60°,,
∴,
∴S阴影=S扇形AOO′+S扇形AO′O﹣S△OO′A
,
故答案为:.
10.(2025 洛宁县模拟)如图,点A,B,C在⊙O上,OA⊥BC,若∠ABC=35°,则∠BCO的度数为 20° .
【解答】解:如下图所示,连接OB,
∵OA⊥BC,
根据垂径定理可得:,
由条件可知∠AOC=2∠ABC=70°,
∴∠BOC=2∠AOC=140°,
又∵OC=OB,
∴.
故答案为:20°.
11.(2025 辽宁模拟)如图,在△ABC中,∠C=60°,∠A=45°,BC=2,分别以B、A为圆心,大于的长为半径作弧,连接弧的两个交点;分别以A、C为圆心,大于的长为半径作弧,连接弧的两个交点,取所作两条直线的交点,以该交点为圆心,该交点到A的距离为半径作弧交于B,则弧AB的长为 .
【解答】解:如图,由作图可知,点O为△ABC的外接圆圆心,连接OB,OC,
由条件可知∠AOB=2∠ACB=120°,∠BOC=2∠BAC=90°,
∴,
∴,
∴弧AB的长为,
故答案为:.
12.(2025 南关区二模)如图,将△ABC折叠,使点B与点A重合,折痕为DE.若AC=4,BC=7,则△ACD的周长为 11 .
【解答】解:根据折叠的性质得:BD=AD,
∴AD+DC=BC=7.
∴△ACD的周长=CD+AD+AC=BC+AC=7+4=11,
故答案为:11.
13.(2025 柯桥区二模)一副三角板ABC和CDE按如图方式摆放,其中∠BAC=∠DCE=90°,∠D=30°,∠B=45°,点A恰好落在DE上,且BC∥DE,则∠ACE的度数为 75° .
【解答】解:∵∠B=45°,∠BAC=90°,
∴∠ACB=90°﹣45°=45°,
∵BC∥DE,
∴∠CAE=∠ACB=45°,
∵∠D=30°,∠DCE=90°,
∴∠E=90°﹣30°=60°,
∴∠ACE=180°﹣60°﹣45°=75°.
故答案为:75°.
14.(2025 南关区二模)《九章算术》中记载了一道数学问题,其译文为:有人合伙购物,每人出8钱,多余3钱;每人出7钱,还缺4钱,问合伙人数是多少?为解决此问题,设合伙人数为x人,根据题意,可列方程为 8x﹣3=7x+4 .
【解答】解:∵每人出8钱,会多出3钱;每人出7钱,又差4钱,设人数为x,
∴8x﹣3=7x+4,
故答案为:8x﹣3=7x+4.
15.(2025 江阳区校级模拟)在平面直角坐标系中,若点P(n,1)与点Q(﹣2,m)关于原点对称,则m+n的值是 1 .
【解答】解:∵点P(n,1)与点Q(﹣2,m)关于原点对称,
∴m=﹣1,n=2,
∴m+n=﹣1+2=1.
故答案为:1.
16.(2025 辽宁模拟)一次函数y=2x+5与抛物线y=2x2﹣4x+3的交点个数为 2 个.
【解答】解:联立方程组,
整理得x2﹣3x﹣1=0,
∴Δ=(﹣3)2﹣4×(﹣1)=13>0,
∴函数y=2x+5与抛物线y=2x2﹣4x+3的交点个数为2个,
故答案为:2.
17.(2025 台江区模拟)如图,一个正五边形纸片可裁成五个全等的等腰三角形和一个五边形,则图中∠α的度数是 36 °.
【解答】解:∵等腰三角形的底角72°,
∴∠α=180°﹣72°﹣72°=36°.
故答案为:36.
18.(2025 台江区模拟)如图,在平面直角坐标系中,△ABO与△A′B′O是以原点O为位似中心的位似图形.点B(﹣6,3)的对应点为B′(2,﹣1),若AA′=12,则A的坐标为 (﹣9,0) .
【解答】解:∵△ABO与△A′B′O是以原点O为位似中心的位似图形,点B(﹣6,3)的对应点为B′(2,﹣1),
∴△ABO与△A′B′O的位似比为3,
∴OA:OA′=3:1,
∵AA′为12,
∴OA=9,
∴点A的坐标为(﹣9,0).
故答案为:(﹣9,0).
19.(2025 成华区校级三模)如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2,分别以AB,BC为直径画半圆,则图中阴影部分的面积为 4 .
【解答】解:连接BD,如图所示,
由图可得,∠ADB=∠BDC=90°,
∵AB=4,BC=2,
∴图中阴影部分的面积为:S半圆ADB﹣S△ABD+S半圆BCD﹣S△BDC
=S半圆ADB+S半圆BCD﹣S△ABC
=π×()2π×()2
4,
故答案为:4.
20.(2025 开州区模拟)如图,△OAB是等边三角形,点B的坐标是(2,0),若反比例函数图象的一支经过点A,则k的值是 .
【解答】解:如图,过点A作AD⊥OB于点D,
∵△OAB是等边三角形,点B的坐标是(2,0),
∴OB=OA=2,
∴ODOB=1,
∴AD,
∴A(1,),
∵反比例函数图象的一支经过点A,
∴k=1.
故答案为:.
21.(2025 天河区校级二模)一个几何体的三视图如图所示,根据图示的数据计算该几何体的侧面积为 65π (结果保留π).
【解答】解:由图示可知,圆锥的高为12,底面圆的直径为10,
∴圆锥的母线为:,
∴圆锥的侧面积为:πrl=π×5×13=65π,
故答案为:65π.
22.(2025 包河区三模)如图,△ABC中,∠BAC=90°,BC=5,D为AB边的中点,将线段BD以B点中心逆时针旋转90°得到线段BD’,连接CD’.
(1)若AC=3,则BD′长为 2 ;
(2)CD′长最大为 .
【解答】解:(1)由勾股定理得,
∵D为AB边的中点,
∴,
故答案为:2;
(2)如图,以BC为直径画⊙O,则点A在⊙O上,
过点B作BH⊥BC,使,
以线段BH的中点I为圆心,BI长为半径画⊙I,
连接CI并延长,交⊙I于点D',此时CD'长最大,
∴,
∴,
由勾股定理得,
∴,
故答案为:.
23.(2025 青羊区校级模拟)在平面直角坐标系xOy中,已知抛物线y=ax2+2a(a﹣3)x(a≠0),设抛物线的对称轴为x=t.点(x1,y1),(x2,y2)是抛物线上两个点,当﹣1<x1<2时,对x1的每一个值,总存在x2,使得﹣1<x2<2,x2>x1,且y2>y1成立,则t的取值范围为 t的取值范围是或t>3 .
【解答】解:抛物线的对称轴为x=t,且t=3﹣a,
当﹣1<x1<2时,对于x1的每一个值,总存在x2,使得﹣1<x2<2x2>x1,且y2>y1成立,
①若a>0,此时t<3,
则当x≥t时,y随x的增大而增大;当x≤t时,y随x的增大而减小,
(i)当t≤﹣1时,
∵t<x1<x2,
∴y2>y1成立,
(ii)当﹣1<t<2时,
∵点(﹣1,m)关于对称轴直线x=t的对称点为(2t+1,m),
∴2t+1≤2,
∴,
∴当时,y2>y1成立,
(ii)当t≥2时,不合题意,舍去,
②若a<0,此时t>3,
则当x≥t时,y随x的增大而减小;当x≤t时,y随x的增大而增大,
∴t>3满足题意,
综上所述,t的取值范围是.
24.(2025 宝应县一模)如图,把R1、R2、R3三个电阻串联起来,线路AB上的电流为I,电压为U,则U=IR1+IR2+IR3,当R1=19.2,R2=35.4,R3=45.4,I=2.2时,U的值为 220 .
【解答】解:当R1=19.2,R2=35.4,R3=45.4,I=2.2时,
U=IR1+IR2+IR3
=I(R1+R2+R3)
=2.2×(19.2+35.4+45.4)
=2.2×100
=220,
故答案为:220.
25.(2025 重庆模拟)若关于x的不等式组所有整数解的和为14,且关于y的分式方程的解为非负整数,则所有满足条件的整数a的值之和为 14 .
【解答】解:,
解不等式①,得,
解不等式②,得x≤5,
∴不等式组的解集为:,
∵不等式组所有整数解的和为14,
∴不等式组的整数解为5,4,3,2或5,4,3,2,1,0,﹣1,
∴或,
解得:4≤a<9或﹣11≤a<﹣6;
,
解得:,
∵解为非负整数,
∴﹣11≤a<﹣6这种情况应舍去,
∴,即a≥2且a为偶数,
由题意得,当a=8时,;
当a=6时,;
当a=4时,(不合题意,舍去);
∴所有满足条件的整数a的值为8、6,
即8+6=14.
故答案为:14.
26.(2025 余姚市三模)如图为七巧板拼成的一个正方形,其边长为,若由其中的六块拼成一个矩形,其周长为整数,则矩形的面积为 6 .
【解答】解:由条件可知正方形的面积为,
结合七巧板,各图形的面积由大到小分别为2,2,1,1,1,,,
∴或或,
则六块拼成的矩形的面积为或7或6,
∵其周长为整数,
∴面积为6,
如图所示:
故答案为:6.
27.(2025 通许县一模)如图,点D为△ABC的边AB上一点,如果∠A=50°,将△ACD沿直线CD翻折后,点A落在A′处,那么当∠ACD= 65 °时,有A′D∥CA.
【解答】解:将△ACD沿直线CD翻折后,点A落在A′处,如果∠A=50°,
∴∠ADC=∠A′DC,
当A′D∥CA,
∴∠A′DC=∠ACD,
∴∠ADC=∠ACD,
∴,
故答案为:65.
28.(2025 鲤城区校级模拟)如图,PA,PB是⊙O的切线,A,B是切点.若∠AOB=130°,则∠APO= 25 °.
【解答】解:由题意可得:∠OAP=∠OBP=90°.
∵OP=OP.AO=BO,
∴Rt△AOP≌Rt△BOP,
∴∠AOP=∠BOP.
∵∠AOB=130°,
∴,
∴∠APO=90°﹣65°=25°.
故答案为:25.
29.(2025 花垣县模拟)如图,在平面直角坐标系中,已知反比例函数的图象上有一点A,过点A作AB⊥x轴于B,且△AOB的面积是6,则反比例函数解析式为 y .
【解答】解:∵反比例函数y的图象的一支在第二象限,
∴k<0,
∵AB⊥x轴,垂足为B,△ABO的面积为6,
∴|k|=2×6=12,
∴k=﹣12,
∴反比例函数的解析式为:y.
故答案为:y.
30.(2025 海珠区校级二模)定义一种新运算“m n”,规定当m≥n时,m n=3n+1;当m<n时,m n=2m+4.例如:3 1=3×1+1=4,(﹣2) 1=2×(﹣2)+4=0.如果(2x﹣3) (﹣2x﹣1)=﹣6,那么x的值为 ﹣1或 .
【解答】解:当2x﹣3≥﹣2x﹣1时,即时,
原式=3×(﹣2x﹣1)+1=﹣6,
解得:,
当2x﹣3<﹣2x﹣1时,即时,
原式=2×(2x﹣3)+4=﹣6,
解得:x=﹣1,
故x的值为﹣1或.
故答案为:﹣1或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
