华师大版的九年级上册第23章 图形的相似—23.6 图形与坐标 1.用坐标确定位置 同步练习
文档属性
| 名称 | 华师大版的九年级上册第23章 图形的相似—23.6 图形与坐标 1.用坐标确定位置 同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 422.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 14:24:52 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学九年级上册第23章第6节23.6.1用坐标确定位置同步练习
一、选择题
1.在平面直角坐标系中,若点P的坐标为(-3,2),则点P所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:B
解析:解答:∵点的横坐标-3<0,纵坐标2>0,
∴这个点在第二象限.
故选:B.
分析:记住平面直角坐标系中各个象限内点的符号:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
2. 若点A(a+1,b-2)在第二象限,则点B(-a,b+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:A
解析:解答:由A(a+1,b-2)在第二象限,得
a+1<0,b-2>0.
解得a<-1,b>2.
由不等式的性质,得
-a>1,b+1>3,
点B(-a,b+1)在第一象限,
故选:A.
分析:根据第二象限内的点的横坐标小于零,纵坐标大于零,可得关于a、b的不等式,再根据不等式的性质,可得B点的坐标符号.
3. 在平面直角坐标系中,点(m-2,m-3)在第三象限,则m的取值范围是( )
A.m>3 B.m<2 C.2<m<3 D.m<3
答案:B
解析:解答:∵点(m-2,m-3)在第三象限,
∴m 2<0
m 3<0
解得:
m<2
m<3
∴m<2.
故选:B.
分析:根据第三象限的点的横坐标与纵坐标都是负数列出不等式组,然后求解即可.
4. 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2015秒时,点P的坐标是( )
A.(2014,0) B.(2015,-1) C.(2015,1) D.(2016,0)
答案:B
解析:解答:半径为1个单位长度的半圆的周长为:×2π×1=π,
∵点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,
∴点P1秒走个半圆,
当点P从原点O出发,沿这条曲线向右运动,运动时间为1秒时,点P的坐标为(1,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为2秒时,点P的坐标为(2,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为3秒时,点P的坐标为(3,-1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为4秒时,点P的坐标为(4,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为5秒时,点P的坐标为(5,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为6秒时,点P的坐标为(6,0),
…,
∵2015÷4=503…3
∴A2015的坐标是(2015,-1),
故选:B.
分析:根据图象可得移动4次图象完成一个循环,从而可得出点A2015的坐标.
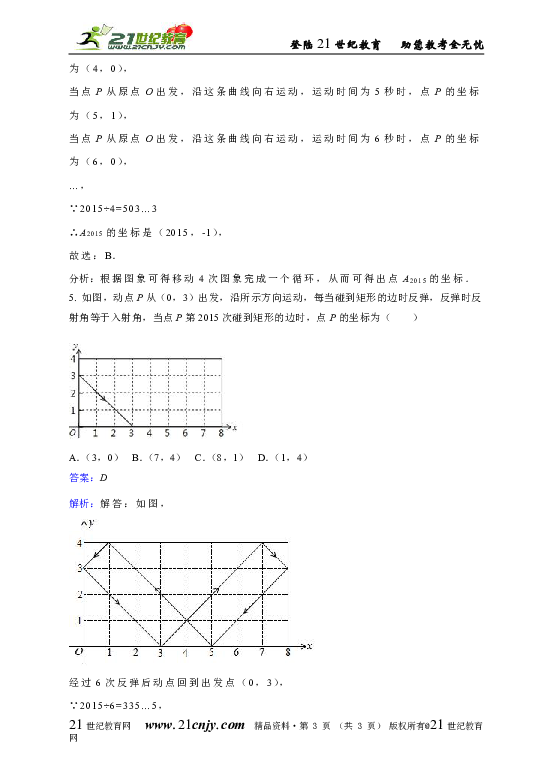
5. 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )
A.(3,0) B.(7,4) C.(8,1) D.(1,4)
答案:D
解析:解答:如图,
经过6次反弹后动点回到出发点(0,3),
∵2015÷6=335…5,
∴当点P第2015次碰到矩形的边时为第336个循环组的第5次反弹,
点P的坐标为(1,4).
故选:D.
分析:根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2015除以6,根据商和余数的情况确定所对应的点的坐标即可.
6. 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )
A.(-2013,2) B.(-2013,-2) C.(-2014,-2) D.(-2014,2)
答案:B
解析:解答:∵正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).
∴对角线交点M的坐标为(2,2),
根据题意得:第1次变换后的点M的对应点的坐标为(2-1,-2),即(1,-2),
第2次变换后的点M的对应点的坐标为:(2-2,2),即(0,2),
第3次变换后的点M的对应点的坐标为(2-3,-2),即(-1,-2),
第n次变换后的点M的对应点的为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2),
∴连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为(-2013,-2).
故选B
分析:首先由正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),然后根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标,即可得规律:第n次变换后的点M的对应点的为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2),继而求得把正方形ABCD连续经过2015次这样的变换得到正方形ABCD的对角线交点M的坐标.
7. 如图所示的网络图中,每个小格的边长是1个单位,点A、B都在格点上,若A(-2,1),则点B应表示为( )
A.(-2,0) B.(0,-2) C.(1,-1) D.(-1,1)
答案:B
解析:解答:如图,
点B表示为(0,-2).
故选B.
分析:先根据点A的坐标画出直角坐标系,然后写出点B的坐标.
8. 课间操时,小华、小军、小刚的位置如图1,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )
A.(5,4) B.(4,5) C.(3,4) D.(4,3)
答案:D
解析:解答:如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,如图所示就是以小华为原点的平面直角坐标系的第一象限,所以小刚的位置为(4,3).
故选D.
分析:根据已知两点的坐标确定平面直角坐标系,然后确定其它各点的坐标.
9. 以下是甲、乙、丙三人看地图时对四个坐标的描述:
甲:从学校向北直走500米,再向东直走100米可到图书馆.
乙:从学校向西直走300米,再向北直走200米可到邮局.
丙:邮局在火车站西200米处.
根据三人的描述,若从图书馆出发,判断下列哪一种走法,其终点是火车站( )
A.向南直走300米,再向西直走200米
B.向南直走300米,再向西直走100米
C.向南直走700米,再向西直走200米
D.向南直走700米,再向西直走600米
答案:A
解析:解答:如图,以学校为坐标原点画出直角坐标系,1个单位长表示100m,
从图书馆出发,向南直走300米,再向西直走200米可到火车站.
故选A.
分析:以学校为坐标原点画出直角坐标系,1个单位长表示100m,描出读书馆、邮局、火车站的位置,然后根据读书馆和火车站的坐标进行判断.
10. 若点A(2,-2),B(-1,-2),则直线AB与x轴和y轴的位置关系分别是( )
A.相交,相交 B.平行,平行
C.平行,垂直相交 D.垂直相交,平行
答案:C
解析:解答:∵点A(2,-2),B(-1,-2),
∴点A、B的纵坐标相同,
∴直线AB与x轴平行,与y轴的垂直.
故选:C.
分析:根据纵坐标相同的点在平行于x轴、垂直于y轴的直线上解答.
11. 过A(-5,-4)和B(-5,4)两点的直线一定( )
A.垂直于x轴
B.与x轴相交但不平行于x轴
C.平行于x轴
D.与x轴、y轴都不平行
答案:A
解析:解答:∵A,B两点的横坐标相等,
∴过这两点的直线一定平行于y轴,垂直于x轴.
故选A.
分析:根据平行于y轴的直线上两点的坐标特点解答.
12. 已知A点的坐标为(n+3,3),B点的坐标为(n-4,n),AB∥x轴,则线段AB的长为( )
A.5 B.6 C.7 D.13
答案:C
解析:解答:由题意得:n=3,
∴n+3=6,n-4=-1,
A(6,3),B(-1,3),
AB=6-(-1)=7,
故选:C.
分析:根据平行于x轴的直线上点的纵坐标相等,可得n=3,值根据同一条直线上两点间的距离是大数减小数,可得答案.
13. 如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )
A.(a-2,b) B.(a+2,b) C.(-a-2,-b) D.(a+2,-b)
答案:C
解析:解答:由图可知,△ABC与△A′B′C′关于点(-1,0)成中心对称,
设点P′的坐标为(x,y),
所以,
解得x=-a-2,y=-b,
所以,P′(-a-2,-b).
故选C.
分析:先根据图形确定出对称中心,然后根据中点公式列式计算即可得解.
14. 平面直角坐标系中,△ABC的顶点坐标分别为A(2,1)、B(-1,0)、C(1,3),现将△ABC绕B点顺时针旋转90°,得到△A′B′C′,则点A的对应点点A′的坐标为( )
A.(2,-1) B.(-2,0) C.(-3,0) D.以上都不对
答案:D
解析:解答:如图,根据旋转的性质可知,将△ABC绕B点顺时针旋转90°得到△A′B′C′,
此时,点A的对应点点A′的坐标为(0,-3).
故选D.
分析:A(2,1)、B(-1,0)两点横坐标相差3,纵坐标相差1,故将△ABC绕B点顺时针旋转90°得到△A′B′C′,点A的对应点点A′的坐标为(0,-3).
15. 在平面直角坐标系中,A、B、C三点的坐标分别为(0,0)、(0,-5)、(-2,-2),以这三点为平行四边形三的三个顶点,则第四个顶点D不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:A
解析:解答:根据平移的性质分两种情况
①从A到B横坐标不变,纵坐标变化5,那么从C到点D,横坐标不变,纵坐标也变化5,则D点为(-2,-7)或(-2,3),即分别在第三象限或第二象限.
②从C到A横坐标加2,纵坐标加2,那么从B到D也应如此,应为(2,-3),即在第四象限.
故选A.
分析:可用点平移的问题来解决,从A到B横坐标不变,纵坐标变化5,那么从C到点D,横坐标不变,纵坐标也变化5,为(-2,-7)或(-2,3)分别在第三象限或第二象限;从C到A横坐标加2,纵坐标加2,那么从B到D也应如此,应为(2,-3),在第四象限,所以不可能在第一象限.
二、填空题
16. 如果点M(3,x)在第一象限,则x的取值范围是 .
答案:x>0
解析:解答:由点M(3,x)在第一象限,得x>0.
故答案为:x>0.
分析:根据第一象限内点的横坐标大于零,点的纵坐标大于零,可得答案.
17. 观察下列一组坐标:
(a,b),(a,c),(b,c),(b,a),(c,a),(c,b),(a,b),(a,c)…,它们是按一定规律排列的,那么第9个坐标是 ,第2015个坐标是
答案:(b,c)|(c,a)
解析:解答:由以上坐标可得,每7个循环一次,
所以第9个坐标是(b,c);
∵2015÷7=287…6,
所以第2015个坐标是(c,a),
故答案为:(b,c);(c,a).
分析:根据观察每7个循环一次,因此解答即可.
18. 如图,这是台州市地图的一部分,分别以正东、正北方向为x轴、y轴的正方向建立直角坐标系,规定一个单位长度表示1km,甲、乙两人对着地图如下描述路桥区A处的位置.
则椒江区B处的坐标是 .
答案:(10,8).
解析:解答:如图:连接AB,作BC⊥x轴于C点,
由题意,得AB=16,∠ABC=30°,
AC=8,BC=8.
OC=OA+AC=10,
B(10,8).
分析:根据A点坐标,可建立平面直角坐标系,根据直角三角形的性质,可得AC的长,根据勾股定理,BC的长.
19. 在平面直角坐标系中,正方形ABCD的顶点A、B、C的坐标分别为(-1,1)、(-1,-1)、(1,-1),则顶点D的坐标为 .
答案:(1,1)
解析:解答:∵正方形两个顶点的坐标为A(-1,1),B(-1,-1),
∴AB=1-(-1)=2,
∵点C的坐标为:(1,-1),
∴第四个顶点D的坐标为:(1,1).
故答案为:(1,1).
分析:根据点的坐标求得正方形的边长,然后根据第三个点的坐标的特点将第四个顶点的坐标求出来即可.
20. 如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形.小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,能使△NMP为等腰直角三角形.那么,在y轴和直线上是否还存在符合条件的点P和点M呢?请你写出其它符合条件的点P的坐标
.
答案:(0,0),(0,),(0,-3)
解析:解答:
当M运动到(-1,1)时,ON=1,MN=1,
∵MN⊥x轴,所以由ON=MN可知,(0,0)就是符合条件的一个P点;
又当M运动到第三象限时,要MN=MP,且PM⊥MN,
设点M(x,2x+3),则有-x=-(2x+3),
解得x=-3,所以点P坐标为(0,-3).
如若MN为斜边时,则∠ONP=45°,所以ON=OP,设点M(x,2x+3),
则有-x=-(2x+3),
化简得-2x=-2x-3,
这方程无解,所以这时不存在符合条件的P点;
又当点M′在第二象限,M′N′为斜边时,这时N′P=M′P,∠M′N′P=45°,
设点M′(x,2x+3),则OP=ON′,而OP=M′N′,
∴有-x=(2x+3),
解得x=-,这时点P的坐标为(0,).
因此,其他符合条件的点P坐标是(0,0),(0,),(0,-3),(0,1).
故答案为:(0,0),(0,),(0,-3).
分析:由题意,应分两类情况讨论:当MN为直角边时和当MN为斜边时.
三、解答题
21. 在平面直角坐标系,点P(3n+2,4-2n)在第四象限,求实数n的取值范围.
答案:解答:∵点P(3n+2,4-2n)在第四象限,
∴3n+2>0
4 2n<0
解得:
n>
n>2
∴实数n的取值范围为:n>2.
解析:根据第四象限内点的坐标特征得到不等式组,然后解不等式组即可.
22. 如图,在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOP内部(不包括边界)的整点个数为m.
(1)当m=3时,求点B坐标的所有可能值;
答案:解答:(1)当B点的横坐标为3或者4时,即B(3,0)或(4,0)如下图所示,只有3个整点,
坐标分别为(1,1),(1,2),(2,1);
(2)当点B的横坐标为4n(n为正整数)时,用含n的代数式表示m.
答案:解答:当n=1时,即B点的横坐标为4,如上图,此时有3个整点;
当n=2时,即B点的横坐标为8,如图1,此时有9个整点;
当n=3时,即B点的横坐标为12,如图2,此时有15个整点;
根据上面的规律,即可得出3,9,15…,
∴整数点m=6n-3,
理由如下:当点B的横坐标为4n(n为正整数)时,
∵以OB为长OA为宽的矩形内(不包括边界)的整点个数为(4n-1)×3=12n-3,对角线AB上的整点个数总为3,
∴△AOB内部(不包括边界)的整点个数m=(12n-3-3)÷2=6n-3.
解析:(1)作出图形,然后根据网格结构确定出点B的可能坐标即可;
(2)作出图形,求出n=1、2、3时的整点个数,即m的值,然后根据矩形内整数点列出算式计算即可得解.
23. 多多和爸爸、妈妈周末到动物园游玩,回到家后,她利用平面直角坐标系画出了动物园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道马场的坐标为(-3,-3),你能帮她建立平面直角坐标系并求出其他各景点的坐标?
答案:解:建立坐标系如图:
∴南门(0,0),狮子(-4,5),飞禽(3,4)两栖动物(4,1).
解析:根据马场的坐标为(-3,-3),建立直角坐标系,找到原点和x轴、y轴.再找到其他各景点的坐标.
24. 如图,四边形OABC各个顶点的坐标分别是O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.
答案:解答:分别过C点和B点作x轴和y轴的平行线,如图,
则E(5,3),
所以S四边形ABCO=S矩形OHEF-S△ABH-S△CBE-S△OCF
=5×3-×2×2-×1×3-×3×2
=.
解析:分别过C点和B点作x轴和y轴的平行线,如图,然后利用S四边形ABCO=S矩形OHEF-S△ABH-S△CBE-S△OCF进行计算.
25. 已知:如图,矩形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A坐标为(0,3),∠OA B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.
答案:解答:由题意得OA=3,∠OAB=60°,
∴OB=3×tan60°=3
∵△ACB≌△ADB
∴AD=AC=OB,
过D作DE⊥y轴于点E
∵∠OAD=30°
∴ED=
∵cos30°=
那么OE=3×-3=1.5
D(,-1.5).
解析:利用三角函数可得到OB长,根据翻折得到的对应线段相等,也就得到了AD、AC长度,过D向y轴引垂线后,利用三角函数,可得到点D的横坐标,AE的值,进而求得OE的长,点E的纵坐标.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 17 页 (共 17 页) 版权所有@21世纪教育网
华师大版数学九年级上册第23章第6节23.6.1用坐标确定位置同步练习
一、选择题
1.在平面直角坐标系中,若点P的坐标为(-3,2),则点P所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:B
解析:解答:∵点的横坐标-3<0,纵坐标2>0,
∴这个点在第二象限.
故选:B.
分析:记住平面直角坐标系中各个象限内点的符号:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
2. 若点A(a+1,b-2)在第二象限,则点B(-a,b+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:A
解析:解答:由A(a+1,b-2)在第二象限,得
a+1<0,b-2>0.
解得a<-1,b>2.
由不等式的性质,得
-a>1,b+1>3,
点B(-a,b+1)在第一象限,
故选:A.
分析:根据第二象限内的点的横坐标小于零,纵坐标大于零,可得关于a、b的不等式,再根据不等式的性质,可得B点的坐标符号.
3. 在平面直角坐标系中,点(m-2,m-3)在第三象限,则m的取值范围是( )
A.m>3 B.m<2 C.2<m<3 D.m<3
答案:B
解析:解答:∵点(m-2,m-3)在第三象限,
∴m 2<0
m 3<0
解得:
m<2
m<3
∴m<2.
故选:B.
分析:根据第三象限的点的横坐标与纵坐标都是负数列出不等式组,然后求解即可.
4. 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2015秒时,点P的坐标是( )
A.(2014,0) B.(2015,-1) C.(2015,1) D.(2016,0)
答案:B
解析:解答:半径为1个单位长度的半圆的周长为:×2π×1=π,
∵点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,
∴点P1秒走个半圆,
当点P从原点O出发,沿这条曲线向右运动,运动时间为1秒时,点P的坐标为(1,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为2秒时,点P的坐标为(2,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为3秒时,点P的坐标为(3,-1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为4秒时,点P的坐标为(4,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为5秒时,点P的坐标为(5,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为6秒时,点P的坐标为(6,0),
…,
∵2015÷4=503…3
∴A2015的坐标是(2015,-1),
故选:B.
分析:根据图象可得移动4次图象完成一个循环,从而可得出点A2015的坐标.
5. 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2015次碰到矩形的边时,点P的坐标为( )
A.(3,0) B.(7,4) C.(8,1) D.(1,4)
答案:D
解析:解答:如图,
经过6次反弹后动点回到出发点(0,3),
∵2015÷6=335…5,
∴当点P第2015次碰到矩形的边时为第336个循环组的第5次反弹,
点P的坐标为(1,4).
故选:D.
分析:根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2015除以6,根据商和余数的情况确定所对应的点的坐标即可.
6. 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )
A.(-2013,2) B.(-2013,-2) C.(-2014,-2) D.(-2014,2)
答案:B
解析:解答:∵正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).
∴对角线交点M的坐标为(2,2),
根据题意得:第1次变换后的点M的对应点的坐标为(2-1,-2),即(1,-2),
第2次变换后的点M的对应点的坐标为:(2-2,2),即(0,2),
第3次变换后的点M的对应点的坐标为(2-3,-2),即(-1,-2),
第n次变换后的点M的对应点的为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2),
∴连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为(-2013,-2).
故选B
分析:首先由正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),然后根据题意求得第1次、2次、3次变换后的对角线交点M的对应点的坐标,即可得规律:第n次变换后的点M的对应点的为:当n为奇数时为(2-n,-2),当n为偶数时为(2-n,2),继而求得把正方形ABCD连续经过2015次这样的变换得到正方形ABCD的对角线交点M的坐标.
7. 如图所示的网络图中,每个小格的边长是1个单位,点A、B都在格点上,若A(-2,1),则点B应表示为( )
A.(-2,0) B.(0,-2) C.(1,-1) D.(-1,1)
答案:B
解析:解答:如图,
点B表示为(0,-2).
故选B.
分析:先根据点A的坐标画出直角坐标系,然后写出点B的坐标.
8. 课间操时,小华、小军、小刚的位置如图1,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )
A.(5,4) B.(4,5) C.(3,4) D.(4,3)
答案:D
解析:解答:如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,如图所示就是以小华为原点的平面直角坐标系的第一象限,所以小刚的位置为(4,3).
故选D.
分析:根据已知两点的坐标确定平面直角坐标系,然后确定其它各点的坐标.
9. 以下是甲、乙、丙三人看地图时对四个坐标的描述:
甲:从学校向北直走500米,再向东直走100米可到图书馆.
乙:从学校向西直走300米,再向北直走200米可到邮局.
丙:邮局在火车站西200米处.
根据三人的描述,若从图书馆出发,判断下列哪一种走法,其终点是火车站( )
A.向南直走300米,再向西直走200米
B.向南直走300米,再向西直走100米
C.向南直走700米,再向西直走200米
D.向南直走700米,再向西直走600米
答案:A
解析:解答:如图,以学校为坐标原点画出直角坐标系,1个单位长表示100m,
从图书馆出发,向南直走300米,再向西直走200米可到火车站.
故选A.
分析:以学校为坐标原点画出直角坐标系,1个单位长表示100m,描出读书馆、邮局、火车站的位置,然后根据读书馆和火车站的坐标进行判断.
10. 若点A(2,-2),B(-1,-2),则直线AB与x轴和y轴的位置关系分别是( )
A.相交,相交 B.平行,平行
C.平行,垂直相交 D.垂直相交,平行
答案:C
解析:解答:∵点A(2,-2),B(-1,-2),
∴点A、B的纵坐标相同,
∴直线AB与x轴平行,与y轴的垂直.
故选:C.
分析:根据纵坐标相同的点在平行于x轴、垂直于y轴的直线上解答.
11. 过A(-5,-4)和B(-5,4)两点的直线一定( )
A.垂直于x轴
B.与x轴相交但不平行于x轴
C.平行于x轴
D.与x轴、y轴都不平行
答案:A
解析:解答:∵A,B两点的横坐标相等,
∴过这两点的直线一定平行于y轴,垂直于x轴.
故选A.
分析:根据平行于y轴的直线上两点的坐标特点解答.
12. 已知A点的坐标为(n+3,3),B点的坐标为(n-4,n),AB∥x轴,则线段AB的长为( )
A.5 B.6 C.7 D.13
答案:C
解析:解答:由题意得:n=3,
∴n+3=6,n-4=-1,
A(6,3),B(-1,3),
AB=6-(-1)=7,
故选:C.
分析:根据平行于x轴的直线上点的纵坐标相等,可得n=3,值根据同一条直线上两点间的距离是大数减小数,可得答案.
13. 如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为( )
A.(a-2,b) B.(a+2,b) C.(-a-2,-b) D.(a+2,-b)
答案:C
解析:解答:由图可知,△ABC与△A′B′C′关于点(-1,0)成中心对称,
设点P′的坐标为(x,y),
所以,
解得x=-a-2,y=-b,
所以,P′(-a-2,-b).
故选C.
分析:先根据图形确定出对称中心,然后根据中点公式列式计算即可得解.
14. 平面直角坐标系中,△ABC的顶点坐标分别为A(2,1)、B(-1,0)、C(1,3),现将△ABC绕B点顺时针旋转90°,得到△A′B′C′,则点A的对应点点A′的坐标为( )
A.(2,-1) B.(-2,0) C.(-3,0) D.以上都不对
答案:D
解析:解答:如图,根据旋转的性质可知,将△ABC绕B点顺时针旋转90°得到△A′B′C′,
此时,点A的对应点点A′的坐标为(0,-3).
故选D.
分析:A(2,1)、B(-1,0)两点横坐标相差3,纵坐标相差1,故将△ABC绕B点顺时针旋转90°得到△A′B′C′,点A的对应点点A′的坐标为(0,-3).
15. 在平面直角坐标系中,A、B、C三点的坐标分别为(0,0)、(0,-5)、(-2,-2),以这三点为平行四边形三的三个顶点,则第四个顶点D不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:A
解析:解答:根据平移的性质分两种情况
①从A到B横坐标不变,纵坐标变化5,那么从C到点D,横坐标不变,纵坐标也变化5,则D点为(-2,-7)或(-2,3),即分别在第三象限或第二象限.
②从C到A横坐标加2,纵坐标加2,那么从B到D也应如此,应为(2,-3),即在第四象限.
故选A.
分析:可用点平移的问题来解决,从A到B横坐标不变,纵坐标变化5,那么从C到点D,横坐标不变,纵坐标也变化5,为(-2,-7)或(-2,3)分别在第三象限或第二象限;从C到A横坐标加2,纵坐标加2,那么从B到D也应如此,应为(2,-3),在第四象限,所以不可能在第一象限.
二、填空题
16. 如果点M(3,x)在第一象限,则x的取值范围是 .
答案:x>0
解析:解答:由点M(3,x)在第一象限,得x>0.
故答案为:x>0.
分析:根据第一象限内点的横坐标大于零,点的纵坐标大于零,可得答案.
17. 观察下列一组坐标:
(a,b),(a,c),(b,c),(b,a),(c,a),(c,b),(a,b),(a,c)…,它们是按一定规律排列的,那么第9个坐标是 ,第2015个坐标是
答案:(b,c)|(c,a)
解析:解答:由以上坐标可得,每7个循环一次,
所以第9个坐标是(b,c);
∵2015÷7=287…6,
所以第2015个坐标是(c,a),
故答案为:(b,c);(c,a).
分析:根据观察每7个循环一次,因此解答即可.
18. 如图,这是台州市地图的一部分,分别以正东、正北方向为x轴、y轴的正方向建立直角坐标系,规定一个单位长度表示1km,甲、乙两人对着地图如下描述路桥区A处的位置.
则椒江区B处的坐标是 .
答案:(10,8).
解析:解答:如图:连接AB,作BC⊥x轴于C点,
由题意,得AB=16,∠ABC=30°,
AC=8,BC=8.
OC=OA+AC=10,
B(10,8).
分析:根据A点坐标,可建立平面直角坐标系,根据直角三角形的性质,可得AC的长,根据勾股定理,BC的长.
19. 在平面直角坐标系中,正方形ABCD的顶点A、B、C的坐标分别为(-1,1)、(-1,-1)、(1,-1),则顶点D的坐标为 .
答案:(1,1)
解析:解答:∵正方形两个顶点的坐标为A(-1,1),B(-1,-1),
∴AB=1-(-1)=2,
∵点C的坐标为:(1,-1),
∴第四个顶点D的坐标为:(1,1).
故答案为:(1,1).
分析:根据点的坐标求得正方形的边长,然后根据第三个点的坐标的特点将第四个顶点的坐标求出来即可.
20. 如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形.小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,能使△NMP为等腰直角三角形.那么,在y轴和直线上是否还存在符合条件的点P和点M呢?请你写出其它符合条件的点P的坐标
.
答案:(0,0),(0,),(0,-3)
解析:解答:
当M运动到(-1,1)时,ON=1,MN=1,
∵MN⊥x轴,所以由ON=MN可知,(0,0)就是符合条件的一个P点;
又当M运动到第三象限时,要MN=MP,且PM⊥MN,
设点M(x,2x+3),则有-x=-(2x+3),
解得x=-3,所以点P坐标为(0,-3).
如若MN为斜边时,则∠ONP=45°,所以ON=OP,设点M(x,2x+3),
则有-x=-(2x+3),
化简得-2x=-2x-3,
这方程无解,所以这时不存在符合条件的P点;
又当点M′在第二象限,M′N′为斜边时,这时N′P=M′P,∠M′N′P=45°,
设点M′(x,2x+3),则OP=ON′,而OP=M′N′,
∴有-x=(2x+3),
解得x=-,这时点P的坐标为(0,).
因此,其他符合条件的点P坐标是(0,0),(0,),(0,-3),(0,1).
故答案为:(0,0),(0,),(0,-3).
分析:由题意,应分两类情况讨论:当MN为直角边时和当MN为斜边时.
三、解答题
21. 在平面直角坐标系,点P(3n+2,4-2n)在第四象限,求实数n的取值范围.
答案:解答:∵点P(3n+2,4-2n)在第四象限,
∴3n+2>0
4 2n<0
解得:
n>
n>2
∴实数n的取值范围为:n>2.
解析:根据第四象限内点的坐标特征得到不等式组,然后解不等式组即可.
22. 如图,在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOP内部(不包括边界)的整点个数为m.
(1)当m=3时,求点B坐标的所有可能值;
答案:解答:(1)当B点的横坐标为3或者4时,即B(3,0)或(4,0)如下图所示,只有3个整点,
坐标分别为(1,1),(1,2),(2,1);
(2)当点B的横坐标为4n(n为正整数)时,用含n的代数式表示m.
答案:解答:当n=1时,即B点的横坐标为4,如上图,此时有3个整点;
当n=2时,即B点的横坐标为8,如图1,此时有9个整点;
当n=3时,即B点的横坐标为12,如图2,此时有15个整点;
根据上面的规律,即可得出3,9,15…,
∴整数点m=6n-3,
理由如下:当点B的横坐标为4n(n为正整数)时,
∵以OB为长OA为宽的矩形内(不包括边界)的整点个数为(4n-1)×3=12n-3,对角线AB上的整点个数总为3,
∴△AOB内部(不包括边界)的整点个数m=(12n-3-3)÷2=6n-3.
解析:(1)作出图形,然后根据网格结构确定出点B的可能坐标即可;
(2)作出图形,求出n=1、2、3时的整点个数,即m的值,然后根据矩形内整数点列出算式计算即可得解.
23. 多多和爸爸、妈妈周末到动物园游玩,回到家后,她利用平面直角坐标系画出了动物园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道马场的坐标为(-3,-3),你能帮她建立平面直角坐标系并求出其他各景点的坐标?
答案:解:建立坐标系如图:
∴南门(0,0),狮子(-4,5),飞禽(3,4)两栖动物(4,1).
解析:根据马场的坐标为(-3,-3),建立直角坐标系,找到原点和x轴、y轴.再找到其他各景点的坐标.
24. 如图,四边形OABC各个顶点的坐标分别是O(0,0),A(3,0),B(5,2),C(2,3).求这个四边形的面积.
答案:解答:分别过C点和B点作x轴和y轴的平行线,如图,
则E(5,3),
所以S四边形ABCO=S矩形OHEF-S△ABH-S△CBE-S△OCF
=5×3-×2×2-×1×3-×3×2
=.
解析:分别过C点和B点作x轴和y轴的平行线,如图,然后利用S四边形ABCO=S矩形OHEF-S△ABH-S△CBE-S△OCF进行计算.
25. 已知:如图,矩形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A坐标为(0,3),∠OA B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.
答案:解答:由题意得OA=3,∠OAB=60°,
∴OB=3×tan60°=3
∵△ACB≌△ADB
∴AD=AC=OB,
过D作DE⊥y轴于点E
∵∠OAD=30°
∴ED=
∵cos30°=
那么OE=3×-3=1.5
D(,-1.5).
解析:利用三角函数可得到OB长,根据翻折得到的对应线段相等,也就得到了AD、AC长度,过D向y轴引垂线后,利用三角函数,可得到点D的横坐标,AE的值,进而求得OE的长,点E的纵坐标.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 17 页 (共 17 页) 版权所有@21世纪教育网
