华师大版的九年级上册第24章 解直角三角形—24.1 测量 同步练习
文档属性
| 名称 | 华师大版的九年级上册第24章 解直角三角形—24.1 测量 同步练习 |
|
|
| 格式 | doc | ||
| 文件大小 | 179.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学九年级上册第24章第1节24.1测量课时练习
一.选择题
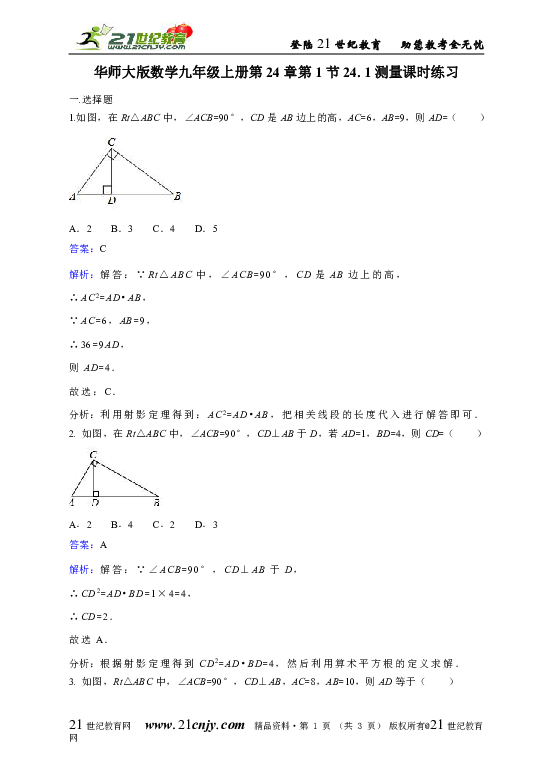
1.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=6,AB=9,则AD=( )
A.2 B.3 C.4 D.5
答案:C
解析:解答:∵Rt△ABC中,∠ACB=90°,CD是AB边上的高,
∴AC2=AD AB,
∵AC=6,AB=9,
∴36=9AD,
则AD=4.
故选:C.
分析:利用射影定理得到:AC2=AD AB,把相关线段的长度代入进行解答即可.
2. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=1,BD=4,则CD=( )
A.2 B.4 C.2 D.3
答案:A
解析:解答:∵∠ACB=90°,CD⊥AB于D,
∴CD2=AD BD=1×4=4,
∴CD=2.
故选A.
分析:根据射影定理得到CD2=AD BD=4,然后利用算术平方根的定义求解.
3. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AC=8,AB=10,则AD等于( )
A.4.4 B.5.5 C.6.4 D.7.4
答案:C
解析:解答:∵∠ACB=90°,CD⊥AB,
∴AC2=AD AB,
∴AD==6.4.
故选C.
分析:根据射影定理得到AC2=AD AB,然后把AC=8,AB=10代入计算即可.
4. 如图,△ABC中,点D在线段AB上,且∠BAD=∠C,则下列结论一定正确的是( )
A.AB2=AC BD B.AB AD=BD BC
C.AB2=BC BD D.AB AD=BD CD
答案:C
解析:解答:∵∠BAD=∠C,
而∠ABD=∠CBA,
∴△BAD∽△BCA,
∴AB:BC=BD:AB,
∴AB2=BC BD.
故选C.
分析:先证明△BAD∽△BCA,则利用相似的性质得AB:BC=BD:AB,然后根据比例性质得到AB2=BC BD.
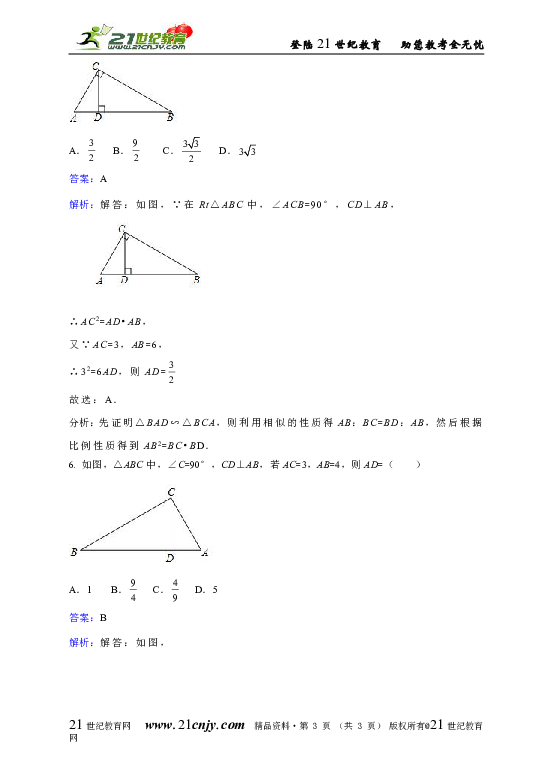
5. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为( )
A. B. C. D.
答案:A
解析:解答:如图,∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴AC2=AD AB,
又∵AC=3,AB=6,
∴32=6AD,则AD=
故选:A.
分析:先证明△BAD∽△BCA,则利用相似的性质得AB:BC=BD:AB,然后根据比例性质得到AB2=BC BD.
6. 如图,△ABC中,∠C=90°,CD⊥AB,若AC=3,AB=4,则AD=( )
A.1 B. C. D.5
答案:B
解析:解答:如图,
∵CD⊥AB,
∴∠ADC=90°,
又∵∠C=90°,
∴∠ACD=∠B(同角的余角相等).
又∵∠A=∠A,
∴△ACB∽△ADC,
∴,即,
∴AD=.
故选:B.
分析:利用两角法证得△ACB∽△ADC,然后由该相似三角形的对应边成比例来求AD的长度.
7. 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,DC=4,BC=9,则AC为( )
A.5 B.6 C.7 D.8
答案:B
解析:解答:由射影定理得,
AC2=CD CB=4×9=36,
∴AC=6.
故选:B.
分析:根据射影定理:直角三角形中,一条直角边是这条直角边在斜边上的射影与斜边的比例中项计算即可.
8. 如图,已知∠ABC=90°,BD⊥AC于D,AB=4,AC=10,则AD=( )
A. B.2 C. D.1
答案:A
解析:解答:根据射影定理得:AB2=AD AC,
∴AD=.
故选A.
分析:根据射影定理每一条直角边是这条直角边在斜边上的射影和斜边的比例中项即可得出BC的长.
9. 如图,在Rt△ABC,∠BAC=90°,AD⊥BC,AB=10,BD=6,则BC的值为( )
A. B.2 C. D.
答案:D
解析:解答:根据射影定理得:AB2=BD×BC,
∴BC=.
故选D.
分析:根据射影定理每一条直角边是这条直角边在斜边上的射影和斜边的比例中项即可得出BC的长.
10. 在Rt△ABC中,AD是斜边BC上的高线,若BD=2,BC=6,则AB=( )
A. B. C.2 D.2
答案:C
解析:解答:根据射影定理,AB2=BC BD,
∵BD=2,BC=6,
∴AB=2.
故选C.
分析:利用:直角三角形斜边上的高把三角形分成的两个三角形与原三角形相似,或射影定理的应用来解答.
11. 用计算器计算cos44°的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
答案:B
解析:解答:用计算器解cos44°=0.72.
故选B.
分析:本题要求熟练应用计算器,对计算器给出的结果,根据有效数字的概念用四舍五入法取近似数.
12. Rt△ABC中,∠C=90°,a:b=3:4,运用计算器计算,∠A的度数(精确到1°)( )
A.30° B.37° C.38° D.39°
答案:B
解析:解答:∵a:b=3:4,
∴设a=3x,b=4x,
由勾股定理知,c=5x.
∴sinA=a:c=3:5=0.6,
运用计算器得,∠A=37°.
故选B.
分析:根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系,可求出各边的长,然后求出∠A.
13. 如果tanα=0.213,那么锐角α的度数大约为( )
A.8° B.10° C.12°
答案:C
解析:解答:∵tanα=0.213,
∴∠α≈12°.
故选C.
分析:正确使用计算器计算即可.使用2nd键,然后按tan-10.213即可求出∠α的度数;
14. 用计算器求sin20°+tan54°33′的结果等于(结果精确到0.01)( )
A.2.25 B.1.55 C.1.73 D.1.75
答案:D
解析:解答:sin20°+tan54°33′
=sin20°+tan54.55°
=0.3420+1.4045
=1.7465
≈1.75.
故选D.
分析:先把54°33′化为54.55°,然后利用计算器分别算出sin20°和tan54.55°的值,相加后四舍五入即可.
15. 按科学记算器MODE MODE 1,使显示器显示D后,求sin90°的值,以下按键顺序正确的是( )
A.sin,9= B.9,sin= C.sin,9,0= D.9,0=
答案:C
解析:解答:显示器显示D后,即弧度制;
求sin90°的值,需按顺序按下:sin,9,0=.
故选C.
分析:要求熟练应用计算器.
二、填空题
16. 用计算器求tan35°的值,按键顺序是 .
答案:先按tan,再按35,最后按=
解析:解答:用计算器求tan35°的值,按键顺序是先按tan,再按35,最后=,
故答案为:先按tan,再按35,最后按=.
分析:先按锐角三角函数的名称,再按角的度数,最后按等号.
17. 利用计算器求值(精确到0.0001):tan27°15′+cos63°42′=
答案:0.9581
解析:解答:tan27°15′+cos63°42′=tan27.25°+cos63.7°≈0.5150+0.4431≈0.9581.
分析:直接利用计算器计算即可.注意把度分秒化为度.
18. 小虎同学在计算a+2cos60°时,因为粗心把“+”看成“-”,结果得2006,那么计算a+2cos60°的正确结果应为 .
答案:2008
解析:解答:∵a-2cos60°=2006,
∴a=2007.
∴a+2cos60°=2007+1=2008.
故答案为:2008.
分析:根据错误的运算先确定a的值,然后求出正确的结果.
19 已知tanβ=sin39°19′+cos80°10′,则锐角β≈ (结果精确到1′).
答案:38°49′
解析:解答:∵tanβ=sin39°19′+cos80°10′,
∴tanβ≈0.6336+0.1708=0.8044,
∠β≈38°49′.
故答案为:38°49′.
分析:首先利用计算器求出sin39°19′+cos80°10′的值,进而求出β的度数.
20 已知sinβ=0.8290,则β的度数约为 .
答案:56°
解析:解答:sinβ=0.8290,
则β的度数约为56°.
故答案为:56°.
分析:一般先按键“SHIFT”,再按键“sin”,输入“0.8290”,再按键“=”即可得到结果.
三、解答题
21 已知∠A为锐角,求满足下列条件的∠A度数.
(1)sinA=0.9816;
(2)tanA=0.1890.
答案:解答:(1)∵sinA=0.9816,∴∠A≈79°;
(2)∵tanA=0.1890,∴∠A≈11°.
解析:(1)正确使用计算器计算即可.使用2nd键,然后按sin-10.9816即可求出∠A的度数;(2)方法同(1).
22 等腰三角形中,两腰和底的长分别是10和13,求三角形的三个内角的度数(精确到l′).
答案:解:如下图所示,
AB=AC=10,BC=13,AD是底边上的高,
∵AD是底边上的高,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD=6.5,∠BAD=∠CAD=∠BAC,
在Rt△ABD中,sin∠BAD==0.65,
∴∠BAD≈40°32′,
∴∠BAC≈2∠BAD≈81°4′,∠B=∠C≈49°28′.
故△ABC的三个内角分别为:81°4′,49°28′,49°28′.
解析:先画图,AB=AC=10,BC=13,AD是底边上的高,利用等腰三角形三线合一定理可知BD=CD=6.5,∠BAD=∠CAD=∠BAC,在Rt△ABD中,利用∠BAD的正弦值的计算,结合计算器,可求∠BAD,从而可求∠B、∠BAC,那么∠C=∠B即可求.
23 用计算器求下列各式的值:
(1)sin59°;
(2)cos68°42′.
答案:解答:(1)sin59°≈0.857,
(2)cos68°42′=cos68.7°≈0.363.
解析:直接利用计算器计算即可.
24 用计算器求下式的值:
(1)tan75°;
(2)tan54°45′.
答案:解答:(1)tan75°≈3.732,
(2)tan54°45′=tan54.75°≈1.415.
故答案是3.732;1.415.
解析:直接利用计算器计算即可.
25利用计算器计算下列各值:(精确到0.001)
(1)sin20°;(2)cos63°35′;(3)sin87°17′.
答案:解答:(1)sin20°≈0.342;
(2)cos63°35′≈0.445;
(3)sin87°17′≈0.999.
解析:直接利用计算器计算即可,注意把度分秒化为度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 10 页 (共 10 页) 版权所有@21世纪教育网
华师大版数学九年级上册第24章第1节24.1测量课时练习
一.选择题
1.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=6,AB=9,则AD=( )
A.2 B.3 C.4 D.5
答案:C
解析:解答:∵Rt△ABC中,∠ACB=90°,CD是AB边上的高,
∴AC2=AD AB,
∵AC=6,AB=9,
∴36=9AD,
则AD=4.
故选:C.
分析:利用射影定理得到:AC2=AD AB,把相关线段的长度代入进行解答即可.
2. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=1,BD=4,则CD=( )
A.2 B.4 C.2 D.3
答案:A
解析:解答:∵∠ACB=90°,CD⊥AB于D,
∴CD2=AD BD=1×4=4,
∴CD=2.
故选A.
分析:根据射影定理得到CD2=AD BD=4,然后利用算术平方根的定义求解.
3. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB,AC=8,AB=10,则AD等于( )
A.4.4 B.5.5 C.6.4 D.7.4
答案:C
解析:解答:∵∠ACB=90°,CD⊥AB,
∴AC2=AD AB,
∴AD==6.4.
故选C.
分析:根据射影定理得到AC2=AD AB,然后把AC=8,AB=10代入计算即可.
4. 如图,△ABC中,点D在线段AB上,且∠BAD=∠C,则下列结论一定正确的是( )
A.AB2=AC BD B.AB AD=BD BC
C.AB2=BC BD D.AB AD=BD CD
答案:C
解析:解答:∵∠BAD=∠C,
而∠ABD=∠CBA,
∴△BAD∽△BCA,
∴AB:BC=BD:AB,
∴AB2=BC BD.
故选C.
分析:先证明△BAD∽△BCA,则利用相似的性质得AB:BC=BD:AB,然后根据比例性质得到AB2=BC BD.
5. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为( )
A. B. C. D.
答案:A
解析:解答:如图,∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴AC2=AD AB,
又∵AC=3,AB=6,
∴32=6AD,则AD=
故选:A.
分析:先证明△BAD∽△BCA,则利用相似的性质得AB:BC=BD:AB,然后根据比例性质得到AB2=BC BD.
6. 如图,△ABC中,∠C=90°,CD⊥AB,若AC=3,AB=4,则AD=( )
A.1 B. C. D.5
答案:B
解析:解答:如图,
∵CD⊥AB,
∴∠ADC=90°,
又∵∠C=90°,
∴∠ACD=∠B(同角的余角相等).
又∵∠A=∠A,
∴△ACB∽△ADC,
∴,即,
∴AD=.
故选:B.
分析:利用两角法证得△ACB∽△ADC,然后由该相似三角形的对应边成比例来求AD的长度.
7. 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,DC=4,BC=9,则AC为( )
A.5 B.6 C.7 D.8
答案:B
解析:解答:由射影定理得,
AC2=CD CB=4×9=36,
∴AC=6.
故选:B.
分析:根据射影定理:直角三角形中,一条直角边是这条直角边在斜边上的射影与斜边的比例中项计算即可.
8. 如图,已知∠ABC=90°,BD⊥AC于D,AB=4,AC=10,则AD=( )
A. B.2 C. D.1
答案:A
解析:解答:根据射影定理得:AB2=AD AC,
∴AD=.
故选A.
分析:根据射影定理每一条直角边是这条直角边在斜边上的射影和斜边的比例中项即可得出BC的长.
9. 如图,在Rt△ABC,∠BAC=90°,AD⊥BC,AB=10,BD=6,则BC的值为( )
A. B.2 C. D.
答案:D
解析:解答:根据射影定理得:AB2=BD×BC,
∴BC=.
故选D.
分析:根据射影定理每一条直角边是这条直角边在斜边上的射影和斜边的比例中项即可得出BC的长.
10. 在Rt△ABC中,AD是斜边BC上的高线,若BD=2,BC=6,则AB=( )
A. B. C.2 D.2
答案:C
解析:解答:根据射影定理,AB2=BC BD,
∵BD=2,BC=6,
∴AB=2.
故选C.
分析:利用:直角三角形斜边上的高把三角形分成的两个三角形与原三角形相似,或射影定理的应用来解答.
11. 用计算器计算cos44°的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
答案:B
解析:解答:用计算器解cos44°=0.72.
故选B.
分析:本题要求熟练应用计算器,对计算器给出的结果,根据有效数字的概念用四舍五入法取近似数.
12. Rt△ABC中,∠C=90°,a:b=3:4,运用计算器计算,∠A的度数(精确到1°)( )
A.30° B.37° C.38° D.39°
答案:B
解析:解答:∵a:b=3:4,
∴设a=3x,b=4x,
由勾股定理知,c=5x.
∴sinA=a:c=3:5=0.6,
运用计算器得,∠A=37°.
故选B.
分析:根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系,可求出各边的长,然后求出∠A.
13. 如果tanα=0.213,那么锐角α的度数大约为( )
A.8° B.10° C.12°
答案:C
解析:解答:∵tanα=0.213,
∴∠α≈12°.
故选C.
分析:正确使用计算器计算即可.使用2nd键,然后按tan-10.213即可求出∠α的度数;
14. 用计算器求sin20°+tan54°33′的结果等于(结果精确到0.01)( )
A.2.25 B.1.55 C.1.73 D.1.75
答案:D
解析:解答:sin20°+tan54°33′
=sin20°+tan54.55°
=0.3420+1.4045
=1.7465
≈1.75.
故选D.
分析:先把54°33′化为54.55°,然后利用计算器分别算出sin20°和tan54.55°的值,相加后四舍五入即可.
15. 按科学记算器MODE MODE 1,使显示器显示D后,求sin90°的值,以下按键顺序正确的是( )
A.sin,9= B.9,sin= C.sin,9,0= D.9,0=
答案:C
解析:解答:显示器显示D后,即弧度制;
求sin90°的值,需按顺序按下:sin,9,0=.
故选C.
分析:要求熟练应用计算器.
二、填空题
16. 用计算器求tan35°的值,按键顺序是 .
答案:先按tan,再按35,最后按=
解析:解答:用计算器求tan35°的值,按键顺序是先按tan,再按35,最后=,
故答案为:先按tan,再按35,最后按=.
分析:先按锐角三角函数的名称,再按角的度数,最后按等号.
17. 利用计算器求值(精确到0.0001):tan27°15′+cos63°42′=
答案:0.9581
解析:解答:tan27°15′+cos63°42′=tan27.25°+cos63.7°≈0.5150+0.4431≈0.9581.
分析:直接利用计算器计算即可.注意把度分秒化为度.
18. 小虎同学在计算a+2cos60°时,因为粗心把“+”看成“-”,结果得2006,那么计算a+2cos60°的正确结果应为 .
答案:2008
解析:解答:∵a-2cos60°=2006,
∴a=2007.
∴a+2cos60°=2007+1=2008.
故答案为:2008.
分析:根据错误的运算先确定a的值,然后求出正确的结果.
19 已知tanβ=sin39°19′+cos80°10′,则锐角β≈ (结果精确到1′).
答案:38°49′
解析:解答:∵tanβ=sin39°19′+cos80°10′,
∴tanβ≈0.6336+0.1708=0.8044,
∠β≈38°49′.
故答案为:38°49′.
分析:首先利用计算器求出sin39°19′+cos80°10′的值,进而求出β的度数.
20 已知sinβ=0.8290,则β的度数约为 .
答案:56°
解析:解答:sinβ=0.8290,
则β的度数约为56°.
故答案为:56°.
分析:一般先按键“SHIFT”,再按键“sin”,输入“0.8290”,再按键“=”即可得到结果.
三、解答题
21 已知∠A为锐角,求满足下列条件的∠A度数.
(1)sinA=0.9816;
(2)tanA=0.1890.
答案:解答:(1)∵sinA=0.9816,∴∠A≈79°;
(2)∵tanA=0.1890,∴∠A≈11°.
解析:(1)正确使用计算器计算即可.使用2nd键,然后按sin-10.9816即可求出∠A的度数;(2)方法同(1).
22 等腰三角形中,两腰和底的长分别是10和13,求三角形的三个内角的度数(精确到l′).
答案:解:如下图所示,
AB=AC=10,BC=13,AD是底边上的高,
∵AD是底边上的高,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD=6.5,∠BAD=∠CAD=∠BAC,
在Rt△ABD中,sin∠BAD==0.65,
∴∠BAD≈40°32′,
∴∠BAC≈2∠BAD≈81°4′,∠B=∠C≈49°28′.
故△ABC的三个内角分别为:81°4′,49°28′,49°28′.
解析:先画图,AB=AC=10,BC=13,AD是底边上的高,利用等腰三角形三线合一定理可知BD=CD=6.5,∠BAD=∠CAD=∠BAC,在Rt△ABD中,利用∠BAD的正弦值的计算,结合计算器,可求∠BAD,从而可求∠B、∠BAC,那么∠C=∠B即可求.
23 用计算器求下列各式的值:
(1)sin59°;
(2)cos68°42′.
答案:解答:(1)sin59°≈0.857,
(2)cos68°42′=cos68.7°≈0.363.
解析:直接利用计算器计算即可.
24 用计算器求下式的值:
(1)tan75°;
(2)tan54°45′.
答案:解答:(1)tan75°≈3.732,
(2)tan54°45′=tan54.75°≈1.415.
故答案是3.732;1.415.
解析:直接利用计算器计算即可.
25利用计算器计算下列各值:(精确到0.001)
(1)sin20°;(2)cos63°35′;(3)sin87°17′.
答案:解答:(1)sin20°≈0.342;
(2)cos63°35′≈0.445;
(3)sin87°17′≈0.999.
解析:直接利用计算器计算即可,注意把度分秒化为度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 10 页 (共 10 页) 版权所有@21世纪教育网
