华师大版的九年级上册第24章 解直角三角形—24.3 锐角三角函数 2.用计算器求锐角三角函数值 同步练习
文档属性
| 名称 | 华师大版的九年级上册第24章 解直角三角形—24.3 锐角三角函数 2.用计算器求锐角三角函数值 同步练习 | 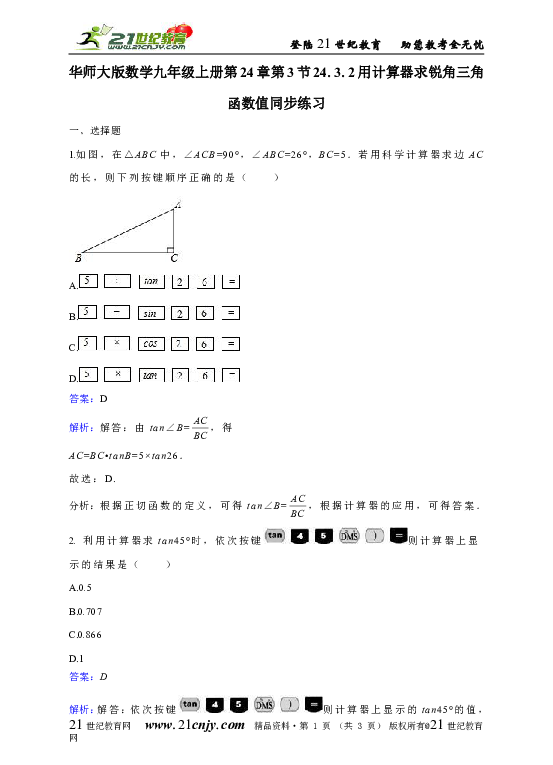 | |
| 格式 | doc | ||
| 文件大小 | 144.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 14:45:46 | ||
图片预览



文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学九年级上册第24章第3节24.3.2用计算器求锐角三角函数值同步练习
一、选择题
1.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.
B.
C.
D.
答案:D
解析:解答:由tan∠B=,得
AC=BC tanB=5×tan26.
故选:D.
分析:根据正切函数的定义,可得tan∠B=,根据计算器的应用,可得答案.
2. 利用计算器求tan45°时,依次按键则计算器上显示的结果是( )
A.0.5
B.0.707
C.0.866
D.1
答案:D
解析:解答:依次按键则计算器上显示的tan45°的值,即1.
故选D.
分析:本题要求熟练应用计算器.
3. 用科学记算器计算锐角α的三角函数值时,不能直接计算出来的三角函数值是( )
A.cotα B.tanα C.cosα D.sinα
答案:A
解析:解答:用科学记算器计算锐角α的三角函数值时,只能计算正弦、余弦、正切的值,要计算余切的值,需先计算正切值,在借助倒数进行计算得出答案,故答案为A.
分析:本题要求熟练应用计算器.
4. Rt△ABC中,∠C=90°,a:b=3:4,运用计算器计算,∠A的度数(精确到1°)( )
A.30° B.37° C.38° D.39°
答案:B
解析:解答:∵a:b=3:4,
∴设a=3x,b=4x,
由勾股定理知,c=5x.
∴sinA=a:c=3:5=0.6,
运用计算器得,∠A=37°.
故选B.
分析:根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系,可求出各边的长,然后求出∠A.
5. 如果tanα=0.213,那么锐角α的度数大约为( )
A.8° B.10° C.12° D.15°
答案:C
解析:解答:∵tanα=0.213,
∴∠α≈12°.
故选C.
分析:正确使用计算器计算即可.使用2nd键,然后按tan-10.213即可求出∠α的度数;
6. 四位学生用计算器求sin62°20′的值正确的是( )
A.0.8857 B.0.8856 C.0.8852 D.0.8851
答案:A
解析:解答:sin62°20′≈0.8857,
故选A.
分析:本题要求熟练应用计算器,根据计算器给出的结果进行判断.
7. 用计算器求sin20°+tan54°33′的结果等于(结果精确到0.01)( )
A.2.25 B.1.55 C.1.73 D.1.75
答案:D
解析:解答:sin20°+tan54°33′
=sin20°+tan54.55°
=0.3420+1.4045
=1.7465
≈1.75.
故选D.
分析:先把54°33′化为54.55°,然后利用计算器分别算出sin20°和tan54.55°的值,相加后四舍五入即可.
8. 一个直角三角形有两条边长为3,4,则较小的锐角约为( )
A.37° B.41°
C.37°或41° D.以上答案均不对
答案:C
解析:解答:①若3、4是直角边,
∵两直角边为3,4,
∴斜边长=
∴较小的锐角所对的直角边为3,则其正弦值为;
②若斜边长为4,则较小边=≈2.65,
∴较小边所对锐角正弦值约==0.6625,
利用计算器求得角约为37°或41°.
故选C.
分析:此题分情况计算:①若3、4是直角边,利用勾股定理可求斜边,从而可求较小锐角的正弦值,再利用计算器可求角;②4是斜边,利用勾股定理可求较小边,从而求出其所对角的正弦值,再利用计算器可求角.
9. 用计算器求tan26°,cos27°,sin28°的值,它们的大小关系是( )
A.tan26°<cos27°<sin28° B.tan26°<sin28°<cos27°
C.sin28°<tan26°<cos27° D.cos27°<sin28°<tan16°
答案:C
解析:解答:∵tan26°≈0.488,
cos27°≈0.891,
sin28°≈0.469.
故sin28°<tan26°<cos27°.
故选C.
分析:先用计算器求出tan26°、cos27°、sin28°的值,比较即可.
10. 按科学记算器MODE MODE 1,使显示器显示D后,求sin90°的值,以下按键顺序正确的是( )
A.sin,9= B.9,sin= C.sin,9,0= D.9,0=
答案:C
解析:解答:显示器显示D后,即弧度制;
求sin90°的值,需按顺序按下:sin,9,0=.
故选C.
分析:要求熟练应用计算器.
11. 用计算器验证,下列等式中正确的是( )
A.sin18°24′+sin35°26′=sin54°
B.sin65°54′-sin35°54′=sin30°
C.2sin15°30′=sin31°
D.sin70°18′-sin12°18′=sin47°42′
答案:D
解析:解答:利用计算器分别计算出各个三角函数的数值,进行分别检验.正确的是sin70°18′-sin12°18′=sin47°42′.
故选D.
分析:本题考查三角函数的加减法运算.
12. 用计算器求cos15°,正确的按键顺序是( )
A.cos15= B.cos15 C.Shift15 D.15cos
答案:A
解析:解答:先按键“cos”,再输入角的度数15,按键“=”即可得到结果.
故选A
分析:根据用计算器算三角函数的方法:先按键“cos”,再输入角的度数,按键“=”即可得到结果.
13. 已知tanα=0.3249,则α约为( )
A.17° B.18° C.19° D.20°
答案:B
解析:解答:tanα=0.3249,
α约为18°.
故选:B.
分析:一般先按键“SHIFT”,再按键“tan”,输入“0.3249”,再按键“=”即可得到结果.
14. 按键,使科学记算器显示回后,求sin90°的值,以下按键顺序正确的是( )
A.
B.
C.
D.
答案:A
解析:解答:第一步按sin,第二步90,最后按=,
故选A.
分析:首先知道用计算器求一个角度的函数值的操作过程,然后作出选择.
15. 已知sinα=,求α,若用计算器计算且结果为“30”,最后按键( )
A.AC10N B.SHIET C.MODE D.SHIFT
答案:D
解析:解答:“SHIET”表示使用该键上方的对应的功能.
故选D.
分析:本题要求熟练应用计算器.
二、填空题
16. 用计算器求tan35°的值,按键顺序是 .
答案:先按tan,再按35,最后按=
解析:解答:用计算器求tan35°的值,按键顺序是先按tan,再按35,最后=,
故答案为:先按tan,再按35,最后按=.
分析:根据计算器的使用,可得答案.
17. 已知tanβ=22.3,则β= (精确到1″)
答案:87°25′56″
解析:解答:∵tanβ=22.3,∴β=87°25′56″.
故答案为:87°25′56″.
分析:利用计算器首先按2ndf,再按tan22.3,即可得出β的角度.
18. 如果cosA=0.8888,则∠A≈ (精确到1″)
答案:27°16′38″
解析:解答:如果cosA=0.8888,则∠A≈27°16′38″.
故答案为:27°16′38″
分析:首先按2ndF键,再按cos键,再输入0.8888,再按DMS即可得出答案
19. cos35°≈ (结果保留四个有效数字).
答案:0.8192
解析:解答:cos35°≈0.8192.
故答案为:0.8192.
分析:利用计算器,先按35,再按cos即可求出(计算器的型号不同可能按键的顺序有所不同,要具体情况具体对待).
20. 小虎同学在计算a+2cos60°时,因为粗心把“+”看成“-”,结果得2006,那么计算a+2cos60°的正确结果应为 .
答案:2008
解析:解答:∵a-2cos60°=2006,
∴a=2007.
∴a+2cos60°=2007+1=2008.
故答案为:2008.
分析:根据错误的运算先确定a的值,然后求出正确的结果.
三、解答题
21. 已知下列锐角三角函数值,用计算器求锐角A,B的度数.
(1)sinA=0.7,sinB=0.01;
答案:解答:(1)sinA=0.7,得A=44.4°;
sinB=0.01得B=0.57°;
(2)cosA=0.15,cosB=0.8;
答案:解答:cosA=0.15,得A=81.3°;
cosB=0.8,得B=36.8°;
(3)tanA=2.4,tanB=0.5.
答案:解答:由tanA=2.4,得A=67.4°;
由tanB=0.5,得B=26.5°.
解析:熟练应用计算器,对计算器给出的结果,根据有效数字的概念用四舍五入法取近似数.
22. (1)验证下列两组数值的关系:
2sin30° cos30°与sin60°;
2sin22.5° cos22.5°与sin45°.
答案:解答:∵2sin30° cos30°=2××=,sin60°=.
2sin22.5° cos22.5≈2×0.38×0.92≈0.7,sin45°=≈0.7,
∴2sin30° cos30°=sin60°,2sin22.5° cos22.5=sin45°;
(2)用一句话概括上面的关系.
答案:解答: 由(1)可知,一个角正弦与余弦积的2倍,等于该角2倍的正弦值;
(3)试一试:你自己任选一个锐角,用计算器验证上述结论是否成立.
答案:解答: 2sin15° cos15°≈2×0.26×0.97≈,sin30°=;
故结论成立;
(4)如果结论成立,试用α表示一个锐角,写出这个关系式.
答案:解答:2sinα cosα=sin2α.
解析:(1)分别计算出各数,进而可得出结论;
(2)根据(1)中的关系可得出结论;
(3)任选一个角验证(3)的结论即可;
(4)用α表示一个锐角,写出这个关系式即可.
23. 已知下列锐角三角函数值,用计算器求其相应的锐角:
(1)sinA=0.7325,sinB=0.0547;
答案:解答:(1)∵sinA=0.7325,∴∠A≈47.1°,
∵sinB=0.0547,∴∠B≈3.1°;
(2)cosA=0.6054,cosB=0.1659;
答案:解答: ∵cosA=0.6054,
∴∠A≈52.7°,
∵cosB=0.1659,
∴∠B≈80.5°;
(3)tanA=4.8425,tanB=0.8816.
答案:解答:∵tanA=4.8425,
∴∠A≈78.3°,
∵tanB=0.8816,
∴∠B≈41.4°.
解析:(1)直接利用计算器借助sin-1求出即可;
(2)直接利用计算器借助cos-1求出即可;
(3)直接利用计算器借助tan-1求出即可.
24. 已知∠A为锐角,求满足下列条件的∠A的度数(精确到1″).
(1)sinA=0.9816;
答案:解答:∵sinA=0.9816,
∴∠A≈78.991°≈78°59′28″;
(2)cosA=0.8607;
答案:解答:∵cosA=0.8607,
∴∠A≈30.605°=30°36′18″;
(3)tanA=0.1890;
答案:解答: ∵tanA=0.1890,
∴∠A≈10.703°≈10°42′11″;
(4)tanA=56.78.
答案:解答:∵tanA=56.78,
∴∠A≈88.991°≈88°59′28″.
解析:(1)熟练应用计算器,使用2nd键,然后按sin-10.9816,即可求出∠A的度数,对计算器给出的结果,用四舍五入法取近似数.
(2)、(3)、(4)方法同(1).
25. 等腰三角形中,两腰和底的长分别是10和13,求三角形的三个内角的度数(精确到1′).
答案:解答:如图所示,AB=AC=10,BC=13,AD是底边上的高,
∵AD是底边上的高,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD=6.5,∠BAD=∠CAD=∠BAC,
在Rt△ABD中,sin∠BAD==0.65,
∴∠BAD≈40°32′,
∴∠BAC≈2∠BAD≈81°4′,∠B=∠C≈49°28′.
故△ABC的三个内角分别为:81°4′,49°28′,49°28′.
解析:先画图,AB=AC=10,BC=13,AD是底边上的高,利用等腰三角形三线合一定理可知BD=CD=6.5,∠BAD=∠CAD=∠BAC,在Rt△ABD中,利用∠BAD的正弦值的计算,结合计算器,可求∠BAD,从而可求∠B、∠BAC,那么∠C=∠B即可求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 10 页 (共 10 页) 版权所有@21世纪教育网
华师大版数学九年级上册第24章第3节24.3.2用计算器求锐角三角函数值同步练习
一、选择题
1.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.
B.
C.
D.
答案:D
解析:解答:由tan∠B=,得
AC=BC tanB=5×tan26.
故选:D.
分析:根据正切函数的定义,可得tan∠B=,根据计算器的应用,可得答案.
2. 利用计算器求tan45°时,依次按键则计算器上显示的结果是( )
A.0.5
B.0.707
C.0.866
D.1
答案:D
解析:解答:依次按键则计算器上显示的tan45°的值,即1.
故选D.
分析:本题要求熟练应用计算器.
3. 用科学记算器计算锐角α的三角函数值时,不能直接计算出来的三角函数值是( )
A.cotα B.tanα C.cosα D.sinα
答案:A
解析:解答:用科学记算器计算锐角α的三角函数值时,只能计算正弦、余弦、正切的值,要计算余切的值,需先计算正切值,在借助倒数进行计算得出答案,故答案为A.
分析:本题要求熟练应用计算器.
4. Rt△ABC中,∠C=90°,a:b=3:4,运用计算器计算,∠A的度数(精确到1°)( )
A.30° B.37° C.38° D.39°
答案:B
解析:解答:∵a:b=3:4,
∴设a=3x,b=4x,
由勾股定理知,c=5x.
∴sinA=a:c=3:5=0.6,
运用计算器得,∠A=37°.
故选B.
分析:根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系,可求出各边的长,然后求出∠A.
5. 如果tanα=0.213,那么锐角α的度数大约为( )
A.8° B.10° C.12° D.15°
答案:C
解析:解答:∵tanα=0.213,
∴∠α≈12°.
故选C.
分析:正确使用计算器计算即可.使用2nd键,然后按tan-10.213即可求出∠α的度数;
6. 四位学生用计算器求sin62°20′的值正确的是( )
A.0.8857 B.0.8856 C.0.8852 D.0.8851
答案:A
解析:解答:sin62°20′≈0.8857,
故选A.
分析:本题要求熟练应用计算器,根据计算器给出的结果进行判断.
7. 用计算器求sin20°+tan54°33′的结果等于(结果精确到0.01)( )
A.2.25 B.1.55 C.1.73 D.1.75
答案:D
解析:解答:sin20°+tan54°33′
=sin20°+tan54.55°
=0.3420+1.4045
=1.7465
≈1.75.
故选D.
分析:先把54°33′化为54.55°,然后利用计算器分别算出sin20°和tan54.55°的值,相加后四舍五入即可.
8. 一个直角三角形有两条边长为3,4,则较小的锐角约为( )
A.37° B.41°
C.37°或41° D.以上答案均不对
答案:C
解析:解答:①若3、4是直角边,
∵两直角边为3,4,
∴斜边长=
∴较小的锐角所对的直角边为3,则其正弦值为;
②若斜边长为4,则较小边=≈2.65,
∴较小边所对锐角正弦值约==0.6625,
利用计算器求得角约为37°或41°.
故选C.
分析:此题分情况计算:①若3、4是直角边,利用勾股定理可求斜边,从而可求较小锐角的正弦值,再利用计算器可求角;②4是斜边,利用勾股定理可求较小边,从而求出其所对角的正弦值,再利用计算器可求角.
9. 用计算器求tan26°,cos27°,sin28°的值,它们的大小关系是( )
A.tan26°<cos27°<sin28° B.tan26°<sin28°<cos27°
C.sin28°<tan26°<cos27° D.cos27°<sin28°<tan16°
答案:C
解析:解答:∵tan26°≈0.488,
cos27°≈0.891,
sin28°≈0.469.
故sin28°<tan26°<cos27°.
故选C.
分析:先用计算器求出tan26°、cos27°、sin28°的值,比较即可.
10. 按科学记算器MODE MODE 1,使显示器显示D后,求sin90°的值,以下按键顺序正确的是( )
A.sin,9= B.9,sin= C.sin,9,0= D.9,0=
答案:C
解析:解答:显示器显示D后,即弧度制;
求sin90°的值,需按顺序按下:sin,9,0=.
故选C.
分析:要求熟练应用计算器.
11. 用计算器验证,下列等式中正确的是( )
A.sin18°24′+sin35°26′=sin54°
B.sin65°54′-sin35°54′=sin30°
C.2sin15°30′=sin31°
D.sin70°18′-sin12°18′=sin47°42′
答案:D
解析:解答:利用计算器分别计算出各个三角函数的数值,进行分别检验.正确的是sin70°18′-sin12°18′=sin47°42′.
故选D.
分析:本题考查三角函数的加减法运算.
12. 用计算器求cos15°,正确的按键顺序是( )
A.cos15= B.cos15 C.Shift15 D.15cos
答案:A
解析:解答:先按键“cos”,再输入角的度数15,按键“=”即可得到结果.
故选A
分析:根据用计算器算三角函数的方法:先按键“cos”,再输入角的度数,按键“=”即可得到结果.
13. 已知tanα=0.3249,则α约为( )
A.17° B.18° C.19° D.20°
答案:B
解析:解答:tanα=0.3249,
α约为18°.
故选:B.
分析:一般先按键“SHIFT”,再按键“tan”,输入“0.3249”,再按键“=”即可得到结果.
14. 按键,使科学记算器显示回后,求sin90°的值,以下按键顺序正确的是( )
A.
B.
C.
D.
答案:A
解析:解答:第一步按sin,第二步90,最后按=,
故选A.
分析:首先知道用计算器求一个角度的函数值的操作过程,然后作出选择.
15. 已知sinα=,求α,若用计算器计算且结果为“30”,最后按键( )
A.AC10N B.SHIET C.MODE D.SHIFT
答案:D
解析:解答:“SHIET”表示使用该键上方的对应的功能.
故选D.
分析:本题要求熟练应用计算器.
二、填空题
16. 用计算器求tan35°的值,按键顺序是 .
答案:先按tan,再按35,最后按=
解析:解答:用计算器求tan35°的值,按键顺序是先按tan,再按35,最后=,
故答案为:先按tan,再按35,最后按=.
分析:根据计算器的使用,可得答案.
17. 已知tanβ=22.3,则β= (精确到1″)
答案:87°25′56″
解析:解答:∵tanβ=22.3,∴β=87°25′56″.
故答案为:87°25′56″.
分析:利用计算器首先按2ndf,再按tan22.3,即可得出β的角度.
18. 如果cosA=0.8888,则∠A≈ (精确到1″)
答案:27°16′38″
解析:解答:如果cosA=0.8888,则∠A≈27°16′38″.
故答案为:27°16′38″
分析:首先按2ndF键,再按cos键,再输入0.8888,再按DMS即可得出答案
19. cos35°≈ (结果保留四个有效数字).
答案:0.8192
解析:解答:cos35°≈0.8192.
故答案为:0.8192.
分析:利用计算器,先按35,再按cos即可求出(计算器的型号不同可能按键的顺序有所不同,要具体情况具体对待).
20. 小虎同学在计算a+2cos60°时,因为粗心把“+”看成“-”,结果得2006,那么计算a+2cos60°的正确结果应为 .
答案:2008
解析:解答:∵a-2cos60°=2006,
∴a=2007.
∴a+2cos60°=2007+1=2008.
故答案为:2008.
分析:根据错误的运算先确定a的值,然后求出正确的结果.
三、解答题
21. 已知下列锐角三角函数值,用计算器求锐角A,B的度数.
(1)sinA=0.7,sinB=0.01;
答案:解答:(1)sinA=0.7,得A=44.4°;
sinB=0.01得B=0.57°;
(2)cosA=0.15,cosB=0.8;
答案:解答:cosA=0.15,得A=81.3°;
cosB=0.8,得B=36.8°;
(3)tanA=2.4,tanB=0.5.
答案:解答:由tanA=2.4,得A=67.4°;
由tanB=0.5,得B=26.5°.
解析:熟练应用计算器,对计算器给出的结果,根据有效数字的概念用四舍五入法取近似数.
22. (1)验证下列两组数值的关系:
2sin30° cos30°与sin60°;
2sin22.5° cos22.5°与sin45°.
答案:解答:∵2sin30° cos30°=2××=,sin60°=.
2sin22.5° cos22.5≈2×0.38×0.92≈0.7,sin45°=≈0.7,
∴2sin30° cos30°=sin60°,2sin22.5° cos22.5=sin45°;
(2)用一句话概括上面的关系.
答案:解答: 由(1)可知,一个角正弦与余弦积的2倍,等于该角2倍的正弦值;
(3)试一试:你自己任选一个锐角,用计算器验证上述结论是否成立.
答案:解答: 2sin15° cos15°≈2×0.26×0.97≈,sin30°=;
故结论成立;
(4)如果结论成立,试用α表示一个锐角,写出这个关系式.
答案:解答:2sinα cosα=sin2α.
解析:(1)分别计算出各数,进而可得出结论;
(2)根据(1)中的关系可得出结论;
(3)任选一个角验证(3)的结论即可;
(4)用α表示一个锐角,写出这个关系式即可.
23. 已知下列锐角三角函数值,用计算器求其相应的锐角:
(1)sinA=0.7325,sinB=0.0547;
答案:解答:(1)∵sinA=0.7325,∴∠A≈47.1°,
∵sinB=0.0547,∴∠B≈3.1°;
(2)cosA=0.6054,cosB=0.1659;
答案:解答: ∵cosA=0.6054,
∴∠A≈52.7°,
∵cosB=0.1659,
∴∠B≈80.5°;
(3)tanA=4.8425,tanB=0.8816.
答案:解答:∵tanA=4.8425,
∴∠A≈78.3°,
∵tanB=0.8816,
∴∠B≈41.4°.
解析:(1)直接利用计算器借助sin-1求出即可;
(2)直接利用计算器借助cos-1求出即可;
(3)直接利用计算器借助tan-1求出即可.
24. 已知∠A为锐角,求满足下列条件的∠A的度数(精确到1″).
(1)sinA=0.9816;
答案:解答:∵sinA=0.9816,
∴∠A≈78.991°≈78°59′28″;
(2)cosA=0.8607;
答案:解答:∵cosA=0.8607,
∴∠A≈30.605°=30°36′18″;
(3)tanA=0.1890;
答案:解答: ∵tanA=0.1890,
∴∠A≈10.703°≈10°42′11″;
(4)tanA=56.78.
答案:解答:∵tanA=56.78,
∴∠A≈88.991°≈88°59′28″.
解析:(1)熟练应用计算器,使用2nd键,然后按sin-10.9816,即可求出∠A的度数,对计算器给出的结果,用四舍五入法取近似数.
(2)、(3)、(4)方法同(1).
25. 等腰三角形中,两腰和底的长分别是10和13,求三角形的三个内角的度数(精确到1′).
答案:解答:如图所示,AB=AC=10,BC=13,AD是底边上的高,
∵AD是底边上的高,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD=6.5,∠BAD=∠CAD=∠BAC,
在Rt△ABD中,sin∠BAD==0.65,
∴∠BAD≈40°32′,
∴∠BAC≈2∠BAD≈81°4′,∠B=∠C≈49°28′.
故△ABC的三个内角分别为:81°4′,49°28′,49°28′.
解析:先画图,AB=AC=10,BC=13,AD是底边上的高,利用等腰三角形三线合一定理可知BD=CD=6.5,∠BAD=∠CAD=∠BAC,在Rt△ABD中,利用∠BAD的正弦值的计算,结合计算器,可求∠BAD,从而可求∠B、∠BAC,那么∠C=∠B即可求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 10 页 (共 10 页) 版权所有@21世纪教育网
