华师大版的九年级上册第24章 解直角三角形—24.4 解直角三角形 同步练习
文档属性
| 名称 | 华师大版的九年级上册第24章 解直角三角形—24.4 解直角三角形 同步练习 |
|
|
| 格式 | doc | ||
| 文件大小 | 766.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学九年级上册第24章第4节24.4解直角三角形课时练习
一、选择题
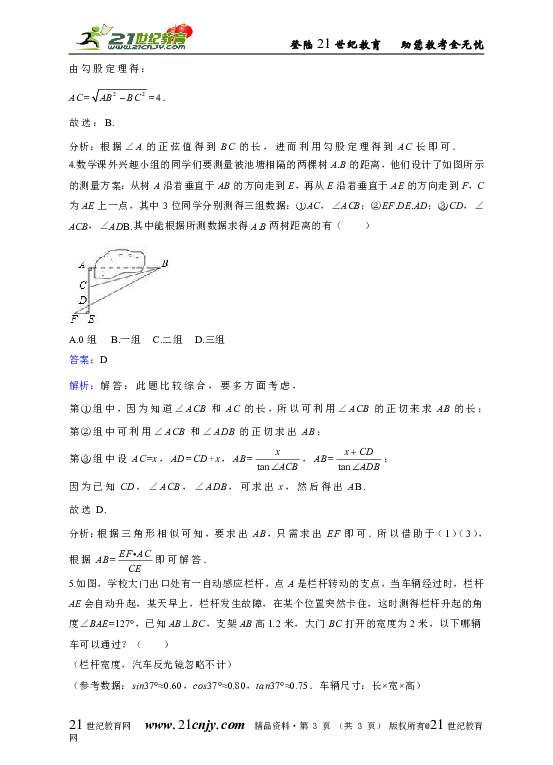
1.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AB=c,∠a=α,则CD长为( )
A.c sin2α B.c cos2α
C.c sinα tanα D.c sinα cosα
答案:D
解析:解答:在Rt△ABC中,∠ACB=90°,AB=c,∠A=α,
sinα=,BC=c sinα,
∠A+∠B=90°,∠DCB+∠B=90°,
∴∠DCB=∠A=α,
在Rt△DCB中,∠CDB=90°,
cos∠DCB=,
CD=BC cosα=c sinα cosα,
故选:D.
分析:根据已知条件在Rt△ABC中,用AB和α表示BC,在Rt△DCB中,根据余弦求出CD的长,得到答案.
2.数学活动课上,小敏.小颖分别画了△ABC和△DEF,尺寸如图.如果两个三角形的面积分别记作S△ABC.S△DEF,那么它们的大小关系是( )
A.S△ABC>S△DEF B.S△ABC<S△DEF
C.S△ABC=S△DEF D.不能确定
答案:C
解析:解答:如图,过点A.D分别作AG⊥BC,DH⊥EF,垂足分别为G.H,
在Rt△ABG中,AG=ABsinB=5×sin 50°=5sin 50°,
在Rt△DHE中,∠DEH=180°-130°=50°,
DH=DEsin∠DEH=5sin 50°,
∴AG=DH.
∵BC=4,EF=4,
∴S△ABC=S△DEF.
故选C.
分析:在两个图形中分别作BC.EF边上的高,欲比较面积,由于底边相等,所以只需比较两条高即可.
3.如图,Rt△ABC中,∠C=90°,若AB=5,sinA=,则AC的长是( )
A.3 B.4 C.5 D.6
答案:B
解析:解答:∵∠C=90°,sinA=,AB=5,
∴BC=AB×sinA=5×=3,
由勾股定理得:
AC==4.
故选:B.
分析:根据∠A的正弦值得到BC的长,进而利用勾股定理得到AC长即可.
4.数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A.B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF.DE.AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A.B两树距离的有( )
A.0组 B.一组 C.二组 D.三组
答案:D
解析:解答:此题比较综合,要多方面考虑,
第①组中,因为知道∠ACB和AC的长,所以可利用∠ACB的正切来求AB的长;
第②组中可利用∠ACB和∠ADB的正切求出AB;
第③组中设AC=x,AD=CD+x,AB=,AB=;
因为已知CD,∠ACB,∠ADB,可求出x,然后得出AB.
故选D.
分析:根据三角形相似可知,要求出AB,只需求出EF即可.所以借助于(1)(3),根据AB=即可解答.
5.如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( )
(栏杆宽度,汽车反光镜忽略不计)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)
A.宝马Z4(4200mm×1800mm×1360mm)
B.奇瑞QQ(4000mm×1600mm×1520mm)
C.大众朗逸(4600mm×1700mm×1400mm)
D.奥迪A4(4700mm×1800mm×1400mm)
答案:C
解析:解答:如图,过点A作BC的平行线AG,过点N作NQ⊥BC于Q,交AG于点R,
则∠BAG=90°,
∵∠BAE=127°,∠BAG=90°,
∴∠EAH=∠EAB-∠BAG=37°.
在△NAR中,∠ARN=90°,∠EAG=37°,
当车宽为1.8m,则GR=1.8m,故AR=2-1.8=0.2(m),
∴NR=ARtan37°=0.2×0.75=0.15(m),
∴NQ=1.2+0.15=1.35<1.36,
∴宝马Z4(4200mm×1800mm×1360mm)无法通过,
∴奥迪A4(4700mm×1800mm×1400mm)无法通过,
故此选项A,D不合题意;
当车宽为1.6m,则GR=1.6m,故AR=2-1.6=0.4(m),
∴NR=ARtan37°=0.4×0.75=0.3(m),
∴NQ=1.2+0.3=1.5<1.52,
∴奇瑞QQ(4000mm×1600mm×1520mm)无法通过,故此选项不合题意;
当车宽为1.7m,则GR=1.7m,故AR=2-1.7=0.3(m),
∴NR=ARtan37°=0.3×0.75=0.225(m),
∴NQ=1.2+0.225=1.425>1.4,
∴大众朗逸(4600mm×1700mm×1400mm)可以通过,故此选项符合题意;
故选:C.
分析:根据由题意只要车辆靠左行驶,车的最大高度小于AE抬起的高度NQ,即可通过,进而分别计算判断得出即可.
6.在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( )
A.1.2米 B.1.5米 C.1.9米 D.2.5米
答案:B
解析:解答:设CD为x,
在Rt△BCD中,∠BDC=α=18°,
∵tan∠BDC=,
∴BC=CD tan∠BDC=0.32x,
在Rt△ACD中,∠ADC=β=66°,
∵tan∠ADC=,
∴AC=CD tan∠ADC=2.2x,
∵AB=AC-BC,
∴2.82=2.2x-0.32x,
解得:x=1.5.
答:CD长约为1.5米.
故选:B.
分析:如图所示,假设CD为x,则有在Rt△BCD中可利用tan∠BDC=得到BC=CD tan∠BDC=0.32x,在Rt△ACD中利用tan∠ADC=,得到AC=CD tan∠ADC=2.2x,则AB=AC-BC,列方程可得2.82=2.2x-0.32x,解得x的值即可.
7.如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
A.5米 B.6米 C.8米 D.(3+)米
答案:A
解析:解答:设CD=x,则AD=2x,
由勾股定理可得,AC=
∵AC=3米,
∴x=3,
∴x=3米,
∴CD=3米,
∴AD=2×3=6米,
在Rt△ABD中,BD==8米,
∴BC=8-3=5米.
故选A.
分析:设CD=x,则AD=2x,根据勾股定理求出AC的长,从而求出CD.AC的长,然后根据勾股定理求出BD的长,即可求出BC的长.
8.如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )
A.0.55 B.0.8 C.0.6 D.0.75
答案:D
解析:解答:
如图;过点E作EM⊥GH于点M,
∵水渠的横断面是等腰梯形,
∴GM=×(GH-EF)=×(2.1-1.2)=0.45,
∵斜坡AD的坡度为1:0.6,
∴EM:GM=1:0.6,
∴EM:0.45=1:0.6,
∴EM=0.75,
故选:D.
分析:先过点E作EM⊥GH于点M,根据水渠的横断面是等腰梯形,求出GM,再根据斜坡AD的坡度为1:0.6,得出EM:GM=1:0.6,最后代入计算即可.
9.四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300m,250m,200m,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )
A.A的最高 B.B的最高 C.C的最高 D.D的最高
答案:B
解析:解答:A.的高度为:300×sin30°=150(米).
B.的高度为:250×sin45°=125≈176.75(米).
C.的高度为:200×sin45°=100≈141.4(米).
D.的高度为:200×sin60°=100≈173.2(米).
所以B的最高.
故选:B.
分析:利用所给角的正弦值求出每个滑板的高度,比较即可.
10.湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB底部50米的C处,测得桥塔顶部A的仰角为41.5°(如图).已知测量仪器CD的高度为1米,则桥塔AB的高度约为( )(参考数据:sin41.5°≈0.663,cos41.5°≈0.749,tan41.5°≈0.885)
A.34米 B.38米 C.45米 D.50米
答案:C
解析:解答:过D作DE⊥AB于E,
∴DE=BC=50米,
在Rt△ADE中,AE=DE tan41,5°≈50×0.88=44(米),
∵CD=1米,
∴BE=1米,
∴AB=AE+BE=44+1=45(米),
∴桥塔AB的高度为45米.
分析:Rt△ADE中利用三角函数即可求得AE的长,则AB的长度即可求解.
11.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10m,楼高AB=24m,则树CD高约为( )
A.5m B.6m C.7m D.8m
答案:C
解析:解答:过C作CE⊥AB,交AB于点E,
在Rt△ACE中,∠EAC=30°,CE=10m,
∴AC=2CE=20m,AE=m,
则CD=EB=AB-AE=24-10≈7m.
故选C
分析:过C作CE⊥AB,交AB于点E,在直角三角形ACE中,利用30度所对的直角边等于斜边的一半求出AC的长,再利用勾股定理求出AE的长,由AB-AE求出EB的长,即为CD的长.
12.如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高(AB)为1.6m,则这棵树的高度为( )(结果精确到0.1m,≈1.73).
A.3.5m B.3.6m C.4.3m D.5.1m
答案:D
解析:解答:设CD=x,
在Rt△ACD中,CD=x,∠CAD=30°,
则tan30°=CD:AD=x:AD
故AD=x,
在Rt△CED中,CD=x,∠CED=60°,
则tan60°=CD:ED=x:ED
故ED=x,
由题意得,AD-ED=x-x=4,
解得:x=2,
则这棵树的高度=2+1.6≈5.1m.
故选D.
分析:设CD=x,在Rt△ACD中求出AD,在Rt△CED中求出ED,再由AE=4m,可求出x的值,再由树高=CD+FD即可得出答案.
13.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海里C到航线AB的距离CD是( )
A.20海里 B.40海里 C.20海里 D.40海里
答案:C
解析:解答:根据题意可知∠CAD=30°,∠CBD=60°,
∵∠CBD=∠CAD+∠ACB,
∴∠CAD=30°=∠ACB,
∴AB=BC=40海里,
在Rt△CBD中,∠BDC=90°,∠DBC=60°,sin∠DBC=,
∴sin60°=,
∴CD=40×sin60°=40×=20(海里).
故选:C.
分析:根据方向角的定义及余角的性质求出∠CAD=30°,∠CBD=60°,再由三角形外角的性质得到∠CAD=30°=∠ACB,根据等角对等边得出AB=BC=20,然后解Rt△BCD,求出CD即可解答.
14.如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )
A.10分钟 B.15分钟 C.20分钟 D.25分钟
答案:B
解析:解答:作MN⊥AB于点N.
∵在直角△BMN中,∠MBN=90°-30°=60°,∠BMN=30°,
又∵∠MAN=90°-60°=30°,
∴∠AMN=30°,
∴∠MAB=∠M,
∴AB=BM,
∴BN=BM,
又∵由A到B航行半小时,即30分钟,
∴由B到N是15分钟.
故选B.
分析:作MN⊥AB于点N,即可证明△ABM是等腰三角形,然后在直角△BMN中,求得BM和BN之间的关系,则AB与N的大小关系即可求得,从而求得时间.
15.在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A.北偏东20°方向上 B.北偏西20°方向上
C.北偏西30°方向上 D.北偏西40°方向上
答案:B
解析:解答:如图,
∵AC=10千米,AB=8千米,BC=6千米,
∴AC2=AB2+BC2,
∴△ABC为直角三角形,即∠ABC=90°,
又∵B点在A的北偏东70°方向,
∴∠1=90°-70°=20°,
∴∠2=∠1=20°,
即C点在B的北偏西20°的方向上.
故选B.
分析:由AC=10千米,AB=8千米,BC=6千米得AC2=AB2+BC2,根据勾股定理的逆定理得到∠ABC=90°,再利用平行线的性质和互余的性质得到∠1,求得∠2.
二、填空题
16. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是
答案:
解析:解答:在Rt△ABC与Rt△BCD中,∠A+∠B=90°,∠BCD+∠B=90°.
∴∠A=∠BCD.
∴tan∠BCD=tan∠A=.
故答案为.
分析:先求得∠A=∠BCD,然后根据锐角三角函数的概念求解即可.
17. 如图,身高1.6m的小丽用一个两锐角分别为30°和60°的三角尺测量一棵树的高度,已知她与树之间的距离为6m,那么这棵树高为(其中小丽眼睛距离地面高度近似为身高)
m
答案:(2+1.6)
解析:解答:由题意得:AD=6m,
在Rt△ACD中,tanA=
∴CD=2,又AB=1.6m
∴CE=CD+DE=CD+AB=2+1.6,
所以树的高度为(2+1.6)m.
分析:已知小丽与树之间的距离为6m即AD=7m,可由直角三角形ACD及三角函数的关系可求出CD的长度,再由AB=1.6m可得出树的高度.
18. 如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了 米.
答案:1000
解析:解答:过点B作BC⊥水平面于点C,
在Rt△ABC中,
∵AB=2000米,∠A=30°,
∴BC=ABsin30°=2000×=1000.
故答案为:1000.
分析:过点B作BC⊥水平面于点C,在Rt△ABC中,根据AB=200米,∠A=30°,求出BC的长度即可.
19. 观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.
答案:135
解析:解答:∵爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°,
∴∠ADB=30°,
在Rt△ABD中,
tan30°=,
解得,,
∴AD=45,
∵在一楼房的底端A点处观测观光塔顶端C处的仰角是60°,
∴在Rt△ACD中,
CD=AD tan60°=45×=135米.
故答案为135米.
分析:根据“爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°”可以求出AD的长,然后根据“在一楼房的底端A点处观测观光塔顶端C处的仰角是60°”可以求出CD的长.
20. 如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 km.
答案:2
解析:解答:如图,过点A作AD⊥OB于D.
在Rt△AOD中,∵∠ADO=90°,∠AOD=30°,OA=4km,
∴AD=OA=2km.
在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB-∠AOB=75°-30°=45°,
∴BD=AD=2km,
∴AB=AD=2km.
即该船航行的距离(即AB的长)为2km.
故答案为2km.
分析:过点A作AD⊥OB于D.先解Rt△AOD,得出AD=OA=2km,再由△ABD是等腰直角三角形,得出BD=AD=2km,则AB=AD=2km.
三、解答题
21. 如图,矩形ABCD的对角线AC.BD相交于点O,过点O作OE⊥AC交AD于E,若AB=6,AD=8,求sin∠OEA的值.
答案:解答:连接EC,
∵四边形ABCD为矩形,
∴OA=OC,∠ABC=90°,
利用勾股定理得:AC==10,即OA=5,
∵OE⊥AC,
∴AE=CE,
在Rt△EDC中,设EC=AE=x,则有ED=AD-AE=8-x,DC=AB=6,
根据勾股定理得:x2=(8-x)2+62,
解得:x=,
∴AE=,
在Rt△AOE中,sin∠OEA=.
解析:连接EC,由四边形ABCD为矩形,得到对角线互相平分,即O为AC中点,再由OE垂直AC,得到OE垂直平分AC,即AE=CE,在直角三角形EDC中,设EC=AE=x,利用勾股定理列出关于x的方程,求出方程的解得到EC的长,即为AE的长,利用勾股定理求出AC的长,进而求出OA的长,在直角三角形AOE中,利用锐角三角函数定义即可求出sin∠OEA的值.
22. 如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D,E,F,G,已知∠CGD=42°
(1)求∠CEF的度数;
答案:解:∵∠CGD=42°,∠C=90°,
∴∠CDG=90°-42°=48°,
∵DG∥EF,
∴∠CEF=∠CDG=48°;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示,点H,B在直尺上的度数分别为4,13.4,求BC的长(结果保留两位小数).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
答案:解:∵点H,B的读数分别为4,13.4,
∴HB=13.4-4=9.4(m),
∴BC=HBcos42°≈9.4×0.74≈6.96(m).
答:BC的长为6.96m.
解析:(1)先根据直角三角形的两锐角互为求出∠CDG的度数,再根据两直线平行,同位角相等求出∠DEF,然后根据三角形的一个外角等于与它不相邻的两个内角的和即可求出∠EFA;
(2)根据度数求出HB的长度,再根据∠CBH=∠CGD=42°,利用42°的余弦值进求解.
23. 如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:≈1.414,≈1.732)
答案:解答:需要拆除,理由为:
∵CB⊥AB,∠CAB=45°,
∴△ABC为等腰直角三角形,
∴AB=BC=10米,
在Rt△BCD中,新坡面DC的坡度为i=:3,即∠CDB=30°,
∴DC=2BC=20米,BD=米,
∴AD=BD-AB=(10-10)米≈7.32米,
∵3+7.32=10.32>10,
∴需要拆除.
解析:需要拆除,理由为:根据题意得到三角形ABC为等腰直角三角形,求出AB的长,在直角三角形BCD中,根据新坡面的坡度求出∠BDC的度数为30,利用30度所对的直角边等于斜边的一半求出DC的长,再利用勾股定理求出DB的长,由DB-AB求出AD的长,由AD+3与10比较即可得到结果.
24. 小丽为了测旗杆AB的高度,小丽眼睛距地图1.5米,小丽站在C点,测出旗杆A的仰角为30°,小丽向前走了10米到达点E,此时的仰角为60°,求旗杆的高度.
答案:解答:如图,
∵∠ADG=30°,AFG=60°,
∴∠DAF=30°,
∴AF=DF=10,
在Rt△FGA中,
AG=AF sin∠AFG=10×=5,
∴AB=1.5+5.
答:旗杆AB的高度为(1.5+5)米.
解析:关键三角形外角的性质求得∠DAF=30°,得出AF=DF=10,在Rt△FGA中,根据正弦函数求出AG的长,加上BG的长即为旗杆高度.
25. 如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
答案:解答:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,
则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.
在Rt△BCE中,∵∠E=90°,∠CBE=60°,
∴∠BCE=30°,
∴BE=BC=×1000=500米;
在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=AB=1000米,
∴CF=CD=500米,
∴DA=BE+CF=(500+500)米,
故拦截点D处到公路的距离是(500+500)米.
解析:过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.解Rt△BCE,求出BE=BC=×1000=500米;解Rt△CDF,求出CF=CD=500米,则DA=BE+CF=(500+500)米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 22 页 (共 22 页) 版权所有@21世纪教育网
华师大版数学九年级上册第24章第4节24.4解直角三角形课时练习
一、选择题
1.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AB=c,∠a=α,则CD长为( )
A.c sin2α B.c cos2α
C.c sinα tanα D.c sinα cosα
答案:D
解析:解答:在Rt△ABC中,∠ACB=90°,AB=c,∠A=α,
sinα=,BC=c sinα,
∠A+∠B=90°,∠DCB+∠B=90°,
∴∠DCB=∠A=α,
在Rt△DCB中,∠CDB=90°,
cos∠DCB=,
CD=BC cosα=c sinα cosα,
故选:D.
分析:根据已知条件在Rt△ABC中,用AB和α表示BC,在Rt△DCB中,根据余弦求出CD的长,得到答案.
2.数学活动课上,小敏.小颖分别画了△ABC和△DEF,尺寸如图.如果两个三角形的面积分别记作S△ABC.S△DEF,那么它们的大小关系是( )
A.S△ABC>S△DEF B.S△ABC<S△DEF
C.S△ABC=S△DEF D.不能确定
答案:C
解析:解答:如图,过点A.D分别作AG⊥BC,DH⊥EF,垂足分别为G.H,
在Rt△ABG中,AG=ABsinB=5×sin 50°=5sin 50°,
在Rt△DHE中,∠DEH=180°-130°=50°,
DH=DEsin∠DEH=5sin 50°,
∴AG=DH.
∵BC=4,EF=4,
∴S△ABC=S△DEF.
故选C.
分析:在两个图形中分别作BC.EF边上的高,欲比较面积,由于底边相等,所以只需比较两条高即可.
3.如图,Rt△ABC中,∠C=90°,若AB=5,sinA=,则AC的长是( )
A.3 B.4 C.5 D.6
答案:B
解析:解答:∵∠C=90°,sinA=,AB=5,
∴BC=AB×sinA=5×=3,
由勾股定理得:
AC==4.
故选:B.
分析:根据∠A的正弦值得到BC的长,进而利用勾股定理得到AC长即可.
4.数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A.B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF.DE.AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A.B两树距离的有( )
A.0组 B.一组 C.二组 D.三组
答案:D
解析:解答:此题比较综合,要多方面考虑,
第①组中,因为知道∠ACB和AC的长,所以可利用∠ACB的正切来求AB的长;
第②组中可利用∠ACB和∠ADB的正切求出AB;
第③组中设AC=x,AD=CD+x,AB=,AB=;
因为已知CD,∠ACB,∠ADB,可求出x,然后得出AB.
故选D.
分析:根据三角形相似可知,要求出AB,只需求出EF即可.所以借助于(1)(3),根据AB=即可解答.
5.如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( )
(栏杆宽度,汽车反光镜忽略不计)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)
A.宝马Z4(4200mm×1800mm×1360mm)
B.奇瑞QQ(4000mm×1600mm×1520mm)
C.大众朗逸(4600mm×1700mm×1400mm)
D.奥迪A4(4700mm×1800mm×1400mm)
答案:C
解析:解答:如图,过点A作BC的平行线AG,过点N作NQ⊥BC于Q,交AG于点R,
则∠BAG=90°,
∵∠BAE=127°,∠BAG=90°,
∴∠EAH=∠EAB-∠BAG=37°.
在△NAR中,∠ARN=90°,∠EAG=37°,
当车宽为1.8m,则GR=1.8m,故AR=2-1.8=0.2(m),
∴NR=ARtan37°=0.2×0.75=0.15(m),
∴NQ=1.2+0.15=1.35<1.36,
∴宝马Z4(4200mm×1800mm×1360mm)无法通过,
∴奥迪A4(4700mm×1800mm×1400mm)无法通过,
故此选项A,D不合题意;
当车宽为1.6m,则GR=1.6m,故AR=2-1.6=0.4(m),
∴NR=ARtan37°=0.4×0.75=0.3(m),
∴NQ=1.2+0.3=1.5<1.52,
∴奇瑞QQ(4000mm×1600mm×1520mm)无法通过,故此选项不合题意;
当车宽为1.7m,则GR=1.7m,故AR=2-1.7=0.3(m),
∴NR=ARtan37°=0.3×0.75=0.225(m),
∴NQ=1.2+0.225=1.425>1.4,
∴大众朗逸(4600mm×1700mm×1400mm)可以通过,故此选项符合题意;
故选:C.
分析:根据由题意只要车辆靠左行驶,车的最大高度小于AE抬起的高度NQ,即可通过,进而分别计算判断得出即可.
6.在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( )
A.1.2米 B.1.5米 C.1.9米 D.2.5米
答案:B
解析:解答:设CD为x,
在Rt△BCD中,∠BDC=α=18°,
∵tan∠BDC=,
∴BC=CD tan∠BDC=0.32x,
在Rt△ACD中,∠ADC=β=66°,
∵tan∠ADC=,
∴AC=CD tan∠ADC=2.2x,
∵AB=AC-BC,
∴2.82=2.2x-0.32x,
解得:x=1.5.
答:CD长约为1.5米.
故选:B.
分析:如图所示,假设CD为x,则有在Rt△BCD中可利用tan∠BDC=得到BC=CD tan∠BDC=0.32x,在Rt△ACD中利用tan∠ADC=,得到AC=CD tan∠ADC=2.2x,则AB=AC-BC,列方程可得2.82=2.2x-0.32x,解得x的值即可.
7.如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
A.5米 B.6米 C.8米 D.(3+)米
答案:A
解析:解答:设CD=x,则AD=2x,
由勾股定理可得,AC=
∵AC=3米,
∴x=3,
∴x=3米,
∴CD=3米,
∴AD=2×3=6米,
在Rt△ABD中,BD==8米,
∴BC=8-3=5米.
故选A.
分析:设CD=x,则AD=2x,根据勾股定理求出AC的长,从而求出CD.AC的长,然后根据勾股定理求出BD的长,即可求出BC的长.
8.如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )
A.0.55 B.0.8 C.0.6 D.0.75
答案:D
解析:解答:
如图;过点E作EM⊥GH于点M,
∵水渠的横断面是等腰梯形,
∴GM=×(GH-EF)=×(2.1-1.2)=0.45,
∵斜坡AD的坡度为1:0.6,
∴EM:GM=1:0.6,
∴EM:0.45=1:0.6,
∴EM=0.75,
故选:D.
分析:先过点E作EM⊥GH于点M,根据水渠的横断面是等腰梯形,求出GM,再根据斜坡AD的坡度为1:0.6,得出EM:GM=1:0.6,最后代入计算即可.
9.四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300m,250m,200m,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )
A.A的最高 B.B的最高 C.C的最高 D.D的最高
答案:B
解析:解答:A.的高度为:300×sin30°=150(米).
B.的高度为:250×sin45°=125≈176.75(米).
C.的高度为:200×sin45°=100≈141.4(米).
D.的高度为:200×sin60°=100≈173.2(米).
所以B的最高.
故选:B.
分析:利用所给角的正弦值求出每个滑板的高度,比较即可.
10.湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线.某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB底部50米的C处,测得桥塔顶部A的仰角为41.5°(如图).已知测量仪器CD的高度为1米,则桥塔AB的高度约为( )(参考数据:sin41.5°≈0.663,cos41.5°≈0.749,tan41.5°≈0.885)
A.34米 B.38米 C.45米 D.50米
答案:C
解析:解答:过D作DE⊥AB于E,
∴DE=BC=50米,
在Rt△ADE中,AE=DE tan41,5°≈50×0.88=44(米),
∵CD=1米,
∴BE=1米,
∴AB=AE+BE=44+1=45(米),
∴桥塔AB的高度为45米.
分析:Rt△ADE中利用三角函数即可求得AE的长,则AB的长度即可求解.
11.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10m,楼高AB=24m,则树CD高约为( )
A.5m B.6m C.7m D.8m
答案:C
解析:解答:过C作CE⊥AB,交AB于点E,
在Rt△ACE中,∠EAC=30°,CE=10m,
∴AC=2CE=20m,AE=m,
则CD=EB=AB-AE=24-10≈7m.
故选C
分析:过C作CE⊥AB,交AB于点E,在直角三角形ACE中,利用30度所对的直角边等于斜边的一半求出AC的长,再利用勾股定理求出AE的长,由AB-AE求出EB的长,即为CD的长.
12.如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高(AB)为1.6m,则这棵树的高度为( )(结果精确到0.1m,≈1.73).
A.3.5m B.3.6m C.4.3m D.5.1m
答案:D
解析:解答:设CD=x,
在Rt△ACD中,CD=x,∠CAD=30°,
则tan30°=CD:AD=x:AD
故AD=x,
在Rt△CED中,CD=x,∠CED=60°,
则tan60°=CD:ED=x:ED
故ED=x,
由题意得,AD-ED=x-x=4,
解得:x=2,
则这棵树的高度=2+1.6≈5.1m.
故选D.
分析:设CD=x,在Rt△ACD中求出AD,在Rt△CED中求出ED,再由AE=4m,可求出x的值,再由树高=CD+FD即可得出答案.
13.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海里C到航线AB的距离CD是( )
A.20海里 B.40海里 C.20海里 D.40海里
答案:C
解析:解答:根据题意可知∠CAD=30°,∠CBD=60°,
∵∠CBD=∠CAD+∠ACB,
∴∠CAD=30°=∠ACB,
∴AB=BC=40海里,
在Rt△CBD中,∠BDC=90°,∠DBC=60°,sin∠DBC=,
∴sin60°=,
∴CD=40×sin60°=40×=20(海里).
故选:C.
分析:根据方向角的定义及余角的性质求出∠CAD=30°,∠CBD=60°,再由三角形外角的性质得到∠CAD=30°=∠ACB,根据等角对等边得出AB=BC=20,然后解Rt△BCD,求出CD即可解答.
14.如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )
A.10分钟 B.15分钟 C.20分钟 D.25分钟
答案:B
解析:解答:作MN⊥AB于点N.
∵在直角△BMN中,∠MBN=90°-30°=60°,∠BMN=30°,
又∵∠MAN=90°-60°=30°,
∴∠AMN=30°,
∴∠MAB=∠M,
∴AB=BM,
∴BN=BM,
又∵由A到B航行半小时,即30分钟,
∴由B到N是15分钟.
故选B.
分析:作MN⊥AB于点N,即可证明△ABM是等腰三角形,然后在直角△BMN中,求得BM和BN之间的关系,则AB与N的大小关系即可求得,从而求得时间.
15.在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A.北偏东20°方向上 B.北偏西20°方向上
C.北偏西30°方向上 D.北偏西40°方向上
答案:B
解析:解答:如图,
∵AC=10千米,AB=8千米,BC=6千米,
∴AC2=AB2+BC2,
∴△ABC为直角三角形,即∠ABC=90°,
又∵B点在A的北偏东70°方向,
∴∠1=90°-70°=20°,
∴∠2=∠1=20°,
即C点在B的北偏西20°的方向上.
故选B.
分析:由AC=10千米,AB=8千米,BC=6千米得AC2=AB2+BC2,根据勾股定理的逆定理得到∠ABC=90°,再利用平行线的性质和互余的性质得到∠1,求得∠2.
二、填空题
16. 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB,垂足为D,则tan∠BCD的值是
答案:
解析:解答:在Rt△ABC与Rt△BCD中,∠A+∠B=90°,∠BCD+∠B=90°.
∴∠A=∠BCD.
∴tan∠BCD=tan∠A=.
故答案为.
分析:先求得∠A=∠BCD,然后根据锐角三角函数的概念求解即可.
17. 如图,身高1.6m的小丽用一个两锐角分别为30°和60°的三角尺测量一棵树的高度,已知她与树之间的距离为6m,那么这棵树高为(其中小丽眼睛距离地面高度近似为身高)
m
答案:(2+1.6)
解析:解答:由题意得:AD=6m,
在Rt△ACD中,tanA=
∴CD=2,又AB=1.6m
∴CE=CD+DE=CD+AB=2+1.6,
所以树的高度为(2+1.6)m.
分析:已知小丽与树之间的距离为6m即AD=7m,可由直角三角形ACD及三角函数的关系可求出CD的长度,再由AB=1.6m可得出树的高度.
18. 如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了 米.
答案:1000
解析:解答:过点B作BC⊥水平面于点C,
在Rt△ABC中,
∵AB=2000米,∠A=30°,
∴BC=ABsin30°=2000×=1000.
故答案为:1000.
分析:过点B作BC⊥水平面于点C,在Rt△ABC中,根据AB=200米,∠A=30°,求出BC的长度即可.
19. 观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.
答案:135
解析:解答:∵爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°,
∴∠ADB=30°,
在Rt△ABD中,
tan30°=,
解得,,
∴AD=45,
∵在一楼房的底端A点处观测观光塔顶端C处的仰角是60°,
∴在Rt△ACD中,
CD=AD tan60°=45×=135米.
故答案为135米.
分析:根据“爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°”可以求出AD的长,然后根据“在一楼房的底端A点处观测观光塔顶端C处的仰角是60°”可以求出CD的长.
20. 如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 km.
答案:2
解析:解答:如图,过点A作AD⊥OB于D.
在Rt△AOD中,∵∠ADO=90°,∠AOD=30°,OA=4km,
∴AD=OA=2km.
在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB-∠AOB=75°-30°=45°,
∴BD=AD=2km,
∴AB=AD=2km.
即该船航行的距离(即AB的长)为2km.
故答案为2km.
分析:过点A作AD⊥OB于D.先解Rt△AOD,得出AD=OA=2km,再由△ABD是等腰直角三角形,得出BD=AD=2km,则AB=AD=2km.
三、解答题
21. 如图,矩形ABCD的对角线AC.BD相交于点O,过点O作OE⊥AC交AD于E,若AB=6,AD=8,求sin∠OEA的值.
答案:解答:连接EC,
∵四边形ABCD为矩形,
∴OA=OC,∠ABC=90°,
利用勾股定理得:AC==10,即OA=5,
∵OE⊥AC,
∴AE=CE,
在Rt△EDC中,设EC=AE=x,则有ED=AD-AE=8-x,DC=AB=6,
根据勾股定理得:x2=(8-x)2+62,
解得:x=,
∴AE=,
在Rt△AOE中,sin∠OEA=.
解析:连接EC,由四边形ABCD为矩形,得到对角线互相平分,即O为AC中点,再由OE垂直AC,得到OE垂直平分AC,即AE=CE,在直角三角形EDC中,设EC=AE=x,利用勾股定理列出关于x的方程,求出方程的解得到EC的长,即为AE的长,利用勾股定理求出AC的长,进而求出OA的长,在直角三角形AOE中,利用锐角三角函数定义即可求出sin∠OEA的值.
22. 如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D,E,F,G,已知∠CGD=42°
(1)求∠CEF的度数;
答案:解:∵∠CGD=42°,∠C=90°,
∴∠CDG=90°-42°=48°,
∵DG∥EF,
∴∠CEF=∠CDG=48°;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示,点H,B在直尺上的度数分别为4,13.4,求BC的长(结果保留两位小数).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
答案:解:∵点H,B的读数分别为4,13.4,
∴HB=13.4-4=9.4(m),
∴BC=HBcos42°≈9.4×0.74≈6.96(m).
答:BC的长为6.96m.
解析:(1)先根据直角三角形的两锐角互为求出∠CDG的度数,再根据两直线平行,同位角相等求出∠DEF,然后根据三角形的一个外角等于与它不相邻的两个内角的和即可求出∠EFA;
(2)根据度数求出HB的长度,再根据∠CBH=∠CGD=42°,利用42°的余弦值进求解.
23. 如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:≈1.414,≈1.732)
答案:解答:需要拆除,理由为:
∵CB⊥AB,∠CAB=45°,
∴△ABC为等腰直角三角形,
∴AB=BC=10米,
在Rt△BCD中,新坡面DC的坡度为i=:3,即∠CDB=30°,
∴DC=2BC=20米,BD=米,
∴AD=BD-AB=(10-10)米≈7.32米,
∵3+7.32=10.32>10,
∴需要拆除.
解析:需要拆除,理由为:根据题意得到三角形ABC为等腰直角三角形,求出AB的长,在直角三角形BCD中,根据新坡面的坡度求出∠BDC的度数为30,利用30度所对的直角边等于斜边的一半求出DC的长,再利用勾股定理求出DB的长,由DB-AB求出AD的长,由AD+3与10比较即可得到结果.
24. 小丽为了测旗杆AB的高度,小丽眼睛距地图1.5米,小丽站在C点,测出旗杆A的仰角为30°,小丽向前走了10米到达点E,此时的仰角为60°,求旗杆的高度.
答案:解答:如图,
∵∠ADG=30°,AFG=60°,
∴∠DAF=30°,
∴AF=DF=10,
在Rt△FGA中,
AG=AF sin∠AFG=10×=5,
∴AB=1.5+5.
答:旗杆AB的高度为(1.5+5)米.
解析:关键三角形外角的性质求得∠DAF=30°,得出AF=DF=10,在Rt△FGA中,根据正弦函数求出AG的长,加上BG的长即为旗杆高度.
25. 如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
答案:解答:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,
则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.
在Rt△BCE中,∵∠E=90°,∠CBE=60°,
∴∠BCE=30°,
∴BE=BC=×1000=500米;
在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=AB=1000米,
∴CF=CD=500米,
∴DA=BE+CF=(500+500)米,
故拦截点D处到公路的距离是(500+500)米.
解析:过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.解Rt△BCE,求出BE=BC=×1000=500米;解Rt△CDF,求出CF=CD=500米,则DA=BE+CF=(500+500)米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 22 页 (共 22 页) 版权所有@21世纪教育网
