【期末真题汇编】期末核心考点 计算题(口算+竖式+递等式)(含解析)-江苏省2024-2025学年五年级下册数学苏教版
文档属性
| 名称 | 【期末真题汇编】期末核心考点 计算题(口算+竖式+递等式)(含解析)-江苏省2024-2025学年五年级下册数学苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 119.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 20:13:22 | ||
图片预览
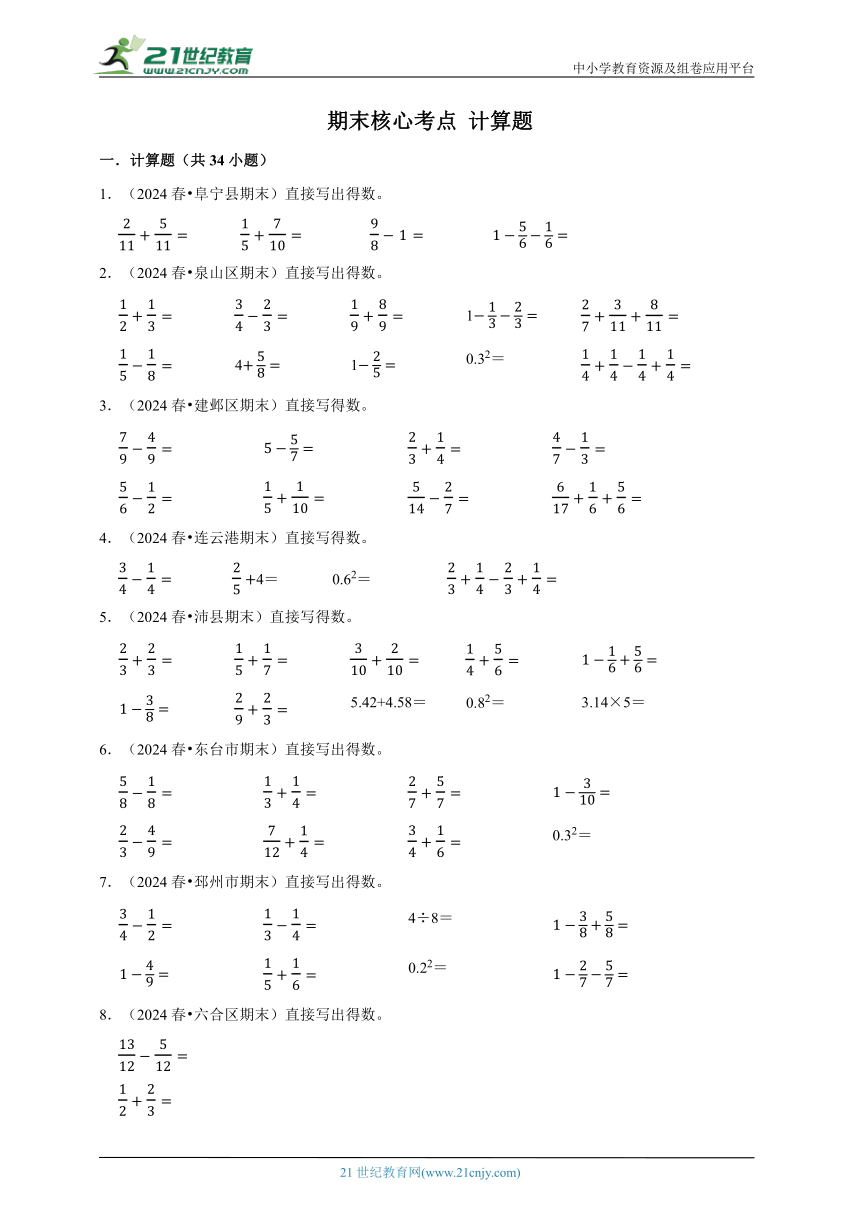




文档简介
中小学教育资源及组卷应用平台
期末核心考点 计算题
一.计算题(共34小题)
1.(2024春 阜宁县期末)直接写出得数。
2.(2024春 泉山区期末)直接写出得数。
1
4 1 0.32=
3.(2024春 建邺区期末)直接写得数。
4.(2024春 连云港期末)直接写得数。
4= 0.62=
5.(2024春 沛县期末)直接写得数。
5.42+4.58= 0.82= 3.14×5=
6.(2024春 东台市期末)直接写出得数。
0.32=
7.(2024春 邳州市期末)直接写出得数。
4÷8=
0.22=
8.(2024春 六合区期末)直接写出得数。
9.(2024春 梁溪区期末)直接写出得数。
0.22= 3.6x﹣2.6x=
10.(2024春 海安市期末)直接写得数。
0.32=
11.(2024春 南京期末)直接写出得数。
5÷8= 1﹣0.49=
0.42= 2 1
12.(2024春 建邺区期末)计算下面各题,能简算的要简算。
13.(2024春 泉山区期末)计算下列各题,能简算的要简算。
1
14.(2024春 连云港期末)怎样算简便就怎样算。
2.5×24
15.(2024春 东台市期末)计算下面各题,能简算的要简算。
16.(2024春 邳州市期末)下面各题怎样算简便就怎样算。
17.(2024春 阜宁县期末)先计算下面各题,怎样简便就怎样算。
18.(2024春 梁溪区期末)递等式计算,能简算的要简算。
19.(2024春 海安市期末)怎样算简便就怎样算。
20.(2024春 沛县期末)计算下面各题,怎样算简便就怎样算。
21.(2024春 南京期末)计算下面各题,能简算的要简算。
22.(2024春 六合区期末)计算下面各题,能简算的要简算。
23.(2024春 建邺区期末)解方程。
2x÷2.5=0.8 4.2x+0.6x=24
5x﹣0.4×30=48 x﹣63+37=150
24.(2024春 泉山区期末)解方程。
1.6x÷3=3.2
1﹣0.5x=0.2
25.(2024春 连云港期末)解方程。
x
2.9x+0.2x=93
4x﹣7×0.5=5.3
26.(2024春 东台市期末)解方程。
5x﹣3x=5.2
2x﹣0.5×6=7
27.(2024春 阜宁县期末)解方程。
x÷40=14
2.7x﹣1.2x=7.5
4x﹣4×0.5=30
28.(2024春 邳州市期末)
5.5x﹣3x=15
2.5x﹣0.5×8=6
29.(2022春 瑶海区期末)解方程。
6.3﹣x=5 1.5x+4=10 2x﹣0.5x=45
30.(2024春 海安市期末)解方程。
0.8x+0.6x=21
2.2x﹣0.3×5=9.5
0.75+0.25x=2
31.(2024春 梁溪区期末)求未知数的值。
0.4x+0.2x=3 2.5x﹣0.5×8=6
32.(2024春 沛县期末)解方程。
0.5+x=2.5
x÷15=1.8
12x+19x=155
2.5x﹣0.5×8=6
33.(2024春 南京期末)解方程。
x1
5.6+4x=10
0.9x﹣3×1.2=7.2
34.(2024春 六合区期末)解方程。
24x+38x=310
3.6x÷2=2.16
7x﹣4.5×2=271
期末核心考点 计算题
参考答案与试题解析
一.计算题(共34小题)
1.(2024春 阜宁县期末)直接写出得数。
【答案】;;;0。
【分析】根据分数加减法的计算方法进行计算。
【解答】解:
0
【点评】口算时,注意运算符号和数据,然后再进一步计算。
2.(2024春 泉山区期末)直接写出得数。
1
4 1 0.32=
【答案】;;1;0;1;;4;;0.09;。
【分析】根据分数加减法、小数乘法的计算方法进行计算。
【解答】解:
1 10 1
44 1 0.32=0.09
【点评】口算时,注意运算符号和数据,然后再进一步计算。
3.(2024春 建邺区期末)直接写得数。
【答案】;4;;;;;;1。
【分析】根据分数加减法的计算方法,直接进行口算即可;,按照加法结合律进行简算即可。
【解答】解:
4
1
【点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
4.(2024春 连云港期末)直接写得数。
4=
0.62=
【答案】;;0.36;。
【分析】根据分数的加减法的运算法则计算即可。
【解答】解:
4
0.62=0.36
【点评】本题考查分数加减法的运算,注意计算的准确性。
5.(2024春 沛县期末)直接写得数。
5.42+4.58= 0.82= 3.14×5=
【答案】,,,,,,,10,0.64,15.7。
【分析】根据分数加法、分数减法、数的乘方、小数加法、小数乘法的计算方法直接写出得数即可。
【解答】解:
5.42+4.58=10 0.82=0.64 3.14×5=15.7
【点评】本题主要考查了分数加法、分数减法、数的乘方、小数加法、小数乘法的运算,属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性。
6.(2024春 东台市期末)直接写出得数。
0.32=
【答案】;;1;;;;;0.09。
【分析】根据分数加减法、小数乘法的计算方法进行计算。
【解答】解:
1
0.32=0.09
【点评】口算时,注意运算符号和数据,然后再进一步计算。
7.(2024春 邳州市期末)直接写出得数。
4÷8=
0.22=
【答案】;;;1;;;0.04;0。
【分析】根据异分母分数相加减的计算方法以及乘方的计算方法口算后写出答案即可。
【解答】解:
4÷8 1
0.22=0.04 0
【点评】本题考查了异分母分数相加减以及乘方的计算。
8.(2024春 六合区期末)直接写出得数。
【答案】;;;3;。
【分析】根据分数加减法的计算方法进行计算。
【解答】解:
3
【点评】口算时,注意运算符号和数据,然后再进一步计算。
9.(2024春 梁溪区期末)直接写出得数。
0.22= 3.6x﹣2.6x=
【答案】;;;1;0.04;;x;1。
【分析】根据分数加减法、小数乘法和减法的计算方法进行计算。
【解答】解:
1
0.22=0.04 3.6x﹣2.6x=x 1
【点评】口算时,注意运算符号和数据,然后再进一步计算。
10.(2024春 海安市期末)直接写得数。
0.32=
【答案】;;3;;;;0.09;;;。
【分析】根据分数加减法、四则混合运算的顺序以及小数乘法的计算方法,直接进行口算即可。
【解答】解:
3
0.32=0.09
【点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
11.(2024春 南京期末)直接写出得数。
5÷8= 1﹣0.49=
0.42= 2 1
【答案】;;0.51;;0.16;;;。
【分析】根据分数加、减法的计算方法,乘方的计算方法和分数与除法的关系,依次口算结果。
【解答】解:
5÷8 1﹣0.49=0.51
0.42=0.16 21 1
【点评】本题解题的关键是熟练掌握分数加、减法的计算方法,乘方的计算方法和分数与除法的关系。
12.(2024春 建邺区期末)计算下面各题,能简算的要简算。
【答案】,,,。
【分析】①,先通分,再按照分数加、减法的计算法则计算;
②(),先算括号里面的减法,再算括号外面的减法;
③,首先将运算顺序调整为:(),据此简算;
④,根据分数的拆项公式进行简算;
【解答】解:①
②()
③
()
=1
④
=(1)+()+()+()+()
=1
=1
【点评】此题考查的目的是理解掌握分数加、减混合运算的顺序以及它们的计算法则,并且能够灵活选择简便方法进行计算。
13.(2024春 泉山区期末)计算下列各题,能简算的要简算。
1
【答案】;2;;。
【分析】(1)根据减法的性质进行计算;
(2)根据加法交换律和结合律进行计算;
(3)(4)根据加法交换律和结合律以及减法的性质进行计算。
【解答】解:(1)
=1
(2)
=()+()
=1+1
=2
(3)
=()﹣()
=1
(4)1
=(1)﹣()
=11
【点评】本题考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
14.(2024春 连云港期末)怎样算简便就怎样算。
2.5×24
【答案】3;60;。
【分析】(1)根据加法交换律、结合律,把同分母的分数先相加。
(2)把24改写成4×6,先算2.5×4=10,再算10×6=60。
(3)根据减法的性质a﹣(b﹣c)=a﹣b+c进行计算简便。
【解答】解:(1)
=()+()
=2+1
=3
(2)2.5×24
=2.5×4×6
=10×6
=60
(3)
【点评】本题考查了分数、小数简便计算的能力。
15.(2024春 东台市期末)计算下面各题,能简算的要简算。
【答案】;;2;。
【分析】(1)(2)(4)根据减法的性质进行计算;
(3)根据加法交换律和结合律进行计算。
【解答】解:(1)
(2)
=1
(3)
=()+()
=1+1
=2
(4)
()
1
【点评】本题考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
16.(2024春 邳州市期末)下面各题怎样算简便就怎样算。
【答案】1;;;。
【分析】(1)根据加法交换律进行计算;
(2)根据加法交换律和结合律以及减法的性质进行计算;
(3)根据减法的性质进行计算;
(4)根据分数的拆项公式进行计算。
【解答】解:(1)
=1
=1
(2)
=()﹣()
(3)
(4)
=(1)+()+()+()+()+()
=1
=1
【点评】本题考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
17.(2024春 阜宁县期末)先计算下面各题,怎样简便就怎样算。
【答案】;;。
【分析】第一题、从左往右依次计算;
第二题、根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c)进行简算;
第三题、根据减法的性质a﹣(b+c)=a﹣b﹣c进行简算。
【解答】解:
【点评】此题考查分数混合运算及运用运算定律进行简算。
18.(2024春 梁溪区期末)递等式计算,能简算的要简算。
【答案】;2;。
【分析】按照从左到右的顺序计算;
按照加法交换律和结合律计算;
先算小括号里面的减法,再算括号外里面的减法。
【解答】解:
=()+()
=1+1
=2
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
19.(2024春 海安市期末)怎样算简便就怎样算。
【答案】;1;1;。
【分析】先算小括号里面的减法,再算括号外面的减法;
按照加法结合律计算;
按照加法交换律和结合律计算;
把分数写成两数相减的形式,然后再抵消计算即可。
【解答】解:
()
1
=1
=()+()
=1+0
=1
=(1)﹣()﹣()﹣()﹣()
=1
【点评】此题是考查四则混合运算,要仔细观察算式的特点,灵活运用一些定律进行简便计算。
20.(2024春 沛县期末)计算下面各题,怎样算简便就怎样算。
【答案】;;2;。
【分析】第1小题,先通分,再计算。
第2小题,先算小括号里面的减法,再算小括号外面的减法。
第3小题,交换加数的位置,结果不变,据此作答。
第4小题,裂项,将每个加数转化为两个分数单位相减的形式,据此作答。
【解答】解:
=1+1
=2
【点评】本题考查了分数加减混合运算与简算问题,解答时一定要熟练掌握并灵活运用相关的计算法则、运算定律或性质。
21.(2024春 南京期末)计算下面各题,能简算的要简算。
【答案】;0;;。
【分析】按照减法的性质计算;
按照加法交换律和减法的性质计算;
按照从左到右的顺序计算;
把分数写成两数相减的形式,然后再抵消计算即可。
【解答】解:
=1
()
=1﹣1
=0
=1
=1
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
22.(2024春 六合区期末)计算下面各题,能简算的要简算。
【答案】,,2,0,,。
【分析】第一题,先通分再计算;第二题同分母分数先相减,再通分计算;第三题把同分母分数先相加;第四题把括号去掉变成连减计算;第五题把括号去掉,括号里的减法变加法;第六题把变成(),变成()以此类推即可简便运算。
【解答】解:
=1+1
=2
=1﹣1
=0
=()
=1
【点评】此题考查了分数运算的简便运算。
23.(2024春 建邺区期末)解方程。
2x÷2.5=0.8 4.2x+0.6x=24
5x﹣0.4×30=48 x﹣63+37=150
【答案】x=1;x=5;x=12;x=176。
【分析】根据等式的性质,方程两端同时乘2.5,再同时除以2,求出方程的解。
先化简,再根据等式的性质,方程两端同时除以4.8,求出方程的解。
先化简,再根据等式的性质,方程两端同时加上12,再同时除以5,求出方程的解。
根据等式的性质,方程两端同时减去37,再同时加上63,求出方程的解。
【解答】解:2x÷2.5=0.8
2x÷2.5×2.5=0.8×2.5
2x=2
2x÷2=2÷2
x=1
4.2x+0.6x=24
4.8x=24
4.8x÷4.8=24÷4.8
x=5
5x﹣0.4×30=48
5x﹣12=48
5x﹣12+12=48+12
5x=60
5x÷5=60÷5
x=12
x﹣63+37=150
x﹣63+37﹣37=150﹣37
x﹣63=113
x﹣63+63=113+63
x=176
【点评】本题解题的关键是熟练掌握解方程的方法。
24.(2024春 泉山区期末)解方程。
1.6x÷3=3.2
1﹣0.5x=0.2
【答案】x;x=6;x=1.6。
【分析】x,根据等式的基本性质,方程两边同时加上,然后计算求出x的值;
1.6x÷3=3.2,根据等式的基本性质,方程两边同时乘3,然后再同时除以1.6,最后计算求出x的值;
1﹣0.5x=0.2,根据等式的基本性质可得0.5x=1﹣0.2,然后等式两边同时除以0.5,最后计算求出x的值。
【解答】解:x
1.6x÷3=3.2
1.6x=3.2×3
1.6x=9.6
x=9.6÷1.6
x=6
1﹣0.5x=0.2
0.5x=1﹣0.2
0.5x=0.8
x=0.8÷0.5
x=1.6
【点评】解答此题要运用等式的基本性质。
25.(2024春 连云港期末)解方程。
x
2.9x+0.2x=93
4x﹣7×0.5=5.3
【答案】x=2;x=30;x=2.2。
【分析】根据等式的性质,方程两端同时加上,算出方程的解。
先化简,再根据等式的性质,方程两端同时除以3.1,算出方程的解。
先化简,再根据等式的性质,方程两端同时加上3.5,再同时除以4,算出方程的解。
【解答】解:x
x
x=2
2.9x+0.2x=93
3.1x=93
3.1x÷3.1=93÷3.1
x=30
4x﹣7×0.5=5.3
4x﹣3.5=5.3
4x﹣3.5+3.5=5.3+3.5
4x=8.8
4x÷4=8.8÷4
x=2.2
【点评】本题解题的关键是熟练掌握解方程的方法。
26.(2024春 东台市期末)解方程。
5x﹣3x=5.2
2x﹣0.5×6=7
【答案】x;x=2.6;x=5。
【分析】,根据等式的基本性质,方程两边同时减去,然后计算求出x的值;
5x﹣3x=5.2,先计算5x﹣3x=2x,根据等式的基本性质,方程两边同时除以2,然后计算求出x的值;
2x﹣0.5×6=7,先计算0.5×6=3,根据等式的基本性质,方程两边同时加上3,然后再同时除以2,最后计算求出x的值。
【解答】解:
5x﹣3x=5.2
2x=5.2
x=5.2÷2
x=2.6
2x﹣0.5×6=7
2x﹣3=7
2x=7+3
2x=10
x=10÷2
x=5
【点评】解答此题要运用等式的基本性质。
27.(2024春 阜宁县期末)解方程。
x÷40=14
2.7x﹣1.2x=7.5
4x﹣4×0.5=30
【答案】x;x=560;x=5;x=8。
【分析】根据等式的性质解方程:
方程两边同时减去,求出方程的解;
方程两边同时乘40,求出方程的解;
先把方程化简成1.5x=7.5,方程两边同时除以1.5,求出方程的解;
先把方程化简成4x﹣2=30,然后方程两边先同时加上2,再同时除以4,求出方程的解。
【解答】解:
x÷40=14
x÷40×40=14×40
x=560
2.7x﹣1.2x=7.5
1.5x=7.5
1.5x÷1.5=7.5÷1.5
x=5
4x﹣4×0.5=30
4x﹣2=30
4x﹣2+2=30+2
4x=32
4x÷4=32÷4
x=8
【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去,同时乘或同时除以一个数(0除外),两边仍相等。
28.(2024春 邳州市期末)
5.5x﹣3x=15
2.5x﹣0.5×8=6
【答案】x;x=6;x=4。
【分析】,根据等式的基本性质,方程两边同时加上,然后计算求出x的值;
5.5x﹣3x=15,先计算5.5x﹣3x=2.5x,根据等式的基本性质,方程两边同时除以2.5,然后计算求出x的值;
2.5x﹣0.5×8=6,先计算0.5×8=4,根据等式的基本性质,方程两边同时加上4,然后再同时除以2.5,最后计算求出x的值。
【解答】解:
5.5x﹣3x=15
2.5x=15
2.5x÷2.5=15÷2.5
x=6
2.5x﹣0.5×8=6
2.5x﹣4=6
2.5x=6+4
2.5x=10
x=10÷2.5
x=4
【点评】解答此题要运用等式的基本性质。
29.(2022春 瑶海区期末)解方程。
6.3﹣x=5 1.5x+4=10 2x﹣0.5x=45
【答案】见试题解答内容
【分析】第1题,根据减数=被减数﹣差,算出方程的解。
第2题,根据等式的性质,方程两边同时减去4,再同时除以1.5,算出方程的解。
第3题,先计算出2x﹣0.5x的结果,再根据等式的性质,方程两边同时除以1.5,算出方程的解。
【解答】解:6.3﹣x=5
x=6.3﹣5
x=1.3
1.5x+4=10
1.5x+4﹣4=10﹣4
1.5x=6
1.5x÷1.5=6÷1.5
x=4
2x﹣0.5x=45
1.5x=45
1.5x÷1.5=45÷1.5
x=30
【点评】本题解题的关键是熟练掌握解方程的方法。
30.(2024春 海安市期末)解方程。
0.8x+0.6x=21
2.2x﹣0.3×5=9.5
0.75+0.25x=2
【答案】x=15;x;x=5;x=5。
【分析】(1)先计算0.8x+0.6x=1.4x,根据等式的性质,方程的两边同时除以1.4求解;
(2)根据等式的性质,方程的两边同时减去,然后方程的两边同时加上求解;
(3)先计算0.3×5=1.5,根据等式的性质,方程的两边同时加上1.5,然后方程的两边同时除以2.2求解;
(4)根据等式的性质,方程的两边同时减去0.75,然后方程的两边同时除以0.25求解。
【解答】解:(1)0.8x+0.6x=21
1.4x=21
1.4x÷1.4=21÷1.4
x=15
(2)
x1
x
x
x
(3)2.2x﹣0.3×5=9.5
2.2x﹣1.5=9.5
2.2x﹣1.5+1.5=9.5+1.5
2.2x=11
2.2x÷2.2=11÷2.2
x=5
(4)0.75+0.25x=2
0.75+0.25x﹣0.75=2﹣0.75
0.25x=1.25
0.25x÷0.25=1.25÷0.25
x=5
【点评】本题考查解方程,解题的关键是掌握等式的性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立。
31.(2024春 梁溪区期末)求未知数的值。
0.4x+0.2x=3 2.5x﹣0.5×8=6
【答案】x=5;x=4;x。
【分析】0.4x+0.2x=3,先计算0.4x+0.2x=0.6x,根据等式的基本性质,方程两边同时除以0.6,然后计算即可求出x的值;
2.5x﹣0.5×8=6,先计算0.5×8=4,根据等式的基本性质,方程两边同时加上4,然后同时除以2.5,最后计算即可求出x的值;
,根据等式的基本性质,方程两边同时加上,然后计算即可求出x的值。
【解答】解:0.4x+0.2x=3
0.6x=3
0.6x÷0.6=3÷0.6
x=5
2.5x﹣0.5×8=6
2.5x﹣4=6
2.5x﹣4+4=6+4
2.5x=10
2.5x÷2.5=10÷2.5
x=4
【点评】解答此题要运用等式的基本性质。
32.(2024春 沛县期末)解方程。
0.5+x=2.5
x÷15=1.8
12x+19x=155
2.5x﹣0.5×8=6
【答案】x=2;x=27;x=5;x=4。
【分析】0.5+x=2.5,根据等式的基本性质,方程两边同时减去0.5,然后计算求出x的值;
x÷15=1.8,根据等式的基本性质,方程两边同时乘15,然后计算求出x的值;
12x+19x=155,先计算12x+19x=31x,根据等式的基本性质,方程两边同时除以31,然后计算求出x的值;
2.5x﹣0.5×8=6,先计算0.5×8=4,根据等式的基本性质,方程两边同时加上4,然后再同时除以2.5,最后计算求出x的值。
【解答】解:0.5+x=2.5
x=2.5﹣0.5
x=2
x÷15=1.8
x=15×1.8
x=27
12x+19x=155
31x=155
x=155÷31
x=5
2.5x﹣0.5×8=6
2.5x﹣4=6
2.5x=6+4
2.5x=10
x=10÷2.5
x=4
【点评】解答此题要运用等式的基本性质。
33.(2024春 南京期末)解方程。
x1
5.6+4x=10
0.9x﹣3×1.2=7.2
【答案】x;x=1.1;x=12。
【分析】根据等式的性质等式的两边同时加,减,求解即可;
根据等式的性质等式的两边同时减5.6,再同时除以4,求解即可;
先计算等式左边的乘法算式,再根据等式的性质等式的两边同时加3.6,再同时除以0.9,求解即可。
【解答】解:
5.6+4x=10
5.6+4x﹣5.6=10﹣5.6
4x=4.4
4x÷4=4.4÷4
x=1.1
0.9x﹣3×1.2=7.2
0.9x﹣3.6=7.2
0.9x﹣3.6+3.6=7.2+3.6
0.9x=10.8
0.9x÷0.9=10.8÷0.9
x=12
【点评】熟练掌握根据等式的性质求方程的解是解答本题的关键。
34.(2024春 六合区期末)解方程。
24x+38x=310
3.6x÷2=2.16
7x﹣4.5×2=271
【答案】x=5;x=1.2;x=40。
【分析】24x+38x=310,先计算24x+38x=62x,根据等式的基本性质,方程两边同时除以62,然后计算即可求出x的值;
3.6x÷2=2.16,根据等式的基本性质,方程两边同时乘2,然后再同时除以3.6,最后计算即可求出x的值;
7x﹣4.5×2=271,先计算4.5×2=9,根据等式的基本性质,方程两边同时加上9,然后再同时除以7,最后计算即可求出x的值。
【解答】解:24x+38x=310
62x=310
62x÷62=310÷62
x=5
3.6x÷2=2.16
3.6x÷2×2=2.16×2
3.6x=4.32
3.6x÷3.6=4.32÷3.6
x=1.2
7x﹣4.5×2=271
7x﹣9=271
7x﹣9+9=271+9
7x=280
7x÷7=280÷7
x=40
【点评】解答此题要运用等式的基本性质。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 计算题
一.计算题(共34小题)
1.(2024春 阜宁县期末)直接写出得数。
2.(2024春 泉山区期末)直接写出得数。
1
4 1 0.32=
3.(2024春 建邺区期末)直接写得数。
4.(2024春 连云港期末)直接写得数。
4= 0.62=
5.(2024春 沛县期末)直接写得数。
5.42+4.58= 0.82= 3.14×5=
6.(2024春 东台市期末)直接写出得数。
0.32=
7.(2024春 邳州市期末)直接写出得数。
4÷8=
0.22=
8.(2024春 六合区期末)直接写出得数。
9.(2024春 梁溪区期末)直接写出得数。
0.22= 3.6x﹣2.6x=
10.(2024春 海安市期末)直接写得数。
0.32=
11.(2024春 南京期末)直接写出得数。
5÷8= 1﹣0.49=
0.42= 2 1
12.(2024春 建邺区期末)计算下面各题,能简算的要简算。
13.(2024春 泉山区期末)计算下列各题,能简算的要简算。
1
14.(2024春 连云港期末)怎样算简便就怎样算。
2.5×24
15.(2024春 东台市期末)计算下面各题,能简算的要简算。
16.(2024春 邳州市期末)下面各题怎样算简便就怎样算。
17.(2024春 阜宁县期末)先计算下面各题,怎样简便就怎样算。
18.(2024春 梁溪区期末)递等式计算,能简算的要简算。
19.(2024春 海安市期末)怎样算简便就怎样算。
20.(2024春 沛县期末)计算下面各题,怎样算简便就怎样算。
21.(2024春 南京期末)计算下面各题,能简算的要简算。
22.(2024春 六合区期末)计算下面各题,能简算的要简算。
23.(2024春 建邺区期末)解方程。
2x÷2.5=0.8 4.2x+0.6x=24
5x﹣0.4×30=48 x﹣63+37=150
24.(2024春 泉山区期末)解方程。
1.6x÷3=3.2
1﹣0.5x=0.2
25.(2024春 连云港期末)解方程。
x
2.9x+0.2x=93
4x﹣7×0.5=5.3
26.(2024春 东台市期末)解方程。
5x﹣3x=5.2
2x﹣0.5×6=7
27.(2024春 阜宁县期末)解方程。
x÷40=14
2.7x﹣1.2x=7.5
4x﹣4×0.5=30
28.(2024春 邳州市期末)
5.5x﹣3x=15
2.5x﹣0.5×8=6
29.(2022春 瑶海区期末)解方程。
6.3﹣x=5 1.5x+4=10 2x﹣0.5x=45
30.(2024春 海安市期末)解方程。
0.8x+0.6x=21
2.2x﹣0.3×5=9.5
0.75+0.25x=2
31.(2024春 梁溪区期末)求未知数的值。
0.4x+0.2x=3 2.5x﹣0.5×8=6
32.(2024春 沛县期末)解方程。
0.5+x=2.5
x÷15=1.8
12x+19x=155
2.5x﹣0.5×8=6
33.(2024春 南京期末)解方程。
x1
5.6+4x=10
0.9x﹣3×1.2=7.2
34.(2024春 六合区期末)解方程。
24x+38x=310
3.6x÷2=2.16
7x﹣4.5×2=271
期末核心考点 计算题
参考答案与试题解析
一.计算题(共34小题)
1.(2024春 阜宁县期末)直接写出得数。
【答案】;;;0。
【分析】根据分数加减法的计算方法进行计算。
【解答】解:
0
【点评】口算时,注意运算符号和数据,然后再进一步计算。
2.(2024春 泉山区期末)直接写出得数。
1
4 1 0.32=
【答案】;;1;0;1;;4;;0.09;。
【分析】根据分数加减法、小数乘法的计算方法进行计算。
【解答】解:
1 10 1
44 1 0.32=0.09
【点评】口算时,注意运算符号和数据,然后再进一步计算。
3.(2024春 建邺区期末)直接写得数。
【答案】;4;;;;;;1。
【分析】根据分数加减法的计算方法,直接进行口算即可;,按照加法结合律进行简算即可。
【解答】解:
4
1
【点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
4.(2024春 连云港期末)直接写得数。
4=
0.62=
【答案】;;0.36;。
【分析】根据分数的加减法的运算法则计算即可。
【解答】解:
4
0.62=0.36
【点评】本题考查分数加减法的运算,注意计算的准确性。
5.(2024春 沛县期末)直接写得数。
5.42+4.58= 0.82= 3.14×5=
【答案】,,,,,,,10,0.64,15.7。
【分析】根据分数加法、分数减法、数的乘方、小数加法、小数乘法的计算方法直接写出得数即可。
【解答】解:
5.42+4.58=10 0.82=0.64 3.14×5=15.7
【点评】本题主要考查了分数加法、分数减法、数的乘方、小数加法、小数乘法的运算,属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性。
6.(2024春 东台市期末)直接写出得数。
0.32=
【答案】;;1;;;;;0.09。
【分析】根据分数加减法、小数乘法的计算方法进行计算。
【解答】解:
1
0.32=0.09
【点评】口算时,注意运算符号和数据,然后再进一步计算。
7.(2024春 邳州市期末)直接写出得数。
4÷8=
0.22=
【答案】;;;1;;;0.04;0。
【分析】根据异分母分数相加减的计算方法以及乘方的计算方法口算后写出答案即可。
【解答】解:
4÷8 1
0.22=0.04 0
【点评】本题考查了异分母分数相加减以及乘方的计算。
8.(2024春 六合区期末)直接写出得数。
【答案】;;;3;。
【分析】根据分数加减法的计算方法进行计算。
【解答】解:
3
【点评】口算时,注意运算符号和数据,然后再进一步计算。
9.(2024春 梁溪区期末)直接写出得数。
0.22= 3.6x﹣2.6x=
【答案】;;;1;0.04;;x;1。
【分析】根据分数加减法、小数乘法和减法的计算方法进行计算。
【解答】解:
1
0.22=0.04 3.6x﹣2.6x=x 1
【点评】口算时,注意运算符号和数据,然后再进一步计算。
10.(2024春 海安市期末)直接写得数。
0.32=
【答案】;;3;;;;0.09;;;。
【分析】根据分数加减法、四则混合运算的顺序以及小数乘法的计算方法,直接进行口算即可。
【解答】解:
3
0.32=0.09
【点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
11.(2024春 南京期末)直接写出得数。
5÷8= 1﹣0.49=
0.42= 2 1
【答案】;;0.51;;0.16;;;。
【分析】根据分数加、减法的计算方法,乘方的计算方法和分数与除法的关系,依次口算结果。
【解答】解:
5÷8 1﹣0.49=0.51
0.42=0.16 21 1
【点评】本题解题的关键是熟练掌握分数加、减法的计算方法,乘方的计算方法和分数与除法的关系。
12.(2024春 建邺区期末)计算下面各题,能简算的要简算。
【答案】,,,。
【分析】①,先通分,再按照分数加、减法的计算法则计算;
②(),先算括号里面的减法,再算括号外面的减法;
③,首先将运算顺序调整为:(),据此简算;
④,根据分数的拆项公式进行简算;
【解答】解:①
②()
③
()
=1
④
=(1)+()+()+()+()
=1
=1
【点评】此题考查的目的是理解掌握分数加、减混合运算的顺序以及它们的计算法则,并且能够灵活选择简便方法进行计算。
13.(2024春 泉山区期末)计算下列各题,能简算的要简算。
1
【答案】;2;;。
【分析】(1)根据减法的性质进行计算;
(2)根据加法交换律和结合律进行计算;
(3)(4)根据加法交换律和结合律以及减法的性质进行计算。
【解答】解:(1)
=1
(2)
=()+()
=1+1
=2
(3)
=()﹣()
=1
(4)1
=(1)﹣()
=11
【点评】本题考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
14.(2024春 连云港期末)怎样算简便就怎样算。
2.5×24
【答案】3;60;。
【分析】(1)根据加法交换律、结合律,把同分母的分数先相加。
(2)把24改写成4×6,先算2.5×4=10,再算10×6=60。
(3)根据减法的性质a﹣(b﹣c)=a﹣b+c进行计算简便。
【解答】解:(1)
=()+()
=2+1
=3
(2)2.5×24
=2.5×4×6
=10×6
=60
(3)
【点评】本题考查了分数、小数简便计算的能力。
15.(2024春 东台市期末)计算下面各题,能简算的要简算。
【答案】;;2;。
【分析】(1)(2)(4)根据减法的性质进行计算;
(3)根据加法交换律和结合律进行计算。
【解答】解:(1)
(2)
=1
(3)
=()+()
=1+1
=2
(4)
()
1
【点评】本题考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
16.(2024春 邳州市期末)下面各题怎样算简便就怎样算。
【答案】1;;;。
【分析】(1)根据加法交换律进行计算;
(2)根据加法交换律和结合律以及减法的性质进行计算;
(3)根据减法的性质进行计算;
(4)根据分数的拆项公式进行计算。
【解答】解:(1)
=1
=1
(2)
=()﹣()
(3)
(4)
=(1)+()+()+()+()+()
=1
=1
【点评】本题考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
17.(2024春 阜宁县期末)先计算下面各题,怎样简便就怎样算。
【答案】;;。
【分析】第一题、从左往右依次计算;
第二题、根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c)进行简算;
第三题、根据减法的性质a﹣(b+c)=a﹣b﹣c进行简算。
【解答】解:
【点评】此题考查分数混合运算及运用运算定律进行简算。
18.(2024春 梁溪区期末)递等式计算,能简算的要简算。
【答案】;2;。
【分析】按照从左到右的顺序计算;
按照加法交换律和结合律计算;
先算小括号里面的减法,再算括号外里面的减法。
【解答】解:
=()+()
=1+1
=2
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
19.(2024春 海安市期末)怎样算简便就怎样算。
【答案】;1;1;。
【分析】先算小括号里面的减法,再算括号外面的减法;
按照加法结合律计算;
按照加法交换律和结合律计算;
把分数写成两数相减的形式,然后再抵消计算即可。
【解答】解:
()
1
=1
=()+()
=1+0
=1
=(1)﹣()﹣()﹣()﹣()
=1
【点评】此题是考查四则混合运算,要仔细观察算式的特点,灵活运用一些定律进行简便计算。
20.(2024春 沛县期末)计算下面各题,怎样算简便就怎样算。
【答案】;;2;。
【分析】第1小题,先通分,再计算。
第2小题,先算小括号里面的减法,再算小括号外面的减法。
第3小题,交换加数的位置,结果不变,据此作答。
第4小题,裂项,将每个加数转化为两个分数单位相减的形式,据此作答。
【解答】解:
=1+1
=2
【点评】本题考查了分数加减混合运算与简算问题,解答时一定要熟练掌握并灵活运用相关的计算法则、运算定律或性质。
21.(2024春 南京期末)计算下面各题,能简算的要简算。
【答案】;0;;。
【分析】按照减法的性质计算;
按照加法交换律和减法的性质计算;
按照从左到右的顺序计算;
把分数写成两数相减的形式,然后再抵消计算即可。
【解答】解:
=1
()
=1﹣1
=0
=1
=1
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
22.(2024春 六合区期末)计算下面各题,能简算的要简算。
【答案】,,2,0,,。
【分析】第一题,先通分再计算;第二题同分母分数先相减,再通分计算;第三题把同分母分数先相加;第四题把括号去掉变成连减计算;第五题把括号去掉,括号里的减法变加法;第六题把变成(),变成()以此类推即可简便运算。
【解答】解:
=1+1
=2
=1﹣1
=0
=()
=1
【点评】此题考查了分数运算的简便运算。
23.(2024春 建邺区期末)解方程。
2x÷2.5=0.8 4.2x+0.6x=24
5x﹣0.4×30=48 x﹣63+37=150
【答案】x=1;x=5;x=12;x=176。
【分析】根据等式的性质,方程两端同时乘2.5,再同时除以2,求出方程的解。
先化简,再根据等式的性质,方程两端同时除以4.8,求出方程的解。
先化简,再根据等式的性质,方程两端同时加上12,再同时除以5,求出方程的解。
根据等式的性质,方程两端同时减去37,再同时加上63,求出方程的解。
【解答】解:2x÷2.5=0.8
2x÷2.5×2.5=0.8×2.5
2x=2
2x÷2=2÷2
x=1
4.2x+0.6x=24
4.8x=24
4.8x÷4.8=24÷4.8
x=5
5x﹣0.4×30=48
5x﹣12=48
5x﹣12+12=48+12
5x=60
5x÷5=60÷5
x=12
x﹣63+37=150
x﹣63+37﹣37=150﹣37
x﹣63=113
x﹣63+63=113+63
x=176
【点评】本题解题的关键是熟练掌握解方程的方法。
24.(2024春 泉山区期末)解方程。
1.6x÷3=3.2
1﹣0.5x=0.2
【答案】x;x=6;x=1.6。
【分析】x,根据等式的基本性质,方程两边同时加上,然后计算求出x的值;
1.6x÷3=3.2,根据等式的基本性质,方程两边同时乘3,然后再同时除以1.6,最后计算求出x的值;
1﹣0.5x=0.2,根据等式的基本性质可得0.5x=1﹣0.2,然后等式两边同时除以0.5,最后计算求出x的值。
【解答】解:x
1.6x÷3=3.2
1.6x=3.2×3
1.6x=9.6
x=9.6÷1.6
x=6
1﹣0.5x=0.2
0.5x=1﹣0.2
0.5x=0.8
x=0.8÷0.5
x=1.6
【点评】解答此题要运用等式的基本性质。
25.(2024春 连云港期末)解方程。
x
2.9x+0.2x=93
4x﹣7×0.5=5.3
【答案】x=2;x=30;x=2.2。
【分析】根据等式的性质,方程两端同时加上,算出方程的解。
先化简,再根据等式的性质,方程两端同时除以3.1,算出方程的解。
先化简,再根据等式的性质,方程两端同时加上3.5,再同时除以4,算出方程的解。
【解答】解:x
x
x=2
2.9x+0.2x=93
3.1x=93
3.1x÷3.1=93÷3.1
x=30
4x﹣7×0.5=5.3
4x﹣3.5=5.3
4x﹣3.5+3.5=5.3+3.5
4x=8.8
4x÷4=8.8÷4
x=2.2
【点评】本题解题的关键是熟练掌握解方程的方法。
26.(2024春 东台市期末)解方程。
5x﹣3x=5.2
2x﹣0.5×6=7
【答案】x;x=2.6;x=5。
【分析】,根据等式的基本性质,方程两边同时减去,然后计算求出x的值;
5x﹣3x=5.2,先计算5x﹣3x=2x,根据等式的基本性质,方程两边同时除以2,然后计算求出x的值;
2x﹣0.5×6=7,先计算0.5×6=3,根据等式的基本性质,方程两边同时加上3,然后再同时除以2,最后计算求出x的值。
【解答】解:
5x﹣3x=5.2
2x=5.2
x=5.2÷2
x=2.6
2x﹣0.5×6=7
2x﹣3=7
2x=7+3
2x=10
x=10÷2
x=5
【点评】解答此题要运用等式的基本性质。
27.(2024春 阜宁县期末)解方程。
x÷40=14
2.7x﹣1.2x=7.5
4x﹣4×0.5=30
【答案】x;x=560;x=5;x=8。
【分析】根据等式的性质解方程:
方程两边同时减去,求出方程的解;
方程两边同时乘40,求出方程的解;
先把方程化简成1.5x=7.5,方程两边同时除以1.5,求出方程的解;
先把方程化简成4x﹣2=30,然后方程两边先同时加上2,再同时除以4,求出方程的解。
【解答】解:
x÷40=14
x÷40×40=14×40
x=560
2.7x﹣1.2x=7.5
1.5x=7.5
1.5x÷1.5=7.5÷1.5
x=5
4x﹣4×0.5=30
4x﹣2=30
4x﹣2+2=30+2
4x=32
4x÷4=32÷4
x=8
【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去,同时乘或同时除以一个数(0除外),两边仍相等。
28.(2024春 邳州市期末)
5.5x﹣3x=15
2.5x﹣0.5×8=6
【答案】x;x=6;x=4。
【分析】,根据等式的基本性质,方程两边同时加上,然后计算求出x的值;
5.5x﹣3x=15,先计算5.5x﹣3x=2.5x,根据等式的基本性质,方程两边同时除以2.5,然后计算求出x的值;
2.5x﹣0.5×8=6,先计算0.5×8=4,根据等式的基本性质,方程两边同时加上4,然后再同时除以2.5,最后计算求出x的值。
【解答】解:
5.5x﹣3x=15
2.5x=15
2.5x÷2.5=15÷2.5
x=6
2.5x﹣0.5×8=6
2.5x﹣4=6
2.5x=6+4
2.5x=10
x=10÷2.5
x=4
【点评】解答此题要运用等式的基本性质。
29.(2022春 瑶海区期末)解方程。
6.3﹣x=5 1.5x+4=10 2x﹣0.5x=45
【答案】见试题解答内容
【分析】第1题,根据减数=被减数﹣差,算出方程的解。
第2题,根据等式的性质,方程两边同时减去4,再同时除以1.5,算出方程的解。
第3题,先计算出2x﹣0.5x的结果,再根据等式的性质,方程两边同时除以1.5,算出方程的解。
【解答】解:6.3﹣x=5
x=6.3﹣5
x=1.3
1.5x+4=10
1.5x+4﹣4=10﹣4
1.5x=6
1.5x÷1.5=6÷1.5
x=4
2x﹣0.5x=45
1.5x=45
1.5x÷1.5=45÷1.5
x=30
【点评】本题解题的关键是熟练掌握解方程的方法。
30.(2024春 海安市期末)解方程。
0.8x+0.6x=21
2.2x﹣0.3×5=9.5
0.75+0.25x=2
【答案】x=15;x;x=5;x=5。
【分析】(1)先计算0.8x+0.6x=1.4x,根据等式的性质,方程的两边同时除以1.4求解;
(2)根据等式的性质,方程的两边同时减去,然后方程的两边同时加上求解;
(3)先计算0.3×5=1.5,根据等式的性质,方程的两边同时加上1.5,然后方程的两边同时除以2.2求解;
(4)根据等式的性质,方程的两边同时减去0.75,然后方程的两边同时除以0.25求解。
【解答】解:(1)0.8x+0.6x=21
1.4x=21
1.4x÷1.4=21÷1.4
x=15
(2)
x1
x
x
x
(3)2.2x﹣0.3×5=9.5
2.2x﹣1.5=9.5
2.2x﹣1.5+1.5=9.5+1.5
2.2x=11
2.2x÷2.2=11÷2.2
x=5
(4)0.75+0.25x=2
0.75+0.25x﹣0.75=2﹣0.75
0.25x=1.25
0.25x÷0.25=1.25÷0.25
x=5
【点评】本题考查解方程,解题的关键是掌握等式的性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立。
31.(2024春 梁溪区期末)求未知数的值。
0.4x+0.2x=3 2.5x﹣0.5×8=6
【答案】x=5;x=4;x。
【分析】0.4x+0.2x=3,先计算0.4x+0.2x=0.6x,根据等式的基本性质,方程两边同时除以0.6,然后计算即可求出x的值;
2.5x﹣0.5×8=6,先计算0.5×8=4,根据等式的基本性质,方程两边同时加上4,然后同时除以2.5,最后计算即可求出x的值;
,根据等式的基本性质,方程两边同时加上,然后计算即可求出x的值。
【解答】解:0.4x+0.2x=3
0.6x=3
0.6x÷0.6=3÷0.6
x=5
2.5x﹣0.5×8=6
2.5x﹣4=6
2.5x﹣4+4=6+4
2.5x=10
2.5x÷2.5=10÷2.5
x=4
【点评】解答此题要运用等式的基本性质。
32.(2024春 沛县期末)解方程。
0.5+x=2.5
x÷15=1.8
12x+19x=155
2.5x﹣0.5×8=6
【答案】x=2;x=27;x=5;x=4。
【分析】0.5+x=2.5,根据等式的基本性质,方程两边同时减去0.5,然后计算求出x的值;
x÷15=1.8,根据等式的基本性质,方程两边同时乘15,然后计算求出x的值;
12x+19x=155,先计算12x+19x=31x,根据等式的基本性质,方程两边同时除以31,然后计算求出x的值;
2.5x﹣0.5×8=6,先计算0.5×8=4,根据等式的基本性质,方程两边同时加上4,然后再同时除以2.5,最后计算求出x的值。
【解答】解:0.5+x=2.5
x=2.5﹣0.5
x=2
x÷15=1.8
x=15×1.8
x=27
12x+19x=155
31x=155
x=155÷31
x=5
2.5x﹣0.5×8=6
2.5x﹣4=6
2.5x=6+4
2.5x=10
x=10÷2.5
x=4
【点评】解答此题要运用等式的基本性质。
33.(2024春 南京期末)解方程。
x1
5.6+4x=10
0.9x﹣3×1.2=7.2
【答案】x;x=1.1;x=12。
【分析】根据等式的性质等式的两边同时加,减,求解即可;
根据等式的性质等式的两边同时减5.6,再同时除以4,求解即可;
先计算等式左边的乘法算式,再根据等式的性质等式的两边同时加3.6,再同时除以0.9,求解即可。
【解答】解:
5.6+4x=10
5.6+4x﹣5.6=10﹣5.6
4x=4.4
4x÷4=4.4÷4
x=1.1
0.9x﹣3×1.2=7.2
0.9x﹣3.6=7.2
0.9x﹣3.6+3.6=7.2+3.6
0.9x=10.8
0.9x÷0.9=10.8÷0.9
x=12
【点评】熟练掌握根据等式的性质求方程的解是解答本题的关键。
34.(2024春 六合区期末)解方程。
24x+38x=310
3.6x÷2=2.16
7x﹣4.5×2=271
【答案】x=5;x=1.2;x=40。
【分析】24x+38x=310,先计算24x+38x=62x,根据等式的基本性质,方程两边同时除以62,然后计算即可求出x的值;
3.6x÷2=2.16,根据等式的基本性质,方程两边同时乘2,然后再同时除以3.6,最后计算即可求出x的值;
7x﹣4.5×2=271,先计算4.5×2=9,根据等式的基本性质,方程两边同时加上9,然后再同时除以7,最后计算即可求出x的值。
【解答】解:24x+38x=310
62x=310
62x÷62=310÷62
x=5
3.6x÷2=2.16
3.6x÷2×2=2.16×2
3.6x=4.32
3.6x÷3.6=4.32÷3.6
x=1.2
7x﹣4.5×2=271
7x﹣9=271
7x﹣9+9=271+9
7x=280
7x÷7=280÷7
x=40
【点评】解答此题要运用等式的基本性质。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
