2025年江西省新余市分宜县中考模拟数学卷(无答案)
文档属性
| 名称 | 2025年江西省新余市分宜县中考模拟数学卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 801.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 09:05:52 | ||
图片预览

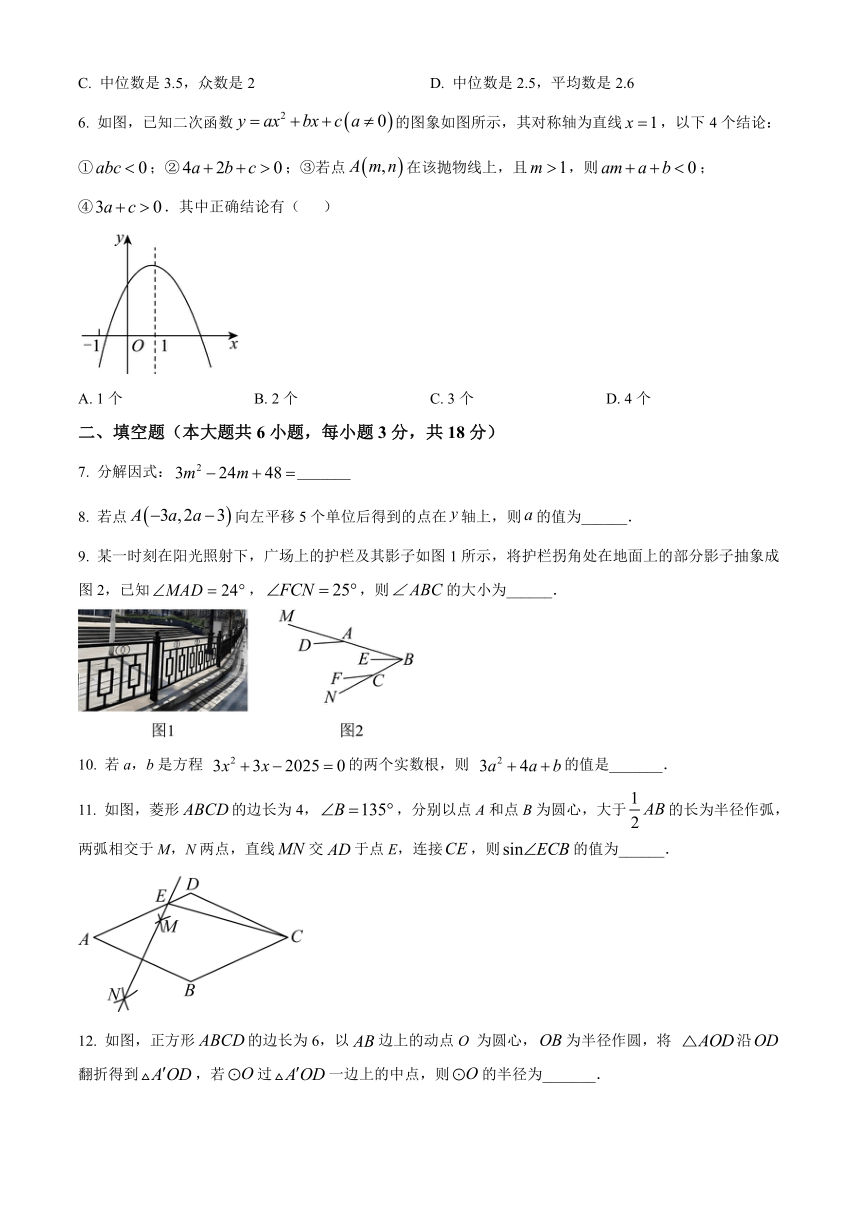

文档简介
2024-2025学年江西省新余市分宜县中考模拟数学卷
说明:
1.全卷满分120分,考试时间120分钟.
2.请将答案写在答题卡上,否则不给分.
一、选择题(本大题共6小题,每小题3分,共18分)
1. ﹣18的相反数是( )
A. 18 B. ﹣18 C. D. ﹣
2. 下列计算正确的是( )
A. B.
C. D.
3. 榫卯)是中国传统建筑、家具及其它器械的一种结构方式,它通过两个构件上凹凸部位相结合来将不同构件组合在一起,凸出部分叫榫,凹进部分叫卯,其特点是在物件上不使用钉子,利用榫卯加固物件,体现出中国古老的文化和智慧.如图是其中一种榫,其俯视图是( )
A. B. C. D.
4. 江西夏粮以水稻为主,2024年我省夏粮播种总产量和播种面积双双增加.全省夏粮播种面积为126.3万亩.126.3万用科学记数法表示为( )
A. B. C. D. 1.263×10
5. 某校为了解同学们课外阅读名著的情况,在某年级随机抽查了20名同学每学期的课外阅读名著的情况,调查结果如表所示:
课外名著阅读量(本) 0 1 2 3 4 5
学生数 1 4 5 4 4 2
关于这20名同学课外阅读名著情况,下列说法正确的是( )
A. 中位数是2.5,众数是4 B. 众数是2,平均数是2.5
C. 中位数是3.5,众数是2 D. 中位数是2.5,平均数是2.6
6. 如图,已知二次函数的图象如图所示,其对称轴为直线,以下4个结论:①;②;③若点在该抛物线上,且,则;④.其中正确结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(本大题共6小题,每小题3分,共18分)
7. 分解因式:_______
8. 若点向左平移5个单位后得到的点在轴上,则的值为______.
9. 某一时刻在阳光照射下,广场上的护栏及其影子如图1所示,将护栏拐角处在地面上的部分影子抽象成图2,已知,,则的大小为______.
10. 若a,b是方程 的两个实数根,则 的值是_______.
11. 如图,菱形的边长为4,,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M,N两点,直线交于点E,连接,则的值为______.
12. 如图,正方形的边长为6,以边上的动点O 为圆心,为半径作圆,将 沿翻折得到,若过一边上的中点,则的半径为_______.
三、解答题(本大题共5小题,每小题6分,共30分)
13. (1)计算∶
(2)解不等式组:
14. 以下是小华化简分式 的过程:
解:原式 …①
②
……… ……③
. . ……………④
(1)小华的解答过程在第 步出现错误;
(2)请你帮助小华写出正确的解答过程,并选择一个合适的x值代入求值.
15. 南昌,作为中国革命历史上的重要城市,蕴藏着丰富的红色旅游资源.这些景点不仅是历史的见证,更是进行爱国主义教育、传承红色文化血脉的神圣殿堂.某校建议同学们利用周末时间自主到以下四个基地开展研学活动.
A.南昌八一起义纪念馆;
B.八一广场;
C.南昌红色记忆展示馆;
D.南昌新四军军部旧址.
小杨和小金各自随机选择一个基地作为本次研学活动的第一站.
(1)小金选择基地A 概率为 ;
(2)用画树状图或列表方法,求小杨和小金选择不同基地的概率.
16. 如图是 的正方形网格,已知格点 (顶点在小正方形顶点处的三角形称为格点三角形),请仅用无刻度直尺完成下列作图(要求保留作图痕迹,不要求写作法).
(1)在图1中,作边的垂直平分线;
(2)在图2中,在边上找一点,作线段,使得
17. 如图,一次函数,是反比例函数 图象上的两点,点 的坐标为,点 的坐标为,线段的延长线交轴于点 .
(1)求反比例函数函数关系式;
(2)求 的面积.
四、解答题(本大题共3小题,每小题8分,共24分)
18. 某商店准备购进A、B两种纪念品.若购进A种纪念品11件,B种纪念品6件,需要222元;若购进A种纪念品5件,B种纪念品12件,需要240元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店本次购进B种纪念品的数量比购进A种纪念品的数量的2倍还少8个,购进两种纪念品的总金额不超过972元,则该商店本次最多购进A种纪念品多少个?
19. 如图,,点O在上,过点B,分别与,交于D,E两点,过点D作的切线交于点F.
(1)求证∶;
(2)若与相切于点G,,,求的半径.
20. 绳金塔位于南昌市西湖区,是南昌的标志性建筑.它始建于唐代,历经风雨,如今已成为集历史、文化、旅游于一体的景区.某兴趣小组开展了测量绳金塔高度的实践活动.如图所示,斜坡 BE 的坡度 ,在B 处测得绳金塔 顶部 D 的仰角为 ,在 E 处测得绳金塔 顶部 D的仰角为
(1)求点 B 离水平地面的高度;
(2)求绳金塔的高度(结果精确到0.1m,参考数据:
五、解答题(本大题共2小题,每小题9分,共18分)
21. 12月2日是第十三个122“全国交通安全日”,主题是“文明交通,携手共创”.12月2日上午,江西省2024年122“全国交通安全日”主题宣传活动在南昌举行.为了增强学生的交通安全意识,某校组织了一次全校2000名学生都参加的“交通安全知识”竞赛,从中随机抽取n名学生的竞赛成绩进行了分析,把成绩分成五个等级(A∶;B∶;C∶;D∶;E∶),并根据分析结果绘制了不完整的频数分布直方图和扇形统计图.
请根据以上信息,解答下列问题:
(1)填空: , ;在扇形统计图中C等级所在扇形的圆心角度数为 ;
(2)补全频数分布直方图;
(3)该校对考试成绩为的学生进行颁发获奖证书,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为,请你估计全校获得二等奖的学生有多少名.
22. 定义:对角互补且有一组邻边相等的四边形称为奇异四边形.
(1)如图1,四边形是奇异四边形, ,求证:平分;
(2)如图1,四边形是奇异四边形, ,求四边形的面积;
(3)如图2,四边形是奇异四边形, 外角的平分线交的延长线于点 E, 20,,求的长.
六、解答题(本大题共12分)
23. 抛物线 与y轴相交于点 与x轴相交于点 、,点 D 是抛物线的顶点.
(1)求抛物线的解析式;
(2)在y轴上有一点 P,求出使值最小时点 P 的坐标,并求出此时 的最小值;
(3)在(2)的条件下,在第四象限中的抛物线上是否存在一点 E,过点E作轴 交x轴于点 F,使 与 相似?若存在,求出点 E 的坐标;若不存在,请说明理由.
说明:
1.全卷满分120分,考试时间120分钟.
2.请将答案写在答题卡上,否则不给分.
一、选择题(本大题共6小题,每小题3分,共18分)
1. ﹣18的相反数是( )
A. 18 B. ﹣18 C. D. ﹣
2. 下列计算正确的是( )
A. B.
C. D.
3. 榫卯)是中国传统建筑、家具及其它器械的一种结构方式,它通过两个构件上凹凸部位相结合来将不同构件组合在一起,凸出部分叫榫,凹进部分叫卯,其特点是在物件上不使用钉子,利用榫卯加固物件,体现出中国古老的文化和智慧.如图是其中一种榫,其俯视图是( )
A. B. C. D.
4. 江西夏粮以水稻为主,2024年我省夏粮播种总产量和播种面积双双增加.全省夏粮播种面积为126.3万亩.126.3万用科学记数法表示为( )
A. B. C. D. 1.263×10
5. 某校为了解同学们课外阅读名著的情况,在某年级随机抽查了20名同学每学期的课外阅读名著的情况,调查结果如表所示:
课外名著阅读量(本) 0 1 2 3 4 5
学生数 1 4 5 4 4 2
关于这20名同学课外阅读名著情况,下列说法正确的是( )
A. 中位数是2.5,众数是4 B. 众数是2,平均数是2.5
C. 中位数是3.5,众数是2 D. 中位数是2.5,平均数是2.6
6. 如图,已知二次函数的图象如图所示,其对称轴为直线,以下4个结论:①;②;③若点在该抛物线上,且,则;④.其中正确结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(本大题共6小题,每小题3分,共18分)
7. 分解因式:_______
8. 若点向左平移5个单位后得到的点在轴上,则的值为______.
9. 某一时刻在阳光照射下,广场上的护栏及其影子如图1所示,将护栏拐角处在地面上的部分影子抽象成图2,已知,,则的大小为______.
10. 若a,b是方程 的两个实数根,则 的值是_______.
11. 如图,菱形的边长为4,,分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于M,N两点,直线交于点E,连接,则的值为______.
12. 如图,正方形的边长为6,以边上的动点O 为圆心,为半径作圆,将 沿翻折得到,若过一边上的中点,则的半径为_______.
三、解答题(本大题共5小题,每小题6分,共30分)
13. (1)计算∶
(2)解不等式组:
14. 以下是小华化简分式 的过程:
解:原式 …①
②
……… ……③
. . ……………④
(1)小华的解答过程在第 步出现错误;
(2)请你帮助小华写出正确的解答过程,并选择一个合适的x值代入求值.
15. 南昌,作为中国革命历史上的重要城市,蕴藏着丰富的红色旅游资源.这些景点不仅是历史的见证,更是进行爱国主义教育、传承红色文化血脉的神圣殿堂.某校建议同学们利用周末时间自主到以下四个基地开展研学活动.
A.南昌八一起义纪念馆;
B.八一广场;
C.南昌红色记忆展示馆;
D.南昌新四军军部旧址.
小杨和小金各自随机选择一个基地作为本次研学活动的第一站.
(1)小金选择基地A 概率为 ;
(2)用画树状图或列表方法,求小杨和小金选择不同基地的概率.
16. 如图是 的正方形网格,已知格点 (顶点在小正方形顶点处的三角形称为格点三角形),请仅用无刻度直尺完成下列作图(要求保留作图痕迹,不要求写作法).
(1)在图1中,作边的垂直平分线;
(2)在图2中,在边上找一点,作线段,使得
17. 如图,一次函数,是反比例函数 图象上的两点,点 的坐标为,点 的坐标为,线段的延长线交轴于点 .
(1)求反比例函数函数关系式;
(2)求 的面积.
四、解答题(本大题共3小题,每小题8分,共24分)
18. 某商店准备购进A、B两种纪念品.若购进A种纪念品11件,B种纪念品6件,需要222元;若购进A种纪念品5件,B种纪念品12件,需要240元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店本次购进B种纪念品的数量比购进A种纪念品的数量的2倍还少8个,购进两种纪念品的总金额不超过972元,则该商店本次最多购进A种纪念品多少个?
19. 如图,,点O在上,过点B,分别与,交于D,E两点,过点D作的切线交于点F.
(1)求证∶;
(2)若与相切于点G,,,求的半径.
20. 绳金塔位于南昌市西湖区,是南昌的标志性建筑.它始建于唐代,历经风雨,如今已成为集历史、文化、旅游于一体的景区.某兴趣小组开展了测量绳金塔高度的实践活动.如图所示,斜坡 BE 的坡度 ,在B 处测得绳金塔 顶部 D 的仰角为 ,在 E 处测得绳金塔 顶部 D的仰角为
(1)求点 B 离水平地面的高度;
(2)求绳金塔的高度(结果精确到0.1m,参考数据:
五、解答题(本大题共2小题,每小题9分,共18分)
21. 12月2日是第十三个122“全国交通安全日”,主题是“文明交通,携手共创”.12月2日上午,江西省2024年122“全国交通安全日”主题宣传活动在南昌举行.为了增强学生的交通安全意识,某校组织了一次全校2000名学生都参加的“交通安全知识”竞赛,从中随机抽取n名学生的竞赛成绩进行了分析,把成绩分成五个等级(A∶;B∶;C∶;D∶;E∶),并根据分析结果绘制了不完整的频数分布直方图和扇形统计图.
请根据以上信息,解答下列问题:
(1)填空: , ;在扇形统计图中C等级所在扇形的圆心角度数为 ;
(2)补全频数分布直方图;
(3)该校对考试成绩为的学生进行颁发获奖证书,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为,请你估计全校获得二等奖的学生有多少名.
22. 定义:对角互补且有一组邻边相等的四边形称为奇异四边形.
(1)如图1,四边形是奇异四边形, ,求证:平分;
(2)如图1,四边形是奇异四边形, ,求四边形的面积;
(3)如图2,四边形是奇异四边形, 外角的平分线交的延长线于点 E, 20,,求的长.
六、解答题(本大题共12分)
23. 抛物线 与y轴相交于点 与x轴相交于点 、,点 D 是抛物线的顶点.
(1)求抛物线的解析式;
(2)在y轴上有一点 P,求出使值最小时点 P 的坐标,并求出此时 的最小值;
(3)在(2)的条件下,在第四象限中的抛物线上是否存在一点 E,过点E作轴 交x轴于点 F,使 与 相似?若存在,求出点 E 的坐标;若不存在,请说明理由.
同课章节目录
