2025年四川省乐山市峨边彝族自治县初中学业水平模拟测试数学试题(无答案)
文档属性
| 名称 | 2025年四川省乐山市峨边彝族自治县初中学业水平模拟测试数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 619.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 12:01:53 | ||
图片预览


文档简介
峨边彝族自治县九年级调查研究考试
数学试题
注意事项:
本试卷分为“选择题”和“非选择题”两部分,“选择题”请用2B铅笔在答题卡上对应题目标号的位置填涂.非选择题必须将答案写在答题卡上对应位置内,作图题可先用铅笔画线,确认后再用签字笔描绘清楚.在对应区域以外的地方作答或在本试题卷、草稿纸上答题无效.切记!
考试时间120分钟,满分150分
第Ⅰ卷选择题(共30分)
一、选择题:(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求)
1. 的值为( )
A. B. C. D.
2. 下列几何体三种视图都是圆形的是( )
A. B.
C. D.
3. 下列计算正确的是( )
A. B.
C. D.
4. 第七次全国人口普查统计,乐山市常住人口约为3147000人,将3147000用科学记数法表示为( )
A. B. C. D.
5. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(‘两’我国古代货币单位);马二匹、牛五头,共价三十八两,阀马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为( )
A. B. C. D.
6. 已知,则值为( )
A. B. C. D.
7. 若方程有实数根,则m值的取值范围是( )
A. B. C. D.
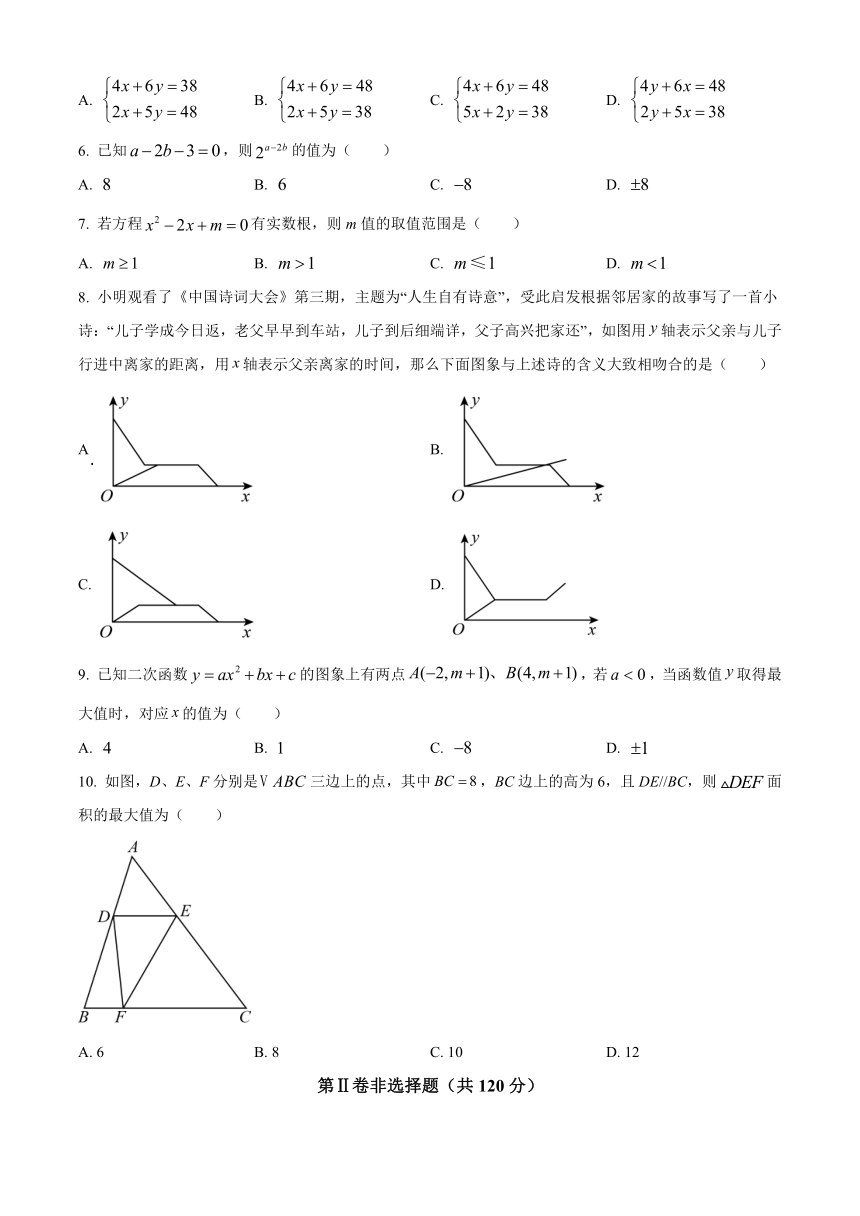
8. 小明观看了《中国诗词大会》第三期,主题为“人生自有诗意”,受此启发根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”,如图用轴表示父亲与儿子行进中离家的距离,用轴表示父亲离家的时间,那么下面图象与上述诗的含义大致相吻合的是( )
A B.
C. D.
9. 已知二次函数的图象上有两点,若,当函数值取得最大值时,对应的值为( )
A. B. C. D.
10. 如图,D、E、F分别是三边上的点,其中,BC边上的高为6,且DE//BC,则面积的最大值为( )
A. 6 B. 8 C. 10 D. 12
第Ⅱ卷非选择题(共120分)
二、填空题(每小题3分,共18分)
11. 计算:_______.
12. 九年级二班进行了一次数学模拟测试,其中优等学生共有9人,成绩分别为:136,138,139,139,140,141,142,145,150,那么这9人成绩的众数是_______.
13. 已知菱形的对角线为和,菱形面积为,其中,则______.
14. 已知点在一次函数的图像上,那么的值是__________.
15. 已知关于的一元二次方程的两根为,,则的值为________.
16. 已知抛物线图象与轴交于点、,若以为直径的圆与在x轴下方的抛物线有交点,则a的取值范围是_______.
三、解答题:本大题共10个小题,总分102分.
17. 计算:.
18. 解不等式组:
19. 如图,已知点分别在平行四边形的边上,且,求证:.
20. 先化简:,再从,,中选择一个合适的数代入并求值.
21. 为了解学生每周参加课外兴趣小组活动的累计时间(单位:小时),学校采用随机抽样的方法,对部分学生进行了问卷调查,调查结果按,,,分为四个等级,分别用A、B、C、D表示;下图是受损的调查统计图,请根据图上残存信息解决以下问题:
(1)求参与问卷调查的学生人数 ,并将条形统计图补充完整;
(2)全校共有学生2000人,试估计学校每周参加课外兴趣小组活动累计时间不少于4小时的学生人数;
(3)某小组有4名同学,A、D等级各2人,从中任选2人向老师汇报兴趣活动情况,请用画树状图或列表法求这2人均属D等级的概率.
22. 如图,一次函数的图象与反比例函数的图象交于、两点,与轴交于点,且,.连结并延长交双曲线于点,连结.
(1)直接写出一次函数的解析式以及点的坐标;
(2)求的面积.
23. 如图,是直径,,连接,过点作射线的垂线,垂足为点,交的延长线于点.
(1)求证:;
(2)若,求的长.
24. 某数学兴趣班研究锐角三角函数在代数与几何中的应用.
第一小组研究锐角三角函数在测量中的应用,如图①,同学们在观测点K处测得顶端P的仰角,观测点与树的距离KH为m米,点O到地面的距离OK为h米,从而通过计算可得树高PH的值.请你根据测量数据,写出PH=_______.(用含α、m、h的式子表示)
第二小组通过学习得知,当α为锐角时有:,,则关于锐角α的代数式有最小值,请你写出当______°时,代数式的最小值为______.
第三小组通过对第一、第二小组的研究结果学习,进行综合研究如图②,半径为的与直线l相切于点,P是上的一个动点(不与点A重合),过点作,垂足为,连接.设,,求出了的最大值.请你书写出第三小组求解最大值的过程.
25. 如图,在矩形中,,点E是边上一动点(点E不与A,D重合),连接,以为边在直线的右侧作矩形,使得矩形矩形,交直线于点H.
(1)【尝试初探】在点E的运动过程中,与始终保持相似关系,请说明理由.
(2)【深入探究】若,随着E点位置的变化,H点的位置随之发生变化,当H是线段中点时,求的值.
(3)【拓展延伸】连接,,当是以为腰的等腰三角形时,求的值(用含n的代数式表示).
26. 定义:在平面直角坐标系中,图形G上点P的纵坐标与其横坐标的差称为P点的“坐标差”,记作Zp,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.
(1)①点A(3,1)的“坐标差”为 ;
②求抛物线的“特征值”;
(2)某二次函数的“特征值”为,点B,与点C分别是此二次函数的图象与轴和轴的交点,且点B与点C的“坐标差”相等.
①直接写出 ;(用含的式子表示)
②求此二次函数的表达式.
数学试题
注意事项:
本试卷分为“选择题”和“非选择题”两部分,“选择题”请用2B铅笔在答题卡上对应题目标号的位置填涂.非选择题必须将答案写在答题卡上对应位置内,作图题可先用铅笔画线,确认后再用签字笔描绘清楚.在对应区域以外的地方作答或在本试题卷、草稿纸上答题无效.切记!
考试时间120分钟,满分150分
第Ⅰ卷选择题(共30分)
一、选择题:(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求)
1. 的值为( )
A. B. C. D.
2. 下列几何体三种视图都是圆形的是( )
A. B.
C. D.
3. 下列计算正确的是( )
A. B.
C. D.
4. 第七次全国人口普查统计,乐山市常住人口约为3147000人,将3147000用科学记数法表示为( )
A. B. C. D.
5. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(‘两’我国古代货币单位);马二匹、牛五头,共价三十八两,阀马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为( )
A. B. C. D.
6. 已知,则值为( )
A. B. C. D.
7. 若方程有实数根,则m值的取值范围是( )
A. B. C. D.
8. 小明观看了《中国诗词大会》第三期,主题为“人生自有诗意”,受此启发根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”,如图用轴表示父亲与儿子行进中离家的距离,用轴表示父亲离家的时间,那么下面图象与上述诗的含义大致相吻合的是( )
A B.
C. D.
9. 已知二次函数的图象上有两点,若,当函数值取得最大值时,对应的值为( )
A. B. C. D.
10. 如图,D、E、F分别是三边上的点,其中,BC边上的高为6,且DE//BC,则面积的最大值为( )
A. 6 B. 8 C. 10 D. 12
第Ⅱ卷非选择题(共120分)
二、填空题(每小题3分,共18分)
11. 计算:_______.
12. 九年级二班进行了一次数学模拟测试,其中优等学生共有9人,成绩分别为:136,138,139,139,140,141,142,145,150,那么这9人成绩的众数是_______.
13. 已知菱形的对角线为和,菱形面积为,其中,则______.
14. 已知点在一次函数的图像上,那么的值是__________.
15. 已知关于的一元二次方程的两根为,,则的值为________.
16. 已知抛物线图象与轴交于点、,若以为直径的圆与在x轴下方的抛物线有交点,则a的取值范围是_______.
三、解答题:本大题共10个小题,总分102分.
17. 计算:.
18. 解不等式组:
19. 如图,已知点分别在平行四边形的边上,且,求证:.
20. 先化简:,再从,,中选择一个合适的数代入并求值.
21. 为了解学生每周参加课外兴趣小组活动的累计时间(单位:小时),学校采用随机抽样的方法,对部分学生进行了问卷调查,调查结果按,,,分为四个等级,分别用A、B、C、D表示;下图是受损的调查统计图,请根据图上残存信息解决以下问题:
(1)求参与问卷调查的学生人数 ,并将条形统计图补充完整;
(2)全校共有学生2000人,试估计学校每周参加课外兴趣小组活动累计时间不少于4小时的学生人数;
(3)某小组有4名同学,A、D等级各2人,从中任选2人向老师汇报兴趣活动情况,请用画树状图或列表法求这2人均属D等级的概率.
22. 如图,一次函数的图象与反比例函数的图象交于、两点,与轴交于点,且,.连结并延长交双曲线于点,连结.
(1)直接写出一次函数的解析式以及点的坐标;
(2)求的面积.
23. 如图,是直径,,连接,过点作射线的垂线,垂足为点,交的延长线于点.
(1)求证:;
(2)若,求的长.
24. 某数学兴趣班研究锐角三角函数在代数与几何中的应用.
第一小组研究锐角三角函数在测量中的应用,如图①,同学们在观测点K处测得顶端P的仰角,观测点与树的距离KH为m米,点O到地面的距离OK为h米,从而通过计算可得树高PH的值.请你根据测量数据,写出PH=_______.(用含α、m、h的式子表示)
第二小组通过学习得知,当α为锐角时有:,,则关于锐角α的代数式有最小值,请你写出当______°时,代数式的最小值为______.
第三小组通过对第一、第二小组的研究结果学习,进行综合研究如图②,半径为的与直线l相切于点,P是上的一个动点(不与点A重合),过点作,垂足为,连接.设,,求出了的最大值.请你书写出第三小组求解最大值的过程.
25. 如图,在矩形中,,点E是边上一动点(点E不与A,D重合),连接,以为边在直线的右侧作矩形,使得矩形矩形,交直线于点H.
(1)【尝试初探】在点E的运动过程中,与始终保持相似关系,请说明理由.
(2)【深入探究】若,随着E点位置的变化,H点的位置随之发生变化,当H是线段中点时,求的值.
(3)【拓展延伸】连接,,当是以为腰的等腰三角形时,求的值(用含n的代数式表示).
26. 定义:在平面直角坐标系中,图形G上点P的纵坐标与其横坐标的差称为P点的“坐标差”,记作Zp,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.
(1)①点A(3,1)的“坐标差”为 ;
②求抛物线的“特征值”;
(2)某二次函数的“特征值”为,点B,与点C分别是此二次函数的图象与轴和轴的交点,且点B与点C的“坐标差”相等.
①直接写出 ;(用含的式子表示)
②求此二次函数的表达式.
同课章节目录
