华师大版数学九年级上册第23章 23.3.1相似三角形课时作业
文档属性
| 名称 | 华师大版数学九年级上册第23章 23.3.1相似三角形课时作业 |
|
|
| 格式 | docx | ||
| 文件大小 | 317.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 15:25:51 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学九年级上册第23章第3节 23.3.1相似三角形
课时作业
一、选择题
1. 若△ABC∽△A′B′C′且 = ,△ABC的周长为15cm,则△A′B′C′的周长为( )
A.18 B.20 C. D.
答案:B
解析:解答:∵△ABC∽△A′B′C′,
∴= =
∴==,
∵△ABC的周长为15cm,
∴△A′B′C′的周长为20cm.
故选B.
分析:根据比例的等比性质可得相似三角形周长的比等于相似比,可得 == ,由△ABC的周长为15cm,即可求得△A′B′C′的周长.
2. 一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则其它两边的和是( )
A.19 B.17 C.24 D.21
答案:C
解析:解答:设另一个三角形的最短边为x,第二短边为y,根据相似三角形的三边对应成比例,知==,
∴x=9,y=15,
∴x+y=24.
故选C.
分析:根据相似三角形的性质三边对应成比例作答即.
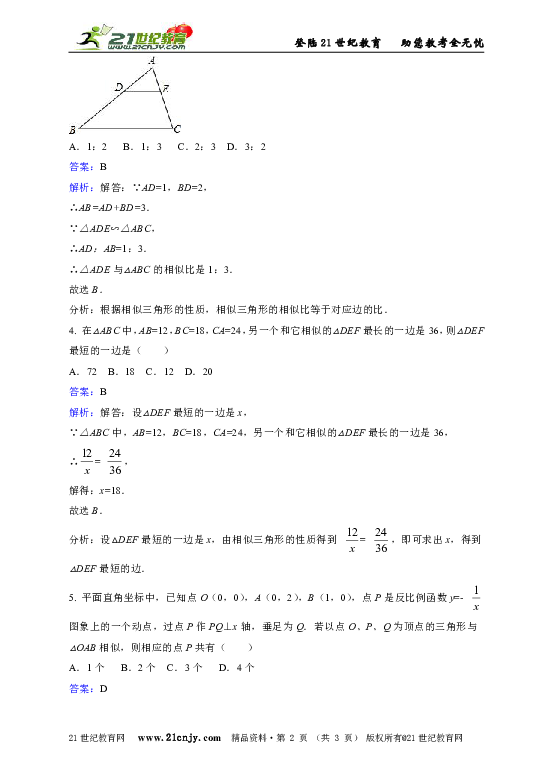
3. 如图,△ADE∽△ABC,若AD=1,BD=2,则△ADE与△ABC的相似比是( )
A.1:2 B.1:3 C.2:3 D.3:2
答案:B
解析:解答:∵AD=1,BD=2,
∴AB=AD+BD=3.
∵△ADE∽△ABC,
∴AD:AB=1:3.
∴△ADE与△ABC的相似比是1:3.
故选B.
分析:根据相似三角形的性质,相似三角形的相似比等于对应边的比.
4. 在△ABC中,AB=12,BC=18,CA=24,另一个和它相似的△DEF最长的一边是36,则△DEF最短的一边是( )
A.72 B.18 C.12 D.20
答案:B
解析:解答:设△DEF最短的一边是x,
∵△ABC中,AB=12,BC=18,CA=24,另一个和它相似的△DEF最长的一边是36,
∴= ,
解得:x=18.
故选B.
分析:设△DEF最短的一边是x,由相似三角形的性质得到 = ,即可求出x,得到△DEF最短的边.
5. 平面直角坐标中,已知点O(0,0),A(0,2),B(1,0),点P是反比例函数y=-
图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( )
A.1个 B.2个 C.3个 D.4个
答案:D
解析:解答:∵点P是反比例函数y=-图象上,
∴设点P(x,y),
当△PQO∽△AOB时,则=,
又PQ=y,OQ=-x,OA=2,OB=1,
即=,即y=-2x,
∵xy=-1,即-2x2=-1,
∴x=±,
∴点P为(,-)或(-,);
同理,当△PQO∽△BOA时,
求得P(-,)或(,-);
故相应的点P共有4个.
故选:D.
分析:可以分别从△PQO∽△AOB与△PQO∽△BOA去分析,首先设点P(x,y),根据相似三角形的对应边成比例与反比例函数的解析式,联立可得方程组,解方程组即可求得点P的坐标,即可求得答案.
6. △ABC∽△A′B′C′,且∠A=68°,则∠A′=( )
A.22° B.44° C.68° D.80°
答案:C
解析:解答:因为△ABC∽△A′B′C′,则∠A与∠A′是对应角,根据相似三角形的性质得到∠A=∠A′=68°,故选C.
分析:根据相似三角形的对应角相等即可求得∠A′的度数.
7. 如图,若△ACD∽△ABC,以下4个等式错误的是( )
A. B. C.CD2=AD DB D.AC2=AD AB
答案:C
解析:解答:∵△ACD∽△ABC,
∴==;
A.= =,故A正确;
B.= =,故B正确;
C.CD2=AD DB =,与相似三角形所得结论不符,故C错误;
D.AC2=AD AB =,故D正确;
故选C.
分析:可根据相似三角形的对应边成比例来进行判断.
8. △ABC和△DEF相似,且相似比为,那么它们的周长比是( )
A. B. C. D.
答案:A
解析:解答:∵△ABC∽△A′B′C′,它们的相似比为2:3,
∴它们的周长比是2:3.
故选A.
分析:根据相似三角形性质,相似三角形周长的比等于相似比可求.
9.点D、E分别在△ABC的边AB、AC上,AD=2,DB=8,AC=5.若△ADE与△ABC相似,则AE的长为( )
A.1.25 B.1 C.4 D.1或4
答案:D
解析:解答:①若∠AED对应∠B时,=,即=,
解得AE=4;
②当∠ADE对应∠B时,= ,即= ,
解得AE=1.
故选D.
分析:由于△ADE与△ABC相似,但其对应角不能确定,所以应分两种情况进行讨论.
10.如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12.在AB上取一点E.使A、D、E三点组成的三角形与△ABC相似,则AE的长为( )
A.16 B.14 C.16或14 D.16或9
答案:D
解析:解答:本题分两种情况:
①△ADE∽△ACB
∴
∵AB=24,AC=18,AD=12,
∴AE=16;
②△ADE∽△ABC
∴
∵AB=24,AC=18,AD=12,
∴AE=9.
故选D
分析:本题应分两种情况进行讨论,①△ABC∽△AED;②△ABC∽△ADE;可根据各相似三角形得出的关于AE、AE、AB、AC四条线段的比例关系式求出AE的长.
11. 如图,Rt△ABC∽Rt△DEF,∠A=35°,则∠E的度数为( )
A.35° B.45° C.55° D.65°
答案:C
解析:解答:∵Rt△ABC∽Rt△DEF,∠A=35°,
∴∠D=∠A=35°.
∵∠F=90°,
∴∠E=55°.
故选C.
分析:由Rt△ABC∽Rt△DEF,∠A=35°,根据相似三角形的对应角相等,即可求得∠D的度数,又由∠F=90°,即可求得∠E的度数.
12. 如图,已知△ACD∽△ABC,∠1=∠B,下列各式正确的是( )
A. = =
B.= =
C.==
D.==
答案:B
解析:解答:∵△ACD∽△ABC,
∴= =.
故选B.
分析:根据相似三角形的性质:相似三角形的对应边成比例作答.
13. 若△ABC与△DEF的相似比是3:2,△DEF的最长边是6cm,那么△ABC的最长边是( )
A.4cm B.9cm C.4cm或9cm D.以上答案都不对
答案:B
解析:解答:∵△ABC与△DEF的相似比是3:2,△DEF的最长边是6cm,
∴△ABC的最长边:△DEF的最长边=3:2,
即△ABC的最长边是9cm.
故选B.
分析:根据相似三角形的相似比的概念,即对应边的比即为相似比,进行求解.
14. 若△ABC∽△A B C ,∠A=40°,∠B=110°,则∠C =( )
A.40° B.110° C.70° D.30°
答案:D
解析:解答:∵∠A=40°,∠B=110°,
∴∠C=180°-∠A-∠B=180°-40°-110°=30°
又∵△ABC∽△A B C ,
∴∠C =∠C=30°.
故选D.
分析:根据相似三角形的性质:相似三角形的对应角相等,即可解答.
15. 如图,在5×5的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上,作一个与△ABC相似的△DEF,使它的三个顶点都在小正方形的顶点上,则△DEF的最大面积是( )
A.5 B.10 C. D.
答案:A
解析:解答:从图中可以看出△ABC的三边分别是2,,,
要让△ABC的相似三角形最大,就要让DF为网格最大的对角线,即是,
所以这两,相似三角形的相似比是:=:5
△ABC的面积为2×1÷2=1,
所以△DEF的最大面积是5.故选A.
分析:要让△ABC的相似三角形最大,就要让AC为网格最大的对角线,据此可根据相似三角形的性质解答.
二、填空题
16. 已知△ABC∽△DEF,∠A=∠D,∠C=∠F且AB:DE=1:2,则EF:BC= 2:1.
答案:2:1
解析:解答:∵△ABC∽△DEF,∠A=∠D,∠C=∠F,
∴==,
∵AB:DE=1:2,
∴EF:BC=2:1,
故答案为2:1.
分析:利用相似三角形的对应边的比相等可以求得两条线段的比.
17. 若两个三角形相似,其中一个三角形的两个角分别为60°、50°,则另一个三角形的最小的内角为 50度.
答案:50
解析:解答:∵一个三角形的两个角分别为60°、50°,
∴另一个角为180°-(60°+50°)=70°,
∴三角形的最小的内角为50°.
∵两个三角形相似,
∴相似的另一个三角形的最小的内角为50°.
分析:先求出三角形的另一个角,比较后得出三角形的最小的内角为50°.再根据相似三角形的性质得出结论.
18. 已知△ABC∽△A′B′C′,∠A=50°,则∠A的对应角∠A′= 50度.
答案:50
解析:解答:∵△ABC∽△A′B′C′,∠A=50°,
∴∠A′=50度.
分析:根据相似三角形的对应角相等解答.
19. 如图,已知△ABC∽△DEF,且相似比为k,则k= ,直线y=kx+k的图象必经过 一、二、三
象限.
答案:|一、二、三
解析:解答:k===,
∴=k,
∴c=(a+b)k,
b=(a+c)k,
a=(c+b)k,
相加得:(a+b+c)=2k(a+b+c),
当a+b+c=0时,k===-1,
∵相似比是k,∴k=-1舍去;
当a+b+c≠0时,k=,此时y=x+图象经过一、二、三象限;
故答案为:,一、二、三.
分析:根据相似比的定义得出=k,推出c=(a+b)k,b=(a+c)k,a=(c+b)k,求出k的值,即可求出答案.
20. 已知:△ABC∽△A′B′C′,△ABC的三边之比为3:4:5.若△A′B′C′的最长边为20cm,则它的最短边长为 12cm.
答案:12
解析:解答:设△A′B′C′的最短的边是x,
根据相似三角形的对应边的比相等,
得到x:20=3:5,
解得:x=12cm.
它的最短边长为12cm.
分析:设△A′B′C′的最短的边是x,根据相似三角形的性质,可得x:20=3:5,解方程即可.
三、解答题
21. 如图,已知△ABC中,AB=8,BC=7,AC=6,点D、E分别在AB、AC上,如果以A、D、E为顶点的三角形和△ABC相似,且相似比为 ,试求AD、AE的长.
答案:解答:当△ABC∽△ADE时,相似比为,==,
即:==,
解得:AD=2,AE=1.5;
当△ABC∽△AED时,
==,
即:==,
解得:AD=1.5,AE=2.
分析:利用三角形相似的性质分△ABC∽△ADE和△ABC∽△AED两种情况讨论即可求得AD、AE的长.
22. 一个三角形三边长分别为5cm,8cm,12cm,另一个与它相似的三角形的最长边为4.8cm,求另外两边长.
答案:解答:设另一个三角形的两边长是xcm,ycm,由题意,得:
x:5=y:8=4.8:12,
解得x=2cm,y=3.2cm.
因此另两条边的边长为2cm,3.2cm.
分析:根据两个相似三角形的最长边的值,可求出它们的相似比,由此可求出另两条边的长.
23. 已知:如图,△ABC∽△ADE,∠A=45°,∠C=40°.求:∠ADE的度数.
答案:解答:∵△ABC∽△ADE,∠C=40°,
∴∠AED=∠C=40°.
在△ADE中,
∵∠AED+∠ADE+∠A=180°,∠A=45°
即40°+∠ADE+45°=180°,
∴∠ADE=95°.
分析:由△ABC∽△ADE,∠C=40°,根据相似三角形的对应角相等,即可求得∠AED的度数,又由三角形的内角和等于180°,即可求得∠ADE的度数.
24. 如图,点D、E分别在△ABC的边AB、AC上,且AB=9,AC=6,AD=3,若使△ADE与△ABC相似,求AE的长.
答案:解答:①若∠AED对应∠B时,
=,即=,
解得AE=;
②当∠ADE对应∠B时,
=,即=,
解得AE=2.
所以AE的长为2或.
分析:由于△ADE与△ABC相似,但其对应角不能确定,所以应分两种情况进行讨论.
25. 如图,在△ABC中,AB=6cm,AC=12cm,动点M从点A出发,以1cm∕秒的速度向点B运动,动点N从点C出发,以2cm∕秒的速度向点A运动,若两点同时运动,是否存在某一时刻t,使得以点A、M、N为顶点的三角形与△ABC相似,若存在,求出t的值;若不存在,请说明理由.
答案:解答:存在t=3秒或4.8秒,使以点A、M、N为顶点的三角形与△ABC相似(无此过程不扣分)
设经过t秒时,△AMN与△ABC相似,
此时,AM=t,CN=2t,AN=12-2t(0≤t≤6),
(1)当MN∥BC时,△AMN∽△ABC,
则=,即=,
解得t=3;
(2)当∠AMN=∠C时,△ANM∽△ABC,
则=,即 = ,
解得t=4.8;
故所求t的值为3秒或4.8秒.
分析:首先设经过t秒时,△AMN与△ABC相似,可得AM=t,CN=2t,AN=12-2t(0≤t≤6),然后分别从当MN∥BC时,△AMN∽△ABC与当∠AMN=∠C时,△ANM∽△ABC去分析,根据相似三角形的对应边成比例即可求得答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 12 页 (共 12 页) 版权所有@21世纪教育网
华师大版数学九年级上册第23章第3节 23.3.1相似三角形
课时作业
一、选择题
1. 若△ABC∽△A′B′C′且 = ,△ABC的周长为15cm,则△A′B′C′的周长为( )
A.18 B.20 C. D.
答案:B
解析:解答:∵△ABC∽△A′B′C′,
∴= =
∴==,
∵△ABC的周长为15cm,
∴△A′B′C′的周长为20cm.
故选B.
分析:根据比例的等比性质可得相似三角形周长的比等于相似比,可得 == ,由△ABC的周长为15cm,即可求得△A′B′C′的周长.
2. 一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则其它两边的和是( )
A.19 B.17 C.24 D.21
答案:C
解析:解答:设另一个三角形的最短边为x,第二短边为y,根据相似三角形的三边对应成比例,知==,
∴x=9,y=15,
∴x+y=24.
故选C.
分析:根据相似三角形的性质三边对应成比例作答即.
3. 如图,△ADE∽△ABC,若AD=1,BD=2,则△ADE与△ABC的相似比是( )
A.1:2 B.1:3 C.2:3 D.3:2
答案:B
解析:解答:∵AD=1,BD=2,
∴AB=AD+BD=3.
∵△ADE∽△ABC,
∴AD:AB=1:3.
∴△ADE与△ABC的相似比是1:3.
故选B.
分析:根据相似三角形的性质,相似三角形的相似比等于对应边的比.
4. 在△ABC中,AB=12,BC=18,CA=24,另一个和它相似的△DEF最长的一边是36,则△DEF最短的一边是( )
A.72 B.18 C.12 D.20
答案:B
解析:解答:设△DEF最短的一边是x,
∵△ABC中,AB=12,BC=18,CA=24,另一个和它相似的△DEF最长的一边是36,
∴= ,
解得:x=18.
故选B.
分析:设△DEF最短的一边是x,由相似三角形的性质得到 = ,即可求出x,得到△DEF最短的边.
5. 平面直角坐标中,已知点O(0,0),A(0,2),B(1,0),点P是反比例函数y=-
图象上的一个动点,过点P作PQ⊥x轴,垂足为Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( )
A.1个 B.2个 C.3个 D.4个
答案:D
解析:解答:∵点P是反比例函数y=-图象上,
∴设点P(x,y),
当△PQO∽△AOB时,则=,
又PQ=y,OQ=-x,OA=2,OB=1,
即=,即y=-2x,
∵xy=-1,即-2x2=-1,
∴x=±,
∴点P为(,-)或(-,);
同理,当△PQO∽△BOA时,
求得P(-,)或(,-);
故相应的点P共有4个.
故选:D.
分析:可以分别从△PQO∽△AOB与△PQO∽△BOA去分析,首先设点P(x,y),根据相似三角形的对应边成比例与反比例函数的解析式,联立可得方程组,解方程组即可求得点P的坐标,即可求得答案.
6. △ABC∽△A′B′C′,且∠A=68°,则∠A′=( )
A.22° B.44° C.68° D.80°
答案:C
解析:解答:因为△ABC∽△A′B′C′,则∠A与∠A′是对应角,根据相似三角形的性质得到∠A=∠A′=68°,故选C.
分析:根据相似三角形的对应角相等即可求得∠A′的度数.
7. 如图,若△ACD∽△ABC,以下4个等式错误的是( )
A. B. C.CD2=AD DB D.AC2=AD AB
答案:C
解析:解答:∵△ACD∽△ABC,
∴==;
A.= =,故A正确;
B.= =,故B正确;
C.CD2=AD DB =,与相似三角形所得结论不符,故C错误;
D.AC2=AD AB =,故D正确;
故选C.
分析:可根据相似三角形的对应边成比例来进行判断.
8. △ABC和△DEF相似,且相似比为,那么它们的周长比是( )
A. B. C. D.
答案:A
解析:解答:∵△ABC∽△A′B′C′,它们的相似比为2:3,
∴它们的周长比是2:3.
故选A.
分析:根据相似三角形性质,相似三角形周长的比等于相似比可求.
9.点D、E分别在△ABC的边AB、AC上,AD=2,DB=8,AC=5.若△ADE与△ABC相似,则AE的长为( )
A.1.25 B.1 C.4 D.1或4
答案:D
解析:解答:①若∠AED对应∠B时,=,即=,
解得AE=4;
②当∠ADE对应∠B时,= ,即= ,
解得AE=1.
故选D.
分析:由于△ADE与△ABC相似,但其对应角不能确定,所以应分两种情况进行讨论.
10.如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12.在AB上取一点E.使A、D、E三点组成的三角形与△ABC相似,则AE的长为( )
A.16 B.14 C.16或14 D.16或9
答案:D
解析:解答:本题分两种情况:
①△ADE∽△ACB
∴
∵AB=24,AC=18,AD=12,
∴AE=16;
②△ADE∽△ABC
∴
∵AB=24,AC=18,AD=12,
∴AE=9.
故选D
分析:本题应分两种情况进行讨论,①△ABC∽△AED;②△ABC∽△ADE;可根据各相似三角形得出的关于AE、AE、AB、AC四条线段的比例关系式求出AE的长.
11. 如图,Rt△ABC∽Rt△DEF,∠A=35°,则∠E的度数为( )
A.35° B.45° C.55° D.65°
答案:C
解析:解答:∵Rt△ABC∽Rt△DEF,∠A=35°,
∴∠D=∠A=35°.
∵∠F=90°,
∴∠E=55°.
故选C.
分析:由Rt△ABC∽Rt△DEF,∠A=35°,根据相似三角形的对应角相等,即可求得∠D的度数,又由∠F=90°,即可求得∠E的度数.
12. 如图,已知△ACD∽△ABC,∠1=∠B,下列各式正确的是( )
A. = =
B.= =
C.==
D.==
答案:B
解析:解答:∵△ACD∽△ABC,
∴= =.
故选B.
分析:根据相似三角形的性质:相似三角形的对应边成比例作答.
13. 若△ABC与△DEF的相似比是3:2,△DEF的最长边是6cm,那么△ABC的最长边是( )
A.4cm B.9cm C.4cm或9cm D.以上答案都不对
答案:B
解析:解答:∵△ABC与△DEF的相似比是3:2,△DEF的最长边是6cm,
∴△ABC的最长边:△DEF的最长边=3:2,
即△ABC的最长边是9cm.
故选B.
分析:根据相似三角形的相似比的概念,即对应边的比即为相似比,进行求解.
14. 若△ABC∽△A B C ,∠A=40°,∠B=110°,则∠C =( )
A.40° B.110° C.70° D.30°
答案:D
解析:解答:∵∠A=40°,∠B=110°,
∴∠C=180°-∠A-∠B=180°-40°-110°=30°
又∵△ABC∽△A B C ,
∴∠C =∠C=30°.
故选D.
分析:根据相似三角形的性质:相似三角形的对应角相等,即可解答.
15. 如图,在5×5的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上,作一个与△ABC相似的△DEF,使它的三个顶点都在小正方形的顶点上,则△DEF的最大面积是( )
A.5 B.10 C. D.
答案:A
解析:解答:从图中可以看出△ABC的三边分别是2,,,
要让△ABC的相似三角形最大,就要让DF为网格最大的对角线,即是,
所以这两,相似三角形的相似比是:=:5
△ABC的面积为2×1÷2=1,
所以△DEF的最大面积是5.故选A.
分析:要让△ABC的相似三角形最大,就要让AC为网格最大的对角线,据此可根据相似三角形的性质解答.
二、填空题
16. 已知△ABC∽△DEF,∠A=∠D,∠C=∠F且AB:DE=1:2,则EF:BC= 2:1.
答案:2:1
解析:解答:∵△ABC∽△DEF,∠A=∠D,∠C=∠F,
∴==,
∵AB:DE=1:2,
∴EF:BC=2:1,
故答案为2:1.
分析:利用相似三角形的对应边的比相等可以求得两条线段的比.
17. 若两个三角形相似,其中一个三角形的两个角分别为60°、50°,则另一个三角形的最小的内角为 50度.
答案:50
解析:解答:∵一个三角形的两个角分别为60°、50°,
∴另一个角为180°-(60°+50°)=70°,
∴三角形的最小的内角为50°.
∵两个三角形相似,
∴相似的另一个三角形的最小的内角为50°.
分析:先求出三角形的另一个角,比较后得出三角形的最小的内角为50°.再根据相似三角形的性质得出结论.
18. 已知△ABC∽△A′B′C′,∠A=50°,则∠A的对应角∠A′= 50度.
答案:50
解析:解答:∵△ABC∽△A′B′C′,∠A=50°,
∴∠A′=50度.
分析:根据相似三角形的对应角相等解答.
19. 如图,已知△ABC∽△DEF,且相似比为k,则k= ,直线y=kx+k的图象必经过 一、二、三
象限.
答案:|一、二、三
解析:解答:k===,
∴=k,
∴c=(a+b)k,
b=(a+c)k,
a=(c+b)k,
相加得:(a+b+c)=2k(a+b+c),
当a+b+c=0时,k===-1,
∵相似比是k,∴k=-1舍去;
当a+b+c≠0时,k=,此时y=x+图象经过一、二、三象限;
故答案为:,一、二、三.
分析:根据相似比的定义得出=k,推出c=(a+b)k,b=(a+c)k,a=(c+b)k,求出k的值,即可求出答案.
20. 已知:△ABC∽△A′B′C′,△ABC的三边之比为3:4:5.若△A′B′C′的最长边为20cm,则它的最短边长为 12cm.
答案:12
解析:解答:设△A′B′C′的最短的边是x,
根据相似三角形的对应边的比相等,
得到x:20=3:5,
解得:x=12cm.
它的最短边长为12cm.
分析:设△A′B′C′的最短的边是x,根据相似三角形的性质,可得x:20=3:5,解方程即可.
三、解答题
21. 如图,已知△ABC中,AB=8,BC=7,AC=6,点D、E分别在AB、AC上,如果以A、D、E为顶点的三角形和△ABC相似,且相似比为 ,试求AD、AE的长.
答案:解答:当△ABC∽△ADE时,相似比为,==,
即:==,
解得:AD=2,AE=1.5;
当△ABC∽△AED时,
==,
即:==,
解得:AD=1.5,AE=2.
分析:利用三角形相似的性质分△ABC∽△ADE和△ABC∽△AED两种情况讨论即可求得AD、AE的长.
22. 一个三角形三边长分别为5cm,8cm,12cm,另一个与它相似的三角形的最长边为4.8cm,求另外两边长.
答案:解答:设另一个三角形的两边长是xcm,ycm,由题意,得:
x:5=y:8=4.8:12,
解得x=2cm,y=3.2cm.
因此另两条边的边长为2cm,3.2cm.
分析:根据两个相似三角形的最长边的值,可求出它们的相似比,由此可求出另两条边的长.
23. 已知:如图,△ABC∽△ADE,∠A=45°,∠C=40°.求:∠ADE的度数.
答案:解答:∵△ABC∽△ADE,∠C=40°,
∴∠AED=∠C=40°.
在△ADE中,
∵∠AED+∠ADE+∠A=180°,∠A=45°
即40°+∠ADE+45°=180°,
∴∠ADE=95°.
分析:由△ABC∽△ADE,∠C=40°,根据相似三角形的对应角相等,即可求得∠AED的度数,又由三角形的内角和等于180°,即可求得∠ADE的度数.
24. 如图,点D、E分别在△ABC的边AB、AC上,且AB=9,AC=6,AD=3,若使△ADE与△ABC相似,求AE的长.
答案:解答:①若∠AED对应∠B时,
=,即=,
解得AE=;
②当∠ADE对应∠B时,
=,即=,
解得AE=2.
所以AE的长为2或.
分析:由于△ADE与△ABC相似,但其对应角不能确定,所以应分两种情况进行讨论.
25. 如图,在△ABC中,AB=6cm,AC=12cm,动点M从点A出发,以1cm∕秒的速度向点B运动,动点N从点C出发,以2cm∕秒的速度向点A运动,若两点同时运动,是否存在某一时刻t,使得以点A、M、N为顶点的三角形与△ABC相似,若存在,求出t的值;若不存在,请说明理由.
答案:解答:存在t=3秒或4.8秒,使以点A、M、N为顶点的三角形与△ABC相似(无此过程不扣分)
设经过t秒时,△AMN与△ABC相似,
此时,AM=t,CN=2t,AN=12-2t(0≤t≤6),
(1)当MN∥BC时,△AMN∽△ABC,
则=,即=,
解得t=3;
(2)当∠AMN=∠C时,△ANM∽△ABC,
则=,即 = ,
解得t=4.8;
故所求t的值为3秒或4.8秒.
分析:首先设经过t秒时,△AMN与△ABC相似,可得AM=t,CN=2t,AN=12-2t(0≤t≤6),然后分别从当MN∥BC时,△AMN∽△ABC与当∠AMN=∠C时,△ANM∽△ABC去分析,根据相似三角形的对应边成比例即可求得答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 12 页 (共 12 页) 版权所有@21世纪教育网
