华师大版数学九年级上册第23章 23.3.2相似三角形的判定课时作业
文档属性
| 名称 | 华师大版数学九年级上册第23章 23.3.2相似三角形的判定课时作业 |  | |
| 格式 | docx | ||
| 文件大小 | 255.6KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 15:30:02 | ||
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学九年级上册第23章第3节23.3.2相似三角形的判定
课时作业
一、选择题
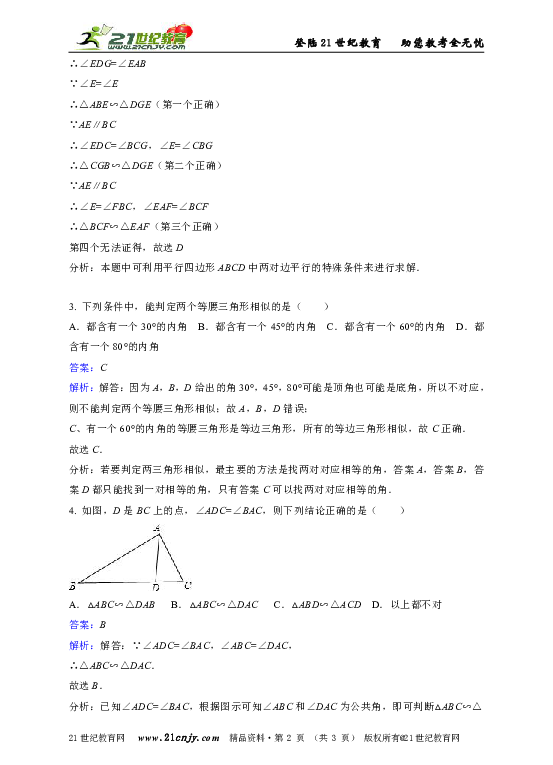
1. 如图,在大小为4×4的正方形网格中,是相似三角形的是( )
A.①和② B.②和③ C.①和③ D.②和④
答案:C
解析:解答:①和③相似,
∵由勾股定理求出①的三角形的各边长分别为2、、;
由勾股定理求出③的各边长分别为2、2、2,
∴=,=,
即==,
∴两三角形的三边对应边成比例,
∴①③相似.
故选C.
分析:本题主要应用两三角形相似的判定定理,有两个对应角相等的三角形相似,即可完成题目.
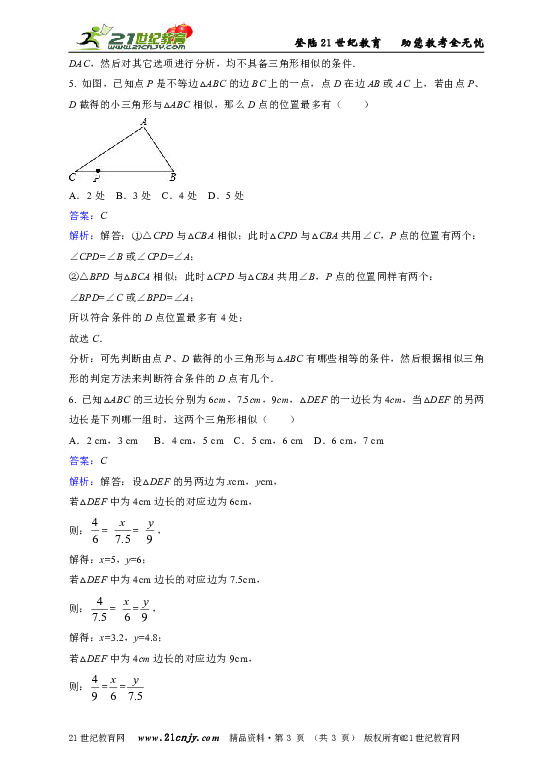
2. 如图,□ABCD中,E是AD延长线上一点,BE交AC于点F,交DC于点G,则下列结论中错误的是( )
A.△ABE∽△DGE B.△CGB∽△DGE C.△BCF∽△EAF D.△ACD∽△GCF
答案:D
解析:解答:∵四边形ABCD是平行四边形
∴AB∥CD
∴∠EDG=∠EAB
∵∠E=∠E
∴△ABE∽△DGE(第一个正确)
∵AE∥BC
∴∠EDC=∠BCG,∠E=∠CBG
∴△CGB∽△DGE(第二个正确)
∵AE∥BC
∴∠E=∠FBC,∠EAF=∠BCF
∴△BCF∽△EAF(第三个正确)
第四个无法证得,故选D
分析:本题中可利用平行四边形ABCD中两对边平行的特殊条件来进行求解.
3. 下列条件中,能判定两个等腰三角形相似的是( )
A.都含有一个30°的内角 B.都含有一个45°的内角 C.都含有一个60°的内角 D.都含有一个80°的内角
答案:C
解析:解答:因为A,B,D给出的角30°,45°,80°可能是顶角也可能是底角,所以不对应,则不能判定两个等腰三角形相似;故A,B,D错误;
C、有一个60°的内角的等腰三角形是等边三角形,所有的等边三角形相似,故C正确.
故选C.
分析:若要判定两三角形相似,最主要的方法是找两对对应相等的角,答案A,答案B,答案D都只能找到一对相等的角,只有答案C可以找两对对应相等的角.
4. 如图,D是BC上的点,∠ADC=∠BAC,则下列结论正确的是( )
A.△ABC∽△DAB B.△ABC∽△DAC C.△ABD∽△ACD D.以上都不对
答案:B
解析:解答:∵∠ADC=∠BAC,∠ABC=∠DAC,
∴△ABC∽△DAC.
故选B.
分析:已知∠ADC=∠BAC,根据图示可知∠ABC和∠DAC为公共角,即可判断△ABC∽△DAC,然后对其它选项进行分析,均不具备三角形相似的条件.
5. 如图,已知点P是不等边△ABC的边BC上的一点,点D在边AB或AC上,若由点P、D截得的小三角形与△ABC相似,那么D点的位置最多有( )
A.2处 B.3处 C.4处 D.5处
答案:C
解析:解答:①△CPD与△CBA相似;此时△CPD与△CBA共用∠C,P点的位置有两个:
∠CPD=∠B或∠CPD=∠A;
②△BPD与△BCA相似;此时△CPD与△CBA共用∠B,P点的位置同样有两个:
∠BPD=∠C或∠BPD=∠A;
所以符合条件的D点位置最多有4处;
故选C.
分析:可先判断由点P、D截得的小三角形与△ABC有哪些相等的条件,然后根据相似三角形的判定方法来判断符合条件的D点有几个.
6. 已知△ABC的三边长分别为6cm,7.5cm,9cm,△DEF的一边长为4cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm B.4 cm,5 cm C.5 cm,6 cm D.6 cm,7 cm
答案:C
解析:解答:设△DEF的另两边为xcm,ycm,
若△DEF中为4cm边长的对应边为6cm,
则:= = ,
解得:x=5,y=6;
若△DEF中为4cm边长的对应边为7.5cm,
则:= =,
解得:x=3.2,y=4.8;
若△DEF中为4cm边长的对应边为9cm,
则:==
解得:x=,y=;
故选C.
分析:根据三边对应成比例的三角形相似,即可求得.注意△DEF中为4cm边长的对应边可能是6cm或7.5cm或9cm,所以有三种情况.
7. 如图,在正△ABC中,D、E分别在AC、AB上,且 = ,AE=BE,则有( )
A.△AED∽△ABC B.△ADB∽△BED C.△BCD∽△ABC D.△AED∽△CBD
答案:D
解析:解答:∵△ABC是等边三角形,=,
∴AB=BC=AC,∠A=∠C,
设AD=x,AC=3x,
则BC=3x,CD=2x,
∵AE=BE=x,
∴=,=,
∴=,
∴△AED∽△CBD;
故选:D.
分析:根据等边三角形的性质得出角相等,再由已知条件求出 =
即两边对应成比例并且夹角相等,因此两个三角形相似.
8. 如图,△ACD和△ABC相似需具备的条件是( )
A. =
B. =
C.AC2=AD AB
D.=AD BD
答案:C
解析:解答:∵在△ACD和△ABC中,∠A=∠A,
∴根据有两边对应成比例,且夹角相等的两三角形相似,得出添加的条件是:= ,
∴AC2=AD AB.
故选C.
分析:题目中隐含条件∠A=∠A,根据有两边对应成比例,且夹角相等的两三角形相似,得出添加的条件只能是 = ,根据比例性质即可推出答案.
9. 下列条件,不能判定△ABC与△DEF相似的是( )
A.∠C=∠F=90°,∠A=55°,∠D=35°
B.∠C=∠F=90°,AB=10,BC=6,DE=15,EF=9
C.∠C=∠F=90°, =
D.∠B=∠E=90°,=
答案:D
解析:解答:A相似:∵∠A=55°∴∠B=90°-55°=35°∵∠D=35°∴∠B=∠D∵∠C=∠F∴△ABC∽△DEF
B相似:∵AB=10,BC=6,DE=15,EF=9,= = ,==
∴=
∵∠C=∠F∴△ABC∽△DEF
C相似:∵∠C=∠F=90°, =
∴△ABC∽△DEF
D不相似:
∵=,有一组角相等两边对应成比例,但该组角不是这两边的夹角,故不相似.
故选D.
分析:根据相似三角形的判定方法对各个选项进行分析即可.
10. 下列命题正确的有( )个
①40°角为内角的两个等腰三角形必相似;
②若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为75°;
③一组对边平行,另一组对边相等的四边形是平行四边形;
④一个等腰直角三角形的三边是a、b、c,(a>b=c),那么a2:b2:c2=2:1:1;
⑤若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c,则此△为等腰直角三角形.
A.1个 B.2个 C.3个 D.4个
答案:A
解析:解答:①40°角为内角两个等腰三角形有2种情况,
一是顶角为40°的一个等腰三角形,二是底角为40°的一个等腰三角形,那么这两个三角形不相似,所以此结论不正确;
②高在内部时,顶角为30度,底角75度高在外部时,顶角的外角30度,底角15度.所以有2种情况:15度或75度,所以此结论不正确;
③一组对边平行,另一组对边相等的四边形也可以是梯形,所以此结论不正确;
④∵一个等腰直角三角形的三边是a、b、c,(a>b=c),
∴a为等腰直角三角形的斜边,
∴a2=2b2=2c2
∴a2:b2:c2=2:1:1;
∴此结论正确;
⑤∵a2+b2+c2=10a+24b+26c-338,∴(a-5)2+(b-12)2+(c-13)2=0,
∴a-5=0,b-12=0,c-13=0,即a=5,b=12,c=13.
∵52+122=132,
∴△ABC是直角三角形.而不是等腰直角三角形.
∴此结论不正确;
因此命题正确的有1个.
故选A.
分析:根据三角形的内角和定理,平行四边形的判定定理,相似三角形的判定定理,等腰三角形的性质,等腰直角三角形的性质,配方法的应用对5个结论逐一分析即可.
11. 下列各组图形必相似的是( )
A.任意两个等腰三角形
B.有两边对应成比例,且有一个角对应相等的两三角形
C.两边为4和5的直角三角形与两边为8和10的直角三角形
D.两边及其中一边上的中线对应成比例的两三角形
答案:D
解析:解答:A、任意两个等腰三角形,各内角的值不确定,故无法证明三角形相似,故本选项错误;
B、两边对应成比例,必须夹角相等才能判定三角形相似,故本选项错误;
C、两边为4和5的直角三角形与两边为8和10的直角三角形,因为不确定边长为5和边长为10的边是斜边,故无法判定三角形相似,故本选项错误;
D、两边和一边的中线均对应成比例,即可判定两三角形中对应成比例的边的夹角相等,因此可判定三角形相似,正确,
故选D.
分析:分别根据相似三角形的判定判断A、B、C、D是否可以证明相似三角形,即可判断A、B、C、D选项的正确性,即可解题.
12. 如图,锐角△ABC中,BE,CD是高,它们相交于O,则图中与△BOD相似的三角形有( )
A.4个 B.3个 C.2个 D.1个
答案:B
解析:解答:①∵∠BDO=90°,∠BEA=90°
∴∠BDO=∠BEA
∴△BOD∽△BAE
②∵∠BDO=90°,∠CDA=90°
∴∠BDO=∠CDA
∴△BOD∽△CAD
③∵∠BDO=90°,∠CEO=90
∴∠BDO=∠CEO
∴△BOD∽△COE
∴有3个
故选B.
分析:根据已知及相似三角形的判定方法从而找到图中存在的相似三角形即可.
13. 下列4组条件中,能判定△ABC∽△DEF的是( )
A.AB=5,BC=4,∠A=45°;DE=10,EF=8,∠D=45°
B.∠A=45°,∠B=55°;∠D=45°,∠F=75°
C.BC=4,AC=6,AB=9;DE=18,EF=8,DF=12
D.AB=6,BC=5,∠B=40°;DE=5,EF=4,∠E=40°
答案:C
解析:解答:
A.= = ,夹角是∠B和∠E,两角不一定相等,故本选项错误;
B.应符合∠A=∠D=45°,∠B和∠E相等才能证两三角形相似,故本选项错误;
C.根据===,得到两三角形相似,故本选项正确;
D.∠B=∠E=40°,但夹此角的两边不成比例,故本选项错误;
故选C.
分析:根据已知条件推出证三角形相似的条件,根据相似三角形的判定判断即可.
14. 如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有( )
A.4对 B.5对 C.6对 D.7对
答案:B
解析:解答:图中相似三角形有△ABC∽△CDA,△AGE∽△ABC,△AFE∽△CBE,△BGE∽△BAF,△AGE∽△CDA共5对,
理由是:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,AB=CD,∠D=∠ABC,
∴△ABC≌△CDA,即△ABC∽△CDA,
∵GE∥BC,
∴△AGE∽△ABC∽△CDA,
∵GE∥BC,AD∥BC,
∴GE∥AD,
∴△BGE∽△BAF,
∵AD∥BC,
∴△AFE∽△CBE.
故选B.
分析:根据平行四边形的性质得出AD∥BC,AB∥CD,AD=BC,AB=CD,∠D=∠ABC,推出△ABC≌△CDA,即可推出△ABC∽△CDA,根据相似三角形的判定定理:平行于三角形一边的直线截其它两边或其它两边的延长线,所截的三角形与原三角形相似即可推出其它各对三角形相似.
15. 如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB延长线于E,则图中一定相似的三角形是( )
A.△AED与△ACB B.△AEB与△ACD C.△BAE与△ACE D.△AEC与△DAC
答案:C
解析:解答:∵斜边中线长为斜边的一半,
∴AD=BD=CD,
∴∠C=∠DAC,
∵∠BAE+∠BAD=90°,∠DAC+∠BAD=90°,
∴∠BAE=∠DAC,
∴∠C=∠BAE,
∵∠E=∠E,
∴△BAE∽△ACE.
故选C
分析:根据等腰三角形底角相等的性质可得∠C=∠DAC,易证∠BAE=∠DAC,即可证明∠C=∠BAE,∴即可证明△AEB与△ACD.
二、填容题
16. 如图,AD是直角△ABC (∠C=90°)的角平分线,EF⊥AD于D,与AB及AC的延长线分别交于E,F,写出图中的一对全等三角形是 △AED和△AFD;一对相似三角形是 △AED和△DFC.
答案:△AED和△AFD|△AED和△DFC
解析:解答:∵AD是∠BAC的角平分线,∴∠DAE=∠DAF,
在△AED和△AFD中,DAE=DAF,AD=AD, ADE=ADF=,
∴△AED≌△AFD(ASA),
∴∠AED=∠DFC,
∵∠FDC+∠CDA=90°,∠CDA+∠CAD=90°,∠DAC=∠DAE,
∴∠FDC=∠DAE,
∴△AED∽△DFC(AA),
故答案为△AED≌△AFD、△AED∽△DFC.
分析:根据角平分线的性质可以求得∠DAE=∠DAF,易证△AED≌△AFD,得∠AED=∠DFC,再求得∠FDC=∠DAE即可判定△AED∽△DFC,即可解题.
17. △ABC中,D为AB上一点,E为AC上一点,添加一个条件 DE∥AC(只能填一个)可以使得△ABC与△ADE相似.
答案:DE∥AC
解析:解答:∵DE∥BC,
∴∠ADE=∠ABC,∠ACB=∠AED,
∴△ABC∽△ADE(AA),
故添加条件DE∥BC,可以证明△ABC∽△ADE.
故答案为:DE∥BC.
分析:添加DE∥BC,根据同位角相等的性质,可以求得∠ADE=∠ABC,∠ACB=∠AED,即可判定△ABC∽△ADE,即可解题.
18. △ABC和△A′B′C′中,∠A=60°,∠B=40°,∠A’=60°,当∠C′= 80°时,△ABC∽△A′B′C′.
答案:80°
解析:解答:∵∠A=60°,∠B=40°,
∴∠C=180°-60°-40°=80°,
∵△ABC∽△A′B′C′
∴∠C=∠C′=80°,
∴当∠C′=80°时,△ABC∽△A′B′C′.
故答案为:80°.
分析:利用两对对应角相等的三角形相似判定即可.
19. 如图,AB⊥CB于点B,AC⊥CD于点C,AB=6,AC=10,当CD= 时,△ABC∽△ACD.
答案:
解析:解答:∵AB⊥CB,AC⊥CD,AB=6,AC=10,
∴∠B=∠ACD=90°,BC=8,
∵△ABC∽△ACD
∴当AB:BC=AC:CD时
∴=,
解得CD=.
分析:根据已知,利用两组对应边的比相等且相应的夹角相等的两个三角形相似来判定,根据相似三角形的边对应成比例求得CD的长.
20. □ABCD中,点P在对角线BD上(不与点B,D重合),添加一个条件,使得△BCD与△ADP相似,这个条件可以是 ∠APD=∠C.
答案:∠APD=∠C
解析:解答:∵AD∥BC,
∴∠ADP=∠CBD,
∵∠APD=∠C,
∴∠DAP=∠CDB,
∴△BCD∽△ADP.
故答案为∠APD=∠C.
分析:根据平行四边形对边平行性质可得一堆角相等,让另两对角中有一对相等即可证明△BCD与△ADP相似.
三、解答题
21. 如图,D为△ABC内一点,E为△ABC外一点,且∠1=∠2,∠3=∠4,找出图中的两对相似三角形并说明理由.
答案:解答:△ABD∽△CBE,△ABC∽△DBE.
∵∠1=∠2,∠3=∠4,
∴△ABD∽△CBE,
∴=
∵∠1=∠2,
∴∠ABC=∠DBE,
∴△ABC∽△DBE
分析:根据相似三角形的判定定理:两角相等;对应边成比例且夹角相等即可证明.
22. 已知:在Rt△ABC中∠C=90°,CD为AB边上的高.
求证:Rt△ADC∽Rt△CDB.
答案:解答:∵CD为AB边上的高,
∴∠ADC=∠CDB=90°,
∵∠ACB=90°,
∴∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∵∠ADC=∠CDB=90°,
∴Rt△ADC∽Rt△CDB.
分析:求出∠ADC=∠CDB=90°,根据∠A+∠ACD=90°,∠ACD+∠BCD=90°,推出∠A=∠BCD,根据相似三角形的判定推出即可.
23. 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
答案:解答:(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
答案:解答:答:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC-∠BAD=∠CBA-∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
分析:(1)根据等边三角形各边长相等和各内角为60°的性质可以求证△ABD≌△BCE;
(2)根据全等三角形对应角相等性质可得∠BAD=∠CBE,进而可以求得∠EAF=∠EBA,即可求证△EAF∽△EBA,即可解题.
24. 如图,在△ABC和△ADE中,已知∠B=∠D,∠BAD=∠CAE,求证:△ABC∽△ADE.
答案:解答:如图,∵∠BAD=∠CAE,
∴∠BAD+∠BAE=∠CAE+∠BAE,即∠DAE=∠BAC.
又∵∠B=∠D,
∴△ABC∽△ADE.
分析:利用“两角法”来证:△ABC∽△ADE.
25. 如图,在△ABC中,已知AB=AC,D、E、B、C在同一条直线上,且AB2=BD CE,求证:△ABD∽△ECA.
答案:解答:∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
∵AB2=BD CE,
∴=,即=,
∴△ABD∽△ECA.
分析:由条件可得到∠ABD=∠ACE,结合AB2=BD CE和AB=AC,可得到 = ,即可证得结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 15 页 (共 15 页) 版权所有@21世纪教育网
华师大版数学九年级上册第23章第3节23.3.2相似三角形的判定
课时作业
一、选择题
1. 如图,在大小为4×4的正方形网格中,是相似三角形的是( )
A.①和② B.②和③ C.①和③ D.②和④
答案:C
解析:解答:①和③相似,
∵由勾股定理求出①的三角形的各边长分别为2、、;
由勾股定理求出③的各边长分别为2、2、2,
∴=,=,
即==,
∴两三角形的三边对应边成比例,
∴①③相似.
故选C.
分析:本题主要应用两三角形相似的判定定理,有两个对应角相等的三角形相似,即可完成题目.
2. 如图,□ABCD中,E是AD延长线上一点,BE交AC于点F,交DC于点G,则下列结论中错误的是( )
A.△ABE∽△DGE B.△CGB∽△DGE C.△BCF∽△EAF D.△ACD∽△GCF
答案:D
解析:解答:∵四边形ABCD是平行四边形
∴AB∥CD
∴∠EDG=∠EAB
∵∠E=∠E
∴△ABE∽△DGE(第一个正确)
∵AE∥BC
∴∠EDC=∠BCG,∠E=∠CBG
∴△CGB∽△DGE(第二个正确)
∵AE∥BC
∴∠E=∠FBC,∠EAF=∠BCF
∴△BCF∽△EAF(第三个正确)
第四个无法证得,故选D
分析:本题中可利用平行四边形ABCD中两对边平行的特殊条件来进行求解.
3. 下列条件中,能判定两个等腰三角形相似的是( )
A.都含有一个30°的内角 B.都含有一个45°的内角 C.都含有一个60°的内角 D.都含有一个80°的内角
答案:C
解析:解答:因为A,B,D给出的角30°,45°,80°可能是顶角也可能是底角,所以不对应,则不能判定两个等腰三角形相似;故A,B,D错误;
C、有一个60°的内角的等腰三角形是等边三角形,所有的等边三角形相似,故C正确.
故选C.
分析:若要判定两三角形相似,最主要的方法是找两对对应相等的角,答案A,答案B,答案D都只能找到一对相等的角,只有答案C可以找两对对应相等的角.
4. 如图,D是BC上的点,∠ADC=∠BAC,则下列结论正确的是( )
A.△ABC∽△DAB B.△ABC∽△DAC C.△ABD∽△ACD D.以上都不对
答案:B
解析:解答:∵∠ADC=∠BAC,∠ABC=∠DAC,
∴△ABC∽△DAC.
故选B.
分析:已知∠ADC=∠BAC,根据图示可知∠ABC和∠DAC为公共角,即可判断△ABC∽△DAC,然后对其它选项进行分析,均不具备三角形相似的条件.
5. 如图,已知点P是不等边△ABC的边BC上的一点,点D在边AB或AC上,若由点P、D截得的小三角形与△ABC相似,那么D点的位置最多有( )
A.2处 B.3处 C.4处 D.5处
答案:C
解析:解答:①△CPD与△CBA相似;此时△CPD与△CBA共用∠C,P点的位置有两个:
∠CPD=∠B或∠CPD=∠A;
②△BPD与△BCA相似;此时△CPD与△CBA共用∠B,P点的位置同样有两个:
∠BPD=∠C或∠BPD=∠A;
所以符合条件的D点位置最多有4处;
故选C.
分析:可先判断由点P、D截得的小三角形与△ABC有哪些相等的条件,然后根据相似三角形的判定方法来判断符合条件的D点有几个.
6. 已知△ABC的三边长分别为6cm,7.5cm,9cm,△DEF的一边长为4cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm B.4 cm,5 cm C.5 cm,6 cm D.6 cm,7 cm
答案:C
解析:解答:设△DEF的另两边为xcm,ycm,
若△DEF中为4cm边长的对应边为6cm,
则:= = ,
解得:x=5,y=6;
若△DEF中为4cm边长的对应边为7.5cm,
则:= =,
解得:x=3.2,y=4.8;
若△DEF中为4cm边长的对应边为9cm,
则:==
解得:x=,y=;
故选C.
分析:根据三边对应成比例的三角形相似,即可求得.注意△DEF中为4cm边长的对应边可能是6cm或7.5cm或9cm,所以有三种情况.
7. 如图,在正△ABC中,D、E分别在AC、AB上,且 = ,AE=BE,则有( )
A.△AED∽△ABC B.△ADB∽△BED C.△BCD∽△ABC D.△AED∽△CBD
答案:D
解析:解答:∵△ABC是等边三角形,=,
∴AB=BC=AC,∠A=∠C,
设AD=x,AC=3x,
则BC=3x,CD=2x,
∵AE=BE=x,
∴=,=,
∴=,
∴△AED∽△CBD;
故选:D.
分析:根据等边三角形的性质得出角相等,再由已知条件求出 =
即两边对应成比例并且夹角相等,因此两个三角形相似.
8. 如图,△ACD和△ABC相似需具备的条件是( )
A. =
B. =
C.AC2=AD AB
D.=AD BD
答案:C
解析:解答:∵在△ACD和△ABC中,∠A=∠A,
∴根据有两边对应成比例,且夹角相等的两三角形相似,得出添加的条件是:= ,
∴AC2=AD AB.
故选C.
分析:题目中隐含条件∠A=∠A,根据有两边对应成比例,且夹角相等的两三角形相似,得出添加的条件只能是 = ,根据比例性质即可推出答案.
9. 下列条件,不能判定△ABC与△DEF相似的是( )
A.∠C=∠F=90°,∠A=55°,∠D=35°
B.∠C=∠F=90°,AB=10,BC=6,DE=15,EF=9
C.∠C=∠F=90°, =
D.∠B=∠E=90°,=
答案:D
解析:解答:A相似:∵∠A=55°∴∠B=90°-55°=35°∵∠D=35°∴∠B=∠D∵∠C=∠F∴△ABC∽△DEF
B相似:∵AB=10,BC=6,DE=15,EF=9,= = ,==
∴=
∵∠C=∠F∴△ABC∽△DEF
C相似:∵∠C=∠F=90°, =
∴△ABC∽△DEF
D不相似:
∵=,有一组角相等两边对应成比例,但该组角不是这两边的夹角,故不相似.
故选D.
分析:根据相似三角形的判定方法对各个选项进行分析即可.
10. 下列命题正确的有( )个
①40°角为内角的两个等腰三角形必相似;
②若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为75°;
③一组对边平行,另一组对边相等的四边形是平行四边形;
④一个等腰直角三角形的三边是a、b、c,(a>b=c),那么a2:b2:c2=2:1:1;
⑤若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c,则此△为等腰直角三角形.
A.1个 B.2个 C.3个 D.4个
答案:A
解析:解答:①40°角为内角两个等腰三角形有2种情况,
一是顶角为40°的一个等腰三角形,二是底角为40°的一个等腰三角形,那么这两个三角形不相似,所以此结论不正确;
②高在内部时,顶角为30度,底角75度高在外部时,顶角的外角30度,底角15度.所以有2种情况:15度或75度,所以此结论不正确;
③一组对边平行,另一组对边相等的四边形也可以是梯形,所以此结论不正确;
④∵一个等腰直角三角形的三边是a、b、c,(a>b=c),
∴a为等腰直角三角形的斜边,
∴a2=2b2=2c2
∴a2:b2:c2=2:1:1;
∴此结论正确;
⑤∵a2+b2+c2=10a+24b+26c-338,∴(a-5)2+(b-12)2+(c-13)2=0,
∴a-5=0,b-12=0,c-13=0,即a=5,b=12,c=13.
∵52+122=132,
∴△ABC是直角三角形.而不是等腰直角三角形.
∴此结论不正确;
因此命题正确的有1个.
故选A.
分析:根据三角形的内角和定理,平行四边形的判定定理,相似三角形的判定定理,等腰三角形的性质,等腰直角三角形的性质,配方法的应用对5个结论逐一分析即可.
11. 下列各组图形必相似的是( )
A.任意两个等腰三角形
B.有两边对应成比例,且有一个角对应相等的两三角形
C.两边为4和5的直角三角形与两边为8和10的直角三角形
D.两边及其中一边上的中线对应成比例的两三角形
答案:D
解析:解答:A、任意两个等腰三角形,各内角的值不确定,故无法证明三角形相似,故本选项错误;
B、两边对应成比例,必须夹角相等才能判定三角形相似,故本选项错误;
C、两边为4和5的直角三角形与两边为8和10的直角三角形,因为不确定边长为5和边长为10的边是斜边,故无法判定三角形相似,故本选项错误;
D、两边和一边的中线均对应成比例,即可判定两三角形中对应成比例的边的夹角相等,因此可判定三角形相似,正确,
故选D.
分析:分别根据相似三角形的判定判断A、B、C、D是否可以证明相似三角形,即可判断A、B、C、D选项的正确性,即可解题.
12. 如图,锐角△ABC中,BE,CD是高,它们相交于O,则图中与△BOD相似的三角形有( )
A.4个 B.3个 C.2个 D.1个
答案:B
解析:解答:①∵∠BDO=90°,∠BEA=90°
∴∠BDO=∠BEA
∴△BOD∽△BAE
②∵∠BDO=90°,∠CDA=90°
∴∠BDO=∠CDA
∴△BOD∽△CAD
③∵∠BDO=90°,∠CEO=90
∴∠BDO=∠CEO
∴△BOD∽△COE
∴有3个
故选B.
分析:根据已知及相似三角形的判定方法从而找到图中存在的相似三角形即可.
13. 下列4组条件中,能判定△ABC∽△DEF的是( )
A.AB=5,BC=4,∠A=45°;DE=10,EF=8,∠D=45°
B.∠A=45°,∠B=55°;∠D=45°,∠F=75°
C.BC=4,AC=6,AB=9;DE=18,EF=8,DF=12
D.AB=6,BC=5,∠B=40°;DE=5,EF=4,∠E=40°
答案:C
解析:解答:
A.= = ,夹角是∠B和∠E,两角不一定相等,故本选项错误;
B.应符合∠A=∠D=45°,∠B和∠E相等才能证两三角形相似,故本选项错误;
C.根据===,得到两三角形相似,故本选项正确;
D.∠B=∠E=40°,但夹此角的两边不成比例,故本选项错误;
故选C.
分析:根据已知条件推出证三角形相似的条件,根据相似三角形的判定判断即可.
14. 如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有( )
A.4对 B.5对 C.6对 D.7对
答案:B
解析:解答:图中相似三角形有△ABC∽△CDA,△AGE∽△ABC,△AFE∽△CBE,△BGE∽△BAF,△AGE∽△CDA共5对,
理由是:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,AB=CD,∠D=∠ABC,
∴△ABC≌△CDA,即△ABC∽△CDA,
∵GE∥BC,
∴△AGE∽△ABC∽△CDA,
∵GE∥BC,AD∥BC,
∴GE∥AD,
∴△BGE∽△BAF,
∵AD∥BC,
∴△AFE∽△CBE.
故选B.
分析:根据平行四边形的性质得出AD∥BC,AB∥CD,AD=BC,AB=CD,∠D=∠ABC,推出△ABC≌△CDA,即可推出△ABC∽△CDA,根据相似三角形的判定定理:平行于三角形一边的直线截其它两边或其它两边的延长线,所截的三角形与原三角形相似即可推出其它各对三角形相似.
15. 如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB延长线于E,则图中一定相似的三角形是( )
A.△AED与△ACB B.△AEB与△ACD C.△BAE与△ACE D.△AEC与△DAC
答案:C
解析:解答:∵斜边中线长为斜边的一半,
∴AD=BD=CD,
∴∠C=∠DAC,
∵∠BAE+∠BAD=90°,∠DAC+∠BAD=90°,
∴∠BAE=∠DAC,
∴∠C=∠BAE,
∵∠E=∠E,
∴△BAE∽△ACE.
故选C
分析:根据等腰三角形底角相等的性质可得∠C=∠DAC,易证∠BAE=∠DAC,即可证明∠C=∠BAE,∴即可证明△AEB与△ACD.
二、填容题
16. 如图,AD是直角△ABC (∠C=90°)的角平分线,EF⊥AD于D,与AB及AC的延长线分别交于E,F,写出图中的一对全等三角形是 △AED和△AFD;一对相似三角形是 △AED和△DFC.
答案:△AED和△AFD|△AED和△DFC
解析:解答:∵AD是∠BAC的角平分线,∴∠DAE=∠DAF,
在△AED和△AFD中,DAE=DAF,AD=AD, ADE=ADF=,
∴△AED≌△AFD(ASA),
∴∠AED=∠DFC,
∵∠FDC+∠CDA=90°,∠CDA+∠CAD=90°,∠DAC=∠DAE,
∴∠FDC=∠DAE,
∴△AED∽△DFC(AA),
故答案为△AED≌△AFD、△AED∽△DFC.
分析:根据角平分线的性质可以求得∠DAE=∠DAF,易证△AED≌△AFD,得∠AED=∠DFC,再求得∠FDC=∠DAE即可判定△AED∽△DFC,即可解题.
17. △ABC中,D为AB上一点,E为AC上一点,添加一个条件 DE∥AC(只能填一个)可以使得△ABC与△ADE相似.
答案:DE∥AC
解析:解答:∵DE∥BC,
∴∠ADE=∠ABC,∠ACB=∠AED,
∴△ABC∽△ADE(AA),
故添加条件DE∥BC,可以证明△ABC∽△ADE.
故答案为:DE∥BC.
分析:添加DE∥BC,根据同位角相等的性质,可以求得∠ADE=∠ABC,∠ACB=∠AED,即可判定△ABC∽△ADE,即可解题.
18. △ABC和△A′B′C′中,∠A=60°,∠B=40°,∠A’=60°,当∠C′= 80°时,△ABC∽△A′B′C′.
答案:80°
解析:解答:∵∠A=60°,∠B=40°,
∴∠C=180°-60°-40°=80°,
∵△ABC∽△A′B′C′
∴∠C=∠C′=80°,
∴当∠C′=80°时,△ABC∽△A′B′C′.
故答案为:80°.
分析:利用两对对应角相等的三角形相似判定即可.
19. 如图,AB⊥CB于点B,AC⊥CD于点C,AB=6,AC=10,当CD= 时,△ABC∽△ACD.
答案:
解析:解答:∵AB⊥CB,AC⊥CD,AB=6,AC=10,
∴∠B=∠ACD=90°,BC=8,
∵△ABC∽△ACD
∴当AB:BC=AC:CD时
∴=,
解得CD=.
分析:根据已知,利用两组对应边的比相等且相应的夹角相等的两个三角形相似来判定,根据相似三角形的边对应成比例求得CD的长.
20. □ABCD中,点P在对角线BD上(不与点B,D重合),添加一个条件,使得△BCD与△ADP相似,这个条件可以是 ∠APD=∠C.
答案:∠APD=∠C
解析:解答:∵AD∥BC,
∴∠ADP=∠CBD,
∵∠APD=∠C,
∴∠DAP=∠CDB,
∴△BCD∽△ADP.
故答案为∠APD=∠C.
分析:根据平行四边形对边平行性质可得一堆角相等,让另两对角中有一对相等即可证明△BCD与△ADP相似.
三、解答题
21. 如图,D为△ABC内一点,E为△ABC外一点,且∠1=∠2,∠3=∠4,找出图中的两对相似三角形并说明理由.
答案:解答:△ABD∽△CBE,△ABC∽△DBE.
∵∠1=∠2,∠3=∠4,
∴△ABD∽△CBE,
∴=
∵∠1=∠2,
∴∠ABC=∠DBE,
∴△ABC∽△DBE
分析:根据相似三角形的判定定理:两角相等;对应边成比例且夹角相等即可证明.
22. 已知:在Rt△ABC中∠C=90°,CD为AB边上的高.
求证:Rt△ADC∽Rt△CDB.
答案:解答:∵CD为AB边上的高,
∴∠ADC=∠CDB=90°,
∵∠ACB=90°,
∴∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∵∠ADC=∠CDB=90°,
∴Rt△ADC∽Rt△CDB.
分析:求出∠ADC=∠CDB=90°,根据∠A+∠ACD=90°,∠ACD+∠BCD=90°,推出∠A=∠BCD,根据相似三角形的判定推出即可.
23. 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
(1)试说明△ABD≌△BCE;
答案:解答:(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
答案:解答:答:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC-∠BAD=∠CBA-∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
分析:(1)根据等边三角形各边长相等和各内角为60°的性质可以求证△ABD≌△BCE;
(2)根据全等三角形对应角相等性质可得∠BAD=∠CBE,进而可以求得∠EAF=∠EBA,即可求证△EAF∽△EBA,即可解题.
24. 如图,在△ABC和△ADE中,已知∠B=∠D,∠BAD=∠CAE,求证:△ABC∽△ADE.
答案:解答:如图,∵∠BAD=∠CAE,
∴∠BAD+∠BAE=∠CAE+∠BAE,即∠DAE=∠BAC.
又∵∠B=∠D,
∴△ABC∽△ADE.
分析:利用“两角法”来证:△ABC∽△ADE.
25. 如图,在△ABC中,已知AB=AC,D、E、B、C在同一条直线上,且AB2=BD CE,求证:△ABD∽△ECA.
答案:解答:∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
∵AB2=BD CE,
∴=,即=,
∴△ABD∽△ECA.
分析:由条件可得到∠ABD=∠ACE,结合AB2=BD CE和AB=AC,可得到 = ,即可证得结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 15 页 (共 15 页) 版权所有@21世纪教育网
