贵州省贵阳市南明区华附初级中学九年级数学2025年学业水平检测模拟试卷(无答案)
文档属性
| 名称 | 贵州省贵阳市南明区华附初级中学九年级数学2025年学业水平检测模拟试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 15:50:04 | ||
图片预览


文档简介
贵州省2025年学业水平检测押题卷九年级数学
同学你好!答题前请认真阅读以下内容:
1.全卷共6页,三个大题,共25题,满分150分,考试时间为120分钟. 考试形式闭卷.
2.一律在答题卡相应位置作答,在试题卷上答题视为无效.
3.不能使用计算器.
一、选择题:以下每小题均有 A、B、C、D 四个选项,其中只有一个选项正确,请在答题卡 相应位置作答,每小题 3 分,共 36 分.
1. 下表记录的是某一天中四个城市的平均气温,其中气温最低的是( )
北京 哈尔滨 贵阳 重庆
A. 北京 B. 哈尔滨 C. 贵阳 D. 重庆
2. 下列各图中,经过折叠可以得到正方体是( )
A B.
C. D.
3. 23表示( )
A. 2×2×2 B. 2×3 C. 3×3 D. 2+2+2
4. 党的二十大报告中指出,我国全社会研发经费支出从一万亿元增加到二万八千亿元,居世界第二位,研发人员总量居世界首位.将2800000000000用科学记数法表示为( )
A. B. C. D.
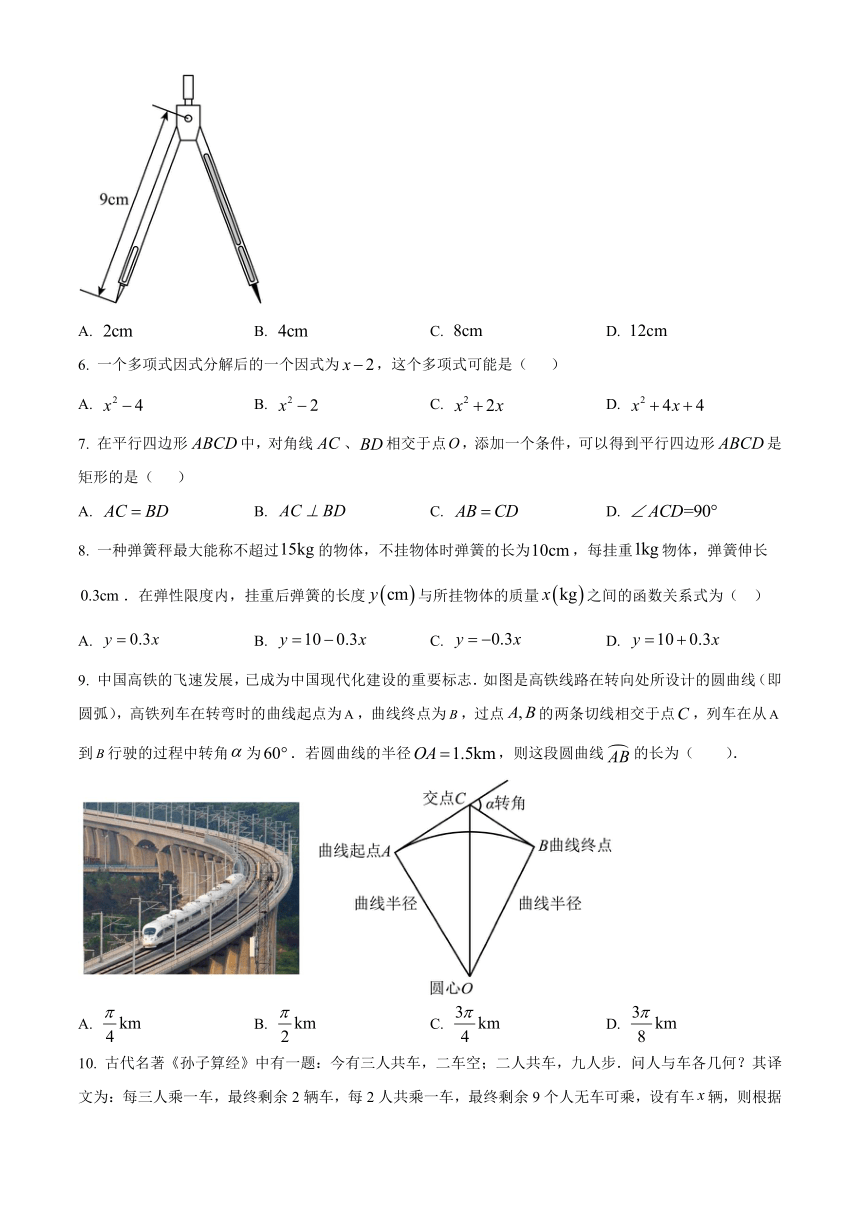
5. 如图所示,小华测得一个圆规的一条支脚长为,另一只脚长为,则该圆规不可能画出圆的半径为( )
A. B. C. D.
6. 一个多项式因式分解后的一个因式为,这个多项式可能是( )
A. B. C. D.
7. 在平行四边形中,对角线、相交于点,添加一个条件,可以得到平行四边形是矩形的是( )
A. B. C. D.
8. 一种弹簧秤最大能称不超过的物体,不挂物体时弹簧的长为,每挂重物体,弹簧伸长.在弹性限度内,挂重后弹簧的长度与所挂物体的质量之间的函数关系式为( )
A. B. C. D.
9. 中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为,曲线终点为,过点的两条切线相交于点,列车在从到行驶的过程中转角为.若圆曲线的半径,则这段圆曲线的长为( ).
A. B. C. D.
10. 古代名著《孙子算经》中有一题:今有三人共车,二车空;二人共车,九人步.问人与车各几何?其译文为:每三人乘一车,最终剩余2辆车,每2人共乘一车,最终剩余9个人无车可乘,设有车辆,则根据题意,可列出方程( )
A. B. C. D.
11. 如图,与在一条直线上,,将图(2)的三角形截去一块,使他变为与图(1)相似的图形,下列做法不正确的是( )
A. 过点E作,交于点G,则
B. 取的中点M,连接,则
C. 在线段和上分别取点M、N,使得,则
D. 在上取一点G,使得,则
12. 若方程的两根分别为,,且,则m的取值范围为( )
A. B. 或 C. D.
二、填空题:每小题4分,共16分.
13. 若公共汽车上车人数记为“+”,下车人数记为“-” ,一辆公共汽车原有18名乘客,经过某一站时,乘客变化为:,,这时车上乘客人数为______.
14. 如图,在等腰中,,分别以A、B圆心,大于长为半径画弧,交于点D,连接交于点E,则______.
15. 在一次活动课上,老师拿来一个不透明的袋子,对学生说:里面只有红球和白球,它们除颜色外没有其他区别,已知白球有个,你能估算出红球的数量吗?小聪与他的小组成员设计了如下方案:先摸出一个小球,记录下颜色后放回,摇均匀后再摸一个小球,记下颜色,如此反复,他们记录表格如下:
摸球次数
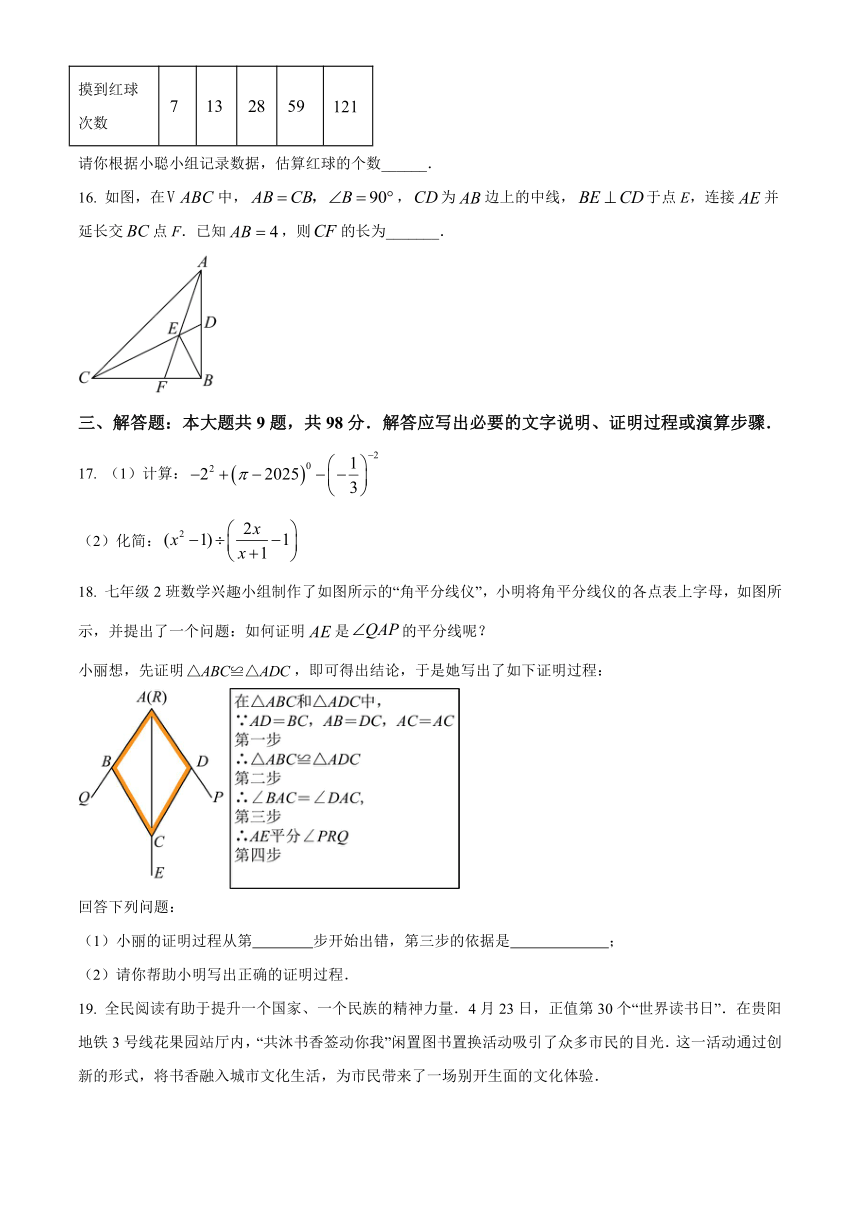
摸到红球次数
请你根据小聪小组记录数据,估算红球的个数______.
16. 如图,在中,,为边上的中线,于点E,连接并延长交点F.已知,则的长为_______.
三、解答题:本大题共9题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
17. (1)计算:
(2)化简:
18. 七年级2班数学兴趣小组制作了如图所示的“角平分线仪”,小明将角平分线仪的各点表上字母,如图所示,并提出了一个问题:如何证明是的平分线呢?
小丽想,先证明,即可得出结论,于是她写出了如下证明过程:
回答下列问题:
(1)小丽的证明过程从第 步开始出错,第三步的依据是 ;
(2)请你帮助小明写出正确的证明过程.
19. 全民阅读有助于提升一个国家、一个民族的精神力量.4月23日,正值第30个“世界读书日”.在贵阳地铁3号线花果园站厅内,“共沐书香签动你我”闲置图书置换活动吸引了众多市民的目光.这一活动通过创新的形式,将书香融入城市文化生活,为市民带来了一场别开生面的文化体验.
某校“综合与实践”小组为了解全校1200名学生的读书情况,随机抽取部分学生进行问卷调查,形成了如下调查报告(不完整):
××中学学生读书情况调查报告
调查主题 ××中学学生读书情况
调查方式 抽样调查 调查对象 ××中学学生
数据收集、 整理与描述 第一项 您平均每周阅读课外书的时间大约是(只能单选,每项含最小值,不含最大值) A.8小时及以上; B.6~8小时; C.4~6小时; D.0~4小时.
第二项 您阅读的课外书的主要来源是(可多选) E.自行购买; F.从图书馆借阅; G.免费数字阅读; H.向他人借阅.
调查结论 ……
请根据以上调查报告,解答下列问题:
(1)参与本次抽样调查的学生人数为 ;这些学生中选择“免费数字阅读”的人数 ;
(2)估计该校1200名学生中,平均每周阅读课外书时间在“6小时及以上”的人数;
(3)该小组要根据以上调查报告在全班进行交流,假如你是小组成员,请结合以上两项调查数据分别写出一条你获取的信息.
20. 已知反比例函数()与正比例函数交于、两点,且点坐标为;
(1)求、的值;
(2)直线与一次函数的图象相交于点,与反比例函数的图象相交于点,若,结合函数图象,直接写出的取值范围: .
21. 推动绿色发展,促进人与自然和谐共生,某地区政府牢记习总书记“绿水青山就是金山银山”嘱托,鼓励村民牢记生态发展的同时,“甩开膀子加油干”积极脱贫致富,该地区政府购进了甲、乙两种果苗分发给村民,已知第一批果苗共1.2万株;第一批果苗分发后,发现村民种植果苗热情很高,于是该区政府决定购进第二批果苗,已知第二批甲种果苗的数量比第一批多,第二批乙种果苗比第一批多,且第二批果苗总数为万株.
(1)分别求出第一批两种树苗各多少株;
(2)市场调研发现,甲种果苗每株售价3元,乙种果苗每株售价2元,该区政府计划明年拿出不高于4.8万元购进两种果苗2万株,则最多购买甲种果苗多少株?
22. 贵州是一个多桥梁的省份,如图 1 是全球最高的桥——北盘江大桥.现某数学兴趣小组打算利用所学的数学知识测量它的桥长和桥高.数学小组的同学们绘制出了如图 2 的几何图形:为桥面,,为两个桥墩在桥上方的部分,满足且 . C为桥下方的最低点.同学们在 B点处用测角仪测出了F的仰角为, G的仰角为 , C的俯角为,从 A点又测得 C的俯角为.
(1)桥面 长为 ;(结果保留整数,参考数据:,,
)
(2)请计算 C点到桥面的距离.(结果保留整数,参考数据:,,,,, )
23. 如图,点A、B、C分别是○O上的三点,连接交线段于点D.
(1)若,则 ;
(2)若D是的中点,延长至点E,使得,连接,求证;
(3)在(2)的条件下,若,,求的长.
24. 再一次校运会上,一名男同学仍铅球时,其运动轨迹为如图所示的一条抛物线,已知仍出铅球时,铅球距离男同学的水平距离长为x(单位:m),距离地面高度为y(单位:m)满足下表关系:.
x 0 1 2 3 4
y 1.4 1.9 2.2 2.3 2.2
(1)求出铅球的运动轨迹的解析式;
(2)若铅球落地的沙坑低于水平面,沙坑边缘与男同学的距离,计算裁判员测量的铅球落地位置G到F的距离;
(3)为了使铅球抛出距离更远,该男同学计划让铅球扔出后,达到的最大高度在B的下方米处,试计算说明,该男同学的抛出的铅球距离是增大还是减少?增大(或减少)多少.
25. 综合与探究
小红根据学习轴对称的经验,发现其中线段之间、角之间存在着紧密的联系,他以等腰三角形为背景展开了拓展探究.如图①,在等腰直角三角形中,,,点D是直线左侧的一动点.作点C关于直线的对称点为点E,连接,直线与直线交于点F,连接,.
【动手操作】
(1)当时,根据题意,用尺规在图①上画出图形;若,,则 ;
【问题探究】
(2)根据(1)所画图形,猜想的大小以及,,的数量关系,并说明理由;
【拓展延伸】
(3)如图②,在等腰三角形中,,,其余条件不变,当时,若,,直接写出,,的数量关系以及的值.
同学你好!答题前请认真阅读以下内容:
1.全卷共6页,三个大题,共25题,满分150分,考试时间为120分钟. 考试形式闭卷.
2.一律在答题卡相应位置作答,在试题卷上答题视为无效.
3.不能使用计算器.
一、选择题:以下每小题均有 A、B、C、D 四个选项,其中只有一个选项正确,请在答题卡 相应位置作答,每小题 3 分,共 36 分.
1. 下表记录的是某一天中四个城市的平均气温,其中气温最低的是( )
北京 哈尔滨 贵阳 重庆
A. 北京 B. 哈尔滨 C. 贵阳 D. 重庆
2. 下列各图中,经过折叠可以得到正方体是( )
A B.
C. D.
3. 23表示( )
A. 2×2×2 B. 2×3 C. 3×3 D. 2+2+2
4. 党的二十大报告中指出,我国全社会研发经费支出从一万亿元增加到二万八千亿元,居世界第二位,研发人员总量居世界首位.将2800000000000用科学记数法表示为( )
A. B. C. D.
5. 如图所示,小华测得一个圆规的一条支脚长为,另一只脚长为,则该圆规不可能画出圆的半径为( )
A. B. C. D.
6. 一个多项式因式分解后的一个因式为,这个多项式可能是( )
A. B. C. D.
7. 在平行四边形中,对角线、相交于点,添加一个条件,可以得到平行四边形是矩形的是( )
A. B. C. D.
8. 一种弹簧秤最大能称不超过的物体,不挂物体时弹簧的长为,每挂重物体,弹簧伸长.在弹性限度内,挂重后弹簧的长度与所挂物体的质量之间的函数关系式为( )
A. B. C. D.
9. 中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为,曲线终点为,过点的两条切线相交于点,列车在从到行驶的过程中转角为.若圆曲线的半径,则这段圆曲线的长为( ).
A. B. C. D.
10. 古代名著《孙子算经》中有一题:今有三人共车,二车空;二人共车,九人步.问人与车各几何?其译文为:每三人乘一车,最终剩余2辆车,每2人共乘一车,最终剩余9个人无车可乘,设有车辆,则根据题意,可列出方程( )
A. B. C. D.
11. 如图,与在一条直线上,,将图(2)的三角形截去一块,使他变为与图(1)相似的图形,下列做法不正确的是( )
A. 过点E作,交于点G,则
B. 取的中点M,连接,则
C. 在线段和上分别取点M、N,使得,则
D. 在上取一点G,使得,则
12. 若方程的两根分别为,,且,则m的取值范围为( )
A. B. 或 C. D.
二、填空题:每小题4分,共16分.
13. 若公共汽车上车人数记为“+”,下车人数记为“-” ,一辆公共汽车原有18名乘客,经过某一站时,乘客变化为:,,这时车上乘客人数为______.
14. 如图,在等腰中,,分别以A、B圆心,大于长为半径画弧,交于点D,连接交于点E,则______.
15. 在一次活动课上,老师拿来一个不透明的袋子,对学生说:里面只有红球和白球,它们除颜色外没有其他区别,已知白球有个,你能估算出红球的数量吗?小聪与他的小组成员设计了如下方案:先摸出一个小球,记录下颜色后放回,摇均匀后再摸一个小球,记下颜色,如此反复,他们记录表格如下:
摸球次数
摸到红球次数
请你根据小聪小组记录数据,估算红球的个数______.
16. 如图,在中,,为边上的中线,于点E,连接并延长交点F.已知,则的长为_______.
三、解答题:本大题共9题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
17. (1)计算:
(2)化简:
18. 七年级2班数学兴趣小组制作了如图所示的“角平分线仪”,小明将角平分线仪的各点表上字母,如图所示,并提出了一个问题:如何证明是的平分线呢?
小丽想,先证明,即可得出结论,于是她写出了如下证明过程:
回答下列问题:
(1)小丽的证明过程从第 步开始出错,第三步的依据是 ;
(2)请你帮助小明写出正确的证明过程.
19. 全民阅读有助于提升一个国家、一个民族的精神力量.4月23日,正值第30个“世界读书日”.在贵阳地铁3号线花果园站厅内,“共沐书香签动你我”闲置图书置换活动吸引了众多市民的目光.这一活动通过创新的形式,将书香融入城市文化生活,为市民带来了一场别开生面的文化体验.
某校“综合与实践”小组为了解全校1200名学生的读书情况,随机抽取部分学生进行问卷调查,形成了如下调查报告(不完整):
××中学学生读书情况调查报告
调查主题 ××中学学生读书情况
调查方式 抽样调查 调查对象 ××中学学生
数据收集、 整理与描述 第一项 您平均每周阅读课外书的时间大约是(只能单选,每项含最小值,不含最大值) A.8小时及以上; B.6~8小时; C.4~6小时; D.0~4小时.
第二项 您阅读的课外书的主要来源是(可多选) E.自行购买; F.从图书馆借阅; G.免费数字阅读; H.向他人借阅.
调查结论 ……
请根据以上调查报告,解答下列问题:
(1)参与本次抽样调查的学生人数为 ;这些学生中选择“免费数字阅读”的人数 ;
(2)估计该校1200名学生中,平均每周阅读课外书时间在“6小时及以上”的人数;
(3)该小组要根据以上调查报告在全班进行交流,假如你是小组成员,请结合以上两项调查数据分别写出一条你获取的信息.
20. 已知反比例函数()与正比例函数交于、两点,且点坐标为;
(1)求、的值;
(2)直线与一次函数的图象相交于点,与反比例函数的图象相交于点,若,结合函数图象,直接写出的取值范围: .
21. 推动绿色发展,促进人与自然和谐共生,某地区政府牢记习总书记“绿水青山就是金山银山”嘱托,鼓励村民牢记生态发展的同时,“甩开膀子加油干”积极脱贫致富,该地区政府购进了甲、乙两种果苗分发给村民,已知第一批果苗共1.2万株;第一批果苗分发后,发现村民种植果苗热情很高,于是该区政府决定购进第二批果苗,已知第二批甲种果苗的数量比第一批多,第二批乙种果苗比第一批多,且第二批果苗总数为万株.
(1)分别求出第一批两种树苗各多少株;
(2)市场调研发现,甲种果苗每株售价3元,乙种果苗每株售价2元,该区政府计划明年拿出不高于4.8万元购进两种果苗2万株,则最多购买甲种果苗多少株?
22. 贵州是一个多桥梁的省份,如图 1 是全球最高的桥——北盘江大桥.现某数学兴趣小组打算利用所学的数学知识测量它的桥长和桥高.数学小组的同学们绘制出了如图 2 的几何图形:为桥面,,为两个桥墩在桥上方的部分,满足且 . C为桥下方的最低点.同学们在 B点处用测角仪测出了F的仰角为, G的仰角为 , C的俯角为,从 A点又测得 C的俯角为.
(1)桥面 长为 ;(结果保留整数,参考数据:,,
)
(2)请计算 C点到桥面的距离.(结果保留整数,参考数据:,,,,, )
23. 如图,点A、B、C分别是○O上的三点,连接交线段于点D.
(1)若,则 ;
(2)若D是的中点,延长至点E,使得,连接,求证;
(3)在(2)的条件下,若,,求的长.
24. 再一次校运会上,一名男同学仍铅球时,其运动轨迹为如图所示的一条抛物线,已知仍出铅球时,铅球距离男同学的水平距离长为x(单位:m),距离地面高度为y(单位:m)满足下表关系:.
x 0 1 2 3 4
y 1.4 1.9 2.2 2.3 2.2
(1)求出铅球的运动轨迹的解析式;
(2)若铅球落地的沙坑低于水平面,沙坑边缘与男同学的距离,计算裁判员测量的铅球落地位置G到F的距离;
(3)为了使铅球抛出距离更远,该男同学计划让铅球扔出后,达到的最大高度在B的下方米处,试计算说明,该男同学的抛出的铅球距离是增大还是减少?增大(或减少)多少.
25. 综合与探究
小红根据学习轴对称的经验,发现其中线段之间、角之间存在着紧密的联系,他以等腰三角形为背景展开了拓展探究.如图①,在等腰直角三角形中,,,点D是直线左侧的一动点.作点C关于直线的对称点为点E,连接,直线与直线交于点F,连接,.
【动手操作】
(1)当时,根据题意,用尺规在图①上画出图形;若,,则 ;
【问题探究】
(2)根据(1)所画图形,猜想的大小以及,,的数量关系,并说明理由;
【拓展延伸】
(3)如图②,在等腰三角形中,,,其余条件不变,当时,若,,直接写出,,的数量关系以及的值.
同课章节目录
