华师大版数学九年级上册第23章 23.3.3相似三角形的性质课时作业
文档属性
| 名称 | 华师大版数学九年级上册第23章 23.3.3相似三角形的性质课时作业 |

|
|
| 格式 | docx | ||
| 文件大小 | 394.2KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 00:00:00 | ||
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学九年级上册第23章第3节23.3.3相似三角形的性质
课时作业
一、选择题
1. 如图,F是平行四边形ABCD对角线BD上的点,BF:FD=1:3,则BE:EC=( )
A. B. C. D.
答案:A
解析:解答:∵ABCD是平行四边形
∴AD∥BC
∴△BFE∽△DFA
∴BE:AD=BF:FD=1:3
∴BE:EC=BE:(BC-BE)=BE:(AD-BE)=1:(3-1)
∴BE:EC=1:2
故选A.
分析:由平行四边形的性质易证两三角形相似,根据相似三角形的性质可解.
2. 如图,△ABC中,∠ACB=90°,AB=5,D是AB延长线上一点,连接CD,若∠DCB=∠A,BD:DC=1:2,则△ABC的面积为( )
A.4 B.5 C.6 D.7
答案:B
解析:解答:∵∠DCB=∠A,∠CDB=∠ADC
∴△DCB∽△DAC
∴==
∵AB=5
∴BC=,AC=2
∴△ABC的面积=BC AC=5.故选B.
分析:由三角形相似,利用相似比,结合勾股定理就可以求出△ABC的面积.
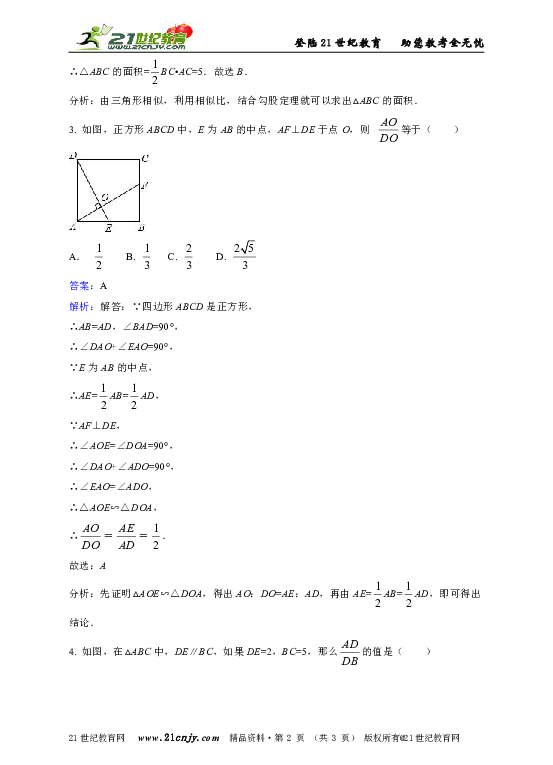
3. 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则 等于( )
A. B. C. D.
答案:A
解析:解答:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠DAO+∠EAO=90°,
∵E为AB的中点,
∴AE=AB=AD,
∵AF⊥DE,
∴∠AOE=∠DOA=90°,
∴∠DAO+∠ADO=90°,
∴∠EAO=∠ADO,
∴△AOE∽△DOA,
∴==.
故选:A
分析:先证明△AOE∽△DOA,得出AO:DO=AE:AD,再由AE=AB=AD,即可得出结论.
4. 如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么的值是( )
A. B. C. D.
答案:B
解析:解答:∵DE∥BC,
∴△ADE∽△ABC,
∴==,
∴=;
故选:B.
分析:先由平行线证明△ADE∽△ABC,得出对应边成比例 = = ,即可得出 的值.
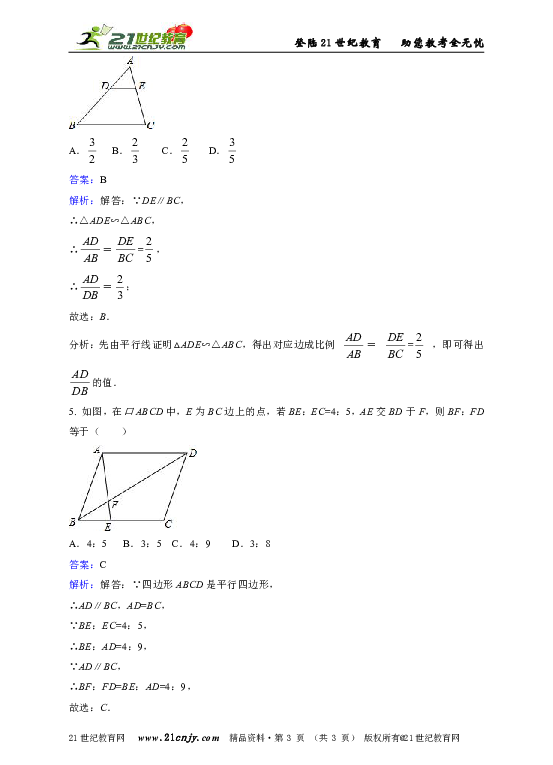
5. 如图,在口ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
A.4:5 B.3:5 C.4:9 D.3:8
答案:C
解析:解答:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵BE:EC=4:5,
∴BE:AD=4:9,
∵AD∥BC,
∴BF:FD=BE:AD=4:9,
故选:C.
分析:根据BE:EC=4:5和AD=BC,证明BE:AD=4:9,根据AD∥BC,得到BF:FD=BE:AD,得到答案.
6. 如图,点D、E分别在线段AB、AC上且∠ABC=∠AED,若DE=4,AE=5,BC=8,则AB的长为( )
A. B.10 C. D.
答案:B
解析:解答:∵∠ABC=∠AED,∠A=∠A,
∴ADE∽△ACB,
∴=,
∵DE=4,AE=5,BC=8,
∴AB=10,
故选:B.
分析:根据已知∠ABC=∠AED,∠A=∠A,证明△ADE∽△ACB,根据相似三角形的性质,列出比例式,代入已知数据求出AB的长.
7. 如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )
A.1:2 B.1:3 C.2:1 D.2:3
答案:B
解析:解答:∵AD:BD=1:2,
∴AD:AB=1:3,
∵DE∥BC,
∴△ADE∽△ABC,
则△ADE和△ABC的相似比为:AD:AB=1:3,
故选:B.
分析:根据AD:BD=1:2,得到AD:AB=1:3,根据DE∥BC,得到△ADE∽△ABC,根据相似比的概念求出相似比.
8. 如图,在△ABC中,点D,E分别在AB,AC上,DE∥BC,AD=CE.若AB:AC=3:2,BC=10,则DE的长为( )
A.3 B.4 C.5 D.6
答案:B
解析:解答:∵DE∥BC,
∴AD:AE=AB:AC=3:2,
∵AD=CE.
∴CE:AE=3:2,
∴AE:AC=2:5,
∴DE:BC=2:5,
∵BC=10,
∴DE:10=2:5,
解得DE=4.
故选:B.
分析:运用DE∥BC,可得出AD:AE的值,由AD=CE,求出CE:AE,可得出AE:AC即DE:BC,利用BC=10,即可求出DE的长.
9. 如图,在 ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=2:3,则S△DEF:S△ABF=( )
A.2:3 B.4:9 C.2:5 D.4:25
答案:D
解析:解答:如图,∵四边形ABCD是平行四边形,
∴DC∥AB,CD=AB.
∴△DFE∽△BFA,
∴S△DEF:S△ABF=DE2:AB2,
∵DE:EC=2:3,
∴DE:DC=DE:AB=2:5,
∴S△DEF:S△ABF=4:25
故选:D.
分析:据已知可得到相似三角形,从而可得到其相似比,再根据相似三角形的面积比等于相似比的平方就可得到答案.
10. 如图,若D、E分别为△ABC中AB、AC边上的点,且∠AED=∠B,AD=3,AC=6,DB=5,则AE的长度为( )
A. B. C. D.4
答案:D
解析:解答:∵∠A=∠A,∠AED=∠B,
∴△ADE∽△ACB,
∴AE:AB=AD:AC,
又∵AD=3,AC=6,DB=5,
∴AB=AD+DB=8,
∴AE=8×3÷6=4.
故选D.
分析:根据相似三角形的判定首先证出△ADE∽△ACB,然后根据相似三角形的性质得出AE:AB=AD:AC,从而求出AE的长度.
11. 如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A,BC=3,AC=6,则CD的长为( )
A. 1 B. 2 C. D.
答案:C
解析:解答:∵∠DBC=∠A,∠C=∠C,
∴△BCD∽△ACB,
∴= ,
∴=
∴CD=,
故选:C.
分析:由∠DBC=∠A,∠C=∠C,可证得△BCD∽△ACB,所以有=,代入数据可求得.
12. 如图,四边形ABCD是平行四边形,∠BAD的平分线交BD于点E,交CD于点F,交BC的延长线于点G,则下列结论中正确的是( )
A.AE2=EF FG B.AE2=EF EG C.AE2=EG FG D.AE2=EF AG
答案:B
解析:解答:∵四边形ABCD是平行四边形,
∴△ADE∽△EGB,△DEF∽△AEB,
∴=,=,
∴=,
即AE2=EF EG.
所以选项B正确,
故选B.
分析:解答此题的关键是利用平行四边形证明出△ADE∽△EGB,△DEF∽△AEB,然后利用对应边成比例即可解答此题.
13. 如图,△ABC中,AD⊥BC于D,下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③= ;④AB2=BD BC.其中一定能够判定△ABC是直角三角形的有( )
A. 1 B. 2 C. 3 D. 4
答案:B
解析:解答:(1)∠B+∠DAC=90°,该条件无法判定△ABC是直角三角形;
(2)∵∠B=∠DAC,∠BAD+∠B=90°,
∴∠BAD+∠DAC=90°,即∠BAC=90°,故该条件可以判定△ABC是直角三角形;
(3)=,该条件无法判定△ABC是直角三角形;
(4)∵AB2=BD BC,
∴=,
∵∠B=∠B,
∴△ABD∽△CBA,
∴∠BAC=90°,故该条件可以判定△ABC是直角三角形;
故选 B
分析:对题干中给出的条件逐一验证,证明∠BAC=90°即可解题.
14. 如图,在△ABC中,点D是AB边上一点,DE∥BC交AC于E,AD:DB=1:2,则△ADE与△ABC的面积之比为( )
A.1:2 B.1:4 C.1:8 D.1:9
答案:D
解析:解答:∵DE∥BC,
∴△ADE∽△ABC,
∴= ,
∵AD:DB=1:2,
∴==,
∴△ADE与△ABC的面积之比为:.
故选:D.
分析:首先利用相似三角形的判定与性质得出 = = ,进而利用相似三角形的面积比等于相似比的平方,得出答案即可.
15. 如图,△ABC中,E、D分别是AC、BC的中点,AD、BE交于点O,则S△DOE:S△AOB=( )
A.1:2 B.2:3 C.1:3 D.1:4
答案:D
解析:解答:∵△ABC中,E、D分别是AC、BC的中点,
∴DE=AB,DE∥AB,
∴△DOE∽△AOB,
∴S△DOE:S△AOB=1:4.
故选:D.
分析:根据三角形中位线定理可得DE= AB,DE∥AB,再根据平行线性质和相似三角形的判定与性质即可求解.
二、填空题
16. 如图,已知△ABC中,DE∥BC,AE:AC=1:3,EM、CN分别是∠AED、∠ACB的角平分线,EM=5,则CN= 15.
答案:15
解析:解答:∵EM、CN分别是∠AED、∠ACB的角平分线,
∴∠AEM=∠AED,∠ACN=∠ACB,
∵DE∥BC,
∴∠AED=∠ACB,
∴∠AEM=∠ACN,
∴EM∥CN,
∴△AEM∽△ACN,
∴=,
∵AE:AC=1:3,EM=5,
∴=,CN=15,
故答案为:15.
分析:根据角平分线定义得出∠AEM=∠AED,∠ACN=∠ACB,根据平行线性质得出∠AED=∠ACB,求出∠AEM=∠ACN,推出EM∥CN,得出△AEM∽△ACN,得出比例式= ,代入求出即可.
17. 如图,D是△ABC的边AC上的一点,若∠ABD=∠C,AB=6,AD=4,则线段CD的长为 5.
答案:5
解析:解答:∵∠ABD=∠C,∠BAD=∠CAB,
∴△ABD∽△ACB,
∴=,即=,
∴AC=9,
∴CD=AC-AD=5.
分析:由∠ABD=∠C,∠BAD=∠CAB,证出△ABD∽△ACB,得出AB:AC=AD:AB,求出AC的长,即可求出CD的长.
18. 如图,O是四边形ABCD对角线的交点,已知∠BAD+∠BCA=180°,AB=5,AC=4,AD=3,=,则BC= .
答案:
解析:解答:过D点作AO的平行线,交BA延长线于E点.
∵AO∥ED,
∴=,求得AE=,
∵AO∥ED,
∴∠BAC=∠AED,
∵∠BAD+∠BCA=180°,∠BAD+∠EAD=180°,
∴∠BCA=∠EAD,
∴△EAD∽△ACB,
∴=,
求得BC=.
故答案为:.
分析:过D点作AO的平行线,交BA延长线于E点,构建△ADE,根据题干中条件可证明△EAD∽△ACB,可以求得BC的值.
19. 如图,△ABC和△ECD均为等边三角形,B、C、D三点在一直线上,AD、BE相交于点F,DF=3,AF=4,则线段FE的长为 1.
答案:1
解析:解答:如图
可以认为△BCE是由△ACD逆时针转60°而得;那么CF的起始位是CF′,
∴CF=CF',
∵∠FCF'=60°,
∴△CFF′是等边△,
∴∠BFC=∠CFD=CF'F=60°,
∴CF平分∠DFB.
∵∠CAD+∠ACF=60°,∠ACF+∠FCE=60°,
∴△ACF∽△CEF,
∴= ,
∵△EFC∽△DF'C,EC=CD,
∴EF=F'D
∴FD=FF'+F'D=CF+EF=3,
解得EF=1.
分析:可证△CFF′是等边△,可得=,可证FD=CF+EF=3,根据EF,FC的关系即可求得EF的值.
20. 如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为 .
答案:
解析:解答::∵△ABC是等边三角形,
∴AB=BC=AC=3,∠B=∠C=60°,
∴∠BAP+∠APB=180°-60°=120°,
∵∠APD=60°,
∴∠APB+∠DPC=180°-60°=120°,
∴∠BAP=∠DPC,
即∠B=∠C,∠BAP=∠DPC,
∴△BAP∽△CPD,
∴=,
∵AB=BC=3,CP=BC-BP=3-1=2,BP=1,
即=,
解得:CD=,
故答案为:.
分析:根据等边三角形性质求出AB=BC=AC=3,∠B=∠C=60°,推出∠BAP=∠DPC,证△BAP∽△CPD,得出=,代入求出即可.
三、解答题
21. 如图,在平行四边形ABCD中,BC=6,点M在对角线AC上,AM=AC,过点M作EF∥AB,交AD于点E,交BC于点F,求ED的长.
答案:解答:∵四边形ABCD是平行四边形,
∴BC=AD=6,AB∥CD,
∵EF∥AB,
∴EM∥DC,
∴△AEM∽△ADC,
∴=,
∵AM=AC,
∴AE=AD=×6=2,
∴DE=6-2=4.
解析:
分析:根据平行四边形性质求出AD=6,推出EM∥CD,得出相似三角形,推出= ,根据AM=AC,求出AE= AD=2,即可求出答案.
22. 如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.
(1)求证:2EF=BD,
答案:解答:(1)∵DC=AC,CF为∠ACB的平分线,
∴AF=DF,
∵AE=EB,AF=DF,
∴EF为△ABD的中位线,
∴2EF=BD.
(2)四边形BDFE的面积为6,求△ABD的面积.
答案:解答:∵EF为△ABD的中位线,
∴EF∥BD,2EF=BD,
∴△AEF∽△ABD
∴两三角形相似比K=1:2,
∴=K2=,
则4(S△ABD-6)=S△ABD,
解得:S△ABD=8.
解析: 分析:(1)根据等腰三角形性质推出F为AD中点,根据三角形的中位线定理推出即可;
(2)根据三角形中位线推出EF∥BD,推出△AEF∽△ABD且两三角形相似比K=1:2,得出面积比是,代入求出即可.
23. 如图,梯形ABCD中,AB∥CD,AD=BC,点E在边AD上,BE与AC相交于点O,且∠ABE=∠BCA.
求证:(1)△BAE∽△BOA;
答案:解答:在梯形ABCD中,
∵AB∥CD,AD=BC,
∴∠EAB=∠CBA
∵∠EBA=∠BCA,
∴△EBA∽△ACB
∴∠AEB=∠BAC
∵∠ABE=∠OBA
∴△BAE∽△BOA
(2)BO BE=BC AE.
答案:解答:∵△BAE∽△BOA,
∴=
∵∠BAC=∠OAB,
∠EBA=∠BCA
∴△OAB∽△BAC
∴=
∴=
∴BE BO=AE BC
分析:(1)利用梯形的性质得到∠EAB=∠CBA,从而证得△EBA∽△ACB,然后利用相似三角形的性质得到∠AEB=∠BAC,从而证明△BAE∽△BOA;
(2)根据上题证得的△BAE∽△BOA得到= ,然后再利用∠BAC=∠OAB、∠EBA=∠BCA证得△OAB∽△BAC,从而得到= ,再根据=
得到BE BO=AE BC即可.
24. 如图,梯形ABCD中,AB∥DC,∠B=90°,E为BC上一点,且AE⊥ED.若BC=12,DC=7,BE:EC=1:2,
(1)求AB的长.
答案:解答:(1)∵AB∥DC,且∠B=90°,
∴∠AEB+∠BAE=90°及∠C=90度.
∴∠AEB+∠CED=90度.
故∠BAE=∠CED.
∴△EAB∽△DEC.
∴=
又BE:EC=1:2,且BC=12及DC=7,
故=
则AB=.
(2)求△AED的面积.
答案:解答:∵△EAB∽△DEC,
∴=
即:=
解得:CD=7
∴S△AED=S梯形ABCD-S△ABE-S△ECD=(AB+CD) BC-AB BE-EC CD=
(+7) 12-××4-×8×7=
分析:(1)由题意易知AB和CD所在的两个三角形相似,再利用相似比即可求出所求线段的长度.
(2)根据证得的△EAB∽△DEC利用相似三角形对应边的比成比例求得线段CD的长,利用梯形的面积减去两个三角形的面积即可求得三角形AED的面积.
25. 如图,已知E是正方形ABCD的边CD上一点,BF⊥AE于F,求证:AB2=AE BF.
答案:解答:∵∠ABF+∠DAE=90°,∠DAE+∠BAF=90°,
∴△ABF∽△AED,
∴=,
∴AD2=AE BF,
∵AB=AD,
∴AB2=AE BF.
分析:根据正方形内角为90°的性质可以求证△ABF∽△EAD,即可求得AD2=AE BF,AB=AD即可解题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 17 页 (共 18 页) 版权所有@21世纪教育网
华师大版数学九年级上册第23章第3节23.3.3相似三角形的性质
课时作业
一、选择题
1. 如图,F是平行四边形ABCD对角线BD上的点,BF:FD=1:3,则BE:EC=( )
A. B. C. D.
答案:A
解析:解答:∵ABCD是平行四边形
∴AD∥BC
∴△BFE∽△DFA
∴BE:AD=BF:FD=1:3
∴BE:EC=BE:(BC-BE)=BE:(AD-BE)=1:(3-1)
∴BE:EC=1:2
故选A.
分析:由平行四边形的性质易证两三角形相似,根据相似三角形的性质可解.
2. 如图,△ABC中,∠ACB=90°,AB=5,D是AB延长线上一点,连接CD,若∠DCB=∠A,BD:DC=1:2,则△ABC的面积为( )
A.4 B.5 C.6 D.7
答案:B
解析:解答:∵∠DCB=∠A,∠CDB=∠ADC
∴△DCB∽△DAC
∴==
∵AB=5
∴BC=,AC=2
∴△ABC的面积=BC AC=5.故选B.
分析:由三角形相似,利用相似比,结合勾股定理就可以求出△ABC的面积.
3. 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则 等于( )
A. B. C. D.
答案:A
解析:解答:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠DAO+∠EAO=90°,
∵E为AB的中点,
∴AE=AB=AD,
∵AF⊥DE,
∴∠AOE=∠DOA=90°,
∴∠DAO+∠ADO=90°,
∴∠EAO=∠ADO,
∴△AOE∽△DOA,
∴==.
故选:A
分析:先证明△AOE∽△DOA,得出AO:DO=AE:AD,再由AE=AB=AD,即可得出结论.
4. 如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么的值是( )
A. B. C. D.
答案:B
解析:解答:∵DE∥BC,
∴△ADE∽△ABC,
∴==,
∴=;
故选:B.
分析:先由平行线证明△ADE∽△ABC,得出对应边成比例 = = ,即可得出 的值.
5. 如图,在口ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
A.4:5 B.3:5 C.4:9 D.3:8
答案:C
解析:解答:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵BE:EC=4:5,
∴BE:AD=4:9,
∵AD∥BC,
∴BF:FD=BE:AD=4:9,
故选:C.
分析:根据BE:EC=4:5和AD=BC,证明BE:AD=4:9,根据AD∥BC,得到BF:FD=BE:AD,得到答案.
6. 如图,点D、E分别在线段AB、AC上且∠ABC=∠AED,若DE=4,AE=5,BC=8,则AB的长为( )
A. B.10 C. D.
答案:B
解析:解答:∵∠ABC=∠AED,∠A=∠A,
∴ADE∽△ACB,
∴=,
∵DE=4,AE=5,BC=8,
∴AB=10,
故选:B.
分析:根据已知∠ABC=∠AED,∠A=∠A,证明△ADE∽△ACB,根据相似三角形的性质,列出比例式,代入已知数据求出AB的长.
7. 如图,DE∥BC,AD:DB=1:2,则△ADE和△ABC的相似比为( )
A.1:2 B.1:3 C.2:1 D.2:3
答案:B
解析:解答:∵AD:BD=1:2,
∴AD:AB=1:3,
∵DE∥BC,
∴△ADE∽△ABC,
则△ADE和△ABC的相似比为:AD:AB=1:3,
故选:B.
分析:根据AD:BD=1:2,得到AD:AB=1:3,根据DE∥BC,得到△ADE∽△ABC,根据相似比的概念求出相似比.
8. 如图,在△ABC中,点D,E分别在AB,AC上,DE∥BC,AD=CE.若AB:AC=3:2,BC=10,则DE的长为( )
A.3 B.4 C.5 D.6
答案:B
解析:解答:∵DE∥BC,
∴AD:AE=AB:AC=3:2,
∵AD=CE.
∴CE:AE=3:2,
∴AE:AC=2:5,
∴DE:BC=2:5,
∵BC=10,
∴DE:10=2:5,
解得DE=4.
故选:B.
分析:运用DE∥BC,可得出AD:AE的值,由AD=CE,求出CE:AE,可得出AE:AC即DE:BC,利用BC=10,即可求出DE的长.
9. 如图,在 ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=2:3,则S△DEF:S△ABF=( )
A.2:3 B.4:9 C.2:5 D.4:25
答案:D
解析:解答:如图,∵四边形ABCD是平行四边形,
∴DC∥AB,CD=AB.
∴△DFE∽△BFA,
∴S△DEF:S△ABF=DE2:AB2,
∵DE:EC=2:3,
∴DE:DC=DE:AB=2:5,
∴S△DEF:S△ABF=4:25
故选:D.
分析:据已知可得到相似三角形,从而可得到其相似比,再根据相似三角形的面积比等于相似比的平方就可得到答案.
10. 如图,若D、E分别为△ABC中AB、AC边上的点,且∠AED=∠B,AD=3,AC=6,DB=5,则AE的长度为( )
A. B. C. D.4
答案:D
解析:解答:∵∠A=∠A,∠AED=∠B,
∴△ADE∽△ACB,
∴AE:AB=AD:AC,
又∵AD=3,AC=6,DB=5,
∴AB=AD+DB=8,
∴AE=8×3÷6=4.
故选D.
分析:根据相似三角形的判定首先证出△ADE∽△ACB,然后根据相似三角形的性质得出AE:AB=AD:AC,从而求出AE的长度.
11. 如图所示,在△ABC中D为AC边上一点,若∠DBC=∠A,BC=3,AC=6,则CD的长为( )
A. 1 B. 2 C. D.
答案:C
解析:解答:∵∠DBC=∠A,∠C=∠C,
∴△BCD∽△ACB,
∴= ,
∴=
∴CD=,
故选:C.
分析:由∠DBC=∠A,∠C=∠C,可证得△BCD∽△ACB,所以有=,代入数据可求得.
12. 如图,四边形ABCD是平行四边形,∠BAD的平分线交BD于点E,交CD于点F,交BC的延长线于点G,则下列结论中正确的是( )
A.AE2=EF FG B.AE2=EF EG C.AE2=EG FG D.AE2=EF AG
答案:B
解析:解答:∵四边形ABCD是平行四边形,
∴△ADE∽△EGB,△DEF∽△AEB,
∴=,=,
∴=,
即AE2=EF EG.
所以选项B正确,
故选B.
分析:解答此题的关键是利用平行四边形证明出△ADE∽△EGB,△DEF∽△AEB,然后利用对应边成比例即可解答此题.
13. 如图,△ABC中,AD⊥BC于D,下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③= ;④AB2=BD BC.其中一定能够判定△ABC是直角三角形的有( )
A. 1 B. 2 C. 3 D. 4
答案:B
解析:解答:(1)∠B+∠DAC=90°,该条件无法判定△ABC是直角三角形;
(2)∵∠B=∠DAC,∠BAD+∠B=90°,
∴∠BAD+∠DAC=90°,即∠BAC=90°,故该条件可以判定△ABC是直角三角形;
(3)=,该条件无法判定△ABC是直角三角形;
(4)∵AB2=BD BC,
∴=,
∵∠B=∠B,
∴△ABD∽△CBA,
∴∠BAC=90°,故该条件可以判定△ABC是直角三角形;
故选 B
分析:对题干中给出的条件逐一验证,证明∠BAC=90°即可解题.
14. 如图,在△ABC中,点D是AB边上一点,DE∥BC交AC于E,AD:DB=1:2,则△ADE与△ABC的面积之比为( )
A.1:2 B.1:4 C.1:8 D.1:9
答案:D
解析:解答:∵DE∥BC,
∴△ADE∽△ABC,
∴= ,
∵AD:DB=1:2,
∴==,
∴△ADE与△ABC的面积之比为:.
故选:D.
分析:首先利用相似三角形的判定与性质得出 = = ,进而利用相似三角形的面积比等于相似比的平方,得出答案即可.
15. 如图,△ABC中,E、D分别是AC、BC的中点,AD、BE交于点O,则S△DOE:S△AOB=( )
A.1:2 B.2:3 C.1:3 D.1:4
答案:D
解析:解答:∵△ABC中,E、D分别是AC、BC的中点,
∴DE=AB,DE∥AB,
∴△DOE∽△AOB,
∴S△DOE:S△AOB=1:4.
故选:D.
分析:根据三角形中位线定理可得DE= AB,DE∥AB,再根据平行线性质和相似三角形的判定与性质即可求解.
二、填空题
16. 如图,已知△ABC中,DE∥BC,AE:AC=1:3,EM、CN分别是∠AED、∠ACB的角平分线,EM=5,则CN= 15.
答案:15
解析:解答:∵EM、CN分别是∠AED、∠ACB的角平分线,
∴∠AEM=∠AED,∠ACN=∠ACB,
∵DE∥BC,
∴∠AED=∠ACB,
∴∠AEM=∠ACN,
∴EM∥CN,
∴△AEM∽△ACN,
∴=,
∵AE:AC=1:3,EM=5,
∴=,CN=15,
故答案为:15.
分析:根据角平分线定义得出∠AEM=∠AED,∠ACN=∠ACB,根据平行线性质得出∠AED=∠ACB,求出∠AEM=∠ACN,推出EM∥CN,得出△AEM∽△ACN,得出比例式= ,代入求出即可.
17. 如图,D是△ABC的边AC上的一点,若∠ABD=∠C,AB=6,AD=4,则线段CD的长为 5.
答案:5
解析:解答:∵∠ABD=∠C,∠BAD=∠CAB,
∴△ABD∽△ACB,
∴=,即=,
∴AC=9,
∴CD=AC-AD=5.
分析:由∠ABD=∠C,∠BAD=∠CAB,证出△ABD∽△ACB,得出AB:AC=AD:AB,求出AC的长,即可求出CD的长.
18. 如图,O是四边形ABCD对角线的交点,已知∠BAD+∠BCA=180°,AB=5,AC=4,AD=3,=,则BC= .
答案:
解析:解答:过D点作AO的平行线,交BA延长线于E点.
∵AO∥ED,
∴=,求得AE=,
∵AO∥ED,
∴∠BAC=∠AED,
∵∠BAD+∠BCA=180°,∠BAD+∠EAD=180°,
∴∠BCA=∠EAD,
∴△EAD∽△ACB,
∴=,
求得BC=.
故答案为:.
分析:过D点作AO的平行线,交BA延长线于E点,构建△ADE,根据题干中条件可证明△EAD∽△ACB,可以求得BC的值.
19. 如图,△ABC和△ECD均为等边三角形,B、C、D三点在一直线上,AD、BE相交于点F,DF=3,AF=4,则线段FE的长为 1.
答案:1
解析:解答:如图
可以认为△BCE是由△ACD逆时针转60°而得;那么CF的起始位是CF′,
∴CF=CF',
∵∠FCF'=60°,
∴△CFF′是等边△,
∴∠BFC=∠CFD=CF'F=60°,
∴CF平分∠DFB.
∵∠CAD+∠ACF=60°,∠ACF+∠FCE=60°,
∴△ACF∽△CEF,
∴= ,
∵△EFC∽△DF'C,EC=CD,
∴EF=F'D
∴FD=FF'+F'D=CF+EF=3,
解得EF=1.
分析:可证△CFF′是等边△,可得=,可证FD=CF+EF=3,根据EF,FC的关系即可求得EF的值.
20. 如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为 .
答案:
解析:解答::∵△ABC是等边三角形,
∴AB=BC=AC=3,∠B=∠C=60°,
∴∠BAP+∠APB=180°-60°=120°,
∵∠APD=60°,
∴∠APB+∠DPC=180°-60°=120°,
∴∠BAP=∠DPC,
即∠B=∠C,∠BAP=∠DPC,
∴△BAP∽△CPD,
∴=,
∵AB=BC=3,CP=BC-BP=3-1=2,BP=1,
即=,
解得:CD=,
故答案为:.
分析:根据等边三角形性质求出AB=BC=AC=3,∠B=∠C=60°,推出∠BAP=∠DPC,证△BAP∽△CPD,得出=,代入求出即可.
三、解答题
21. 如图,在平行四边形ABCD中,BC=6,点M在对角线AC上,AM=AC,过点M作EF∥AB,交AD于点E,交BC于点F,求ED的长.
答案:解答:∵四边形ABCD是平行四边形,
∴BC=AD=6,AB∥CD,
∵EF∥AB,
∴EM∥DC,
∴△AEM∽△ADC,
∴=,
∵AM=AC,
∴AE=AD=×6=2,
∴DE=6-2=4.
解析:
分析:根据平行四边形性质求出AD=6,推出EM∥CD,得出相似三角形,推出= ,根据AM=AC,求出AE= AD=2,即可求出答案.
22. 如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.
(1)求证:2EF=BD,
答案:解答:(1)∵DC=AC,CF为∠ACB的平分线,
∴AF=DF,
∵AE=EB,AF=DF,
∴EF为△ABD的中位线,
∴2EF=BD.
(2)四边形BDFE的面积为6,求△ABD的面积.
答案:解答:∵EF为△ABD的中位线,
∴EF∥BD,2EF=BD,
∴△AEF∽△ABD
∴两三角形相似比K=1:2,
∴=K2=,
则4(S△ABD-6)=S△ABD,
解得:S△ABD=8.
解析: 分析:(1)根据等腰三角形性质推出F为AD中点,根据三角形的中位线定理推出即可;
(2)根据三角形中位线推出EF∥BD,推出△AEF∽△ABD且两三角形相似比K=1:2,得出面积比是,代入求出即可.
23. 如图,梯形ABCD中,AB∥CD,AD=BC,点E在边AD上,BE与AC相交于点O,且∠ABE=∠BCA.
求证:(1)△BAE∽△BOA;
答案:解答:在梯形ABCD中,
∵AB∥CD,AD=BC,
∴∠EAB=∠CBA
∵∠EBA=∠BCA,
∴△EBA∽△ACB
∴∠AEB=∠BAC
∵∠ABE=∠OBA
∴△BAE∽△BOA
(2)BO BE=BC AE.
答案:解答:∵△BAE∽△BOA,
∴=
∵∠BAC=∠OAB,
∠EBA=∠BCA
∴△OAB∽△BAC
∴=
∴=
∴BE BO=AE BC
分析:(1)利用梯形的性质得到∠EAB=∠CBA,从而证得△EBA∽△ACB,然后利用相似三角形的性质得到∠AEB=∠BAC,从而证明△BAE∽△BOA;
(2)根据上题证得的△BAE∽△BOA得到= ,然后再利用∠BAC=∠OAB、∠EBA=∠BCA证得△OAB∽△BAC,从而得到= ,再根据=
得到BE BO=AE BC即可.
24. 如图,梯形ABCD中,AB∥DC,∠B=90°,E为BC上一点,且AE⊥ED.若BC=12,DC=7,BE:EC=1:2,
(1)求AB的长.
答案:解答:(1)∵AB∥DC,且∠B=90°,
∴∠AEB+∠BAE=90°及∠C=90度.
∴∠AEB+∠CED=90度.
故∠BAE=∠CED.
∴△EAB∽△DEC.
∴=
又BE:EC=1:2,且BC=12及DC=7,
故=
则AB=.
(2)求△AED的面积.
答案:解答:∵△EAB∽△DEC,
∴=
即:=
解得:CD=7
∴S△AED=S梯形ABCD-S△ABE-S△ECD=(AB+CD) BC-AB BE-EC CD=
(+7) 12-××4-×8×7=
分析:(1)由题意易知AB和CD所在的两个三角形相似,再利用相似比即可求出所求线段的长度.
(2)根据证得的△EAB∽△DEC利用相似三角形对应边的比成比例求得线段CD的长,利用梯形的面积减去两个三角形的面积即可求得三角形AED的面积.
25. 如图,已知E是正方形ABCD的边CD上一点,BF⊥AE于F,求证:AB2=AE BF.
答案:解答:∵∠ABF+∠DAE=90°,∠DAE+∠BAF=90°,
∴△ABF∽△AED,
∴=,
∴AD2=AE BF,
∵AB=AD,
∴AB2=AE BF.
分析:根据正方形内角为90°的性质可以求证△ABF∽△EAD,即可求得AD2=AE BF,AB=AD即可解题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 17 页 (共 18 页) 版权所有@21世纪教育网
