华师大版数学九年级上册第23章 23.3.4相似三角形的应用课时作业
文档属性
| 名称 | 华师大版数学九年级上册第23章 23.3.4相似三角形的应用课时作业 |
|
|
| 格式 | docx | ||
| 文件大小 | 350.8KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 00:00:00 | ||
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学九年级上册第23章第3节23.3.4相似三角形的应用
课时作业
一、选择题
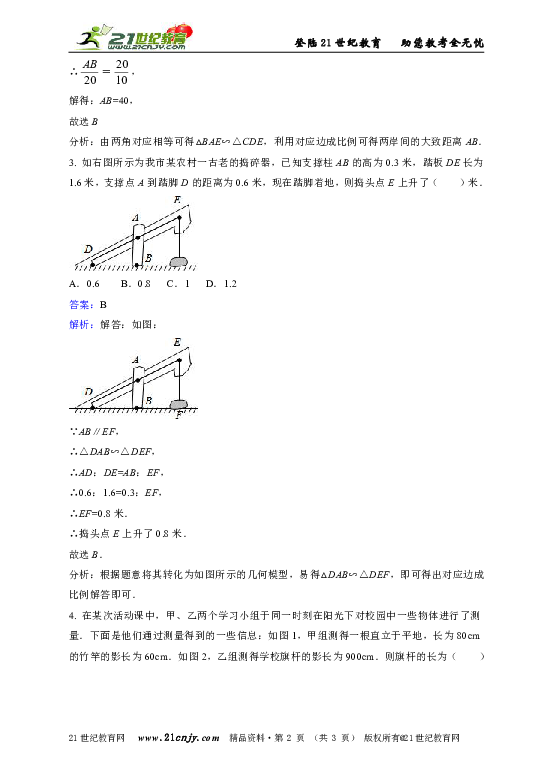
1. 如图,为估算学校的旗杆的高度,身高1.6米的小红同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m,BC=8m,则旗杆的高度是( )
A.6.4m B.7m C.8m D.9m
答案:C
解析:解答:设旗杆高度为h,
由题意得,h=8米.
故选:C.
分析:因为人和旗杆均垂直于地面,所以构成相似三角形,利用相似比解题即可.
2. 如图,为估算某河的宽度,在河岸边选定一个目标点A,在对岸取点B、C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A、E、D在同一条直线上,若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于( )
A.60m B.40m C.30m D.20m
答案:B
解析:解答:∵AB⊥BC,CD⊥BC,
∴△BAE∽△CDE,
∴=,
∵BE=20m,CE=10m,CD=20m,
∴=,
解得:AB=40,
故选B
分析:由两角对应相等可得△BAE∽△CDE,利用对应边成比例可得两岸间的大致距离AB.
3. 如右图所示为我市某农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1.6米,支撑点A到踏脚D的距离为0.6米,现在踏脚着地,则捣头点E上升了( )米.
A.0.6 B.0.8 C.1 D.1.2
答案:B
解析:解答:如图:
∵AB∥EF,
∴△DAB∽△DEF,
∴AD:DE=AB:EF,
∴0.6:1.6=0.3:EF,
∴EF=0.8米.
∴捣头点E上升了0.8米.
故选B.
分析:根据题意将其转化为如图所示的几何模型,易得△DAB∽△DEF,即可得出对应边成比例解答即可.
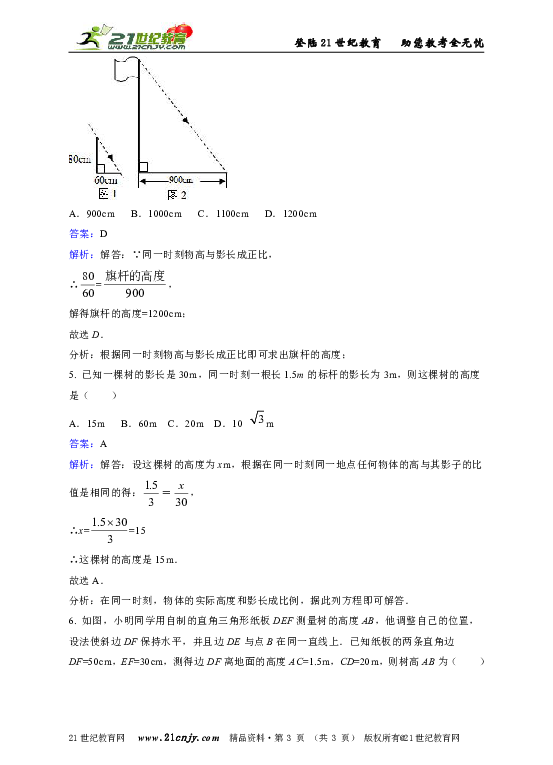
4. 在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为( )
A.900cm B.1000cm C.1100cm D.1200cm
答案:D
解析:解答:∵同一时刻物高与影长成正比,
∴=,
解得旗杆的高度=1200cm;
故选D.
分析:根据同一时刻物高与影长成正比即可求出旗杆的高度;
5. 已知一棵树的影长是30m,同一时刻一根长1.5m的标杆的影长为3m,则这棵树的高度是( )
A.15m B.60m C.20m D.10 m
答案:A
解析:解答:设这棵树的高度为xm,根据在同一时刻同一地点任何物体的高与其影子的比值是相同的得:=,
∴x==15
∴这棵树的高度是15m.
故选A.
分析:在同一时刻,物体的实际高度和影长成比例,据此列方程即可解答.
6. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树高AB为( )
A.12 m B.13.5 m C.15 m D.16.5 m
答案:D
解析:解答:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴=
∵DF=50cm=0.5m,EF=30cm=0.3m,AC=1.5m,CD=20m,
∴由勾股定理求得DE=40cm,
∴=
∴BC=15米,
∴AB=AC+BC=1.5+15=16.5米,
故选D.
分析:利用直角三角形DEF和直角三角形BCD相似求得BC的长后加上小明同学的身高即可求得树高AB.
7. 冬至时是一年中太阳相对于地球位置最低的时刻,只要此时能采到阳光,一年四季就均能受到阳光照射.此时竖一根a米长的竹杆,其影长为b米,某单位计划想建m米高的南北两幢宿舍楼(如图所示).当两幢楼相距多少米时,后楼的采光一年四季不受影响?( )
A. 米 B.米 C.米 D.abm米
答案:A
解析:解答:根据题意可得:=,
∵AB=m,
∴BC=,
∴两幢楼相距米时,后楼的采光一年四季不受影响.
故选A.
分析:运用同一时刻物体与影长成比例,得出=,进而求出即可.
8. 身高为1.8m的墨墨站在离路灯底部6m处时发现自己的影长恰好为2m,如图所示,则该路灯的高度是( )
A.5.4m B.6m C.7.2m D.8m
答案:C
解析:解答:如图,AB=1.8m,DB=6米,BE=2米,
∵△EAB∽△ECD,
∴=,
即:=,
解得:CD=7.2米,
故选C.
分析:如图,设AB为小亮,CD为路灯,DB=10米,利用相似三角形求得CD的长即可.
9. 在相同的时刻,太阳光下物高与影长成正比.如果高为1.5米的人的影长为2.5米,那么影长为30米的旗杆的高是( )
A.18米 B.16米 C.20米 D.15米
答案:A
解析:解答:根据题意解:标杆的高:标杆的影长=旗杆的高:旗杆的影长,
即1.5:2.5=旗杆的高:30,
∴旗杆的高= =18米.
故选A.
分析:在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
10. 如图,有一块锐角三角形材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使其一边在BC上,其余两个顶点分别在AB、AC上,则这个正方形零件的边长为( )
A.40mm B.45mm C.48mm D.60mm
答案:C
解析:解答:设正方形的边长为xmm,
则AK=AD-x=80-x,
∵EFGH是正方形,
∴EH∥FG,
∴△AEH∽△ABC,
∴= ,
即,
解得x=48mm,
故选C.
分析:设正方形的边长为x,表示出AI的长度,然后根据相似三角形对应高的比等于相似比列出比例式,然后进行计算即可得解.
11. 如图是小莹设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.4米,P=2.1米,PD=12米.那么该古城墙CD的高度是( )
A.6米 B.8米 C.10米 D.12米
答案:B
解析:解答:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP
∴=
即=
解得:CD=8米.
分析:由光学知识反射角等于入射角不难分析得出∠APB=∠CPD,再由∠ABP=∠CDP=90°得到△ABP∽△CDP,得到= 代入数值求的CD=8.
故选B.
12. 一个钢筋三角形框架三边长分别为20厘米,50厘米、60厘米,现要再做一个与其相似的钢筋三角形框架,而只有长是30厘米和50厘米的两根钢筋,要求以其中一根为边,从另一根上截下两段(允许有余料)作为两边,则不同的截法有( )
A.一种 B.二种 C.三种 D.四种
答案:B
解析:解答:①当把30厘米的钢筋作为最长边,把50厘米的钢筋按10厘米与25厘米两部分截,则:===;
②当30厘米的钢筋作为中长边,把50厘米分截出12厘米和36厘米两部分,
则有===.
③当30cm作为最短边:则另两边都会超过50cm,此时不合题意,
∴一共有两种截法.
故选B.
分析:①当把30厘米作为最长边,50厘米的钢筋截成10与25即可,利用三组对应边的相似比相等即可得所求三角形;②当把30厘米作为中长边,50厘米的钢筋截成12与36即可,③当30cm作为最短边,分别利用三组对应边的相似比相等即可得所求三角形.
13. 王大爷家有一块梯形形状土地,如图,AD∥BC,对角线AD,BC相交于点O,王大爷量得AD长3米,BC长9米,王大爷准备在△AOD处种大白菜,那么王大爷种大白菜的面积与整个土地的面积比为( )
A.1:14 B.3:14 C.1:16 D.3:16
答案:C
解析:解答:∵梯形ABCD中,AD∥BC,
∴△AOD∽△COB,
∵AD=3,BC=9,
即AD:BC=1:3,
∴△AOD与△BOC的面积比等于:1:9.
∵△ADO与△ABO等高,
∴S△ADO:S△ABO=OD:OB=AD:BC=1:3,
同理可得:S△ADO:S△DCO=OA:OC=AD:BC=1:3
∴王大爷种大白菜的面积与整个土地的面积比为1:16
故选C.
分析:由梯形ABCD中,AD∥BC,可得△AOD∽△COB,又由AD=3,BC=9,根据相似三角形的面积比等于相似比的平方,即可求得△AOD与△BOC的面积比.
14. 如图,AB是斜靠在墙上的一个梯子,梯脚B距墙1.4m,梯上点D距墙1.2m,BD长0.5m,则梯子的长为( )
A.3.5m B.3.85m C.4m D.4.2m
答案:A
解析:解答:∵△ADE∽△ABC,
∴AD:AB=DE:BC,
∴(AB-0.5):AB=1.2:1.4,
∴AB=3.5m.
∴梯子AB的长为3.5m.
故选A.
分析:有条件△ADE∽△ABC,可得相似三角形对应边成比例,解答即可.
15. 如图,路边有一根电线杆AB和一块正方形广告牌(不用考虑牌子的厚度).有一天,小明突然发现,在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上E点,已知BC=5米,正方形边长为2米,DE=4米.则此时电线杆的高度是( )米.
A.8 B.7 C.6 D.5
答案:D
解析:解答:过点G作GH∥BC,GM⊥BE,
根据题意,四边形BMGH是矩形,
∴BH=GM=2米,
△AHG∽△FDE,
∴=,
∴AH=3,
∴AB=2+3=5米.
故选D.
分析:过点G作GH∥BC,可得四边形BCGH是矩形,然后且△AHG与△FDE相似,然后根据相似三角形对应边成比例列式求出AH的长度,再加上BH即可.
二、填空题
16. 现有一个测试距离为5m的视力表,根据这个视力表,小华想制作一个测试距离为3m的视力表,则图中的= .
答案:
解析:解答:如图,依题意得△OAB∽△OCD
∴=
∴=.
分析:如图,易得△OAB∽△OCD,利用它们对应边成比例,即可容易得到题目的结论.
17. 晚上,身高1.6米的小华站在D处(如图),测得他的影长DE=1.5米,BD=4.5米,那么灯到地面的距离AB= 6.4米.
答案:6.4
解析:解答:根据题意画出图形,列方程.
设灯到地面的高度为h,根据相似三角形的性质可得到= ,
即= ,解得h=6.4米.
分析:根据题意,可以得出△ABE∽△CDE,根据相似三角形的对应边成比例,列出方程,通过解方程求出灯到地面的高度即可.
18. 如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,则小方行走的路程AC= 7.5米.
答案:7.5米
解析:解答:
∵AE⊥OD,FC⊥OD,
∴△AEB∽△OGB,
∴=,即 =
解得AB=2m;
∵OA所在的直线行走到点C时,人影长度增长3米,
∴DC=5m
同理可得△DFC∽△DGO,
∴=,即 =,
解得AC=7.5m.
故答案为7.5m.
分析:设出影长AB的长,利用身高与影长成正比可以求得AB的长,然后在利用相似三角形求得AC的长即可.
19. 如图,身高为1.6m的小李AB站在河的一岸,利用树的倒影去测对岸一棵树CD的高度,CD的倒影是C′D,且AEC′在一条视线上,河宽BD=12m,且BE=2m,则树高CD= 8m.
答案:8
解析:解答:利用△ABE∽△CDE,对应线段成比例解题,
因为AB,CD均垂直于地面,所以AB∥CD,
则有△ABE∽△CDE,
∵△ABE∽△CDE,
∴=,
又∵AB=1.6,BE=2,BD=12,
∴DE=10,
∴=,
∴CD=8.
故填8.
分析:利用相似三角形求对应线段成比例,求解即可.
20. 为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度为 5.6米.
答案:5.6
解析:解答:根据题意,易得∠CDE=∠ABE=90°,∠CED=∠AEB,
则△ABE∽△CDE,
则=,即=,
解得:AB=5.6米.
故答案为:5.6.
分析:根据镜面反射的性质求出△ABE∽△CDE,再根据其相似比解答.
三、解答题
21. 在同一时刻,身高1.6m的小强的影长是1.2m,旗杆的影长是15m,求旗杆高.
答案:解答:根据题意可得:设旗杆高为x.
根据在同一时刻身高与影长成比例可得:=
解得:x=20.
答:旗杆高20米.
分析:利用在同一时刻身高与影长成比例计算.
22. 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
答案:解答:根据题意得出:QR∥ST,
则△PQR∽△PST,
故= ,
∵QS=45m,ST=90m,QR=60m,
∴=,
解得:PQ=90(m),
∴河的宽度为90米.
分析:根据相似三角形的性质得出 = ,进而代入求出即可.
23. 如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积.
答案:解答:由已知得,DG∥BC
∴△ADG∽△ABC,
∵AH⊥BC
∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m)
=,
即DG==50(m),
∴S矩形DEFG=DE×DG=2000(m2).
分析:由于四边形DEFG是矩形,即DG∥EF,此时有∠ADG=∠B,∠AGD=∠C,所以△ADG∽△ABC,利用相似三角形的性质求得线段DG的长,最后求得矩形的面积.
24. 求证:一个人在两个高度相同的路灯之间行走,他前后的两个影子的长度之和是一个定值.
答案:解答:如图所示,CD、EF为路灯高度,AB为该人高度,BM、BN为该人前后的两个影子.
∵AB∥CD,
∴=,
∴=,
即 MB=DB.
同理BN=FB.
∴MB+BN=(DB+FB)=常数(定值).
分析:根据题意作出图象,利用相似三角形的性质说明即可.
25. 要测量旗杆高CD,在B处立标杆AB=2.5cm,人在F处.眼睛E、标杆顶A、旗杆顶C在一条直线上.已知BD=3.6m,FB=2.2m,EF=1.5m.求旗杆的高度.
答案:解答:过E作EH∥FD分别交AB、CD于G、H.
因为EF∥AB∥CD,所以EF=GB=HD.
所以AG=AB-GB=AB-EF=2.5-1.5=1m
EG=FB=2.2m,GH=BD=3.6m
CH=CD-1.5m
又因为=,
所以=
所以CD=4m,即旗杆的高4m
分析:过E作EH∥FD分别交AB、CD于G、H,根据EF∥AB∥CD可求出AG、EG、GH,再根据相似三角形的判定定理可得△EAG∽△ECH,再根据三角形的相似比解答即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 15 页 (共 15 页) 版权所有@21世纪教育网
华师大版数学九年级上册第23章第3节23.3.4相似三角形的应用
课时作业
一、选择题
1. 如图,为估算学校的旗杆的高度,身高1.6米的小红同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m,BC=8m,则旗杆的高度是( )
A.6.4m B.7m C.8m D.9m
答案:C
解析:解答:设旗杆高度为h,
由题意得,h=8米.
故选:C.
分析:因为人和旗杆均垂直于地面,所以构成相似三角形,利用相似比解题即可.
2. 如图,为估算某河的宽度,在河岸边选定一个目标点A,在对岸取点B、C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A、E、D在同一条直线上,若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于( )
A.60m B.40m C.30m D.20m
答案:B
解析:解答:∵AB⊥BC,CD⊥BC,
∴△BAE∽△CDE,
∴=,
∵BE=20m,CE=10m,CD=20m,
∴=,
解得:AB=40,
故选B
分析:由两角对应相等可得△BAE∽△CDE,利用对应边成比例可得两岸间的大致距离AB.
3. 如右图所示为我市某农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1.6米,支撑点A到踏脚D的距离为0.6米,现在踏脚着地,则捣头点E上升了( )米.
A.0.6 B.0.8 C.1 D.1.2
答案:B
解析:解答:如图:
∵AB∥EF,
∴△DAB∽△DEF,
∴AD:DE=AB:EF,
∴0.6:1.6=0.3:EF,
∴EF=0.8米.
∴捣头点E上升了0.8米.
故选B.
分析:根据题意将其转化为如图所示的几何模型,易得△DAB∽△DEF,即可得出对应边成比例解答即可.
4. 在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为( )
A.900cm B.1000cm C.1100cm D.1200cm
答案:D
解析:解答:∵同一时刻物高与影长成正比,
∴=,
解得旗杆的高度=1200cm;
故选D.
分析:根据同一时刻物高与影长成正比即可求出旗杆的高度;
5. 已知一棵树的影长是30m,同一时刻一根长1.5m的标杆的影长为3m,则这棵树的高度是( )
A.15m B.60m C.20m D.10 m
答案:A
解析:解答:设这棵树的高度为xm,根据在同一时刻同一地点任何物体的高与其影子的比值是相同的得:=,
∴x==15
∴这棵树的高度是15m.
故选A.
分析:在同一时刻,物体的实际高度和影长成比例,据此列方程即可解答.
6. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树高AB为( )
A.12 m B.13.5 m C.15 m D.16.5 m
答案:D
解析:解答:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴=
∵DF=50cm=0.5m,EF=30cm=0.3m,AC=1.5m,CD=20m,
∴由勾股定理求得DE=40cm,
∴=
∴BC=15米,
∴AB=AC+BC=1.5+15=16.5米,
故选D.
分析:利用直角三角形DEF和直角三角形BCD相似求得BC的长后加上小明同学的身高即可求得树高AB.
7. 冬至时是一年中太阳相对于地球位置最低的时刻,只要此时能采到阳光,一年四季就均能受到阳光照射.此时竖一根a米长的竹杆,其影长为b米,某单位计划想建m米高的南北两幢宿舍楼(如图所示).当两幢楼相距多少米时,后楼的采光一年四季不受影响?( )
A. 米 B.米 C.米 D.abm米
答案:A
解析:解答:根据题意可得:=,
∵AB=m,
∴BC=,
∴两幢楼相距米时,后楼的采光一年四季不受影响.
故选A.
分析:运用同一时刻物体与影长成比例,得出=,进而求出即可.
8. 身高为1.8m的墨墨站在离路灯底部6m处时发现自己的影长恰好为2m,如图所示,则该路灯的高度是( )
A.5.4m B.6m C.7.2m D.8m
答案:C
解析:解答:如图,AB=1.8m,DB=6米,BE=2米,
∵△EAB∽△ECD,
∴=,
即:=,
解得:CD=7.2米,
故选C.
分析:如图,设AB为小亮,CD为路灯,DB=10米,利用相似三角形求得CD的长即可.
9. 在相同的时刻,太阳光下物高与影长成正比.如果高为1.5米的人的影长为2.5米,那么影长为30米的旗杆的高是( )
A.18米 B.16米 C.20米 D.15米
答案:A
解析:解答:根据题意解:标杆的高:标杆的影长=旗杆的高:旗杆的影长,
即1.5:2.5=旗杆的高:30,
∴旗杆的高= =18米.
故选A.
分析:在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.
10. 如图,有一块锐角三角形材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使其一边在BC上,其余两个顶点分别在AB、AC上,则这个正方形零件的边长为( )
A.40mm B.45mm C.48mm D.60mm
答案:C
解析:解答:设正方形的边长为xmm,
则AK=AD-x=80-x,
∵EFGH是正方形,
∴EH∥FG,
∴△AEH∽△ABC,
∴= ,
即,
解得x=48mm,
故选C.
分析:设正方形的边长为x,表示出AI的长度,然后根据相似三角形对应高的比等于相似比列出比例式,然后进行计算即可得解.
11. 如图是小莹设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.4米,P=2.1米,PD=12米.那么该古城墙CD的高度是( )
A.6米 B.8米 C.10米 D.12米
答案:B
解析:解答:∵∠APB=∠CPD,∠ABP=∠CDP,
∴△ABP∽△CDP
∴=
即=
解得:CD=8米.
分析:由光学知识反射角等于入射角不难分析得出∠APB=∠CPD,再由∠ABP=∠CDP=90°得到△ABP∽△CDP,得到= 代入数值求的CD=8.
故选B.
12. 一个钢筋三角形框架三边长分别为20厘米,50厘米、60厘米,现要再做一个与其相似的钢筋三角形框架,而只有长是30厘米和50厘米的两根钢筋,要求以其中一根为边,从另一根上截下两段(允许有余料)作为两边,则不同的截法有( )
A.一种 B.二种 C.三种 D.四种
答案:B
解析:解答:①当把30厘米的钢筋作为最长边,把50厘米的钢筋按10厘米与25厘米两部分截,则:===;
②当30厘米的钢筋作为中长边,把50厘米分截出12厘米和36厘米两部分,
则有===.
③当30cm作为最短边:则另两边都会超过50cm,此时不合题意,
∴一共有两种截法.
故选B.
分析:①当把30厘米作为最长边,50厘米的钢筋截成10与25即可,利用三组对应边的相似比相等即可得所求三角形;②当把30厘米作为中长边,50厘米的钢筋截成12与36即可,③当30cm作为最短边,分别利用三组对应边的相似比相等即可得所求三角形.
13. 王大爷家有一块梯形形状土地,如图,AD∥BC,对角线AD,BC相交于点O,王大爷量得AD长3米,BC长9米,王大爷准备在△AOD处种大白菜,那么王大爷种大白菜的面积与整个土地的面积比为( )
A.1:14 B.3:14 C.1:16 D.3:16
答案:C
解析:解答:∵梯形ABCD中,AD∥BC,
∴△AOD∽△COB,
∵AD=3,BC=9,
即AD:BC=1:3,
∴△AOD与△BOC的面积比等于:1:9.
∵△ADO与△ABO等高,
∴S△ADO:S△ABO=OD:OB=AD:BC=1:3,
同理可得:S△ADO:S△DCO=OA:OC=AD:BC=1:3
∴王大爷种大白菜的面积与整个土地的面积比为1:16
故选C.
分析:由梯形ABCD中,AD∥BC,可得△AOD∽△COB,又由AD=3,BC=9,根据相似三角形的面积比等于相似比的平方,即可求得△AOD与△BOC的面积比.
14. 如图,AB是斜靠在墙上的一个梯子,梯脚B距墙1.4m,梯上点D距墙1.2m,BD长0.5m,则梯子的长为( )
A.3.5m B.3.85m C.4m D.4.2m
答案:A
解析:解答:∵△ADE∽△ABC,
∴AD:AB=DE:BC,
∴(AB-0.5):AB=1.2:1.4,
∴AB=3.5m.
∴梯子AB的长为3.5m.
故选A.
分析:有条件△ADE∽△ABC,可得相似三角形对应边成比例,解答即可.
15. 如图,路边有一根电线杆AB和一块正方形广告牌(不用考虑牌子的厚度).有一天,小明突然发现,在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上E点,已知BC=5米,正方形边长为2米,DE=4米.则此时电线杆的高度是( )米.
A.8 B.7 C.6 D.5
答案:D
解析:解答:过点G作GH∥BC,GM⊥BE,
根据题意,四边形BMGH是矩形,
∴BH=GM=2米,
△AHG∽△FDE,
∴=,
∴AH=3,
∴AB=2+3=5米.
故选D.
分析:过点G作GH∥BC,可得四边形BCGH是矩形,然后且△AHG与△FDE相似,然后根据相似三角形对应边成比例列式求出AH的长度,再加上BH即可.
二、填空题
16. 现有一个测试距离为5m的视力表,根据这个视力表,小华想制作一个测试距离为3m的视力表,则图中的= .
答案:
解析:解答:如图,依题意得△OAB∽△OCD
∴=
∴=.
分析:如图,易得△OAB∽△OCD,利用它们对应边成比例,即可容易得到题目的结论.
17. 晚上,身高1.6米的小华站在D处(如图),测得他的影长DE=1.5米,BD=4.5米,那么灯到地面的距离AB= 6.4米.
答案:6.4
解析:解答:根据题意画出图形,列方程.
设灯到地面的高度为h,根据相似三角形的性质可得到= ,
即= ,解得h=6.4米.
分析:根据题意,可以得出△ABE∽△CDE,根据相似三角形的对应边成比例,列出方程,通过解方程求出灯到地面的高度即可.
18. 如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,则小方行走的路程AC= 7.5米.
答案:7.5米
解析:解答:
∵AE⊥OD,FC⊥OD,
∴△AEB∽△OGB,
∴=,即 =
解得AB=2m;
∵OA所在的直线行走到点C时,人影长度增长3米,
∴DC=5m
同理可得△DFC∽△DGO,
∴=,即 =,
解得AC=7.5m.
故答案为7.5m.
分析:设出影长AB的长,利用身高与影长成正比可以求得AB的长,然后在利用相似三角形求得AC的长即可.
19. 如图,身高为1.6m的小李AB站在河的一岸,利用树的倒影去测对岸一棵树CD的高度,CD的倒影是C′D,且AEC′在一条视线上,河宽BD=12m,且BE=2m,则树高CD= 8m.
答案:8
解析:解答:利用△ABE∽△CDE,对应线段成比例解题,
因为AB,CD均垂直于地面,所以AB∥CD,
则有△ABE∽△CDE,
∵△ABE∽△CDE,
∴=,
又∵AB=1.6,BE=2,BD=12,
∴DE=10,
∴=,
∴CD=8.
故填8.
分析:利用相似三角形求对应线段成比例,求解即可.
20. 为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度为 5.6米.
答案:5.6
解析:解答:根据题意,易得∠CDE=∠ABE=90°,∠CED=∠AEB,
则△ABE∽△CDE,
则=,即=,
解得:AB=5.6米.
故答案为:5.6.
分析:根据镜面反射的性质求出△ABE∽△CDE,再根据其相似比解答.
三、解答题
21. 在同一时刻,身高1.6m的小强的影长是1.2m,旗杆的影长是15m,求旗杆高.
答案:解答:根据题意可得:设旗杆高为x.
根据在同一时刻身高与影长成比例可得:=
解得:x=20.
答:旗杆高20米.
分析:利用在同一时刻身高与影长成比例计算.
22. 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
答案:解答:根据题意得出:QR∥ST,
则△PQR∽△PST,
故= ,
∵QS=45m,ST=90m,QR=60m,
∴=,
解得:PQ=90(m),
∴河的宽度为90米.
分析:根据相似三角形的性质得出 = ,进而代入求出即可.
23. 如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积.
答案:解答:由已知得,DG∥BC
∴△ADG∽△ABC,
∵AH⊥BC
∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m)
=,
即DG==50(m),
∴S矩形DEFG=DE×DG=2000(m2).
分析:由于四边形DEFG是矩形,即DG∥EF,此时有∠ADG=∠B,∠AGD=∠C,所以△ADG∽△ABC,利用相似三角形的性质求得线段DG的长,最后求得矩形的面积.
24. 求证:一个人在两个高度相同的路灯之间行走,他前后的两个影子的长度之和是一个定值.
答案:解答:如图所示,CD、EF为路灯高度,AB为该人高度,BM、BN为该人前后的两个影子.
∵AB∥CD,
∴=,
∴=,
即 MB=DB.
同理BN=FB.
∴MB+BN=(DB+FB)=常数(定值).
分析:根据题意作出图象,利用相似三角形的性质说明即可.
25. 要测量旗杆高CD,在B处立标杆AB=2.5cm,人在F处.眼睛E、标杆顶A、旗杆顶C在一条直线上.已知BD=3.6m,FB=2.2m,EF=1.5m.求旗杆的高度.
答案:解答:过E作EH∥FD分别交AB、CD于G、H.
因为EF∥AB∥CD,所以EF=GB=HD.
所以AG=AB-GB=AB-EF=2.5-1.5=1m
EG=FB=2.2m,GH=BD=3.6m
CH=CD-1.5m
又因为=,
所以=
所以CD=4m,即旗杆的高4m
分析:过E作EH∥FD分别交AB、CD于G、H,根据EF∥AB∥CD可求出AG、EG、GH,再根据相似三角形的判定定理可得△EAG∽△ECH,再根据三角形的相似比解答即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 15 页 (共 15 页) 版权所有@21世纪教育网
