期末素养质量检测卷(三)(含解析)-2024-2025学年六年级下册数学北师大版
文档属性
| 名称 | 期末素养质量检测卷(三)(含解析)-2024-2025学年六年级下册数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 398.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 05:10:59 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末素养质量检测卷(三)-2024-2025学年六年级下册数学北师大版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个等底等高的圆柱和圆锥,如果圆锥的高增加18cm,那么圆柱和圆锥的体积相等。已知圆锥的底面半径是5cm,则原来圆锥的体积是( )立方厘米。
A.50π B.75π C.100π D.200π
2.一袋盐的价格是2.5元,妈妈买的盐的袋数和所花钱的总数( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
3.下列不能用比例“2∶4=3∶X”解决的是( )。
A.2支铅笔可以换4块橡皮,3支铅笔可以换X块橡皮。
B.一辆汽车2分钟行驶4千米,按这个速度,3分钟可以行驶X千米。
C.一根钢筋,截成2段要4分钟,按这个速度,截成3段要X分钟。
D.长4厘米,宽2厘米的长方形按一定的比放大后,长是X厘米,宽是3厘米。
4.从4时到7时,钟表上的时针绕中心点( )。
A.顺时针旋转60° B.逆时针旋转60°
C.顺时针旋转90° D.逆时针旋转90°
5.一个底面半径为6cm、高为10cm的圆柱,将它的侧面沿虚线剪开(如图),得到的平行四边形的面积是( )cm2。
A.60π B.120π C.360π D.无法确定
二、填空题
6.去年6月17日我国第三艘航空母舰“福建号”成功下水,据悉它的长是320米,宽是78米,排水量8万余吨。如果按照的比例尺制作“福建号”模型,长应是( )厘米,宽应是( )厘米。
7.把一根圆柱形木料截成3段,表面积比原来增加了45.12平方厘米,这根木料的底面积是( )平方厘米。
8.我国首艘国产航母山东舰的长度约是315m,宽度约是75m,如果按照1∶500的比例尺制作山东舰模型,长应是( )cm,宽应是( )cm。
9.一个圆柱的底面周长是25.12分米,侧面积是251.2平方分米。这个圆柱的高是( )分米,体积是( )立方分米。
10.一个数与3、6、9正好可以组成比例,那么这个数可能( )。(不止一种情况,请写完整哟。)
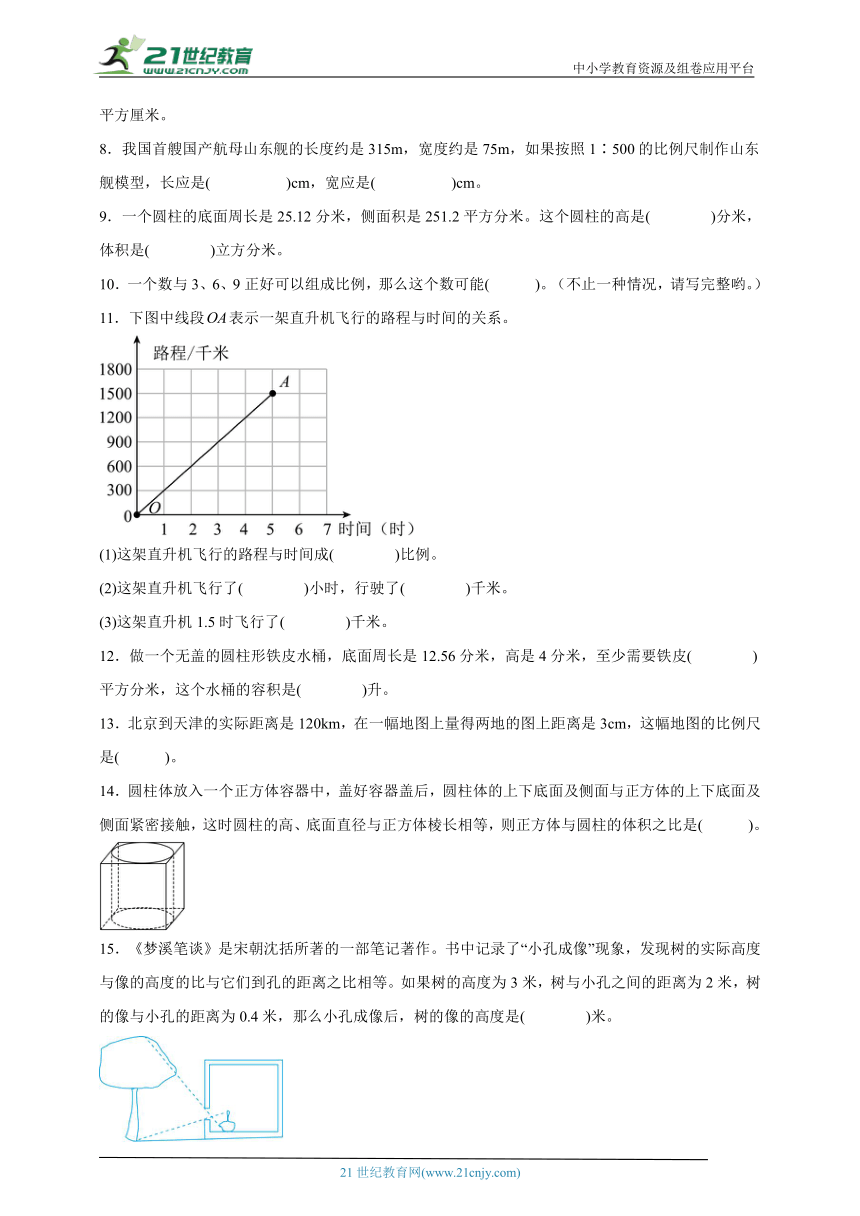
11.下图中线段表示一架直升机飞行的路程与时间的关系。
(1)这架直升机飞行的路程与时间成( )比例。
(2)这架直升机飞行了( )小时,行驶了( )千米。
(3)这架直升机1.5时飞行了( )千米。
12.做一个无盖的圆柱形铁皮水桶,底面周长是12.56分米,高是4分米,至少需要铁皮( )平方分米,这个水桶的容积是( )升。
13.北京到天津的实际距离是120km,在一幅地图上量得两地的图上距离是3cm,这幅地图的比例尺是( )。
14.圆柱体放入一个正方体容器中,盖好容器盖后,圆柱体的上下底面及侧面与正方体的上下底面及侧面紧密接触,这时圆柱的高、底面直径与正方体棱长相等,则正方体与圆柱的体积之比是( )。
15.《梦溪笔谈》是宋朝沈括所著的一部笔记著作。书中记录了“小孔成像”现象,发现树的实际高度与像的高度的比与它们到孔的距离之比相等。如果树的高度为3米,树与小孔之间的距离为2米,树的像与小孔的距离为0.4米,那么小孔成像后,树的像的高度是( )米。
三、判断题
16.一个圆柱侧面沿一条高剪开后展开是一个正方形,这个圆柱底面周长与高的比是1∶1。( )
17.一个圆柱和一个圆锥等底等高,体积和是251.2立方米,这个圆锥的体积是62.8立方米。( )
18.在钟表上,时针从“5”指向“7”绕中心点按顺时针方向旋转了30°。( )
19.车轮直径一定,所行驶的路程和车轮转数成正比例。( )
20.在一个比例中,两个内项互为倒数,如果其中一个外项是4,那么另一个外项是0.25。( )
四、计算题
21.直接写出得数.
1.6×0.4 = 4.2÷= ×= 10-0.09=
÷36= += ×4÷×4= 3.34+66%=
22.计算下面各题。
1.8×+2.2×25%
9∶3=x∶4
23.解方程。
24.计算下面图形的体积。
五、解答题
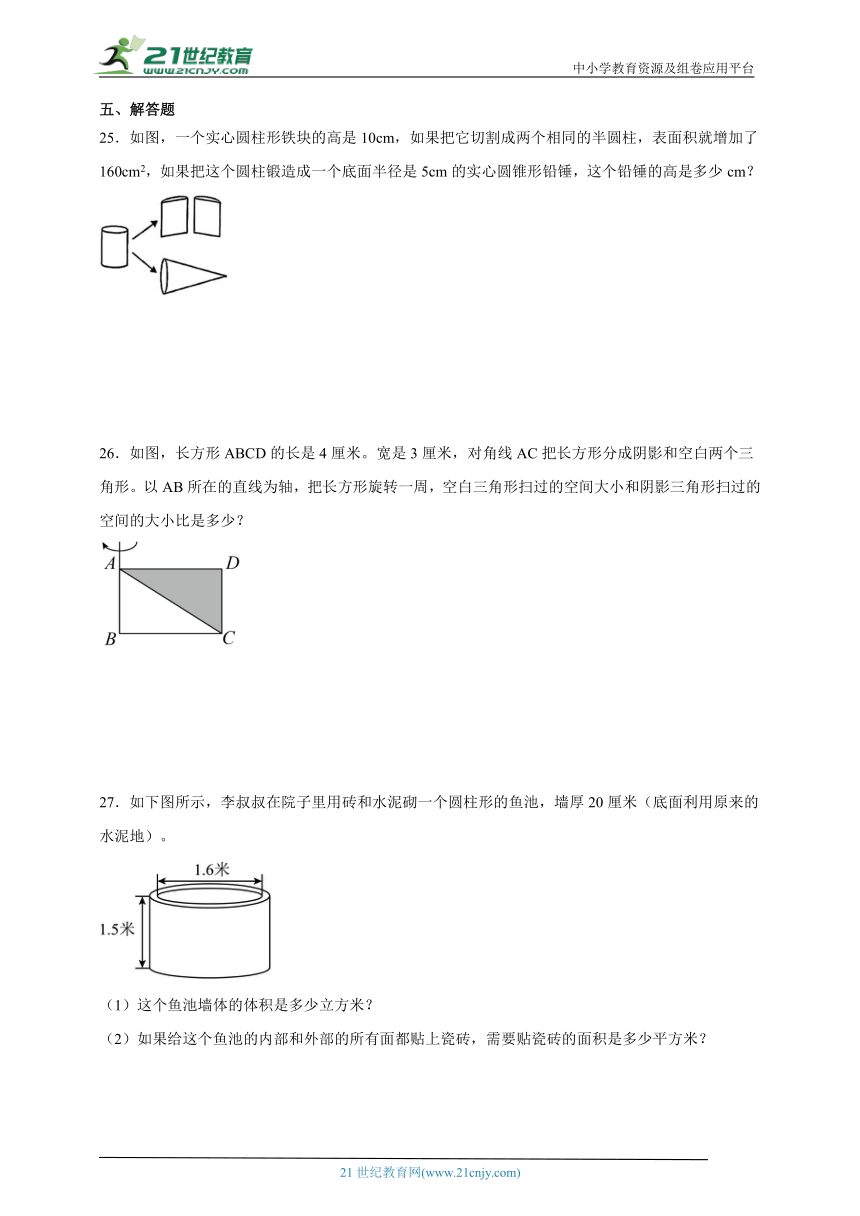
25.如图,一个实心圆柱形铁块的高是10cm,如果把它切割成两个相同的半圆柱,表面积就增加了160cm2,如果把这个圆柱锻造成一个底面半径是5cm的实心圆锥形铅锤,这个铅锤的高是多少cm?
26.如图,长方形ABCD的长是4厘米。宽是3厘米,对角线AC把长方形分成阴影和空白两个三角形。以AB所在的直线为轴,把长方形旋转一周,空白三角形扫过的空间大小和阴影三角形扫过的空间的大小比是多少?
27.如下图所示,李叔叔在院子里用砖和水泥砌一个圆柱形的鱼池,墙厚20厘米(底面利用原来的水泥地)。
(1)这个鱼池墙体的体积是多少立方米?
(2)如果给这个鱼池的内部和外部的所有面都贴上瓷砖,需要贴瓷砖的面积是多少平方米?
28.青白江区城市森林和谐广场位于青白江区华金大道二段,是青白江百姓休闲、娱乐的重要场所。把它绘制在比例尺为1∶5000的地图上,该广场平面图是一个长约是5厘米,宽约是3厘米的长方形。请问该广场实际面积约是多少平方米?
29.小明家把今年收获的小麦堆成了圆锥形,高3米,底面直径是4米。
(1)如果每立方米小麦重700千克,这堆小麦重多少千克?
(2)如果把这堆小麦倒入一个底面直径为2米的圆柱形铁桶中刚好装满,那么铁桶高多少米?
30.一个圆柱沿直径切开表面积增加12平方厘米,如果切成三个小圆柱,表面积增加48平方厘米,则原来圆柱的体积是多少立方厘米?(π取3)
31.师徒两人加工一批零件,由师傅独做需37小时,徒弟每小时能加工30个零件,现由师徒两人同时加工,完成任务时,徒弟加工的个数是师傅的。这批零件共有多少个?
32.陀螺是中国民间最早的娱乐工具之一,下图是一种木制玩具陀螺,可以看作是一个近似的圆锥和圆柱组合起来的立体图形。它的底面半径是3厘米,圆柱部分的高是6厘米(即AB=6厘米),圆锥部分的高是3厘米(即BC=3厘米)。这个木质陀螺的体积是多少立方厘米?
《期末素养质量检测卷(三)-2024-2025学年六年级下册数学北师大版》参考答案
1.B
【分析】等底等高的圆柱的体积是圆锥体积的3倍,圆锥的高增加18厘米后,圆锥与圆柱的体积相等,说明圆锥体积增加了2倍,即高增加了2倍,先算出圆锥原来的高,再根据公式:圆锥的体积=×底面积×高,算出原来圆锥的体积,据此解答。
【详解】18÷2=9(厘米)
×π×52×9
=×π×25×9
=75π(立方厘米)
即原来圆锥的体积是75π立方厘米。
故答案为:B
2.A
【分析】当两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,这两种量就成正比例关系;如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,这两种量就成反比例关系。
【详解】根据总价÷数量=单价可知,妈妈所花钱的总数÷买的盐的袋数=2.5(元/袋),一袋盐的价格是固定的,所以妈妈所花钱的总数与买的盐的袋数的比值一定,因此妈妈买的盐的袋数和所花钱的总数成正比例关系。因为妈妈所花钱的总数与买的盐的袋数的比值一定,而不是积一定,因此妈妈所花钱的总数与买的盐的袋数不成反比例。
故答案为:A
3.C
【分析】表示两个比相等的式子叫作比例;
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,这两种量就成正比例关系。
通过判断每个选项是否能构成比例关系来解决问题,据此解答。
【详解】A.因为2支铅笔可以换4块橡皮,所以每支铅笔能换的橡皮数是一定的,可列出比例2∶4=3∶X,所以此选项能用该比例解决;
B.汽车速度一定,路程与时间成正比例,可列出比例2∶4=3∶X,所以此选项能用该比例解决;
C.一根钢筋截成2段需要截1次,用时4分钟,截成3段需要截2次,总共用时8分钟,因为截的次数比段数少1,截的次数与段数之间的关系并不是正比例关系,所以不能列出比例2∶4=3∶X,所以此选项不能用该比例解决。
D.长方形放大比例一定,长和宽成正比例,可列出比例2∶4=3∶X,所以此选项能用该比例解决。
故答案为:C
4.C
【分析】钟表的表盘是圆形,圆心角是360°,上面有12大格,则每大格的圆心角是360°÷12=30°。从4时到7时,时针绕中心点顺时针走了3大格,30°×3=90°,即顺时针旋转90°。
【详解】通过分析可得:
360°÷12=30°
7-4=3
30°×3=90°
则钟表上的时针绕中心点顺时针旋转90°。
故答案为:C
5.B
【分析】平行四边形的面积就是圆柱的侧面积,根据圆柱的侧面积公式,代入数据计算即可。
【详解】2×π×6×10
=12π×10
=120π(cm2)
这个平行四边形的面积是(120π)cm2。
故答案为:B
6. 16 3.9
【分析】根据图上距离实际距离比例尺,代入数据解答。同时注意答案中单位,根据1米=100厘米,在答案中做相应变化。
【详解】320米=32000厘米
78米=7800厘米
(厘米)
(厘米)
长应是16厘米,宽应是3.9厘米。
7.11.28
【分析】根据题意,圆柱形木料截成3段后,总的表面积增加了4个底面积,所以用45.12平方厘米除以4,即可求出这根木料的底面积。
【详解】(平方厘米)
即这根木料的底面积是11.28平方厘米。
8. 63 15
【分析】图上距离=实际距离×比例尺,1米=100厘米,据此进行换算即可。
【详解】315×=0.63(m)=63(cm)
75×=0.15(m)=15(cm)
长应是63cm,宽应是15cm。
9. 10 502.4
【分析】根据圆柱的高=侧面积÷底面周长,底面半径=底面周长÷圆周率÷2,圆柱的体积=底面积×高,列式计算即可。
【详解】251.2÷25.12=10(分米)
3.14×(25.12÷3.14÷2)2×10
=3.14×42×10
=3.14×16×10
=502.4(立方分米)
这个圆柱的高是10分米,体积是502.4立方分米。
10.4.5、2、18
【分析】比值相等的两个比组成比例,比的比值等于前项除以后项,可先将3、6、9三个数组成一个比,得到比值后,再计算得出另一个比。据此可得出答案。
【详解】一个数与3、6、9可以组成比例:3∶6=,,即3∶6=4.5∶9;
3∶9=,,即组成比例:;
6∶9=,,即组成比例:。
3∶6=,,即组成比例:
即这个数可能是:4.5、2、18。
11.(1)正
(2) 5 1500
(3)450
【分析】(1)正比例图像是一条经过原点的射线,反比例图像是一条平滑的曲线,据此解答即可;
(2)点A可以用数对(5,1500)表示,即直升机飞行了5小时,行驶了1500千米;
(3)根据路程÷时间=速度,据此求出直升机的速度,再根据速度×时间=路程,据此解答即可。
【详解】(1)这架直升机飞行的路程与时间成正比例。
(2)这架直升机飞行了5小时,行驶了1500千米。
(3)1500÷5×1.5
=300×1.5
=450(千米)
这架直升机1.5时飞行了450千米。
12. 62.8 50.24
【分析】将底面周长除以3.14再除以2,求出底面半径。根据“圆面积=πr2”求出圆柱形水桶的底面积,根据“圆柱侧面积=底面周长×高”求出圆柱的侧面积。将底面积和侧面积相加,求出需要的铁皮面积。圆柱容积=底面积×高,据此列式求出这个水桶的容积。
【详解】12.56÷3.14÷2=2(分米)
3.14×22+12.56×4
=3.14×4+50.24
=12.56+50.24
=62.8(平方分米)
3.14×22×4
=3.14×4×4
=50.24(立方分米)
50.24立方分米=50.24升
所以,至少需要铁皮62.8平方分米,这个水桶的容积是50.24升。
13.1∶4000000
【分析】一幅图的图上距离与实际距离的比,叫作这幅图的比例尺,比例尺=图上距离∶实际距离,据此解答。
【详解】比例尺:3cm∶120km
=3cm∶12000000cm
=3∶120000000
=1∶4000000
所以这幅地图的比例尺是:1∶4000000。
【点睛】本题考查比例尺,解答本题的关键是掌握比例尺的计算方法。
14.200∶157
【分析】圆柱的高、底面直径与正方体的棱长相等,可设正方体的棱长为具体数字,则可分别计算出正方体的体积与圆柱的体积,再计算正方体与圆柱的体积比。
【详解】假设正方体的棱长为6厘米,则圆柱的高和底面直径也为6厘米。
正方体的体积:6×6×6=216(立方厘米)
圆柱的体积:3.14×(6÷2)2×6
=3.14×32×6
=3.14×9×6
=28.26×6
=169.56(立方厘米)
216∶169.56=200∶157
故正方体与圆柱的体积之比是200∶157。
15.0.6/
【分析】设小孔成像后,树的像的高度是x米,根据“小孔成像”现象:树的实际高度与像的高度的比与它们到孔的距离之比相等,据此列出比例,解比例即可解答。
【详解】解:设小孔成像后,树的像的高度是x米。
因此小孔成像后,树的像的高度是0.6米。
16.√
【分析】如果圆柱的侧面展开是一个正方形,那么圆柱的底面周长=圆柱的高,再根据比的意义即可求出圆柱的底面周长与高的比是多少。
【详解】由分析可知:
圆柱的底面周长=圆柱的高,所以这个圆柱底面周长与高的比是1∶1。
故答案为:√
【点睛】本题主要考查圆柱的展开图的特点,要清楚的知道圆柱展开图的特点是解题的关键。
17.√
【分析】根据圆柱与圆锥的体积关系:等底等高的圆柱体积是圆锥体积的3倍,则等底等高圆柱体积+圆锥体积=圆锥体积×4,据此可计算得出答案。
【详解】等地等高的圆柱体积是圆锥体积的3倍,则等底等高圆柱体积+圆锥体积=圆锥体积×4,体积和是251.2立方米,则圆锥体积为:251.2÷4=62.8(立方米)。题干表述正确。
故答案为:√
18.×
【分析】钟表上有12大格,每大格的圆心角是360°÷12=30°。时针从“5”指向“7”走了2大格,30°×2=60°,则时针从“5”指向“7”绕中心点按顺时针方向旋转了60°。
【详解】通过分析可得:
360°÷12=30°
30°×2=60°
时针从“5”指向“7”绕中心点按顺时针方向旋转了60°。原题说法错误。
故答案为:×
19.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为直径一定,π是定值,所以π×直径=周长,周长一定,即路程÷转数=周长(一定),所以,所行路程和车轮转数成正比例。
故答案为:√
20.√
【分析】在比例里,两外项之积等于两内项之积,如果两个内项互为倒数,则积是1,两外项的积也是1,用1除以其中的一个外项,看是否等于另一个外项即可判断。
【详解】1÷4=0.25
所以在一个比例中,两个内项互为倒数,如果其中一个外项是4,那么另一个外项是0.25。
原题说法正确。
故答案为:√
21.6.4 ;21 ; ;9.91 ; ; ;16 ;4
【详解】略
22.;49;1
x=12;x=12.25
【分析】将除以转化成乘,再根据乘法分配律进行简算;
根据乘法分配律进行简算;
将和25%都转换成0.25,再根据乘法分配律进行简算;
根据比例的性质,即内项之积等于外项之积,把比例转换成方程后,利用等式的性质,方程两边同时除以3进行计算即可;
根据比例的性质,即内项之积等于外项之积,把比例转换成方程后,利用等式的性质,方程两边同时除以8进行计算即可。
【详解】
=×+×
=×(+)
=×1
=
=×36+×36-×36
=28+30-9
=58-9
=49
1.8×+2.2×25%
=1.8×0.25+2.2×0.25
=(1.8+2.2)×0.25
=4×0.25
=1
9∶3=x∶4
解:3x=4×9
3x=36
x=36÷3
x=12
解:8x=7×14
8x=98
x=98÷8
x=12.25
23.;;
【分析】,根据等式的性质1和2,两边同时-39,再同时÷13即可;
,先将左边合并成,根据等式的性质2,两边同时÷3即可;
,根据比例的基本性质,比例的两内项积=两外项积,先写成的形式,两边同时÷即可。
【详解】
解:
解:
解:
24.84.56立方厘米
【分析】根据题意,图中有2个立体图形:圆锥体、长方体,那么他们的体积之和即为整个图形的体积。圆锥体的体积:圆锥体积=底面积×高÷3,长方体的体积=长×宽×高,将数值代入公式计算出结果即可。
【详解】圆锥体积=底面积×高÷3=πr2×3÷3
底面圆半径=4÷2=2(厘米)
3.14×22×3÷3
=3.14×4×3÷3
=12.56(立方厘米)
长方体的体积=长×宽×高
=6×6×2
=36×2
=72(立方厘米)
12.56+72=84.56(立方厘米)
答:图形的体积是84.56立方厘米。
25.19.2cm
【分析】增加的面积是以圆柱形铁块的高为长、圆柱的底面直径为宽的两个长方形的面积,据此用160除以2,求出一个长方形的面积,再用一个长方形的面积除以圆柱形铁块的高就是底面直径,再除以2就是圆柱形铁块的底面半径,再根据圆柱的体积=求出圆柱形铁块的体积,也就是半径是5cm的实心圆锥形铅锤的体积,再根据圆锥的高=圆锥体积的3倍÷底面积解答即可。
【详解】160÷2÷10÷2
=80÷10÷2
=8÷2
=4(cm)
=16×10×3÷25
=160×3÷25
=480÷25
=19.2(cm)
答:这个铅锤的高是19.2cm。
26.1∶2
【分析】根据题意可知,长方形扫过的空间是一个底面半径是4厘米,高是3厘米的圆柱;空白三角形出扫过的空间是一个底面半径是4厘米,高是3厘米的圆锥,由此可知,圆柱与圆锥的等底等高;圆柱的体积是圆锥体积的3倍;阴影三角形扫过的体积等于圆柱的体积-圆锥的体积;可以将圆锥的体积看做1,那么圆柱的体积就是3,那么阴影扫过的空间的大小就是3-1=2,据此求出空白三角形扫过的空间大小和阴影三角形扫过的空间的大小的比。
【详解】长方形扫过的空间是一个圆柱体;空白三角形扫过的空间是一个圆锥体;它们是等底等高;
设圆锥的体积是1;
则圆柱的体积是:1×3=3;
阴影三角形扫过的体积是:3-1=2;
三角形扫过的空间大小和阴影三角形扫过的空间的大小比是=1∶2。
答:三角形扫过的空间大小和阴影三角形扫过的空间的大小比是1∶2。
27.(1)1.6956立方米
(2)20.096平方米
【分析】(1)根据题意可知,鱼池墙体的体积=大圆柱的体积-小圆柱的体积;根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答,注意单位名数的统一。
(2)需要贴瓷砖的面积=大圆柱的侧面积+大圆柱的底面积+小圆柱侧面积,根据圆柱的侧面积公式:侧面积=底面周长×高,圆柱的底面积公式:底面积=,代入数据,即可解答。
【详解】(1)20厘米=0.2米
1.6÷2=0.8(米)
0.8+0.2=1(米)
3.14×12×1.5-3.14×0.82×1.5
=3.14×1×1.5-3.14×0.64×1.5
=3.14×1.5-2.0096×1.5
=4.71-3.0144
=1.6956(立方米)
答:这个鱼池墙的体积是1.6956立方米。
(2)3.14×1×2×1.5+3.14×12+3.14×1.6×1.5
=3.14×2×1.5+3.14×1+5.024×1.5
=6.28×1.5+3.14+7.536
=9.42+3.14+7.536
=12.56+7.356
=20.096(平方米)
答:需要贴瓷砖的面积是20.096平方米。
28.37500平方米
【分析】由题可知该广场的长和宽的图上距离分别是5厘米和3厘米,根据公式:实际距离=图上距离÷比例尺,代入数据进行计算,可以求出该广场的长和宽的实际距离,再根据1米=100厘米进行单位换算,最后根据长方形的面积=长×宽,代入数据计算,即可求出该广场实际面积,据此解答。
【详解】(厘米)
(厘米)
25000厘米=250米
15000厘米=150米
250×150=37500(平方米)
答:该广场实际面积约是37500平方米。
29.(1)8792千克
(2)4米
【分析】(1)根据圆锥体积=底面积×高÷3,求出小麦体积,小麦体积×每立方米质量=这堆小麦的质量;
(2)根据圆柱的高=体积÷底面积,列式解答即可。
【详解】(1)3.14×(4÷2)2×3÷3
=3.14×22×3÷3
=3.14×4×3÷3
=12.56(立方米)
12.56×700=8792(千克)
答:这堆小麦重8792千克。
(2)12.56÷[3.14×(2÷2)2]
=12.56÷[3.14×12]
=12.56÷[3.14×1]
=12.56÷3.14
=4(米)
答:铁桶高4米。
30.18立方厘米
【分析】切成三个小圆柱,则增加了4个底面积,用求出底面积,再根据圆的面积公式的逆运算,求出半径,再用半径乘2得到直径;圆柱沿直径切开表面积增加12平方厘米,即增加了2个底面直径乘高的面积,用12除以2,再除以直径得到高;最后根据,代入数据计算即可得解。
【详解】48÷4÷3=4(平方厘米)
因为2×2=4,所以这个圆柱的底面半径是2厘米。
所以圆柱的高是:12÷2÷(2×2)
=12÷2÷4
=6÷4
=1.5(厘米)
则圆柱的体积是:48÷4×1.5
=12×1.5
=18(立方厘米)
答:原来圆柱的体积是18立方厘米。
31.1998个
【分析】师徒两人同时开始加工到完成任务所花的时间相同。因为工作时间一定,工作效率和工作总量成正比例所以徒弟的工作效率与师傅的比值还是,把师傅的工作效率看作单位“1”,根据已知一个数的几分之几是多少,求这个数用除法计算,可求出师傅的工作效率,再根据,代入数据计算即可得解。
【详解】
(个)
答:这批零件共有1998个。
32.197.82立方厘米
【分析】从图中可知,这个陀螺的体积等于圆柱部分的体积加上圆锥部分的体积,其中圆柱部分的底面半径和圆锥部分的底面半径相等;根据圆柱的体积=πr2h1 ,圆锥的体积=×πr2h2,代入相应数值计算,即可解答。
【详解】3.14×32×6+×3.14×32×3
=3.14×9×6+×3.14×9×3
=3.14×9×(6+×3)
=28.26×(6+1)
=28.26×7
=197.82(立方厘米)
答:这个木质陀螺的体积是197.82立方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末素养质量检测卷(三)-2024-2025学年六年级下册数学北师大版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个等底等高的圆柱和圆锥,如果圆锥的高增加18cm,那么圆柱和圆锥的体积相等。已知圆锥的底面半径是5cm,则原来圆锥的体积是( )立方厘米。
A.50π B.75π C.100π D.200π
2.一袋盐的价格是2.5元,妈妈买的盐的袋数和所花钱的总数( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
3.下列不能用比例“2∶4=3∶X”解决的是( )。
A.2支铅笔可以换4块橡皮,3支铅笔可以换X块橡皮。
B.一辆汽车2分钟行驶4千米,按这个速度,3分钟可以行驶X千米。
C.一根钢筋,截成2段要4分钟,按这个速度,截成3段要X分钟。
D.长4厘米,宽2厘米的长方形按一定的比放大后,长是X厘米,宽是3厘米。
4.从4时到7时,钟表上的时针绕中心点( )。
A.顺时针旋转60° B.逆时针旋转60°
C.顺时针旋转90° D.逆时针旋转90°
5.一个底面半径为6cm、高为10cm的圆柱,将它的侧面沿虚线剪开(如图),得到的平行四边形的面积是( )cm2。
A.60π B.120π C.360π D.无法确定
二、填空题
6.去年6月17日我国第三艘航空母舰“福建号”成功下水,据悉它的长是320米,宽是78米,排水量8万余吨。如果按照的比例尺制作“福建号”模型,长应是( )厘米,宽应是( )厘米。
7.把一根圆柱形木料截成3段,表面积比原来增加了45.12平方厘米,这根木料的底面积是( )平方厘米。
8.我国首艘国产航母山东舰的长度约是315m,宽度约是75m,如果按照1∶500的比例尺制作山东舰模型,长应是( )cm,宽应是( )cm。
9.一个圆柱的底面周长是25.12分米,侧面积是251.2平方分米。这个圆柱的高是( )分米,体积是( )立方分米。
10.一个数与3、6、9正好可以组成比例,那么这个数可能( )。(不止一种情况,请写完整哟。)
11.下图中线段表示一架直升机飞行的路程与时间的关系。
(1)这架直升机飞行的路程与时间成( )比例。
(2)这架直升机飞行了( )小时,行驶了( )千米。
(3)这架直升机1.5时飞行了( )千米。
12.做一个无盖的圆柱形铁皮水桶,底面周长是12.56分米,高是4分米,至少需要铁皮( )平方分米,这个水桶的容积是( )升。
13.北京到天津的实际距离是120km,在一幅地图上量得两地的图上距离是3cm,这幅地图的比例尺是( )。
14.圆柱体放入一个正方体容器中,盖好容器盖后,圆柱体的上下底面及侧面与正方体的上下底面及侧面紧密接触,这时圆柱的高、底面直径与正方体棱长相等,则正方体与圆柱的体积之比是( )。
15.《梦溪笔谈》是宋朝沈括所著的一部笔记著作。书中记录了“小孔成像”现象,发现树的实际高度与像的高度的比与它们到孔的距离之比相等。如果树的高度为3米,树与小孔之间的距离为2米,树的像与小孔的距离为0.4米,那么小孔成像后,树的像的高度是( )米。
三、判断题
16.一个圆柱侧面沿一条高剪开后展开是一个正方形,这个圆柱底面周长与高的比是1∶1。( )
17.一个圆柱和一个圆锥等底等高,体积和是251.2立方米,这个圆锥的体积是62.8立方米。( )
18.在钟表上,时针从“5”指向“7”绕中心点按顺时针方向旋转了30°。( )
19.车轮直径一定,所行驶的路程和车轮转数成正比例。( )
20.在一个比例中,两个内项互为倒数,如果其中一个外项是4,那么另一个外项是0.25。( )
四、计算题
21.直接写出得数.
1.6×0.4 = 4.2÷= ×= 10-0.09=
÷36= += ×4÷×4= 3.34+66%=
22.计算下面各题。
1.8×+2.2×25%
9∶3=x∶4
23.解方程。
24.计算下面图形的体积。
五、解答题
25.如图,一个实心圆柱形铁块的高是10cm,如果把它切割成两个相同的半圆柱,表面积就增加了160cm2,如果把这个圆柱锻造成一个底面半径是5cm的实心圆锥形铅锤,这个铅锤的高是多少cm?
26.如图,长方形ABCD的长是4厘米。宽是3厘米,对角线AC把长方形分成阴影和空白两个三角形。以AB所在的直线为轴,把长方形旋转一周,空白三角形扫过的空间大小和阴影三角形扫过的空间的大小比是多少?
27.如下图所示,李叔叔在院子里用砖和水泥砌一个圆柱形的鱼池,墙厚20厘米(底面利用原来的水泥地)。
(1)这个鱼池墙体的体积是多少立方米?
(2)如果给这个鱼池的内部和外部的所有面都贴上瓷砖,需要贴瓷砖的面积是多少平方米?
28.青白江区城市森林和谐广场位于青白江区华金大道二段,是青白江百姓休闲、娱乐的重要场所。把它绘制在比例尺为1∶5000的地图上,该广场平面图是一个长约是5厘米,宽约是3厘米的长方形。请问该广场实际面积约是多少平方米?
29.小明家把今年收获的小麦堆成了圆锥形,高3米,底面直径是4米。
(1)如果每立方米小麦重700千克,这堆小麦重多少千克?
(2)如果把这堆小麦倒入一个底面直径为2米的圆柱形铁桶中刚好装满,那么铁桶高多少米?
30.一个圆柱沿直径切开表面积增加12平方厘米,如果切成三个小圆柱,表面积增加48平方厘米,则原来圆柱的体积是多少立方厘米?(π取3)
31.师徒两人加工一批零件,由师傅独做需37小时,徒弟每小时能加工30个零件,现由师徒两人同时加工,完成任务时,徒弟加工的个数是师傅的。这批零件共有多少个?
32.陀螺是中国民间最早的娱乐工具之一,下图是一种木制玩具陀螺,可以看作是一个近似的圆锥和圆柱组合起来的立体图形。它的底面半径是3厘米,圆柱部分的高是6厘米(即AB=6厘米),圆锥部分的高是3厘米(即BC=3厘米)。这个木质陀螺的体积是多少立方厘米?
《期末素养质量检测卷(三)-2024-2025学年六年级下册数学北师大版》参考答案
1.B
【分析】等底等高的圆柱的体积是圆锥体积的3倍,圆锥的高增加18厘米后,圆锥与圆柱的体积相等,说明圆锥体积增加了2倍,即高增加了2倍,先算出圆锥原来的高,再根据公式:圆锥的体积=×底面积×高,算出原来圆锥的体积,据此解答。
【详解】18÷2=9(厘米)
×π×52×9
=×π×25×9
=75π(立方厘米)
即原来圆锥的体积是75π立方厘米。
故答案为:B
2.A
【分析】当两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,这两种量就成正比例关系;如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,这两种量就成反比例关系。
【详解】根据总价÷数量=单价可知,妈妈所花钱的总数÷买的盐的袋数=2.5(元/袋),一袋盐的价格是固定的,所以妈妈所花钱的总数与买的盐的袋数的比值一定,因此妈妈买的盐的袋数和所花钱的总数成正比例关系。因为妈妈所花钱的总数与买的盐的袋数的比值一定,而不是积一定,因此妈妈所花钱的总数与买的盐的袋数不成反比例。
故答案为:A
3.C
【分析】表示两个比相等的式子叫作比例;
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,这两种量就成正比例关系。
通过判断每个选项是否能构成比例关系来解决问题,据此解答。
【详解】A.因为2支铅笔可以换4块橡皮,所以每支铅笔能换的橡皮数是一定的,可列出比例2∶4=3∶X,所以此选项能用该比例解决;
B.汽车速度一定,路程与时间成正比例,可列出比例2∶4=3∶X,所以此选项能用该比例解决;
C.一根钢筋截成2段需要截1次,用时4分钟,截成3段需要截2次,总共用时8分钟,因为截的次数比段数少1,截的次数与段数之间的关系并不是正比例关系,所以不能列出比例2∶4=3∶X,所以此选项不能用该比例解决。
D.长方形放大比例一定,长和宽成正比例,可列出比例2∶4=3∶X,所以此选项能用该比例解决。
故答案为:C
4.C
【分析】钟表的表盘是圆形,圆心角是360°,上面有12大格,则每大格的圆心角是360°÷12=30°。从4时到7时,时针绕中心点顺时针走了3大格,30°×3=90°,即顺时针旋转90°。
【详解】通过分析可得:
360°÷12=30°
7-4=3
30°×3=90°
则钟表上的时针绕中心点顺时针旋转90°。
故答案为:C
5.B
【分析】平行四边形的面积就是圆柱的侧面积,根据圆柱的侧面积公式,代入数据计算即可。
【详解】2×π×6×10
=12π×10
=120π(cm2)
这个平行四边形的面积是(120π)cm2。
故答案为:B
6. 16 3.9
【分析】根据图上距离实际距离比例尺,代入数据解答。同时注意答案中单位,根据1米=100厘米,在答案中做相应变化。
【详解】320米=32000厘米
78米=7800厘米
(厘米)
(厘米)
长应是16厘米,宽应是3.9厘米。
7.11.28
【分析】根据题意,圆柱形木料截成3段后,总的表面积增加了4个底面积,所以用45.12平方厘米除以4,即可求出这根木料的底面积。
【详解】(平方厘米)
即这根木料的底面积是11.28平方厘米。
8. 63 15
【分析】图上距离=实际距离×比例尺,1米=100厘米,据此进行换算即可。
【详解】315×=0.63(m)=63(cm)
75×=0.15(m)=15(cm)
长应是63cm,宽应是15cm。
9. 10 502.4
【分析】根据圆柱的高=侧面积÷底面周长,底面半径=底面周长÷圆周率÷2,圆柱的体积=底面积×高,列式计算即可。
【详解】251.2÷25.12=10(分米)
3.14×(25.12÷3.14÷2)2×10
=3.14×42×10
=3.14×16×10
=502.4(立方分米)
这个圆柱的高是10分米,体积是502.4立方分米。
10.4.5、2、18
【分析】比值相等的两个比组成比例,比的比值等于前项除以后项,可先将3、6、9三个数组成一个比,得到比值后,再计算得出另一个比。据此可得出答案。
【详解】一个数与3、6、9可以组成比例:3∶6=,,即3∶6=4.5∶9;
3∶9=,,即组成比例:;
6∶9=,,即组成比例:。
3∶6=,,即组成比例:
即这个数可能是:4.5、2、18。
11.(1)正
(2) 5 1500
(3)450
【分析】(1)正比例图像是一条经过原点的射线,反比例图像是一条平滑的曲线,据此解答即可;
(2)点A可以用数对(5,1500)表示,即直升机飞行了5小时,行驶了1500千米;
(3)根据路程÷时间=速度,据此求出直升机的速度,再根据速度×时间=路程,据此解答即可。
【详解】(1)这架直升机飞行的路程与时间成正比例。
(2)这架直升机飞行了5小时,行驶了1500千米。
(3)1500÷5×1.5
=300×1.5
=450(千米)
这架直升机1.5时飞行了450千米。
12. 62.8 50.24
【分析】将底面周长除以3.14再除以2,求出底面半径。根据“圆面积=πr2”求出圆柱形水桶的底面积,根据“圆柱侧面积=底面周长×高”求出圆柱的侧面积。将底面积和侧面积相加,求出需要的铁皮面积。圆柱容积=底面积×高,据此列式求出这个水桶的容积。
【详解】12.56÷3.14÷2=2(分米)
3.14×22+12.56×4
=3.14×4+50.24
=12.56+50.24
=62.8(平方分米)
3.14×22×4
=3.14×4×4
=50.24(立方分米)
50.24立方分米=50.24升
所以,至少需要铁皮62.8平方分米,这个水桶的容积是50.24升。
13.1∶4000000
【分析】一幅图的图上距离与实际距离的比,叫作这幅图的比例尺,比例尺=图上距离∶实际距离,据此解答。
【详解】比例尺:3cm∶120km
=3cm∶12000000cm
=3∶120000000
=1∶4000000
所以这幅地图的比例尺是:1∶4000000。
【点睛】本题考查比例尺,解答本题的关键是掌握比例尺的计算方法。
14.200∶157
【分析】圆柱的高、底面直径与正方体的棱长相等,可设正方体的棱长为具体数字,则可分别计算出正方体的体积与圆柱的体积,再计算正方体与圆柱的体积比。
【详解】假设正方体的棱长为6厘米,则圆柱的高和底面直径也为6厘米。
正方体的体积:6×6×6=216(立方厘米)
圆柱的体积:3.14×(6÷2)2×6
=3.14×32×6
=3.14×9×6
=28.26×6
=169.56(立方厘米)
216∶169.56=200∶157
故正方体与圆柱的体积之比是200∶157。
15.0.6/
【分析】设小孔成像后,树的像的高度是x米,根据“小孔成像”现象:树的实际高度与像的高度的比与它们到孔的距离之比相等,据此列出比例,解比例即可解答。
【详解】解:设小孔成像后,树的像的高度是x米。
因此小孔成像后,树的像的高度是0.6米。
16.√
【分析】如果圆柱的侧面展开是一个正方形,那么圆柱的底面周长=圆柱的高,再根据比的意义即可求出圆柱的底面周长与高的比是多少。
【详解】由分析可知:
圆柱的底面周长=圆柱的高,所以这个圆柱底面周长与高的比是1∶1。
故答案为:√
【点睛】本题主要考查圆柱的展开图的特点,要清楚的知道圆柱展开图的特点是解题的关键。
17.√
【分析】根据圆柱与圆锥的体积关系:等底等高的圆柱体积是圆锥体积的3倍,则等底等高圆柱体积+圆锥体积=圆锥体积×4,据此可计算得出答案。
【详解】等地等高的圆柱体积是圆锥体积的3倍,则等底等高圆柱体积+圆锥体积=圆锥体积×4,体积和是251.2立方米,则圆锥体积为:251.2÷4=62.8(立方米)。题干表述正确。
故答案为:√
18.×
【分析】钟表上有12大格,每大格的圆心角是360°÷12=30°。时针从“5”指向“7”走了2大格,30°×2=60°,则时针从“5”指向“7”绕中心点按顺时针方向旋转了60°。
【详解】通过分析可得:
360°÷12=30°
30°×2=60°
时针从“5”指向“7”绕中心点按顺时针方向旋转了60°。原题说法错误。
故答案为:×
19.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为直径一定,π是定值,所以π×直径=周长,周长一定,即路程÷转数=周长(一定),所以,所行路程和车轮转数成正比例。
故答案为:√
20.√
【分析】在比例里,两外项之积等于两内项之积,如果两个内项互为倒数,则积是1,两外项的积也是1,用1除以其中的一个外项,看是否等于另一个外项即可判断。
【详解】1÷4=0.25
所以在一个比例中,两个内项互为倒数,如果其中一个外项是4,那么另一个外项是0.25。
原题说法正确。
故答案为:√
21.6.4 ;21 ; ;9.91 ; ; ;16 ;4
【详解】略
22.;49;1
x=12;x=12.25
【分析】将除以转化成乘,再根据乘法分配律进行简算;
根据乘法分配律进行简算;
将和25%都转换成0.25,再根据乘法分配律进行简算;
根据比例的性质,即内项之积等于外项之积,把比例转换成方程后,利用等式的性质,方程两边同时除以3进行计算即可;
根据比例的性质,即内项之积等于外项之积,把比例转换成方程后,利用等式的性质,方程两边同时除以8进行计算即可。
【详解】
=×+×
=×(+)
=×1
=
=×36+×36-×36
=28+30-9
=58-9
=49
1.8×+2.2×25%
=1.8×0.25+2.2×0.25
=(1.8+2.2)×0.25
=4×0.25
=1
9∶3=x∶4
解:3x=4×9
3x=36
x=36÷3
x=12
解:8x=7×14
8x=98
x=98÷8
x=12.25
23.;;
【分析】,根据等式的性质1和2,两边同时-39,再同时÷13即可;
,先将左边合并成,根据等式的性质2,两边同时÷3即可;
,根据比例的基本性质,比例的两内项积=两外项积,先写成的形式,两边同时÷即可。
【详解】
解:
解:
解:
24.84.56立方厘米
【分析】根据题意,图中有2个立体图形:圆锥体、长方体,那么他们的体积之和即为整个图形的体积。圆锥体的体积:圆锥体积=底面积×高÷3,长方体的体积=长×宽×高,将数值代入公式计算出结果即可。
【详解】圆锥体积=底面积×高÷3=πr2×3÷3
底面圆半径=4÷2=2(厘米)
3.14×22×3÷3
=3.14×4×3÷3
=12.56(立方厘米)
长方体的体积=长×宽×高
=6×6×2
=36×2
=72(立方厘米)
12.56+72=84.56(立方厘米)
答:图形的体积是84.56立方厘米。
25.19.2cm
【分析】增加的面积是以圆柱形铁块的高为长、圆柱的底面直径为宽的两个长方形的面积,据此用160除以2,求出一个长方形的面积,再用一个长方形的面积除以圆柱形铁块的高就是底面直径,再除以2就是圆柱形铁块的底面半径,再根据圆柱的体积=求出圆柱形铁块的体积,也就是半径是5cm的实心圆锥形铅锤的体积,再根据圆锥的高=圆锥体积的3倍÷底面积解答即可。
【详解】160÷2÷10÷2
=80÷10÷2
=8÷2
=4(cm)
=16×10×3÷25
=160×3÷25
=480÷25
=19.2(cm)
答:这个铅锤的高是19.2cm。
26.1∶2
【分析】根据题意可知,长方形扫过的空间是一个底面半径是4厘米,高是3厘米的圆柱;空白三角形出扫过的空间是一个底面半径是4厘米,高是3厘米的圆锥,由此可知,圆柱与圆锥的等底等高;圆柱的体积是圆锥体积的3倍;阴影三角形扫过的体积等于圆柱的体积-圆锥的体积;可以将圆锥的体积看做1,那么圆柱的体积就是3,那么阴影扫过的空间的大小就是3-1=2,据此求出空白三角形扫过的空间大小和阴影三角形扫过的空间的大小的比。
【详解】长方形扫过的空间是一个圆柱体;空白三角形扫过的空间是一个圆锥体;它们是等底等高;
设圆锥的体积是1;
则圆柱的体积是:1×3=3;
阴影三角形扫过的体积是:3-1=2;
三角形扫过的空间大小和阴影三角形扫过的空间的大小比是=1∶2。
答:三角形扫过的空间大小和阴影三角形扫过的空间的大小比是1∶2。
27.(1)1.6956立方米
(2)20.096平方米
【分析】(1)根据题意可知,鱼池墙体的体积=大圆柱的体积-小圆柱的体积;根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答,注意单位名数的统一。
(2)需要贴瓷砖的面积=大圆柱的侧面积+大圆柱的底面积+小圆柱侧面积,根据圆柱的侧面积公式:侧面积=底面周长×高,圆柱的底面积公式:底面积=,代入数据,即可解答。
【详解】(1)20厘米=0.2米
1.6÷2=0.8(米)
0.8+0.2=1(米)
3.14×12×1.5-3.14×0.82×1.5
=3.14×1×1.5-3.14×0.64×1.5
=3.14×1.5-2.0096×1.5
=4.71-3.0144
=1.6956(立方米)
答:这个鱼池墙的体积是1.6956立方米。
(2)3.14×1×2×1.5+3.14×12+3.14×1.6×1.5
=3.14×2×1.5+3.14×1+5.024×1.5
=6.28×1.5+3.14+7.536
=9.42+3.14+7.536
=12.56+7.356
=20.096(平方米)
答:需要贴瓷砖的面积是20.096平方米。
28.37500平方米
【分析】由题可知该广场的长和宽的图上距离分别是5厘米和3厘米,根据公式:实际距离=图上距离÷比例尺,代入数据进行计算,可以求出该广场的长和宽的实际距离,再根据1米=100厘米进行单位换算,最后根据长方形的面积=长×宽,代入数据计算,即可求出该广场实际面积,据此解答。
【详解】(厘米)
(厘米)
25000厘米=250米
15000厘米=150米
250×150=37500(平方米)
答:该广场实际面积约是37500平方米。
29.(1)8792千克
(2)4米
【分析】(1)根据圆锥体积=底面积×高÷3,求出小麦体积,小麦体积×每立方米质量=这堆小麦的质量;
(2)根据圆柱的高=体积÷底面积,列式解答即可。
【详解】(1)3.14×(4÷2)2×3÷3
=3.14×22×3÷3
=3.14×4×3÷3
=12.56(立方米)
12.56×700=8792(千克)
答:这堆小麦重8792千克。
(2)12.56÷[3.14×(2÷2)2]
=12.56÷[3.14×12]
=12.56÷[3.14×1]
=12.56÷3.14
=4(米)
答:铁桶高4米。
30.18立方厘米
【分析】切成三个小圆柱,则增加了4个底面积,用求出底面积,再根据圆的面积公式的逆运算,求出半径,再用半径乘2得到直径;圆柱沿直径切开表面积增加12平方厘米,即增加了2个底面直径乘高的面积,用12除以2,再除以直径得到高;最后根据,代入数据计算即可得解。
【详解】48÷4÷3=4(平方厘米)
因为2×2=4,所以这个圆柱的底面半径是2厘米。
所以圆柱的高是:12÷2÷(2×2)
=12÷2÷4
=6÷4
=1.5(厘米)
则圆柱的体积是:48÷4×1.5
=12×1.5
=18(立方厘米)
答:原来圆柱的体积是18立方厘米。
31.1998个
【分析】师徒两人同时开始加工到完成任务所花的时间相同。因为工作时间一定,工作效率和工作总量成正比例所以徒弟的工作效率与师傅的比值还是,把师傅的工作效率看作单位“1”,根据已知一个数的几分之几是多少,求这个数用除法计算,可求出师傅的工作效率,再根据,代入数据计算即可得解。
【详解】
(个)
答:这批零件共有1998个。
32.197.82立方厘米
【分析】从图中可知,这个陀螺的体积等于圆柱部分的体积加上圆锥部分的体积,其中圆柱部分的底面半径和圆锥部分的底面半径相等;根据圆柱的体积=πr2h1 ,圆锥的体积=×πr2h2,代入相应数值计算,即可解答。
【详解】3.14×32×6+×3.14×32×3
=3.14×9×6+×3.14×9×3
=3.14×9×(6+×3)
=28.26×(6+1)
=28.26×7
=197.82(立方厘米)
答:这个木质陀螺的体积是197.82立方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
