人教版五年级下册数学第8单元素养提优卷(含答案)
文档属性
| 名称 | 人教版五年级下册数学第8单元素养提优卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
五年级下册数学第8单元素养提优卷
(满分:100分+10分 时间:80分钟)
一、填空题。(第3题4分,其余每空1分,共16分)
1.用天平找次品时,每一次天平两边放的物品数量应该要( )。
2.要找到30个待测物品中的次品(次品重一些),先按( )个一组进行分组并称重,至少称( )次能保证找到次品。
3.用尽可能少的次数找次品,你会对待测物品的个数进行分组吗?在○中填一填。
4.有五个零件,其中有一个是次品(次品重一些),根据下图可以推断出( )号零件一定是正品。
5.有6个小球,其中1个是次品,称重过程如图所示。如果次品重一些,那么次品是( );如果次品轻一些,那么次品是( )。
6.学校象棋兴趣小组买来33副象棋,其中一副少了3颗棋子,用天平称,至少称( )次能保证找出少了棋子的那副。
7.4袋饼干中有1袋次品(次品轻一些),完成下面找次品的过程。
8.有9盒牛奶,其中1盒是次品(次品轻一些),无法直接估测出来,需要用一架天平来称。如果按(2,2,2,3)分成4份,至少称( )次能保证找到次品。如果按(4,4,1)分成3份,至少称( )次能保证找到次品。
9.有10瓶饮料其中1瓶是次品(次品轻一些),至少用天平称( )次能保证找到次品。
二、判断题。(第3题6分,其余每题2分,共10分)
1.找次品时,把物品的个数平均分成的份数越少,称的次数就越少。( )
2.11盒饼干中,有1盒被小明吃了几块,用天平称,不可能一次就把这盒找出来。( )
3.小宁的12个零件中有1个次品(次品重一些),小亮的20个零件中也有1个次品(次品轻一些),他们要分别找出次品。
(1)小宁用的次数一定比小亮少。( )
(2)小宁用的次数不一定比小亮少。( )
(3)他们用的次数可能相等。( )
三、选择题。(每题2分,共10分)
1.药店有72瓶维生素,其中1瓶少了几粒,用天平称,至少要( )次才能保证找到这瓶。
A. 3 B. 4 C. 5 D. 6
2.有一些玻璃球,其中1个是次品(次品轻一些),小强要利用天平找到这个次品,他把这些玻璃球分成了下面三组。用小强的分组方法,至少称( )次能保证找到这个次品。
A. 2 B. 3 C. 4 D. 5
3.有一些零件,其中有一个次品略轻一些,小希用天平至少称4次能保证找到次品,这些零件最多有( )个。
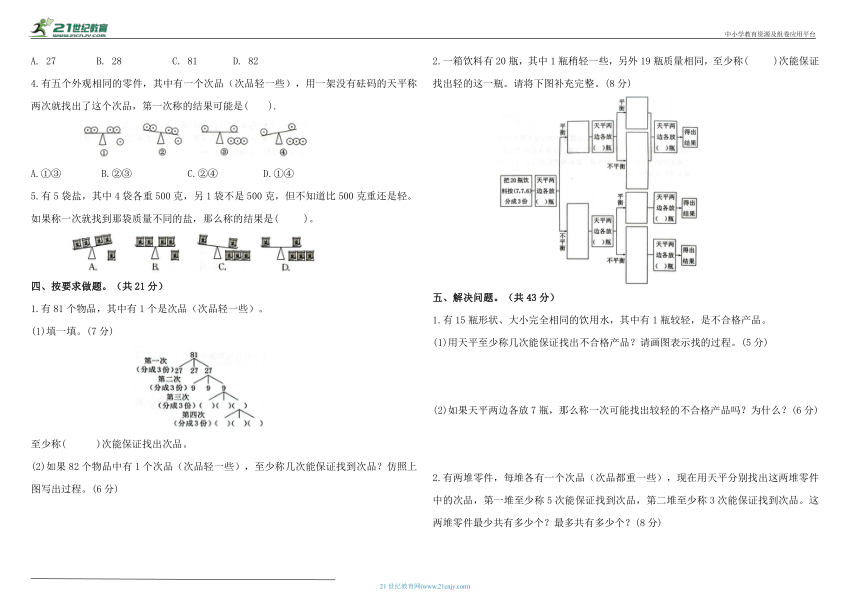
A. 27 B. 28 C. 81 D. 82
4.有五个外观相同的零件,其中有一个次品(次品轻一些),用一架没有砝码的天平称两次就找出了这个次品,第一次称的结果可能是( ).
A.①③ B.②③ C.②④ D.①④
5.有5袋盐,其中4袋各重500克,另1袋不是500克,但不知道比500克重还是轻。如果称一次就找到那袋质量不同的盐,那么称的结果是( )。
四、按要求做题。(共21分)
1.有81个物品,其中有1个是次品(次品轻一些)。
(1)填一填。(7分)
至少称( )次能保证找出次品。
(2)如果82个物品中有1个次品(次品轻一些),至少称几次能保证找到次品?仿照上图写出过程。(6分)
2.一箱饮料有20瓶,其中1瓶稍轻一些,另外19瓶质量相同,至少称( )次能保证找出轻的这一瓶。请将下图补充完整。(8分)
五、解决问题。(共43分)
1.有15瓶形状、大小完全相同的饮用水,其中有1瓶较轻,是不合格产品。
(1)用天平至少称几次能保证找出不合格产品?请画图表示找的过程。(5分)
(2)如果天平两边各放7瓶,那么称一次可能找出较轻的不合格产品吗?为什么?(6分)
2.有两堆零件,每堆各有一个次品(次品都重一些),现在用天平分别找出这两堆零件中的次品,第一堆至少称5次能保证找到次品,第二堆至少称3次能保证找到次品。这两堆零件最少共有多少个?最多共有多少个?(8分)
3.有A,B,C三个金属球,它们的质量关系是A4.桌上有八个球,编号分别是①②③④⑤⑥⑦⑧,其中六个球一样重,另外两个球都轻一些且一样重。为了找出轻的球,壮壮用天平称了三次,结果如下:(8分)
第一次:①+②比③+④轻;
第二次:⑤+⑥比⑦+⑧轻;
第三次:①+③+⑤与②+④+⑧一样重。
5.有五个砝码,它们的质量分别为100克、101克、102克、104克、107克,但外观完全相同,无法直接估出轻重。现有一台带指针的秤,它可以称出300克以内的物体的质量。至少称几次能保证找出质量为100克的砝码?怎样称?(8分)
附加题
1.小明有五个物品,分别用P,Q,R,S,T表示它们的质量,从这五个物品中选两个放到秤上称,得到下面的结果:Q+S=700克,R+T=700克,Q+T=500克,Q+R=600克,P+T=400克。这五个物品的质量(用字母表示)按从大到小的顺序排列为( )。(4分)
2.快乐的周末又到了,丁丁和妈妈一起做面包。规定每个面包用的面粉一样重,并且要求每6个放一屉。丁丁和妈妈共做了4屉,其中妈妈做了3屉,丁丁做了1屉,但丁丁由于粗心听错了要求,每个面包都比规定的少了5g,你有办法用秤称一次就找出哪一屉面包是丁丁做的吗?(6分)
参考答案
一、1.相等 2.10 4 3.2 2 2 6 6 6 8 8 7 10 10 9 4.③④⑤
5.⑤ ③ 6.4 7.轻的 轻的 8.3 3 9.3
二、1.× 2.× 3. (1)× (2)√ (3)√
三、1. B 2. B 3. C 4.B 5. B
四、1.(1)3 3 3 1 1 1 4 (2)称5次
2.3
五、1.(1)3次
(2)可能因为如果天平两边各放7瓶,天平恰好平衡,那么剩下的1瓶就是不合格产品
2.第一堆最少:3×3×3×3+1=82(个) 第二堆最少:3×3+1=10(个)
两堆最少:82+10=92(个) 第一堆最多:3×3×3×3×3=243(个)
第二堆最多:3×3×3=27(个) 两堆最多:243+27=270(个)
3.先用天平称B和D,若D和B一样重,则A4.②和⑤
5.三次 从100,101,102,104,107中任选两个数求和,可以得到10个不同的和,即任选两个砝码一起称,都可以得出这两个砝码的质量。第一次,任选两个砝码一起称,若称得的质量是201克、202克、204克或207克,则质量为100克的砝码就在其中,第二次再从其中任选一个砝码来称,即可找出质量为100克的砝码。若第一次称得的质量不是201克、202克、204克或207克,则质量为100克的砝码在剩余的三个砝码中,第二次从剩余的三个砝码中任选两个一起称,若第二次称得的质量不是201克、202克、204克或207克,则剩下的一个砝码质量为100克;若第二次称得的质量是201克、202克、204克或207克,则质量为100克的砝码就在其中,第三次再从其中任选一个砝码来称,即可找出质量为100克的砝码
附加题
1. S>R>T>Q>P 解析:由Q+S=700克,Q+T=500克,Q+R=600克可知,S-T=200 克,S-R=100克,所以S>R>T。由Q+T=500 克,P+T=400 克可知,Q-P=100克,所以Q>P。由R+T=700克,Q+R=600克可知,T-Q=100 克,所以T>Q。所以 S>R>T>Q>P.
2.答案不唯一,如先将4屉面包依次编号为①②③④,按编号分别从里面拿出1个面包、2个面包、3个面包、4个面包,再将这10个面包一起称重,看跟规定的总质量相差多少,若差5g,则第一屉面包是丁丁做的;若差10g,则第二屉面包是丁丁做的;若差15g,则第三屉面包是丁丁做的;若差20g,则第四屉面包是丁丁做的
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
五年级下册数学第8单元素养提优卷
(满分:100分+10分 时间:80分钟)
一、填空题。(第3题4分,其余每空1分,共16分)
1.用天平找次品时,每一次天平两边放的物品数量应该要( )。
2.要找到30个待测物品中的次品(次品重一些),先按( )个一组进行分组并称重,至少称( )次能保证找到次品。
3.用尽可能少的次数找次品,你会对待测物品的个数进行分组吗?在○中填一填。
4.有五个零件,其中有一个是次品(次品重一些),根据下图可以推断出( )号零件一定是正品。
5.有6个小球,其中1个是次品,称重过程如图所示。如果次品重一些,那么次品是( );如果次品轻一些,那么次品是( )。
6.学校象棋兴趣小组买来33副象棋,其中一副少了3颗棋子,用天平称,至少称( )次能保证找出少了棋子的那副。
7.4袋饼干中有1袋次品(次品轻一些),完成下面找次品的过程。
8.有9盒牛奶,其中1盒是次品(次品轻一些),无法直接估测出来,需要用一架天平来称。如果按(2,2,2,3)分成4份,至少称( )次能保证找到次品。如果按(4,4,1)分成3份,至少称( )次能保证找到次品。
9.有10瓶饮料其中1瓶是次品(次品轻一些),至少用天平称( )次能保证找到次品。
二、判断题。(第3题6分,其余每题2分,共10分)
1.找次品时,把物品的个数平均分成的份数越少,称的次数就越少。( )
2.11盒饼干中,有1盒被小明吃了几块,用天平称,不可能一次就把这盒找出来。( )
3.小宁的12个零件中有1个次品(次品重一些),小亮的20个零件中也有1个次品(次品轻一些),他们要分别找出次品。
(1)小宁用的次数一定比小亮少。( )
(2)小宁用的次数不一定比小亮少。( )
(3)他们用的次数可能相等。( )
三、选择题。(每题2分,共10分)
1.药店有72瓶维生素,其中1瓶少了几粒,用天平称,至少要( )次才能保证找到这瓶。
A. 3 B. 4 C. 5 D. 6
2.有一些玻璃球,其中1个是次品(次品轻一些),小强要利用天平找到这个次品,他把这些玻璃球分成了下面三组。用小强的分组方法,至少称( )次能保证找到这个次品。
A. 2 B. 3 C. 4 D. 5
3.有一些零件,其中有一个次品略轻一些,小希用天平至少称4次能保证找到次品,这些零件最多有( )个。
A. 27 B. 28 C. 81 D. 82
4.有五个外观相同的零件,其中有一个次品(次品轻一些),用一架没有砝码的天平称两次就找出了这个次品,第一次称的结果可能是( ).
A.①③ B.②③ C.②④ D.①④
5.有5袋盐,其中4袋各重500克,另1袋不是500克,但不知道比500克重还是轻。如果称一次就找到那袋质量不同的盐,那么称的结果是( )。
四、按要求做题。(共21分)
1.有81个物品,其中有1个是次品(次品轻一些)。
(1)填一填。(7分)
至少称( )次能保证找出次品。
(2)如果82个物品中有1个次品(次品轻一些),至少称几次能保证找到次品?仿照上图写出过程。(6分)
2.一箱饮料有20瓶,其中1瓶稍轻一些,另外19瓶质量相同,至少称( )次能保证找出轻的这一瓶。请将下图补充完整。(8分)
五、解决问题。(共43分)
1.有15瓶形状、大小完全相同的饮用水,其中有1瓶较轻,是不合格产品。
(1)用天平至少称几次能保证找出不合格产品?请画图表示找的过程。(5分)
(2)如果天平两边各放7瓶,那么称一次可能找出较轻的不合格产品吗?为什么?(6分)
2.有两堆零件,每堆各有一个次品(次品都重一些),现在用天平分别找出这两堆零件中的次品,第一堆至少称5次能保证找到次品,第二堆至少称3次能保证找到次品。这两堆零件最少共有多少个?最多共有多少个?(8分)
3.有A,B,C三个金属球,它们的质量关系是A
第一次:①+②比③+④轻;
第二次:⑤+⑥比⑦+⑧轻;
第三次:①+③+⑤与②+④+⑧一样重。
5.有五个砝码,它们的质量分别为100克、101克、102克、104克、107克,但外观完全相同,无法直接估出轻重。现有一台带指针的秤,它可以称出300克以内的物体的质量。至少称几次能保证找出质量为100克的砝码?怎样称?(8分)
附加题
1.小明有五个物品,分别用P,Q,R,S,T表示它们的质量,从这五个物品中选两个放到秤上称,得到下面的结果:Q+S=700克,R+T=700克,Q+T=500克,Q+R=600克,P+T=400克。这五个物品的质量(用字母表示)按从大到小的顺序排列为( )。(4分)
2.快乐的周末又到了,丁丁和妈妈一起做面包。规定每个面包用的面粉一样重,并且要求每6个放一屉。丁丁和妈妈共做了4屉,其中妈妈做了3屉,丁丁做了1屉,但丁丁由于粗心听错了要求,每个面包都比规定的少了5g,你有办法用秤称一次就找出哪一屉面包是丁丁做的吗?(6分)
参考答案
一、1.相等 2.10 4 3.2 2 2 6 6 6 8 8 7 10 10 9 4.③④⑤
5.⑤ ③ 6.4 7.轻的 轻的 8.3 3 9.3
二、1.× 2.× 3. (1)× (2)√ (3)√
三、1. B 2. B 3. C 4.B 5. B
四、1.(1)3 3 3 1 1 1 4 (2)称5次
2.3
五、1.(1)3次
(2)可能因为如果天平两边各放7瓶,天平恰好平衡,那么剩下的1瓶就是不合格产品
2.第一堆最少:3×3×3×3+1=82(个) 第二堆最少:3×3+1=10(个)
两堆最少:82+10=92(个) 第一堆最多:3×3×3×3×3=243(个)
第二堆最多:3×3×3=27(个) 两堆最多:243+27=270(个)
3.先用天平称B和D,若D和B一样重,则A
5.三次 从100,101,102,104,107中任选两个数求和,可以得到10个不同的和,即任选两个砝码一起称,都可以得出这两个砝码的质量。第一次,任选两个砝码一起称,若称得的质量是201克、202克、204克或207克,则质量为100克的砝码就在其中,第二次再从其中任选一个砝码来称,即可找出质量为100克的砝码。若第一次称得的质量不是201克、202克、204克或207克,则质量为100克的砝码在剩余的三个砝码中,第二次从剩余的三个砝码中任选两个一起称,若第二次称得的质量不是201克、202克、204克或207克,则剩下的一个砝码质量为100克;若第二次称得的质量是201克、202克、204克或207克,则质量为100克的砝码就在其中,第三次再从其中任选一个砝码来称,即可找出质量为100克的砝码
附加题
1. S>R>T>Q>P 解析:由Q+S=700克,Q+T=500克,Q+R=600克可知,S-T=200 克,S-R=100克,所以S>R>T。由Q+T=500 克,P+T=400 克可知,Q-P=100克,所以Q>P。由R+T=700克,Q+R=600克可知,T-Q=100 克,所以T>Q。所以 S>R>T>Q>P.
2.答案不唯一,如先将4屉面包依次编号为①②③④,按编号分别从里面拿出1个面包、2个面包、3个面包、4个面包,再将这10个面包一起称重,看跟规定的总质量相差多少,若差5g,则第一屉面包是丁丁做的;若差10g,则第二屉面包是丁丁做的;若差15g,则第三屉面包是丁丁做的;若差20g,则第四屉面包是丁丁做的
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
