2025年湖北省黄冈市部分学校九年级下学期6月质量监测数学试卷(word版含答案)
文档属性
| 名称 | 2025年湖北省黄冈市部分学校九年级下学期6月质量监测数学试卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 307.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 00:00:00 | ||
图片预览


文档简介
2024—2025年中考数学模拟测试题E
一、选择题(每小题3分,共30分)
1. “二十四节气”是中华农耕文明的结晶,被国际气象界誉为“中国第五大发明”. 立春为二十四节气之首,2025年立春这天北京、武汉、哈尔滨、长沙四地最低气温分别为-8℃,-1℃,-16℃,4℃,这些气温中最低的是( )
A.-8℃ B.-1℃ C.-16℃ D.4℃
2. 芯片是半导体元件产品的统称,是一种将电路小型化的技术,常制造在半导体晶圆表面上.下列关于芯片的图标中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3. 下列计算正确的是( )
A.x2·x3=x5 B.(x3)2=x5 C.x(x-1)=x2-1 D.(2a-1)2=2a2-4a+1
4. 如图,两个平面镜平行放置,光线经过平面镜反射时,∠1=∠2=40 ,则∠3的度数为( )
A.80 B.90 C.100 D.120
5. “月壤砖”是我国科学家模拟月壤成分烧制而成的一种建筑材料,拟用于未来建造月球基地. 据介绍,“月壤砖”呈榫卯结构,密度与普通砖块相当,抗压强度却是普通砖的三倍以上.如图,这是“月壤砖”的示意图,其俯视图为( )
A. B. C. D.
6. 不等式组的解集在数轴上的表示正确的是( )
A. B. C. D.
7. 下列说法错误的是( )
A.“在平面上任意画一个六边形,其内角和为360”这一事件是必然事件
B.对“神舟二十号”载人飞船发射前的零部件的检查,采用全面调查的方式
C.在大量重复试验中,随着试验次数的增加,随机事件发生的频率一般会越来越接近概率
D.在“吾辈当自强,唯我少年郎”的演讲比赛计分中,通常采用去掉一个最高分和一个最低分,然后计算平均分的办法,是因为平均数易受极端数据的影响
8. 我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗. 今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗?如果设清酒x斗,醑酒y斗,那么可列方程组为( )
A. B. C. D.
9. 已知∠ADB,作图. 步骤1:以点D为圆心,适当长为半径画弧,分别交DA,DB 于点M,N;再分别以点M,N为圆心,大于MN长为半径画弧交于点E,画射线DE. 步骤 2:在DB上任取一点O,以点O 为圆心,OD长为半径画半圆,分别交DA,DB,DE 于点P,Q,C;步骤3:连接PQ,OC.则下列结论不正确的是( )
A.= B.OC∥DA C.OC垂直平分PQ D.DP=PQ
10.二次函数y=ax2+bx+c(a、b、c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
x … -2 -1 0 1 2 …
y=ax2+bx+c … t m -2 -2 n …
且当x=-0.5时,其对应的函数值y>0,有下列结论:①abc>0;②-2和3是关于x的方程ax2+bx+c=t的两个根;③b2-4ac>0;④当0<x<1时,y<-2;⑤0<m+n<. 其中正确结论的个数是( )个.
A.1 B.2 C.3 D.4
二、填空题(每小题5分,共15分)
11.代数式中x的取值范围是_________.
12.计算:-=_________.
13.任意写出一个满足“当x>0时,y随工增大而减小”的函数为___________.
14.截止 2024年9月,我国共13位共和国勋章获得者. 老师制作了正面分别书写有孙家栋、于敏、袁隆平、黄旭华四位共和国勋章获得者为国奉献的事迹的四张卡片,除此之外背面完全相同,把这4张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片上分别写有袁隆平和黄旭华事迹的概率是_________.
15.在矩形ABCD的对角线BD上取一点E,使得DE=2BE,连接CE,将△CEB沿CE翻折得到△CEF,连接AF,BF,⑴∠AFB=_______;⑵若AB=6,BC=9,则AF=________.
三、解答题(共75分).
16.(6分)计算:-22+2cos60 +(-2025)0-(-)-1.
17.(6分)如图,□ABCD的对角线相交于点O,AE⊥BD于点E,CF⊥BD于点F,求证:BE=DF.
18.(6分)风能是一种消洁能源,我国风能资源非常丰富. 风力发电发展迅速,习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和,某校数学综合与实践小组成员查阅资料得知,在风力发电机组中,电塔简是风力发电设施中不可或缺的重要组成部分,它的高度是一个重要的设计参数.于是该小组成员开展了测量风电塔筒高度(即风力发电的塔杆)的实践活动.形成了如下不完整的实践报告:
测量对象 风电塔筒的高度
测量目的 运用三角函数有关知识解决实际问题
测量工具 测角仪、激光测距仪等
测量示意图
测量方案 1. 在风电塔筒的空地上取测量点C,利用测角仪PC测得此时点A的仰角∠APQ=53 ; 2. 改变测量点,在风电塔筒另一侧空地上取点D,利用测角仪MD测得此时点A的仰角∠AMN=45 ; 3. 测得PC=1米,MD=0.5米,CD=200米.(图中各点均在同一竖直平面内)
请根据以上测量数据,求风电塔筒AB的高度(参考数据:sin53 ≈0.80,cos53 ≈0.60,tan53 ≈).
19.(8分)学校开展了以“生活中的数学”为主题的知识竟赛活动,现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,其分为四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95<x≤100),下面给出了部分信息.
七年级10名学生的竞赛成绩:80、96、99、99、90、99、89、82、86、100.
八年级10名学生的竞赛成绩: 94、90、94 (部分数据被墨水污染)
七、八年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 方差
七年级 92 93 a 52
八年级 92 b 100 50.4
根据以上信息,解答下列问题.
⑴ 填空:a=_______,b=_______,c=_______,并补
全条形统计图.
⑵ 若规定竞赛成绩在90分及以上为优秀,该校七、八年级参加此次活动的学生分别有800人和860人,估计在本次活动中七、八年级竞赛成绩为优秀的学生人数共多少人?
⑶ 分析上述信息,你认为该校七、八年级中哪个年级的学生对“生活中的数学”知识竞赛掌握得更好?请说明理由(写一条即可).
20.(8分)如图,正比例函数y=-x的图象与反比例函数y=(k≠0)的图象相交于点A(a ,2),B.
⑴ ①求点A 的坐标和反比例函数表达式;
②填空:点B的坐标为____________;
⑵ 若点 P(m,n)在该反比例函数图象上,且它到x轴距离大于3,请根据图象直接写出m的取值范围.
21.(8分)如图,直线AB经过⊙O上的点E,直线AO交⊙O于点D,OB⊙O于点G,连接 DE交OB于点F,连接EG,若点G是弧DE的中点,∠BEF=∠DOG.
⑴ 求证:AB 是⊙O的切线;
⑵ 若BE=6,EG=GB,求图中阴影部分面积.
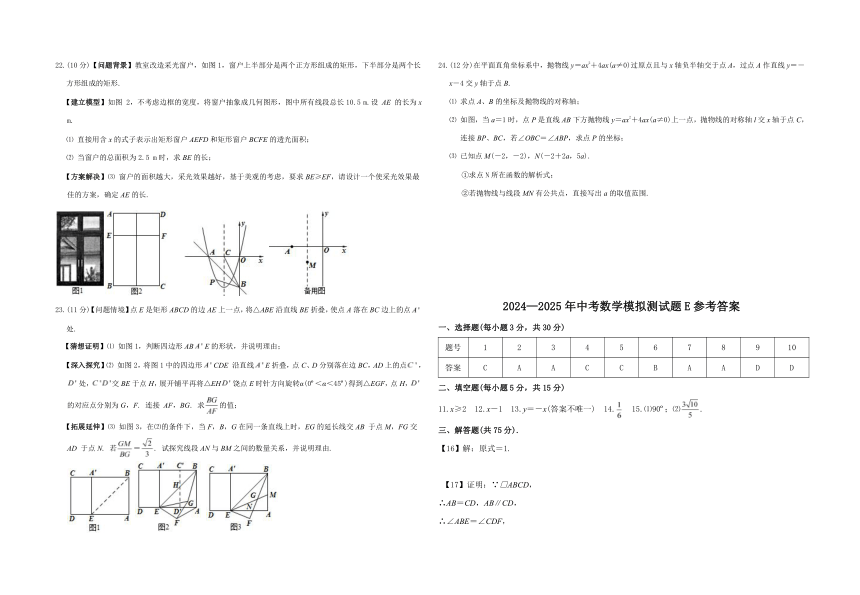
22.(10分)【问题背景】教室改造采光窗户,如图1,窗户上半部分是两个正方形组成的矩形,下半部分是两个长方形组成的矩形.
【建立模型】如图 2,不考虑边框的宽度,将窗户抽象成几何图形,图中所有线段总长10.5 m.设 AE 的长为x m.
⑴ 直接用含x的式子表示出矩形窗户AEFD和矩形窗户BCFE的透光面积;
⑵ 当窗户的总面积为2.5 m时,求BE的长;
【方案解决】⑶ 窗户的面积越大,采光效果越好,基于美观的考虑,要求BE≥EF,请设计一个使采光效果最佳的方案,确定AE的长.
23.(11分)【问题情境】点E是矩形ABCD的边AE上一点,将△ABE沿直线BE折叠,使点A落在BC边上的点处.
【猜想证明】⑴ 如图1,判断四边形ABE的形状,并说明理由;
【深入探究】⑵ 如图2,将图1中的四边形CDE 沿直线E折叠,点C、D分别落在边BC,AD上的点,处,交BE于点H,展开铺平再将△EH饶点E时针方向旋转α(0 <α<45 )得到△EGF,点H,的对应点分别为G,F. 连接 AF,BG. 求的值;
【拓展延伸】⑶ 如图3,在⑵的条件下,当F,B,G在同一条直线上时,EG的延长线交AB 于点M,FG交AD 于点N. 若=. 试探究线段AN与BM之间的数量关系,并说明理由.
24.(12分)在平面直角坐标系中,抛物线y=ax2+4ax(a≠0)过原点且与x轴负半轴交于点A,过点A作直线y=-x-4交y轴于点B.
⑴ 求点A、B的坐标及抛物线的对称轴;
⑵ 如图,当a=1时,点P是直线AB下方抛物线y=ax2+4ax(a≠0)上一点,抛物线的对称轴l交x轴于点C,连接BP、BC,若∠OBC=∠ABP,求点P的坐标;
⑶ 已知点M(-2,-2),N(-2+2a,5a).
①求点N所在函数的解析式;
②若抛物线与线段MN有公共点,直接写出a的取值范围.
2024—2025年中考数学模拟测试题E参考答案
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A C C B A A D D
二、填空题(每小题5分,共15分)
11.x≥2 12.x-1 13.y=-x(答案不唯一) 14. 15.⑴90 ;⑵.
三、解答题(共75分).
【16】解:原式=1.
【17】证明:∵□ABCD,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90 ,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=DF.
【18】解:115 m.
【19】解:⑴99,94,补图略(1);
⑵1082;
⑶从表格来看,八年级的中位数比七年级的中位数大,说明八年级获得94分的比七年级多,所以八年级学生对“生活中的数学”知识竞赛掌握的更好.
【21】解:⑴①A(-3,2),y=-.
②(3,-2).
⑵-2<m<0或0<m<2.
【21】⑴证明:连接OE,
∵G是弧DE的中点,
∴弧DG=弧EG,
∴∠EOG=∠DOG,
∵OE=OD,
∴OF⊥DE,
∴∠EOF+∠OEF=90 ,
∵∠BEF=∠DOG=∠EOF,
∴∠OEB=∠OEF+∠BEF=∠OEF+∠EOF=90 ,
∴OE⊥AB,
∵OE是⊙O的半径,
∴AB是⊙O的切线.
⑵解:∵∠EFB=90 ,
∴∠DEB+∠B=90 ,
∴∠DEB+∠B=90 ,
∵EG=GB,
∴∠GEB=∠B,
∴∠GEB=∠B,
∵∠DEG=∠BEG,
∴∠DEG=∠BEG=∠B=30 ,
∴∠DEG=∠BEG=∠B=30 ,
在Rt△EFB中,BE=6,
∴EF=BE=3,
∵OG⊥DE,
∴EF=DF=3,
在Rt△OFD中,∠DOB=2∠DEG=60 ,
∴OF===,
∴OD=2OF=,
∴S阴影=S扇形DOG-S△DOF
=-××3=2π-.
【22】解:⑴由题意,矩形窗户AEFD的长EF=2x,宽AE=x,
∴矩形窗户AEFD的面积=2x2.
又∵所有线段总长10.5 m,矩形窗户AEFD的周长为7x,
∴矩形窗户BCFE的BC为2x,BE为(3.5-x).
∴矩形窗户BCFE的面积=2x(3.5-x)=7x-6x2.
⑵由题意,2x2+7x-6x2=2.5,
∴x1=0.5,x2=1.25,
当 x=1.25时,BE=3.5-3x=-0.25,不合题意,舍去,
当x=0.5时,BE=3.5-3x=2.
⑶由题意,窗户采光面积y=-4x2+7x=-4(x-)2+,
∵BE≥EF,
∴3.5-3x≥2x,
∴x≤0.7,
∵-4<0,抛物线开口向下,
∴当x<时,y随x的增加而增加,
∴在x≤0.7的范围内,当x=0.7时,采光面积最大,
答:当AE为0.7时,采光面积最大.
【23】解:⑴四边形ABE是正方形,
理由:∵四边形ABCD是矩形,
∴∠A=∠ABC=90 ,
由折叠性质得:∠BE=∠A=90 ,BA=B,
∴四边形ABE是矩形.
∴四边形ABE是正方形.
⑵∵四边形ABCD是矩形,
∴∠BAD=∠D=90 ,
由折叠性质得:∠E=∠D=90 ,
∴∠E=∠BAE=90 ,
∴∥AB,
∴=,
由旋转性质得 EF=EH,E=EF,∠BEG=∠AEF,
∴=,
∴△EBG∽△EAF,
∴=,
由折叠性质知∠ABE=∠ABC=45 ,
∴在 Rt△ABE 中,sin45 ==,
∴==,
即=.
(法二)直接用三函更简单.
⑶过M作MP⊥BG于P,
∵=,
∴令GM=,BG=3,
由题意知:∠AEB=∠FEN=45 ,∠F=90 ,
∵B、G、F三点共线,
∴∠BGM=∠EGF=45 ,
∴PG=PM=GM·sin∠PGM=1,
∴BP=BG-PG=2,
∴BM==,
∵∠BNG=∠EMB,∠MGB=∠MBE,
∴△MBG∽MBE,
∴=,即=,
∴BE=,
∴AB=BE·sin∠AEB=,
∵∠A=90 ,MP⊥BG,
∴tan∠ABN==,即=,
∴AN=,
∴==,
即3BM=4AN.
【24】解:⑴当y=-x-4=0时,x=-4,
当x=0时,y=-x-4=-4,
∴A(-4,0),B(0,-4),
抛物线对称轴为x=-=-2.
⑵当a=1时,y=x2+4x,
过P作PD⊥x轴于D,过C作CE⊥AB于E,延长BP交x轴于F,
由⑴知:A(-4,0),B(0,-4),抛物线对称轴为x=-2,
∴OA=OB=4,AC=2,
∴∠OAB=∠OBA=45 ,AB==,
∴AE=CE=AC·sin∠OAB=,
∴BE=AB-AE=,
∴∠tan∠ABC==,
∵∠ABP=∠OBC,
∴∠ABC+∠ABP=∠OBC+∠ABC=45 =∠CBP,
∵∠OAB=∠OFB+∠ABF=45 ,
∴∠OFB=∠ABC,即tan∠OFB=tan∠ABC,
∴=,即OF=3OB=12,
∴F(-12,0),
设P(x,x2+4x),则PD=x2-4x,DF=x+12,
∴tan∠OFB==,即=,
∴x1=-,x2=-3,
∴P(-,-)或(3,-3).
(法二)联立直线BP(过C作CE⊥CB,在CE上取点E,使CE=CB,过E作EF⊥x轴于F,则y=-3x-4)与抛物线解析式也可以.
(法三)延长PD交x轴于F,过P作PD⊥x轴于D,证△CBA∽△CFB求出CF的长,可得点F的坐标.
⑶①∵N(-2+2a,5a),
∴x=-2+2a,y=5a,
∴y=x+5.
②a≤-或0<a≤或a≥.
解法:当(-2,-2)在y=ax2+4ax上时,
∴-2=4a-8a,
∴a=,
当N(-2+2a,5a)在y=ax2+4ax上时,
∴5a=a(-2+2a)+4a(-2+2a),
∵a≠0,
∴a1=-,a2=,
结合函数图象知:当a≤-或0<a≤或a≥时,抛物线与线段MN有公共点.
一、选择题(每小题3分,共30分)
1. “二十四节气”是中华农耕文明的结晶,被国际气象界誉为“中国第五大发明”. 立春为二十四节气之首,2025年立春这天北京、武汉、哈尔滨、长沙四地最低气温分别为-8℃,-1℃,-16℃,4℃,这些气温中最低的是( )
A.-8℃ B.-1℃ C.-16℃ D.4℃
2. 芯片是半导体元件产品的统称,是一种将电路小型化的技术,常制造在半导体晶圆表面上.下列关于芯片的图标中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3. 下列计算正确的是( )
A.x2·x3=x5 B.(x3)2=x5 C.x(x-1)=x2-1 D.(2a-1)2=2a2-4a+1
4. 如图,两个平面镜平行放置,光线经过平面镜反射时,∠1=∠2=40 ,则∠3的度数为( )
A.80 B.90 C.100 D.120
5. “月壤砖”是我国科学家模拟月壤成分烧制而成的一种建筑材料,拟用于未来建造月球基地. 据介绍,“月壤砖”呈榫卯结构,密度与普通砖块相当,抗压强度却是普通砖的三倍以上.如图,这是“月壤砖”的示意图,其俯视图为( )
A. B. C. D.
6. 不等式组的解集在数轴上的表示正确的是( )
A. B. C. D.
7. 下列说法错误的是( )
A.“在平面上任意画一个六边形,其内角和为360”这一事件是必然事件
B.对“神舟二十号”载人飞船发射前的零部件的检查,采用全面调查的方式
C.在大量重复试验中,随着试验次数的增加,随机事件发生的频率一般会越来越接近概率
D.在“吾辈当自强,唯我少年郎”的演讲比赛计分中,通常采用去掉一个最高分和一个最低分,然后计算平均分的办法,是因为平均数易受极端数据的影响
8. 我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗. 今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗?如果设清酒x斗,醑酒y斗,那么可列方程组为( )
A. B. C. D.
9. 已知∠ADB,作图. 步骤1:以点D为圆心,适当长为半径画弧,分别交DA,DB 于点M,N;再分别以点M,N为圆心,大于MN长为半径画弧交于点E,画射线DE. 步骤 2:在DB上任取一点O,以点O 为圆心,OD长为半径画半圆,分别交DA,DB,DE 于点P,Q,C;步骤3:连接PQ,OC.则下列结论不正确的是( )
A.= B.OC∥DA C.OC垂直平分PQ D.DP=PQ
10.二次函数y=ax2+bx+c(a、b、c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
x … -2 -1 0 1 2 …
y=ax2+bx+c … t m -2 -2 n …
且当x=-0.5时,其对应的函数值y>0,有下列结论:①abc>0;②-2和3是关于x的方程ax2+bx+c=t的两个根;③b2-4ac>0;④当0<x<1时,y<-2;⑤0<m+n<. 其中正确结论的个数是( )个.
A.1 B.2 C.3 D.4
二、填空题(每小题5分,共15分)
11.代数式中x的取值范围是_________.
12.计算:-=_________.
13.任意写出一个满足“当x>0时,y随工增大而减小”的函数为___________.
14.截止 2024年9月,我国共13位共和国勋章获得者. 老师制作了正面分别书写有孙家栋、于敏、袁隆平、黄旭华四位共和国勋章获得者为国奉献的事迹的四张卡片,除此之外背面完全相同,把这4张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片上分别写有袁隆平和黄旭华事迹的概率是_________.
15.在矩形ABCD的对角线BD上取一点E,使得DE=2BE,连接CE,将△CEB沿CE翻折得到△CEF,连接AF,BF,⑴∠AFB=_______;⑵若AB=6,BC=9,则AF=________.
三、解答题(共75分).
16.(6分)计算:-22+2cos60 +(-2025)0-(-)-1.
17.(6分)如图,□ABCD的对角线相交于点O,AE⊥BD于点E,CF⊥BD于点F,求证:BE=DF.
18.(6分)风能是一种消洁能源,我国风能资源非常丰富. 风力发电发展迅速,习近平总书记于2021年指出,中国将力争2030年前实现碳达峰、2060年前实现碳中和,某校数学综合与实践小组成员查阅资料得知,在风力发电机组中,电塔简是风力发电设施中不可或缺的重要组成部分,它的高度是一个重要的设计参数.于是该小组成员开展了测量风电塔筒高度(即风力发电的塔杆)的实践活动.形成了如下不完整的实践报告:
测量对象 风电塔筒的高度
测量目的 运用三角函数有关知识解决实际问题
测量工具 测角仪、激光测距仪等
测量示意图
测量方案 1. 在风电塔筒的空地上取测量点C,利用测角仪PC测得此时点A的仰角∠APQ=53 ; 2. 改变测量点,在风电塔筒另一侧空地上取点D,利用测角仪MD测得此时点A的仰角∠AMN=45 ; 3. 测得PC=1米,MD=0.5米,CD=200米.(图中各点均在同一竖直平面内)
请根据以上测量数据,求风电塔筒AB的高度(参考数据:sin53 ≈0.80,cos53 ≈0.60,tan53 ≈).
19.(8分)学校开展了以“生活中的数学”为主题的知识竟赛活动,现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,其分为四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95<x≤100),下面给出了部分信息.
七年级10名学生的竞赛成绩:80、96、99、99、90、99、89、82、86、100.
八年级10名学生的竞赛成绩: 94、90、94 (部分数据被墨水污染)
七、八年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 方差
七年级 92 93 a 52
八年级 92 b 100 50.4
根据以上信息,解答下列问题.
⑴ 填空:a=_______,b=_______,c=_______,并补
全条形统计图.
⑵ 若规定竞赛成绩在90分及以上为优秀,该校七、八年级参加此次活动的学生分别有800人和860人,估计在本次活动中七、八年级竞赛成绩为优秀的学生人数共多少人?
⑶ 分析上述信息,你认为该校七、八年级中哪个年级的学生对“生活中的数学”知识竞赛掌握得更好?请说明理由(写一条即可).
20.(8分)如图,正比例函数y=-x的图象与反比例函数y=(k≠0)的图象相交于点A(a ,2),B.
⑴ ①求点A 的坐标和反比例函数表达式;
②填空:点B的坐标为____________;
⑵ 若点 P(m,n)在该反比例函数图象上,且它到x轴距离大于3,请根据图象直接写出m的取值范围.
21.(8分)如图,直线AB经过⊙O上的点E,直线AO交⊙O于点D,OB⊙O于点G,连接 DE交OB于点F,连接EG,若点G是弧DE的中点,∠BEF=∠DOG.
⑴ 求证:AB 是⊙O的切线;
⑵ 若BE=6,EG=GB,求图中阴影部分面积.
22.(10分)【问题背景】教室改造采光窗户,如图1,窗户上半部分是两个正方形组成的矩形,下半部分是两个长方形组成的矩形.
【建立模型】如图 2,不考虑边框的宽度,将窗户抽象成几何图形,图中所有线段总长10.5 m.设 AE 的长为x m.
⑴ 直接用含x的式子表示出矩形窗户AEFD和矩形窗户BCFE的透光面积;
⑵ 当窗户的总面积为2.5 m时,求BE的长;
【方案解决】⑶ 窗户的面积越大,采光效果越好,基于美观的考虑,要求BE≥EF,请设计一个使采光效果最佳的方案,确定AE的长.
23.(11分)【问题情境】点E是矩形ABCD的边AE上一点,将△ABE沿直线BE折叠,使点A落在BC边上的点处.
【猜想证明】⑴ 如图1,判断四边形ABE的形状,并说明理由;
【深入探究】⑵ 如图2,将图1中的四边形CDE 沿直线E折叠,点C、D分别落在边BC,AD上的点,处,交BE于点H,展开铺平再将△EH饶点E时针方向旋转α(0 <α<45 )得到△EGF,点H,的对应点分别为G,F. 连接 AF,BG. 求的值;
【拓展延伸】⑶ 如图3,在⑵的条件下,当F,B,G在同一条直线上时,EG的延长线交AB 于点M,FG交AD 于点N. 若=. 试探究线段AN与BM之间的数量关系,并说明理由.
24.(12分)在平面直角坐标系中,抛物线y=ax2+4ax(a≠0)过原点且与x轴负半轴交于点A,过点A作直线y=-x-4交y轴于点B.
⑴ 求点A、B的坐标及抛物线的对称轴;
⑵ 如图,当a=1时,点P是直线AB下方抛物线y=ax2+4ax(a≠0)上一点,抛物线的对称轴l交x轴于点C,连接BP、BC,若∠OBC=∠ABP,求点P的坐标;
⑶ 已知点M(-2,-2),N(-2+2a,5a).
①求点N所在函数的解析式;
②若抛物线与线段MN有公共点,直接写出a的取值范围.
2024—2025年中考数学模拟测试题E参考答案
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A C C B A A D D
二、填空题(每小题5分,共15分)
11.x≥2 12.x-1 13.y=-x(答案不唯一) 14. 15.⑴90 ;⑵.
三、解答题(共75分).
【16】解:原式=1.
【17】证明:∵□ABCD,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90 ,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=DF.
【18】解:115 m.
【19】解:⑴99,94,补图略(1);
⑵1082;
⑶从表格来看,八年级的中位数比七年级的中位数大,说明八年级获得94分的比七年级多,所以八年级学生对“生活中的数学”知识竞赛掌握的更好.
【21】解:⑴①A(-3,2),y=-.
②(3,-2).
⑵-2<m<0或0<m<2.
【21】⑴证明:连接OE,
∵G是弧DE的中点,
∴弧DG=弧EG,
∴∠EOG=∠DOG,
∵OE=OD,
∴OF⊥DE,
∴∠EOF+∠OEF=90 ,
∵∠BEF=∠DOG=∠EOF,
∴∠OEB=∠OEF+∠BEF=∠OEF+∠EOF=90 ,
∴OE⊥AB,
∵OE是⊙O的半径,
∴AB是⊙O的切线.
⑵解:∵∠EFB=90 ,
∴∠DEB+∠B=90 ,
∴∠DEB+∠B=90 ,
∵EG=GB,
∴∠GEB=∠B,
∴∠GEB=∠B,
∵∠DEG=∠BEG,
∴∠DEG=∠BEG=∠B=30 ,
∴∠DEG=∠BEG=∠B=30 ,
在Rt△EFB中,BE=6,
∴EF=BE=3,
∵OG⊥DE,
∴EF=DF=3,
在Rt△OFD中,∠DOB=2∠DEG=60 ,
∴OF===,
∴OD=2OF=,
∴S阴影=S扇形DOG-S△DOF
=-××3=2π-.
【22】解:⑴由题意,矩形窗户AEFD的长EF=2x,宽AE=x,
∴矩形窗户AEFD的面积=2x2.
又∵所有线段总长10.5 m,矩形窗户AEFD的周长为7x,
∴矩形窗户BCFE的BC为2x,BE为(3.5-x).
∴矩形窗户BCFE的面积=2x(3.5-x)=7x-6x2.
⑵由题意,2x2+7x-6x2=2.5,
∴x1=0.5,x2=1.25,
当 x=1.25时,BE=3.5-3x=-0.25,不合题意,舍去,
当x=0.5时,BE=3.5-3x=2.
⑶由题意,窗户采光面积y=-4x2+7x=-4(x-)2+,
∵BE≥EF,
∴3.5-3x≥2x,
∴x≤0.7,
∵-4<0,抛物线开口向下,
∴当x<时,y随x的增加而增加,
∴在x≤0.7的范围内,当x=0.7时,采光面积最大,
答:当AE为0.7时,采光面积最大.
【23】解:⑴四边形ABE是正方形,
理由:∵四边形ABCD是矩形,
∴∠A=∠ABC=90 ,
由折叠性质得:∠BE=∠A=90 ,BA=B,
∴四边形ABE是矩形.
∴四边形ABE是正方形.
⑵∵四边形ABCD是矩形,
∴∠BAD=∠D=90 ,
由折叠性质得:∠E=∠D=90 ,
∴∠E=∠BAE=90 ,
∴∥AB,
∴=,
由旋转性质得 EF=EH,E=EF,∠BEG=∠AEF,
∴=,
∴△EBG∽△EAF,
∴=,
由折叠性质知∠ABE=∠ABC=45 ,
∴在 Rt△ABE 中,sin45 ==,
∴==,
即=.
(法二)直接用三函更简单.
⑶过M作MP⊥BG于P,
∵=,
∴令GM=,BG=3,
由题意知:∠AEB=∠FEN=45 ,∠F=90 ,
∵B、G、F三点共线,
∴∠BGM=∠EGF=45 ,
∴PG=PM=GM·sin∠PGM=1,
∴BP=BG-PG=2,
∴BM==,
∵∠BNG=∠EMB,∠MGB=∠MBE,
∴△MBG∽MBE,
∴=,即=,
∴BE=,
∴AB=BE·sin∠AEB=,
∵∠A=90 ,MP⊥BG,
∴tan∠ABN==,即=,
∴AN=,
∴==,
即3BM=4AN.
【24】解:⑴当y=-x-4=0时,x=-4,
当x=0时,y=-x-4=-4,
∴A(-4,0),B(0,-4),
抛物线对称轴为x=-=-2.
⑵当a=1时,y=x2+4x,
过P作PD⊥x轴于D,过C作CE⊥AB于E,延长BP交x轴于F,
由⑴知:A(-4,0),B(0,-4),抛物线对称轴为x=-2,
∴OA=OB=4,AC=2,
∴∠OAB=∠OBA=45 ,AB==,
∴AE=CE=AC·sin∠OAB=,
∴BE=AB-AE=,
∴∠tan∠ABC==,
∵∠ABP=∠OBC,
∴∠ABC+∠ABP=∠OBC+∠ABC=45 =∠CBP,
∵∠OAB=∠OFB+∠ABF=45 ,
∴∠OFB=∠ABC,即tan∠OFB=tan∠ABC,
∴=,即OF=3OB=12,
∴F(-12,0),
设P(x,x2+4x),则PD=x2-4x,DF=x+12,
∴tan∠OFB==,即=,
∴x1=-,x2=-3,
∴P(-,-)或(3,-3).
(法二)联立直线BP(过C作CE⊥CB,在CE上取点E,使CE=CB,过E作EF⊥x轴于F,则y=-3x-4)与抛物线解析式也可以.
(法三)延长PD交x轴于F,过P作PD⊥x轴于D,证△CBA∽△CFB求出CF的长,可得点F的坐标.
⑶①∵N(-2+2a,5a),
∴x=-2+2a,y=5a,
∴y=x+5.
②a≤-或0<a≤或a≥.
解法:当(-2,-2)在y=ax2+4ax上时,
∴-2=4a-8a,
∴a=,
当N(-2+2a,5a)在y=ax2+4ax上时,
∴5a=a(-2+2a)+4a(-2+2a),
∵a≠0,
∴a1=-,a2=,
结合函数图象知:当a≤-或0<a≤或a≥时,抛物线与线段MN有公共点.
同课章节目录
