华师大版九年级下册数学第27章第3节圆中的计算问题
文档属性
| 名称 | 华师大版九年级下册数学第27章第3节圆中的计算问题 |  | |
| 格式 | doc | ||
| 文件大小 | 316.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 16:49:35 | ||
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学九年级下册第27章第3节圆中的计算问题课时练习
一、单选题(共15小题)
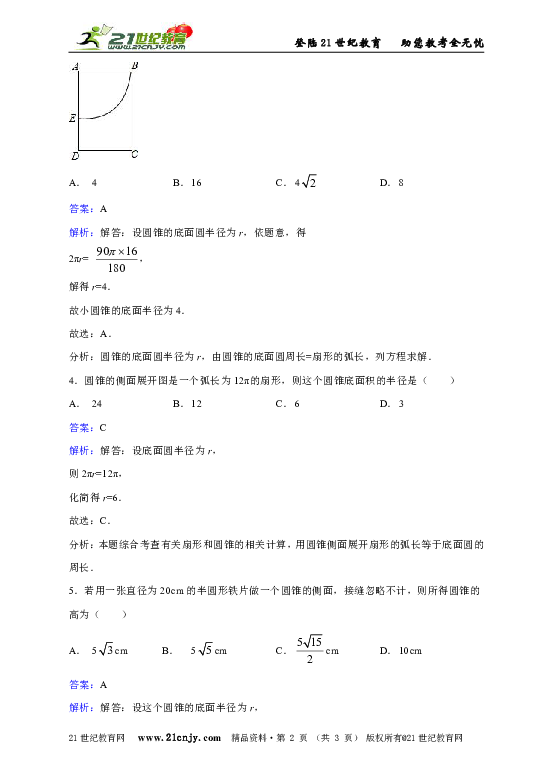
1.如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
A. 288° B. 144° C. 216° D. 120°
答案: A
解析:解答:∵底面圆的半径与母线长的比是4:5,
∴设底面圆的半径为4x,
则母线长是5x,
设圆心角为n°,
则2×4x= ,
解得:n=288,
故选:A.
分析:由底面圆的半径与母线长比的关系去设,然后利用底面圆的周长等于弧长列式计算.
2.已知一块圆心角为300°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥的底面圆的直径是80cm,则这块扇形铁皮的半径是( )
A. 24cm B. 48cm C. 96cm D. 192cm
答案:B
解析:解答:设这个扇形铁皮的半径为rcm,由题意得=π×80,
解得r=48.
故这个扇形铁皮的半径为48cm.
故选:B.
分析:底面周长=展开图的弧长
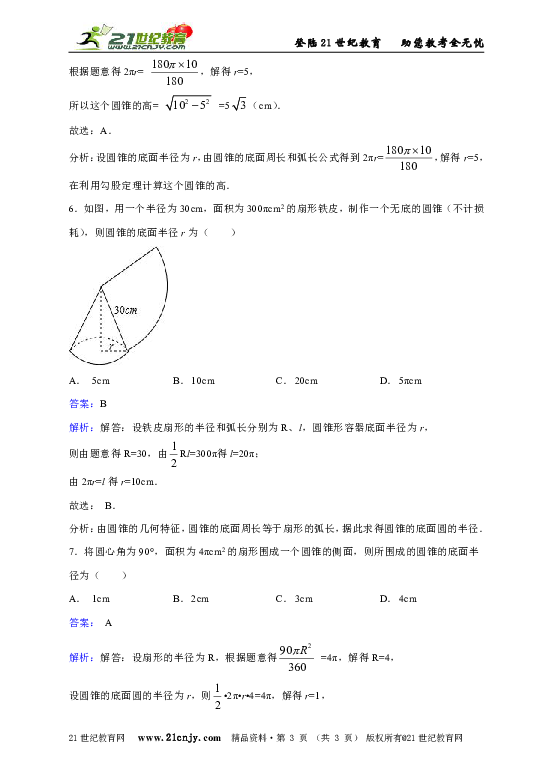
3.在长方形ABCD中AB=16,如图所示裁出一扇形ABE,将扇形围成一个圆锥(AB和AE重合),则此圆锥的底面半径为( )
A. 4 B. 16 C. 4 D. 8
答案:A
解析:解答:设圆锥的底面圆半径为r,依题意,得
2πr= ,
解得r=4.
故小圆锥的底面半径为4.
故选:A.
分析:圆锥的底面圆半径为r,由圆锥的底面圆周长=扇形的弧长,列方程求解.
4.圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面积的半径是( )
A. 24 B. 12 C. 6 D. 3
答案:C
解析:解答:设底面圆半径为r,
则2πr=12π,
化简得r=6.
故选:C.
分析:本题综合考查有关扇形和圆锥的相关计算,用圆锥侧面展开扇形的弧长等于底面圆的周长.
5.若用一张直径为20cm的半圆形铁片做一个圆锥的侧面,接缝忽略不计,则所得圆锥的高为( )
A. 5cm B. 5cm C. cm D. 10cm
答案:A
解析:解答:设这个圆锥的底面半径为r,
根据题意得2πr= ,解得r=5,
所以这个圆锥的高= =5(cm).
故选:A.
分析:设圆锥的底面半径为r,由圆锥的底面周长和弧长公式得到2πr=,解得r=5,在利用勾股定理计算这个圆锥的高.
6.如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
A. 5cm B. 10cm C. 20cm D. 5πcm
答案:B
解析:解答:设铁皮扇形的半径和弧长分别为R、l,圆锥形容器底面半径为r,
则由题意得R=30,由Rl=300π得l=20π;
由2πr=l得r=10cm.
故选: B.
分析:由圆锥的几何特征,圆锥的底面周长等于扇形的弧长,据此求得圆锥的底面圆的半径.
7.将圆心角为90°,面积为4πcm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面半径为( )
A. 1cm B. 2cm C. 3cm D. 4cm
答案: A
解析:解答:设扇形的半径为R,根据题意得 =4π,解得R=4,
设圆锥的底面圆的半径为r,则 2π r 4=4π,解得r=1,
即所围成的圆锥的底面半径为1cm.
故选:A.
分析:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
8.若一个圆锥的侧面展开图是半径为18cm,圆心角为240°的扇形,则这个圆锥的底面半径长是( )
A. 6cm B. 9cm C. 12cm D. 18cm
答案:C
解析:解答:圆锥的弧长为:=24π,
∴圆锥的底面半径为24π÷2π=12.
故选: C
分析:圆锥的侧面展开图的弧长等于圆锥的底面周长.
9.将弧长为2πcm,圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高及侧面积分别是( )
A. cm,3πcm2 B.2cm,3πcm2 C.2cm,6πcm2 D.cm,6πcm2
答案:B
解析:解答:(2π×180)÷120π=3(cm),
2π÷π÷2=1(cm),
=2(cm),
=3π(cm2).
故这个圆锥的高是2cm,侧面积是3πcm2.
故选:B.
分析:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.
10.已知圆锥的侧面积是20πcm2,母线长为5cm,则圆锥的底面半径为( )
A. 2cm B. 3cm C. 4cm D. 6cm
答案:C
解析:解答:∵圆锥的母线长是5cm,侧面积是20πcm2,
∴圆锥的侧面展开扇形的弧长为:l===8π,
∵锥的侧面展开扇形的弧长等于圆锥的底面周长,
∴r===4(cm).
故选:C
分析:圆锥的侧面积和圆锥的母线长求得圆锥的弧长,利用圆锥的侧面展开扇形的弧长等于圆锥的底面周长求得圆锥的底面半径.
11.一个圆锥的底面圆的周长是2π,母线长是3,它侧面展开图的圆心角的度数是( )
A. 60° B. 90° C. 120° D. 150°
答案:C
解析:解答:圆锥侧面展开图的扇形面积半径为6cm,弧长为4πcm,
代入扇形弧长公式l=,
即2π=,
解得n=120,
即扇形圆心角为120度.
故选:C.
分析:圆锥的母线长等于扇形的半径,圆锥的底面周长等于扇形的弧长.因而根据扇形的弧长公式就可以求出n的值.
12.如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
A. m B. m C. m D. 1m
答案:A
解析:解答:如图所示
连接OA,作OD⊥AB于点D.
在直角△OAD中,OA=1,∠OAD=∠BAC=30°,
则AD=OA cos30°=.
则AB=2AD=,
则扇形的弧长是:=,
设底面圆的半径是r,则2πr=,
解得:r=.
故选:A.
分析:连接OA,作OD⊥AB于点D,利用三角函数即可求得AD的长,则AB的长可以求得,利用弧长公式即可求得弧长;再利用圆的周长公式即可求得半径.
13.已知圆锥的侧面积为10πcm2,侧面展开图的圆心角为36°,则该圆锥的母线长为( )A. 100cm B. cm C. 10cm D. cm
答案:C
解析:解答:设母线长为R,圆锥的侧面积==10π,
∴R=10cm
故选:C
分析:利用了扇形的面积公式求解,扇形的面积公式=.
14.如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长均为1厘米,则这个圆锥的底面半径为( )厘米.
A. B. C. D.2
答案:B
解析:解答:扇形的半径为=2厘米,
∴扇形的弧长为=π厘米,
∴这个圆锥的底面半径为π÷2π=厘米.
故选:B
分析:利用弧长公式可求得扇形的弧长,圆锥的侧面展开图的弧长等于圆锥的底面周长.
15.已知圆锥形模具的母线长、半径分别是12cm、4cm,求得这个模具的侧面积是( )
A. 100πcm2 B. 80πcm2 C. 60πcm2 D. 48πcm2
答案:D
解析:解答:半径是4cm,则底面周长=8πcm,侧面积=×8π×12=48πcm2.
故选:D
分析:利用了圆的周长公式和扇形面积公式求解.
二、填空题(共5小题)
16.已知圆锥的底面圆半径为3,母线长为5,则圆锥的全面积是 .
答案:24π
解析:解答:底面周长是:2×3π=6π,
则侧面积是:×6π×5=15π,
底面积是:π×32=9π,
则全面积是:15π+9π=24π.
故答案为:24π.
分析:首先求得底面周长,即侧面展开图的扇形弧长,然后根据扇形的面积公式即可求得侧面积,即圆锥的侧面积,再求得圆锥的底面积,侧面积与底面积的和就是全面积.
17.用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是 .
答案:2
解析:解答:扇形的弧长==4π,
∴圆锥的底面半径为4π÷2π=2.
故答案为:2
分析:圆锥的弧长等于底面周长.
18.已知圆锥的侧面积等于60πcm2,母线长10cm,则圆锥的高是 cm.
答案:8
解析:解答:设圆锥的底面圆的半径为r,
根据题意得 2π r 10=60π,
解得r=6,
所以圆锥的高==8(cm).
故答案为8
分析:设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,扇形的半径等于圆锥的母线长和扇形面积公式得到r,然后根据勾股定理计算圆锥的高.
19.用一个圆心角为90°,半径为4的扇形围成一个圆锥的侧面,该圆锥底面圆的半径 .
答案:1
解析:解答:根据扇形的弧长公式l===2π,
设底面圆的半径是r,
则2π=2πr
∴r=1.
故答案为:1
分析:圆锥的底面周长等于扇形的弧长.
20.已知圆锥的底面半径是1cm,母线长为3cm,则该圆锥的侧面积为 cm2.
答案:3π
解析:解答:圆锥的侧面积=2π×3×1÷2=3π.
故答案为:3π
分析:圆锥的底面周长等于圆锥的侧面扇形的弧长.
三、解答题(共5小题)
21.如图所示的粮仓可以看成圆柱体与圆锥体的组合体,已知其底面半径为6米,高为4米,下方圆柱高为3米.
(1)求该粮仓的容积;
答案:解答:体积V=π×62×3+×π×62×(4﹣3)=108π+12π=120π;
(2)求上方圆锥的侧面积.(计算结果保留根号)
答案:解答:圆锥的母线长为l==,
所以圆锥的侧面积为s=π×6×=6π.
解析:分析:(1)确定该几何体为圆锥和圆柱的组合体,然后计算圆锥和圆柱的体积的和;(2)利用圆锥的侧面积公式直接计算.
22.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
答案:解答:如图所示:
,而r=2,
∴AB=12,
∴由勾股定理得:
AO2=AB2﹣OB2,而AB=12,OB=2,
∴AO=2.
即该圆锥的高为2.
解析:分析:运用弧长公式求出AB的长度,即可.
23.一个几何体的三视图如图所示,根据图示的数据计算出该几何体的表面积.
答案:解答:由三视图可知该几何体是圆锥,圆锥的高为12,圆锥的底面圆的半径为5,
圆锥的母线长==13,
圆锥的表面积=π 52+ 2π 5 13=90π.
解析:分析:根据三视图可判断该几何体是圆锥,利用勾股定理计算出母线长,然后求底面积与侧面积的和即可.
24.已知一个几何体的三视图如图,根据图示的数据计算该几何体的全面积及侧面展开图的圆心角(结果保留π).
答案:解答:∵如图所示可知,圆锥的高为4,底面圆的直径为6,
∴圆锥的母线为:5,
∴根据圆锥的侧面积公式:πrl=π×3×5=15π,
底面圆的面积为:πr2=9π,
∴该几何体的表面积为24π.
∴圆心角的度数:
解析:分析:根据圆锥侧面积公式首先求出圆锥的侧面积,再求出底面圆的面积,即可得出表面积.
25.在△ABC中,AB=,AC=,BC=1.
(1)求证:∠A≠30°;
答案:解答:证明:∵BC2+AC2=1+2=3=AB2,
∴△ABC是直角三角形,且∠C=90°.
∵,
∴∠A≠30°.
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积.
答案:解答:将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,
∴圆锥的底面圆的半径=,
∴圆锥的底面圆的周长=2π =2π;母线长为,
∴几何体的表面积π+π×()2=π+2π.
解析:分析:(1)根据勾股定理的逆定理得到△ABC是直角三角形,利用三角函数计算出sinA,然后与sin30°进行比较判断∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,几何体的表面积分为底面积和侧面积,分别根据圆的面积公式和扇形的面积公式进行计算.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 12 页 (共 12 页) 版权所有@21世纪教育网
华师大版数学九年级下册第27章第3节圆中的计算问题课时练习
一、单选题(共15小题)
1.如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
A. 288° B. 144° C. 216° D. 120°
答案: A
解析:解答:∵底面圆的半径与母线长的比是4:5,
∴设底面圆的半径为4x,
则母线长是5x,
设圆心角为n°,
则2×4x= ,
解得:n=288,
故选:A.
分析:由底面圆的半径与母线长比的关系去设,然后利用底面圆的周长等于弧长列式计算.
2.已知一块圆心角为300°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥的底面圆的直径是80cm,则这块扇形铁皮的半径是( )
A. 24cm B. 48cm C. 96cm D. 192cm
答案:B
解析:解答:设这个扇形铁皮的半径为rcm,由题意得=π×80,
解得r=48.
故这个扇形铁皮的半径为48cm.
故选:B.
分析:底面周长=展开图的弧长
3.在长方形ABCD中AB=16,如图所示裁出一扇形ABE,将扇形围成一个圆锥(AB和AE重合),则此圆锥的底面半径为( )
A. 4 B. 16 C. 4 D. 8
答案:A
解析:解答:设圆锥的底面圆半径为r,依题意,得
2πr= ,
解得r=4.
故小圆锥的底面半径为4.
故选:A.
分析:圆锥的底面圆半径为r,由圆锥的底面圆周长=扇形的弧长,列方程求解.
4.圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面积的半径是( )
A. 24 B. 12 C. 6 D. 3
答案:C
解析:解答:设底面圆半径为r,
则2πr=12π,
化简得r=6.
故选:C.
分析:本题综合考查有关扇形和圆锥的相关计算,用圆锥侧面展开扇形的弧长等于底面圆的周长.
5.若用一张直径为20cm的半圆形铁片做一个圆锥的侧面,接缝忽略不计,则所得圆锥的高为( )
A. 5cm B. 5cm C. cm D. 10cm
答案:A
解析:解答:设这个圆锥的底面半径为r,
根据题意得2πr= ,解得r=5,
所以这个圆锥的高= =5(cm).
故选:A.
分析:设圆锥的底面半径为r,由圆锥的底面周长和弧长公式得到2πr=,解得r=5,在利用勾股定理计算这个圆锥的高.
6.如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
A. 5cm B. 10cm C. 20cm D. 5πcm
答案:B
解析:解答:设铁皮扇形的半径和弧长分别为R、l,圆锥形容器底面半径为r,
则由题意得R=30,由Rl=300π得l=20π;
由2πr=l得r=10cm.
故选: B.
分析:由圆锥的几何特征,圆锥的底面周长等于扇形的弧长,据此求得圆锥的底面圆的半径.
7.将圆心角为90°,面积为4πcm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面半径为( )
A. 1cm B. 2cm C. 3cm D. 4cm
答案: A
解析:解答:设扇形的半径为R,根据题意得 =4π,解得R=4,
设圆锥的底面圆的半径为r,则 2π r 4=4π,解得r=1,
即所围成的圆锥的底面半径为1cm.
故选:A.
分析:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
8.若一个圆锥的侧面展开图是半径为18cm,圆心角为240°的扇形,则这个圆锥的底面半径长是( )
A. 6cm B. 9cm C. 12cm D. 18cm
答案:C
解析:解答:圆锥的弧长为:=24π,
∴圆锥的底面半径为24π÷2π=12.
故选: C
分析:圆锥的侧面展开图的弧长等于圆锥的底面周长.
9.将弧长为2πcm,圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高及侧面积分别是( )
A. cm,3πcm2 B.2cm,3πcm2 C.2cm,6πcm2 D.cm,6πcm2
答案:B
解析:解答:(2π×180)÷120π=3(cm),
2π÷π÷2=1(cm),
=2(cm),
=3π(cm2).
故这个圆锥的高是2cm,侧面积是3πcm2.
故选:B.
分析:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.
10.已知圆锥的侧面积是20πcm2,母线长为5cm,则圆锥的底面半径为( )
A. 2cm B. 3cm C. 4cm D. 6cm
答案:C
解析:解答:∵圆锥的母线长是5cm,侧面积是20πcm2,
∴圆锥的侧面展开扇形的弧长为:l===8π,
∵锥的侧面展开扇形的弧长等于圆锥的底面周长,
∴r===4(cm).
故选:C
分析:圆锥的侧面积和圆锥的母线长求得圆锥的弧长,利用圆锥的侧面展开扇形的弧长等于圆锥的底面周长求得圆锥的底面半径.
11.一个圆锥的底面圆的周长是2π,母线长是3,它侧面展开图的圆心角的度数是( )
A. 60° B. 90° C. 120° D. 150°
答案:C
解析:解答:圆锥侧面展开图的扇形面积半径为6cm,弧长为4πcm,
代入扇形弧长公式l=,
即2π=,
解得n=120,
即扇形圆心角为120度.
故选:C.
分析:圆锥的母线长等于扇形的半径,圆锥的底面周长等于扇形的弧长.因而根据扇形的弧长公式就可以求出n的值.
12.如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
A. m B. m C. m D. 1m
答案:A
解析:解答:如图所示
连接OA,作OD⊥AB于点D.
在直角△OAD中,OA=1,∠OAD=∠BAC=30°,
则AD=OA cos30°=.
则AB=2AD=,
则扇形的弧长是:=,
设底面圆的半径是r,则2πr=,
解得:r=.
故选:A.
分析:连接OA,作OD⊥AB于点D,利用三角函数即可求得AD的长,则AB的长可以求得,利用弧长公式即可求得弧长;再利用圆的周长公式即可求得半径.
13.已知圆锥的侧面积为10πcm2,侧面展开图的圆心角为36°,则该圆锥的母线长为( )A. 100cm B. cm C. 10cm D. cm
答案:C
解析:解答:设母线长为R,圆锥的侧面积==10π,
∴R=10cm
故选:C
分析:利用了扇形的面积公式求解,扇形的面积公式=.
14.如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长均为1厘米,则这个圆锥的底面半径为( )厘米.
A. B. C. D.2
答案:B
解析:解答:扇形的半径为=2厘米,
∴扇形的弧长为=π厘米,
∴这个圆锥的底面半径为π÷2π=厘米.
故选:B
分析:利用弧长公式可求得扇形的弧长,圆锥的侧面展开图的弧长等于圆锥的底面周长.
15.已知圆锥形模具的母线长、半径分别是12cm、4cm,求得这个模具的侧面积是( )
A. 100πcm2 B. 80πcm2 C. 60πcm2 D. 48πcm2
答案:D
解析:解答:半径是4cm,则底面周长=8πcm,侧面积=×8π×12=48πcm2.
故选:D
分析:利用了圆的周长公式和扇形面积公式求解.
二、填空题(共5小题)
16.已知圆锥的底面圆半径为3,母线长为5,则圆锥的全面积是 .
答案:24π
解析:解答:底面周长是:2×3π=6π,
则侧面积是:×6π×5=15π,
底面积是:π×32=9π,
则全面积是:15π+9π=24π.
故答案为:24π.
分析:首先求得底面周长,即侧面展开图的扇形弧长,然后根据扇形的面积公式即可求得侧面积,即圆锥的侧面积,再求得圆锥的底面积,侧面积与底面积的和就是全面积.
17.用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是 .
答案:2
解析:解答:扇形的弧长==4π,
∴圆锥的底面半径为4π÷2π=2.
故答案为:2
分析:圆锥的弧长等于底面周长.
18.已知圆锥的侧面积等于60πcm2,母线长10cm,则圆锥的高是 cm.
答案:8
解析:解答:设圆锥的底面圆的半径为r,
根据题意得 2π r 10=60π,
解得r=6,
所以圆锥的高==8(cm).
故答案为8
分析:设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,扇形的半径等于圆锥的母线长和扇形面积公式得到r,然后根据勾股定理计算圆锥的高.
19.用一个圆心角为90°,半径为4的扇形围成一个圆锥的侧面,该圆锥底面圆的半径 .
答案:1
解析:解答:根据扇形的弧长公式l===2π,
设底面圆的半径是r,
则2π=2πr
∴r=1.
故答案为:1
分析:圆锥的底面周长等于扇形的弧长.
20.已知圆锥的底面半径是1cm,母线长为3cm,则该圆锥的侧面积为 cm2.
答案:3π
解析:解答:圆锥的侧面积=2π×3×1÷2=3π.
故答案为:3π
分析:圆锥的底面周长等于圆锥的侧面扇形的弧长.
三、解答题(共5小题)
21.如图所示的粮仓可以看成圆柱体与圆锥体的组合体,已知其底面半径为6米,高为4米,下方圆柱高为3米.
(1)求该粮仓的容积;
答案:解答:体积V=π×62×3+×π×62×(4﹣3)=108π+12π=120π;
(2)求上方圆锥的侧面积.(计算结果保留根号)
答案:解答:圆锥的母线长为l==,
所以圆锥的侧面积为s=π×6×=6π.
解析:分析:(1)确定该几何体为圆锥和圆柱的组合体,然后计算圆锥和圆柱的体积的和;(2)利用圆锥的侧面积公式直接计算.
22.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
答案:解答:如图所示:
,而r=2,
∴AB=12,
∴由勾股定理得:
AO2=AB2﹣OB2,而AB=12,OB=2,
∴AO=2.
即该圆锥的高为2.
解析:分析:运用弧长公式求出AB的长度,即可.
23.一个几何体的三视图如图所示,根据图示的数据计算出该几何体的表面积.
答案:解答:由三视图可知该几何体是圆锥,圆锥的高为12,圆锥的底面圆的半径为5,
圆锥的母线长==13,
圆锥的表面积=π 52+ 2π 5 13=90π.
解析:分析:根据三视图可判断该几何体是圆锥,利用勾股定理计算出母线长,然后求底面积与侧面积的和即可.
24.已知一个几何体的三视图如图,根据图示的数据计算该几何体的全面积及侧面展开图的圆心角(结果保留π).
答案:解答:∵如图所示可知,圆锥的高为4,底面圆的直径为6,
∴圆锥的母线为:5,
∴根据圆锥的侧面积公式:πrl=π×3×5=15π,
底面圆的面积为:πr2=9π,
∴该几何体的表面积为24π.
∴圆心角的度数:
解析:分析:根据圆锥侧面积公式首先求出圆锥的侧面积,再求出底面圆的面积,即可得出表面积.
25.在△ABC中,AB=,AC=,BC=1.
(1)求证:∠A≠30°;
答案:解答:证明:∵BC2+AC2=1+2=3=AB2,
∴△ABC是直角三角形,且∠C=90°.
∵,
∴∠A≠30°.
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积.
答案:解答:将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,
∴圆锥的底面圆的半径=,
∴圆锥的底面圆的周长=2π =2π;母线长为,
∴几何体的表面积π+π×()2=π+2π.
解析:分析:(1)根据勾股定理的逆定理得到△ABC是直角三角形,利用三角函数计算出sinA,然后与sin30°进行比较判断∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,几何体的表面积分为底面积和侧面积,分别根据圆的面积公式和扇形的面积公式进行计算.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 12 页 (共 12 页) 版权所有@21世纪教育网
