华师大版数学九年级下册第27章27.1圆的认识1.圆的基本元素同步练习
文档属性
| 名称 | 华师大版数学九年级下册第27章27.1圆的认识1.圆的基本元素同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 129.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学九年级下册第27章27.1圆的认识1.圆的基本元素
同步练习
一、选择题
1. 如图,AB是⊙O的直径,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则∠DAC等于( )
A.15° B.30° C.45° D.60°
答案:B
解析:解答:∵OA=OC,
∴∠CAO=∠ACO,
∵AD∥OC,
∴∠DAC=∠ACO,
∴∠DAC=∠CAB,
∵∠DAB=60°,
∴∠DAC=∠DAB=30°,
故选:B
分析:首先利用同一圆的半径相等和平行线的性质得到∠DAC=∠CAB,然后利用已知角求解即可.
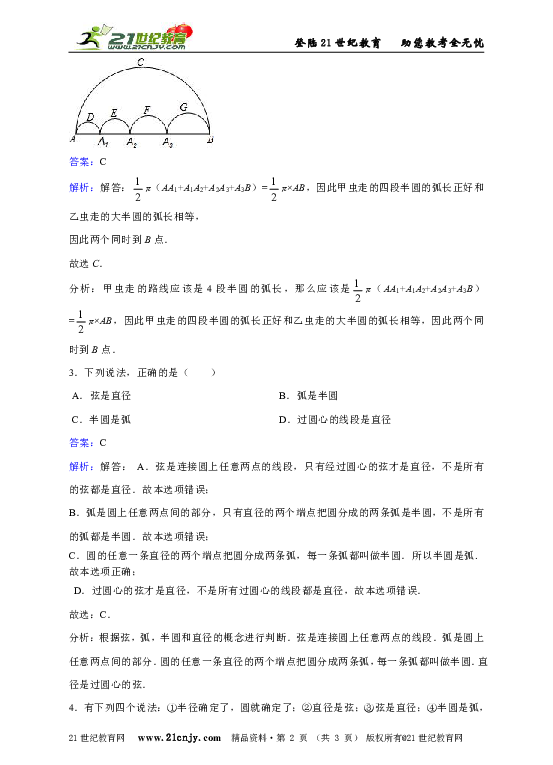
2.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B点 D.无法确定
答案:C
解析:解答:π(AA1+A1A2+A2A3+A3B)=π×AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,
因此两个同时到B点.
故选C.
分析:甲虫走的路线应该是4段半圆的弧长,那么应该是π(AA1+A1A2+A2A3+A3B)=π×AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,因此两个同时到B点.
3.下列说法,正确的是( )
A.弦是直径 B.弧是半圆
C.半圆是弧 D.过圆心的线段是直径
答案:C
解析:解答: A.弦是连接圆上任意两点的线段,只有经过圆心的弦才是直径,不是所有的弦都是直径.故本选项错误;
B.弧是圆上任意两点间的部分,只有直径的两个端点把圆分成的两条弧是半圆,不是所有的弧都是半圆.故本选项错误;
C.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.所以半圆是弧.故本选项正确;
D.过圆心的弦才是直径,不是所有过圆心的线段都是直径,故本选项错误.
故选:C.
分析:根据弦,弧,半圆和直径的概念进行判断.弦是连接圆上任意两点的线段.弧是圆上任意两点间的部分.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.直径是过圆心的弦.
4.有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中错误说法的个数是( )
A.1个 B.2个 C.3个 D.4个
答案:B
解析:解答:①圆确定的条件是确定圆心与半径,是假命题,故此说法错误;
②直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;
③弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;
④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.
其中错误说法的是①③两个.
故选:B.
分析:根据弦的定义、弧的定义、以及确定圆的条件即可解决.
5.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是( )
A.4 B.5 C.6 D.10
答案:C
解析:解答:因为五边形的各边长都和小圆的周长相等,所有小圆在每一边上滚动正好一周,在五条边上共滚动了5周.由于每次小圆从五边形的一边滚动到另一边时,都会翻转72°,所以小圆在五个角处共滚动一周.因此,总共是滚动了6周.
故选:C.
分析:因为五边形的各边长都和小圆的周长相等,所以小圆在每一边上滚动正好一周,另外五边形的外角和为360°,所以小圆在五个角处共滚动一周,可以求出小圆滚动的圈数.
6. 下列说法中,结论错误的是( )
A.直径相等的两个圆是等圆
B.长度相等的两条弧是等弧
C.圆中最长的弦是直径
D.一条直经把圆分成两条弧,这两条弧是等弧
答案:B
解析:解答:A.直径相等的两个圆是等圆,正确,不符合题意;
B.长度相等的两条弧圆周角不一定相等,它们不一定是等弧,原题的说法是错误的,符合题意;
C.圆中最长的弦是直径,正确,不符合题意;
D.一条直径把圆分成两条弧,这两条弧是等弧,正确,不符合题意,
故选:B.
分析:利用圆的有关定义进行判断,后利用排除法即可得到正确的答案;
7. 如图,在半圆的直径上作4个正三角形,如这半圆周长为C1,这4个正三角形的周长和为C2,则C1和C2的大小关系是( )
A.C1>C2 B.C1<C2 C.C1=C2 D.不能确定
答案:B
解析:解答:设半圆的直径为a,则半圆周长C1为:aπ,
4个正三角形的周长和C2为:3a,
∵aπ<3a,
∴C1<C2
故选:B.
分析:首先设圆的直径,然后表示出半圆的弧长和三个正三角形的周长和,比较后即可得到答案.
8.下列语句中,不正确的个数是( )
①直径是弦;②弧是半圆;③长度相等的弧是等弧;④经过圆内一定点可以作无数条直径.
A.1个 B.2个 C.3个 D.4个
答案:C
解析:解答: ①根据直径的概念,知直径是特殊的弦,故正确;
②根据弧的概念,知半圆是弧,但弧不一定是半圆,故错误;
③根据等弧的概念:在同圆或等圆中,能够互相重合的弧是等弧.长度相等的两条弧不一定能够重合,故错误;
④如果该定点和圆心不重合,根据两点确定一条直线,则只能作一条直径,故错误.
故选C.
分析:根据弦、弧、等弧的定义即可求解.
9. 过圆内一点A可以作出圆的最长弦有( )
A.1条 B.2条
C.3条 D.1条或无数条
答案:D
解析:解答:分两种情况:
①点A不是圆心时,由于两点确定一条直线,所以过点A的最长弦只有1条;
②点A是圆心时,由于过一点可以作无数条直线,所以过点A的最长弦有无数条.
即过圆内一点A可以作出圆的最长弦有1条或无数条.
故选D.
分析:由于直径是圆中最长的弦,过圆心的弦即是直径,根据点A与圆心的位置分两种情况进行讨论:①点A不是圆心;②点A是圆心.
10.A、B是半径为5cm的⊙O上两个不同的点,则弦AB的取值范围是( )
A.AB>0 B.0<AB<5 C.0<AB<10 D.0<AB≤10
答案:D
解析:解答:∵圆中最长的弦为直径,
∴0<AB≤10.
故选:D.
分析:根据直径是圆中最长的弦求解.
11. 已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm B.等于12cm C.小于6cm D.大于12cm
答案:B
解析:解答:根据点和圆的位置关系,得OP=6cm,再根据线段的中点的概念,得OA=2OP=12.
故选B.
分析:点在圆上,则d=r;点在圆外,d>r;点在圆内,d<r(d即点到圆心的距离,r即圆的半径).
12.下列结论错误的是( )
A.圆是轴对称图形
B.圆是中心对称图形
C.半圆不是弧
D.同圆中,等弧所对的圆心角相等
答案:C
解析:解答: A.圆是轴对称图形,说法正确;
B.圆是中心对称图形,说法正确;
C.半圆不是弧,说法错误;
D.同圆中,等弧所对的圆心角相等,说法正确;
故选:C.
分析:根据圆既是轴对称图形,也是中心对称图形,圆上任意两点间的部分叫圆弧,简称弧,圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆,大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧,进行分析.
13.车轮要做成圆形,实际上就是根据圆的特征( )
A.圆上各点到圆心的距离相等
B.直径是圆中最长的弦
C.同弧所对的圆周角相等
D.圆是中心对称图形
答案:A
解析:解答:车轮做成圆形是为了在行进过程中保持和地面的高度不变,
是利用了圆上各点到圆心的距离相等,
故选A.
分析:根据车轮的特点和功能进行解答.
14.下列说法中,结论错误的是( )
A.直径相等的两个圆是等圆
B.三角形的外心是这个三角形三条角平分线的交点
C.圆中最长的弦是直径
D.一条弦把圆分成两条弧,这两条弧可能是等弧
答案:B
解析:解答:A.直径相等的两个圆是等圆,所以A选项的说法正确;
B.三角形的外心是这个三角形三边的中垂线的交点,所以B选项的说法错误;
C.圆中最长的弦是直径,所以C选项的说法正确;
D.一条直径弦圆分成两条弧,这两条弧是等弧,所以D选项的说法正确.
故选B.
分析:根据等圆的定义对A进行判断;根据三角形外心的定义对B进行判断;根据直径的定义对C进行判断;根据等弧的定义对D进行判断.
15.下列说法中,正确的是( )
A.同一条弦所对的两条弧一定是等弧
B.长度相等的两条弧是等弧
C.正多边形一定是轴对称图形
D.三角形的外心到三角形各边的距离相等
答案:C
解析:解答: A.在同圆或等圆中,同一条弦所对的两条弧可能有一条是劣弧,一条是优弧,所以A选项错误;
B.在同圆或等圆中,长度相等的两条弧是等弧,所以B选项错误;
C.正多边形一定是轴对称图形,对称轴的条数等于它的边数,所以C选项正确;
D.三角形的外心到三角形三个顶点的距离相等,所以D选项错误.
故选C.
分析:根据等弧的定义对A、B进行判断;根据正多边的性质对C进行判断;根据三角形外心的性质对D进行判断.
二、填空题
16.如图,MN为⊙O的弦,∠M=50°,则∠MON等于 .
答案:80°
解析:解答:∵OM=ON,
∴∠N=∠M=50°,
∴∠MON=180°-∠M-∠N=80°,
故答案为:80°.
分析:利用等腰三角形的性质可得∠N的度数,根据三角形的内角和定理可得所求角的度数.
17.若⊙O的半径为6cm,则⊙O中最长的弦为 cm.
答案:12
解析:解答:∵⊙O的半径为6cm,
∴⊙O的直径为12cm,
即圆中最长的弦长为12cm.
故答案为:12.
分析:根据直径为圆的最长弦求解.
18.已知⊙O中最长的弦为16cm,则⊙O的半径为 cm.
答案:8
解析:解答: ∵⊙O中最长的弦为16cm,即直径为16cm,
∴⊙O的半径为8cm.
故答案为:8.
分析:⊙O最长的弦就是直径从而不难求得半径的长.
19.如果圆的半径为4厘米,那么它的面积为 平方厘米.
答案:16π
解析:解答:圆的面积=π 42=16π(cm2).
故答案为16π.
分析:根据圆的面积公式计算.
20. 过圆内的一点(非圆心)有 条直径.
答案:且只有一
解析:解答:过圆内的一点(非圆心)有且只有一条直径.
故答案为且只有一.
分析:根据直径的定义求解.
三、解答题
21. 已知:如图,AB是⊙O的直径,AC是⊙O的弦,AB=2,∠BAC=30°.在图中作弦AD,使AD=1,并求∠CAD的度数.
答案:解答:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=30°,
∴BC=AB=1,∠B=60°,
以A圆心BC长为半径画弧可得点D,再连接AD即可;
∵AD=BC,
∴,
∴∠DAB=∠B=60°,
∴∠DAC=60°-30°=30°;
同理可得:∠D′AC=60°+30°=90°;
综上所述:∠CAD的度数为30°或90°.
解析:分析:利用圆周角定理、圆弧、弧所对的弦的关系,进而得出∠DAB=∠B=60°,进而得出答案.
22. 如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
答案:证明: ∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
解析:分析:根据AB、CD为⊙O中两条直径,得出OA=OB,OC=OD,再根据CE=DF,得出OE=OF,从而证出△AOF和△BOE全等,即可得出答案.
23.如图,点A、B、C是⊙0上的三点,B0平分∠ABC.求证:BA=BC.
答案:证明:连OA、OC,如图,
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO,
∵B0平分∠ABC,
∴∠ABO=∠CBO,
∴∠BAO=∠BCO,
∴△OAB≌△OCB,
∴AB=BC.
解析:分析:连OA、OC,利用半径都相等得到OA=OB,OB=OC,根据等腰三角形的性质有∠ABO=∠BAO,∠CBO=∠BCO,而BO平分∠ABC,则∠ABO=∠CBO,根据三角形全等的判定得到△OAB≌△OCB,即可得到结论.
24.如图,半圆O的直径AB=8,半径OC⊥AB,D为弧AC上一点,DE⊥OC,DF⊥OA,垂足分别为E、F,求EF的长.
答案:解答:连接OD.
∵OC⊥AB ,DE⊥OC,DF⊥OA
∴∠AOC=∠DEO=∠DFO=90°,
∴四边形DEOF是矩形,
∴EF=OD.
∵OD=OA
∴EF=OA=4.
解析:分析:连接OD,利用三个角是直角的四边形是矩形判定四边形DEOF是矩形,利用矩形的对角线相等即可得到所求结论.
25.一个花坛,直径5米,在它的周围有一条宽1米的环形小路,小路的面积是多少平方米?
答案:解答:∵环形小路的宽为1米,花坛的直径为5米,
∴R=3.5m,r=2.5m;
则圆环的面积为:π×(3.5)2-π×(2.5)2=6πm2,
所以小路的面积为6πm2.
解析:分析:由题意知,求环形小路的面积,实际是求一个圆环的面积.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 12 页 (共 12 页) 版权所有@21世纪教育网
华师大版数学九年级下册第27章27.1圆的认识1.圆的基本元素
同步练习
一、选择题
1. 如图,AB是⊙O的直径,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则∠DAC等于( )
A.15° B.30° C.45° D.60°
答案:B
解析:解答:∵OA=OC,
∴∠CAO=∠ACO,
∵AD∥OC,
∴∠DAC=∠ACO,
∴∠DAC=∠CAB,
∵∠DAB=60°,
∴∠DAC=∠DAB=30°,
故选:B
分析:首先利用同一圆的半径相等和平行线的性质得到∠DAC=∠CAB,然后利用已知角求解即可.
2.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B点 D.无法确定
答案:C
解析:解答:π(AA1+A1A2+A2A3+A3B)=π×AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,
因此两个同时到B点.
故选C.
分析:甲虫走的路线应该是4段半圆的弧长,那么应该是π(AA1+A1A2+A2A3+A3B)=π×AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,因此两个同时到B点.
3.下列说法,正确的是( )
A.弦是直径 B.弧是半圆
C.半圆是弧 D.过圆心的线段是直径
答案:C
解析:解答: A.弦是连接圆上任意两点的线段,只有经过圆心的弦才是直径,不是所有的弦都是直径.故本选项错误;
B.弧是圆上任意两点间的部分,只有直径的两个端点把圆分成的两条弧是半圆,不是所有的弧都是半圆.故本选项错误;
C.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.所以半圆是弧.故本选项正确;
D.过圆心的弦才是直径,不是所有过圆心的线段都是直径,故本选项错误.
故选:C.
分析:根据弦,弧,半圆和直径的概念进行判断.弦是连接圆上任意两点的线段.弧是圆上任意两点间的部分.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.直径是过圆心的弦.
4.有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中错误说法的个数是( )
A.1个 B.2个 C.3个 D.4个
答案:B
解析:解答:①圆确定的条件是确定圆心与半径,是假命题,故此说法错误;
②直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;
③弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;
④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.
其中错误说法的是①③两个.
故选:B.
分析:根据弦的定义、弧的定义、以及确定圆的条件即可解决.
5.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是( )
A.4 B.5 C.6 D.10
答案:C
解析:解答:因为五边形的各边长都和小圆的周长相等,所有小圆在每一边上滚动正好一周,在五条边上共滚动了5周.由于每次小圆从五边形的一边滚动到另一边时,都会翻转72°,所以小圆在五个角处共滚动一周.因此,总共是滚动了6周.
故选:C.
分析:因为五边形的各边长都和小圆的周长相等,所以小圆在每一边上滚动正好一周,另外五边形的外角和为360°,所以小圆在五个角处共滚动一周,可以求出小圆滚动的圈数.
6. 下列说法中,结论错误的是( )
A.直径相等的两个圆是等圆
B.长度相等的两条弧是等弧
C.圆中最长的弦是直径
D.一条直经把圆分成两条弧,这两条弧是等弧
答案:B
解析:解答:A.直径相等的两个圆是等圆,正确,不符合题意;
B.长度相等的两条弧圆周角不一定相等,它们不一定是等弧,原题的说法是错误的,符合题意;
C.圆中最长的弦是直径,正确,不符合题意;
D.一条直径把圆分成两条弧,这两条弧是等弧,正确,不符合题意,
故选:B.
分析:利用圆的有关定义进行判断,后利用排除法即可得到正确的答案;
7. 如图,在半圆的直径上作4个正三角形,如这半圆周长为C1,这4个正三角形的周长和为C2,则C1和C2的大小关系是( )
A.C1>C2 B.C1<C2 C.C1=C2 D.不能确定
答案:B
解析:解答:设半圆的直径为a,则半圆周长C1为:aπ,
4个正三角形的周长和C2为:3a,
∵aπ<3a,
∴C1<C2
故选:B.
分析:首先设圆的直径,然后表示出半圆的弧长和三个正三角形的周长和,比较后即可得到答案.
8.下列语句中,不正确的个数是( )
①直径是弦;②弧是半圆;③长度相等的弧是等弧;④经过圆内一定点可以作无数条直径.
A.1个 B.2个 C.3个 D.4个
答案:C
解析:解答: ①根据直径的概念,知直径是特殊的弦,故正确;
②根据弧的概念,知半圆是弧,但弧不一定是半圆,故错误;
③根据等弧的概念:在同圆或等圆中,能够互相重合的弧是等弧.长度相等的两条弧不一定能够重合,故错误;
④如果该定点和圆心不重合,根据两点确定一条直线,则只能作一条直径,故错误.
故选C.
分析:根据弦、弧、等弧的定义即可求解.
9. 过圆内一点A可以作出圆的最长弦有( )
A.1条 B.2条
C.3条 D.1条或无数条
答案:D
解析:解答:分两种情况:
①点A不是圆心时,由于两点确定一条直线,所以过点A的最长弦只有1条;
②点A是圆心时,由于过一点可以作无数条直线,所以过点A的最长弦有无数条.
即过圆内一点A可以作出圆的最长弦有1条或无数条.
故选D.
分析:由于直径是圆中最长的弦,过圆心的弦即是直径,根据点A与圆心的位置分两种情况进行讨论:①点A不是圆心;②点A是圆心.
10.A、B是半径为5cm的⊙O上两个不同的点,则弦AB的取值范围是( )
A.AB>0 B.0<AB<5 C.0<AB<10 D.0<AB≤10
答案:D
解析:解答:∵圆中最长的弦为直径,
∴0<AB≤10.
故选:D.
分析:根据直径是圆中最长的弦求解.
11. 已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm B.等于12cm C.小于6cm D.大于12cm
答案:B
解析:解答:根据点和圆的位置关系,得OP=6cm,再根据线段的中点的概念,得OA=2OP=12.
故选B.
分析:点在圆上,则d=r;点在圆外,d>r;点在圆内,d<r(d即点到圆心的距离,r即圆的半径).
12.下列结论错误的是( )
A.圆是轴对称图形
B.圆是中心对称图形
C.半圆不是弧
D.同圆中,等弧所对的圆心角相等
答案:C
解析:解答: A.圆是轴对称图形,说法正确;
B.圆是中心对称图形,说法正确;
C.半圆不是弧,说法错误;
D.同圆中,等弧所对的圆心角相等,说法正确;
故选:C.
分析:根据圆既是轴对称图形,也是中心对称图形,圆上任意两点间的部分叫圆弧,简称弧,圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆,大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧,进行分析.
13.车轮要做成圆形,实际上就是根据圆的特征( )
A.圆上各点到圆心的距离相等
B.直径是圆中最长的弦
C.同弧所对的圆周角相等
D.圆是中心对称图形
答案:A
解析:解答:车轮做成圆形是为了在行进过程中保持和地面的高度不变,
是利用了圆上各点到圆心的距离相等,
故选A.
分析:根据车轮的特点和功能进行解答.
14.下列说法中,结论错误的是( )
A.直径相等的两个圆是等圆
B.三角形的外心是这个三角形三条角平分线的交点
C.圆中最长的弦是直径
D.一条弦把圆分成两条弧,这两条弧可能是等弧
答案:B
解析:解答:A.直径相等的两个圆是等圆,所以A选项的说法正确;
B.三角形的外心是这个三角形三边的中垂线的交点,所以B选项的说法错误;
C.圆中最长的弦是直径,所以C选项的说法正确;
D.一条直径弦圆分成两条弧,这两条弧是等弧,所以D选项的说法正确.
故选B.
分析:根据等圆的定义对A进行判断;根据三角形外心的定义对B进行判断;根据直径的定义对C进行判断;根据等弧的定义对D进行判断.
15.下列说法中,正确的是( )
A.同一条弦所对的两条弧一定是等弧
B.长度相等的两条弧是等弧
C.正多边形一定是轴对称图形
D.三角形的外心到三角形各边的距离相等
答案:C
解析:解答: A.在同圆或等圆中,同一条弦所对的两条弧可能有一条是劣弧,一条是优弧,所以A选项错误;
B.在同圆或等圆中,长度相等的两条弧是等弧,所以B选项错误;
C.正多边形一定是轴对称图形,对称轴的条数等于它的边数,所以C选项正确;
D.三角形的外心到三角形三个顶点的距离相等,所以D选项错误.
故选C.
分析:根据等弧的定义对A、B进行判断;根据正多边的性质对C进行判断;根据三角形外心的性质对D进行判断.
二、填空题
16.如图,MN为⊙O的弦,∠M=50°,则∠MON等于 .
答案:80°
解析:解答:∵OM=ON,
∴∠N=∠M=50°,
∴∠MON=180°-∠M-∠N=80°,
故答案为:80°.
分析:利用等腰三角形的性质可得∠N的度数,根据三角形的内角和定理可得所求角的度数.
17.若⊙O的半径为6cm,则⊙O中最长的弦为 cm.
答案:12
解析:解答:∵⊙O的半径为6cm,
∴⊙O的直径为12cm,
即圆中最长的弦长为12cm.
故答案为:12.
分析:根据直径为圆的最长弦求解.
18.已知⊙O中最长的弦为16cm,则⊙O的半径为 cm.
答案:8
解析:解答: ∵⊙O中最长的弦为16cm,即直径为16cm,
∴⊙O的半径为8cm.
故答案为:8.
分析:⊙O最长的弦就是直径从而不难求得半径的长.
19.如果圆的半径为4厘米,那么它的面积为 平方厘米.
答案:16π
解析:解答:圆的面积=π 42=16π(cm2).
故答案为16π.
分析:根据圆的面积公式计算.
20. 过圆内的一点(非圆心)有 条直径.
答案:且只有一
解析:解答:过圆内的一点(非圆心)有且只有一条直径.
故答案为且只有一.
分析:根据直径的定义求解.
三、解答题
21. 已知:如图,AB是⊙O的直径,AC是⊙O的弦,AB=2,∠BAC=30°.在图中作弦AD,使AD=1,并求∠CAD的度数.
答案:解答:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=30°,
∴BC=AB=1,∠B=60°,
以A圆心BC长为半径画弧可得点D,再连接AD即可;
∵AD=BC,
∴,
∴∠DAB=∠B=60°,
∴∠DAC=60°-30°=30°;
同理可得:∠D′AC=60°+30°=90°;
综上所述:∠CAD的度数为30°或90°.
解析:分析:利用圆周角定理、圆弧、弧所对的弦的关系,进而得出∠DAB=∠B=60°,进而得出答案.
22. 如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
答案:证明: ∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
解析:分析:根据AB、CD为⊙O中两条直径,得出OA=OB,OC=OD,再根据CE=DF,得出OE=OF,从而证出△AOF和△BOE全等,即可得出答案.
23.如图,点A、B、C是⊙0上的三点,B0平分∠ABC.求证:BA=BC.
答案:证明:连OA、OC,如图,
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO,
∵B0平分∠ABC,
∴∠ABO=∠CBO,
∴∠BAO=∠BCO,
∴△OAB≌△OCB,
∴AB=BC.
解析:分析:连OA、OC,利用半径都相等得到OA=OB,OB=OC,根据等腰三角形的性质有∠ABO=∠BAO,∠CBO=∠BCO,而BO平分∠ABC,则∠ABO=∠CBO,根据三角形全等的判定得到△OAB≌△OCB,即可得到结论.
24.如图,半圆O的直径AB=8,半径OC⊥AB,D为弧AC上一点,DE⊥OC,DF⊥OA,垂足分别为E、F,求EF的长.
答案:解答:连接OD.
∵OC⊥AB ,DE⊥OC,DF⊥OA
∴∠AOC=∠DEO=∠DFO=90°,
∴四边形DEOF是矩形,
∴EF=OD.
∵OD=OA
∴EF=OA=4.
解析:分析:连接OD,利用三个角是直角的四边形是矩形判定四边形DEOF是矩形,利用矩形的对角线相等即可得到所求结论.
25.一个花坛,直径5米,在它的周围有一条宽1米的环形小路,小路的面积是多少平方米?
答案:解答:∵环形小路的宽为1米,花坛的直径为5米,
∴R=3.5m,r=2.5m;
则圆环的面积为:π×(3.5)2-π×(2.5)2=6πm2,
所以小路的面积为6πm2.
解析:分析:由题意知,求环形小路的面积,实际是求一个圆环的面积.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 12 页 (共 12 页) 版权所有@21世纪教育网
