华师大版数学九年级下册第27章27.1圆的认识2.圆的对称性同步练习
文档属性
| 名称 | 华师大版数学九年级下册第27章27.1圆的认识2.圆的对称性同步练习 |
|
|
| 格式 | doc | ||
| 文件大小 | 446.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 17:12:57 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学九年级下册第27章27.1圆的认识2.圆的对称性
同步练习
一、选择题
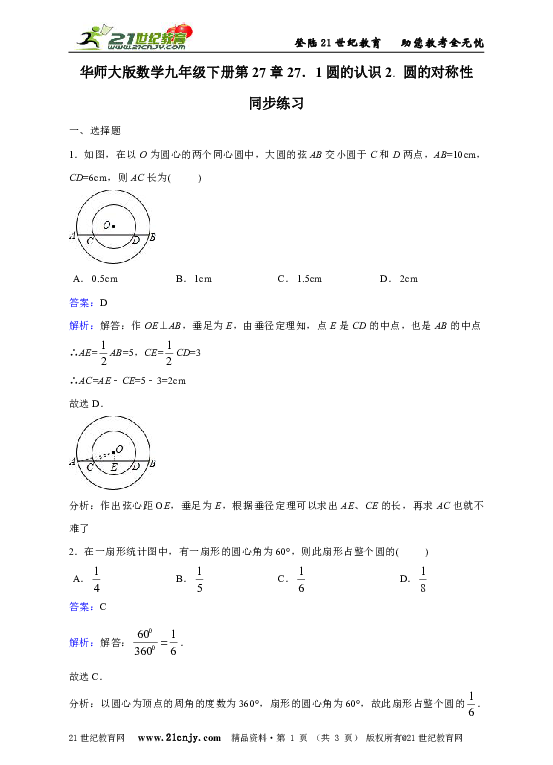
1.如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C和D两点,AB=10cm,CD=6cm,则AC长为( )
A. 0.5cm B. 1cm C. 1.5cm D. 2cm
答案:D
解析:解答:作OE⊥AB,垂足为E,由垂径定理知,点E是CD的中点,也是AB的中点
∴AE=AB=5,CE=CD=3
∴AC=AE﹣CE=5﹣3=2cm
故选D.
分析:作出弦心距OE,垂足为E,根据垂径定理可以求出AE、CE的长,再求AC也就不难了
2.在一扇形统计图中,有一扇形的圆心角为60°,则此扇形占整个圆的( )
A. B. C. D.
答案:C
解析:解答:.
故选C.
分析:以圆心为顶点的周角的度数为360°,扇形的圆心角为60°,故此扇形占整个圆的.
3.如图,在⊙O中,AB为弦,OC⊥AB,垂足为C,若AO=5,OC=3,则弦AB的长为( )
A. 10 B. 8 C. 6 D. 4
答案:B
解析:解答:Rt△OAC中,OA=5,OC=3;
根据勾股定理,得:AC==4;
所以AB=2AC=8,故选B.
分析: 在Rt△OAC中,根据勾股定理易求得AC的长;由垂径定理知AB=2AC,由此可求得AB的值.
4.下列语句中正确的是( )
A. 相等的圆心角所对的弧相等
B. 平分弦的直径垂直于弦
C. 长度相等的两条弧是等弧
D. 经过圆心的每一条直线都是圆的对称轴
答案:D
解析:解答:A.在同圆或等圆中,相等的圆心角所对的弧相等;故A错误;
B.平分弦(不是直径)的直径垂直于弦;故B错误;
C.在同圆或等圆中,能够重合的两条弧是等弧;故C错误;
D.圆是轴对称图形,过圆心的任意一条直线都是圆的对称轴,故D正确;
故选D.
分析:根据圆、圆心角、弧、弦的相关知识进行解答即可.
5.如图,半径为4的⊙O中有弦AB,以AB为折痕对折,劣弧恰好经过圆心O,则弦AB的长度等于( )
A. B. 4 C. D.
答案:C
解析:解答:过O作OC⊥AB于D,交折叠前的AB弧于C,
根据折叠后劣弧恰好经过圆心O,那么可得出的是OD=CD=2,
直角三角形OAD中,OA=4,OD=2,
AD==,
AB=2AD=.
故选C.
分析:如果过O作OC⊥AB于D,交折叠前的AB弧于C,根据折叠后劣弧恰好经过圆心O,根据垂径定理及勾股定理即可求出AC的长,进而求出AB的长.
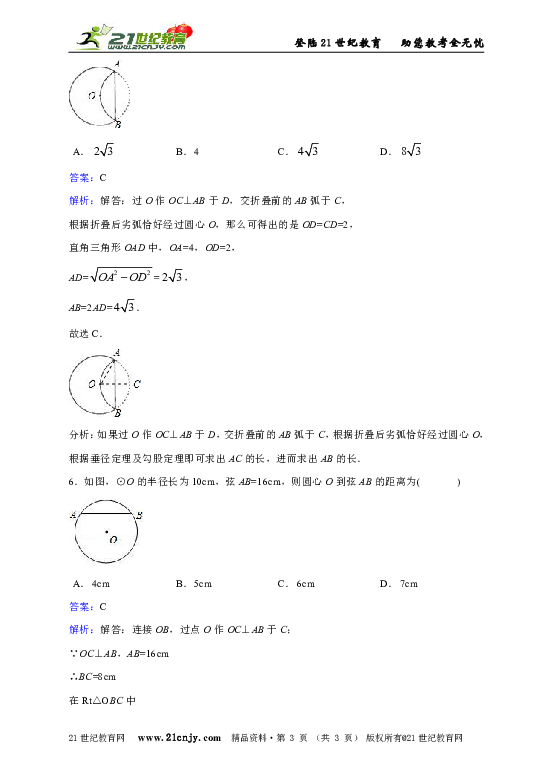
6.如图,⊙O的半径长为10cm,弦AB=16cm,则圆心O到弦AB的距离为( )
A. 4cm B. 5cm C. 6cm D. 7cm
答案:C
解析:解答:连接OB,过点O作OC⊥AB于C;
∵OC⊥AB,AB=16cm
∴BC=8cm
在Rt△OBC中
OB=10cm,CB=8cm
OC===6cm
故选C.
分析:连接OB,过点O作OC⊥AB于C,构造Rt△OBC,利用垂径定理可求得弦的一半是8,利用勾股定理即可求得弦心距.
7.下列说法不正确的是( )
A. 圆是轴对称图形,它有无数条对称轴
B. 圆的半径、弦长的一半、弦上的弦心距能组成一直角三角形,且圆的半径是此直角三角形的斜边
C. 弦长相等,则弦所对的弦心距也相等
D. 垂直于弦的直径平分这条弦,并且平分弦所对的弧
答案:C
解析:解答:A、圆是轴对称图形,过圆心的每条直线都是圆的对称轴,故A正确;
B、若圆的半径、弦长的一半、弦上的弦心距能组成一直角三角形,则此弦一定不是直径,由垂径定理知,B正确;
C、在同圆或等圆中,弦长相等,则弦所对的弦心距才相等;故C错误;
D、此结论是垂径定理,故D正确;
故选C.
分析: 根据垂径定理以及圆的相关知识进行解答.
8.如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为( )
A. B.4 C. D.8
答案:C
解析:解答:∵∠A=22.5°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=OC=,
∴CD=2CE=.
故选:C.
分析:根据圆周角定理得∠BOC=2∠A=45°,由于⊙O的直径AB垂直于弦CD,根据垂径定理得CE=DE,且可判断△OCE为等腰直角三角形,所以CE= OC=,然后利用CD=2CE进行计算.
9.如图,AB为圆O的直径,BC为圆O的一弦,自O点作BC的垂线,且交BC于D点.若AB=16,BC=12,则△OBD的面积为何?( )
A. B.12 C.15 D.30
答案:A
解析:解答:∵OD⊥BC,
∴BD=CD=BC=×12=6,
在Rt△BOD中,∵OB=AB=8,BD=6,
∴OD==2,
∴S△OBD=OD BD=×2×6=6.
故选A.
分析:根据垂径定理,由OD⊥BC得到BD=CD=BC=6,再在Rt△BOD中利用勾股定理计算出OD=2,然后根据三角形面积公式求解.
10.在⊙O中,圆心O到弦AB的距离为AB长度的一半,则弦AB所对圆心角的大小为( )
A.30° B.45° C.60° D.90°
答案:D
解析:解答:如图所示:连接BO,AO,
∵圆心O到弦AB的距离为AB长度的一半,
∴DO=DB,DO⊥AB,
∴∠BOC=∠BOC=45°,
则∠A=∠AOC=45°,
∴∠AOB=90°.
故选:D.
分析:利用等腰直角三角形的性质以及垂径定理得出∠BOC的度数进而求出.
11.如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
A.3cm B.4cm C.5cm D.6cm
答案:B
解析:解答:连接OA,
∵AB=6cm,OC⊥AB于点C,
∴AC=AB=×6=3cm,
∵⊙O的半径为5cm,
∴OC===4cm,
故选B.
分析:连接OA,先利用垂径定理得出AC的长,再由勾股定理得出OC的长即可解答.
12.如图,在⊙O内有折线OABC,点B、C在圆上,点A在⊙O内,其中OA=4cm,BC=10cm,∠A=∠B=60°,则AB的长为( )
A.5cm B.6cm C.7cm D.8cm
答案:B
解析:解答:延长AO交BC于D,作OE⊥BC于E,
设AB的长为xcm,
∵∠A=∠B=60°,∴∠ADB=60°;
∴△ADB为等边三角形;
∴BD=AD=AB=x;
∵OA=4cm,BC=10cm,
∴BE=5cm,DE=(x-5)cm,OD=(x-4)cm,
又∵∠ADB=60°,
∴DE=OD,
∴x-5=(x-4),
解得:x=6.
故选B.
分析:延长AO交BC于D,过O作BC的垂线,设垂足为E,根据∠A、∠B的度数易证得△ABD是等边三角形,设AB的长为xcm,由此可表示出OD、BD和DE的长;在Rt△ODE中,根据∠ODE的度数,可得出OD=2DE,进而可求出x的值.
13. 下列下列说法中,正确的是( )
A.平分一条直径的弦必垂直于这条直径
B.平分一条弧的直线垂直于这条弧所对的弦
C.弦的垂线必经过这条弦所在圆的圆心
D.在一个圆内平分一条弧和平分它所对的弦的直线必经过这个圆的圆心
答案:D
解析:解答:A两条直径互相平分,但不一定垂直,故本选项错误;
B.平分一条弧的直径垂直于这条弧所对的弦,故本选项错误;
C.弦的垂直平分线必经过这条弦所在圆的圆心,故本选项错误;
D.在一个圆内平分一条弧和平分它所对的弦的直线必经过这个圆的圆心,故本选项正确.
故选D.
分析:根据垂径定理对各选项进行逐一分析即可.
14.如图,⊙O的半径为5,弦AB=8,则圆上到弦AB所在的直线距离为2的点有( )个.
A.1 B.2 C.3 D.0
答案:C
解析:解答:作圆的直径CE⊥AB于点D,连接OA,
∵AB=8,
∴AD=4.
∵OA=5,
∴OD==3,
∴CD=OC-3=5-3=2,即C到弦AB所在的直线距离为2,
∴在劣弧AB上,到弦AB所在的直线距离为2的点只有C;
∵DE=5+3=8>2,
∴在优弧AEB上到弦AB所在的直线距离为2的点有2个,即圆上到弦AB所在的直线距离为2的点有3个.
故选C.
分析:作圆的直径CE⊥AB于点D,连接OA,根据勾股定理求出OE的长,求得C、E到弦AB所在的直线距离,与2比较大小,即可判断.
15.在⊙O上作一条弦AB,再作一条与弦AB垂直的直径CD,CD与AB交于点E,则下列结论中不一定正确是( )
A.AE=BE B. C.CE=EO D.
答案:C
解析:解答:由垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两段弧知:
AE=BE,,,故A,B,D正确,
故选C.
分析:根据垂径定理,垂直于弦的直径平分这条弦,并且平分这条弦所对的两段弧得出结论.
二、填空题
16. 如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦AB的长是 .
答案:6
解析:解答:连接AO,
∵半径是5,CD=1,
∴OD=5-1=4,
根据勾股定理,
AD===3,
∴AB=3×2=6,
因此弦AB的长是6.
故答案为:6.
分析:连接AO,得到直角三角形,再求出OD的长,就可以利用勾股定理求解.
17.如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为 .
答案:
解析:解答:连接OC,如图所示:
∵AB是⊙O的直径,CD⊥AB,
∴CE=CD=2,∠OEC=90°,
设OC=OA=x,则OE=x-1,
根据勾股定理得:CE2+OE2=OC2,
即22+(x-1)2=x2,
解得:x=;
故答案为:.
分析:连接OC,由垂径定理得出CE=CD=2,设OC=OA=x,则OE=x-1,由勾股定理得出CE2+OE2=OC2,得出方程,解方程即可.
18.如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为 .
答案:4
解析:解答: ∵OD⊥BC,
∴BD=CD=BC=3,
∵OB=AB=5,
∴OD==4.
故答案为:4.
分析:根据垂径定理求得BD,然后根据勾股定理求得即可.
19.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE= .
答案:4-
解析:解答:如图,连接OC.
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3.
∵在Rt△OEC中,∠OEC=90°,CE=3,OC=4,
∴OE==,
∴BE=OB-OE=4-.
故答案为4-.
分析:连接OC,根据垂径定理得出CE=ED=CD=3,然后在Rt△OEC中由勾股定理求出OE的长度,最后由BE=OB-OE,即可求出BE的长度.
20.赵洲桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R= 米.
答案:25
解析:解答:根据垂径定理,得AD=AB=20米.
设圆的半径是r,根据勾股定理,
得R2=202+(R-10)2,
解得R=25(米).
故答案为25.
分析:根据垂径定理和勾股定理求解即可.
三、解答题
21.如图,AB为半圆直径,O为圆心,C为半圆上一点,E是弧AC的中点,OE交弦AC于点D,若AC=8cm,DE=2cm,求OD的长.
答案: 解答:∵E为弧AC的中点,∴OE⊥AC,∴AD=AC=4cm,
∵OD=OE-DE=(OE-2)cm,OA=OE,
∴在Rt△OAD中,OA2=OD2+AD2即OA2=(OE-2)2+42,又知0A=OE,解得:OE=5,
∴OD=OE-DE=3cm.
解析:分析:由E是弧AC的中点,可得:OE⊥AC.根据垂径定理得:AD=AC,又OD=OE-DE,故在Rt△OAD中,运用勾股定理可将OA的长求出.
22.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
答案: 解答:过O作OF⊥CD,交CD于点F,连接OD,
∴F为CD的中点,即CF=DF,
∵AE=2,EB=6,
∴AB=AE+EB=2+6=8,
∴OA=4,
∴OE=OA-AE=4-2=2,
在Rt△OEF中,∠DEB=30°,
∴OF=OE=1,
在Rt△ODF中,OF=1,OD=4,
根据勾股定理得:DF==,
则CD=2DF=2.
解析:分析:过O作OF垂直于CD,连接OD,利用垂径定理得到F为CD的中点,由AE+EB求出直径AB的长,进而确定出半径OA与OD的长,由OA-AE求出OE的长,在直角三角形OEF中,利用30°所对的直角边等于斜边的一半求出OF的长,在直角三角形ODF中,利用勾股定理求出DF的长,由CD=2DF即可求出CD的长.
23. 如图,在⊙O中,点C是的中点,弦AB与半径OC相交于点D,AB=12,CD=2.求⊙O半径的长.
答案: 解答:连接AO,
∵点C是弧AB的中点,半径OC与AB相交于点D,
∴OC⊥AB,
∵AB=12,
∴AD=BD=6,
设⊙O的半径为R,
∵CD=2,
∴在Rt△AOD中,由勾股定理得:AD2=OD2+AD2,
即:R2=(R-2)2+62,
∴R=10
答:⊙O的半径长为10.
解析:分析:连接OA,根据垂径定理求出AD=6,∠ADO=90°,根据勾股定理得出方程,求出方程的解即可.
24. 如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
答案: 证明:作OH⊥AB于H,如图,
则AH=BH,CH=DH,
∴AH-CH=BH-DH,
即AC=BD.
解析:分析:作OH⊥AB于H,根据垂径定理得到AH=BH,CH=DH,然后利用等量减等量差相等可得到结论.
25.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
答案: 解答:(1)连接AC,如图
∵直径AB垂直于弦CD于点E,
∴,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点
(2)若AB=8,求CD的长.
答案: 在Rt△OCE中,AB=8,
∴OC=AB=4,
又∵BE=OE,
∴OE=2,
∴CE===2,
∴CD=2CE=4.
解析:分析:(1)要证明:E是OB的中点,只要求证OE=OB=OC,即证明∠OCE=30°即可.
(2)在直角△OCE中,根据勾股定理就可以解得CE的长,进而求出CD的长.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 18 页 (共 18 页) 版权所有@21世纪教育网
华师大版数学九年级下册第27章27.1圆的认识2.圆的对称性
同步练习
一、选择题
1.如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C和D两点,AB=10cm,CD=6cm,则AC长为( )
A. 0.5cm B. 1cm C. 1.5cm D. 2cm
答案:D
解析:解答:作OE⊥AB,垂足为E,由垂径定理知,点E是CD的中点,也是AB的中点
∴AE=AB=5,CE=CD=3
∴AC=AE﹣CE=5﹣3=2cm
故选D.
分析:作出弦心距OE,垂足为E,根据垂径定理可以求出AE、CE的长,再求AC也就不难了
2.在一扇形统计图中,有一扇形的圆心角为60°,则此扇形占整个圆的( )
A. B. C. D.
答案:C
解析:解答:.
故选C.
分析:以圆心为顶点的周角的度数为360°,扇形的圆心角为60°,故此扇形占整个圆的.
3.如图,在⊙O中,AB为弦,OC⊥AB,垂足为C,若AO=5,OC=3,则弦AB的长为( )
A. 10 B. 8 C. 6 D. 4
答案:B
解析:解答:Rt△OAC中,OA=5,OC=3;
根据勾股定理,得:AC==4;
所以AB=2AC=8,故选B.
分析: 在Rt△OAC中,根据勾股定理易求得AC的长;由垂径定理知AB=2AC,由此可求得AB的值.
4.下列语句中正确的是( )
A. 相等的圆心角所对的弧相等
B. 平分弦的直径垂直于弦
C. 长度相等的两条弧是等弧
D. 经过圆心的每一条直线都是圆的对称轴
答案:D
解析:解答:A.在同圆或等圆中,相等的圆心角所对的弧相等;故A错误;
B.平分弦(不是直径)的直径垂直于弦;故B错误;
C.在同圆或等圆中,能够重合的两条弧是等弧;故C错误;
D.圆是轴对称图形,过圆心的任意一条直线都是圆的对称轴,故D正确;
故选D.
分析:根据圆、圆心角、弧、弦的相关知识进行解答即可.
5.如图,半径为4的⊙O中有弦AB,以AB为折痕对折,劣弧恰好经过圆心O,则弦AB的长度等于( )
A. B. 4 C. D.
答案:C
解析:解答:过O作OC⊥AB于D,交折叠前的AB弧于C,
根据折叠后劣弧恰好经过圆心O,那么可得出的是OD=CD=2,
直角三角形OAD中,OA=4,OD=2,
AD==,
AB=2AD=.
故选C.
分析:如果过O作OC⊥AB于D,交折叠前的AB弧于C,根据折叠后劣弧恰好经过圆心O,根据垂径定理及勾股定理即可求出AC的长,进而求出AB的长.
6.如图,⊙O的半径长为10cm,弦AB=16cm,则圆心O到弦AB的距离为( )
A. 4cm B. 5cm C. 6cm D. 7cm
答案:C
解析:解答:连接OB,过点O作OC⊥AB于C;
∵OC⊥AB,AB=16cm
∴BC=8cm
在Rt△OBC中
OB=10cm,CB=8cm
OC===6cm
故选C.
分析:连接OB,过点O作OC⊥AB于C,构造Rt△OBC,利用垂径定理可求得弦的一半是8,利用勾股定理即可求得弦心距.
7.下列说法不正确的是( )
A. 圆是轴对称图形,它有无数条对称轴
B. 圆的半径、弦长的一半、弦上的弦心距能组成一直角三角形,且圆的半径是此直角三角形的斜边
C. 弦长相等,则弦所对的弦心距也相等
D. 垂直于弦的直径平分这条弦,并且平分弦所对的弧
答案:C
解析:解答:A、圆是轴对称图形,过圆心的每条直线都是圆的对称轴,故A正确;
B、若圆的半径、弦长的一半、弦上的弦心距能组成一直角三角形,则此弦一定不是直径,由垂径定理知,B正确;
C、在同圆或等圆中,弦长相等,则弦所对的弦心距才相等;故C错误;
D、此结论是垂径定理,故D正确;
故选C.
分析: 根据垂径定理以及圆的相关知识进行解答.
8.如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为( )
A. B.4 C. D.8
答案:C
解析:解答:∵∠A=22.5°,
∴∠BOC=2∠A=45°,
∵⊙O的直径AB垂直于弦CD,
∴CE=DE,△OCE为等腰直角三角形,
∴CE=OC=,
∴CD=2CE=.
故选:C.
分析:根据圆周角定理得∠BOC=2∠A=45°,由于⊙O的直径AB垂直于弦CD,根据垂径定理得CE=DE,且可判断△OCE为等腰直角三角形,所以CE= OC=,然后利用CD=2CE进行计算.
9.如图,AB为圆O的直径,BC为圆O的一弦,自O点作BC的垂线,且交BC于D点.若AB=16,BC=12,则△OBD的面积为何?( )
A. B.12 C.15 D.30
答案:A
解析:解答:∵OD⊥BC,
∴BD=CD=BC=×12=6,
在Rt△BOD中,∵OB=AB=8,BD=6,
∴OD==2,
∴S△OBD=OD BD=×2×6=6.
故选A.
分析:根据垂径定理,由OD⊥BC得到BD=CD=BC=6,再在Rt△BOD中利用勾股定理计算出OD=2,然后根据三角形面积公式求解.
10.在⊙O中,圆心O到弦AB的距离为AB长度的一半,则弦AB所对圆心角的大小为( )
A.30° B.45° C.60° D.90°
答案:D
解析:解答:如图所示:连接BO,AO,
∵圆心O到弦AB的距离为AB长度的一半,
∴DO=DB,DO⊥AB,
∴∠BOC=∠BOC=45°,
则∠A=∠AOC=45°,
∴∠AOB=90°.
故选:D.
分析:利用等腰直角三角形的性质以及垂径定理得出∠BOC的度数进而求出.
11.如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
A.3cm B.4cm C.5cm D.6cm
答案:B
解析:解答:连接OA,
∵AB=6cm,OC⊥AB于点C,
∴AC=AB=×6=3cm,
∵⊙O的半径为5cm,
∴OC===4cm,
故选B.
分析:连接OA,先利用垂径定理得出AC的长,再由勾股定理得出OC的长即可解答.
12.如图,在⊙O内有折线OABC,点B、C在圆上,点A在⊙O内,其中OA=4cm,BC=10cm,∠A=∠B=60°,则AB的长为( )
A.5cm B.6cm C.7cm D.8cm
答案:B
解析:解答:延长AO交BC于D,作OE⊥BC于E,
设AB的长为xcm,
∵∠A=∠B=60°,∴∠ADB=60°;
∴△ADB为等边三角形;
∴BD=AD=AB=x;
∵OA=4cm,BC=10cm,
∴BE=5cm,DE=(x-5)cm,OD=(x-4)cm,
又∵∠ADB=60°,
∴DE=OD,
∴x-5=(x-4),
解得:x=6.
故选B.
分析:延长AO交BC于D,过O作BC的垂线,设垂足为E,根据∠A、∠B的度数易证得△ABD是等边三角形,设AB的长为xcm,由此可表示出OD、BD和DE的长;在Rt△ODE中,根据∠ODE的度数,可得出OD=2DE,进而可求出x的值.
13. 下列下列说法中,正确的是( )
A.平分一条直径的弦必垂直于这条直径
B.平分一条弧的直线垂直于这条弧所对的弦
C.弦的垂线必经过这条弦所在圆的圆心
D.在一个圆内平分一条弧和平分它所对的弦的直线必经过这个圆的圆心
答案:D
解析:解答:A两条直径互相平分,但不一定垂直,故本选项错误;
B.平分一条弧的直径垂直于这条弧所对的弦,故本选项错误;
C.弦的垂直平分线必经过这条弦所在圆的圆心,故本选项错误;
D.在一个圆内平分一条弧和平分它所对的弦的直线必经过这个圆的圆心,故本选项正确.
故选D.
分析:根据垂径定理对各选项进行逐一分析即可.
14.如图,⊙O的半径为5,弦AB=8,则圆上到弦AB所在的直线距离为2的点有( )个.
A.1 B.2 C.3 D.0
答案:C
解析:解答:作圆的直径CE⊥AB于点D,连接OA,
∵AB=8,
∴AD=4.
∵OA=5,
∴OD==3,
∴CD=OC-3=5-3=2,即C到弦AB所在的直线距离为2,
∴在劣弧AB上,到弦AB所在的直线距离为2的点只有C;
∵DE=5+3=8>2,
∴在优弧AEB上到弦AB所在的直线距离为2的点有2个,即圆上到弦AB所在的直线距离为2的点有3个.
故选C.
分析:作圆的直径CE⊥AB于点D,连接OA,根据勾股定理求出OE的长,求得C、E到弦AB所在的直线距离,与2比较大小,即可判断.
15.在⊙O上作一条弦AB,再作一条与弦AB垂直的直径CD,CD与AB交于点E,则下列结论中不一定正确是( )
A.AE=BE B. C.CE=EO D.
答案:C
解析:解答:由垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两段弧知:
AE=BE,,,故A,B,D正确,
故选C.
分析:根据垂径定理,垂直于弦的直径平分这条弦,并且平分这条弦所对的两段弧得出结论.
二、填空题
16. 如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=1,则弦AB的长是 .
答案:6
解析:解答:连接AO,
∵半径是5,CD=1,
∴OD=5-1=4,
根据勾股定理,
AD===3,
∴AB=3×2=6,
因此弦AB的长是6.
故答案为:6.
分析:连接AO,得到直角三角形,再求出OD的长,就可以利用勾股定理求解.
17.如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为 .
答案:
解析:解答:连接OC,如图所示:
∵AB是⊙O的直径,CD⊥AB,
∴CE=CD=2,∠OEC=90°,
设OC=OA=x,则OE=x-1,
根据勾股定理得:CE2+OE2=OC2,
即22+(x-1)2=x2,
解得:x=;
故答案为:.
分析:连接OC,由垂径定理得出CE=CD=2,设OC=OA=x,则OE=x-1,由勾股定理得出CE2+OE2=OC2,得出方程,解方程即可.
18.如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为 .
答案:4
解析:解答: ∵OD⊥BC,
∴BD=CD=BC=3,
∵OB=AB=5,
∴OD==4.
故答案为:4.
分析:根据垂径定理求得BD,然后根据勾股定理求得即可.
19.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE= .
答案:4-
解析:解答:如图,连接OC.
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=CD=3.
∵在Rt△OEC中,∠OEC=90°,CE=3,OC=4,
∴OE==,
∴BE=OB-OE=4-.
故答案为4-.
分析:连接OC,根据垂径定理得出CE=ED=CD=3,然后在Rt△OEC中由勾股定理求出OE的长度,最后由BE=OB-OE,即可求出BE的长度.
20.赵洲桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R= 米.
答案:25
解析:解答:根据垂径定理,得AD=AB=20米.
设圆的半径是r,根据勾股定理,
得R2=202+(R-10)2,
解得R=25(米).
故答案为25.
分析:根据垂径定理和勾股定理求解即可.
三、解答题
21.如图,AB为半圆直径,O为圆心,C为半圆上一点,E是弧AC的中点,OE交弦AC于点D,若AC=8cm,DE=2cm,求OD的长.
答案: 解答:∵E为弧AC的中点,∴OE⊥AC,∴AD=AC=4cm,
∵OD=OE-DE=(OE-2)cm,OA=OE,
∴在Rt△OAD中,OA2=OD2+AD2即OA2=(OE-2)2+42,又知0A=OE,解得:OE=5,
∴OD=OE-DE=3cm.
解析:分析:由E是弧AC的中点,可得:OE⊥AC.根据垂径定理得:AD=AC,又OD=OE-DE,故在Rt△OAD中,运用勾股定理可将OA的长求出.
22.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.
答案: 解答:过O作OF⊥CD,交CD于点F,连接OD,
∴F为CD的中点,即CF=DF,
∵AE=2,EB=6,
∴AB=AE+EB=2+6=8,
∴OA=4,
∴OE=OA-AE=4-2=2,
在Rt△OEF中,∠DEB=30°,
∴OF=OE=1,
在Rt△ODF中,OF=1,OD=4,
根据勾股定理得:DF==,
则CD=2DF=2.
解析:分析:过O作OF垂直于CD,连接OD,利用垂径定理得到F为CD的中点,由AE+EB求出直径AB的长,进而确定出半径OA与OD的长,由OA-AE求出OE的长,在直角三角形OEF中,利用30°所对的直角边等于斜边的一半求出OF的长,在直角三角形ODF中,利用勾股定理求出DF的长,由CD=2DF即可求出CD的长.
23. 如图,在⊙O中,点C是的中点,弦AB与半径OC相交于点D,AB=12,CD=2.求⊙O半径的长.
答案: 解答:连接AO,
∵点C是弧AB的中点,半径OC与AB相交于点D,
∴OC⊥AB,
∵AB=12,
∴AD=BD=6,
设⊙O的半径为R,
∵CD=2,
∴在Rt△AOD中,由勾股定理得:AD2=OD2+AD2,
即:R2=(R-2)2+62,
∴R=10
答:⊙O的半径长为10.
解析:分析:连接OA,根据垂径定理求出AD=6,∠ADO=90°,根据勾股定理得出方程,求出方程的解即可.
24. 如图,两个圆都以点O为圆心,大圆的弦AB交小圆于C、D两点.
求证:AC=BD.
答案: 证明:作OH⊥AB于H,如图,
则AH=BH,CH=DH,
∴AH-CH=BH-DH,
即AC=BD.
解析:分析:作OH⊥AB于H,根据垂径定理得到AH=BH,CH=DH,然后利用等量减等量差相等可得到结论.
25.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
答案: 解答:(1)连接AC,如图
∵直径AB垂直于弦CD于点E,
∴,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点
(2)若AB=8,求CD的长.
答案: 在Rt△OCE中,AB=8,
∴OC=AB=4,
又∵BE=OE,
∴OE=2,
∴CE===2,
∴CD=2CE=4.
解析:分析:(1)要证明:E是OB的中点,只要求证OE=OB=OC,即证明∠OCE=30°即可.
(2)在直角△OCE中,根据勾股定理就可以解得CE的长,进而求出CD的长.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 18 页 (共 18 页) 版权所有@21世纪教育网
