【期末专项训练】第二单元测试(含解析)2024-2025学年四年级下册数学北师大版
文档属性
| 名称 | 【期末专项训练】第二单元测试(含解析)2024-2025学年四年级下册数学北师大版 | 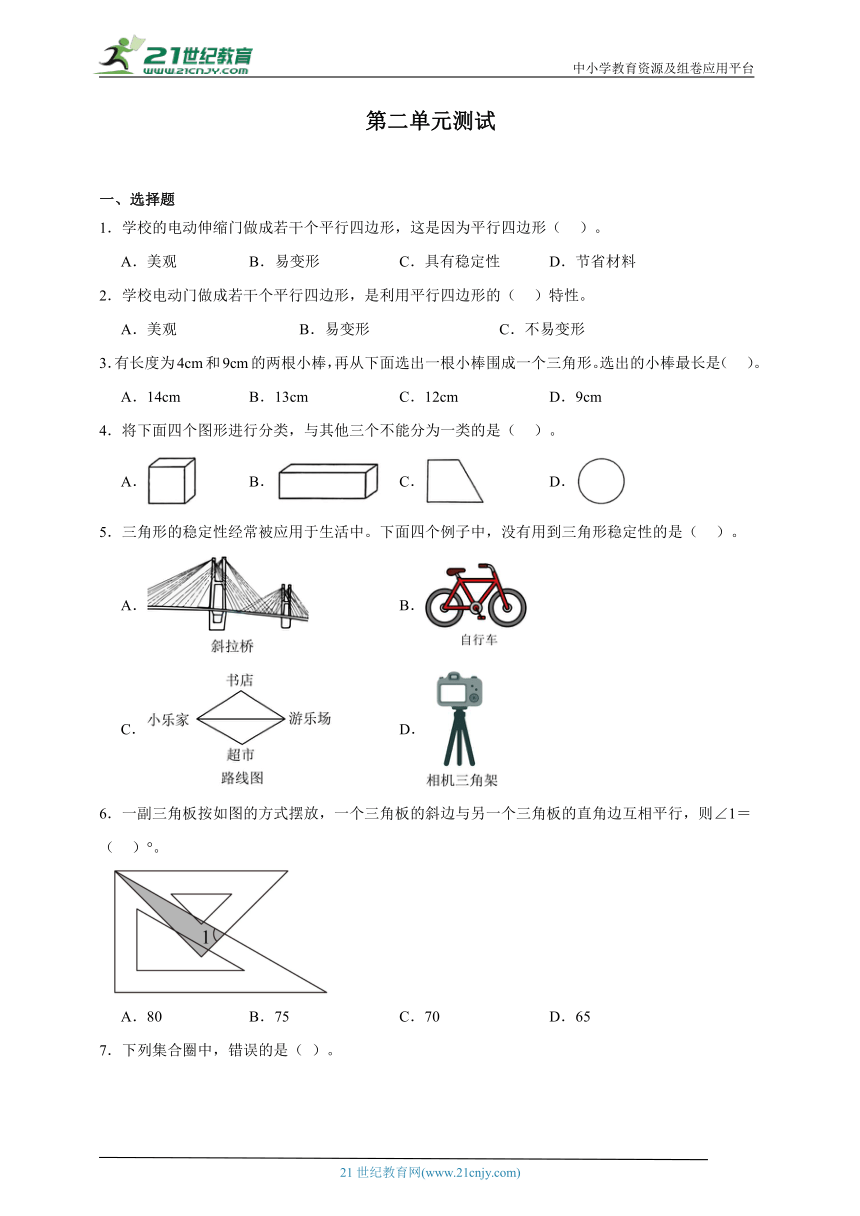 | |
| 格式 | docx | ||
| 文件大小 | 320.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 10:33:05 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
第二单元测试
一、选择题
1.学校的电动伸缩门做成若干个平行四边形,这是因为平行四边形( )。
A.美观 B.易变形 C.具有稳定性 D.节省材料
2.学校电动门做成若干个平行四边形,是利用平行四边形的( )特性。
A.美观 B.易变形 C.不易变形
3.有长度为4cm和9cm的两根小棒,再从下面选出一根小棒围成一个三角形。选出的小棒最长是( )。
A.14cm B.13cm C.12cm D.9cm
4.将下面四个图形进行分类,与其他三个不能分为一类的是( )。
A. B. C. D.
5.三角形的稳定性经常被应用于生活中。下面四个例子中,没有用到三角形稳定性的是( )。
A. B.
C. D.
6.一副三角板按如图的方式摆放,一个三角板的斜边与另一个三角板的直角边互相平行,则∠1=( )°。
A.80 B.75 C.70 D.65
7.下列集合圈中,错误的是( )。
A. B. C.
8.已知三条线段的长度分别是3米、2米和d米,如果用这样的三条线段围成一个三角形,那么满足条件的整数d有( )个。
A.3 B.4 C.5 D.6
9.被遮住的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
10.用5个长6厘米、宽4厘米的长方形可以拼成的大长方形中周长最小的是( )厘米.
A.68 B.52 C.44 D.40
二、填空题
11.三角形是由三条( )首尾相接围成的图形.
12.由 围成的图形叫做三角形。
13.如果两个内角相等,那么这个三角形是( )三角形。
14.一个等腰三角形,它的一个顶角是80,它的底角是( ) °。这个三角形是( )三角形。(填“钝角”、“锐角”、“直角”)
15.如图,凳子摇晃了,在凳子下边斜着钉木条,凳子就可以正常使用了,这是运用了( )知识。
16.一个三角形两条边分别长5厘米和9厘米,第三条边最短是( )厘米,最长可以是( )厘米。(答案均为整数)
17.如下图,一个四边形被遮住了一部分,这个图形可能是( )。
18.在一张长10厘米,宽4厘米的长方形纸上剪下一个最大的正方形,这个正方形的边长是 厘米,周长是 厘米.
19.一个等边三角形的三条边之和是18厘米,它的边长是( )厘米。
20. 有 个四边形.
三、判断题
21.平行四边形的两组对边互相平行。( )
22.有两组对边平行的四边形是平行四边形,有一组对边平行的四边形是梯形。( )
23.淘气用5厘米、2厘米、2厘米的三根小棒围成了一个等腰三角形。( )
24.在一个直角三角形中,已知其中一个锐角是43°则另一个锐角是47°。( )
25.用三根分别长7厘米、12厘米和5厘米的小木棒,头尾相连,一定能摆出一个三角形。( )
26.钝角三角形的内角和大于锐角三角形的内角和. .(判断对错)
四、计算题
27.在三角形ABC中,∠B=135 ,∠C=20 。求∠A的度数。
28.计算下面各角的度数。
五、连线题
29.小鸟回家。(连一连)
两组对边分别平行的四边形 只有一组对边平行的四边形 有一个内角是90°的三角形
钝角三角形 锐角三角形 直角三角形 平行四边形 梯形
最大的内角是72°的三角形 其中两个内角之和是82°的三角形
六、解答题
30.在学校“变废为宝”活动中,小明用铁丝围成边长6厘米的正方形当作品底座的外边。老师建议改成更稳的等边三角形,且铁丝长度不变,那改成后的等边三角形边长是多少厘米?
31.小红认为,下图中被遮住的三角形不可能是钝角三角形。你同意小红的观点吗?请说明理由。
32.在一块长方形菜地(如图)的四周围上竹篱笆,竹篱笆至少需要多少米?
33.一块直角三角形的菜地,已知一个锐角是另一个锐角的4倍,这两个锐角的度数分别是多少度?
34.(1)三个安装工人,6天一共安装了72台空调,平均每人每天安装了多少台?
(2)用两个长5厘米,宽3厘米的小长方形,拼成一个大长方形,拼成的大长方形的周长最少是多少厘米?
(3)右图是一块长方形菜地,它的一边靠墙,其它三面用篱笆围成,算一算,围成的篱笆长 米.
《第二单元测试》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C D C B A A D C
1.B
【分析】根据平行四边形的易变性(不稳定性)进行解答即可。
【详解】学校的电动伸缩门做成若干个平行四边形,这是因为平行四边形易变形;
故答案为:B
【点睛】此题考查了平行四边形的易变性。
2.B
【分析】学校大门做成的若干个平行四边形,这是应用了平行四边形不稳定性,即易变形的特性进行制作的。
【详解】由分析可知,学校电动门做成若干个平行四边形,是利用平行四边形的易变形特性。
故答案为:B
3.C
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】4+9=13(cm),9-4=5(cm)
则第三条边应小于13cm,大于5cm,最长是12cm。
故答案为:C
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
4.D
【分析】观察上图可知,前面三个图形都是由线段组成的,最后一个图形由轴线组成的,据此即可解答。
【详解】
根据分析可知,与其他三个不能分为一类的是。
故答案为:D
5.C
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点,据此解答即可。
【详解】A.支撑桥梁结构的结构图形采用三角形,这是利用三角形的稳定;
B.自行车车架是一个三角形,应用了三角形的稳定性;
C.虽然图中出现三角形,但是描述的是路径问题,不属于利用三角形稳定性;
D.相机三脚架的三个脚在地面形成一个三角形,可以起到稳定相机的作用,利用了三角形的稳定。
故答案为:C
6.B
【分析】观察上图可知,图上一个45°的角和一个60°的角叠放在一起,形成一个90°的角,所以重叠部分的∠2为45°+60°-90°=15°,阴影部分是一个直角三角形,所以∠1等于180°减90°,再减∠2;据此即可解答。
【详解】∠2=45°+60°-90°=105°-90°=15°
∠1=180°-90°-∠2=90°-15°=75°
故答案为:B
7.A
【详解】略
8.A
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】3+2=5(米),3-2=1(米)
则第三条线段的长度应大于1米,小于5米。即满足条件的整数d有2、3、4,共3个。
故答案为:A。
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
9.D
【分析】有一个角是直角的三角形是直角三角形,有一个角是钝角的三角形是钝角三角形,三个角都是锐角的三角形是锐角三角形,题目中没有提供任何角的信息,所以都有可能。
【详解】根据分析可得,被遮住的三角形可能是钝角三角形也可能是锐角三角形,还可能是直角三角形形,不能确定。
故答案选:D
10.C
【详解】略
11.线段
【详解】解决这类题的关键是掌握三角形的特征.
12.三条线段
【详解】由不在同一直线的三条线段首尾相连围成的图形叫做三角形。
如图:
13.等腰
【分析】等腰三角形的两个底角相等,据此作答即可。
【详解】如果两个内角相等,这个三角形是等腰三角形。
【点睛】此题主要考查等腰三角形的特点的灵活应用。
14. 50 锐角
【分析】已知顶角为80°,根据等腰三角形的两底角相等的性质及三角形内角和定理,即可求出它的一个底角的值,即一个底角的度数是:(180°-80°)÷2=50°;再根据三个内角都是锐角的三角形叫做锐角三角形,据此解答。
【详解】一个等腰三角形,它的一个顶角是80°,它的底角是50°,这个三角形是锐角三角形。
【点睛】熟练掌握等腰三角形的性质、三角形内角和定理及锐角三角形的定义是本题解答的关键。
15.三角形具有稳定性
【分析】根据题意在桌子腿上斜着钉木条后,可以看出组成一个三角形,那么利用三角形具有稳定性的性质进行解答。
【详解】在桌子腿上斜着钉木条后,组成一个三角形,所以运用了三角形的稳定性知识。
【点睛】本题主要考查三角形的性质,熟练应用三角形的稳定性是解本题的关键。
16. 5 13
【分析】三角形任意两边之和大于第三边,任意两边之差小于第三边,据此即可解答。
【详解】9-5=4(厘米)
9+5=14(厘米)
4厘米<第三边<14厘米,所以第三条边最短是5厘米,最长是13厘米。
17.梯形
【分析】两组对边分别平行且相等的四边形叫做平行四边形;只有一组对边平行的四边形叫做梯形;长方形的对边分别平行且相等,四个角都是直角;正方形四条边都相等,四个角都是直角。从四边形露出部分可以看出,这个四边形有一个角不是直角,这个四边形不可能是长方形或正方形,这个四边形露出的对边不平行,不可能是平行四边形,这个四边形可能是梯形。
【详解】如下图,一个四边形被遮住了一部分,这个图形可能是(梯形)。
【点睛】熟记常见四边形的特征是解题关键。
18.4、16
【详解】试题分析:长方形中最大的正方形的边长应等于长方形的宽,长方形的宽已知,于是得解;再据正方形的周长公式即可得解.
解:因为长方形中最大的正方形的边长应等于长方形的宽,
所以正方形的边长为4厘米,
4×4=16(厘米);
答:这个正方形的边长是4厘米,周长是16厘米.
故答案为4、16.
点评:解答此题的关键是明白:长方形中最大的正方形的边长应等于长方形的宽.
19.6
【分析】由题意可得,等边三角形的周长除以3等于它的边长,据此即可解答。
【详解】18÷3=6(厘米)
【点睛】解答本题的关键是要掌握等边三角形的定义,三条边都相等的三角形叫等边三角形。
20.14
【分析】由四条线段首位顺次相接组成的图形是四边形,据此即可解答问题.
【详解】解:观察图形可知,单个的四边形是5个,2个图形组成的有7个,三个图形组成的有2个,
5+7+2=14(个)
故图中有11个四边形.
【点评】此题考查了图形的计数,要注意分类计数,做到不重不漏.
21.√
【分析】两组对边分别平行的四边形是平行四边形。如下图:
由图可知,平行四边形的两组对边互相平行。
【详解】由分析可知,平行四边形的两组对边互相平行。
故答案为:√
22.×
【详解】有两组对边平行的四边形是平行四边形,正方形、长方形是特殊的平行四边形;只有一组对边平行的四边形叫做梯形,一组对边平行,另一组对边不平行。所以判断错误。
23.×
【分析】根据三角形三边的关系:两边之和大于第三边,两边之差小于第三边,计算两边之和再与第三边比较大小即可判断。
【详解】2+2=4(厘米)
4<5
所以5厘米、2厘米、2厘米的三根小棒不能围成等腰三角形。
故答案为:×
24.√
【分析】有一个角是直角的三角形是直角三角形,三角形内角和是180°,用180°减去90°再减去43°,即可算出另一个锐角是(180°-90°-43°)。
【详解】180°-90°-43°
=90°-43°
=47°
故答案为:√
【点睛】熟记直角三角形特征和三角形内角和是180°是解题关键。
25.×
【分析】三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边。由此解答即可。
【详解】7+5=12(cm)
不符合三角形的三边关系。
所以用三根分别长7厘米、12厘米和5厘米的小木棒,头尾相连,不能摆出三角形。
故答案为:×
【点睛】此题关键是根据三角形的三边关系进行分析、解答,只需验证较小的两条边之和是否大于最长边即可。
26.×
【详解】试题分析:根据任何三角形内角和都是180°即可解决.
解:因为任何三角形内角和都是180°,所以这个说法是错误的.
故答案为×.
【点评】此题考查了三角形的内角和是180°.
27.25°
【分析】三角形的内角和是180°,用180°减去135°再减去20°即可求出∠A的度数。
【详解】180°-135°-20°
=45°-20°
=25°
28.125°
【分析】三角形的内角和为180°。由题意得,三角形的两个内角分别是28°和27°,那么直接用180°减去两个内角的度数即可算出未知角的度数。
【详解】180°-28°-27°
=152°-27°
=125°
29.见详解
【分析】(1)两组对边分别平行的四边形是平行四边形;
(2)只有一组对边平行的四边形是梯形;
(3)有一个角是直角的三角形是直角三角形,所以有一个内角是90°的三角形是直角三角形;
(4)三个角都是锐角的三角形是锐角三角形。一个三角形,最大的内角是72°,是一个锐角,说明它的其它两个角也是锐角。所以它是一个锐角三角形;
(5)有一个角是钝角的三角形是钝角三角形。一个三角形,两个内角之和为82°,根据三角形的内角和为180°可知,可以用减法算出第三个角。第三个角=180°-82°=98°,是一个钝角。所以这个三角形是钝角三角形。
【详解】
30.8厘米
【分析】正方形的周长=边长×4,据此将数据带入求出铁丝的长度,再根据等边三角形三边相等,用铁丝的长度除以3即可求出等边三角形的边长。
【详解】6×4=24(厘米)
24÷3=8(厘米)
答:改成后的等边三角形边长是8厘米。
31.不同意;理由见详解
【分析】三角形的内角和是180°,露出的角是30°,用180°-30°可求出遮住的两个角之和,据此举例即可解答。
【详解】答:我不同意小红的观点。理由:另外两个角的和是180°-30°=150°,如果遮住的两个角中有一个角是钝角,那么这个三角形是钝角三角形,如另外两个角分别是40°和110°,110°是钝角,则这个三角形是钝角三角形。
32.96米
【详解】试题分析:根据长方形的周长公式C=(a+b)×2,把菜地的长30米,宽18米代入公式即可求出篱笆的长.
解:(30+18)×2,
=48×2,
=96(米),
答:篱笆长96米.
点评:此题主要考查了长方形的周长公式C=(a+b)×2的实际应用.
33.72°;18°
【分析】直角三角形的两锐角之和等于90°,一个锐角是另一个锐角的4倍,所以90°是较小锐角的(1+4)倍,90°除以(1+4)等于较小锐角的度数,90°减较小的锐角的度数等于较大锐角的度数,据此即可解答。
【详解】90°÷(1+4)
=90°÷5
=18°
90°-18°=72°
答:两个锐角的度数分别是72°和18°。
34.(1)72÷3÷6,
=24÷6,
=4(台);
答:平均每人每天安装了4台.
(2)(3×2+5)×2,
=11×2,
=22(厘米);
答:拼成的大长方形的周长最少是22厘米.
(3)(12+5)×2﹣12,
=17×2﹣12,
=34﹣12,
=22(米);
【详解】试题分析:(1)先求每人6天安装的台数,再求每人每天安装的台数,列式为72÷3÷6,计算即可;
(2)要使周长最少,应把长边作为后来长方形的宽,拼成的大长方形的周长最少是(3×2+5)×2,解决问题;
(3)先求出长方形菜地的周长,然后减去靠墙的边长即可,列式为(12+5)×2﹣12,计算即可.
解:(1)72÷3÷6,
=24÷6,
=4(台);
答:平均每人每天安装了4台.
(2)(3×2+5)×2,
=11×2,
=22(厘米);
答:拼成的大长方形的周长最少是22厘米.
(3)(12+5)×2﹣12,
=17×2﹣12,
=34﹣12,
=22(米);
答:围成的篱笆长22米.
故答案为22.
点评:(1)此题也可先求3人每天一共安装的台数,再求每人每天安装的台数,列式为72÷6÷3;
(2)此题考查学生的空间想象力以及动手操作能力;
(3)此题考查了长方形周长计算的应用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二单元测试
一、选择题
1.学校的电动伸缩门做成若干个平行四边形,这是因为平行四边形( )。
A.美观 B.易变形 C.具有稳定性 D.节省材料
2.学校电动门做成若干个平行四边形,是利用平行四边形的( )特性。
A.美观 B.易变形 C.不易变形
3.有长度为4cm和9cm的两根小棒,再从下面选出一根小棒围成一个三角形。选出的小棒最长是( )。
A.14cm B.13cm C.12cm D.9cm
4.将下面四个图形进行分类,与其他三个不能分为一类的是( )。
A. B. C. D.
5.三角形的稳定性经常被应用于生活中。下面四个例子中,没有用到三角形稳定性的是( )。
A. B.
C. D.
6.一副三角板按如图的方式摆放,一个三角板的斜边与另一个三角板的直角边互相平行,则∠1=( )°。
A.80 B.75 C.70 D.65
7.下列集合圈中,错误的是( )。
A. B. C.
8.已知三条线段的长度分别是3米、2米和d米,如果用这样的三条线段围成一个三角形,那么满足条件的整数d有( )个。
A.3 B.4 C.5 D.6
9.被遮住的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
10.用5个长6厘米、宽4厘米的长方形可以拼成的大长方形中周长最小的是( )厘米.
A.68 B.52 C.44 D.40
二、填空题
11.三角形是由三条( )首尾相接围成的图形.
12.由 围成的图形叫做三角形。
13.如果两个内角相等,那么这个三角形是( )三角形。
14.一个等腰三角形,它的一个顶角是80,它的底角是( ) °。这个三角形是( )三角形。(填“钝角”、“锐角”、“直角”)
15.如图,凳子摇晃了,在凳子下边斜着钉木条,凳子就可以正常使用了,这是运用了( )知识。
16.一个三角形两条边分别长5厘米和9厘米,第三条边最短是( )厘米,最长可以是( )厘米。(答案均为整数)
17.如下图,一个四边形被遮住了一部分,这个图形可能是( )。
18.在一张长10厘米,宽4厘米的长方形纸上剪下一个最大的正方形,这个正方形的边长是 厘米,周长是 厘米.
19.一个等边三角形的三条边之和是18厘米,它的边长是( )厘米。
20. 有 个四边形.
三、判断题
21.平行四边形的两组对边互相平行。( )
22.有两组对边平行的四边形是平行四边形,有一组对边平行的四边形是梯形。( )
23.淘气用5厘米、2厘米、2厘米的三根小棒围成了一个等腰三角形。( )
24.在一个直角三角形中,已知其中一个锐角是43°则另一个锐角是47°。( )
25.用三根分别长7厘米、12厘米和5厘米的小木棒,头尾相连,一定能摆出一个三角形。( )
26.钝角三角形的内角和大于锐角三角形的内角和. .(判断对错)
四、计算题
27.在三角形ABC中,∠B=135 ,∠C=20 。求∠A的度数。
28.计算下面各角的度数。
五、连线题
29.小鸟回家。(连一连)
两组对边分别平行的四边形 只有一组对边平行的四边形 有一个内角是90°的三角形
钝角三角形 锐角三角形 直角三角形 平行四边形 梯形
最大的内角是72°的三角形 其中两个内角之和是82°的三角形
六、解答题
30.在学校“变废为宝”活动中,小明用铁丝围成边长6厘米的正方形当作品底座的外边。老师建议改成更稳的等边三角形,且铁丝长度不变,那改成后的等边三角形边长是多少厘米?
31.小红认为,下图中被遮住的三角形不可能是钝角三角形。你同意小红的观点吗?请说明理由。
32.在一块长方形菜地(如图)的四周围上竹篱笆,竹篱笆至少需要多少米?
33.一块直角三角形的菜地,已知一个锐角是另一个锐角的4倍,这两个锐角的度数分别是多少度?
34.(1)三个安装工人,6天一共安装了72台空调,平均每人每天安装了多少台?
(2)用两个长5厘米,宽3厘米的小长方形,拼成一个大长方形,拼成的大长方形的周长最少是多少厘米?
(3)右图是一块长方形菜地,它的一边靠墙,其它三面用篱笆围成,算一算,围成的篱笆长 米.
《第二单元测试》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C D C B A A D C
1.B
【分析】根据平行四边形的易变性(不稳定性)进行解答即可。
【详解】学校的电动伸缩门做成若干个平行四边形,这是因为平行四边形易变形;
故答案为:B
【点睛】此题考查了平行四边形的易变性。
2.B
【分析】学校大门做成的若干个平行四边形,这是应用了平行四边形不稳定性,即易变形的特性进行制作的。
【详解】由分析可知,学校电动门做成若干个平行四边形,是利用平行四边形的易变形特性。
故答案为:B
3.C
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】4+9=13(cm),9-4=5(cm)
则第三条边应小于13cm,大于5cm,最长是12cm。
故答案为:C
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
4.D
【分析】观察上图可知,前面三个图形都是由线段组成的,最后一个图形由轴线组成的,据此即可解答。
【详解】
根据分析可知,与其他三个不能分为一类的是。
故答案为:D
5.C
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点,据此解答即可。
【详解】A.支撑桥梁结构的结构图形采用三角形,这是利用三角形的稳定;
B.自行车车架是一个三角形,应用了三角形的稳定性;
C.虽然图中出现三角形,但是描述的是路径问题,不属于利用三角形稳定性;
D.相机三脚架的三个脚在地面形成一个三角形,可以起到稳定相机的作用,利用了三角形的稳定。
故答案为:C
6.B
【分析】观察上图可知,图上一个45°的角和一个60°的角叠放在一起,形成一个90°的角,所以重叠部分的∠2为45°+60°-90°=15°,阴影部分是一个直角三角形,所以∠1等于180°减90°,再减∠2;据此即可解答。
【详解】∠2=45°+60°-90°=105°-90°=15°
∠1=180°-90°-∠2=90°-15°=75°
故答案为:B
7.A
【详解】略
8.A
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】3+2=5(米),3-2=1(米)
则第三条线段的长度应大于1米,小于5米。即满足条件的整数d有2、3、4,共3个。
故答案为:A。
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
9.D
【分析】有一个角是直角的三角形是直角三角形,有一个角是钝角的三角形是钝角三角形,三个角都是锐角的三角形是锐角三角形,题目中没有提供任何角的信息,所以都有可能。
【详解】根据分析可得,被遮住的三角形可能是钝角三角形也可能是锐角三角形,还可能是直角三角形形,不能确定。
故答案选:D
10.C
【详解】略
11.线段
【详解】解决这类题的关键是掌握三角形的特征.
12.三条线段
【详解】由不在同一直线的三条线段首尾相连围成的图形叫做三角形。
如图:
13.等腰
【分析】等腰三角形的两个底角相等,据此作答即可。
【详解】如果两个内角相等,这个三角形是等腰三角形。
【点睛】此题主要考查等腰三角形的特点的灵活应用。
14. 50 锐角
【分析】已知顶角为80°,根据等腰三角形的两底角相等的性质及三角形内角和定理,即可求出它的一个底角的值,即一个底角的度数是:(180°-80°)÷2=50°;再根据三个内角都是锐角的三角形叫做锐角三角形,据此解答。
【详解】一个等腰三角形,它的一个顶角是80°,它的底角是50°,这个三角形是锐角三角形。
【点睛】熟练掌握等腰三角形的性质、三角形内角和定理及锐角三角形的定义是本题解答的关键。
15.三角形具有稳定性
【分析】根据题意在桌子腿上斜着钉木条后,可以看出组成一个三角形,那么利用三角形具有稳定性的性质进行解答。
【详解】在桌子腿上斜着钉木条后,组成一个三角形,所以运用了三角形的稳定性知识。
【点睛】本题主要考查三角形的性质,熟练应用三角形的稳定性是解本题的关键。
16. 5 13
【分析】三角形任意两边之和大于第三边,任意两边之差小于第三边,据此即可解答。
【详解】9-5=4(厘米)
9+5=14(厘米)
4厘米<第三边<14厘米,所以第三条边最短是5厘米,最长是13厘米。
17.梯形
【分析】两组对边分别平行且相等的四边形叫做平行四边形;只有一组对边平行的四边形叫做梯形;长方形的对边分别平行且相等,四个角都是直角;正方形四条边都相等,四个角都是直角。从四边形露出部分可以看出,这个四边形有一个角不是直角,这个四边形不可能是长方形或正方形,这个四边形露出的对边不平行,不可能是平行四边形,这个四边形可能是梯形。
【详解】如下图,一个四边形被遮住了一部分,这个图形可能是(梯形)。
【点睛】熟记常见四边形的特征是解题关键。
18.4、16
【详解】试题分析:长方形中最大的正方形的边长应等于长方形的宽,长方形的宽已知,于是得解;再据正方形的周长公式即可得解.
解:因为长方形中最大的正方形的边长应等于长方形的宽,
所以正方形的边长为4厘米,
4×4=16(厘米);
答:这个正方形的边长是4厘米,周长是16厘米.
故答案为4、16.
点评:解答此题的关键是明白:长方形中最大的正方形的边长应等于长方形的宽.
19.6
【分析】由题意可得,等边三角形的周长除以3等于它的边长,据此即可解答。
【详解】18÷3=6(厘米)
【点睛】解答本题的关键是要掌握等边三角形的定义,三条边都相等的三角形叫等边三角形。
20.14
【分析】由四条线段首位顺次相接组成的图形是四边形,据此即可解答问题.
【详解】解:观察图形可知,单个的四边形是5个,2个图形组成的有7个,三个图形组成的有2个,
5+7+2=14(个)
故图中有11个四边形.
【点评】此题考查了图形的计数,要注意分类计数,做到不重不漏.
21.√
【分析】两组对边分别平行的四边形是平行四边形。如下图:
由图可知,平行四边形的两组对边互相平行。
【详解】由分析可知,平行四边形的两组对边互相平行。
故答案为:√
22.×
【详解】有两组对边平行的四边形是平行四边形,正方形、长方形是特殊的平行四边形;只有一组对边平行的四边形叫做梯形,一组对边平行,另一组对边不平行。所以判断错误。
23.×
【分析】根据三角形三边的关系:两边之和大于第三边,两边之差小于第三边,计算两边之和再与第三边比较大小即可判断。
【详解】2+2=4(厘米)
4<5
所以5厘米、2厘米、2厘米的三根小棒不能围成等腰三角形。
故答案为:×
24.√
【分析】有一个角是直角的三角形是直角三角形,三角形内角和是180°,用180°减去90°再减去43°,即可算出另一个锐角是(180°-90°-43°)。
【详解】180°-90°-43°
=90°-43°
=47°
故答案为:√
【点睛】熟记直角三角形特征和三角形内角和是180°是解题关键。
25.×
【分析】三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边。由此解答即可。
【详解】7+5=12(cm)
不符合三角形的三边关系。
所以用三根分别长7厘米、12厘米和5厘米的小木棒,头尾相连,不能摆出三角形。
故答案为:×
【点睛】此题关键是根据三角形的三边关系进行分析、解答,只需验证较小的两条边之和是否大于最长边即可。
26.×
【详解】试题分析:根据任何三角形内角和都是180°即可解决.
解:因为任何三角形内角和都是180°,所以这个说法是错误的.
故答案为×.
【点评】此题考查了三角形的内角和是180°.
27.25°
【分析】三角形的内角和是180°,用180°减去135°再减去20°即可求出∠A的度数。
【详解】180°-135°-20°
=45°-20°
=25°
28.125°
【分析】三角形的内角和为180°。由题意得,三角形的两个内角分别是28°和27°,那么直接用180°减去两个内角的度数即可算出未知角的度数。
【详解】180°-28°-27°
=152°-27°
=125°
29.见详解
【分析】(1)两组对边分别平行的四边形是平行四边形;
(2)只有一组对边平行的四边形是梯形;
(3)有一个角是直角的三角形是直角三角形,所以有一个内角是90°的三角形是直角三角形;
(4)三个角都是锐角的三角形是锐角三角形。一个三角形,最大的内角是72°,是一个锐角,说明它的其它两个角也是锐角。所以它是一个锐角三角形;
(5)有一个角是钝角的三角形是钝角三角形。一个三角形,两个内角之和为82°,根据三角形的内角和为180°可知,可以用减法算出第三个角。第三个角=180°-82°=98°,是一个钝角。所以这个三角形是钝角三角形。
【详解】
30.8厘米
【分析】正方形的周长=边长×4,据此将数据带入求出铁丝的长度,再根据等边三角形三边相等,用铁丝的长度除以3即可求出等边三角形的边长。
【详解】6×4=24(厘米)
24÷3=8(厘米)
答:改成后的等边三角形边长是8厘米。
31.不同意;理由见详解
【分析】三角形的内角和是180°,露出的角是30°,用180°-30°可求出遮住的两个角之和,据此举例即可解答。
【详解】答:我不同意小红的观点。理由:另外两个角的和是180°-30°=150°,如果遮住的两个角中有一个角是钝角,那么这个三角形是钝角三角形,如另外两个角分别是40°和110°,110°是钝角,则这个三角形是钝角三角形。
32.96米
【详解】试题分析:根据长方形的周长公式C=(a+b)×2,把菜地的长30米,宽18米代入公式即可求出篱笆的长.
解:(30+18)×2,
=48×2,
=96(米),
答:篱笆长96米.
点评:此题主要考查了长方形的周长公式C=(a+b)×2的实际应用.
33.72°;18°
【分析】直角三角形的两锐角之和等于90°,一个锐角是另一个锐角的4倍,所以90°是较小锐角的(1+4)倍,90°除以(1+4)等于较小锐角的度数,90°减较小的锐角的度数等于较大锐角的度数,据此即可解答。
【详解】90°÷(1+4)
=90°÷5
=18°
90°-18°=72°
答:两个锐角的度数分别是72°和18°。
34.(1)72÷3÷6,
=24÷6,
=4(台);
答:平均每人每天安装了4台.
(2)(3×2+5)×2,
=11×2,
=22(厘米);
答:拼成的大长方形的周长最少是22厘米.
(3)(12+5)×2﹣12,
=17×2﹣12,
=34﹣12,
=22(米);
【详解】试题分析:(1)先求每人6天安装的台数,再求每人每天安装的台数,列式为72÷3÷6,计算即可;
(2)要使周长最少,应把长边作为后来长方形的宽,拼成的大长方形的周长最少是(3×2+5)×2,解决问题;
(3)先求出长方形菜地的周长,然后减去靠墙的边长即可,列式为(12+5)×2﹣12,计算即可.
解:(1)72÷3÷6,
=24÷6,
=4(台);
答:平均每人每天安装了4台.
(2)(3×2+5)×2,
=11×2,
=22(厘米);
答:拼成的大长方形的周长最少是22厘米.
(3)(12+5)×2﹣12,
=17×2﹣12,
=34﹣12,
=22(米);
答:围成的篱笆长22米.
故答案为22.
点评:(1)此题也可先求3人每天一共安装的台数,再求每人每天安装的台数,列式为72÷6÷3;
(2)此题考查学生的空间想象力以及动手操作能力;
(3)此题考查了长方形周长计算的应用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
