【期末专项训练】第八单元测试(含解析)2024-2025学年五年级下册数学北师大版
文档属性
| 名称 | 【期末专项训练】第八单元测试(含解析)2024-2025学年五年级下册数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 312.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 10:37:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八单元测试
一、选择题
1.水果店老板希望既能清楚看出2022年每季度苹果和香蕉的销售情况,又能了解两种水果销售增减变化情况,他应该选( )比较合适。
A.条形统计图 B.复式条形统计图 C.折线统计图 D.复式折线统计图
2.笑笑参加一次歌唱大奖赛,6位裁判给她评分分别是:9.7,9.8,7.3,9.0,10;8.5。去掉一个最高分和一个最低分求平均分,笑笑得分是( )。
A.9.0 B.9.25 C.9.5 D.9.7
3.六(1)班老师要统计本班期末考试语文、数学成绩中各分数段的人数,应制作( )。
A.单式条形统计图 B.复式条形统计图 C.单式折线统计图 D.复式折线统计图
4.制作某城市2021年和2022年两年6—9月空气质量达到优良情况统计图,应选择( )统计图。
A.条形 B.折线 C.复式条形 D.复式折线
5.下图是三、四年级同学喜爱的课外读物的统计图。根据图中信息,下列结论中( )是正确的。
A.三年级比四年级更喜欢《动物小说》
B.三、四年级喜欢《笑猫日记》的学生比较多
C.参加调查的人中四年级比三年级多
D.三年级喜欢《淘气包马小跳》的学生是四年级的2倍
6.小红参加县举行的中、小学生“美文诵读”比赛,9位评委给她的打分如下:
9.6 9.4 9.6 9.7 9.9 9.7 9.3 9.6 9.6
如果按照“去掉一个最高分,去掉一个最低分,再计算平均分”的评分方法来计算,她的平均分是( )分。
A.9.45 B.9.4 C.9.5 D.9.6
7.某青少年机器人小组成员的平均年龄为13.5岁,又新加入一名成员后,平均年龄变为13.75岁,新加入的成员的年龄可能为( )岁。
A.10 B.12 C.13 D.15
8.8个人进行仰卧起坐比赛,静静做了56个,明明做了42个,庆庆做了10个,另外5个人做的个数比明明少,比庆庆多,这8个人做仰卧起坐的平均数是( )。
A.大于10小于42 B.42 C.大于42小于56
二、填空题
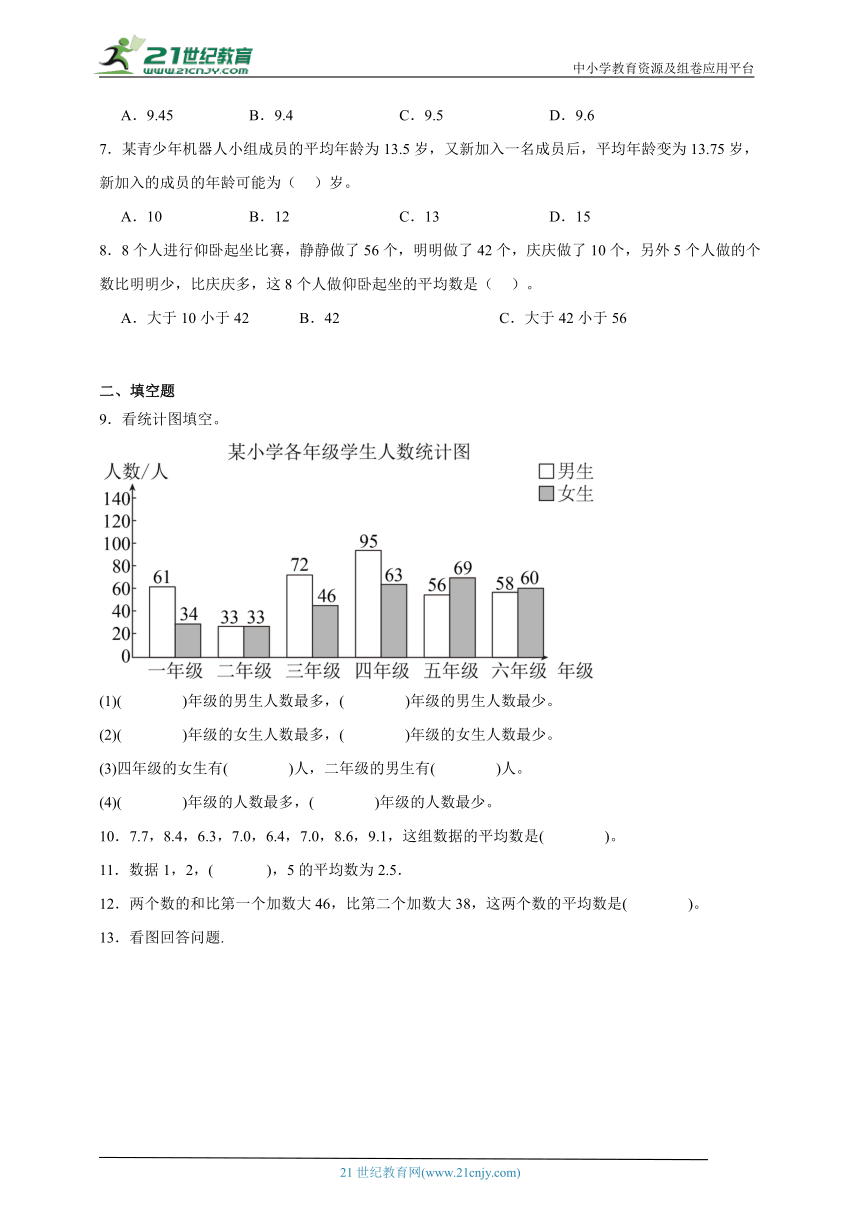
9.看统计图填空。
(1)( )年级的男生人数最多,( )年级的男生人数最少。
(2)( )年级的女生人数最多,( )年级的女生人数最少。
(3)四年级的女生有( )人,二年级的男生有( )人。
(4)( )年级的人数最多,( )年级的人数最少。
10.7.7,8.4,6.3,7.0,6.4,7.0,8.6,9.1,这组数据的平均数是( )。
11.数据1,2,( ),5的平均数为2.5.
12.两个数的和比第一个加数大46,比第二个加数大38,这两个数的平均数是( )。
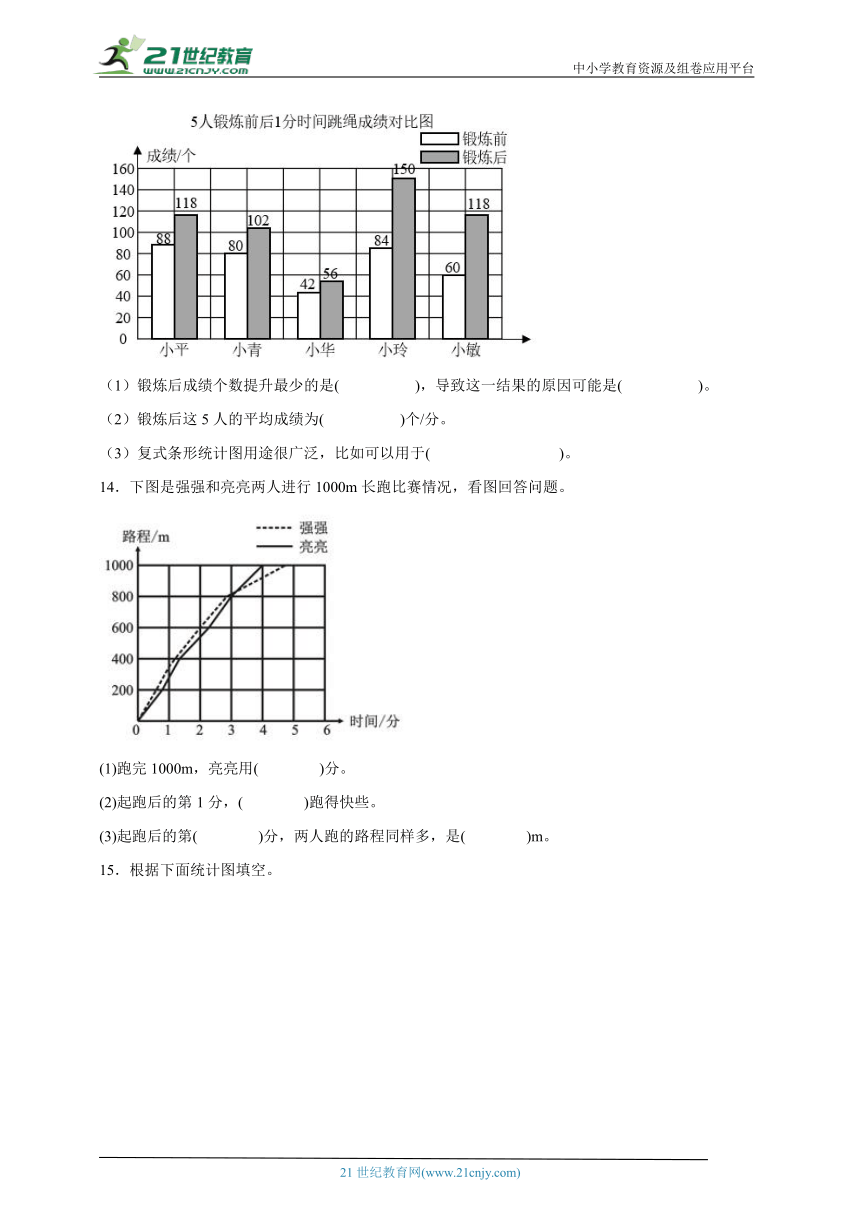
13.看图回答问题.
(1)锻炼后成绩个数提升最少的是( ),导致这一结果的原因可能是( )。
(2)锻炼后这5人的平均成绩为( )个/分。
(3)复式条形统计图用途很广泛,比如可以用于( )。
14.下图是强强和亮亮两人进行1000m长跑比赛情况,看图回答问题。
(1)跑完1000m,亮亮用( )分。
(2)起跑后的第1分,( )跑得快些。
(3)起跑后的第( )分,两人跑的路程同样多,是( )m。
15.根据下面统计图填空。
(1) 先到达终点。
(2)请用“快”“慢”来描述他们的比赛情况,小亮是先 后 。
(3)小亮的平均速度约是 米/分。小明的平均速度约是 米/分。(得数均保留整数)
16.一艘轮船从甲港到乙港,每时行45千米,从乙港到甲港每时行30千米,该艘轮船往返两港的平均速度是( )千米/时。
三、判断题
17.比较成都今年和去年各月空气质量为“优”的天数,宜使用复式条形统计图。( )
18.复式条形统计图、复式折线统计图都必须有图例。 ( )
19.平均数不具代表性。( )
20.平均数往往会受到极端数据的影响。( )
21.求平均数就用总数量除以总份数. ( )
四、计算题
22.33、42、20、53、32这5个数的平均数是多少?33、42、20、53、32、36这6个数的平均数是多少?两个平均数相差多少?
五、解答题
23.下图是甲、乙两位学生在复习阶段数学测试成绩和学习时间分配情况的统计图,请根据图中的信息回答问题。
(1)甲、乙两位学生第( )次测试成绩差距最大,相差( )分。
(2)学生甲五次测试的平均成绩是( )分。
(3)学生乙反思的时间比学生甲少几分之几?( )(填最简分数)
24.下表是甲、乙两城市2012年上半年月平均气温统计表。(单位:摄氏度)
月份 1 2 3 4 5 6
甲市 7 8 11 13 10 9
乙市 10 8 6 9 9 12
(1)完成两市上半年月平均气温变化的复式折线统计图。
(2)回答下面问题。两市月平均气温最大相差( )摄氏度。( )月份两城市平均气温相同,有( )个月乙市平均气温高于甲市,其余( )个月乙市平均气温低于甲市。
25.观察分析条形统计图.
某气压机厂两个车间2012~2015年年产值情况统计图
(1)( )年两个车间产值最高,( )年最少.
(2)2013年第二车间的产值比第一车间多( )万元.
(3)你还能从这个统计图中获得哪些信息?请写在下面.
26.下面是甲、乙两名射击队员连续射击成绩的统计图。
(1)甲、乙两人六次射击的平均成绩分别是多少?
(2)如果要从两人中选一人参加比赛,你觉得选谁合适?写出你的想法。
27.服装加工组有240米布,做了50套儿童服装后,还剩90米,平均每套儿童服装用布多少米?
《第八单元测试》参考答案
题号 1 2 3 4 5 6 7 8
答案 D B B D B D D A
1.D
【分析】条形统计图可以直观地看出数量的多少;折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况。据此可知,要表示两种水果的销售情况和增减变化情况,应选用复式折线统计图。
【详解】根据条形统计图和折线统计图的特点,他应该选复式折线统计图。
故答案为:D
【点睛】本题考查统计图的选择。掌握各统计图的特征是解题的关键。
2.B
【分析】笑笑得分=去掉一个最高分与一个最低分的分数和÷4。
【详解】(9.7+9.8+9.0+8.5)÷4
=37÷4
=9.25(分)
笑笑得分是9.25分。
故答案为:B。
3.B
【分析】条形统计图可以清楚地看出数量的多少。
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
单式统计图通过一组数据表示出来,复式统计图通过两组以上数据进行比较。
【详解】六(1)班老师要统计本班期末考试语文、数学成绩中各分数段的人数,应制作复式条形统计图。
故答案为:B
4.D
【分析】条形统计图能清楚地表示出数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;复式折线统计图表示2个以上的量的增减变化情况,据此解答。
【详解】制作某城市2021年和2022年两年6—9月空气质量达到优良情况统计图,应选择复式折线统计图。
故答案为:D
【点睛】关键是熟悉折线统计图的特征,根据统计图的特征进行选择。
5.B
【分析】A项中,《动物小说》中三年级的条形明显低于四年级,所以四年级比三年级更喜欢《动物小说》;
B项中,在统计图中,《笑猫日记》的三、四年级的人数之和最多,所以三、四年级喜欢《笑猫日记》的学生比较多;
C项中,从图中可以得出,《淘气包马小跳》和《笑猫日记》中三年级明显多于四年级,而《动物小说》中三年级只比四年级少一点,总之,参加调查的人中四年级比三年级少;
D项中,从图中明显看出三年级喜欢《淘气包马小跳》的学生不是四年级的2倍。
【详解】A.四年级比三年级更喜欢《动物小说》;
B.三、四年级喜欢《笑猫日记》的学生比较多;
C.参加调查的人中四年级比三年级少;
D.三年级喜欢《淘气包马小跳》的学生不是四年级的2倍。
故答案为:B
【点睛】本题主要考查从复式条形统计图中提取信息。
6.D
【分析】去掉最高和最低分,是为了不受偏大或偏小数据的影响,使结果更合理。根据“总数÷个数=平均数”,用7个数的和除以7即可。
【详解】(9.6+9.4+9.6+9.7+9.7+9.6+9.6)÷7
=67.2÷7
=9.6(分)
故答案为:D
【点睛】解答此题应结合题意和平均数的计算方法进行解答即可。
7.D
【分析】某青少年机器人小组成员的平均年龄为13.5岁,又新加入一名成员后,平均年龄变为13.75岁,平均数比原来大,说明新加入的成员的年龄要大于原来的平均年龄,据此选择。
【详解】A. 10<13.5,不符合题意。
B. 12<13.5,不符合题意。
C. 13<13.5,不符合题意。
D. 15>13.5,符合题意。
故答案为:D
【点睛】此题考查了平均数的意义,找出新加入的成员的年龄范围是解题关键。
8.A
【分析】已知有8个人进行仰卧起坐比赛,静静做了56个,明明做了42个,庆庆做了10个,另外5个人做的个数比明明少,比庆庆多,可以这样想:另外的5人做的个数的平均数一定在10~42之间,而静静、明明、庆庆三个人做的个数的平均数是(56+42+10)÷3,即36,36在10~42之间,所以8个人做的个数的平均数一定在10~42之间。
【详解】(56+42+10)÷3
=108÷3
=36(个)
即静静、明明、庆庆三个人做的个数的平均数是36,36大于10,小于42;
另外5个人做的个数都大于10个,小于42个,即他们5个人做的个数的平均数大于10,小于42,;
所以这个8个人做仰卧起坐的个数的平均数一定大于10,小于42。
故答案为:A
【点睛】此题考查的目的是理解平均数的意义,掌握求平均数的方法及应用。
9.(1) 四 二
(2) 五 二
(3) 63 33
(4) 四 二
【分析】(1)观察统计图可知,表示男生人数的直条中,四年级的直条最长,二年级的直条最短,说明四年级的男生人数最多,二年级的男生人数最少。
(2)表示女生人数的直条中,五年级的直条最长,二年级的直条最短,说明五年级的女生人数最多,二年级的女生人数最少。
(3)从统计图中可以看出,四年级的女生有63人,二年级的男生有33人。
(4)观察统计图可知,四年级的男生人数最多,女生人数也较多,则四年级的人数最多;二年级的男生和女生人数都是最少的,则二年级的人数最少。
【详解】(1)通过分析可得:四年级的男生人数最多,二年级的男生人数最少。
(2)五年级的女生人数最多,二年级的女生人数最少。
(3)四年级的女生有63人,二年级的男生有33人。
(4)四年级的人数最多,二年级的人数最少。
10.7.5625
【分析】先将这几个数相加求和,再用和除以8,求出这组数据的平均数。
【详解】(7.7+8.4+6.3+7.0+6.4+7.0+8.6+9.1)÷8
=(16.1+6.3+7.0+6.4+7.0+8.6+9.1)÷8
=(22.4+7.0+6.4+7.0+8.6+9.1)÷8
=(29.4+6.4+7.0+8.6+9.1)÷8
=(35.8+7.0+8.6+9.1)÷8
=(42.8+8.6+9.1)÷8
=(51.4+9.1)÷8
=60.5÷8
=7.5625
这组数据的平均数是7.5625。
11.2
【详解】略
12.42
【分析】两个加数的和比第一个加数大46,因为和=加数+加数,和比其中的一个加数多的数就是另一个加数,即另一个加数是46;和比第二个加数大38,即其中的另一个加数是38,再根据平均数的意义,把两个数相加,再除以2,即可解答。
【详解】(46+38)÷2
=84÷2
=42
两个数的和比第一个加数大46,比第二个加数大38,这两个数的平均数是42。
【点睛】解答本题的关键是根据题意找出两个加数分别是多少,进而解答。
13. 小华 小华跳绳方式不对 109 比较两种数据的多少
【分析】(1)分别计算出5人锻炼前后的个数差,再进行比较,即可解答;
(2)把锻炼后5人跳绳的个数相加,再除以5,即可解答;
(3)根据复式条形统计图的认识去解答即可。
【详解】(1)118-88=30(个)
102-80=22(个)
56-42=14(个)
150-84=66(个)
118-60=58(个)
14<22<30<58<66
锻炼后成绩个数提升最少的是小华,导致这一结果的原因可能是小华跳绳方式不对。(答案不唯一)
(2)(118+102+56+150+118)÷5
=544÷5
=108.8
≈109(下)
锻炼后这5人的平均成绩为109个/分。
(3)复式条形统计图用途很广泛,比如可以用于比较两种数据的多少。
【点睛】熟练掌握复式条形统计图的特点是解答此题的关键。
14.(1)4
(2)强强
(3) 3 800
【分析】(1)观察统计图,找出亮亮跑完1000m所用的时间;
(2)观察统计图,找出起跑后1分谁跑得快些;
(3)观察统计图,找出起跑几分后,两人跑的路程同样多,跑了多少m。
【详解】(1)跑完1000m,亮亮用了4分。
(2)起跑后的第1分钟,强强跑得快些。
(3)起跑后的第3分,两人跑的路程同样多,是800m。
【点睛】本题考查复式折线统计图的实际应用,根据折线统计图提供的信息解答问题。
15. 小亮 慢 快 178 145
【分析】(1)由图可知,小亮用的时间短,先到达终点;
(2)观察描述小亮的线段可知,开始线段较缓,后来变陡,说明小亮先慢后快;
(3)用总路程除以总时间即可求出平均速度。
【详解】(1)小亮先到达终点;
(2)小亮是先慢后快;
(3)800÷4.5≈178(米/分);
800÷5.5≈145(米/分);
【点睛】本题主要考查的是如何观察折线统计图并从图中获取信息。
16.36
【分析】把甲港到乙港之间的距离看作单位“1”,从甲港到乙港所用时间为,则返回所用时间为,根据平均速度=总路程÷时间,列式解答即可。
【详解】(1+1)÷(+)
=2÷
=36(千米/时)
该艘轮船往返两港的平均速度是36千米/时。
【点睛】此题考查了平均数的求法,用总数量÷份数解答,不能直接把两个来回速度求平均数。
17.√
【分析】条形统计图能很容易看出数量的多少;因为比较各月空气的质量为“优”的天数,即数量的多少,所以用复式条形统计图;据此解答。
【详解】根据分析可知,比较成都今年和去年各月空气质量为“优”的天数,宜使用复式条形统计图,原题干说法正确。
故答案为:√
【点睛】根据复式条形统计图的特征进行解答。
18.√
【详解】复式条形统计图、复式折线统计图因为是对两组及两组以上的数据进行比较,为了区分,必须要有图例。
故答案为:√
19.×
【分析】根据平均数的意义可知,如果总数量改变,份数不变,平均数一定会改变;据此解答即可。
【详解】因为平均数=总数量÷总份数,所以如果总数量改变,份数不变,平均数一定会改变;平均数有一定的代表性,原题说法错误。
故答案为: ×。
【点睛】考查了平均数的意义,平均数是指在一组数据中所有数据之和再除以数据的个数,它是反映数据集中趋势的一项指标。
20.√
【分析】把一组数据中的所有数据加起来,再除以数据个数,即可得出平均数,平均数易受少数几个极端值的影响,据此解答。
【详解】根据分析可知:平均数容易受偏大或偏小数据的影响。
原题干说法正确。
故答案为√
【点睛】本题考查对平均数的含义的理解。
21.√
【详解】解答本题时,要知道:总数量÷总份数=平均数.
22.36;36;0
【详解】试题分析:(1)先求出5个数的和,进而根据“总数÷个数=平均数”进行解答即可;
(2)先求出6个数的和,进而根据“总数÷个数=平均数”进行解答即可;
(3)求两个平均数相差多少,用减法解答即可.
解:(1)(33+42+20+53+32)÷5,
=180÷5,
=36,
答:这5个数的平均数是36;
(2)(33+42+20+53+32+36)÷6,
=216÷6,
=36,
答:这6个数的平均数是36;
(3)36﹣36=0,
答:两个平均数相差0.
点评:此题考查了平均数的计算方法,应灵活掌握求平均数的方法.
23.(1) 四 10
(2)79.8
(3)
【分析】(1)根据统计图,算出甲、乙每次成绩差,差最大表示成绩差距最大。
(2)用5次成绩的和除以5即可求出平均成绩;
(3)(甲反思的时间-乙反思的时间)÷甲反思的时间即可求解。
(1)
根据统计图,第四次甲、乙成绩差距最大,相差90-80=10(分);
(2)
(65+70+80+90+94)÷5
=399÷5
=79.8(分)
(3)
乙的反思时间是0.2时,甲的反思时间是0.6时,
(0.6-0.2)÷0.6
=0.4÷0.6
=
【点睛】本题主要考查的是统计图、平均数、一个数比另一个数多(少)几分之几的问题。
24.(1)见详解;
(2)5,2、5,2,2
【分析】(1)根据表中已知数据,在统计图上描出各点,制成折线统计图;
(2)观察折线统计图的折线变化情况,高低差距最大的就是气温相差最大的月份,用减法求差即可;折线重合的月份即两城市气温相同的月份;通过观察折线统计图可得有几个月乙市平均气温高于甲市,几个月乙市平均气温低于甲市。
【详解】(1)如图:
(2)1月份温差:10-7=3(摄氏度);
2月份两城市都是8摄氏度;
3月份温差:11-6=5(摄氏度);
4月份温差:13-9=4(摄氏度);
5月份两城市都是10摄氏度;
6月份温差:12-9=3(摄氏度);
5>4>3
温差最大的是3月份,差5摄氏度;
乙市平均气温中1、4月份高于甲市,2、5月份平均气温相同,其余3、4个月份低于甲市。
由此可得,两市月平均气温最大相差5摄氏度。2、5月份两城市平均气温相同,有2个月乙市平均气温高于甲市,其余2个月乙市平均气温低于甲市。
【点睛】解答此题的关键利用表中已知的信息,分析问题以及绘制折线统计图的能力。
25.(1)2015 2012(2)375
【详解】略
26.(1)甲、乙两人六次射击的平均成绩都是9环。
(2)我觉得选乙合适,因为乙的成绩稳步上升。
【分析】(1)通过折线统计图收集数据:甲6次射击的分数为: 8,9,10,9,8,10;乙6次射击的成绩为: 9,8,8, 9,10,10;然后用各自分数的和:射击的次数得到平均数即可。
{2)通过统计图发现,甲的成绩波动较大,而乙的发挥呈上升趋势。
【详解】(1)甲:(8+9+10+9+8+10)÷6
=54÷6
=9(环)
乙:(9+8+8+9+10+10)÷6
=54÷6
=9(环)
答:甲、乙两人六次射击的平均成绩都是9环。
(2)我觉得选乙合适,因为乙的成绩稳步上升。
【点睛】本题考查了从复式折线统计图获取信的能力。折线统计图不但可以表示项目的具体数量,又能清楚地反映事物变化的情况。
27.3米
【分析】要求平均每套儿童服装用布多少米,根据题意,先求出50套儿童服装一共用了多少米布,进而除以服装套数50得解。
【详解】(240-90)÷50
=150÷50
=3(米)
答:平均每套儿童服装用布3米。
【点睛】解决此题关键是先求出50套儿童服装一共用了多少米布,进而根据平均数的求法计算得解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八单元测试
一、选择题
1.水果店老板希望既能清楚看出2022年每季度苹果和香蕉的销售情况,又能了解两种水果销售增减变化情况,他应该选( )比较合适。
A.条形统计图 B.复式条形统计图 C.折线统计图 D.复式折线统计图
2.笑笑参加一次歌唱大奖赛,6位裁判给她评分分别是:9.7,9.8,7.3,9.0,10;8.5。去掉一个最高分和一个最低分求平均分,笑笑得分是( )。
A.9.0 B.9.25 C.9.5 D.9.7
3.六(1)班老师要统计本班期末考试语文、数学成绩中各分数段的人数,应制作( )。
A.单式条形统计图 B.复式条形统计图 C.单式折线统计图 D.复式折线统计图
4.制作某城市2021年和2022年两年6—9月空气质量达到优良情况统计图,应选择( )统计图。
A.条形 B.折线 C.复式条形 D.复式折线
5.下图是三、四年级同学喜爱的课外读物的统计图。根据图中信息,下列结论中( )是正确的。
A.三年级比四年级更喜欢《动物小说》
B.三、四年级喜欢《笑猫日记》的学生比较多
C.参加调查的人中四年级比三年级多
D.三年级喜欢《淘气包马小跳》的学生是四年级的2倍
6.小红参加县举行的中、小学生“美文诵读”比赛,9位评委给她的打分如下:
9.6 9.4 9.6 9.7 9.9 9.7 9.3 9.6 9.6
如果按照“去掉一个最高分,去掉一个最低分,再计算平均分”的评分方法来计算,她的平均分是( )分。
A.9.45 B.9.4 C.9.5 D.9.6
7.某青少年机器人小组成员的平均年龄为13.5岁,又新加入一名成员后,平均年龄变为13.75岁,新加入的成员的年龄可能为( )岁。
A.10 B.12 C.13 D.15
8.8个人进行仰卧起坐比赛,静静做了56个,明明做了42个,庆庆做了10个,另外5个人做的个数比明明少,比庆庆多,这8个人做仰卧起坐的平均数是( )。
A.大于10小于42 B.42 C.大于42小于56
二、填空题
9.看统计图填空。
(1)( )年级的男生人数最多,( )年级的男生人数最少。
(2)( )年级的女生人数最多,( )年级的女生人数最少。
(3)四年级的女生有( )人,二年级的男生有( )人。
(4)( )年级的人数最多,( )年级的人数最少。
10.7.7,8.4,6.3,7.0,6.4,7.0,8.6,9.1,这组数据的平均数是( )。
11.数据1,2,( ),5的平均数为2.5.
12.两个数的和比第一个加数大46,比第二个加数大38,这两个数的平均数是( )。
13.看图回答问题.
(1)锻炼后成绩个数提升最少的是( ),导致这一结果的原因可能是( )。
(2)锻炼后这5人的平均成绩为( )个/分。
(3)复式条形统计图用途很广泛,比如可以用于( )。
14.下图是强强和亮亮两人进行1000m长跑比赛情况,看图回答问题。
(1)跑完1000m,亮亮用( )分。
(2)起跑后的第1分,( )跑得快些。
(3)起跑后的第( )分,两人跑的路程同样多,是( )m。
15.根据下面统计图填空。
(1) 先到达终点。
(2)请用“快”“慢”来描述他们的比赛情况,小亮是先 后 。
(3)小亮的平均速度约是 米/分。小明的平均速度约是 米/分。(得数均保留整数)
16.一艘轮船从甲港到乙港,每时行45千米,从乙港到甲港每时行30千米,该艘轮船往返两港的平均速度是( )千米/时。
三、判断题
17.比较成都今年和去年各月空气质量为“优”的天数,宜使用复式条形统计图。( )
18.复式条形统计图、复式折线统计图都必须有图例。 ( )
19.平均数不具代表性。( )
20.平均数往往会受到极端数据的影响。( )
21.求平均数就用总数量除以总份数. ( )
四、计算题
22.33、42、20、53、32这5个数的平均数是多少?33、42、20、53、32、36这6个数的平均数是多少?两个平均数相差多少?
五、解答题
23.下图是甲、乙两位学生在复习阶段数学测试成绩和学习时间分配情况的统计图,请根据图中的信息回答问题。
(1)甲、乙两位学生第( )次测试成绩差距最大,相差( )分。
(2)学生甲五次测试的平均成绩是( )分。
(3)学生乙反思的时间比学生甲少几分之几?( )(填最简分数)
24.下表是甲、乙两城市2012年上半年月平均气温统计表。(单位:摄氏度)
月份 1 2 3 4 5 6
甲市 7 8 11 13 10 9
乙市 10 8 6 9 9 12
(1)完成两市上半年月平均气温变化的复式折线统计图。
(2)回答下面问题。两市月平均气温最大相差( )摄氏度。( )月份两城市平均气温相同,有( )个月乙市平均气温高于甲市,其余( )个月乙市平均气温低于甲市。
25.观察分析条形统计图.
某气压机厂两个车间2012~2015年年产值情况统计图
(1)( )年两个车间产值最高,( )年最少.
(2)2013年第二车间的产值比第一车间多( )万元.
(3)你还能从这个统计图中获得哪些信息?请写在下面.
26.下面是甲、乙两名射击队员连续射击成绩的统计图。
(1)甲、乙两人六次射击的平均成绩分别是多少?
(2)如果要从两人中选一人参加比赛,你觉得选谁合适?写出你的想法。
27.服装加工组有240米布,做了50套儿童服装后,还剩90米,平均每套儿童服装用布多少米?
《第八单元测试》参考答案
题号 1 2 3 4 5 6 7 8
答案 D B B D B D D A
1.D
【分析】条形统计图可以直观地看出数量的多少;折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况。据此可知,要表示两种水果的销售情况和增减变化情况,应选用复式折线统计图。
【详解】根据条形统计图和折线统计图的特点,他应该选复式折线统计图。
故答案为:D
【点睛】本题考查统计图的选择。掌握各统计图的特征是解题的关键。
2.B
【分析】笑笑得分=去掉一个最高分与一个最低分的分数和÷4。
【详解】(9.7+9.8+9.0+8.5)÷4
=37÷4
=9.25(分)
笑笑得分是9.25分。
故答案为:B。
3.B
【分析】条形统计图可以清楚地看出数量的多少。
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
单式统计图通过一组数据表示出来,复式统计图通过两组以上数据进行比较。
【详解】六(1)班老师要统计本班期末考试语文、数学成绩中各分数段的人数,应制作复式条形统计图。
故答案为:B
4.D
【分析】条形统计图能清楚地表示出数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;复式折线统计图表示2个以上的量的增减变化情况,据此解答。
【详解】制作某城市2021年和2022年两年6—9月空气质量达到优良情况统计图,应选择复式折线统计图。
故答案为:D
【点睛】关键是熟悉折线统计图的特征,根据统计图的特征进行选择。
5.B
【分析】A项中,《动物小说》中三年级的条形明显低于四年级,所以四年级比三年级更喜欢《动物小说》;
B项中,在统计图中,《笑猫日记》的三、四年级的人数之和最多,所以三、四年级喜欢《笑猫日记》的学生比较多;
C项中,从图中可以得出,《淘气包马小跳》和《笑猫日记》中三年级明显多于四年级,而《动物小说》中三年级只比四年级少一点,总之,参加调查的人中四年级比三年级少;
D项中,从图中明显看出三年级喜欢《淘气包马小跳》的学生不是四年级的2倍。
【详解】A.四年级比三年级更喜欢《动物小说》;
B.三、四年级喜欢《笑猫日记》的学生比较多;
C.参加调查的人中四年级比三年级少;
D.三年级喜欢《淘气包马小跳》的学生不是四年级的2倍。
故答案为:B
【点睛】本题主要考查从复式条形统计图中提取信息。
6.D
【分析】去掉最高和最低分,是为了不受偏大或偏小数据的影响,使结果更合理。根据“总数÷个数=平均数”,用7个数的和除以7即可。
【详解】(9.6+9.4+9.6+9.7+9.7+9.6+9.6)÷7
=67.2÷7
=9.6(分)
故答案为:D
【点睛】解答此题应结合题意和平均数的计算方法进行解答即可。
7.D
【分析】某青少年机器人小组成员的平均年龄为13.5岁,又新加入一名成员后,平均年龄变为13.75岁,平均数比原来大,说明新加入的成员的年龄要大于原来的平均年龄,据此选择。
【详解】A. 10<13.5,不符合题意。
B. 12<13.5,不符合题意。
C. 13<13.5,不符合题意。
D. 15>13.5,符合题意。
故答案为:D
【点睛】此题考查了平均数的意义,找出新加入的成员的年龄范围是解题关键。
8.A
【分析】已知有8个人进行仰卧起坐比赛,静静做了56个,明明做了42个,庆庆做了10个,另外5个人做的个数比明明少,比庆庆多,可以这样想:另外的5人做的个数的平均数一定在10~42之间,而静静、明明、庆庆三个人做的个数的平均数是(56+42+10)÷3,即36,36在10~42之间,所以8个人做的个数的平均数一定在10~42之间。
【详解】(56+42+10)÷3
=108÷3
=36(个)
即静静、明明、庆庆三个人做的个数的平均数是36,36大于10,小于42;
另外5个人做的个数都大于10个,小于42个,即他们5个人做的个数的平均数大于10,小于42,;
所以这个8个人做仰卧起坐的个数的平均数一定大于10,小于42。
故答案为:A
【点睛】此题考查的目的是理解平均数的意义,掌握求平均数的方法及应用。
9.(1) 四 二
(2) 五 二
(3) 63 33
(4) 四 二
【分析】(1)观察统计图可知,表示男生人数的直条中,四年级的直条最长,二年级的直条最短,说明四年级的男生人数最多,二年级的男生人数最少。
(2)表示女生人数的直条中,五年级的直条最长,二年级的直条最短,说明五年级的女生人数最多,二年级的女生人数最少。
(3)从统计图中可以看出,四年级的女生有63人,二年级的男生有33人。
(4)观察统计图可知,四年级的男生人数最多,女生人数也较多,则四年级的人数最多;二年级的男生和女生人数都是最少的,则二年级的人数最少。
【详解】(1)通过分析可得:四年级的男生人数最多,二年级的男生人数最少。
(2)五年级的女生人数最多,二年级的女生人数最少。
(3)四年级的女生有63人,二年级的男生有33人。
(4)四年级的人数最多,二年级的人数最少。
10.7.5625
【分析】先将这几个数相加求和,再用和除以8,求出这组数据的平均数。
【详解】(7.7+8.4+6.3+7.0+6.4+7.0+8.6+9.1)÷8
=(16.1+6.3+7.0+6.4+7.0+8.6+9.1)÷8
=(22.4+7.0+6.4+7.0+8.6+9.1)÷8
=(29.4+6.4+7.0+8.6+9.1)÷8
=(35.8+7.0+8.6+9.1)÷8
=(42.8+8.6+9.1)÷8
=(51.4+9.1)÷8
=60.5÷8
=7.5625
这组数据的平均数是7.5625。
11.2
【详解】略
12.42
【分析】两个加数的和比第一个加数大46,因为和=加数+加数,和比其中的一个加数多的数就是另一个加数,即另一个加数是46;和比第二个加数大38,即其中的另一个加数是38,再根据平均数的意义,把两个数相加,再除以2,即可解答。
【详解】(46+38)÷2
=84÷2
=42
两个数的和比第一个加数大46,比第二个加数大38,这两个数的平均数是42。
【点睛】解答本题的关键是根据题意找出两个加数分别是多少,进而解答。
13. 小华 小华跳绳方式不对 109 比较两种数据的多少
【分析】(1)分别计算出5人锻炼前后的个数差,再进行比较,即可解答;
(2)把锻炼后5人跳绳的个数相加,再除以5,即可解答;
(3)根据复式条形统计图的认识去解答即可。
【详解】(1)118-88=30(个)
102-80=22(个)
56-42=14(个)
150-84=66(个)
118-60=58(个)
14<22<30<58<66
锻炼后成绩个数提升最少的是小华,导致这一结果的原因可能是小华跳绳方式不对。(答案不唯一)
(2)(118+102+56+150+118)÷5
=544÷5
=108.8
≈109(下)
锻炼后这5人的平均成绩为109个/分。
(3)复式条形统计图用途很广泛,比如可以用于比较两种数据的多少。
【点睛】熟练掌握复式条形统计图的特点是解答此题的关键。
14.(1)4
(2)强强
(3) 3 800
【分析】(1)观察统计图,找出亮亮跑完1000m所用的时间;
(2)观察统计图,找出起跑后1分谁跑得快些;
(3)观察统计图,找出起跑几分后,两人跑的路程同样多,跑了多少m。
【详解】(1)跑完1000m,亮亮用了4分。
(2)起跑后的第1分钟,强强跑得快些。
(3)起跑后的第3分,两人跑的路程同样多,是800m。
【点睛】本题考查复式折线统计图的实际应用,根据折线统计图提供的信息解答问题。
15. 小亮 慢 快 178 145
【分析】(1)由图可知,小亮用的时间短,先到达终点;
(2)观察描述小亮的线段可知,开始线段较缓,后来变陡,说明小亮先慢后快;
(3)用总路程除以总时间即可求出平均速度。
【详解】(1)小亮先到达终点;
(2)小亮是先慢后快;
(3)800÷4.5≈178(米/分);
800÷5.5≈145(米/分);
【点睛】本题主要考查的是如何观察折线统计图并从图中获取信息。
16.36
【分析】把甲港到乙港之间的距离看作单位“1”,从甲港到乙港所用时间为,则返回所用时间为,根据平均速度=总路程÷时间,列式解答即可。
【详解】(1+1)÷(+)
=2÷
=36(千米/时)
该艘轮船往返两港的平均速度是36千米/时。
【点睛】此题考查了平均数的求法,用总数量÷份数解答,不能直接把两个来回速度求平均数。
17.√
【分析】条形统计图能很容易看出数量的多少;因为比较各月空气的质量为“优”的天数,即数量的多少,所以用复式条形统计图;据此解答。
【详解】根据分析可知,比较成都今年和去年各月空气质量为“优”的天数,宜使用复式条形统计图,原题干说法正确。
故答案为:√
【点睛】根据复式条形统计图的特征进行解答。
18.√
【详解】复式条形统计图、复式折线统计图因为是对两组及两组以上的数据进行比较,为了区分,必须要有图例。
故答案为:√
19.×
【分析】根据平均数的意义可知,如果总数量改变,份数不变,平均数一定会改变;据此解答即可。
【详解】因为平均数=总数量÷总份数,所以如果总数量改变,份数不变,平均数一定会改变;平均数有一定的代表性,原题说法错误。
故答案为: ×。
【点睛】考查了平均数的意义,平均数是指在一组数据中所有数据之和再除以数据的个数,它是反映数据集中趋势的一项指标。
20.√
【分析】把一组数据中的所有数据加起来,再除以数据个数,即可得出平均数,平均数易受少数几个极端值的影响,据此解答。
【详解】根据分析可知:平均数容易受偏大或偏小数据的影响。
原题干说法正确。
故答案为√
【点睛】本题考查对平均数的含义的理解。
21.√
【详解】解答本题时,要知道:总数量÷总份数=平均数.
22.36;36;0
【详解】试题分析:(1)先求出5个数的和,进而根据“总数÷个数=平均数”进行解答即可;
(2)先求出6个数的和,进而根据“总数÷个数=平均数”进行解答即可;
(3)求两个平均数相差多少,用减法解答即可.
解:(1)(33+42+20+53+32)÷5,
=180÷5,
=36,
答:这5个数的平均数是36;
(2)(33+42+20+53+32+36)÷6,
=216÷6,
=36,
答:这6个数的平均数是36;
(3)36﹣36=0,
答:两个平均数相差0.
点评:此题考查了平均数的计算方法,应灵活掌握求平均数的方法.
23.(1) 四 10
(2)79.8
(3)
【分析】(1)根据统计图,算出甲、乙每次成绩差,差最大表示成绩差距最大。
(2)用5次成绩的和除以5即可求出平均成绩;
(3)(甲反思的时间-乙反思的时间)÷甲反思的时间即可求解。
(1)
根据统计图,第四次甲、乙成绩差距最大,相差90-80=10(分);
(2)
(65+70+80+90+94)÷5
=399÷5
=79.8(分)
(3)
乙的反思时间是0.2时,甲的反思时间是0.6时,
(0.6-0.2)÷0.6
=0.4÷0.6
=
【点睛】本题主要考查的是统计图、平均数、一个数比另一个数多(少)几分之几的问题。
24.(1)见详解;
(2)5,2、5,2,2
【分析】(1)根据表中已知数据,在统计图上描出各点,制成折线统计图;
(2)观察折线统计图的折线变化情况,高低差距最大的就是气温相差最大的月份,用减法求差即可;折线重合的月份即两城市气温相同的月份;通过观察折线统计图可得有几个月乙市平均气温高于甲市,几个月乙市平均气温低于甲市。
【详解】(1)如图:
(2)1月份温差:10-7=3(摄氏度);
2月份两城市都是8摄氏度;
3月份温差:11-6=5(摄氏度);
4月份温差:13-9=4(摄氏度);
5月份两城市都是10摄氏度;
6月份温差:12-9=3(摄氏度);
5>4>3
温差最大的是3月份,差5摄氏度;
乙市平均气温中1、4月份高于甲市,2、5月份平均气温相同,其余3、4个月份低于甲市。
由此可得,两市月平均气温最大相差5摄氏度。2、5月份两城市平均气温相同,有2个月乙市平均气温高于甲市,其余2个月乙市平均气温低于甲市。
【点睛】解答此题的关键利用表中已知的信息,分析问题以及绘制折线统计图的能力。
25.(1)2015 2012(2)375
【详解】略
26.(1)甲、乙两人六次射击的平均成绩都是9环。
(2)我觉得选乙合适,因为乙的成绩稳步上升。
【分析】(1)通过折线统计图收集数据:甲6次射击的分数为: 8,9,10,9,8,10;乙6次射击的成绩为: 9,8,8, 9,10,10;然后用各自分数的和:射击的次数得到平均数即可。
{2)通过统计图发现,甲的成绩波动较大,而乙的发挥呈上升趋势。
【详解】(1)甲:(8+9+10+9+8+10)÷6
=54÷6
=9(环)
乙:(9+8+8+9+10+10)÷6
=54÷6
=9(环)
答:甲、乙两人六次射击的平均成绩都是9环。
(2)我觉得选乙合适,因为乙的成绩稳步上升。
【点睛】本题考查了从复式折线统计图获取信的能力。折线统计图不但可以表示项目的具体数量,又能清楚地反映事物变化的情况。
27.3米
【分析】要求平均每套儿童服装用布多少米,根据题意,先求出50套儿童服装一共用了多少米布,进而除以服装套数50得解。
【详解】(240-90)÷50
=150÷50
=3(米)
答:平均每套儿童服装用布3米。
【点睛】解决此题关键是先求出50套儿童服装一共用了多少米布,进而根据平均数的求法计算得解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
