小升初《立体图形》专项训练(含解析)
文档属性
| 名称 | 小升初《立体图形》专项训练(含解析) | 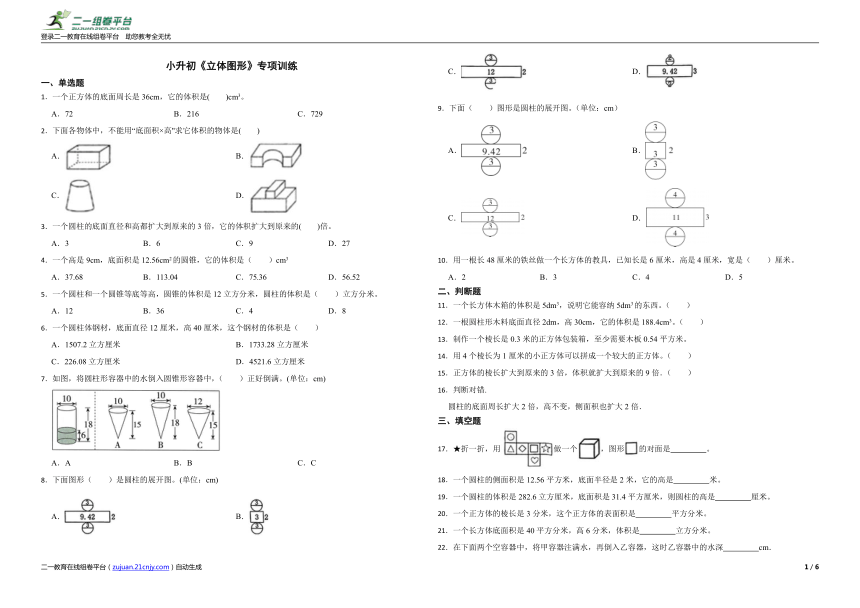 | |
| 格式 | docx | ||
| 文件大小 | 391.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 10:59:57 | ||
图片预览


文档简介
登录二一教育在线组卷平台 助您教考全无忧
小升初《立体图形》专项训练
一、单选题
1.一个正方体的底面周长是36cm,它的体积是( )cm3。
A.72 B.216 C.729
2.下面各物体中,不能用“底面积×高"求它体积的物体是( )
A. B.
C. D.
3.一个圆柱的底面直径和高都扩大到原来的3倍,它的体积扩大到原来的( )倍。
A.3 B.6 C.9 D.27
4.一个高是9cm,底面积是12.56cm2的圆锥,它的体积是( )cm3
A.37.68 B.113.04 C.75.36 D.56.52
5.一个圆柱和一个圆锥等底等高,圆锥的体积是12立方分米,圆柱的体积是( )立方分米。
A.12 B.36 C.4 D.8
6.一个圆柱体钢材,底面直径12厘米,高40厘米,这个钢材的体积是( )
A.1507.2立方厘米 B.1733.28立方厘米
C.226.08立方厘米 D.4521.6立方厘米
7.如图,将圆柱形容器中的水倒入圆锥形容器中,( )正好倒满。(单位:cm)
A.A B.B C.C
8.下面图形( )是圆柱的展开图。(单位:cm)
A. B.
C. D.
9.下面( )图形是圆柱的展开图。(单位:cm)
A. B.
C. D.
10.用一根长48厘米的铁丝做一个长方体的教具,已知长是6厘米,高是4厘米,宽是( )厘米。
A.2 B.3 C.4 D.5
二、判断题
11.一个长方体木箱的体积是5dm3,说明它能容纳5dm3的东西。( )
12.一根圆柱形木料底面直径2dm,高30cm,它的体积是188.4cm3。( )
13.制作一个棱长是0.3米的正方体包装箱,至少需要木板0.54平方米。
14.用4个棱长为1厘米的小正方体可以拼成一个较大的正方体。( )
15.正方体的棱长扩大到原来的3倍,体积就扩大到原来的9倍.( )
16.判断对错.
圆柱的底面周长扩大2倍,高不变,侧面积也扩大2倍.
三、填空题
17.★折一折,用做一个,图形的对面是 。
18.一个圆柱的侧面积是12.56平方米,底面半径是2米,它的高是 米。
19.一个圆柱的体积是282.6立方厘米,底面积是31.4平方厘米,则圆柱的高是 厘米。
20.一个正方体的棱长是3分米,这个正方体的表面积是 平方分米。
21.一个长方体底面积是40平方分米,高6分米,体积是 立方分米。
22.在下面两个空容器中,将甲容器注满水,再倒入乙容器,这时乙容器中的水深 cm.
23.一个圆柱的底面积是24cm,高是6cm,这个圆柱的体积是 cm 。
24.等底等高的圆柱和圆锥的体积相差24立方米,这个圆柱的体积是 立方米,圆锥的体积是 立方米。
25.把一根长2米的长方体钢材沿着横截面锯成三段,表面积比原来增加2.4平方分米,这根钢材原来的体积是 立方分米。
26.如图,下边的木棒底面半径为2dm,高为1m,把它截成2段后,表面积之和比原来增加了 dm2。
四、计算题
27.做一个圆柱形厨师帽底面圆周长为45厘米,高是底面直径的2倍,至少需要多少布料?
五、解答题
28.建筑工地有一个圆锥形沙堆,底面直径是8m,高是3m。如果每立方米沙重1500 kg,那么这堆沙-共重多少千克?
29. 一个正方体容器,从里面量,棱长是6dm。先在该容器底部放一个高为4dm、体积为30cm3的钢坯,再往容器里倒水。当倒入多少升水时,钢坯刚好完全浸没水里?
30.下面4个图形的面积都是36 dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现? (单位:dm)
31.如图是一个无盖长方体纸箱的展开图,请你根据图中的信息求出这个纸箱的容积。(纸板的厚度忽略不计,单位:dm)
32.冰墩墩是2022年北京冬季奥运会的吉祥物,深受小朋友喜爱。一个底面长12 cm、宽15 cm。里面体积为1080 cm3的长方体盒子,能否装下下图尺寸的冰墩墩玩偶?尺寸:11cm×8 cm×12 cm)
六、解决问题
33.一个新建的游泳池长50m,宽25m,深2.5m,现在要在游泳池的四周和底面贴上瓷砖,一共需要贴多少平方米瓷砖?
34.下图是用牛皮纸做成的手提袋,做一个这样的手提袋至少需要多少牛皮纸?
35.求圆锥的体积(单位:厘米)
七、图形计算
36.计算下面立体图形的体积。(单位:cm)
答案解析部分
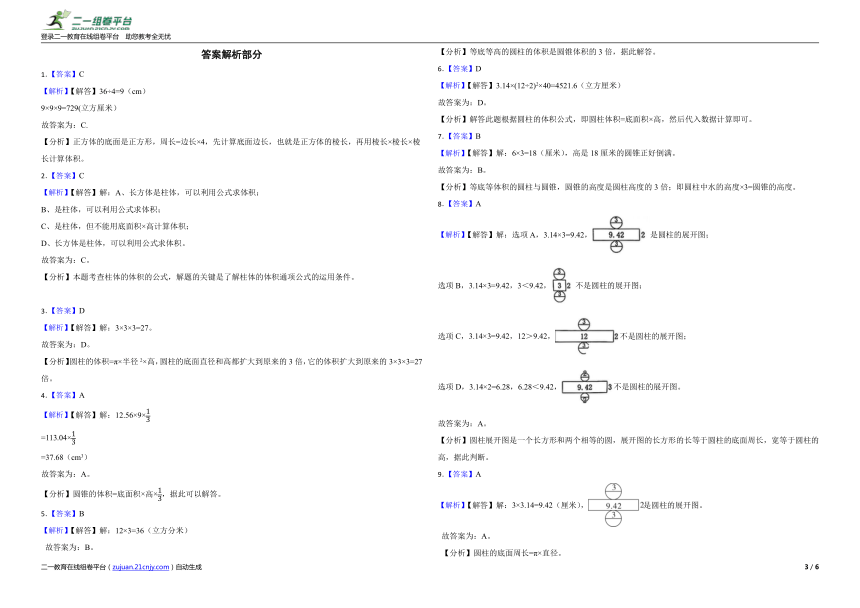
1.【答案】C
【解析】【解答】36÷4=9(cm)
9×9×9=729(立方厘米)
故答案为:C.
【分析】正方体的底面是正方形,周长=边长×4,先计算底面边长,也就是正方体的棱长,再用棱长×棱长×棱长计算体积。
2.【答案】C
【解析】【解答】解:A、长方体是柱体,可以利用公式求体积;
B、是柱体,可以利用公式求体积;
C、是柱体,但不能用底面积×高计算体积;
D、长方体是柱体,可以利用公式求体积。
故答案为:C。
【分析】本题考查柱体的体积的公式,解题的关键是了解柱体的体积通项公式的运用条件。
3.【答案】D
【解析】【解答】解:3×3×3=27。
故答案为:D。
【分析】圆柱的体积=π×半径2×高,圆柱的底面直径和高都扩大到原来的3倍,它的体积扩大到原来的3×3×3=27倍。
4.【答案】A
【解析】【解答】解:12.56×9×
=113.04×
=37.68(cm3)
故答案为:A。
【分析】圆锥的体积=底面积×高×,据此可以解答。
5.【答案】B
【解析】【解答】解:12×3=36(立方分米)
故答案为:B。
【分析】等底等高的圆柱的体积是圆锥体积的3倍,据此解答。
6.【答案】D
【解析】【解答】3.14×(12÷2)2×40=4521.6(立方厘米)
故答案为:D。
【分析】解答此题根据圆柱的体积公式,即圆柱体积=底面积×高,然后代入数据计算即可。
7.【答案】B
【解析】【解答】解:6×3=18(厘米),高是18厘米的圆锥正好倒满。
故答案为:B。
【分析】等底等体积的圆柱与圆锥,圆锥的高度是圆柱高度的3倍;即圆柱中水的高度×3=圆锥的高度。
8.【答案】A
【解析】【解答】解:选项A,3.14×3=9.42,是圆柱的展开图;
选项B,3.14×3=9.42,3<9.42,不是圆柱的展开图;
选项C,3.14×3=9.42,12>9.42,不是圆柱的展开图;
选项D,3.14×2=6.28,6.28<9.42,不是圆柱的展开图。
故答案为:A。
【分析】圆柱展开图是一个长方形和两个相等的圆,展开图的长方形的长等于圆柱的底面周长,宽等于圆柱的高,据此判断。
9.【答案】A
【解析】【解答】解:3×3.14=9.42(厘米),是圆柱的展开图。
故答案为:A。
【分析】圆柱的底面周长=π×直径。
10.【答案】A
【解析】【解答】解:48÷4﹣(6+4)
=12﹣10
=2(厘米),
答:宽是2厘米。
故选:A。
【分析】用一根长48厘米的铁丝做一个长方体的教具,也就是这个长方体的棱长总和是48厘米,因为长方体的棱长总和=(长+宽+高)×4,所以用棱长总和除以4减去长和高即可求出宽,据此解答。
11.【答案】错误
【解析】【解答】解:一个长方体木箱的体积是5dm3,不能说明它能容纳5dm3的东西。
故答案为:错误。
【分析】体积是物体所占空间的体积,容积是指容器所能物体的体积,所以体积和统计不一样。
12.【答案】错误
【解析】【解答】解:2dm=20cm;
3.14×(20÷2)2×30
=3.14×100×30
=314×30
=9420(cm3)
故答案为:错误。
【分析】圆柱的体积=底面积×高,就此计算判断。
13.【答案】正确
【解析】【解答】0.3×0.3×6=0.54(平方米)。
故答案为:正确
【分析】棱长×棱长×6=正方体表面积。
14.【答案】错误
【解析】【解答】解:2×2×2
=4×2
=8(个)
故答案为:错误。
【分析】用棱长为1厘米的小正方体拼成一个较大正方体的棱长是2厘米,至少需要小正方体的个数=棱长×棱长×棱长。
15.【答案】错误
【解析】【解答】3×3×3=27,正方体的棱长扩大到原来的3倍,体积就扩大到原来的27倍,原题说法错误。
故答案为:错误。
【分析】正方体的棱长×棱长×棱长=正方体的体积,据此解答。
16.【答案】正确
【解析】【解答】根据圆柱的侧面积公式可知,圆柱的底面周长扩大2倍,高不变,侧面积也扩大2倍;原题说法正确.
故答案为:正确
【分析】圆柱的侧面积=底面周长×高,高不变,圆柱的侧面积的变化情况与底面周长的变化情况相同.
17.【答案】△
【解析】【解答】解:图形的对面是△。
故答案为:△。
【分析】正方体相对的面不相邻,据此填空。
18.【答案】1
【解析】【解答】解:底面周长:2×3.14×2=12.56(米)
高:12.56÷12.56=1(米)
故答案为:1。
【分析】2×π×底面半径=底面周长,侧面积÷底面周长=高。
19.【答案】9
【解析】【解答】282.6÷31.4=9(厘米)
故答案为:9.
【分析】已知圆柱的体积和底面积,求圆柱的高,用圆柱的体积÷底面积=圆柱的高,据此列式解答.
20.【答案】54
【解析】【解答】解:3×3×6=54(平方分米)
故答案为:54。
【分析】正方体表面积=棱长×棱长×6,根据公式计算表面积即可。
21.【答案】240
【解析】【解答】解:40×6=240(立方分米)。
故答案为:240。
【分析】长方体的体积=底面积×高。
22.【答案】4
【解析】【解答】12× =4(厘米);
故答案为:4.
【分析】体积和底面积相等的圆锥和圆柱,圆柱的高=圆锥的高×。
23.【答案】144
【解析】【解答】解:圆柱的体积=24×6=144(cm3)。
故答案为:144。
【分析】圆柱的体积=圆柱的底面积×圆柱的高,代入数值计算即可得出答案。
24.【答案】12;36
【解析】【解答】解:24÷(3-1)=12(立方厘米),所以这个圆锥的体积是12立方厘米;12×3=36(立方厘米),所以圆柱的体积是36立方厘米。
故答案为:12;36。
【分析】等底等高圆柱的体积是圆锥体积的3倍,它们相差2个圆锥的面积,所以圆锥的体积=它们的面积之差÷2,圆柱的体积=圆锥的体积×3。
25.【答案】12
【解析】【解答】解:2米=20分米
2.4÷4×20
=0.6×20
=12(立方分米)。
故答案为:12。
【分析】这根钢材原来的体积=横截面的面积×原来的高度;其中,横截面的面积=增加的表面积÷增加横截面的个数。
26.【答案】25.12
【解析】【解答】解:3.14×22×2
=3.14×4×2
=12.56×2
=25.12(dm2)
故答案为:25.12。
【分析】把它截成2段后,表面积之和比原来增加了两个横截面的面积;其中,一个横截面的面积=底面积=π×半径2。
27.【答案】1451.03平方厘米
【解析】【解答】45×[2×(45÷π)]+(45÷2π) π≈1451.03(平方厘米)
【分析】先求出底面圆的直径进而得到帽子的高度,根据圆柱侧面是长方形,用底面圆的周长即长方形的长乘以高度即长方形的宽,得到了侧面面积再加上一个冒顶即圆柱的底面积。
28.【答案】解:×3.14×(8÷2)2×3×1500
=×3.14×16×3×1500
=50.24×1500
=75360(千克);
答:这堆沙一共重75360千克。
【解析】【分析】首先根据圆锥的体积公式:V=πr2h,求出沙堆的体积,然后用沙的体积乘每立方米沙的质量即可。
29.【答案】解:6×6×4=144(立方分米)
144-30=114(立方分米)
114立方分米=114L
答:当倒入114升水时,钢坯刚好完全浸没水里。
【解析】【分析】钢坯刚好浸没在水里时,水面的高度与钢坯高度相等,都是4dm。此时容器内钢坯和水的体积和就是底面边长6dm,高4dm的长方体体积。因此用水和钢坯的体积和减去钢坯的体积就是倒入水的体积。
30.【答案】解:第1个图形:
第2个图形:
第3个图形:
第4个图形:
发现:用第1个图形的长作为圆柱的底面周长围成的圆柱的体积最大;用第1个图形的宽作为圆柱的底面周长围成的圆柱的体积最小。
【解析】【分析】用长方形卷成圆柱共有两种方法,一种是用长方形的长作为圓柱的底面周长,宽作为圆柱的高;另一种是用长方形的宽作为圆柱的底面周长,长作为圆柱的高。用正方形卷成圆柱只有一种方法。
31.【答案】解:3-1=2(分米)
5-2=3(分米)
2×3×1=6(立方分米)
答:这个纸箱的容积是6立方分米。
【解析】【分析】这个纸箱的容积=长×宽×高;其中,这个长方体的高是1分米,宽+高=3分米,也就是宽=3-1=2分米,又因为长+宽=5分米,可知长是3分米。
32.【答案】解:1080÷12÷15
=90÷15
=6(cm)
8>6
答:不能。
【解析】【分析】根据题意可得:长方体盒子的体积÷长÷宽=长方体盒子的高,再将盒子的长、宽、高分别与冰墩墩的尺寸进行比较即可判断。
33.【答案】解:50×25+50×2.5×2+2.5×25×2
=1250+125×2+62.5×2
=1250+250+125
=1500+125
=1625(平方米)
答:一共需要贴1625平方米瓷砖。
【解析】【分析】一共需要贴瓷砖的面积=长×宽+长×高×2+宽×高×2。
34.【答案】解:35×45×2+15×45×2+35×15
=3150+1350+525
=5025(平方厘米)
答:做一个这样的手提袋至少需要5025平方厘米牛皮纸。
【解析】【分析】至少需要牛皮纸的数量=四周的面积+底面的面积=长×高×2+宽×高×2+长×宽,据此代入数据解答即可。
35.【答案】解:3.14×(6÷2)2 ×9÷3
=3.14×9×3
=3.14×27
=84.78(立方厘米)
答:圆锥的体积是84.78立方厘米。
【解析】【分析】圆锥体积=π×半径的平方×高÷3,据此解答。
36.【答案】解:高:4-1=3(cm)
3.14×(3÷2)2×3×
=3.14×1.52×3×
=3.14×2.25
=7.065(cm3)
答:体积是7.065cm3。
【解析】【分析】该立体图形是一个圆锥,圆锥的高是4-1=3(cm),底面直径是3cm,根据圆锥的体积=π×半径2×高×,代入数值计算解答。
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
小升初《立体图形》专项训练
一、单选题
1.一个正方体的底面周长是36cm,它的体积是( )cm3。
A.72 B.216 C.729
2.下面各物体中,不能用“底面积×高"求它体积的物体是( )
A. B.
C. D.
3.一个圆柱的底面直径和高都扩大到原来的3倍,它的体积扩大到原来的( )倍。
A.3 B.6 C.9 D.27
4.一个高是9cm,底面积是12.56cm2的圆锥,它的体积是( )cm3
A.37.68 B.113.04 C.75.36 D.56.52
5.一个圆柱和一个圆锥等底等高,圆锥的体积是12立方分米,圆柱的体积是( )立方分米。
A.12 B.36 C.4 D.8
6.一个圆柱体钢材,底面直径12厘米,高40厘米,这个钢材的体积是( )
A.1507.2立方厘米 B.1733.28立方厘米
C.226.08立方厘米 D.4521.6立方厘米
7.如图,将圆柱形容器中的水倒入圆锥形容器中,( )正好倒满。(单位:cm)
A.A B.B C.C
8.下面图形( )是圆柱的展开图。(单位:cm)
A. B.
C. D.
9.下面( )图形是圆柱的展开图。(单位:cm)
A. B.
C. D.
10.用一根长48厘米的铁丝做一个长方体的教具,已知长是6厘米,高是4厘米,宽是( )厘米。
A.2 B.3 C.4 D.5
二、判断题
11.一个长方体木箱的体积是5dm3,说明它能容纳5dm3的东西。( )
12.一根圆柱形木料底面直径2dm,高30cm,它的体积是188.4cm3。( )
13.制作一个棱长是0.3米的正方体包装箱,至少需要木板0.54平方米。
14.用4个棱长为1厘米的小正方体可以拼成一个较大的正方体。( )
15.正方体的棱长扩大到原来的3倍,体积就扩大到原来的9倍.( )
16.判断对错.
圆柱的底面周长扩大2倍,高不变,侧面积也扩大2倍.
三、填空题
17.★折一折,用做一个,图形的对面是 。
18.一个圆柱的侧面积是12.56平方米,底面半径是2米,它的高是 米。
19.一个圆柱的体积是282.6立方厘米,底面积是31.4平方厘米,则圆柱的高是 厘米。
20.一个正方体的棱长是3分米,这个正方体的表面积是 平方分米。
21.一个长方体底面积是40平方分米,高6分米,体积是 立方分米。
22.在下面两个空容器中,将甲容器注满水,再倒入乙容器,这时乙容器中的水深 cm.
23.一个圆柱的底面积是24cm,高是6cm,这个圆柱的体积是 cm 。
24.等底等高的圆柱和圆锥的体积相差24立方米,这个圆柱的体积是 立方米,圆锥的体积是 立方米。
25.把一根长2米的长方体钢材沿着横截面锯成三段,表面积比原来增加2.4平方分米,这根钢材原来的体积是 立方分米。
26.如图,下边的木棒底面半径为2dm,高为1m,把它截成2段后,表面积之和比原来增加了 dm2。
四、计算题
27.做一个圆柱形厨师帽底面圆周长为45厘米,高是底面直径的2倍,至少需要多少布料?
五、解答题
28.建筑工地有一个圆锥形沙堆,底面直径是8m,高是3m。如果每立方米沙重1500 kg,那么这堆沙-共重多少千克?
29. 一个正方体容器,从里面量,棱长是6dm。先在该容器底部放一个高为4dm、体积为30cm3的钢坯,再往容器里倒水。当倒入多少升水时,钢坯刚好完全浸没水里?
30.下面4个图形的面积都是36 dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现? (单位:dm)
31.如图是一个无盖长方体纸箱的展开图,请你根据图中的信息求出这个纸箱的容积。(纸板的厚度忽略不计,单位:dm)
32.冰墩墩是2022年北京冬季奥运会的吉祥物,深受小朋友喜爱。一个底面长12 cm、宽15 cm。里面体积为1080 cm3的长方体盒子,能否装下下图尺寸的冰墩墩玩偶?尺寸:11cm×8 cm×12 cm)
六、解决问题
33.一个新建的游泳池长50m,宽25m,深2.5m,现在要在游泳池的四周和底面贴上瓷砖,一共需要贴多少平方米瓷砖?
34.下图是用牛皮纸做成的手提袋,做一个这样的手提袋至少需要多少牛皮纸?
35.求圆锥的体积(单位:厘米)
七、图形计算
36.计算下面立体图形的体积。(单位:cm)
答案解析部分
1.【答案】C
【解析】【解答】36÷4=9(cm)
9×9×9=729(立方厘米)
故答案为:C.
【分析】正方体的底面是正方形,周长=边长×4,先计算底面边长,也就是正方体的棱长,再用棱长×棱长×棱长计算体积。
2.【答案】C
【解析】【解答】解:A、长方体是柱体,可以利用公式求体积;
B、是柱体,可以利用公式求体积;
C、是柱体,但不能用底面积×高计算体积;
D、长方体是柱体,可以利用公式求体积。
故答案为:C。
【分析】本题考查柱体的体积的公式,解题的关键是了解柱体的体积通项公式的运用条件。
3.【答案】D
【解析】【解答】解:3×3×3=27。
故答案为:D。
【分析】圆柱的体积=π×半径2×高,圆柱的底面直径和高都扩大到原来的3倍,它的体积扩大到原来的3×3×3=27倍。
4.【答案】A
【解析】【解答】解:12.56×9×
=113.04×
=37.68(cm3)
故答案为:A。
【分析】圆锥的体积=底面积×高×,据此可以解答。
5.【答案】B
【解析】【解答】解:12×3=36(立方分米)
故答案为:B。
【分析】等底等高的圆柱的体积是圆锥体积的3倍,据此解答。
6.【答案】D
【解析】【解答】3.14×(12÷2)2×40=4521.6(立方厘米)
故答案为:D。
【分析】解答此题根据圆柱的体积公式,即圆柱体积=底面积×高,然后代入数据计算即可。
7.【答案】B
【解析】【解答】解:6×3=18(厘米),高是18厘米的圆锥正好倒满。
故答案为:B。
【分析】等底等体积的圆柱与圆锥,圆锥的高度是圆柱高度的3倍;即圆柱中水的高度×3=圆锥的高度。
8.【答案】A
【解析】【解答】解:选项A,3.14×3=9.42,是圆柱的展开图;
选项B,3.14×3=9.42,3<9.42,不是圆柱的展开图;
选项C,3.14×3=9.42,12>9.42,不是圆柱的展开图;
选项D,3.14×2=6.28,6.28<9.42,不是圆柱的展开图。
故答案为:A。
【分析】圆柱展开图是一个长方形和两个相等的圆,展开图的长方形的长等于圆柱的底面周长,宽等于圆柱的高,据此判断。
9.【答案】A
【解析】【解答】解:3×3.14=9.42(厘米),是圆柱的展开图。
故答案为:A。
【分析】圆柱的底面周长=π×直径。
10.【答案】A
【解析】【解答】解:48÷4﹣(6+4)
=12﹣10
=2(厘米),
答:宽是2厘米。
故选:A。
【分析】用一根长48厘米的铁丝做一个长方体的教具,也就是这个长方体的棱长总和是48厘米,因为长方体的棱长总和=(长+宽+高)×4,所以用棱长总和除以4减去长和高即可求出宽,据此解答。
11.【答案】错误
【解析】【解答】解:一个长方体木箱的体积是5dm3,不能说明它能容纳5dm3的东西。
故答案为:错误。
【分析】体积是物体所占空间的体积,容积是指容器所能物体的体积,所以体积和统计不一样。
12.【答案】错误
【解析】【解答】解:2dm=20cm;
3.14×(20÷2)2×30
=3.14×100×30
=314×30
=9420(cm3)
故答案为:错误。
【分析】圆柱的体积=底面积×高,就此计算判断。
13.【答案】正确
【解析】【解答】0.3×0.3×6=0.54(平方米)。
故答案为:正确
【分析】棱长×棱长×6=正方体表面积。
14.【答案】错误
【解析】【解答】解:2×2×2
=4×2
=8(个)
故答案为:错误。
【分析】用棱长为1厘米的小正方体拼成一个较大正方体的棱长是2厘米,至少需要小正方体的个数=棱长×棱长×棱长。
15.【答案】错误
【解析】【解答】3×3×3=27,正方体的棱长扩大到原来的3倍,体积就扩大到原来的27倍,原题说法错误。
故答案为:错误。
【分析】正方体的棱长×棱长×棱长=正方体的体积,据此解答。
16.【答案】正确
【解析】【解答】根据圆柱的侧面积公式可知,圆柱的底面周长扩大2倍,高不变,侧面积也扩大2倍;原题说法正确.
故答案为:正确
【分析】圆柱的侧面积=底面周长×高,高不变,圆柱的侧面积的变化情况与底面周长的变化情况相同.
17.【答案】△
【解析】【解答】解:图形的对面是△。
故答案为:△。
【分析】正方体相对的面不相邻,据此填空。
18.【答案】1
【解析】【解答】解:底面周长:2×3.14×2=12.56(米)
高:12.56÷12.56=1(米)
故答案为:1。
【分析】2×π×底面半径=底面周长,侧面积÷底面周长=高。
19.【答案】9
【解析】【解答】282.6÷31.4=9(厘米)
故答案为:9.
【分析】已知圆柱的体积和底面积,求圆柱的高,用圆柱的体积÷底面积=圆柱的高,据此列式解答.
20.【答案】54
【解析】【解答】解:3×3×6=54(平方分米)
故答案为:54。
【分析】正方体表面积=棱长×棱长×6,根据公式计算表面积即可。
21.【答案】240
【解析】【解答】解:40×6=240(立方分米)。
故答案为:240。
【分析】长方体的体积=底面积×高。
22.【答案】4
【解析】【解答】12× =4(厘米);
故答案为:4.
【分析】体积和底面积相等的圆锥和圆柱,圆柱的高=圆锥的高×。
23.【答案】144
【解析】【解答】解:圆柱的体积=24×6=144(cm3)。
故答案为:144。
【分析】圆柱的体积=圆柱的底面积×圆柱的高,代入数值计算即可得出答案。
24.【答案】12;36
【解析】【解答】解:24÷(3-1)=12(立方厘米),所以这个圆锥的体积是12立方厘米;12×3=36(立方厘米),所以圆柱的体积是36立方厘米。
故答案为:12;36。
【分析】等底等高圆柱的体积是圆锥体积的3倍,它们相差2个圆锥的面积,所以圆锥的体积=它们的面积之差÷2,圆柱的体积=圆锥的体积×3。
25.【答案】12
【解析】【解答】解:2米=20分米
2.4÷4×20
=0.6×20
=12(立方分米)。
故答案为:12。
【分析】这根钢材原来的体积=横截面的面积×原来的高度;其中,横截面的面积=增加的表面积÷增加横截面的个数。
26.【答案】25.12
【解析】【解答】解:3.14×22×2
=3.14×4×2
=12.56×2
=25.12(dm2)
故答案为:25.12。
【分析】把它截成2段后,表面积之和比原来增加了两个横截面的面积;其中,一个横截面的面积=底面积=π×半径2。
27.【答案】1451.03平方厘米
【解析】【解答】45×[2×(45÷π)]+(45÷2π) π≈1451.03(平方厘米)
【分析】先求出底面圆的直径进而得到帽子的高度,根据圆柱侧面是长方形,用底面圆的周长即长方形的长乘以高度即长方形的宽,得到了侧面面积再加上一个冒顶即圆柱的底面积。
28.【答案】解:×3.14×(8÷2)2×3×1500
=×3.14×16×3×1500
=50.24×1500
=75360(千克);
答:这堆沙一共重75360千克。
【解析】【分析】首先根据圆锥的体积公式:V=πr2h,求出沙堆的体积,然后用沙的体积乘每立方米沙的质量即可。
29.【答案】解:6×6×4=144(立方分米)
144-30=114(立方分米)
114立方分米=114L
答:当倒入114升水时,钢坯刚好完全浸没水里。
【解析】【分析】钢坯刚好浸没在水里时,水面的高度与钢坯高度相等,都是4dm。此时容器内钢坯和水的体积和就是底面边长6dm,高4dm的长方体体积。因此用水和钢坯的体积和减去钢坯的体积就是倒入水的体积。
30.【答案】解:第1个图形:
第2个图形:
第3个图形:
第4个图形:
发现:用第1个图形的长作为圆柱的底面周长围成的圆柱的体积最大;用第1个图形的宽作为圆柱的底面周长围成的圆柱的体积最小。
【解析】【分析】用长方形卷成圆柱共有两种方法,一种是用长方形的长作为圓柱的底面周长,宽作为圆柱的高;另一种是用长方形的宽作为圆柱的底面周长,长作为圆柱的高。用正方形卷成圆柱只有一种方法。
31.【答案】解:3-1=2(分米)
5-2=3(分米)
2×3×1=6(立方分米)
答:这个纸箱的容积是6立方分米。
【解析】【分析】这个纸箱的容积=长×宽×高;其中,这个长方体的高是1分米,宽+高=3分米,也就是宽=3-1=2分米,又因为长+宽=5分米,可知长是3分米。
32.【答案】解:1080÷12÷15
=90÷15
=6(cm)
8>6
答:不能。
【解析】【分析】根据题意可得:长方体盒子的体积÷长÷宽=长方体盒子的高,再将盒子的长、宽、高分别与冰墩墩的尺寸进行比较即可判断。
33.【答案】解:50×25+50×2.5×2+2.5×25×2
=1250+125×2+62.5×2
=1250+250+125
=1500+125
=1625(平方米)
答:一共需要贴1625平方米瓷砖。
【解析】【分析】一共需要贴瓷砖的面积=长×宽+长×高×2+宽×高×2。
34.【答案】解:35×45×2+15×45×2+35×15
=3150+1350+525
=5025(平方厘米)
答:做一个这样的手提袋至少需要5025平方厘米牛皮纸。
【解析】【分析】至少需要牛皮纸的数量=四周的面积+底面的面积=长×高×2+宽×高×2+长×宽,据此代入数据解答即可。
35.【答案】解:3.14×(6÷2)2 ×9÷3
=3.14×9×3
=3.14×27
=84.78(立方厘米)
答:圆锥的体积是84.78立方厘米。
【解析】【分析】圆锥体积=π×半径的平方×高÷3,据此解答。
36.【答案】解:高:4-1=3(cm)
3.14×(3÷2)2×3×
=3.14×1.52×3×
=3.14×2.25
=7.065(cm3)
答:体积是7.065cm3。
【解析】【分析】该立体图形是一个圆锥,圆锥的高是4-1=3(cm),底面直径是3cm,根据圆锥的体积=π×半径2×高×,代入数值计算解答。
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
同课章节目录
