小升初奥数《几何》专项训练(含解析)
文档属性
| 名称 | 小升初奥数《几何》专项训练(含解析) | 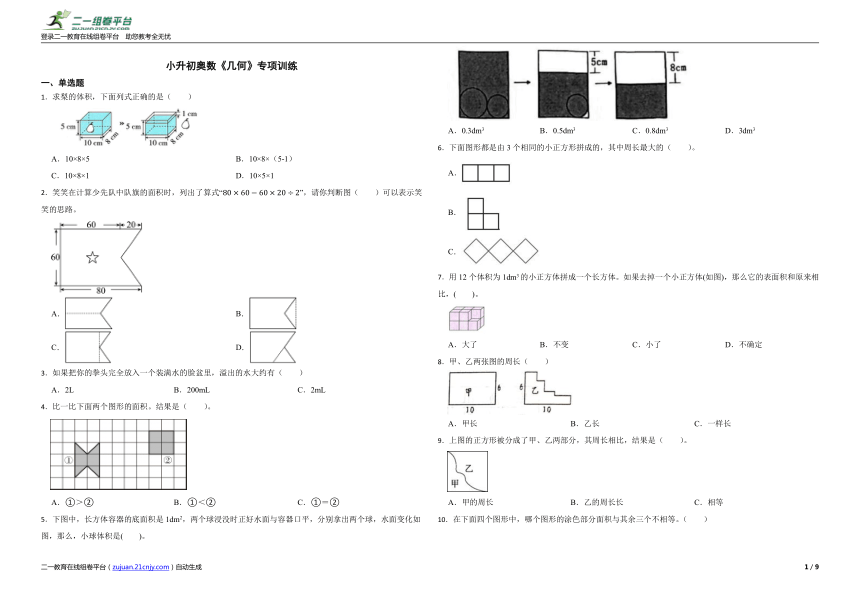 | |
| 格式 | docx | ||
| 文件大小 | 666.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 11:07:54 | ||
图片预览


文档简介
登录二一教育在线组卷平台 助您教考全无忧
小升初奥数《几何》专项训练
一、单选题
1.求梨的体积,下面列式正确的是( )
A.10×8×5 B.10×8×(5-1)
C.10×8×1 D.10×5×1
2.笑笑在计算少先队中队旗的面积时,列出了算式“”,请你判断图( )可以表示笑笑的思路。
A. B.
C. D.
3.如果把你的拳头完全放入一个装满水的脸盆里,溢出的水大约有( )
A.2L B.200mL C.2mL
4.比一比下面两个图形的面积。结果是( )。
A.①>② B.①<② C.①=②
5.下图中,长方体容器的底面积是1dm2,两个球浸没时正好水面与容器口平,分别拿出两个球,水面变化如图,那么,小球体积是( )。
A.0.3dm3 B.0.5dm3 C.0.8dm3 D.3dm3
6.下面图形都是由3个相同的小正方形拼成的,其中周长最大的( )。
A.
B.
C.
7.用12个体积为1dm3的小正方体拼成一个长方体。如果去掉一个小正方体(如图),那么它的表面积和原来相比,( )。
A.大了 B.不变 C.小了 D.不确定
8.甲、乙两张图的周长( )
A.甲长 B.乙长 C.一样长
9.上图的正方形被分成了甲、乙两部分,其周长相比,结果是( )。
A.甲的周长 B.乙的周长长 C.相等
10.在下面四个图形中,哪个图形的涂色部分面积与其余三个不相等。( )
A. B.
C. D.
二、判断题
11.把一个正方体橡皮泥捏成长方体,体积变大了。( )
12.将一个圆柱形铁块熔铸成一个圆锥,它的体积变小了。( )
13.如下图,大正方形的边长是2厘米,小正方形的边长是1厘米,则阴影部分的面积是2平方厘米。(
)
14.球从哪个方向看都一样。( )
15.判断对错
把一块正方体的橡皮泥捏成一个长方体后,它的形状改变了,但它所占的空间大小不变.
16.图中涂色的两个三角形面积是一样大的。
三、填空题
17. 将两个棱长为1cm的小正方体叠放在墙角处,有 个面露在外面,露在外面的面积是
18.下面这个组合图形的面积是 cm2。
19.将一根长80厘米的草绳对折一次后,用剪刀在中点处剪开,则其中最长的和最短的各一段,这两段绳的绳长之和是 厘米。
20.填上“>”、“<”或“=”.
88mm 8cm
21.右面的物体是由8个小正方体拼成的,如果把这个物体的表面涂上红色(含底面),那么4个面涂红色的小正方体有 个。
22.(如下图)5个棱长2分米的正方体硬纸箱堆放在墙角,体积一共是 立方分米,露在外面的硬纸面积是 平方分米。
23.一张长方形纸片的周长是32厘米,3张这样的长方形纸片恰好可以拼成一张大正方形纸片,这张大正方形纸片的周长是 厘米。
24.如图,三角形BEF的面积比三角形ADF的面积少12平方厘来,三角形ABD的面积与三角形CDE的面积比是3:5,则平行四边形ABCD的面积等于 平方厘米.
25.如图,在正方形中套一个长方形,如果正方形的边长是4厘米,而且其每条边都被长方形的顶点分成长、短两段,其中长的一段是短的一段的3倍,那么长方形的面积是平方厘米 米。
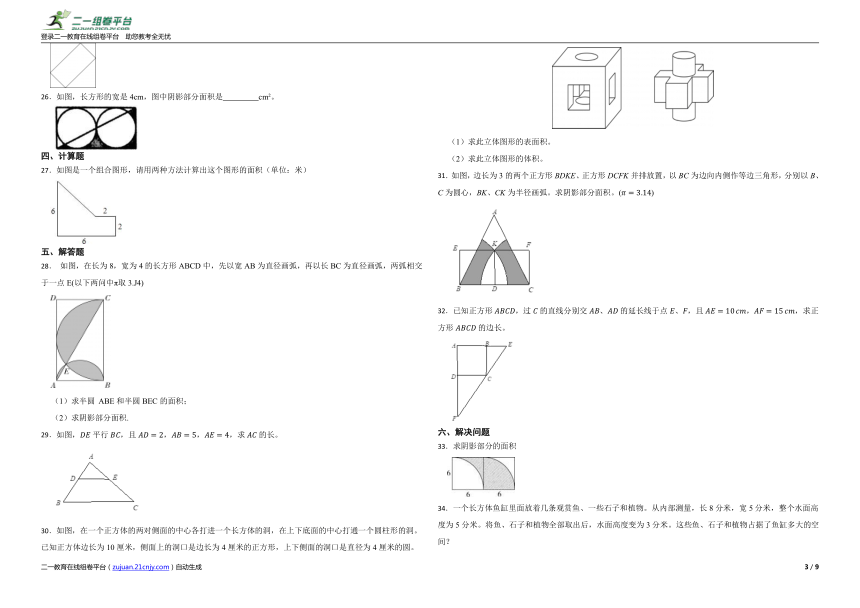
26.如图,长方形的宽是4cm,图中阴影部分面积是 cm2。
四、计算题
27.如图是一个组合图形,请用两种方法计算出这个图形的面积(单位:米)
五、解答题
28. 如图,在长为8,宽为4的长方形ABCD中,先以宽AB为直径画弧,再以长BC为直径画弧,两弧相交于一点E(以下两问中π取3.J4)
(1)求半圆 ABE和半圆BEC的面积;
(2)求阴影部分面积.
29.如图,平行,且,,,求的长。
30.如图,在一个正方体的两对侧面的中心各打进一个长方体的洞,在上下底面的中心打通一个圆柱形的洞。已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下侧面的洞口是直径为4厘米的圆。
(1)求此立体图形的表面积。
(2)求此立体图形的体积。
31.如图,边长为3的两个正方形BDKE、正方形DCFK并排放置,以BC为边向内侧作等边三角形,分别以B、C为圆心,BK、CK为半径画弧。求阴影部分面积。()
32.已知正方形,过的直线分别交、的延长线于点、,且,,求正方形的边长。
六、解决问题
33.求阴影部分的面积
34.一个长方体鱼缸里面放着几条观赏鱼、一些石子和植物。从内部测量,长8分米,宽5分米,整个水面高度为5分米。将鱼、石子和植物全部取出后,水面高度变为3分米。这些鱼、石子和植物占据了鱼缸多大的空间?
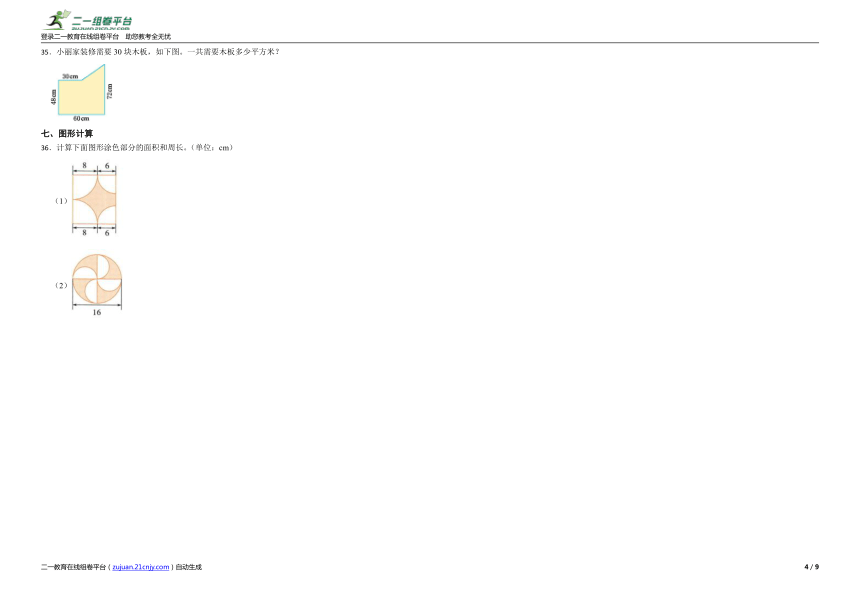
35.小丽家装修需要30块木板,如下图。一共需要木板多少平方米?
七、图形计算
36.计算下面图形涂色部分的面积和周长。(单位:cm)
(1)
(2)
答案解析部分
1.【答案】C
【解析】【解答】解:梨的体积等于下降了的水的体积,列式为10×8×1。
故答案为:C。
【分析】梨的体积=容器的长×容器的宽×水面下降的高度。
2.【答案】B
【解析】【解答】解:80×60-60×20÷2表示:左边长方形的面积-右边三角形的面积。
故答案为:B。
【分析】计算少先队中队旗的面积时,可以列式80×60-60×20÷2表示:左边长方形的面积-右边三角形的面积;其中,长方形的面积=长×宽,三角形的面积=底×高÷2。
3.【答案】B
【解析】【解答】解:把拳头完全放入一个装满水的脸盆里,溢出的水大约有200mL。
故答案为:B。
【分析】根据排水法求体积,溢出的水的体积也就是拳头的体积,结合生活实际选择合适的结果即可。
4.【答案】C
【解析】【解答】解:①和②占的格子数相同,是面积相等。
故答案为:C。
【分析】①占了2个整格和4个半格,也就是4个整格;②占了4个整格。所以它们的面积相等。
5.【答案】D
【解析】【解答】解:1×(8-5)
=1×3
=3(立方分米)。
故答案为:D。
【分析】小球的体积=正方体容器的底面积×(放入大、小球后的总高度-取出大球后的高度) 。
6.【答案】C
【解析】【解答】解:周长最大的是C项中的图形。
故答案为:C。
【分析】把正方形的每条边看成1,A项中图形的周长是8,B项中图形的周长是8,C项中图形的周长是12,所以周长最大的是C项中的图形。
7.【答案】B
【解析】【解答】解:如果去掉一个小正方体(如图),那么它的表面积和原来相比不变。
故答案为:B。
【分析】通过看图可知拿掉小正方体的位置原来有三个小正方体的面,而拿走该位置的小正方体后该位置还是有三个小正方体的面,因此表面积没有改变。
8.【答案】C
【解析】【解答】解:观察图形可得甲、乙两张图的周长一样长。
故答案为:C。
【分析】将图乙的折线进行平移即可得出与图甲一样的图形,进而即可比较出甲、乙两张图的周长。
9.【答案】C
【解析】【解答】解:图中的正方形被分成了甲、乙两部分,其周长相比,结果是相等。
故答案为:C。
【分析】观察图形可得甲的周长=正方形的2条边长+曲线长;乙的周长=正方形的2条边长+曲线长,据此即可得出答案。
10.【答案】D
【解析】【解答】A、B、C三个图形的面积相等,D的面积比另外三个图形的面积小。
故答案为:D。
【分析】A、B、C三个图形,经过平移、旋转后均可得到,D图形是 ,据此解答即可。
11.【答案】错误
【解析】【解答】解:把一个正方体橡皮泥捏成长方体,体积不变。
故答案为:错误。
【分析】把一个正方体橡皮泥捏成长方体,橡皮泥还是原来的,所以体积不变。
12.【答案】错误
【解析】【解答】 将一个圆柱形铁块熔铸成一个圆锥,形状变了,体积不变,原题说法错误。
故答案为:错误。
【分析】此题主要考查了体积的等积变形,在熔铸铁块或其他物体时,形状会发生变化,体积不变。
13.【答案】正确
【解析】【解答】2×2+1×1-(2+1)×2÷2=4+1-3=2(平方厘米),本题对.
故答案为:正确.
【分析】阴影面积=大正方形面积-小正方形面积-空白三角形面积,据此解答.
14.【答案】正确
【解析】【解答】 球从哪个方向看都一样,此题说法正确。
故答案为:正确。
【分析】此题主要考查了球的特征,球从哪个方向看都一样,据此判断。
15.【答案】正确
【解析】【解答】把一块正方体的橡皮泥捏成一个长方体后,它的形状改变了,但它所占的空间大小不变.正确
故答案为:正确
【分析】本题属于体积的等积变形问题,即物体的形状改变,但是体积不变。
16.【答案】正确
【解析】【解答】解:图中涂色的两个三角形面积都是等底等高的两个三角形面积减去两个三角形重叠部分的面积,两部分面积是相等的。
故答案为:正确
【分析】两个三角形的面积都可以看做是等底等高的两个三角形面积减去重叠部分的面积,等底等高的两个三角形面积相等,所以这两个涂色三角形的面积也相等。
17.【答案】5;5
【解析】【解答】解:有5个面露在外面,
1×1×5=1×5=5(平方厘米)
露在外面的面积是5平方厘米。
故答案为:5;5。
【分析】棱长×棱长=1个面的面积,1个面的面积×5=露在外面的面积。
18.【答案】780
【解析】【解答】解:(24+36)×8÷2+36×30÷2
=240+540
=780(平方厘米)。
故答案为:780。
【分析】这个组合图形的面积=上面梯形的面积+下面三角形的面积;其中,梯形的面积=(上底+下底) ×高÷2,三角形的面积=底×高÷2。
19.【答案】60
【解析】【解答】
解:长绳子长度为:80÷2=40(厘米)
短绳子的长度为:40÷2=20
两段绳子的长度和为:40+20=60(厘米)
故答案为:60
【分析】先算出长绳子的长度,再算出短绳子的长度,再求出和即可.
20.【答案】>
21.【答案】5
【解析】【解答】解:如图所示4个面涂红色的小正方体有5个。
故答案为:5。
【分析】4个面涂红色的小正方体在下面一层的标有1、2、3、4、5的5个小正方体。
22.【答案】40;40
【解析】【解答】解:体积:2×2×2×5=40(立方分米);露在外面的面积:2×2×(4+3+3)=4×10=40(平方分米)。
故答案为:40;40。
【分析】正方体体积=棱长×棱长×棱长,用一个硬纸箱的体积乘5即可求出总体积;露在外面的一共有(4+3+3)个面,用每个面的面积乘露在外面面的个数即可求出露在外面的总面积。
23.【答案】48
【解析】【解答】解:32÷2=16(厘米)
16÷4=4(厘米)
4×3=12(厘米)
12×4=48(厘米)
故答案为:48。
【分析】如图,用3张同样的长方形纸片拼成正方形只有一种拼法,即长=宽的3倍,所以长:宽=3:1;
长方形的周长÷2=长与宽的和,根据比的应用可知长与宽的和平均分成了3+1=4份,所以长与宽的和÷4=宽,宽×3=长,而拼成的正方形的边长就是原长方形的长,所以正方形的周长=边长×4=长×4,据此可以解答。
24.【答案】72
【解析】【解答】解:∵△CDE与△BCD的高相等
∴BC:CE=3:5
∴EB:BC=2:3
又∵BC=AD
∴EB:AD=2:3
∴S△BEF:S△ADF=4:9
∴S△BEF=12÷(9-4)×4=9.6(平方厘米)
∵EE:FD=2:3
∴S△BDF=9.6÷2×3=14.4(平方厘米)
∴S平行四边形ABCD=(9.6+12+14.4)×2=72(平方厘米)
故答案为:72。
【分析】在平行四边形ABCD中,三角形ABD与三角形BCD的面积相等。三角形CDE与三角形BCD的高相等,面积比等于底边长度比,那么BC:CE=3:5,EB:BC=2:3,而BC等于AD,那么EB:AD=2:3,三角形BEF与三角形ADF的面积比是4:9,S△BEF=12÷(9-4)×4=9.6(平方厘米),因为EE:FD=2:3,三角形BDF的面积:9.6÷2×3=14.4(平方厘米),故平行四边形ABCD的面积等于(9.6+12+14.4)×2=72(平方厘米)。
25.【答案】6
【解析】【解答】解:
由题意可得:BE=BF=CG=CH=AE=АB=×4=1(厘米)
AE=AH=DF=DG=АС=×4=3(厘米)
所以长方形EFGH的面积是:
4×4-1×1-3×3
=16-1-9
=6(平方厘米)
故答案为:6。
【分析】观察可知,长方形的面积=正方形面积-S-S-S-S,根据题干给出的条件长的一段是短的一段的3倍,易得出三角形的底和高,进而求得面积。
26.【答案】3.44
【解析】【解答】长方形的长是:4×2=8(cm);
三角形的面积:
8×4÷2
=32÷2
=16(cm2)
圆的面积:
3.14×(4÷2)2
=3.14×22
=3.14×4
=12.56(cm2)
阴影部分的面积:16-12.56=3.44(cm2)
故答案为:3.44 。
【分析】观察图可知,长方形的长是宽的2倍,先求出长方形的长,阴影部分的面积=三角形的面积-一个空白圆的面积,据此列式解答。
27.【答案】解:第一种:(2+6)×(6﹣2)÷2+2×2,
=8×4÷2+4,
=32÷2+4,
=20(平方米)
第二种:(6﹣2)×(6﹣2)÷2+6×2,
=4×4÷2+12,
=8+12,
=20(平方米);
答:这个图形的面积是20平方米
【解析】【分析】(1)如图所示,图形的面积=梯形的面积+正方形的面积,代入数据即可求解;
(2)如图所示,图形的面积=三角形的面积+长方形的面积,代入数据即可求解.
解答此题的关键是:将图形分割成容易求面积的图形.
28.【答案】(1)解:S半圆ABE=×π×42
=1.57×16
=25.12
S半圆BEC=×π×22
=1.57×4
=6.28
答:半圆ABE面积为25.12,半圆BEC面积为6.28。
(2)解:S=S半圆ABE+S半圆BEC-×4×8
=25.12+6.28-2×8
=18.84-16
=2.84
答:阴影部分面积为2.84。
【解析】【分析】(1)观察图形,半圆ABE半径为2,半圆BEC半径为4,根据半圆面积=πr2÷2,计算即可;
(2)观察图形,得到阴影部分面积=大半圆面积+小半圆面积-底4高8的三角形面积,根据(1)可得两个半圆的面积,再根据三角形面积公式:S=×底×高,求解即可。
29.【答案】解:由金字塔模型得 ,所以
【解析】【分析】在金字塔模型中,如果一个金字塔被平行于底面的平面分割,那么截面与底面的边长比等于相应高度的比。的比值,即。由于是的,可以通过的长度来计算的长度,进而得到的长度。
30.【答案】(1)解:10×10×6-4×4×4-π×22×2
=600-64-8π
=536-8π(平方厘米)
4×3×16+2×(4×4-π×22)+2π×2×3×2
=192+32-8π+24π
=224+16π(平方厘米)
224+16π+536-8π=
760+8π
=785.12(平方厘米)
答:立体图形的表面积为785.12平方厘米。
(2)解:4×4×3×4+4×4×4+π×22×3×2
=192+ 64+24π
= 256+24π(立方厘米)
10×10×10-(256+24π)
=1000-256-24π
=744-24π
=668.64(立方厘米)
答:立体图形的体积为668.64立方厘米。
【解析】【分析】(1)表面积可分为外侧表面积和内侧表面积。外侧为6个边长10厘米的正方形挖去4个边长4厘米的正方形及2个直径4厘米的圆,所以,外侧表面积为:10×10×6-4×4×4-π×22×2=536-8π(平方厘米);内侧表面积则为右上图所示的立体图形的表面积,需要注意的是这个图形的上下两个圆形底面和前后左右4个正方形面不能计算在内,所以内侧表面积为:4×3×16+2×(4×4-π×22)+2π×2×3×2=192+32-8π+24π=224+16π(平方厘米),所以,总表面积为:224+ 16π+536-8π=760+ 8=785.12(平方厘米);
(2)计算体积时将挖空部分的立体图形取出,如右上图,只要求出这个几何体的体积,用原立方体的体积减去这个体积即可。挖出的几何体体积为:4×4×3×4+4×4×4+π×22×3×2=192+ 64+24π= 256+24π(立方厘米);所求几何体体积为:10×10×10-(256+24π)=668.64(立方厘米)。
31.【答案】解:
如图将左边的阴影翻转右边阴影下部
答:阴影部分的面积为8.58。
【解析】【分析】根据题意可知扇形的半径 恰是正方形的对角线,所以 ,如右图将左边的阴影翻转右边阴影下部,再根据阴影部分的面积等于扇形面积加柳叶部分面积求解即可。
32.【答案】解:方法一:本题有两个金字塔模型,根据这两个模型有 , ,设正方形的边长为 ,所以有 ,即 ,解得 ,所以正方形的边长为 。
方法二:或根据一个金字塔列方程即 ,解得
【解析】【分析】首先识别出题目中的两个金字塔模型,并利用它们的性质来建立方程。使用两个比例关系,即BC:AF = CE:EF 和 DC:AE = CF:EF,将正方形的边长设为x,然后解出了x的值。在方法二中,你使用了一个金字塔的模型,直接建立了x与10和15的关系,解出了x的值。两种方法都得到了正方形边长为6cm的结果。
33.【答案】解:6×6=36
【解析】【分析】把左边正方形中的阴影部分移到右边正方形的空白部分,阴影部分的总面积就是一个正方形的面积,由此根据正方形面积公式计算即可.
34.【答案】80立方分米
35.【答案】解:
48×30+(48+72)×(60-30)÷2
=1440+120×30÷2
=1440+1800
=3240(平方米)
答:一共需要木板3240平方米。
【解析】【分析】可以把木板分成左边长方形和右边梯形,把长方形面积和梯形面积相加求出木板的总面积。
36.【答案】(1)涂色部分的面积:(8+6)×(8+8)-3.14×82÷2-3.14×62÷2=67(cm2)。
涂色部分的周长:(8+8)-(6+6)+3.14×6×2÷2+3.14×8×2÷2=47.96(cm)。
(2)涂色部分的面积:3.14×(16÷2)2-3.14×(16÷2÷2)×2=100.48(cm2)。
涂色部分的周长:3.14×16+3.14×(16÷2)×2+16×2=132.48(cm)。
【解析】【分析】(1)根据圆的周长结合题意即可求出涂色部分的周长,再根据题意用长方形的面积减去四个四分之一圆的面积即可求出涂色部分的面积;
(2)根据题意用大圆的周长减去四个小半圆的周长求出图色部分的面积,进而根据题意用大圆的周长加上四个小半圆的周长即可求出涂色部分的周长。
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
小升初奥数《几何》专项训练
一、单选题
1.求梨的体积,下面列式正确的是( )
A.10×8×5 B.10×8×(5-1)
C.10×8×1 D.10×5×1
2.笑笑在计算少先队中队旗的面积时,列出了算式“”,请你判断图( )可以表示笑笑的思路。
A. B.
C. D.
3.如果把你的拳头完全放入一个装满水的脸盆里,溢出的水大约有( )
A.2L B.200mL C.2mL
4.比一比下面两个图形的面积。结果是( )。
A.①>② B.①<② C.①=②
5.下图中,长方体容器的底面积是1dm2,两个球浸没时正好水面与容器口平,分别拿出两个球,水面变化如图,那么,小球体积是( )。
A.0.3dm3 B.0.5dm3 C.0.8dm3 D.3dm3
6.下面图形都是由3个相同的小正方形拼成的,其中周长最大的( )。
A.
B.
C.
7.用12个体积为1dm3的小正方体拼成一个长方体。如果去掉一个小正方体(如图),那么它的表面积和原来相比,( )。
A.大了 B.不变 C.小了 D.不确定
8.甲、乙两张图的周长( )
A.甲长 B.乙长 C.一样长
9.上图的正方形被分成了甲、乙两部分,其周长相比,结果是( )。
A.甲的周长 B.乙的周长长 C.相等
10.在下面四个图形中,哪个图形的涂色部分面积与其余三个不相等。( )
A. B.
C. D.
二、判断题
11.把一个正方体橡皮泥捏成长方体,体积变大了。( )
12.将一个圆柱形铁块熔铸成一个圆锥,它的体积变小了。( )
13.如下图,大正方形的边长是2厘米,小正方形的边长是1厘米,则阴影部分的面积是2平方厘米。(
)
14.球从哪个方向看都一样。( )
15.判断对错
把一块正方体的橡皮泥捏成一个长方体后,它的形状改变了,但它所占的空间大小不变.
16.图中涂色的两个三角形面积是一样大的。
三、填空题
17. 将两个棱长为1cm的小正方体叠放在墙角处,有 个面露在外面,露在外面的面积是
18.下面这个组合图形的面积是 cm2。
19.将一根长80厘米的草绳对折一次后,用剪刀在中点处剪开,则其中最长的和最短的各一段,这两段绳的绳长之和是 厘米。
20.填上“>”、“<”或“=”.
88mm 8cm
21.右面的物体是由8个小正方体拼成的,如果把这个物体的表面涂上红色(含底面),那么4个面涂红色的小正方体有 个。
22.(如下图)5个棱长2分米的正方体硬纸箱堆放在墙角,体积一共是 立方分米,露在外面的硬纸面积是 平方分米。
23.一张长方形纸片的周长是32厘米,3张这样的长方形纸片恰好可以拼成一张大正方形纸片,这张大正方形纸片的周长是 厘米。
24.如图,三角形BEF的面积比三角形ADF的面积少12平方厘来,三角形ABD的面积与三角形CDE的面积比是3:5,则平行四边形ABCD的面积等于 平方厘米.
25.如图,在正方形中套一个长方形,如果正方形的边长是4厘米,而且其每条边都被长方形的顶点分成长、短两段,其中长的一段是短的一段的3倍,那么长方形的面积是平方厘米 米。
26.如图,长方形的宽是4cm,图中阴影部分面积是 cm2。
四、计算题
27.如图是一个组合图形,请用两种方法计算出这个图形的面积(单位:米)
五、解答题
28. 如图,在长为8,宽为4的长方形ABCD中,先以宽AB为直径画弧,再以长BC为直径画弧,两弧相交于一点E(以下两问中π取3.J4)
(1)求半圆 ABE和半圆BEC的面积;
(2)求阴影部分面积.
29.如图,平行,且,,,求的长。
30.如图,在一个正方体的两对侧面的中心各打进一个长方体的洞,在上下底面的中心打通一个圆柱形的洞。已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下侧面的洞口是直径为4厘米的圆。
(1)求此立体图形的表面积。
(2)求此立体图形的体积。
31.如图,边长为3的两个正方形BDKE、正方形DCFK并排放置,以BC为边向内侧作等边三角形,分别以B、C为圆心,BK、CK为半径画弧。求阴影部分面积。()
32.已知正方形,过的直线分别交、的延长线于点、,且,,求正方形的边长。
六、解决问题
33.求阴影部分的面积
34.一个长方体鱼缸里面放着几条观赏鱼、一些石子和植物。从内部测量,长8分米,宽5分米,整个水面高度为5分米。将鱼、石子和植物全部取出后,水面高度变为3分米。这些鱼、石子和植物占据了鱼缸多大的空间?
35.小丽家装修需要30块木板,如下图。一共需要木板多少平方米?
七、图形计算
36.计算下面图形涂色部分的面积和周长。(单位:cm)
(1)
(2)
答案解析部分
1.【答案】C
【解析】【解答】解:梨的体积等于下降了的水的体积,列式为10×8×1。
故答案为:C。
【分析】梨的体积=容器的长×容器的宽×水面下降的高度。
2.【答案】B
【解析】【解答】解:80×60-60×20÷2表示:左边长方形的面积-右边三角形的面积。
故答案为:B。
【分析】计算少先队中队旗的面积时,可以列式80×60-60×20÷2表示:左边长方形的面积-右边三角形的面积;其中,长方形的面积=长×宽,三角形的面积=底×高÷2。
3.【答案】B
【解析】【解答】解:把拳头完全放入一个装满水的脸盆里,溢出的水大约有200mL。
故答案为:B。
【分析】根据排水法求体积,溢出的水的体积也就是拳头的体积,结合生活实际选择合适的结果即可。
4.【答案】C
【解析】【解答】解:①和②占的格子数相同,是面积相等。
故答案为:C。
【分析】①占了2个整格和4个半格,也就是4个整格;②占了4个整格。所以它们的面积相等。
5.【答案】D
【解析】【解答】解:1×(8-5)
=1×3
=3(立方分米)。
故答案为:D。
【分析】小球的体积=正方体容器的底面积×(放入大、小球后的总高度-取出大球后的高度) 。
6.【答案】C
【解析】【解答】解:周长最大的是C项中的图形。
故答案为:C。
【分析】把正方形的每条边看成1,A项中图形的周长是8,B项中图形的周长是8,C项中图形的周长是12,所以周长最大的是C项中的图形。
7.【答案】B
【解析】【解答】解:如果去掉一个小正方体(如图),那么它的表面积和原来相比不变。
故答案为:B。
【分析】通过看图可知拿掉小正方体的位置原来有三个小正方体的面,而拿走该位置的小正方体后该位置还是有三个小正方体的面,因此表面积没有改变。
8.【答案】C
【解析】【解答】解:观察图形可得甲、乙两张图的周长一样长。
故答案为:C。
【分析】将图乙的折线进行平移即可得出与图甲一样的图形,进而即可比较出甲、乙两张图的周长。
9.【答案】C
【解析】【解答】解:图中的正方形被分成了甲、乙两部分,其周长相比,结果是相等。
故答案为:C。
【分析】观察图形可得甲的周长=正方形的2条边长+曲线长;乙的周长=正方形的2条边长+曲线长,据此即可得出答案。
10.【答案】D
【解析】【解答】A、B、C三个图形的面积相等,D的面积比另外三个图形的面积小。
故答案为:D。
【分析】A、B、C三个图形,经过平移、旋转后均可得到,D图形是 ,据此解答即可。
11.【答案】错误
【解析】【解答】解:把一个正方体橡皮泥捏成长方体,体积不变。
故答案为:错误。
【分析】把一个正方体橡皮泥捏成长方体,橡皮泥还是原来的,所以体积不变。
12.【答案】错误
【解析】【解答】 将一个圆柱形铁块熔铸成一个圆锥,形状变了,体积不变,原题说法错误。
故答案为:错误。
【分析】此题主要考查了体积的等积变形,在熔铸铁块或其他物体时,形状会发生变化,体积不变。
13.【答案】正确
【解析】【解答】2×2+1×1-(2+1)×2÷2=4+1-3=2(平方厘米),本题对.
故答案为:正确.
【分析】阴影面积=大正方形面积-小正方形面积-空白三角形面积,据此解答.
14.【答案】正确
【解析】【解答】 球从哪个方向看都一样,此题说法正确。
故答案为:正确。
【分析】此题主要考查了球的特征,球从哪个方向看都一样,据此判断。
15.【答案】正确
【解析】【解答】把一块正方体的橡皮泥捏成一个长方体后,它的形状改变了,但它所占的空间大小不变.正确
故答案为:正确
【分析】本题属于体积的等积变形问题,即物体的形状改变,但是体积不变。
16.【答案】正确
【解析】【解答】解:图中涂色的两个三角形面积都是等底等高的两个三角形面积减去两个三角形重叠部分的面积,两部分面积是相等的。
故答案为:正确
【分析】两个三角形的面积都可以看做是等底等高的两个三角形面积减去重叠部分的面积,等底等高的两个三角形面积相等,所以这两个涂色三角形的面积也相等。
17.【答案】5;5
【解析】【解答】解:有5个面露在外面,
1×1×5=1×5=5(平方厘米)
露在外面的面积是5平方厘米。
故答案为:5;5。
【分析】棱长×棱长=1个面的面积,1个面的面积×5=露在外面的面积。
18.【答案】780
【解析】【解答】解:(24+36)×8÷2+36×30÷2
=240+540
=780(平方厘米)。
故答案为:780。
【分析】这个组合图形的面积=上面梯形的面积+下面三角形的面积;其中,梯形的面积=(上底+下底) ×高÷2,三角形的面积=底×高÷2。
19.【答案】60
【解析】【解答】
解:长绳子长度为:80÷2=40(厘米)
短绳子的长度为:40÷2=20
两段绳子的长度和为:40+20=60(厘米)
故答案为:60
【分析】先算出长绳子的长度,再算出短绳子的长度,再求出和即可.
20.【答案】>
21.【答案】5
【解析】【解答】解:如图所示4个面涂红色的小正方体有5个。
故答案为:5。
【分析】4个面涂红色的小正方体在下面一层的标有1、2、3、4、5的5个小正方体。
22.【答案】40;40
【解析】【解答】解:体积:2×2×2×5=40(立方分米);露在外面的面积:2×2×(4+3+3)=4×10=40(平方分米)。
故答案为:40;40。
【分析】正方体体积=棱长×棱长×棱长,用一个硬纸箱的体积乘5即可求出总体积;露在外面的一共有(4+3+3)个面,用每个面的面积乘露在外面面的个数即可求出露在外面的总面积。
23.【答案】48
【解析】【解答】解:32÷2=16(厘米)
16÷4=4(厘米)
4×3=12(厘米)
12×4=48(厘米)
故答案为:48。
【分析】如图,用3张同样的长方形纸片拼成正方形只有一种拼法,即长=宽的3倍,所以长:宽=3:1;
长方形的周长÷2=长与宽的和,根据比的应用可知长与宽的和平均分成了3+1=4份,所以长与宽的和÷4=宽,宽×3=长,而拼成的正方形的边长就是原长方形的长,所以正方形的周长=边长×4=长×4,据此可以解答。
24.【答案】72
【解析】【解答】解:∵△CDE与△BCD的高相等
∴BC:CE=3:5
∴EB:BC=2:3
又∵BC=AD
∴EB:AD=2:3
∴S△BEF:S△ADF=4:9
∴S△BEF=12÷(9-4)×4=9.6(平方厘米)
∵EE:FD=2:3
∴S△BDF=9.6÷2×3=14.4(平方厘米)
∴S平行四边形ABCD=(9.6+12+14.4)×2=72(平方厘米)
故答案为:72。
【分析】在平行四边形ABCD中,三角形ABD与三角形BCD的面积相等。三角形CDE与三角形BCD的高相等,面积比等于底边长度比,那么BC:CE=3:5,EB:BC=2:3,而BC等于AD,那么EB:AD=2:3,三角形BEF与三角形ADF的面积比是4:9,S△BEF=12÷(9-4)×4=9.6(平方厘米),因为EE:FD=2:3,三角形BDF的面积:9.6÷2×3=14.4(平方厘米),故平行四边形ABCD的面积等于(9.6+12+14.4)×2=72(平方厘米)。
25.【答案】6
【解析】【解答】解:
由题意可得:BE=BF=CG=CH=AE=АB=×4=1(厘米)
AE=AH=DF=DG=АС=×4=3(厘米)
所以长方形EFGH的面积是:
4×4-1×1-3×3
=16-1-9
=6(平方厘米)
故答案为:6。
【分析】观察可知,长方形的面积=正方形面积-S-S-S-S,根据题干给出的条件长的一段是短的一段的3倍,易得出三角形的底和高,进而求得面积。
26.【答案】3.44
【解析】【解答】长方形的长是:4×2=8(cm);
三角形的面积:
8×4÷2
=32÷2
=16(cm2)
圆的面积:
3.14×(4÷2)2
=3.14×22
=3.14×4
=12.56(cm2)
阴影部分的面积:16-12.56=3.44(cm2)
故答案为:3.44 。
【分析】观察图可知,长方形的长是宽的2倍,先求出长方形的长,阴影部分的面积=三角形的面积-一个空白圆的面积,据此列式解答。
27.【答案】解:第一种:(2+6)×(6﹣2)÷2+2×2,
=8×4÷2+4,
=32÷2+4,
=20(平方米)
第二种:(6﹣2)×(6﹣2)÷2+6×2,
=4×4÷2+12,
=8+12,
=20(平方米);
答:这个图形的面积是20平方米
【解析】【分析】(1)如图所示,图形的面积=梯形的面积+正方形的面积,代入数据即可求解;
(2)如图所示,图形的面积=三角形的面积+长方形的面积,代入数据即可求解.
解答此题的关键是:将图形分割成容易求面积的图形.
28.【答案】(1)解:S半圆ABE=×π×42
=1.57×16
=25.12
S半圆BEC=×π×22
=1.57×4
=6.28
答:半圆ABE面积为25.12,半圆BEC面积为6.28。
(2)解:S=S半圆ABE+S半圆BEC-×4×8
=25.12+6.28-2×8
=18.84-16
=2.84
答:阴影部分面积为2.84。
【解析】【分析】(1)观察图形,半圆ABE半径为2,半圆BEC半径为4,根据半圆面积=πr2÷2,计算即可;
(2)观察图形,得到阴影部分面积=大半圆面积+小半圆面积-底4高8的三角形面积,根据(1)可得两个半圆的面积,再根据三角形面积公式:S=×底×高,求解即可。
29.【答案】解:由金字塔模型得 ,所以
【解析】【分析】在金字塔模型中,如果一个金字塔被平行于底面的平面分割,那么截面与底面的边长比等于相应高度的比。的比值,即。由于是的,可以通过的长度来计算的长度,进而得到的长度。
30.【答案】(1)解:10×10×6-4×4×4-π×22×2
=600-64-8π
=536-8π(平方厘米)
4×3×16+2×(4×4-π×22)+2π×2×3×2
=192+32-8π+24π
=224+16π(平方厘米)
224+16π+536-8π=
760+8π
=785.12(平方厘米)
答:立体图形的表面积为785.12平方厘米。
(2)解:4×4×3×4+4×4×4+π×22×3×2
=192+ 64+24π
= 256+24π(立方厘米)
10×10×10-(256+24π)
=1000-256-24π
=744-24π
=668.64(立方厘米)
答:立体图形的体积为668.64立方厘米。
【解析】【分析】(1)表面积可分为外侧表面积和内侧表面积。外侧为6个边长10厘米的正方形挖去4个边长4厘米的正方形及2个直径4厘米的圆,所以,外侧表面积为:10×10×6-4×4×4-π×22×2=536-8π(平方厘米);内侧表面积则为右上图所示的立体图形的表面积,需要注意的是这个图形的上下两个圆形底面和前后左右4个正方形面不能计算在内,所以内侧表面积为:4×3×16+2×(4×4-π×22)+2π×2×3×2=192+32-8π+24π=224+16π(平方厘米),所以,总表面积为:224+ 16π+536-8π=760+ 8=785.12(平方厘米);
(2)计算体积时将挖空部分的立体图形取出,如右上图,只要求出这个几何体的体积,用原立方体的体积减去这个体积即可。挖出的几何体体积为:4×4×3×4+4×4×4+π×22×3×2=192+ 64+24π= 256+24π(立方厘米);所求几何体体积为:10×10×10-(256+24π)=668.64(立方厘米)。
31.【答案】解:
如图将左边的阴影翻转右边阴影下部
答:阴影部分的面积为8.58。
【解析】【分析】根据题意可知扇形的半径 恰是正方形的对角线,所以 ,如右图将左边的阴影翻转右边阴影下部,再根据阴影部分的面积等于扇形面积加柳叶部分面积求解即可。
32.【答案】解:方法一:本题有两个金字塔模型,根据这两个模型有 , ,设正方形的边长为 ,所以有 ,即 ,解得 ,所以正方形的边长为 。
方法二:或根据一个金字塔列方程即 ,解得
【解析】【分析】首先识别出题目中的两个金字塔模型,并利用它们的性质来建立方程。使用两个比例关系,即BC:AF = CE:EF 和 DC:AE = CF:EF,将正方形的边长设为x,然后解出了x的值。在方法二中,你使用了一个金字塔的模型,直接建立了x与10和15的关系,解出了x的值。两种方法都得到了正方形边长为6cm的结果。
33.【答案】解:6×6=36
【解析】【分析】把左边正方形中的阴影部分移到右边正方形的空白部分,阴影部分的总面积就是一个正方形的面积,由此根据正方形面积公式计算即可.
34.【答案】80立方分米
35.【答案】解:
48×30+(48+72)×(60-30)÷2
=1440+120×30÷2
=1440+1800
=3240(平方米)
答:一共需要木板3240平方米。
【解析】【分析】可以把木板分成左边长方形和右边梯形,把长方形面积和梯形面积相加求出木板的总面积。
36.【答案】(1)涂色部分的面积:(8+6)×(8+8)-3.14×82÷2-3.14×62÷2=67(cm2)。
涂色部分的周长:(8+8)-(6+6)+3.14×6×2÷2+3.14×8×2÷2=47.96(cm)。
(2)涂色部分的面积:3.14×(16÷2)2-3.14×(16÷2÷2)×2=100.48(cm2)。
涂色部分的周长:3.14×16+3.14×(16÷2)×2+16×2=132.48(cm)。
【解析】【分析】(1)根据圆的周长结合题意即可求出涂色部分的周长,再根据题意用长方形的面积减去四个四分之一圆的面积即可求出涂色部分的面积;
(2)根据题意用大圆的周长减去四个小半圆的周长求出图色部分的面积,进而根据题意用大圆的周长加上四个小半圆的周长即可求出涂色部分的周长。
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
同课章节目录
