海南省部分学校2025年九年级下学期中考模拟考试数学试卷(含详解)
文档属性
| 名称 | 海南省部分学校2025年九年级下学期中考模拟考试数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 950.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 22:48:09 | ||
图片预览




文档简介
2025年海南省部分学校中考模拟考试数学科试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如果零上2℃记作,那么零下3℃记作( )
A.2℃ B.5℃ C. D.
2.下列计算正确的是( )
A. B.
C. D.
3.我国南海探明可燃冰储量约19400000000立方米,19400000000用科学记数法表示为( )
A. B. C. D.
4.一个由长方体截去一部分后得到的几何体如图水平放置,其俯视图是( )
A. B.
C. D.
5.计算的结果是( )
A.1 B. C. D.
6.已知点在双曲线上,则a的值是( )
A.2 B. C.1 D.
7.如果一个三角形的两边长分别为3和7,则第三边长可能是( ).
A.3 B.4 C.7 D.10
8.不透明袋子中装有个球,其中有个绿球、个白球,这些球除颜色外无其他差别,从袋子中随机取出个球,则它是绿球的概率是( )
A. B. C. D.
9.如图,,其中,则的度数为( )
A. B. C. D.
10.如图,在中,,点E,F,G分别在边,,上,,,则四边形的周长是( )
A.32 B.24 C.16 D.8
11.如图,菱形的边长为10,,则点到的距离等于( )
A.5 B.6 C.8 D.1
12.如图,是的直径,C,D为上两点,且平分.若,则的大小为( )
A. B. C. D.
二、填空题
13.分解因式:3a2﹣6a+3= .
14.若式子在实数范围内有意义,则x的取值范围是 .
15.如图,在中,,,,,E是边上一点,将沿所在直线翻折得到,交于F.当时, ,的长为 .
三、解答题
16.(1)计算:;
(2)先化简,再求值:,其中.
17.如图,点O是对角线的交点,过点O的直线分别交,于点E,F.
(1)求证:;
(2)当时,,分别连接,,求此时四边形的周长.
18.海南某芒果种植基地为推进智慧农业,采用A、B两款无人机协同喷洒生态农药.已知A型无人机每小时可喷洒12公顷,但电池续航为5小时;B型无人机每小时喷洒10公顷,续航可达6小时.某日,A、B两型无人机共同完成一片芒果园的喷洒任务,总作业面积360公顷,且所有无人机累计飞行35小时.问:A、B两款无人机各出动多少架?
19.2024年1月11日,全球运力最大固体运载火箭“引力一号”遥一商业运载火箭在我国山东海阳附近海域成功发射,将搭载的云遥一号18-20星3颗卫星顺利送入预定轨道,飞行试验任务获得圆满成功.某校为增强学生对航天知识的了解,组织七、八年级学生进行了航天知识的学习并进行了测试,随机从两个年级各随机抽取了50名学生的成绩,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图;
b.七年级成绩在这一组的是:70,72,74,75,76,76,77,77,77,78,79;
c.七、八年级成绩的平均数、中位数如下:
年级 平均数 中位数
七
八
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有________人;
(2)求出表中的值;
(3)在这次测试中,七年级子骁同学与八年级子栋同学的成绩都是78分,请判断两位同学在各自年级的排名谁更靠前,并说明理由;
(4)若该校七年级学生有600人,假设全部参加此次测试,请估计七年级成绩超过平均数分的人数.
20.根据以下素材,完成任务.
探究淋浴喷头的位置
素材1 图1是一种淋浴喷头,淋浴喷头固定器装在升降杆上的某处,手柄与固定器的连接处记为点A(点A与墙之间的距离忽略不计).图2视作淋浴喷头喷水后的截面示意图,线段为手柄,射线为水流,与的夹角为,手柄与墙的夹角为淋浴喷头的“调整角”,记为.已知长为.
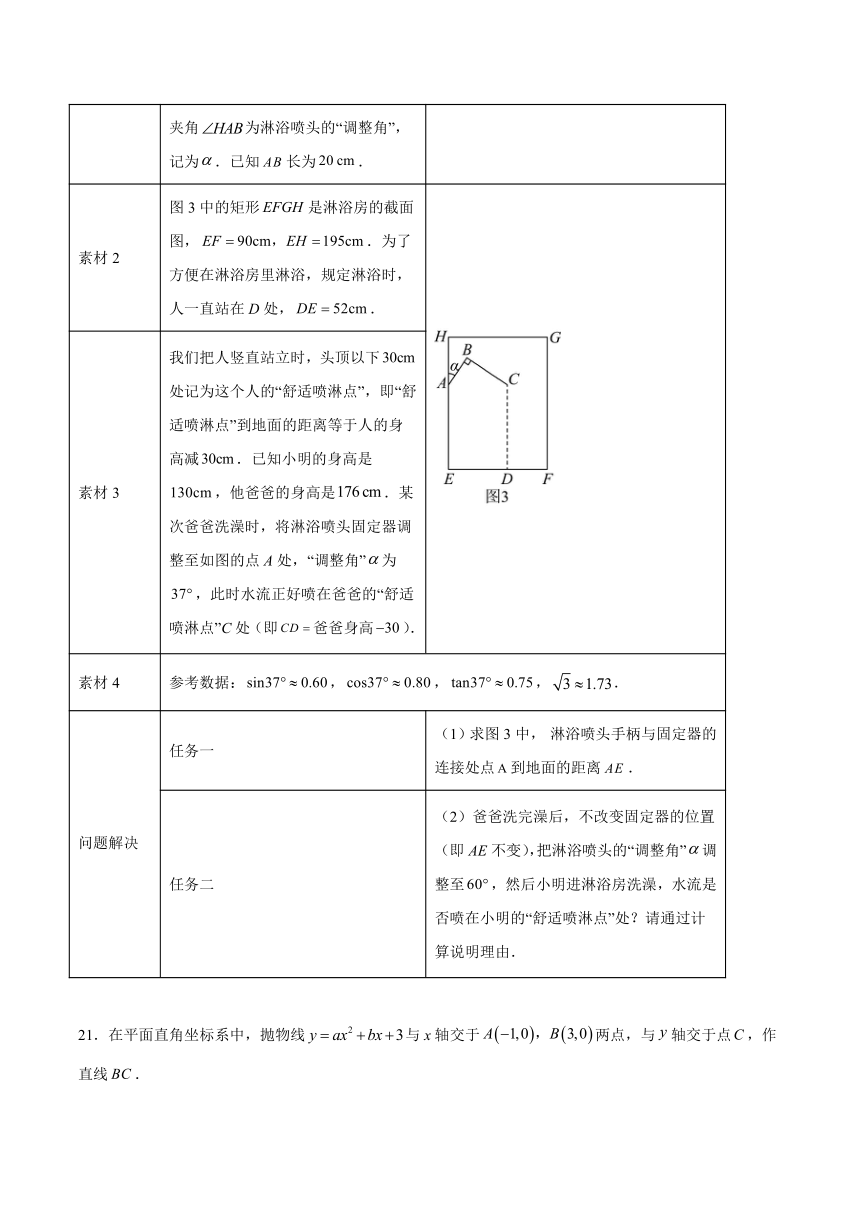
素材2 图3中的矩形是淋浴房的截面图,.为了方便在淋浴房里淋浴,规定淋浴时,人一直站在D处,.
素材3 我们把人竖直站立时,头顶以下处记为这个人的“舒适喷淋点”,即“舒适喷淋点”到地面的距离等于人的身高减.已知小明的身高是,他爸爸的身高是.某次爸爸洗澡时,将淋浴喷头固定器调整至如图的点A处,“调整角”为,此时水流正好喷在爸爸的“舒适喷淋点”C处(即爸爸身高).
素材4 参考数据:,,,.
问题解决 任务一 (1)求图3中, 淋浴喷头手柄与固定器的连接处点到地面的距离.
任务二 (2)爸爸洗完澡后,不改变固定器的位置(即AE不变),把淋浴喷头的“调整角”调整至,然后小明进淋浴房洗澡,水流是否喷在小明的“舒适喷淋点”处?请通过计算说明理由.
21.在平面直角坐标系中,抛物线与x轴交于两点,与轴交于点,作直线.
(1)求抛物线的解析式.
(2)如图1,点是线段上方的抛物线上一动点,过点作,垂足为,请问线段是否存在最大值?若存在,请求出最大值及此时点的坐标;若不存在请说明理由.
(3)如图2,点是直线上一动点,过点作线段(点在直线下方),设点的横坐标为.若,且线段与抛物线有交点,求的取值范围.
22.如图,矩形中,,,点E是边上一动点(不与B、C重合),过点C作交于点G,过点A作的垂线交的延长线于点F,连接.
(1)求证:四边形是平行四边形;
(2)当的长为何值时,四边形是菱形?
(3)当E运动到的中点时,求的长.
《2025年海南省部分学校中考模拟考试数学科试题》参考答案
1.C
解:如果零上2℃记作,那么零下3℃记作,
故选:C.
2.C
解:.,原计算错误,故该选项不符合题意;
.,原计算错误,故该选项不符合题意;
.,原计算正确,故该选项符合题意;
.,原计算错误,故该选项不符合题意;
故选:C.
3.D
解:19400000000;
故选D.
4.A
解:该几何体的俯视图为:
,
故选:A
5.A
解:.
故选:A.
6.A
解:依题意,,
解得:,
故选:A.
7.C
解:设第三边长为x,则4故选:C.
8.D
解:不透明袋子中装有个球,其中有个绿球、个白球,这些球除颜色外无其他差别,
从袋子中随机取出个球,则它是绿球的概率是.
故选:D.
9.B
解:如图:
,
,
,
互为对顶角;
,
故选:B.
10.C
解∶∵,,
∴四边形AEFG是平行四边形,
∴FG=AE,AG=EF,
∵,
∴∠BFE=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠BFE,
∴BE=EF,
∴四边形的周长是2(AE+EF)=2(AE+BE)=2AB=2×8=16.
故选:C
11.A
解:连接交于点,
四边形是菱形,,
,,
,
在中,
,,
,
点A到的距离等于5.
故选:A.
12.A
解:∵,
∴,
∵为的直径,
∴,
∴,
∴,
∵平分,
∴,
∴,
故选:A.
13.3(a﹣1)2.
解:原式=3(a2﹣2a+1)=3(a﹣1)2.
故答案为:3(a﹣1)2.
14.
解:式子在实数范围内有意义,
.
.
故答案为:.
15. 2
解:如图,作于,于,
,,
,
,
,
,
将沿所在直线翻折得到,且,
,,
,
,
.
故答案为:,2.
16.(1);(2),
解:(1)
;
(2)
.
当时,原式.
17.(1)见解析
(2)
(1)∵四边形是平行四边形,
∴,
∴,
∵点O是对角线的交点,
∴,
在△和中,,
∴.
(2)由(1)知,,
∴,
∵,
∴四边形是平行四边形,
∵,
∴是菱形,
∴,
∴,
∴四边形的周长为.
18.型无人机出动架,型无人机出动架
解:设型无人机出动架,型无人机出动架,
由题意可得:,
解得:,
∴型无人机出动架,型无人机出动架.
19.(1)23
(2)
(3)七年级子骁同学在其年级的排名更靠前,理由见解析
(4)估计七年级成绩超过平均数分的有336人
(1)解:成绩在的人数为(人),
故答案为:23;
(2)解:第25,26名学生的成绩分别为77,78,
所以;
(3)解:七年级子骁同学在其年级的排名更靠前,理由如下:
因为七年级子骁同学的成绩大于其中位数分,而八年级子栋同学的成绩小于其中位数分,所以七年级子骁同学在其年级的排名更靠前;
(4)解:(人).
答:估计七年级成绩超过平均数分的有336人.
20.(1);(2)无法喷在小明的“舒适喷淋点”处,理由见解析
解:(1)作于点N,延长交于点M,则,
∵爸爸身高是,此时水流正好喷在爸爸的“舒适喷淋点”C处,
∴,
∵
∴,
∵,
∴,
∴,
∴,
∴,
∴.
答:点A到地面的距离约为;
(2)当时,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∵小明的身高是,
∴小明的舒适距离,
∵,
∴水流无法喷在小明的“舒适喷淋点”处.
21.(1)
(2)线段存在最大值,最大值为,此时点的坐标为,理由见详解
(3)或
(1)解:将代入得,
,
解得,
∴抛物线的解析式为;
(2)解:线段存在最大值,最大值为,此时点的坐标为,理由如下:
如果过点作直线,那么当直线与抛物线相切时,的值最大,
假设直线的解析式为,将代入解析式得,
解得
∴直线的解析式为,
∴直线的,
假设直线的解析式为,
联立得
,
∴,
解得,
∴直线的解析式为,
∴,
解得,
∴,
此时点的坐标为,
直线可以看作直线向上平移了个单位长度得到的,
如果过点作轴的平行线,交直线于一点,此时该点与两点够成了等腰直角三角形,
根据勾股定理得,
解得;
(3)解:假设,
∴,
解得或,
结合二次函数和一次函数图象得,
的取值范围为或.
22.(1)见解析
(2)当时,四边形是菱形
(3)
(1)证明:∵四边形是矩形,
∴,
∵,
∴四边形是平行四边形;
(2)解:∵四边形是平行四边形,
∴当时,四边形是菱形,
设,则,
∵,
∴,
∴,
∴当时,四边形是菱形;
(3)解:∵四边形是矩形,
∴,
∵为的中点,
∴,
∴,
由(1)知,
∴,
∴,
∵,
∴,
又,
∴,
又∵,
∴,
∴,
∴,
∴,
∴.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如果零上2℃记作,那么零下3℃记作( )
A.2℃ B.5℃ C. D.
2.下列计算正确的是( )
A. B.
C. D.
3.我国南海探明可燃冰储量约19400000000立方米,19400000000用科学记数法表示为( )
A. B. C. D.
4.一个由长方体截去一部分后得到的几何体如图水平放置,其俯视图是( )
A. B.
C. D.
5.计算的结果是( )
A.1 B. C. D.
6.已知点在双曲线上,则a的值是( )
A.2 B. C.1 D.
7.如果一个三角形的两边长分别为3和7,则第三边长可能是( ).
A.3 B.4 C.7 D.10
8.不透明袋子中装有个球,其中有个绿球、个白球,这些球除颜色外无其他差别,从袋子中随机取出个球,则它是绿球的概率是( )
A. B. C. D.
9.如图,,其中,则的度数为( )
A. B. C. D.
10.如图,在中,,点E,F,G分别在边,,上,,,则四边形的周长是( )
A.32 B.24 C.16 D.8
11.如图,菱形的边长为10,,则点到的距离等于( )
A.5 B.6 C.8 D.1
12.如图,是的直径,C,D为上两点,且平分.若,则的大小为( )
A. B. C. D.
二、填空题
13.分解因式:3a2﹣6a+3= .
14.若式子在实数范围内有意义,则x的取值范围是 .
15.如图,在中,,,,,E是边上一点,将沿所在直线翻折得到,交于F.当时, ,的长为 .
三、解答题
16.(1)计算:;
(2)先化简,再求值:,其中.
17.如图,点O是对角线的交点,过点O的直线分别交,于点E,F.
(1)求证:;
(2)当时,,分别连接,,求此时四边形的周长.
18.海南某芒果种植基地为推进智慧农业,采用A、B两款无人机协同喷洒生态农药.已知A型无人机每小时可喷洒12公顷,但电池续航为5小时;B型无人机每小时喷洒10公顷,续航可达6小时.某日,A、B两型无人机共同完成一片芒果园的喷洒任务,总作业面积360公顷,且所有无人机累计飞行35小时.问:A、B两款无人机各出动多少架?
19.2024年1月11日,全球运力最大固体运载火箭“引力一号”遥一商业运载火箭在我国山东海阳附近海域成功发射,将搭载的云遥一号18-20星3颗卫星顺利送入预定轨道,飞行试验任务获得圆满成功.某校为增强学生对航天知识的了解,组织七、八年级学生进行了航天知识的学习并进行了测试,随机从两个年级各随机抽取了50名学生的成绩,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图;
b.七年级成绩在这一组的是:70,72,74,75,76,76,77,77,77,78,79;
c.七、八年级成绩的平均数、中位数如下:
年级 平均数 中位数
七
八
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有________人;
(2)求出表中的值;
(3)在这次测试中,七年级子骁同学与八年级子栋同学的成绩都是78分,请判断两位同学在各自年级的排名谁更靠前,并说明理由;
(4)若该校七年级学生有600人,假设全部参加此次测试,请估计七年级成绩超过平均数分的人数.
20.根据以下素材,完成任务.
探究淋浴喷头的位置
素材1 图1是一种淋浴喷头,淋浴喷头固定器装在升降杆上的某处,手柄与固定器的连接处记为点A(点A与墙之间的距离忽略不计).图2视作淋浴喷头喷水后的截面示意图,线段为手柄,射线为水流,与的夹角为,手柄与墙的夹角为淋浴喷头的“调整角”,记为.已知长为.
素材2 图3中的矩形是淋浴房的截面图,.为了方便在淋浴房里淋浴,规定淋浴时,人一直站在D处,.
素材3 我们把人竖直站立时,头顶以下处记为这个人的“舒适喷淋点”,即“舒适喷淋点”到地面的距离等于人的身高减.已知小明的身高是,他爸爸的身高是.某次爸爸洗澡时,将淋浴喷头固定器调整至如图的点A处,“调整角”为,此时水流正好喷在爸爸的“舒适喷淋点”C处(即爸爸身高).
素材4 参考数据:,,,.
问题解决 任务一 (1)求图3中, 淋浴喷头手柄与固定器的连接处点到地面的距离.
任务二 (2)爸爸洗完澡后,不改变固定器的位置(即AE不变),把淋浴喷头的“调整角”调整至,然后小明进淋浴房洗澡,水流是否喷在小明的“舒适喷淋点”处?请通过计算说明理由.
21.在平面直角坐标系中,抛物线与x轴交于两点,与轴交于点,作直线.
(1)求抛物线的解析式.
(2)如图1,点是线段上方的抛物线上一动点,过点作,垂足为,请问线段是否存在最大值?若存在,请求出最大值及此时点的坐标;若不存在请说明理由.
(3)如图2,点是直线上一动点,过点作线段(点在直线下方),设点的横坐标为.若,且线段与抛物线有交点,求的取值范围.
22.如图,矩形中,,,点E是边上一动点(不与B、C重合),过点C作交于点G,过点A作的垂线交的延长线于点F,连接.
(1)求证:四边形是平行四边形;
(2)当的长为何值时,四边形是菱形?
(3)当E运动到的中点时,求的长.
《2025年海南省部分学校中考模拟考试数学科试题》参考答案
1.C
解:如果零上2℃记作,那么零下3℃记作,
故选:C.
2.C
解:.,原计算错误,故该选项不符合题意;
.,原计算错误,故该选项不符合题意;
.,原计算正确,故该选项符合题意;
.,原计算错误,故该选项不符合题意;
故选:C.
3.D
解:19400000000;
故选D.
4.A
解:该几何体的俯视图为:
,
故选:A
5.A
解:.
故选:A.
6.A
解:依题意,,
解得:,
故选:A.
7.C
解:设第三边长为x,则4
8.D
解:不透明袋子中装有个球,其中有个绿球、个白球,这些球除颜色外无其他差别,
从袋子中随机取出个球,则它是绿球的概率是.
故选:D.
9.B
解:如图:
,
,
,
互为对顶角;
,
故选:B.
10.C
解∶∵,,
∴四边形AEFG是平行四边形,
∴FG=AE,AG=EF,
∵,
∴∠BFE=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠BFE,
∴BE=EF,
∴四边形的周长是2(AE+EF)=2(AE+BE)=2AB=2×8=16.
故选:C
11.A
解:连接交于点,
四边形是菱形,,
,,
,
在中,
,,
,
点A到的距离等于5.
故选:A.
12.A
解:∵,
∴,
∵为的直径,
∴,
∴,
∴,
∵平分,
∴,
∴,
故选:A.
13.3(a﹣1)2.
解:原式=3(a2﹣2a+1)=3(a﹣1)2.
故答案为:3(a﹣1)2.
14.
解:式子在实数范围内有意义,
.
.
故答案为:.
15. 2
解:如图,作于,于,
,,
,
,
,
,
将沿所在直线翻折得到,且,
,,
,
,
.
故答案为:,2.
16.(1);(2),
解:(1)
;
(2)
.
当时,原式.
17.(1)见解析
(2)
(1)∵四边形是平行四边形,
∴,
∴,
∵点O是对角线的交点,
∴,
在△和中,,
∴.
(2)由(1)知,,
∴,
∵,
∴四边形是平行四边形,
∵,
∴是菱形,
∴,
∴,
∴四边形的周长为.
18.型无人机出动架,型无人机出动架
解:设型无人机出动架,型无人机出动架,
由题意可得:,
解得:,
∴型无人机出动架,型无人机出动架.
19.(1)23
(2)
(3)七年级子骁同学在其年级的排名更靠前,理由见解析
(4)估计七年级成绩超过平均数分的有336人
(1)解:成绩在的人数为(人),
故答案为:23;
(2)解:第25,26名学生的成绩分别为77,78,
所以;
(3)解:七年级子骁同学在其年级的排名更靠前,理由如下:
因为七年级子骁同学的成绩大于其中位数分,而八年级子栋同学的成绩小于其中位数分,所以七年级子骁同学在其年级的排名更靠前;
(4)解:(人).
答:估计七年级成绩超过平均数分的有336人.
20.(1);(2)无法喷在小明的“舒适喷淋点”处,理由见解析
解:(1)作于点N,延长交于点M,则,
∵爸爸身高是,此时水流正好喷在爸爸的“舒适喷淋点”C处,
∴,
∵
∴,
∵,
∴,
∴,
∴,
∴,
∴.
答:点A到地面的距离约为;
(2)当时,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∵小明的身高是,
∴小明的舒适距离,
∵,
∴水流无法喷在小明的“舒适喷淋点”处.
21.(1)
(2)线段存在最大值,最大值为,此时点的坐标为,理由见详解
(3)或
(1)解:将代入得,
,
解得,
∴抛物线的解析式为;
(2)解:线段存在最大值,最大值为,此时点的坐标为,理由如下:
如果过点作直线,那么当直线与抛物线相切时,的值最大,
假设直线的解析式为,将代入解析式得,
解得
∴直线的解析式为,
∴直线的,
假设直线的解析式为,
联立得
,
∴,
解得,
∴直线的解析式为,
∴,
解得,
∴,
此时点的坐标为,
直线可以看作直线向上平移了个单位长度得到的,
如果过点作轴的平行线,交直线于一点,此时该点与两点够成了等腰直角三角形,
根据勾股定理得,
解得;
(3)解:假设,
∴,
解得或,
结合二次函数和一次函数图象得,
的取值范围为或.
22.(1)见解析
(2)当时,四边形是菱形
(3)
(1)证明:∵四边形是矩形,
∴,
∵,
∴四边形是平行四边形;
(2)解:∵四边形是平行四边形,
∴当时,四边形是菱形,
设,则,
∵,
∴,
∴,
∴当时,四边形是菱形;
(3)解:∵四边形是矩形,
∴,
∵为的中点,
∴,
∴,
由(1)知,
∴,
∴,
∵,
∴,
又,
∴,
又∵,
∴,
∴,
∴,
∴,
∴.
同课章节目录
