河南省平顶山市鲁山县五所学校2025年九年级下学期中考二模数学试卷(含图片答案)
文档属性
| 名称 | 河南省平顶山市鲁山县五所学校2025年九年级下学期中考二模数学试卷(含图片答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 22:59:20 | ||
图片预览



文档简介
2025年河南省鲁山县五所学校中考二模数学试卷
【本卷满分:120分 考试时间:100分钟】
一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的)
1.(2024·扬州)实数2 的倒数是 ( )
A. -2 B.2 D.
2.(2024·陕西)如图,将半圆绕直径所在的虚线旋转一周,得到的立体图形是 ( )
3.(2024·福建)据《人民日报》3 月12 日电,世界知识产权组织近日公布数据显示,2023年,全球PCT(《专利合作条约》)国际专利申请总量为27.26万件,中国申请量为69610件,是申请量最大的来源国.数据69 610 用科学记数法可表示为 ( )
A.6961×10
D.0.6961×10
4.(2024·湖北) 的值是 ( )
A.5x B.5x C.6x D.6x
5.(2024·北京)如图,直线AB 和 CD 相交于点 O,OE⊥OC.若∠AOC=58°,则∠EOB 的大小为
( )
A.29° B.32° C.45° D.58°
6.(2024·江西)如图是某地去年一至六月每月空气质量为优的天数的折线统计图,关于各月空气质量为优的天数,下列结论错误的是 ( )
A.五月份空气质量为优的有16天
B.这组数据的众数是15天
C.这组数据的中位数是15天
D.这组数据的平均数是15天
7.(2024·北京)若关于x的一元二次方程 c=0有两个相等的实数根,则实数c的值为( )
A. -16 B. - 4 C.4 D.16
8.(2024·湖北)《九章算术》中记载这样一个题:牛5头和羊2只共值10金,牛2头和羊5只共值8金,牛和羊各值多少金 设每头牛值x金,每只羊值y金,可列方程组为 ( )
9.(2024·湖北)抛物线 的顶点为(--1,-2),抛物线与y轴的交点位于x轴上方.以下结论正确的是 ( )
A. a<0 B. c<0
C. a-b+c= -2
10.(2024·威海)同一条公路连接A,B,C三地,B地在A,C两地之间.甲、乙两车分别从 A地、B 地同时出发前往 C 地.甲车速度始终保持不变,乙车中途休息一段时间,继续行驶.下图表示甲、乙两车之间的距离y(km)与时间x(h)的函数关系.下列结论正确的是 ( )
A.甲车行驶 h与乙车相遇
B. A,C两地相距220 km
C.甲车的速度是70 km/h
D.乙车中途休息36分钟
二、填空题(每小题3分,共15分)
11.(2024·阜新)函数 中,自变量x的取值范围是 .
12.(2024·山东)写出满足不等式组 的一个整数解: .
13.(2024·湖北)如图,在平面直角坐标系xOy中,点A 的坐标为(-4,6),将线段 OA 绕点 O顺时针旋转90°,则点 A 的对应点 A'的坐标为
14.(2024·威海)如图,在扇形AOB 中,∠AOB =90°,C是AO的中点,过点 C作 CE⊥AO 交 于点E,过点 E作ED⊥OB,垂足为 D.在扇形内随机选取一点 P,则点 P 落在阴影部分的概率是 .
15.(2024·重庆 A卷)如图,以AB 为直径的⊙O与AC 相切于点 A,以AC 为边作平行四边形ACDE,点D,E均在⊙O 上,DE与AB 交于点 F,连接CE,与⊙O 交于点 G,连接DG.若AB=10,DE=8,则AF= ,DG= .
三、解答题(本大题共8个小题,共75分)
16.(2024·重庆 A 卷)(10分)计算:
(1)x(x-2y)+(x+y) ;
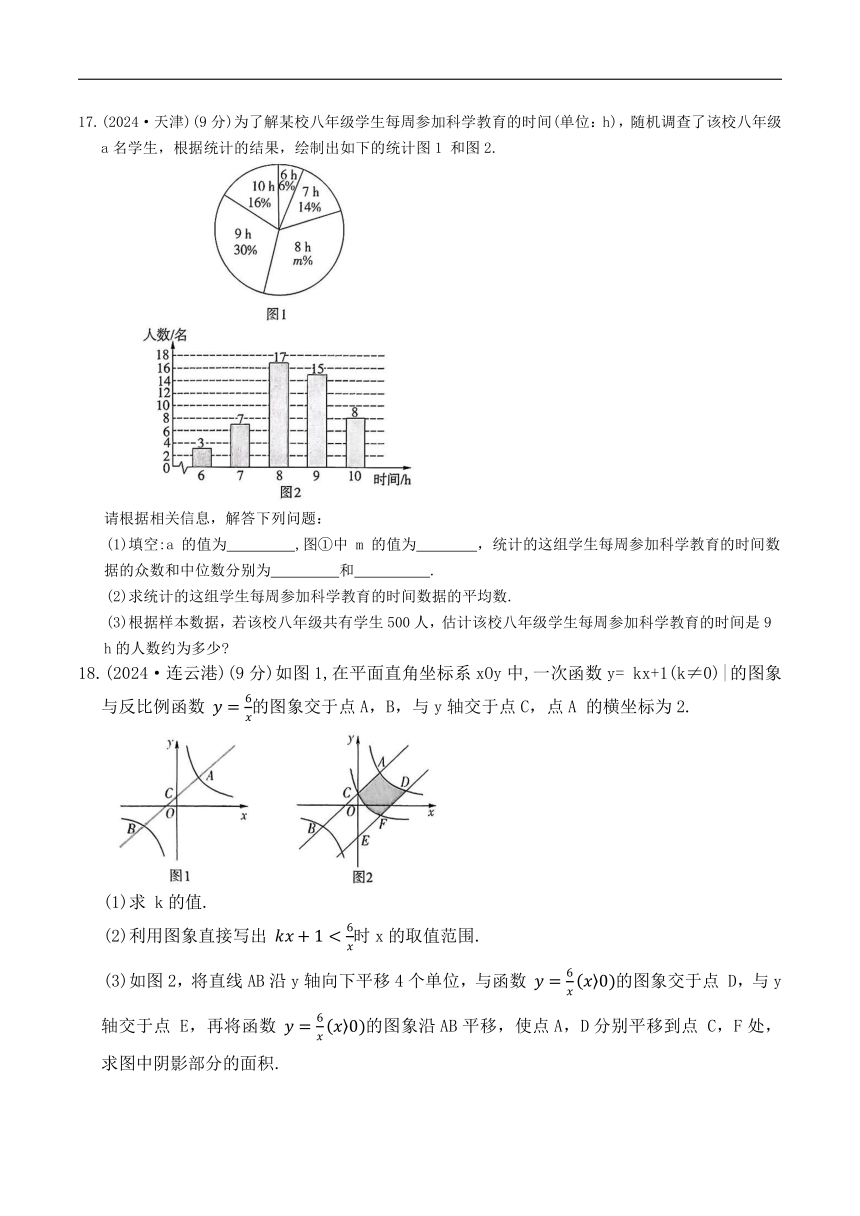
17.(2024·天津)(9分)为了解某校八年级学生每周参加科学教育的时间(单位:h),随机调查了该校八年级a名学生,根据统计的结果,绘制出如下的统计图1 和图2.
请根据相关信息,解答下列问题:
(1)填空:a 的值为 ,图①中 m 的值为 ,统计的这组学生每周参加科学教育的时间数据的众数和中位数分别为 和 .
(2)求统计的这组学生每周参加科学教育的时间数据的平均数.
(3)根据样本数据,若该校八年级共有学生500人,估计该校八年级学生每周参加科学教育的时间是9 h的人数约为多少
18.(2024·连云港)(9分)如图1,在平面直角坐标系xOy中,一次函数y= kx+1(k≠0)|的图象与反比例函数 的图象交于点A,B,与y轴交于点C,点A 的横坐标为2.
(1)求 k的值.
(2)利用图象直接写出 时x的取值范围.
(3)如图2,将直线AB沿y轴向下平移4个单位,与函数 的图象交于点 D,与y轴交于点 E,再将函数 的图象沿AB平移,使点A,D分别平移到点 C,F处,求图中阴影部分的面积.
19.(2024·广东)(9分)如图,Rt△ABC 内接于⊙O,∠ACB=90°,直线l与⊙O 相切于点 C.
(1)尺规作图:过点O 作直线m,使得直线m∥AC交劣弧BC于点D,交弦BC于点E,交直线l于点F.(保留作图痕迹,不写作法)
(2)在(1)的基础上,①求证:∠BCF =∠BAC;②若AB=10,BC=8,求 DF 的长.
20.(2024·达州)(9分)“三汇彩婷会”是达州市渠县三汇镇独有的传统民俗文化活动,起源于汉代,融数学、力学、锻造、绑扎、运载于一体,如图1.在一次展演活动中,某数学综合与实践小组将彩婷抽象成如图2的示意图,AB 是彩婷的中轴.甲同学站在 C处,借助测角仪观察,发现中轴AB上的点 D 的仰角是30°,他与彩婷中轴的距离 BC=6米.乙同学借助无人机技术在观测点 E处进行测量,测得AE 平行于水平线 BC,中轴AB上的点 F 的俯角∠AEF=45°,点 E,F 之间的距离是4米.已知彩婷的中轴AB=6.3米,甲同学的眼睛到地面的距离MC=1.5米,请根据以上数据,求中轴上 DF 的长度.(结果精确到0.1米.参考数据
21.(2024·陕西)(9分)我国新能源汽车快速健康发展,续航里程不断提升,王师傅驾驶一辆纯电动汽车从 A 市前往 B 市,他驾车从 A 市一高速公路入口驶入时,该车的剩余电量是80kW·h,行驶了240 km后,从B市一高速公路出口驶出.已知该车在高速公路上行驶的过程中,剩余电量y(kW·h)与行驶路程x(km)之间的关系如图所示.
(1)求y与x之间的关系式.
(2)已知这辆车的“满电量”为100 kW·h,王师傅驾车从B 市这一高速公路出口驶出时,求该车的剩余电量占“满电量”的百分比.
22.(2024·山东)(10分)在平面直角坐标系xOy中,点P(2,-3)在二次函数 (a0)的图象上,记该二次函数图象的对称轴为直线x=m.
(1)求m的值.
(2)若点 Q(m,-4)在 的图象上,将该二次函数的图象向上平移5个单位长度,得到新的二次函数的图象.当0≤x≤4时,求新的二次函数的最大值与最小值的和.
(3)设 的图象与x轴的交点为 若 求 a的取值范围.
23.(2024·临夏)(10分)如图1,在矩形ABCD中,E为AD边上不与端点重合的一动点,F是对角线BD 上一点,连接 BE 交 AF 于点 O,且∠ABE =∠DAF.
【模型建立】
(1)求证:AF⊥BE.
【模型应用】
(2)若AB=2,/AD=3,DF= BF,求 DE 的长.
【模型迁移】
(3)如图2,若矩形ABCD 是正方形, 求 的值.
【本卷满分:120分 考试时间:100分钟】
一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的)
1.(2024·扬州)实数2 的倒数是 ( )
A. -2 B.2 D.
2.(2024·陕西)如图,将半圆绕直径所在的虚线旋转一周,得到的立体图形是 ( )
3.(2024·福建)据《人民日报》3 月12 日电,世界知识产权组织近日公布数据显示,2023年,全球PCT(《专利合作条约》)国际专利申请总量为27.26万件,中国申请量为69610件,是申请量最大的来源国.数据69 610 用科学记数法可表示为 ( )
A.6961×10
D.0.6961×10
4.(2024·湖北) 的值是 ( )
A.5x B.5x C.6x D.6x
5.(2024·北京)如图,直线AB 和 CD 相交于点 O,OE⊥OC.若∠AOC=58°,则∠EOB 的大小为
( )
A.29° B.32° C.45° D.58°
6.(2024·江西)如图是某地去年一至六月每月空气质量为优的天数的折线统计图,关于各月空气质量为优的天数,下列结论错误的是 ( )
A.五月份空气质量为优的有16天
B.这组数据的众数是15天
C.这组数据的中位数是15天
D.这组数据的平均数是15天
7.(2024·北京)若关于x的一元二次方程 c=0有两个相等的实数根,则实数c的值为( )
A. -16 B. - 4 C.4 D.16
8.(2024·湖北)《九章算术》中记载这样一个题:牛5头和羊2只共值10金,牛2头和羊5只共值8金,牛和羊各值多少金 设每头牛值x金,每只羊值y金,可列方程组为 ( )
9.(2024·湖北)抛物线 的顶点为(--1,-2),抛物线与y轴的交点位于x轴上方.以下结论正确的是 ( )
A. a<0 B. c<0
C. a-b+c= -2
10.(2024·威海)同一条公路连接A,B,C三地,B地在A,C两地之间.甲、乙两车分别从 A地、B 地同时出发前往 C 地.甲车速度始终保持不变,乙车中途休息一段时间,继续行驶.下图表示甲、乙两车之间的距离y(km)与时间x(h)的函数关系.下列结论正确的是 ( )
A.甲车行驶 h与乙车相遇
B. A,C两地相距220 km
C.甲车的速度是70 km/h
D.乙车中途休息36分钟
二、填空题(每小题3分,共15分)
11.(2024·阜新)函数 中,自变量x的取值范围是 .
12.(2024·山东)写出满足不等式组 的一个整数解: .
13.(2024·湖北)如图,在平面直角坐标系xOy中,点A 的坐标为(-4,6),将线段 OA 绕点 O顺时针旋转90°,则点 A 的对应点 A'的坐标为
14.(2024·威海)如图,在扇形AOB 中,∠AOB =90°,C是AO的中点,过点 C作 CE⊥AO 交 于点E,过点 E作ED⊥OB,垂足为 D.在扇形内随机选取一点 P,则点 P 落在阴影部分的概率是 .
15.(2024·重庆 A卷)如图,以AB 为直径的⊙O与AC 相切于点 A,以AC 为边作平行四边形ACDE,点D,E均在⊙O 上,DE与AB 交于点 F,连接CE,与⊙O 交于点 G,连接DG.若AB=10,DE=8,则AF= ,DG= .
三、解答题(本大题共8个小题,共75分)
16.(2024·重庆 A 卷)(10分)计算:
(1)x(x-2y)+(x+y) ;
17.(2024·天津)(9分)为了解某校八年级学生每周参加科学教育的时间(单位:h),随机调查了该校八年级a名学生,根据统计的结果,绘制出如下的统计图1 和图2.
请根据相关信息,解答下列问题:
(1)填空:a 的值为 ,图①中 m 的值为 ,统计的这组学生每周参加科学教育的时间数据的众数和中位数分别为 和 .
(2)求统计的这组学生每周参加科学教育的时间数据的平均数.
(3)根据样本数据,若该校八年级共有学生500人,估计该校八年级学生每周参加科学教育的时间是9 h的人数约为多少
18.(2024·连云港)(9分)如图1,在平面直角坐标系xOy中,一次函数y= kx+1(k≠0)|的图象与反比例函数 的图象交于点A,B,与y轴交于点C,点A 的横坐标为2.
(1)求 k的值.
(2)利用图象直接写出 时x的取值范围.
(3)如图2,将直线AB沿y轴向下平移4个单位,与函数 的图象交于点 D,与y轴交于点 E,再将函数 的图象沿AB平移,使点A,D分别平移到点 C,F处,求图中阴影部分的面积.
19.(2024·广东)(9分)如图,Rt△ABC 内接于⊙O,∠ACB=90°,直线l与⊙O 相切于点 C.
(1)尺规作图:过点O 作直线m,使得直线m∥AC交劣弧BC于点D,交弦BC于点E,交直线l于点F.(保留作图痕迹,不写作法)
(2)在(1)的基础上,①求证:∠BCF =∠BAC;②若AB=10,BC=8,求 DF 的长.
20.(2024·达州)(9分)“三汇彩婷会”是达州市渠县三汇镇独有的传统民俗文化活动,起源于汉代,融数学、力学、锻造、绑扎、运载于一体,如图1.在一次展演活动中,某数学综合与实践小组将彩婷抽象成如图2的示意图,AB 是彩婷的中轴.甲同学站在 C处,借助测角仪观察,发现中轴AB上的点 D 的仰角是30°,他与彩婷中轴的距离 BC=6米.乙同学借助无人机技术在观测点 E处进行测量,测得AE 平行于水平线 BC,中轴AB上的点 F 的俯角∠AEF=45°,点 E,F 之间的距离是4米.已知彩婷的中轴AB=6.3米,甲同学的眼睛到地面的距离MC=1.5米,请根据以上数据,求中轴上 DF 的长度.(结果精确到0.1米.参考数据
21.(2024·陕西)(9分)我国新能源汽车快速健康发展,续航里程不断提升,王师傅驾驶一辆纯电动汽车从 A 市前往 B 市,他驾车从 A 市一高速公路入口驶入时,该车的剩余电量是80kW·h,行驶了240 km后,从B市一高速公路出口驶出.已知该车在高速公路上行驶的过程中,剩余电量y(kW·h)与行驶路程x(km)之间的关系如图所示.
(1)求y与x之间的关系式.
(2)已知这辆车的“满电量”为100 kW·h,王师傅驾车从B 市这一高速公路出口驶出时,求该车的剩余电量占“满电量”的百分比.
22.(2024·山东)(10分)在平面直角坐标系xOy中,点P(2,-3)在二次函数 (a0)的图象上,记该二次函数图象的对称轴为直线x=m.
(1)求m的值.
(2)若点 Q(m,-4)在 的图象上,将该二次函数的图象向上平移5个单位长度,得到新的二次函数的图象.当0≤x≤4时,求新的二次函数的最大值与最小值的和.
(3)设 的图象与x轴的交点为 若 求 a的取值范围.
23.(2024·临夏)(10分)如图1,在矩形ABCD中,E为AD边上不与端点重合的一动点,F是对角线BD 上一点,连接 BE 交 AF 于点 O,且∠ABE =∠DAF.
【模型建立】
(1)求证:AF⊥BE.
【模型应用】
(2)若AB=2,/AD=3,DF= BF,求 DE 的长.
【模型迁移】
(3)如图2,若矩形ABCD 是正方形, 求 的值.
同课章节目录
