1.4 质谱仪与回旋加速器——高二物理人教版(2019)选择性必修二期末易错题集训(含解析)
文档属性
| 名称 | 1.4 质谱仪与回旋加速器——高二物理人教版(2019)选择性必修二期末易错题集训(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 750.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-13 17:37:18 | ||
图片预览



文档简介
1.4 质谱仪与回旋加速器——高二物理人教版(2019)选择性必修二期末易错题集训
易错知识点
一、质谱仪
1.定义:质谱仪是测量带电粒子的质量和分析同位素的重要工具。
2.构造:①带电粒子发射器;②加速电场(U);③速度选择器();④ 偏转磁场();⑤照相底片。
(点拨:进入右侧磁场中的粒子速度相同,电性相同。)
3.工作原理:设加速电压为U,速度选择器内电场强度为E,磁感应强度为,偏转磁场磁感应强度为,有,v不全相同,只有的粒子才被选出进入偏转磁场,根据牛顿第二定律得关系式,由上述式子可得出需要研究的物理量,如粒子轨道半径、粒子质量、比荷,。
二、回旋加速器
1.构造:回旋加速器的核心部件是两个D形扁金属盒,整个装置放在真空容器中,如图所示。
(1)两个D形盒之间留有一个窄缝,在A处放有粒子源。
(2)两个D形盒分别接在高频交流电源的两极上,在两盒间的窄缝中形成一个方向周期性变化的交变电场。
2.原理:利用电场对带电粒子的加速作用和磁场对运动的带电粒子的偏转作用来获得高能粒子。
(1)磁场的作用:带电粒子以某一速度垂直于磁场方向进人匀强磁场时,只在洛伦兹力作用下做匀速圆周运动,其中周期与速度和半径无关,使带电粒子每次进入D形盒中都能运动相等时间(半个周期)后,平行于电场方向进入电场中加速。
(2)交流电压:为了保证每次带电粒子经过狭缝时均被加速,使其能量不断提高,要在狭缝处加一个周期与相同的交流电压。
1.19世纪末,汤姆孙的学生阿斯顿设计了质谱仪,并用质谱仪发现了氖-20、氖-22,这两种粒子在质谱仪磁场部分运动时轨道半径的大小情况是( )
A.氖-20更大 B.氖-22更大 C.一样大 D.不能判断
2.回旋加速器的两个D形金属盒分别和一高频交流电源的两极相接,两盒放在磁感应强度大小为B的匀强磁场中,若粒子源射出粒子的电荷量为q、质量为m,则要使粒子能持续加速,所加交流电源的频率为( )
A. B. C. D.
3.如图所示为回旋加速器工作原理图,置于真空中的D形金属盒半径为R,磁感应强度为B的匀强磁场与盒面垂直,交流加速电压为U。圆心A处粒子源产生初速度为零,质量为m,电荷量为q的质子,质子在加速器中被加速。忽略质子穿过两金属盒间狭缝的时间,忽略相对论效应和重力的影响,下列说法正确的是( )
A.保持B、R、U及交流电频率均不变,该装置也可用于加速粒子
B.若增大加速电压U,质子从D型盒出口射出的动能增大
C.质子从D型盒出口射出时,加速次数
D.质子第n次加速后和第次加速后的运动半径之比为
4.回旋加速器工作原理示意图如图所示,磁感应强度为B的匀强磁场与盒面垂直,两盒间的狭缝很小,粒子穿过的时间可忽略,它们接在电压为U、频率为f的交流电源上;若A处粒子源产生的氘核()能在加速器中被加速到出加速器,下列说法中正确的是( )
A.不改变磁感应强度B和交流电源频率f,该回旋加速器不能用于加速()粒子
B.若只增大磁感应强度B,则氘核获得的最大动能增大
C.若只增大交流电压U,则氘核在回旋加速器中运行时间会变短
D.若只增大交流电压U,则氘核获得的最大动能增大
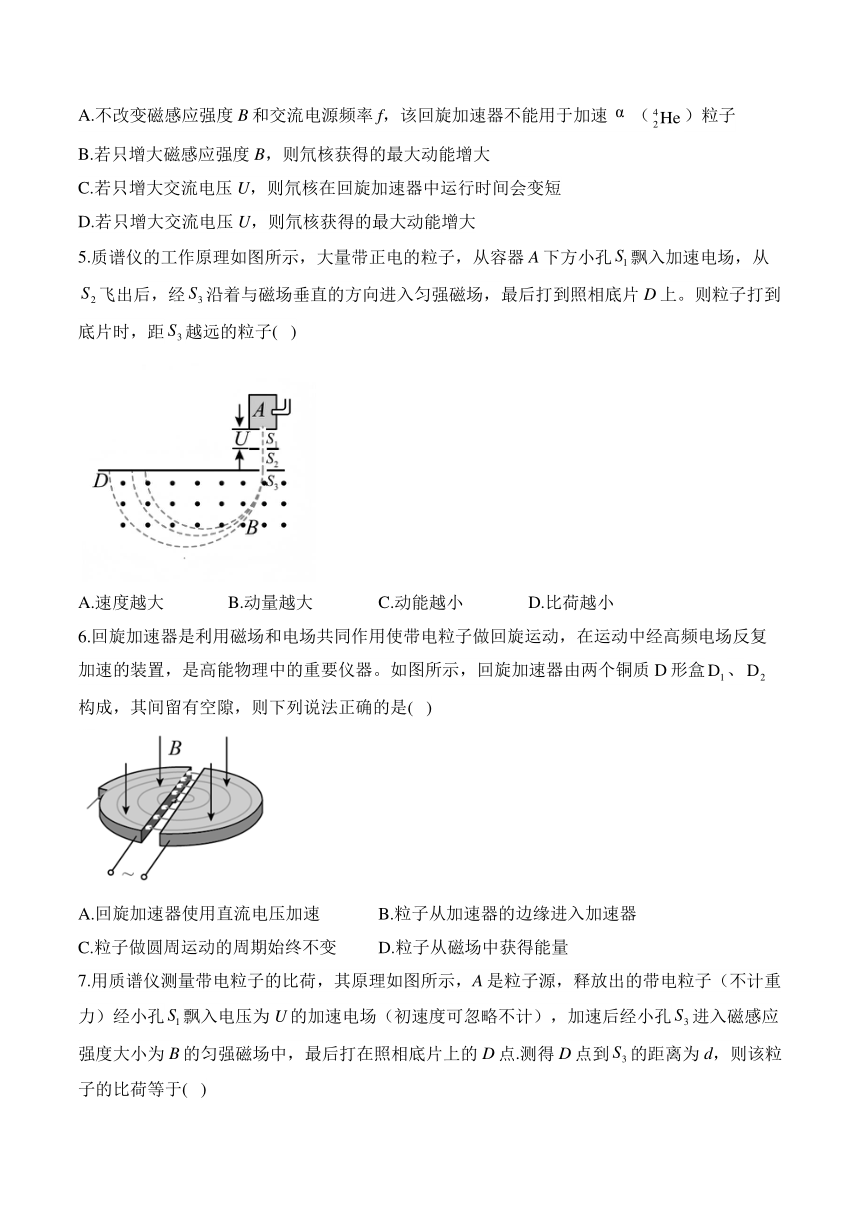
5.质谱仪的工作原理如图所示,大量带正电的粒子,从容器A下方小孔飘入加速电场,从飞出后,经沿着与磁场垂直的方向进入匀强磁场,最后打到照相底片D上。则粒子打到底片时,距越远的粒子( )
A.速度越大 B.动量越大 C.动能越小 D.比荷越小
6.回旋加速器是利用磁场和电场共同作用使带电粒子做回旋运动,在运动中经高频电场反复加速的装置,是高能物理中的重要仪器。如图所示,回旋加速器由两个铜质D形盒、构成,其间留有空隙,则下列说法正确的是( )
A.回旋加速器使用直流电压加速 B.粒子从加速器的边缘进入加速器
C.粒子做圆周运动的周期始终不变 D.粒子从磁场中获得能量
7.用质谱仪测量带电粒子的比荷,其原理如图所示,A是粒子源,释放出的带电粒子(不计重力)经小孔飘入电压为U的加速电场(初速度可忽略不计),加速后经小孔进入磁感应强度大小为B的匀强磁场中,最后打在照相底片上的D点.测得D点到的距离为d,则该粒子的比荷等于( )
A. B. C. D.
8.如图所示为回旋加速器示意图,利用回旋加速器对H粒子进行加速,此时D形盒中的磁场的磁感应强度大小为B,D形盒缝隙间电场变化周期为T,加速电压为U。忽略相对论效应和粒子在D形盒缝隙间的运动时间,下列说法正确的是( )
A.保持B、U和T不变,该回旋加速器可以加速质子
B.只增大加速电压U,H粒子获得的最大动能增大
C.只增大加速电压U,H粒子在回旋加速器中运动的时间变短
D.回旋加速器只能加速带正电的粒子,不能加速带负电的粒子
答案以及解析
1.答案:B
解析:根据粒子在磁场中做圆周运动得解得两种粒子射入磁场时的速度大小相等,同时电荷数相等,由于氖-22的质量数大,即氖-22的质量大,故可知氖-22的轨道半径更大。故选B。
2.答案:C
解析:带电粒子来磁场中运动,洛伦兹力提供向心力,有
其周期为
所加交流电的电源频率与粒子的频率相同,即
故选C。
3.答案:D
解析:A.此加速器加速粒子时的周期与粒子在磁场中的运动周期相同为
粒子的比荷与质子的比荷不同,即粒子与质子在磁场中运动的周期不同,所以保持B、R、U及交流电频率均不变,该装置不能用于加速粒子,故A错误;
B.设质子从D型盒出口射出的速度为,则有
解得质子从D型盒出口射出的动能为
可知质子从D型盒出口射出的动能与加速电压无关,故B错误;
C.设质子从D型盒出口射出时加速了n次,则由动能定理有
解得
故C错误;
D.由动能定理可知,
得第n次加速后和第次加速后的速度分别为,
再由质子在磁场中做圆周运动洛伦兹力提供向心力有
可知
则质子第n次加速后和第次加速后的运动半径分别为,
所以
故D正确。
故选D。
4.答案:C
解析:A.粒子若能被加速,则所加交流电源的频率等于粒子在磁场中做圆周运动的频率,即
不改变磁感应强度B和交流电源频率f,因()粒子的比荷等于氘核()的比荷,则该回旋加速器也能用于加速()粒子,选项A错误;
B.只增大磁感应强度B,则粒子在磁场中做圆周运动的周期改变,则氘核不能被加速,选项B错误;
C.若只增大交流电压U,不会改变质子在回旋加速器中运行的周期,但加速次数减少,则运行时间也会变短,故C正确;
D.粒子在加速器中能获得的最大动能,根据
可得
若只增大交流电压U,则氘核获得的最大动能不变,选项D错误。
故选C。
5.答案:D
解析:D.带电粒子进入磁场的动能,则,带电粒子在磁场中,由牛顿第二定律,联立可知距越远的粒子轨迹半径越大,,速度越比荷越小,故D正确;A.又根据,知带电粒子的比荷越小,速度越小,故A错误;B.带电粒子的动量为,故无法判断动量大小,故B错误;C.在加速电场中,由动能定理可得带电粒子进入磁场的动能为,无法判断带电量的大小关系,故无法判断动能大小,故C错误。故选D。
6.答案:C
解析:A.回旋加速器中粒子每转半圈加速一次,且相邻两次进入加速场时速度方向相反,故使用交流电压加速,故A错误;
B.粒子由加速器的中心附近进入加速器,而从边缘离开加速器,故B错误;
C.粒子做圆周运动,受力分析得
运动的周期
始终不变,故C正确;
D.由于洛伦兹力并不做功,而粒子通过电场时有电能转化为动能,故粒子是从电场中获得能量,故D错误。
故选C。
7.答案:A
解析:电场中,由动能定理得,粒子在磁场中做圆周运动,由洛伦兹力提供向心力得,联立解得,BCD项错误,A项正确.
8.答案:C
解析:A.D形盒缝隙间电场变化周期与H粒子在磁场中做圆周运动的周期相等,为,而质子与H粒子的比荷不相等,所以为了加速器可以加速质子,应对加速器进行参数调节,改变B和T,选项A错误;B.设D形盒半径为r,则H粒子离开回旋加速器的最大速度,所以只增大加速电压U,H粒子获得的最大动能不会增大,选项B错误;C.粒子在回旋加速器回旋一周,增加的动能为2qU,在回旋加速器中运动时间由回旋次数决定,设回旋次数为n,则由,可得,所以粒子运动总时间,故只增大加速电压U,H粒子在回旋加速器中回旋的次数会变少,即运动的时间会变短,选项C正确;D.回旋加速度既能加速带正电的粒子,也能加速带负电的粒子,选项D错误。故选C。
易错知识点
一、质谱仪
1.定义:质谱仪是测量带电粒子的质量和分析同位素的重要工具。
2.构造:①带电粒子发射器;②加速电场(U);③速度选择器();④ 偏转磁场();⑤照相底片。
(点拨:进入右侧磁场中的粒子速度相同,电性相同。)
3.工作原理:设加速电压为U,速度选择器内电场强度为E,磁感应强度为,偏转磁场磁感应强度为,有,v不全相同,只有的粒子才被选出进入偏转磁场,根据牛顿第二定律得关系式,由上述式子可得出需要研究的物理量,如粒子轨道半径、粒子质量、比荷,。
二、回旋加速器
1.构造:回旋加速器的核心部件是两个D形扁金属盒,整个装置放在真空容器中,如图所示。
(1)两个D形盒之间留有一个窄缝,在A处放有粒子源。
(2)两个D形盒分别接在高频交流电源的两极上,在两盒间的窄缝中形成一个方向周期性变化的交变电场。
2.原理:利用电场对带电粒子的加速作用和磁场对运动的带电粒子的偏转作用来获得高能粒子。
(1)磁场的作用:带电粒子以某一速度垂直于磁场方向进人匀强磁场时,只在洛伦兹力作用下做匀速圆周运动,其中周期与速度和半径无关,使带电粒子每次进入D形盒中都能运动相等时间(半个周期)后,平行于电场方向进入电场中加速。
(2)交流电压:为了保证每次带电粒子经过狭缝时均被加速,使其能量不断提高,要在狭缝处加一个周期与相同的交流电压。
1.19世纪末,汤姆孙的学生阿斯顿设计了质谱仪,并用质谱仪发现了氖-20、氖-22,这两种粒子在质谱仪磁场部分运动时轨道半径的大小情况是( )
A.氖-20更大 B.氖-22更大 C.一样大 D.不能判断
2.回旋加速器的两个D形金属盒分别和一高频交流电源的两极相接,两盒放在磁感应强度大小为B的匀强磁场中,若粒子源射出粒子的电荷量为q、质量为m,则要使粒子能持续加速,所加交流电源的频率为( )
A. B. C. D.
3.如图所示为回旋加速器工作原理图,置于真空中的D形金属盒半径为R,磁感应强度为B的匀强磁场与盒面垂直,交流加速电压为U。圆心A处粒子源产生初速度为零,质量为m,电荷量为q的质子,质子在加速器中被加速。忽略质子穿过两金属盒间狭缝的时间,忽略相对论效应和重力的影响,下列说法正确的是( )
A.保持B、R、U及交流电频率均不变,该装置也可用于加速粒子
B.若增大加速电压U,质子从D型盒出口射出的动能增大
C.质子从D型盒出口射出时,加速次数
D.质子第n次加速后和第次加速后的运动半径之比为
4.回旋加速器工作原理示意图如图所示,磁感应强度为B的匀强磁场与盒面垂直,两盒间的狭缝很小,粒子穿过的时间可忽略,它们接在电压为U、频率为f的交流电源上;若A处粒子源产生的氘核()能在加速器中被加速到出加速器,下列说法中正确的是( )
A.不改变磁感应强度B和交流电源频率f,该回旋加速器不能用于加速()粒子
B.若只增大磁感应强度B,则氘核获得的最大动能增大
C.若只增大交流电压U,则氘核在回旋加速器中运行时间会变短
D.若只增大交流电压U,则氘核获得的最大动能增大
5.质谱仪的工作原理如图所示,大量带正电的粒子,从容器A下方小孔飘入加速电场,从飞出后,经沿着与磁场垂直的方向进入匀强磁场,最后打到照相底片D上。则粒子打到底片时,距越远的粒子( )
A.速度越大 B.动量越大 C.动能越小 D.比荷越小
6.回旋加速器是利用磁场和电场共同作用使带电粒子做回旋运动,在运动中经高频电场反复加速的装置,是高能物理中的重要仪器。如图所示,回旋加速器由两个铜质D形盒、构成,其间留有空隙,则下列说法正确的是( )
A.回旋加速器使用直流电压加速 B.粒子从加速器的边缘进入加速器
C.粒子做圆周运动的周期始终不变 D.粒子从磁场中获得能量
7.用质谱仪测量带电粒子的比荷,其原理如图所示,A是粒子源,释放出的带电粒子(不计重力)经小孔飘入电压为U的加速电场(初速度可忽略不计),加速后经小孔进入磁感应强度大小为B的匀强磁场中,最后打在照相底片上的D点.测得D点到的距离为d,则该粒子的比荷等于( )
A. B. C. D.
8.如图所示为回旋加速器示意图,利用回旋加速器对H粒子进行加速,此时D形盒中的磁场的磁感应强度大小为B,D形盒缝隙间电场变化周期为T,加速电压为U。忽略相对论效应和粒子在D形盒缝隙间的运动时间,下列说法正确的是( )
A.保持B、U和T不变,该回旋加速器可以加速质子
B.只增大加速电压U,H粒子获得的最大动能增大
C.只增大加速电压U,H粒子在回旋加速器中运动的时间变短
D.回旋加速器只能加速带正电的粒子,不能加速带负电的粒子
答案以及解析
1.答案:B
解析:根据粒子在磁场中做圆周运动得解得两种粒子射入磁场时的速度大小相等,同时电荷数相等,由于氖-22的质量数大,即氖-22的质量大,故可知氖-22的轨道半径更大。故选B。
2.答案:C
解析:带电粒子来磁场中运动,洛伦兹力提供向心力,有
其周期为
所加交流电的电源频率与粒子的频率相同,即
故选C。
3.答案:D
解析:A.此加速器加速粒子时的周期与粒子在磁场中的运动周期相同为
粒子的比荷与质子的比荷不同,即粒子与质子在磁场中运动的周期不同,所以保持B、R、U及交流电频率均不变,该装置不能用于加速粒子,故A错误;
B.设质子从D型盒出口射出的速度为,则有
解得质子从D型盒出口射出的动能为
可知质子从D型盒出口射出的动能与加速电压无关,故B错误;
C.设质子从D型盒出口射出时加速了n次,则由动能定理有
解得
故C错误;
D.由动能定理可知,
得第n次加速后和第次加速后的速度分别为,
再由质子在磁场中做圆周运动洛伦兹力提供向心力有
可知
则质子第n次加速后和第次加速后的运动半径分别为,
所以
故D正确。
故选D。
4.答案:C
解析:A.粒子若能被加速,则所加交流电源的频率等于粒子在磁场中做圆周运动的频率,即
不改变磁感应强度B和交流电源频率f,因()粒子的比荷等于氘核()的比荷,则该回旋加速器也能用于加速()粒子,选项A错误;
B.只增大磁感应强度B,则粒子在磁场中做圆周运动的周期改变,则氘核不能被加速,选项B错误;
C.若只增大交流电压U,不会改变质子在回旋加速器中运行的周期,但加速次数减少,则运行时间也会变短,故C正确;
D.粒子在加速器中能获得的最大动能,根据
可得
若只增大交流电压U,则氘核获得的最大动能不变,选项D错误。
故选C。
5.答案:D
解析:D.带电粒子进入磁场的动能,则,带电粒子在磁场中,由牛顿第二定律,联立可知距越远的粒子轨迹半径越大,,速度越比荷越小,故D正确;A.又根据,知带电粒子的比荷越小,速度越小,故A错误;B.带电粒子的动量为,故无法判断动量大小,故B错误;C.在加速电场中,由动能定理可得带电粒子进入磁场的动能为,无法判断带电量的大小关系,故无法判断动能大小,故C错误。故选D。
6.答案:C
解析:A.回旋加速器中粒子每转半圈加速一次,且相邻两次进入加速场时速度方向相反,故使用交流电压加速,故A错误;
B.粒子由加速器的中心附近进入加速器,而从边缘离开加速器,故B错误;
C.粒子做圆周运动,受力分析得
运动的周期
始终不变,故C正确;
D.由于洛伦兹力并不做功,而粒子通过电场时有电能转化为动能,故粒子是从电场中获得能量,故D错误。
故选C。
7.答案:A
解析:电场中,由动能定理得,粒子在磁场中做圆周运动,由洛伦兹力提供向心力得,联立解得,BCD项错误,A项正确.
8.答案:C
解析:A.D形盒缝隙间电场变化周期与H粒子在磁场中做圆周运动的周期相等,为,而质子与H粒子的比荷不相等,所以为了加速器可以加速质子,应对加速器进行参数调节,改变B和T,选项A错误;B.设D形盒半径为r,则H粒子离开回旋加速器的最大速度,所以只增大加速电压U,H粒子获得的最大动能不会增大,选项B错误;C.粒子在回旋加速器回旋一周,增加的动能为2qU,在回旋加速器中运动时间由回旋次数决定,设回旋次数为n,则由,可得,所以粒子运动总时间,故只增大加速电压U,H粒子在回旋加速器中回旋的次数会变少,即运动的时间会变短,选项C正确;D.回旋加速度既能加速带正电的粒子,也能加速带负电的粒子,选项D错误。故选C。
