4.2.2平行线的判定 课件(共26张PPT)
文档属性
| 名称 | 4.2.2平行线的判定 课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 19:26:09 | ||
图片预览




文档简介
(共26张PPT)
4.2 平行线
第四章 相交线和平行线
2 平行线的判定
教学目标
1. 熟练掌握平行线的判定方法.
2. 能灵活的利用平行线的判定方法解决些简单的证明问题.
重点:平行线的判定.
难点:平行线的判定应用.
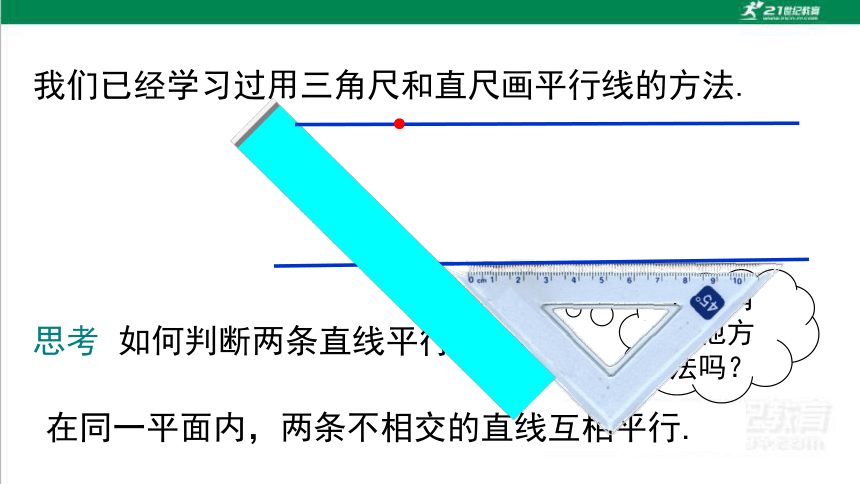
思考 如何判断两条直线平行?
在同一平面内,两条不相交的直线互相平行.
你还有其他方法吗?
我们已经学习过用三角尺和直尺画平行线的方法.
●
平行线的判定
1
●
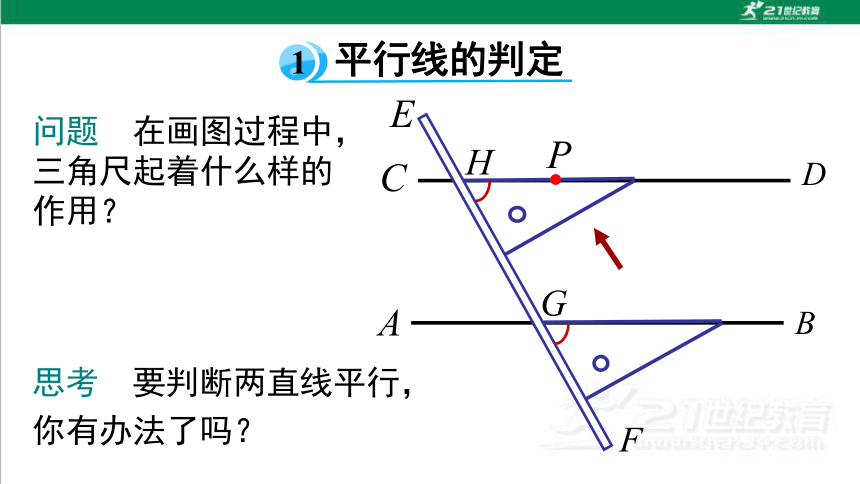
问题 在画图过程中,三角尺起着什么样的作用?
思考 要判断两直线平行,你有办法了吗?
b
A
2
1
a
B
(1)这样的画法可以看作是怎样的图形变换?
(2)画图过程中,什么角始终保持相等?
(3)直线 a,b 位置关系如何?
问题
合作探究
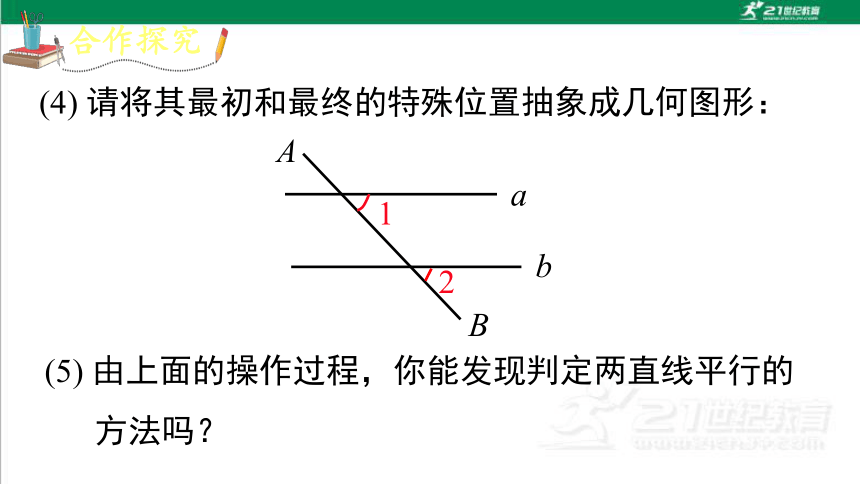
(4) 请将其最初和最终的特殊位置抽象成几何图形:
1
2
a
b
A
B
(5) 由上面的操作过程,你能发现判定两直线平行的
方法吗?
定义总结
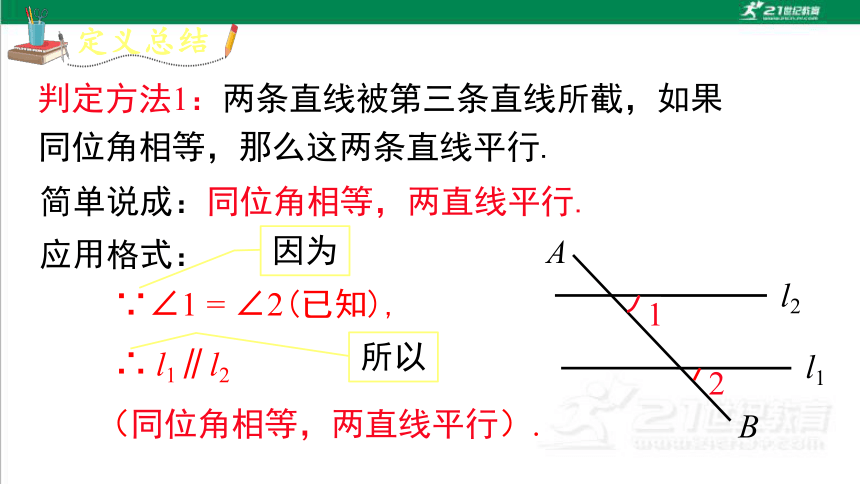
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
应用格式:
∵∠1 = ∠2(已知),
∴ l1∥l2 (同位角相等,两直线平行).
1
2
l2
l1
A
B
因为
所以
典例精析
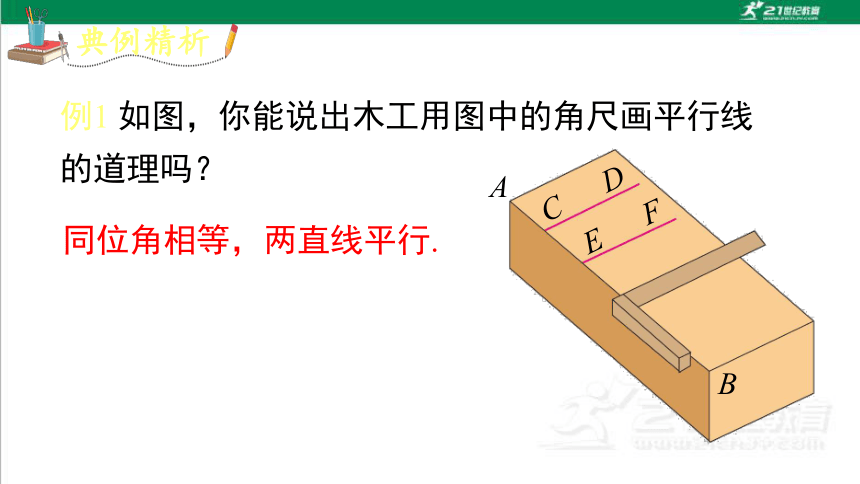
同位角相等,两直线平行.
例1 如图,你能说出木工用图中的角尺画平行线的道理吗?
A
B
C D
E F
思考:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
如图,由 3 = 2,能推得 a∥b 吗?试一试.
解:∵ 1 = 3(对顶角相等),
3 = 2(已知),
∴ 1 = 2.
∴ a∥b(同位角相等,两直线平行).
2
b
a
1
3
定义总结
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠1 = ∠2 (已知),
∴ a∥b (内错角相等,两直线平行).
应用格式:
2
b
a
1
思考:如图,如果 1 + 2 = 180°,能判定 a∥b 吗
解:能. 理由如下:
∵ 1 + 2 = 180°(已知),
1 + 3 = 180°(已知),
∴ 2 = 3(同角的补角相等).
∴ a∥b(同位角相等,两直线平行).
c
2
b
a
1
3
定义总结
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
∵∠1 + ∠2 = 180° (已知),
∴ a∥b (同旁内角互补,两直线平行).
如图,已知直线点 P,试利用尺规作图按下列作法准确地过点 P 作直线 AB 的平行线:
试一试
(1) 在直线 AB 上取一点 Q,经过点 P 和点 Q,作直线 MN;
A
B
P
Q
N
M
(2) 作∠MPD =∠PQB,并使得∠MPD 与∠PQB 是一对同位角;
(3) 反向延长射线 PD,得到直线 CD.
直线 CD 就是过点 P 所要求作的直线 AB 的平行线.
C
D
借助“内错角相等”,是否也可以作出所需要的平行线呢?
(1) 在直线 AB 上取一点 Q,经过点 P 和点 Q,作直线 MN;
A
B
P
Q
N
M
(2) 作∠NPC =∠PQB,并使得∠NPC 与∠PQB 是一对内错角;
(3) 反向延长射线 PD,得到直线 CD.
直线 CD 就是过点 P 所要求作的直线 AB 的平行线.
C
D
例2 如图,直线 a、b 被直线 l 所截,已知∠1 = 115°,∠2= 115°,直线a、b平行吗?为什么?
平行线的判定的运用
2
解:∵∠1 = 115° (已知),∠2 = 115° (已知),
∴∠1=∠2 (等量代换).
∴a // b (内错角相等,两直线平行).
括号内所写的,就是括号前这一结论成立的理由.
等量代换以及等式的性质是我们常用的推理依据.
l
a
b
1
2
“推理”是数学的一种基本思想.
→ 从特殊到一般
→ 从一般到特殊
推理
归纳推理
演绎推理
方法要点
典例精析
例3 如图,在四边形 ABCD 中,已知∠B = 60°,
∠C = 120°,AB 与 CD 平行吗?AD 与 BC 平行吗?
解:∵∠B = 60° (已知), ∠C = 120° (已知),
∴∠B +∠C = 180° (等式的性质).
∴ AB // CD (同旁内角互补,两直线平行).
本题中,根据已知条件,无法判定 AD 与 BC 是否平行.
A
B
C
D
例4 如图,在同一平面内,直线 CD、EF 均与直线 AB 垂直,点 D、F 为垂足. 试判断 CD 与 EF 是否平行.
解:∵CD⊥AB (已知),EF⊥AB (已知),
∴∠ADC =∠AFE = 90°
∴CD // EF (同位角相等,两直线平行).
(垂直的定义).
总结
在同一平面内,垂直于同一条直线的两条直线平行.
典例精析
A
B
E
F
C
D
练一练
2. 光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象,如图,光线 a 从空气中射入水中,再从水中射入空气中,
形成光线 b,根据光学知识有 ∠1=∠2,
∠3=∠4,请判断光线 a 与光线 b 是否
平行,请说明理由.
1
3
5
2
4
6
a
b
∠3 = ∠4
∠5 = ∠6
∠1 = ∠2
∠1+∠5 = ∠2+∠6
a∥b
1
3
5
2
4
6
a
b
总结
在平行线判定的实际应用过程中解题的关键就是将其抽象为几何模型.
平行线的判定
判定方法
__________,两直线平行
定义法
同一个平面内,两条直线_______
同位角相等
___________,两直线平行
同旁内角互补
不相交
__________,两直线平行
内错角相等
1. 如图,可以确定 AB∥CE 的条件是 ( )
A. ∠2 = ∠B
B. ∠1 = ∠A
C. ∠3 = ∠B
D. ∠3 = ∠A
C
1
2
3
A
E
B
C
D
2. 如图,已知∠1 = 30°,若∠2 或∠3 满足条件
____________________,则 a∥b.
2
1
3
a
b
c
∠2 = 150° 或∠3 = 30°
3. 如图.(1)从∠1 = ∠4,可以推出 ∥ ,
理由是 .
(2) 从∠ABC +∠ = 180°,可以推出 AB∥CD,理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
(3) 从∠ =∠ 2 ,可以推出 AD∥BC,
理由是 .
(4) 从∠5 =∠ ,可以推出 AB∥CD,
理由是 .
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
理由如下:
∵ AC 平分∠DAB (已知),
∴ ∠1 =∠2 (角平分线的定义).
∵ ∠1 = ∠3 (已知),
∴ ∠2 =∠3 (等量代换).
∴ AB∥CD (内错角相等,两直线平行).
4. 如图,已知∠1 = ∠3,AC 平分∠DAB,你能判定
哪两条直线平行?请说明理由.
2
3
A
B
C
D
)
)
1
(
解:AB∥CD.
4.2 平行线
第四章 相交线和平行线
2 平行线的判定
教学目标
1. 熟练掌握平行线的判定方法.
2. 能灵活的利用平行线的判定方法解决些简单的证明问题.
重点:平行线的判定.
难点:平行线的判定应用.
思考 如何判断两条直线平行?
在同一平面内,两条不相交的直线互相平行.
你还有其他方法吗?
我们已经学习过用三角尺和直尺画平行线的方法.
●
平行线的判定
1
●
问题 在画图过程中,三角尺起着什么样的作用?
思考 要判断两直线平行,你有办法了吗?
b
A
2
1
a
B
(1)这样的画法可以看作是怎样的图形变换?
(2)画图过程中,什么角始终保持相等?
(3)直线 a,b 位置关系如何?
问题
合作探究
(4) 请将其最初和最终的特殊位置抽象成几何图形:
1
2
a
b
A
B
(5) 由上面的操作过程,你能发现判定两直线平行的
方法吗?
定义总结
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
应用格式:
∵∠1 = ∠2(已知),
∴ l1∥l2 (同位角相等,两直线平行).
1
2
l2
l1
A
B
因为
所以
典例精析
同位角相等,两直线平行.
例1 如图,你能说出木工用图中的角尺画平行线的道理吗?
A
B
C D
E F
思考:两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
如图,由 3 = 2,能推得 a∥b 吗?试一试.
解:∵ 1 = 3(对顶角相等),
3 = 2(已知),
∴ 1 = 2.
∴ a∥b(同位角相等,两直线平行).
2
b
a
1
3
定义总结
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠1 = ∠2 (已知),
∴ a∥b (内错角相等,两直线平行).
应用格式:
2
b
a
1
思考:如图,如果 1 + 2 = 180°,能判定 a∥b 吗
解:能. 理由如下:
∵ 1 + 2 = 180°(已知),
1 + 3 = 180°(已知),
∴ 2 = 3(同角的补角相等).
∴ a∥b(同位角相等,两直线平行).
c
2
b
a
1
3
定义总结
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
∵∠1 + ∠2 = 180° (已知),
∴ a∥b (同旁内角互补,两直线平行).
如图,已知直线点 P,试利用尺规作图按下列作法准确地过点 P 作直线 AB 的平行线:
试一试
(1) 在直线 AB 上取一点 Q,经过点 P 和点 Q,作直线 MN;
A
B
P
Q
N
M
(2) 作∠MPD =∠PQB,并使得∠MPD 与∠PQB 是一对同位角;
(3) 反向延长射线 PD,得到直线 CD.
直线 CD 就是过点 P 所要求作的直线 AB 的平行线.
C
D
借助“内错角相等”,是否也可以作出所需要的平行线呢?
(1) 在直线 AB 上取一点 Q,经过点 P 和点 Q,作直线 MN;
A
B
P
Q
N
M
(2) 作∠NPC =∠PQB,并使得∠NPC 与∠PQB 是一对内错角;
(3) 反向延长射线 PD,得到直线 CD.
直线 CD 就是过点 P 所要求作的直线 AB 的平行线.
C
D
例2 如图,直线 a、b 被直线 l 所截,已知∠1 = 115°,∠2= 115°,直线a、b平行吗?为什么?
平行线的判定的运用
2
解:∵∠1 = 115° (已知),∠2 = 115° (已知),
∴∠1=∠2 (等量代换).
∴a // b (内错角相等,两直线平行).
括号内所写的,就是括号前这一结论成立的理由.
等量代换以及等式的性质是我们常用的推理依据.
l
a
b
1
2
“推理”是数学的一种基本思想.
→ 从特殊到一般
→ 从一般到特殊
推理
归纳推理
演绎推理
方法要点
典例精析
例3 如图,在四边形 ABCD 中,已知∠B = 60°,
∠C = 120°,AB 与 CD 平行吗?AD 与 BC 平行吗?
解:∵∠B = 60° (已知), ∠C = 120° (已知),
∴∠B +∠C = 180° (等式的性质).
∴ AB // CD (同旁内角互补,两直线平行).
本题中,根据已知条件,无法判定 AD 与 BC 是否平行.
A
B
C
D
例4 如图,在同一平面内,直线 CD、EF 均与直线 AB 垂直,点 D、F 为垂足. 试判断 CD 与 EF 是否平行.
解:∵CD⊥AB (已知),EF⊥AB (已知),
∴∠ADC =∠AFE = 90°
∴CD // EF (同位角相等,两直线平行).
(垂直的定义).
总结
在同一平面内,垂直于同一条直线的两条直线平行.
典例精析
A
B
E
F
C
D
练一练
2. 光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象,如图,光线 a 从空气中射入水中,再从水中射入空气中,
形成光线 b,根据光学知识有 ∠1=∠2,
∠3=∠4,请判断光线 a 与光线 b 是否
平行,请说明理由.
1
3
5
2
4
6
a
b
∠3 = ∠4
∠5 = ∠6
∠1 = ∠2
∠1+∠5 = ∠2+∠6
a∥b
1
3
5
2
4
6
a
b
总结
在平行线判定的实际应用过程中解题的关键就是将其抽象为几何模型.
平行线的判定
判定方法
__________,两直线平行
定义法
同一个平面内,两条直线_______
同位角相等
___________,两直线平行
同旁内角互补
不相交
__________,两直线平行
内错角相等
1. 如图,可以确定 AB∥CE 的条件是 ( )
A. ∠2 = ∠B
B. ∠1 = ∠A
C. ∠3 = ∠B
D. ∠3 = ∠A
C
1
2
3
A
E
B
C
D
2. 如图,已知∠1 = 30°,若∠2 或∠3 满足条件
____________________,则 a∥b.
2
1
3
a
b
c
∠2 = 150° 或∠3 = 30°
3. 如图.(1)从∠1 = ∠4,可以推出 ∥ ,
理由是 .
(2) 从∠ABC +∠ = 180°,可以推出 AB∥CD,理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
(3) 从∠ =∠ 2 ,可以推出 AD∥BC,
理由是 .
(4) 从∠5 =∠ ,可以推出 AB∥CD,
理由是 .
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
理由如下:
∵ AC 平分∠DAB (已知),
∴ ∠1 =∠2 (角平分线的定义).
∵ ∠1 = ∠3 (已知),
∴ ∠2 =∠3 (等量代换).
∴ AB∥CD (内错角相等,两直线平行).
4. 如图,已知∠1 = ∠3,AC 平分∠DAB,你能判定
哪两条直线平行?请说明理由.
2
3
A
B
C
D
)
)
1
(
解:AB∥CD.
同课章节目录
