期末押题卷(含解析)-2024-2025学年数学八年级下册人教版
文档属性
| 名称 | 期末押题卷(含解析)-2024-2025学年数学八年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 06:51:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末押题卷-2024-2025学年数学八年级下册人教版
一、单选题
1.若函数的图象上有两点,,则下列说法正确的是( )
A. B. C. D.
2.下列长度的三条线段能组成直角三角形的是( )
A. B. C. D.
3.下列代数式中,是最简二次根式的是( )
A. B. C. D.
4.如图,在中,,,点为斜边上的中点,则的长为( )
A. B. C. D.
5.一次函数的图象如图所示,当时,的取值范围是( )
A. B. C. D.
6.若点,在一次函数的图像上,且.则下列的取值符合条件的是( )
A. B. C. D.
7.下列命题中是假命题的是( )
A.全等三角形的面积相等
B.三角形三个内角的和等于
C.若函数的图象与函数的图象平行,则
D.如果,,那么
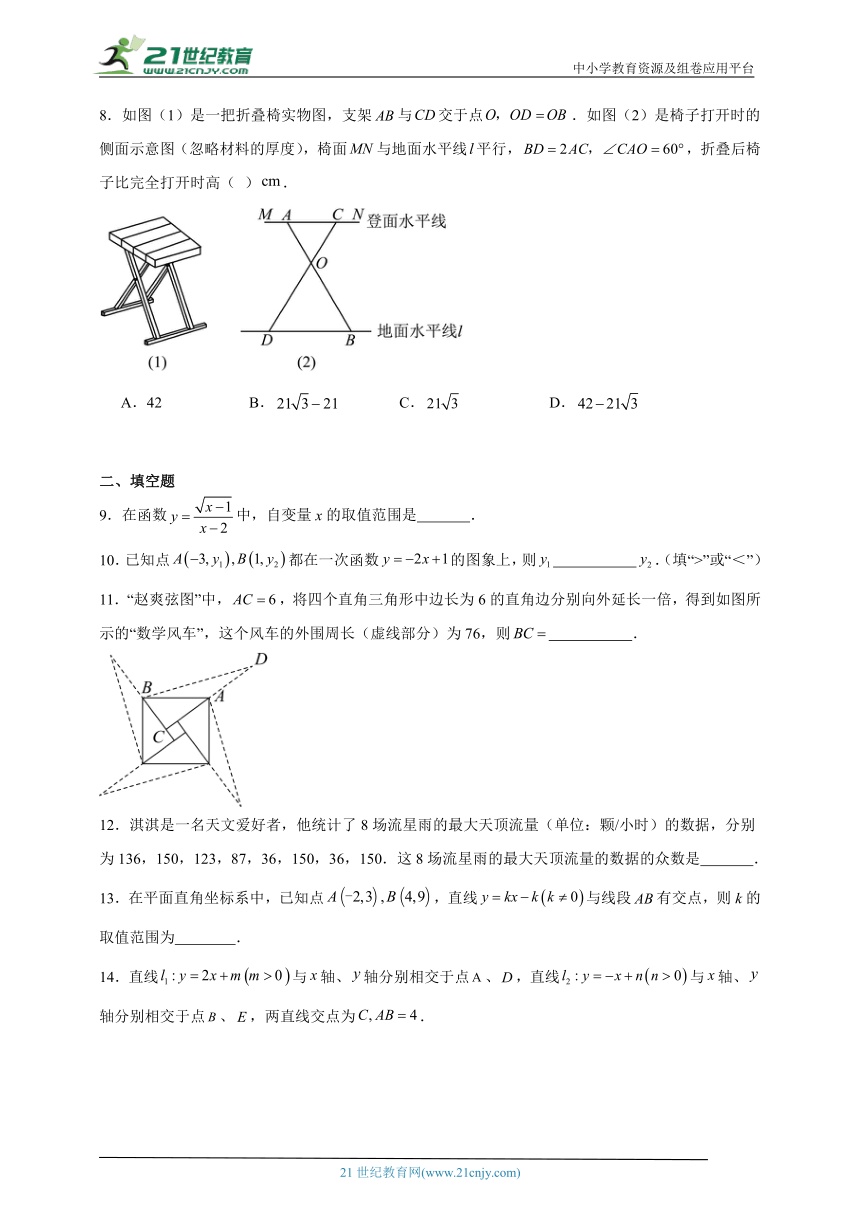
8.如图(1)是一把折叠椅实物图,支架与交于点.如图(2)是椅子打开时的侧面示意图(忽略材料的厚度),椅面与地面水平线平行,,折叠后椅子比完全打开时高( ).
A.42 B. C. D.
二、填空题
9.在函数中,自变量x的取值范围是 .
10.已知点都在一次函数的图象上,则 .(填“>”或“<”)
11.“赵爽弦图”中,,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,这个风车的外围周长(虚线部分)为76,则 .
12.淇淇是一名天文爱好者,他统计了8场流星雨的最大天顶流量(单位:颗/小时)的数据,分别为136,150,123,87,36,150,36,150.这8场流星雨的最大天顶流量的数据的众数是 .
13.在平面直角坐标系中,已知点,直线与线段有交点,则k的取值范围为 .
14.直线与轴、轴分别相交于点、,直线与轴、轴分别相交于点、,两直线交点为.
(1)如图,当时,点的坐标为 ;
(2)若两点之间距离为2,则 .
15.如图,矩形中,,.点是边上一动点,点为线段上一动点.,则的最小值为 .
16.如图,长方形中,,,将此长方形折叠,使点与点重合,折痕为,则折痕的长为 cm.
三、解答题
17.计算:.
18.为了缓解环境污染的问题,某地禁止燃油助力车上路,于是电动自行车的市场需求量日渐增多.某商店计划购进A,B两种型号的电动自行车(两种型号都要购进)共30辆,其中A型电动自行车不少于10辆,A,B两种型号电动自行车的进货单价分别为2500元、3000元,售价分别为2800元、3500元,设该商店计划购进A型电动自行车x辆,两种型号的电动自行车全部销售后可获利润y元.
(1)求出y与x之间的函数关系式.
(2)该商店如何进货才能获得最大利润?此时最大利润是多少元?
19.已知一次函数(k,b为常数,且)的图象经过点.
(1)若,求一次函数的表达式.
(2)当时,该一次函数的最大值为6,求k的值.
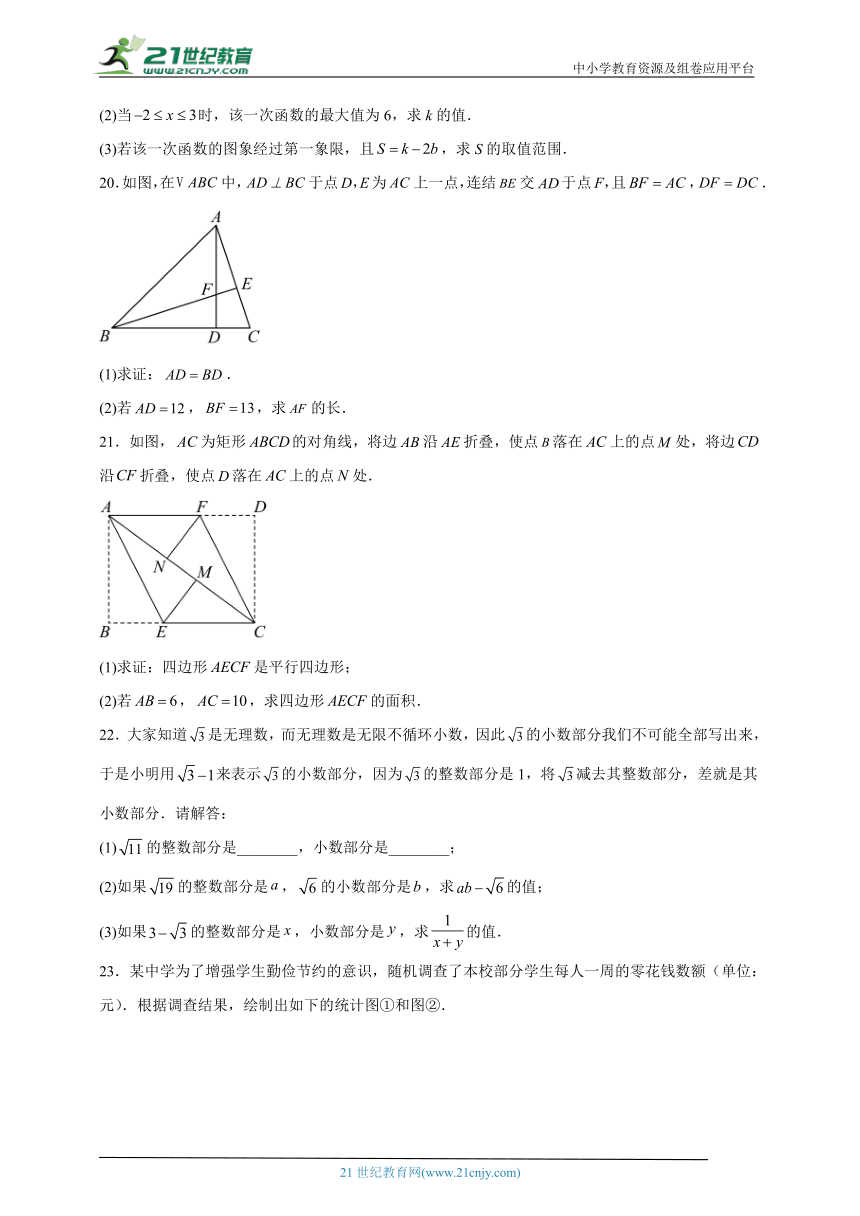
(3)若该一次函数的图象经过第一象限,且,求S的取值范围.
20.如图,在中,于点D,E为上一点,连结交于点F,且,.
(1)求证:.
(2)若,,求的长.
21.如图,为矩形的对角线,将边沿折叠,使点落在上的点处,将边沿折叠,使点落在上的点处.
(1)求证:四边形是平行四边形;
(2)若,,求四边形的面积.
22.大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用来表示的小数部分,因为的整数部分是1,将减去其整数部分,差就是其小数部分.请解答:
(1)的整数部分是________,小数部分是________;
(2)如果的整数部分是,的小数部分是,求的值;
(3)如果的整数部分是,小数部分是,求的值.
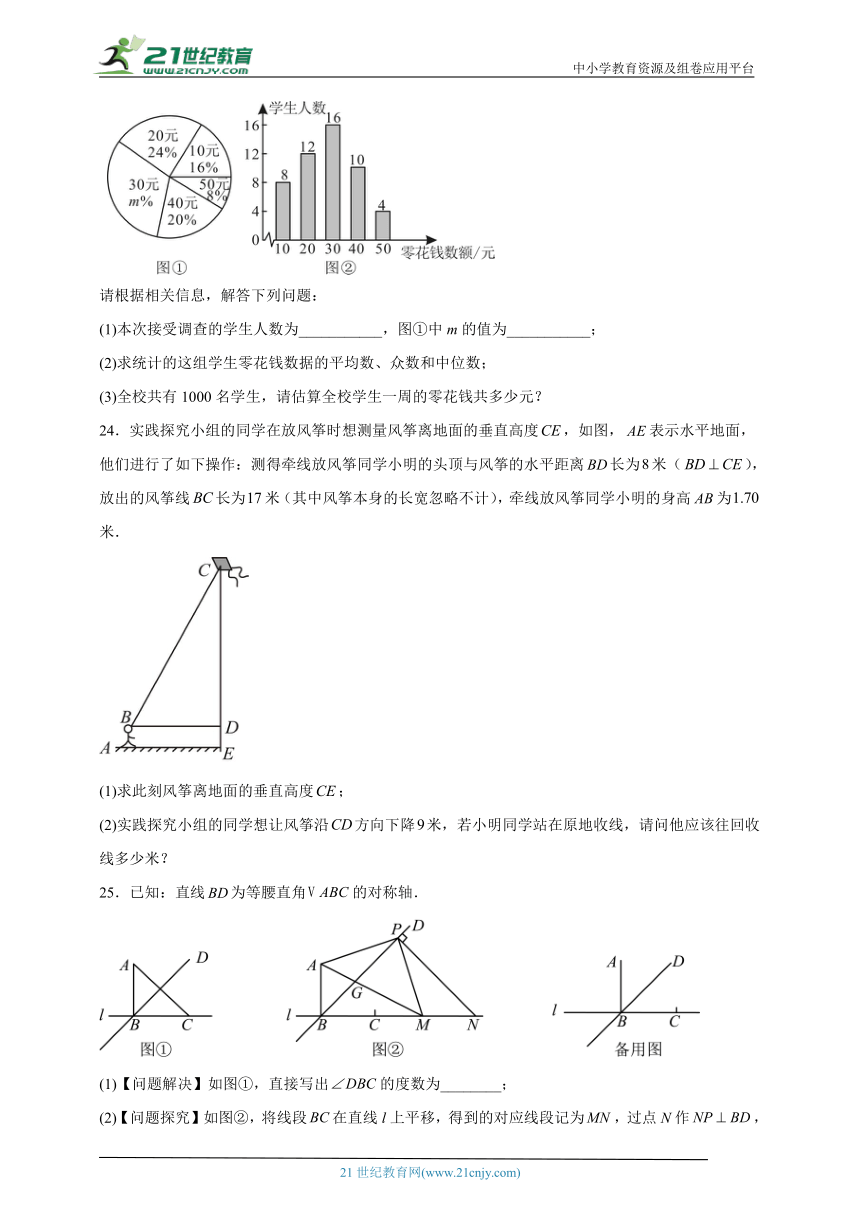
23.某中学为了增强学生勤俭节约的意识,随机调查了本校部分学生每人一周的零花钱数额(单位:元).根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)本次接受调查的学生人数为___________,图①中m的值为___________;
(2)求统计的这组学生零花钱数据的平均数、众数和中位数;
(3)全校共有1000名学生,请估算全校学生一周的零花钱共多少元?
24.实践探究小组的同学在放风筝时想测量风筝离地面的垂直高度,如图,表示水平地面,他们进行了如下操作:测得牵线放风筝同学小明的头顶与风筝的水平距离长为米(),放出的风筝线长为米(其中风筝本身的长宽忽略不计),牵线放风筝同学小明的身高为米.
(1)求此刻风筝离地面的垂直高度;
(2)实践探究小组的同学想让风筝沿方向下降米,若小明同学站在原地收线,请问他应该往回收线多少米?
25.已知:直线为等腰直角的对称轴.
(1)【问题解决】如图①,直接写出的度数为________;
(2)【问题探究】如图②,将线段在直线l上平移,得到的对应线段记为,过点N作,垂足为点P.连接与交于点G.求证:;
(3)【拓展延伸】在(2)的条件下,在直线l上运动,当时,直接写出的值.
《期末押题卷-2024-2025学年数学八年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 B D C C D A D D
1.B
【分析】本题主要考查了一次函数的性质,一次函数(k,b为常数),当时, y随x的增大而增大,当时, y随x的增大而减小,熟练掌握一次函数的性质是解题的关键.根据函数的解析式判断出函数的增减性,再根据即可得出结论.
【详解】解:中,
y随x的增大而增大,
,
,
故选B.
2.D
【分析】本题考查了勾股定理的逆定理,熟练掌握定理是解题的关键.
利用勾股定理的逆定理,进行计算逐一判断即可解答.
【详解】解:∵,
∴三角形不是直角三角形,故A选项不符合题意;
∵,
∴三角形不是直角三角形,故B选项不符合题意;
∵,
∴三角形不是直角三角形,故C选项不符合题意;
∵,
∴三角形是直角三角形,故D选项符合题意;
故选:D.
3.C
【分析】根据最简二次根式的定义判断即可.
本题考查了最简二次根式,熟练掌握定义是解题的关键.
【详解】A. ,不符合题意;
B. ,不是二次根式,不符合题意;
C. ,符合题意;
D. ,不符合题意;
故选:C.
4.C
【分析】本题考查直角三角形斜边上的中线的性质,熟练掌握斜边上的中线等于斜边的一半是解题的关键.
根据斜边上的中线等于斜边的一半即可得出结果.
【详解】解:中,,,点为斜边上的中点,
;
故选:C
5.D
【分析】本题考查一次函数与一元一次不等式,根据一次函数的图象,进行求解即可.
【详解】解:由图象可知,随的增大而减小,当时,,
∴当时,的取值范围是;
故选D.
6.A
【分析】本题主要考查一次函数的图象与性质,熟练掌握一次函数的图象与性质是解题的关键;根据题意易得,则有,然后问题可求解.
【详解】解:由点,在一次函数的图像上,且,可知:,
∴,
故选A.
7.D
【分析】根据全等三角形的性质、三角形内角和定理、一次函数的性质、不等式的性质判断即可.
【详解】解:A、全等三角形的面积相等,是真命题,不符合题意;
B、三角形三个内角的和等于,是真命题,不符合题意;
C、若函数的图象与函数的图象平行,则,是真命题,不符合题意;
D、当,时,或,故本选项命题是假命题,符合题意;
故选: D
【点睛】本题考查的是命题与定理,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
8.D
【分析】本题考查了勾股定理,平行线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.过点作,垂足为点,从而可得,再利用平行线的性质可得,从而可得是等边三角形,然后利用等边三角形的性质可得,,再根据平行线的性质可得:,从而可得,进而可得,最后根据等边三角形的判定可得:是等边三角形,从而可得,再利用直角三角形的两个锐角互余可得:,从而中,利用含30度角的直角三角形性质可得,再利用勾股定理求出的长,从而进行计算即可解答.
【详解】解:过点作,垂足为点,
,
,
,
,
是等边三角形,
,,
,
,
,
,
,
,
是等边三角形,
,
,
,,
,
,
,
,
折叠后椅子比完全打开时高,
故选:D.
9.且
【分析】本题主要考查了求自变量的取值范围,分式和二次根式有意义的条件,分式有意义的条件是被开方数大于等于0,二次根式有意义的条件是分母不为0,据此求解即可.
【详解】解;∵有意义,
∴,
∴且,
故答案为:且.
10.>
【分析】本题主要考查了比较一次函数值的大小,熟练掌握相关知识是解题的关键.
根据函数解析式可得y随x增大而减小,由即可得答案.
【详解】解:∵一次函数解析式为,,
∴y随x增大而减小,
∵点都在一次函数的图象上,,
∴,
故答案为:.
11.5
【分析】本题考查勾股定理在实际情况中应用,解题关键是注意运用隐含的已知条件来解答此类题.
根据风车外围的周长可求出“数学风车”的斜边,再通过勾股定理可将“数学风车”的直角边求出.
【详解】解:根据题意,得,
∴,
,
,即,
,
故答案为:5.
12.150
【分析】本题主要考查了求一组数据的众数,熟练掌握众数的定义,是解题的关键.根据众数是指一组数据中出现次数最多的数,进行解答即可.
【详解】解:136,150,123,87,36,150,36,150中,150出现次数最多,因此这8场流星雨的最大天顶流量的数据的众数是150.
故答案为:150.
13.或
【分析】本题考查了一次函数与线段相交求参数问题,理解经过两点求得的临界值是解题的关键.要使直线与线段有交点,分别将代入,求得的临界值即可.
【详解】解:∵,
∴直线过定点.
当直线经过点时,
解得:
当直线经过点时,
解得:
或
故答案为:或.
14. 或
【分析】本题考查的是一次函数的图象与性质,求解一次函数的解析式以及交点坐标,当时,求解,结合可得,可得直线为,再求解交点坐标即可;求解,,,,利用,,再建立方程组求解即可.
【详解】解:(1)当时,直线为:,
当时,,
解得:,
∴,
∵,
∴,
∴,
∴,
解得:,
∴直线为,
∴,
解得:,
∴;
故答案为:;
(2)∵直线:,直线:,
同理可得:,,,,
∵,,
∴,
解得:或;
故答案为:或.
15.2
【分析】本题考查矩形的性质,勾股定理,直角三角形斜边中线的性质,两点之间,线段最短等知识,解题的关键是学会添加常用辅助线,应用直角三角形性质解决问题.
取的中点O,连接,,证明,推出,点M在以O为圆心,4为半径的上,利用勾股定理求出,可得结论.
【详解】解:如图,取的中点O,连接,.
∵四边形是矩形,
∴,,
∴,
∵,
∴,
∴,
∵点O是的中点
∴,
∴,
∴点M在以O为圆心,4为半径的上,
∵
∴
∴的最小值为2.
故答案为:2.
16.
【分析】连接,,根据折叠性质可求出,设,利用勾股定理求出,再利用勾股定理求出的长,判定出四边形为菱形,根据菱形面积的求解可求出最后结果.
【详解】解:如图,连接,,
∵折叠,点D与点B重合,
,
设,
,,
在中,
,
解得:,
,
,
∵四边形是矩形,,
,,
,
四边形为平行四边形,
四边形为菱形,
,
,
故答案为:.
【点睛】本题考查了平行四边形的判定与性质,等腰三角形的判定与性质,菱形的判定与性质,勾股定理,折叠的性质,熟练掌握相关性质定理为解题关键.
17.
【分析】本题考查了二次根式的混合运算,熟练掌握二次根式的混合运算法则是解答本题的关键.
先计算二次根式的乘法和除法,最后合并同类项即可.
【详解】解:,
,
,
.
18.(1)
(2)购进A型电动自行车10辆、B型电动自行车20辆才能获得最大利润,此时最大利润是13000元
【分析】本题考查一次函数的应用,根据题意写出函数关系式、掌握一次函数的增减性是解题的关键.
(1)根据“利润型电动自行车的总利润型电动自行车的总利润”写出y与x之间的函数关系式,并标明x的取值范围即可;
(2)根据(1)求得的一次函数的增减性和x的取值范围,确定当x为何值时y值最大,求出其最大值及此时的值即可.
【详解】(1)解:根据题意,得,
与x之间的函数关系式为;
(2)解:,
随x的减小而增大,
,
当时,y值最大,,
(辆);
答:购进A型电动自行车10辆、B型电动自行车20辆才能获得最大利润,此时最大利润是13000元.
19.(1)
(2)
(3)
【分析】本题考查了一次函数的图象和性质,待定系数法求解析式,正确求出函数解析式是解题的关键.
(1)一次函数(k,b为常数,且)的图象经过点,得到,再结合,解二元一次方程组求解即可;
(2)根据题意可得一次函数y随x的增大而减小,可得当时,,结合一次函数(k,b为常数,且)的图象经过点,得到,解二元一次方程组求解即可;
(3)根据,即,进而得到,再根据一次函数的图象经过第一象限,可得到,由不等式的性质即可解答.
【详解】(1)解:∵一次函数(k,b为常数,且)的图象经过点,
∴,
∵,
∴,
解得:,
∴一次函数的表达式为:;
(2)解:∵,
∴一次函数y随x的增大而减小,
∵当时,该一次函数的最大值为6,
∴当时,,
∵一次函数(k,b为常数,且)的图象经过点,
∴,
∴,
解得:;
(3)解:根据题意:,即,
∴,
∵一次函数的图象经过第一象限,且,
∴,
∴,
∴.
20.(1)见解析
(2)
【分析】此题考查全等三角形的判定和性质,勾股定理,关键是掌握全等三角形的判定方法.
(1)根据,得出,再根据证明,即可推出结论;
(2)根据,得出,由,利用勾股定理即可求出,进而得到,由即可得到结果.
【详解】(1)证明:∵,
∴,
∵,,
∴,
∴.
(2)解:∵,,,
∴,
∵,
∴,
∴,
∴.
21.(1)见解析;
(2).
【分析】根据矩形的性质可知,所以可证,根据角平分线的性质可证,从而可证,根据两组对边分别平行的四边形是平行四边形可证结论成立;
根据勾股定理可求,设,则,利用勾股定理可得关于的方程,解方程求出的值,即为,可知,利用平行四边形的面积公式可求结果.
【详解】(1)证明:四边形是矩形,
,,
,
根据折叠的性质可知,,
,
,
四边形是平行四边形;
(2)解:,,
,
设,则,
,,
,
在中,,
,
解得:,
,
,
四边形的面积为.
【点睛】本题考查了矩形的性质、平行四边形的判定与性质、角平分线的性质、平行四边形的面积公式.
22.(1)3,
(2)
(3)
【分析】本题主要考查了二次根式运算、无理数的估算等知识点,正确进行无理数的估算是解题的关键,
(1)根据无理数的估算解答即可;
(2)根据无理数的估算求出、,计算即可;
(3)根据无理数的估算求出、,代入所求代数式,再进行分母有理化即可.
【详解】(1)解:,
,
的整数部分是3,小数部分是,
故答案为:3,;
(2)解:,
,
的整数部分为,
,
,
的小数部分是,
;
(3)解:,
,
,
的整数部分是,小数部分是,
.
23.(1)50人,32
(2)28,30,30
(3)28000元
【分析】(1)根据条形统计各组数据相加即可得到接受调查的总人数,用零花钱为30元的人数除以总人数即可其求解;
(2)根据平均数、众数和中位数的定义即可求解;
(3)根据所调查的学生的一周零花钱的平均数乘以全校学生总人数即可求解.
本题考查了扇形统计图和条形统计图、平均数、众数、中位和用样本估计总体的知识,注重数形结合是解答本题的关键.
【详解】(1)解:依题意,接受调查的总人数为:(人),
则零花钱为30元的人数所占的比例为:,
即,
故答案为:50人,32;
(2)解:零花钱数据的平均数为:,
将调查的零花钱的数据从小到大排列:
可知众数为30,中位数为30;
(3)解:全校学生一周的零花钱为:(元).
24.(1)米
(2)米
【分析】此题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键;
(1)在中,由勾股定理得,进而根据,即可求解;
(2)设风筝沿方向下降米至点,进而勾股定理求得,根据,即可求解.
【详解】(1)解:由题意得:米,米,米,
在中,由勾股定理得:(米),
(米),
答:此刻风筝离地面的高度为米;
(2)如图,设风筝沿方向下降米至点,
则米,
(米),
(米),
(米),
答:放风筝的同学要使风筝沿方向下降米,若该同学站在原地收线,他应该往回收线米
25.(1)
(2)见解析
(3)或4
【分析】(1)根据轴对称的性质求解即可;
(2)利用证明,得出,,进而证出,最后根据勾股定理求解即可;
(3)分M在B的右侧和左侧讨论,然后根据勾股定理,角平分线的性质,等面积法等求解即可.
【详解】(1)解:∵直线为等腰直角的对称轴,,
∴,
故答案为:;
(2)证明:∵,,,
∴,,
∴,,
又,
∴,
∴,,
又,
∴,
∴;
(3)解:当M在B的右侧时,过P作于Q,过G作于H,于K,
设,则,,
∴,
由(2)知:,,
∵,
∴,
∴,
∵平分,
∴,
∴,即,
解得,
∵,,
∴,
∴,
∴,
∴;
当M在B的左侧时,过P作于Q,过G作于H,于K,
设,则,,
∴,
同理可求,
,即,
解得,
∵,,
∴,
∴,
∴,
∴;
综上,的值为或4.
【点睛】本题考查了轴对称的性质,平移的性质,勾股定理,全等三角形的判定与性质,等腰直角三角形的判定与性质等知识,添加合适辅助线是截图的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末押题卷-2024-2025学年数学八年级下册人教版
一、单选题
1.若函数的图象上有两点,,则下列说法正确的是( )
A. B. C. D.
2.下列长度的三条线段能组成直角三角形的是( )
A. B. C. D.
3.下列代数式中,是最简二次根式的是( )
A. B. C. D.
4.如图,在中,,,点为斜边上的中点,则的长为( )
A. B. C. D.
5.一次函数的图象如图所示,当时,的取值范围是( )
A. B. C. D.
6.若点,在一次函数的图像上,且.则下列的取值符合条件的是( )
A. B. C. D.
7.下列命题中是假命题的是( )
A.全等三角形的面积相等
B.三角形三个内角的和等于
C.若函数的图象与函数的图象平行,则
D.如果,,那么
8.如图(1)是一把折叠椅实物图,支架与交于点.如图(2)是椅子打开时的侧面示意图(忽略材料的厚度),椅面与地面水平线平行,,折叠后椅子比完全打开时高( ).
A.42 B. C. D.
二、填空题
9.在函数中,自变量x的取值范围是 .
10.已知点都在一次函数的图象上,则 .(填“>”或“<”)
11.“赵爽弦图”中,,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,这个风车的外围周长(虚线部分)为76,则 .
12.淇淇是一名天文爱好者,他统计了8场流星雨的最大天顶流量(单位:颗/小时)的数据,分别为136,150,123,87,36,150,36,150.这8场流星雨的最大天顶流量的数据的众数是 .
13.在平面直角坐标系中,已知点,直线与线段有交点,则k的取值范围为 .
14.直线与轴、轴分别相交于点、,直线与轴、轴分别相交于点、,两直线交点为.
(1)如图,当时,点的坐标为 ;
(2)若两点之间距离为2,则 .
15.如图,矩形中,,.点是边上一动点,点为线段上一动点.,则的最小值为 .
16.如图,长方形中,,,将此长方形折叠,使点与点重合,折痕为,则折痕的长为 cm.
三、解答题
17.计算:.
18.为了缓解环境污染的问题,某地禁止燃油助力车上路,于是电动自行车的市场需求量日渐增多.某商店计划购进A,B两种型号的电动自行车(两种型号都要购进)共30辆,其中A型电动自行车不少于10辆,A,B两种型号电动自行车的进货单价分别为2500元、3000元,售价分别为2800元、3500元,设该商店计划购进A型电动自行车x辆,两种型号的电动自行车全部销售后可获利润y元.
(1)求出y与x之间的函数关系式.
(2)该商店如何进货才能获得最大利润?此时最大利润是多少元?
19.已知一次函数(k,b为常数,且)的图象经过点.
(1)若,求一次函数的表达式.
(2)当时,该一次函数的最大值为6,求k的值.
(3)若该一次函数的图象经过第一象限,且,求S的取值范围.
20.如图,在中,于点D,E为上一点,连结交于点F,且,.
(1)求证:.
(2)若,,求的长.
21.如图,为矩形的对角线,将边沿折叠,使点落在上的点处,将边沿折叠,使点落在上的点处.
(1)求证:四边形是平行四边形;
(2)若,,求四边形的面积.
22.大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用来表示的小数部分,因为的整数部分是1,将减去其整数部分,差就是其小数部分.请解答:
(1)的整数部分是________,小数部分是________;
(2)如果的整数部分是,的小数部分是,求的值;
(3)如果的整数部分是,小数部分是,求的值.
23.某中学为了增强学生勤俭节约的意识,随机调查了本校部分学生每人一周的零花钱数额(单位:元).根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)本次接受调查的学生人数为___________,图①中m的值为___________;
(2)求统计的这组学生零花钱数据的平均数、众数和中位数;
(3)全校共有1000名学生,请估算全校学生一周的零花钱共多少元?
24.实践探究小组的同学在放风筝时想测量风筝离地面的垂直高度,如图,表示水平地面,他们进行了如下操作:测得牵线放风筝同学小明的头顶与风筝的水平距离长为米(),放出的风筝线长为米(其中风筝本身的长宽忽略不计),牵线放风筝同学小明的身高为米.
(1)求此刻风筝离地面的垂直高度;
(2)实践探究小组的同学想让风筝沿方向下降米,若小明同学站在原地收线,请问他应该往回收线多少米?
25.已知:直线为等腰直角的对称轴.
(1)【问题解决】如图①,直接写出的度数为________;
(2)【问题探究】如图②,将线段在直线l上平移,得到的对应线段记为,过点N作,垂足为点P.连接与交于点G.求证:;
(3)【拓展延伸】在(2)的条件下,在直线l上运动,当时,直接写出的值.
《期末押题卷-2024-2025学年数学八年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 B D C C D A D D
1.B
【分析】本题主要考查了一次函数的性质,一次函数(k,b为常数),当时, y随x的增大而增大,当时, y随x的增大而减小,熟练掌握一次函数的性质是解题的关键.根据函数的解析式判断出函数的增减性,再根据即可得出结论.
【详解】解:中,
y随x的增大而增大,
,
,
故选B.
2.D
【分析】本题考查了勾股定理的逆定理,熟练掌握定理是解题的关键.
利用勾股定理的逆定理,进行计算逐一判断即可解答.
【详解】解:∵,
∴三角形不是直角三角形,故A选项不符合题意;
∵,
∴三角形不是直角三角形,故B选项不符合题意;
∵,
∴三角形不是直角三角形,故C选项不符合题意;
∵,
∴三角形是直角三角形,故D选项符合题意;
故选:D.
3.C
【分析】根据最简二次根式的定义判断即可.
本题考查了最简二次根式,熟练掌握定义是解题的关键.
【详解】A. ,不符合题意;
B. ,不是二次根式,不符合题意;
C. ,符合题意;
D. ,不符合题意;
故选:C.
4.C
【分析】本题考查直角三角形斜边上的中线的性质,熟练掌握斜边上的中线等于斜边的一半是解题的关键.
根据斜边上的中线等于斜边的一半即可得出结果.
【详解】解:中,,,点为斜边上的中点,
;
故选:C
5.D
【分析】本题考查一次函数与一元一次不等式,根据一次函数的图象,进行求解即可.
【详解】解:由图象可知,随的增大而减小,当时,,
∴当时,的取值范围是;
故选D.
6.A
【分析】本题主要考查一次函数的图象与性质,熟练掌握一次函数的图象与性质是解题的关键;根据题意易得,则有,然后问题可求解.
【详解】解:由点,在一次函数的图像上,且,可知:,
∴,
故选A.
7.D
【分析】根据全等三角形的性质、三角形内角和定理、一次函数的性质、不等式的性质判断即可.
【详解】解:A、全等三角形的面积相等,是真命题,不符合题意;
B、三角形三个内角的和等于,是真命题,不符合题意;
C、若函数的图象与函数的图象平行,则,是真命题,不符合题意;
D、当,时,或,故本选项命题是假命题,符合题意;
故选: D
【点睛】本题考查的是命题与定理,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
8.D
【分析】本题考查了勾股定理,平行线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.过点作,垂足为点,从而可得,再利用平行线的性质可得,从而可得是等边三角形,然后利用等边三角形的性质可得,,再根据平行线的性质可得:,从而可得,进而可得,最后根据等边三角形的判定可得:是等边三角形,从而可得,再利用直角三角形的两个锐角互余可得:,从而中,利用含30度角的直角三角形性质可得,再利用勾股定理求出的长,从而进行计算即可解答.
【详解】解:过点作,垂足为点,
,
,
,
,
是等边三角形,
,,
,
,
,
,
,
,
是等边三角形,
,
,
,,
,
,
,
,
折叠后椅子比完全打开时高,
故选:D.
9.且
【分析】本题主要考查了求自变量的取值范围,分式和二次根式有意义的条件,分式有意义的条件是被开方数大于等于0,二次根式有意义的条件是分母不为0,据此求解即可.
【详解】解;∵有意义,
∴,
∴且,
故答案为:且.
10.>
【分析】本题主要考查了比较一次函数值的大小,熟练掌握相关知识是解题的关键.
根据函数解析式可得y随x增大而减小,由即可得答案.
【详解】解:∵一次函数解析式为,,
∴y随x增大而减小,
∵点都在一次函数的图象上,,
∴,
故答案为:.
11.5
【分析】本题考查勾股定理在实际情况中应用,解题关键是注意运用隐含的已知条件来解答此类题.
根据风车外围的周长可求出“数学风车”的斜边,再通过勾股定理可将“数学风车”的直角边求出.
【详解】解:根据题意,得,
∴,
,
,即,
,
故答案为:5.
12.150
【分析】本题主要考查了求一组数据的众数,熟练掌握众数的定义,是解题的关键.根据众数是指一组数据中出现次数最多的数,进行解答即可.
【详解】解:136,150,123,87,36,150,36,150中,150出现次数最多,因此这8场流星雨的最大天顶流量的数据的众数是150.
故答案为:150.
13.或
【分析】本题考查了一次函数与线段相交求参数问题,理解经过两点求得的临界值是解题的关键.要使直线与线段有交点,分别将代入,求得的临界值即可.
【详解】解:∵,
∴直线过定点.
当直线经过点时,
解得:
当直线经过点时,
解得:
或
故答案为:或.
14. 或
【分析】本题考查的是一次函数的图象与性质,求解一次函数的解析式以及交点坐标,当时,求解,结合可得,可得直线为,再求解交点坐标即可;求解,,,,利用,,再建立方程组求解即可.
【详解】解:(1)当时,直线为:,
当时,,
解得:,
∴,
∵,
∴,
∴,
∴,
解得:,
∴直线为,
∴,
解得:,
∴;
故答案为:;
(2)∵直线:,直线:,
同理可得:,,,,
∵,,
∴,
解得:或;
故答案为:或.
15.2
【分析】本题考查矩形的性质,勾股定理,直角三角形斜边中线的性质,两点之间,线段最短等知识,解题的关键是学会添加常用辅助线,应用直角三角形性质解决问题.
取的中点O,连接,,证明,推出,点M在以O为圆心,4为半径的上,利用勾股定理求出,可得结论.
【详解】解:如图,取的中点O,连接,.
∵四边形是矩形,
∴,,
∴,
∵,
∴,
∴,
∵点O是的中点
∴,
∴,
∴点M在以O为圆心,4为半径的上,
∵
∴
∴的最小值为2.
故答案为:2.
16.
【分析】连接,,根据折叠性质可求出,设,利用勾股定理求出,再利用勾股定理求出的长,判定出四边形为菱形,根据菱形面积的求解可求出最后结果.
【详解】解:如图,连接,,
∵折叠,点D与点B重合,
,
设,
,,
在中,
,
解得:,
,
,
∵四边形是矩形,,
,,
,
四边形为平行四边形,
四边形为菱形,
,
,
故答案为:.
【点睛】本题考查了平行四边形的判定与性质,等腰三角形的判定与性质,菱形的判定与性质,勾股定理,折叠的性质,熟练掌握相关性质定理为解题关键.
17.
【分析】本题考查了二次根式的混合运算,熟练掌握二次根式的混合运算法则是解答本题的关键.
先计算二次根式的乘法和除法,最后合并同类项即可.
【详解】解:,
,
,
.
18.(1)
(2)购进A型电动自行车10辆、B型电动自行车20辆才能获得最大利润,此时最大利润是13000元
【分析】本题考查一次函数的应用,根据题意写出函数关系式、掌握一次函数的增减性是解题的关键.
(1)根据“利润型电动自行车的总利润型电动自行车的总利润”写出y与x之间的函数关系式,并标明x的取值范围即可;
(2)根据(1)求得的一次函数的增减性和x的取值范围,确定当x为何值时y值最大,求出其最大值及此时的值即可.
【详解】(1)解:根据题意,得,
与x之间的函数关系式为;
(2)解:,
随x的减小而增大,
,
当时,y值最大,,
(辆);
答:购进A型电动自行车10辆、B型电动自行车20辆才能获得最大利润,此时最大利润是13000元.
19.(1)
(2)
(3)
【分析】本题考查了一次函数的图象和性质,待定系数法求解析式,正确求出函数解析式是解题的关键.
(1)一次函数(k,b为常数,且)的图象经过点,得到,再结合,解二元一次方程组求解即可;
(2)根据题意可得一次函数y随x的增大而减小,可得当时,,结合一次函数(k,b为常数,且)的图象经过点,得到,解二元一次方程组求解即可;
(3)根据,即,进而得到,再根据一次函数的图象经过第一象限,可得到,由不等式的性质即可解答.
【详解】(1)解:∵一次函数(k,b为常数,且)的图象经过点,
∴,
∵,
∴,
解得:,
∴一次函数的表达式为:;
(2)解:∵,
∴一次函数y随x的增大而减小,
∵当时,该一次函数的最大值为6,
∴当时,,
∵一次函数(k,b为常数,且)的图象经过点,
∴,
∴,
解得:;
(3)解:根据题意:,即,
∴,
∵一次函数的图象经过第一象限,且,
∴,
∴,
∴.
20.(1)见解析
(2)
【分析】此题考查全等三角形的判定和性质,勾股定理,关键是掌握全等三角形的判定方法.
(1)根据,得出,再根据证明,即可推出结论;
(2)根据,得出,由,利用勾股定理即可求出,进而得到,由即可得到结果.
【详解】(1)证明:∵,
∴,
∵,,
∴,
∴.
(2)解:∵,,,
∴,
∵,
∴,
∴,
∴.
21.(1)见解析;
(2).
【分析】根据矩形的性质可知,所以可证,根据角平分线的性质可证,从而可证,根据两组对边分别平行的四边形是平行四边形可证结论成立;
根据勾股定理可求,设,则,利用勾股定理可得关于的方程,解方程求出的值,即为,可知,利用平行四边形的面积公式可求结果.
【详解】(1)证明:四边形是矩形,
,,
,
根据折叠的性质可知,,
,
,
四边形是平行四边形;
(2)解:,,
,
设,则,
,,
,
在中,,
,
解得:,
,
,
四边形的面积为.
【点睛】本题考查了矩形的性质、平行四边形的判定与性质、角平分线的性质、平行四边形的面积公式.
22.(1)3,
(2)
(3)
【分析】本题主要考查了二次根式运算、无理数的估算等知识点,正确进行无理数的估算是解题的关键,
(1)根据无理数的估算解答即可;
(2)根据无理数的估算求出、,计算即可;
(3)根据无理数的估算求出、,代入所求代数式,再进行分母有理化即可.
【详解】(1)解:,
,
的整数部分是3,小数部分是,
故答案为:3,;
(2)解:,
,
的整数部分为,
,
,
的小数部分是,
;
(3)解:,
,
,
的整数部分是,小数部分是,
.
23.(1)50人,32
(2)28,30,30
(3)28000元
【分析】(1)根据条形统计各组数据相加即可得到接受调查的总人数,用零花钱为30元的人数除以总人数即可其求解;
(2)根据平均数、众数和中位数的定义即可求解;
(3)根据所调查的学生的一周零花钱的平均数乘以全校学生总人数即可求解.
本题考查了扇形统计图和条形统计图、平均数、众数、中位和用样本估计总体的知识,注重数形结合是解答本题的关键.
【详解】(1)解:依题意,接受调查的总人数为:(人),
则零花钱为30元的人数所占的比例为:,
即,
故答案为:50人,32;
(2)解:零花钱数据的平均数为:,
将调查的零花钱的数据从小到大排列:
可知众数为30,中位数为30;
(3)解:全校学生一周的零花钱为:(元).
24.(1)米
(2)米
【分析】此题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键;
(1)在中,由勾股定理得,进而根据,即可求解;
(2)设风筝沿方向下降米至点,进而勾股定理求得,根据,即可求解.
【详解】(1)解:由题意得:米,米,米,
在中,由勾股定理得:(米),
(米),
答:此刻风筝离地面的高度为米;
(2)如图,设风筝沿方向下降米至点,
则米,
(米),
(米),
(米),
答:放风筝的同学要使风筝沿方向下降米,若该同学站在原地收线,他应该往回收线米
25.(1)
(2)见解析
(3)或4
【分析】(1)根据轴对称的性质求解即可;
(2)利用证明,得出,,进而证出,最后根据勾股定理求解即可;
(3)分M在B的右侧和左侧讨论,然后根据勾股定理,角平分线的性质,等面积法等求解即可.
【详解】(1)解:∵直线为等腰直角的对称轴,,
∴,
故答案为:;
(2)证明:∵,,,
∴,,
∴,,
又,
∴,
∴,,
又,
∴,
∴;
(3)解:当M在B的右侧时,过P作于Q,过G作于H,于K,
设,则,,
∴,
由(2)知:,,
∵,
∴,
∴,
∵平分,
∴,
∴,即,
解得,
∵,,
∴,
∴,
∴,
∴;
当M在B的左侧时,过P作于Q,过G作于H,于K,
设,则,,
∴,
同理可求,
,即,
解得,
∵,,
∴,
∴,
∴,
∴;
综上,的值为或4.
【点睛】本题考查了轴对称的性质,平移的性质,勾股定理,全等三角形的判定与性质,等腰直角三角形的判定与性质等知识,添加合适辅助线是截图的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
