北师大版五年级数学下册期末考试满分冲刺质量检测卷一(含解析)
文档属性
| 名称 | 北师大版五年级数学下册期末考试满分冲刺质量检测卷一(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 937.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版五年级数学下册期末考试满分冲刺质量检测卷一
一、填空题(共20分)
1.(2分)一个西瓜,爸爸吃了它的,妈妈吃了它的,爸爸和妈妈一共吃了它的( ),还剩下它的( )。
2.(2分)有两个完全相同的长方体木料,长为20分米,宽为12分米,高为2分米,如果要合成一个长方体,它的表面积最大为( ),最小为( )。
3.(2分)集邮可以加深我们对不同国家、地区、动植物、历史事件等的了解。小周和爸爸都喜欢集邮,小周收集了各种邮票56张,爸爸收集的邮票数比小周多,爸爸比小周多收集( )张邮票。
4.(2分)某风景区票价90元/人,“六一”特价:成人九折,儿童半价。这天小明和爸爸妈妈一块去这里游玩,可以节省( )元。
5.(2分)如图,在一个长方体容器中,放入一个西红柿后(完全浸没),水面高度上升到12厘米(没有溢出)。西红柿的体积是( )立方厘米。
6.(2分)( )cm3 85立方厘米=( )毫升=( )升
7.(2分)小明比姐姐小6岁,姐姐的年龄是小明的3倍,姐姐的年龄是妈妈的,妈妈今年( )岁,小明今年( )岁。
8.(2分)如图,以学校为观察点,博物馆在学校的( )方向上,距离学校( )米。
9.(2分)哥哥和弟弟身上各有一些钱,已知哥哥身上的钱是弟弟的5倍,如果哥哥给弟弟80.5元,则哥哥的钱还比弟弟多21元,原来弟弟身上有( )元。
10.(2分)在演讲比赛中,评委给王明打出的分数分别是87分、93分、94分、95分、98分、85分、 92分、91分。按比赛规则,计算选手的平均得分要先去掉一个最高分和一个最低分,再计算。因此,王明的实际得分是( )分。
二、选择题(共10分)
11.(2分)工厂计划本月生产一批零件。实际生产时发现上半月完成计划的,下半月完成计划的,下面说法正确的是( )。
A.本月生产计划没有完成 B.本月实际产量是计划的
C.本月实际产量超过计划的 D.本月产量超过计划的主要原因是上半月生产效率高
12.(2分)一个长方体木块正好能锯成两个小正方体,如果每个小正方体的表面积是6平方分米,那么原来长方体的表面积是( )平方分米。
A.12 B.10 C.8 D.6
13.(2分)下列算式结果最大的是( )。
A.× B.× C.+ D.-
14.(2分)图中,甲、乙两个立体图形的表面积( ),体积( )。
A.甲>乙;甲<乙 B.甲<乙;甲>乙
C.甲<乙;甲=乙 D.无法判断;无法判断
15.(2分)图书馆在公园西偏南30°的方向,那么公园在图书馆( )的方向。
A.南偏西30° B.东偏北30° C.北偏东30° D.南偏西60°
三、判断题(共10分)
16.(2分)一根绳子对折再对折,量得每段长米,这根绳子原来的长度是5米。( )
17.(2分)根据下图可列方程为。( )
18.(2分)小丽参加“中英文风采”大赛,5个评委给她的评分是:97分,96分,88分,90分,93分,去掉最高分和最低分后她的平均得分是92分。( )
19.(2分)用两个棱长为1厘米的正方体拼成一个长方体,长方体的表面积是12平方厘米。( )
20.(2分)x=1,那么x=。( )
四、计算题(共12分)
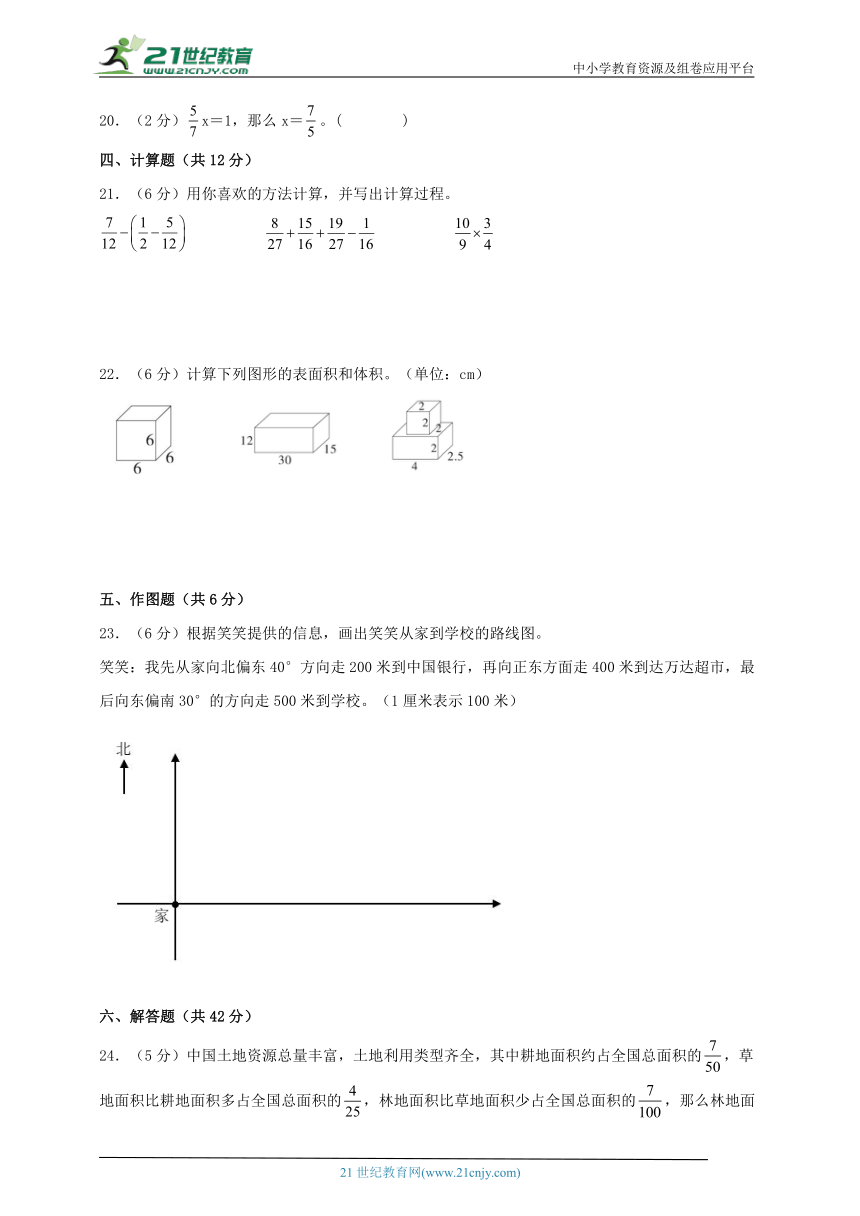
21.(6分)用你喜欢的方法计算,并写出计算过程。
22.(6分)计算下列图形的表面积和体积。(单位:cm)
五、作图题(共6分)
23.(6分)根据笑笑提供的信息,画出笑笑从家到学校的路线图。
笑笑:我先从家向北偏东40°方向走200米到中国银行,再向正东方面走400米到达万达超市,最后向东偏南30°的方向走500米到学校。(1厘米表示100米)
六、解答题(共42分)
24.(5分)中国土地资源总量丰富,土地利用类型齐全,其中耕地面积约占全国总面积的,草地面积比耕地面积多占全国总面积的,林地面积比草地面积少占全国总面积的,那么林地面积约占全国总面积的几分之几?
25.(5分)建设美丽校园,共享绿色文明。桃源小学在今年植树节活动中,共植树1050棵,其中是杨树,是槐树,哪种树种植得多?多多少棵?
26.(5分)将两盒糖果包装成一包,怎样包装才能最节省包装纸?(画出草图)需要包装纸的面积是多少平方厘米?
27.(5分)两袋大米,第二袋比第一袋重15千克,已知第一袋大米的恰好与第二袋的相等,两袋大米各重多少千克?(先写出等量关系式,再列方程解答问题)
等量关系式:
列方程解答:
28.(5分)惠东南站是厦深铁路上18个客运站之一,距离深圳北站88千米,为沿线县级车站之最。已知甲动车从惠东南站出发,每分行驶2千米,行驶11分钟后,乙动车才从深圳北站出发,每分行驶1.3千米,乙动车出发多少分后两车相遇?
29.(8分)AI智能模块化鱼缸是一款科技感十足的智能鱼缸,它拥有自动定时喂食、自动清洁等多种功能,让养鱼这件事变得更加简单。张大爷家的智能鱼缸是长60厘米,宽和高都是40厘米的长方体。
(1)鱼缸的四周是钢化玻璃,为了防止玻璃自爆,需要在玻璃上贴一层防爆膜,一共需要贴多少平方米的防爆膜?(损耗忽略不计)
(2)鱼缸中放有一块高为24厘米,体积为1100立方厘米的假山石(如图),如果向鱼缸内注水,那么至少需要注入多少立方分米的水才能将假山石完全淹没?
30.(9分)下面是某大药房2023年1-5月消毒液、感冒药的销售情况统计表。
(1)根据上表中的数据,画出折线统计图。
(2)( )月到( )月感冒药销售数量降低最多。
(3)消毒液销售数量的变化趋势是( ),消毒液平均每月销售( )箱。
答案解析
一、填空题(共20分)
1.(2分)一个西瓜,爸爸吃了它的,妈妈吃了它的,爸爸和妈妈一共吃了它的( ),还剩下它的( )。
【答案】
【分析】根据题意,将整个西瓜看作单位“1”,爸爸吃了它的,妈妈吃了它的,用加法可以求出爸爸和妈妈一共吃了它的几分之几;用单位“1”减去爸爸妈妈一共吃了它的几分之几,即可求出还剩下它的几分之几。
【详解】由分析可得:
+=+=
1-=
综上所述:一个西瓜,爸爸吃了它的,妈妈吃了它的,爸爸和妈妈一共吃了它的,还剩下它的。
2.(2分)有两个完全相同的长方体木料,长为20分米,宽为12分米,高为2分米,如果要合成一个长方体,它的表面积最大为( ),最小为( )。
【答案】 1168平方分米/1168dm2 736平方分米/736dm2
【分析】将最小的两个面(左右面)拼起来,合成的长方体表面积最大;将最大的两个面(上下面)拼起来,合成的长方体表面积最小。
根据长方体表面积=(长×宽+长×高+宽×高)×2,求出两个长方体木料的面积和,分别减去最小两个面和最大两个面即可。
【详解】(20×12+20×2+12×2)×2×2
=(240+40+24)×2×2
=304×2×2
=1216(平方分米)
1216-12×2×2
=1216-48
=1168(平方分米)
1216-20×12×2
=1216-480
=736(平方分米)
它的表面积最大为1168平方分米,最小为736平方分米。
3.(2分)集邮可以加深我们对不同国家、地区、动植物、历史事件等的了解。小周和爸爸都喜欢集邮,小周收集了各种邮票56张,爸爸收集的邮票数比小周多,爸爸比小周多收集( )张邮票。
【答案】21
【分析】把小周收集的邮票数看作单位“1”,要求爸爸比小周多收集的邮票数,就是求小周邮票数的是多少,用乘法计算。
【详解】56×=21(张)
所以爸爸比小周多收集21张邮票。
4.(2分)某风景区票价90元/人,“六一”特价:成人九折,儿童半价。这天小明和爸爸妈妈一块去这里游玩,可以节省( )元。
【答案】63
【分析】九折就是,半价就是原价的,用原价×,求景区成人一张票价;用原价×,求景区儿童票价;再用原价-九折后的票价,求出一张成人票节省的钱数,再乘2,求出爸爸妈妈节省的钱数;再用原价-儿童票价,求出小明节省的钱数,再把节省的钱数相加,即可解答。
【详解】九折就是,半价就是原价的。
90×=81(元)
90×=45(元)
(90-81)×2+(90-45)
=9×2+45
=18+45
=63(元)
某风景区票价90元/人,“六一”特价:成人九折,儿童半价。这天小明和爸爸妈妈一块去这里游玩,可以节省63元。
5.(2分)如图,在一个长方体容器中,放入一个西红柿后(完全浸没),水面高度上升到12厘米(没有溢出)。西红柿的体积是( )立方厘米。
【答案】300
【分析】通过观察可知,西红柿的体积相当于水面上升的体积,根据水面上升的体积=容器的长×宽×上升部分的高度,代入数据解答。
【详解】15×10×(12-10)
=15×10×2
=300(立方厘米)
西红柿的体积是300立方厘米。
6.(2分)( )cm3 85立方厘米=( )毫升=( )升
【答案】 6020 85 0.085
【分析】1dm3=1000cm3;1立方厘米=1毫升;1升=1000立方厘米;高级单位换算成低级单位,乘进率;低级单位换算成高级单位,除以进率,据此解答。
【详解】6.02dm3=6.02×1000=6020cm3
85立方厘米=85×1=85毫升
85立方厘米=85÷1000=0.085升
85立方厘米=85毫升=0.085升
7.(2分)小明比姐姐小6岁,姐姐的年龄是小明的3倍,姐姐的年龄是妈妈的,妈妈今年( )岁,小明今年( )岁。
【答案】 36 3
【分析】假设小明今年岁,那么姐姐今年岁,姐姐的年龄是小明的3倍,即小明的年龄×3=姐姐的年龄,据此列方程求解,即可算出姐姐和小明今年几岁,姐姐的年龄是妈妈的,所以妈妈的年龄=姐姐的年龄÷,据此解答。
【详解】解:假设小明今年岁,那么姐姐今年岁,
姐姐:(岁)
妈妈:
(岁)
即妈妈今年36岁,小明今年3岁。
8.(2分)如图,以学校为观察点,博物馆在学校的( )方向上,距离学校( )米。
【答案】 东偏北30° 500
【分析】在地图上按照“上北下南,左西右东”确定方向,结合图上标注的信息和数据,注意观测点是学校,据此解答。
【详解】观察图可知:以学校为观察点,博物馆在学校的东偏北30°方向上,距离学校500米。
【点睛】本题主要考查学生的方位感和对基本方向的辨别。
9.(2分)哥哥和弟弟身上各有一些钱,已知哥哥身上的钱是弟弟的5倍,如果哥哥给弟弟80.5元,则哥哥的钱还比弟弟多21元,原来弟弟身上有( )元。
【答案】45.5
【分析】设原来弟弟身上有x元,哥哥身上的钱是弟弟的5倍,则哥哥有5x元;如果哥哥给弟弟80.5元,则哥哥的钱还比弟弟多21元;哥哥钱数-80.5元,比弟弟的钱数+80.5元还多21元,列方程:5x-80.5-(x+80.5)=21,解方程,即可解答。
【详解】解:设原来弟弟身上有x元,则哥哥有5x元。
5x-80.5-(x+80.5)=21
5x-80.5-x-80.5=21
4x-161=21
4x=21+161
4x=182
x=182÷4
x=45.5
哥哥和弟弟身上各有一些钱,已知哥哥身上的钱是弟弟的5倍,如果哥哥给弟弟80.5元,则哥哥的钱还比弟弟多21元,原来弟弟身上有45.5元。
【点睛】根据方程的实际应用,利用哥哥和弟弟身上的钱数之间的关系,设出未知数,找出相关的量,列方程,解方程。
10.(2分)在演讲比赛中,评委给王明打出的分数分别是87分、93分、94分、95分、98分、85分、 92分、91分。按比赛规则,计算选手的平均得分要先去掉一个最高分和一个最低分,再计算。因此,王明的实际得分是( )分。
【答案】92
【分析】去掉最高分98分和最低分85分,根据平均数=总数÷数据个数,代入数据计算即可。
【详解】(87+93+94+95+92+91)÷6
=(180+94+95+92+91)÷6
=(274+95+92+91)÷6
=(369+92+91)÷6
=(461+91)÷6
=552÷6
=92(分)
在演讲比赛中,评委给王明打出的分数分别是87分、93分、94分、95分、98分、85分、 92分、91分。按比赛规则,计算选手的平均得分要先去掉一个最高分和一个最低分,再计算。因此,王明的实际得分是92分。
【点睛】本题主要考查平均数的意义和求法,关键是掌握平均数的相关公式。
二、选择题(共10分)
11.(2分)工厂计划本月生产一批零件。实际生产时发现上半月完成计划的,下半月完成计划的,下面说法正确的是( )。
A.本月生产计划没有完成 B.本月实际产量是计划的
C.本月实际产量超过计划的 D.本月产量超过计划的主要原因是上半月生产效率高
【答案】C
【分析】把本月生产计划产量看作单位“1”,把实际生产时上半月和下半月完成计划的分率相加,再与单位“1”比较即可。
【详解】+=
-1=
所以本月实际产量超过计划的。
故答案为:C
【点睛】本题考查了学生解决简单的分数加法与减法的应用题的能力。
12.(2分)一个长方体木块正好能锯成两个小正方体,如果每个小正方体的表面积是6平方分米,那么原来长方体的表面积是( )平方分米。
A.12 B.10 C.8 D.6
【答案】B
【分析】根据小正方体的表面积为6平方分米,可求出正方体每个面的面积,长方体木块锯成两个正方体后面积增加了两个正方形面积,将两个正方体表面积加起来减去两个正方形面的面积即可得到答案。
【详解】6÷6×2
=1×2
=2(平方分米)
6×2-2
=12-2
=10(平方分米)
原来长方体的表面积是10平方分米。
故答案为:B
13.(2分)下列算式结果最大的是( )。
A.× B.× C.+ D.-
【答案】C
【分析】根据分数加减法及分数乘法法则,分别求出各选项的结果,再比较即可。
【详解】A.×=;
B.×=;
C.+=;
D.-=。
因为<<<,所以,得数最大的算式是+。
故答案为:C
14.(2分)图中,甲、乙两个立体图形的表面积( ),体积( )。
A.甲>乙;甲<乙 B.甲<乙;甲>乙
C.甲<乙;甲=乙 D.无法判断;无法判断
【答案】C
【分析】甲乙都是由同样大小的小正方体组成的,那么它们的表面积可以利用小正方体的个数表示出来,分别从前后、上下、左右观察并计算出它们的小正方体的面的总和;然后进行比较;所占空间的大小就是这个立体图形的体积的大小,它们的体积分别等于组成它的小正方体的体积之和,由此数出各自的小正方体的个数即可进行比较。
【详解】甲的表面积由24个完全相同的正方形的面积组成,乙的表面积由26个完全相同的正方形的面积组成,所以甲的表面积<乙的表面积;
甲乙都是由7个小正方体组成的,所以它们的体积相等。
故答案为:C
15.(2分)图书馆在公园西偏南30°的方向,那么公园在图书馆( )的方向。
A.南偏西30° B.东偏北30° C.北偏东30° D.南偏西60°
【答案】B
【分析】根据位置的相对性可知,它们的方向相反,角度相等,距离相等,据此解答。
【详解】图书馆在公园西偏南30°的方向,那么公园在图书馆东偏北30°的方向。
故答案为:B
【点睛】本题主要考查了学生对位置相对性的掌握情况。
三、判断题(共10分)
16.(2分)一根绳子对折再对折,量得每段长米,这根绳子原来的长度是5米。( )
【答案】×
【分析】把这根绳子的长度看成单位“1”,对折一次,相当于把这根绳子平均分成2份,对折两次,相当于把这根绳子平均分成4份,每段占这根绳子的,量得每段长米,根据分数除法的意义,全长是:÷。
【详解】一根绳子对折再对折,相当于把这根绳子平均分成4份,每段占这根绳子的,所以:
÷=(米)
所以,这根这根绳子原来的长度是米。
故答案为:×
【点睛】本题考查分数的意义及分数除法的应用。
17.(2分)根据下图可列方程为。( )
【答案】√
【分析】观察图形可知,女生人数是x人,男生是女生的4倍,男生人数是4x人,女生和男生一共90人,列方程:x+4x=90,据此解答。
【详解】解:设女生人数是x人,则男生人数是4x人。
x+4x=90
5x=90
x=90÷5
x=18
原题干正确。
故答案为:√
【点睛】根据女生人数和男生人数之间的关系设出未知数,找出相关的量,列方程即可。
18.(2分)小丽参加“中英文风采”大赛,5个评委给她的评分是:97分,96分,88分,90分,93分,去掉最高分和最低分后她的平均得分是92分。( )
【答案】×
【分析】根据题目可知,去掉一个最高分97分和一个最低分88分,把剩下的分数相加,然后再利用分数总数÷总份数=平均分,把数代入公式即可判断。
【详解】(96+90+93)÷3
=279÷3
=93(分)
去掉最高分和最低分后她的平均得分是93分,所以原题说法错误。
故答案为:×
【点睛】解答此题先去掉最高分和最低分是解答的前提。
19.(2分)用两个棱长为1厘米的正方体拼成一个长方体,长方体的表面积是12平方厘米。( )
【答案】×
【分析】用2个棱长是1厘米的正方体拼成的长方体的长为2厘米、宽为1厘米、高为1厘米,根据“长方体表面积=(长×宽+长×高+宽×高)×2”,求出表面积即可。
【详解】(2×1+1×1+2×1)×2
=(2+1+2)×2
=5×2
=10(平方厘米)
所以,用两个棱长为1厘米的正方体拼成一个长方体,长方体的表面积是10平方厘米;原题干说法错误。
故答案为:×
【点睛】本题主要考查立体图形的切拼及长方体表面积公式,解题的关键是构想出拼成的长方体的长、宽、高。
20.(2分)x=1,那么x=。( )
【答案】√
【分析】方程两边同时乘,即可求得x的值,再进行判断。据此解答。
【详解】x=1
解:x=1×
x=
原题说法正确。
故答案为:√
【点睛】本题考查了倒数的认识。明确乘积为1的两个数互为倒数是解答本题的关键。
四、计算题(共12分)
21.(6分)用你喜欢的方法计算,并写出计算过程。
【答案】;;
【分析】(1)先根据减法的性质a-(b-c)=a-b+c把变成,然后交换“”和“”的位置,再按顺序计算;
(2)先根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c),把变成,再按顺序计算;
(3)根据分数乘分数的计算方法,分子和分子相乘的积作为分子,分母与分母相乘的积作为分母;在计算过程中能约分的先约分,再计算。
【详解】(1)
(2)
(3)
22.(6分)计算下列图形的表面积和体积。(单位:cm)
【答案】(1)216cm2;216cm3
(2)1980cm2;5400cm3
(3)62cm2;28cm3
【分析】(1)根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,把数据代入公式解答;
(2)根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,即可解答;
(3)通过观察图形可知,由于正方体和长方体粘合在一起,求表面积时,上面的正方体只求它的4个侧面的面积,下面的长方体求出表面积,然后合并起来,这个组合图形的体积等于正方体的体积加上长方体的体积。根据正方体的表面积公式:S=6a2,体积公式:V=a3,长方体的表面积公式:S=(ab+ah+bh)×2,体积公式:V=abh,把数据代入公式解答。
【详解】(1)6×6×6
=36×6
=216(cm2)
6×6×6
=36×6
=216(cm3)
它的表面积是216 cm2,体积是216 cm3。
(2)(30×12+30×15+15×12)×2
=(360+450+180)×2
=(810+180)×2
=990×2
=1980(cm2)
30×15×12
=450×12
=5400(cm3)
它的表面积是1980cm2,体积是5400 cm3。
(3)2×2×4+(4×2+4×2.5+2×2.5)×2
=4×4+(8+10+5)×2
=16+(18+5)×2
=16+23×2
=16+46
=62(cm2)
2×2×2+4×2.5×2
=4×2+10×2
=8+20
=28(cm3)
它的表面积是62 cm2,体积是28 cm3。
五、作图题(共6分)
23.(6分)根据笑笑提供的信息,画出笑笑从家到学校的路线图。
笑笑:我先从家向北偏东40°方向走200米到中国银行,再向正东方面走400米到达万达超市,最后向东偏南30°的方向走500米到学校。(1厘米表示100米)
【答案】见详解
【分析】结合题意,图上1厘米表示实际100米。先以家为观测点,向北偏东40°方向画一条2厘米的线段,线段末端表示中国银行;再以中国银行为观测点,向正东方向画一条4厘米长的线段,线段末端表示万达超市;再以万达超市为观测点,向东偏南30°画一条5厘米长的线段,线段末端表示学校。
【详解】如图:
200÷100=2(厘米)
400÷100=4(厘米)
500÷100=5(厘米)
【点睛】绘制路线图时,先明确单位长度,然后确定观测点、被观测点,要以观测点为参照物结合具体描述来绘制。
六、解答题(共42分)
24.(5分)中国土地资源总量丰富,土地利用类型齐全,其中耕地面积约占全国总面积的,草地面积比耕地面积多占全国总面积的,林地面积比草地面积少占全国总面积的,那么林地面积约占全国总面积的几分之几?
【答案】
【分析】已知草地面积比耕地面积多占全国总面积的,用耕地面积约占全国总面积的分率加上,求出草地面积约占全国总面积的几分之几;
已知林地面积比草地面积少占全国总面积的,用草地面积约占全国总面积的分率减去,即是林地面积约占全国总面积的几分之几。
【详解】
答:林地面积约占全国总面积的。
25.(5分)建设美丽校园,共享绿色文明。桃源小学在今年植树节活动中,共植树1050棵,其中是杨树,是槐树,哪种树种植得多?多多少棵?
【答案】槐树;70棵
【分析】将总棵数看作单位“1”,总棵数分别乘杨树和槐树的对应分率,即求出杨树和槐树的棵数,比较,求差即可。
【详解】1050×=350(棵)
1050×=420(棵)
420>350
420-350=70(棵)
答:槐树种植的多,多70棵。
26.(5分)将两盒糖果包装成一包,怎样包装才能最节省包装纸?(画出草图)需要包装纸的面积是多少平方厘米?
【答案】将上下两个面拼起来;画图见详解;1300平方厘米
【分析】
想最节省包装纸就是让拼起来的长方体表面积最小,将长方体最大的两个面拼起来表面积最小,观察示意图,上下面最大,将上下两个面拼起来即可。拼起来的大长方体长和宽不变,高=原长方体的高×2,根据长方体表面积=(长×宽+长×高+宽×高)×2,即可求出需要的包装纸的面积。
【详解】
5×2=10(厘米)
(20×15+20×10+15×10)×2
=(300+200+150)×2
=650×2
=1300(平方厘米)
答:将上下两个面拼起来最节省包装纸,需要包装纸的面积是1300平方厘米。
27.(5分)两袋大米,第二袋比第一袋重15千克,已知第一袋大米的恰好与第二袋的相等,两袋大米各重多少千克?(先写出等量关系式,再列方程解答问题)
等量关系式:
列方程解答:
【答案】第一袋大米的质量×=第二袋大米的质量×
第一袋15千克;第二袋30千克
【分析】第一袋大米的恰好与第二袋的相等,所以,第一袋大米的质量×=第二袋大米的质量×。第二袋比第一袋重15千克,设第一袋大米重千克,则第二袋大米重千克,列方程求解即可。
【详解】等量关系式:第一袋大米的质量×=第二袋大米的质量×
列方程解答:解:设第一袋大米重千克,则第二袋大米重千克,
(千克)
答:第一袋大米重15千克,则第二袋大米重30千克。
28.(5分)惠东南站是厦深铁路上18个客运站之一,距离深圳北站88千米,为沿线县级车站之最。已知甲动车从惠东南站出发,每分行驶2千米,行驶11分钟后,乙动车才从深圳北站出发,每分行驶1.3千米,乙动车出发多少分后两车相遇?
【答案】20分
【分析】根据相遇问题中“速度和×相遇时间=路程”可得出等量关系:甲动车的速度×甲先行驶的时间+(甲动车的速度+乙动车的速度)×乙动车出发后的相遇时间=惠东南站与深圳北站的距离,据此列出方程,并求解。
【详解】解:设乙动车出发分后两车相遇。
2×11+(2+1.3)=88
22+3.3=88
22+3.3-22=88-22
3.3=66
3.3÷3.3=66÷3.3
=20
答:乙动车出发20分后两车相遇。
29.(8分)AI智能模块化鱼缸是一款科技感十足的智能鱼缸,它拥有自动定时喂食、自动清洁等多种功能,让养鱼这件事变得更加简单。张大爷家的智能鱼缸是长60厘米,宽和高都是40厘米的长方体。
(1)鱼缸的四周是钢化玻璃,为了防止玻璃自爆,需要在玻璃上贴一层防爆膜,一共需要贴多少平方米的防爆膜?(损耗忽略不计)
(2)鱼缸中放有一块高为24厘米,体积为1100立方厘米的假山石(如图),如果向鱼缸内注水,那么至少需要注入多少立方分米的水才能将假山石完全淹没?
【答案】(1)0.8平方米
(2)56.5立方分米
【分析】(1)求四周需要贴防爆膜的面积,就是求这个长方体鱼缸的侧面积,根据长方体侧面积公式:侧面积=(长×高+宽×高)×2,代入数据,即可解答,注意单位名数的换算;
(2)水能将假山石完全淹没,鱼缸中水的高度等于假山石的高度;根据长方体体积公式:体积=长×宽×高,代入数据,求出高是24厘米的长方体的体积,再减去假山石的体积,即可求出水的体积,注意单位名数的换算。
【详解】(1)(60×40+40×40)×2
=(2400+1600)×2
=4000×2
=8000(平方厘米)
8000平方厘米=0.8平方米
答:一共需要贴0.8平方米的防爆膜。
(2)60×40×24-1100
=2400×24-1100
=57600-1100
=56500(立方厘米)
56500立方厘米=56.5立方分米
答:至少需要注入56.5立方分米的水才能将假山石完全淹没。
30.(9分)下面是某大药房2023年1-5月消毒液、感冒药的销售情况统计表。
(1)根据上表中的数据,画出折线统计图。
(2)( )月到( )月感冒药销售数量降低最多。
(3)消毒液销售数量的变化趋势是( ),消毒液平均每月销售( )箱。
【答案】(1)见详解
(2)1;2
(3)逐渐增加;46
【分析】(1)结合统计表中的数据,先在统计图中描出各点,然后把各点用线段顺次连接起来,完成折线统计图的绘制。
(2)把相邻两个月感冒药销售数量相减,差值最大的,这两个月感冒药销售数量降低最多。
(3)观察折线统计图中消毒液的折线变化情况,据此得出消毒液销售数量的变化趋势。
先用加法求出这五个月消毒液的销售数量总和,再除以5,即是消毒液平均每月的销售数量。
【详解】(1)如图:
(2)32-25=7(箱)
25-22=3(箱)
22-20=2(箱)
20-15=5(箱)
7>5>3>2
1月到2月感冒药销售数量降低最多。
(3)(15+48+52+55+60)÷5
=230÷5
=46(箱)
消毒液销售数量的变化趋势是逐渐增加,消毒液平均每月销售46箱。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版五年级数学下册期末考试满分冲刺质量检测卷一
一、填空题(共20分)
1.(2分)一个西瓜,爸爸吃了它的,妈妈吃了它的,爸爸和妈妈一共吃了它的( ),还剩下它的( )。
2.(2分)有两个完全相同的长方体木料,长为20分米,宽为12分米,高为2分米,如果要合成一个长方体,它的表面积最大为( ),最小为( )。
3.(2分)集邮可以加深我们对不同国家、地区、动植物、历史事件等的了解。小周和爸爸都喜欢集邮,小周收集了各种邮票56张,爸爸收集的邮票数比小周多,爸爸比小周多收集( )张邮票。
4.(2分)某风景区票价90元/人,“六一”特价:成人九折,儿童半价。这天小明和爸爸妈妈一块去这里游玩,可以节省( )元。
5.(2分)如图,在一个长方体容器中,放入一个西红柿后(完全浸没),水面高度上升到12厘米(没有溢出)。西红柿的体积是( )立方厘米。
6.(2分)( )cm3 85立方厘米=( )毫升=( )升
7.(2分)小明比姐姐小6岁,姐姐的年龄是小明的3倍,姐姐的年龄是妈妈的,妈妈今年( )岁,小明今年( )岁。
8.(2分)如图,以学校为观察点,博物馆在学校的( )方向上,距离学校( )米。
9.(2分)哥哥和弟弟身上各有一些钱,已知哥哥身上的钱是弟弟的5倍,如果哥哥给弟弟80.5元,则哥哥的钱还比弟弟多21元,原来弟弟身上有( )元。
10.(2分)在演讲比赛中,评委给王明打出的分数分别是87分、93分、94分、95分、98分、85分、 92分、91分。按比赛规则,计算选手的平均得分要先去掉一个最高分和一个最低分,再计算。因此,王明的实际得分是( )分。
二、选择题(共10分)
11.(2分)工厂计划本月生产一批零件。实际生产时发现上半月完成计划的,下半月完成计划的,下面说法正确的是( )。
A.本月生产计划没有完成 B.本月实际产量是计划的
C.本月实际产量超过计划的 D.本月产量超过计划的主要原因是上半月生产效率高
12.(2分)一个长方体木块正好能锯成两个小正方体,如果每个小正方体的表面积是6平方分米,那么原来长方体的表面积是( )平方分米。
A.12 B.10 C.8 D.6
13.(2分)下列算式结果最大的是( )。
A.× B.× C.+ D.-
14.(2分)图中,甲、乙两个立体图形的表面积( ),体积( )。
A.甲>乙;甲<乙 B.甲<乙;甲>乙
C.甲<乙;甲=乙 D.无法判断;无法判断
15.(2分)图书馆在公园西偏南30°的方向,那么公园在图书馆( )的方向。
A.南偏西30° B.东偏北30° C.北偏东30° D.南偏西60°
三、判断题(共10分)
16.(2分)一根绳子对折再对折,量得每段长米,这根绳子原来的长度是5米。( )
17.(2分)根据下图可列方程为。( )
18.(2分)小丽参加“中英文风采”大赛,5个评委给她的评分是:97分,96分,88分,90分,93分,去掉最高分和最低分后她的平均得分是92分。( )
19.(2分)用两个棱长为1厘米的正方体拼成一个长方体,长方体的表面积是12平方厘米。( )
20.(2分)x=1,那么x=。( )
四、计算题(共12分)
21.(6分)用你喜欢的方法计算,并写出计算过程。
22.(6分)计算下列图形的表面积和体积。(单位:cm)
五、作图题(共6分)
23.(6分)根据笑笑提供的信息,画出笑笑从家到学校的路线图。
笑笑:我先从家向北偏东40°方向走200米到中国银行,再向正东方面走400米到达万达超市,最后向东偏南30°的方向走500米到学校。(1厘米表示100米)
六、解答题(共42分)
24.(5分)中国土地资源总量丰富,土地利用类型齐全,其中耕地面积约占全国总面积的,草地面积比耕地面积多占全国总面积的,林地面积比草地面积少占全国总面积的,那么林地面积约占全国总面积的几分之几?
25.(5分)建设美丽校园,共享绿色文明。桃源小学在今年植树节活动中,共植树1050棵,其中是杨树,是槐树,哪种树种植得多?多多少棵?
26.(5分)将两盒糖果包装成一包,怎样包装才能最节省包装纸?(画出草图)需要包装纸的面积是多少平方厘米?
27.(5分)两袋大米,第二袋比第一袋重15千克,已知第一袋大米的恰好与第二袋的相等,两袋大米各重多少千克?(先写出等量关系式,再列方程解答问题)
等量关系式:
列方程解答:
28.(5分)惠东南站是厦深铁路上18个客运站之一,距离深圳北站88千米,为沿线县级车站之最。已知甲动车从惠东南站出发,每分行驶2千米,行驶11分钟后,乙动车才从深圳北站出发,每分行驶1.3千米,乙动车出发多少分后两车相遇?
29.(8分)AI智能模块化鱼缸是一款科技感十足的智能鱼缸,它拥有自动定时喂食、自动清洁等多种功能,让养鱼这件事变得更加简单。张大爷家的智能鱼缸是长60厘米,宽和高都是40厘米的长方体。
(1)鱼缸的四周是钢化玻璃,为了防止玻璃自爆,需要在玻璃上贴一层防爆膜,一共需要贴多少平方米的防爆膜?(损耗忽略不计)
(2)鱼缸中放有一块高为24厘米,体积为1100立方厘米的假山石(如图),如果向鱼缸内注水,那么至少需要注入多少立方分米的水才能将假山石完全淹没?
30.(9分)下面是某大药房2023年1-5月消毒液、感冒药的销售情况统计表。
(1)根据上表中的数据,画出折线统计图。
(2)( )月到( )月感冒药销售数量降低最多。
(3)消毒液销售数量的变化趋势是( ),消毒液平均每月销售( )箱。
答案解析
一、填空题(共20分)
1.(2分)一个西瓜,爸爸吃了它的,妈妈吃了它的,爸爸和妈妈一共吃了它的( ),还剩下它的( )。
【答案】
【分析】根据题意,将整个西瓜看作单位“1”,爸爸吃了它的,妈妈吃了它的,用加法可以求出爸爸和妈妈一共吃了它的几分之几;用单位“1”减去爸爸妈妈一共吃了它的几分之几,即可求出还剩下它的几分之几。
【详解】由分析可得:
+=+=
1-=
综上所述:一个西瓜,爸爸吃了它的,妈妈吃了它的,爸爸和妈妈一共吃了它的,还剩下它的。
2.(2分)有两个完全相同的长方体木料,长为20分米,宽为12分米,高为2分米,如果要合成一个长方体,它的表面积最大为( ),最小为( )。
【答案】 1168平方分米/1168dm2 736平方分米/736dm2
【分析】将最小的两个面(左右面)拼起来,合成的长方体表面积最大;将最大的两个面(上下面)拼起来,合成的长方体表面积最小。
根据长方体表面积=(长×宽+长×高+宽×高)×2,求出两个长方体木料的面积和,分别减去最小两个面和最大两个面即可。
【详解】(20×12+20×2+12×2)×2×2
=(240+40+24)×2×2
=304×2×2
=1216(平方分米)
1216-12×2×2
=1216-48
=1168(平方分米)
1216-20×12×2
=1216-480
=736(平方分米)
它的表面积最大为1168平方分米,最小为736平方分米。
3.(2分)集邮可以加深我们对不同国家、地区、动植物、历史事件等的了解。小周和爸爸都喜欢集邮,小周收集了各种邮票56张,爸爸收集的邮票数比小周多,爸爸比小周多收集( )张邮票。
【答案】21
【分析】把小周收集的邮票数看作单位“1”,要求爸爸比小周多收集的邮票数,就是求小周邮票数的是多少,用乘法计算。
【详解】56×=21(张)
所以爸爸比小周多收集21张邮票。
4.(2分)某风景区票价90元/人,“六一”特价:成人九折,儿童半价。这天小明和爸爸妈妈一块去这里游玩,可以节省( )元。
【答案】63
【分析】九折就是,半价就是原价的,用原价×,求景区成人一张票价;用原价×,求景区儿童票价;再用原价-九折后的票价,求出一张成人票节省的钱数,再乘2,求出爸爸妈妈节省的钱数;再用原价-儿童票价,求出小明节省的钱数,再把节省的钱数相加,即可解答。
【详解】九折就是,半价就是原价的。
90×=81(元)
90×=45(元)
(90-81)×2+(90-45)
=9×2+45
=18+45
=63(元)
某风景区票价90元/人,“六一”特价:成人九折,儿童半价。这天小明和爸爸妈妈一块去这里游玩,可以节省63元。
5.(2分)如图,在一个长方体容器中,放入一个西红柿后(完全浸没),水面高度上升到12厘米(没有溢出)。西红柿的体积是( )立方厘米。
【答案】300
【分析】通过观察可知,西红柿的体积相当于水面上升的体积,根据水面上升的体积=容器的长×宽×上升部分的高度,代入数据解答。
【详解】15×10×(12-10)
=15×10×2
=300(立方厘米)
西红柿的体积是300立方厘米。
6.(2分)( )cm3 85立方厘米=( )毫升=( )升
【答案】 6020 85 0.085
【分析】1dm3=1000cm3;1立方厘米=1毫升;1升=1000立方厘米;高级单位换算成低级单位,乘进率;低级单位换算成高级单位,除以进率,据此解答。
【详解】6.02dm3=6.02×1000=6020cm3
85立方厘米=85×1=85毫升
85立方厘米=85÷1000=0.085升
85立方厘米=85毫升=0.085升
7.(2分)小明比姐姐小6岁,姐姐的年龄是小明的3倍,姐姐的年龄是妈妈的,妈妈今年( )岁,小明今年( )岁。
【答案】 36 3
【分析】假设小明今年岁,那么姐姐今年岁,姐姐的年龄是小明的3倍,即小明的年龄×3=姐姐的年龄,据此列方程求解,即可算出姐姐和小明今年几岁,姐姐的年龄是妈妈的,所以妈妈的年龄=姐姐的年龄÷,据此解答。
【详解】解:假设小明今年岁,那么姐姐今年岁,
姐姐:(岁)
妈妈:
(岁)
即妈妈今年36岁,小明今年3岁。
8.(2分)如图,以学校为观察点,博物馆在学校的( )方向上,距离学校( )米。
【答案】 东偏北30° 500
【分析】在地图上按照“上北下南,左西右东”确定方向,结合图上标注的信息和数据,注意观测点是学校,据此解答。
【详解】观察图可知:以学校为观察点,博物馆在学校的东偏北30°方向上,距离学校500米。
【点睛】本题主要考查学生的方位感和对基本方向的辨别。
9.(2分)哥哥和弟弟身上各有一些钱,已知哥哥身上的钱是弟弟的5倍,如果哥哥给弟弟80.5元,则哥哥的钱还比弟弟多21元,原来弟弟身上有( )元。
【答案】45.5
【分析】设原来弟弟身上有x元,哥哥身上的钱是弟弟的5倍,则哥哥有5x元;如果哥哥给弟弟80.5元,则哥哥的钱还比弟弟多21元;哥哥钱数-80.5元,比弟弟的钱数+80.5元还多21元,列方程:5x-80.5-(x+80.5)=21,解方程,即可解答。
【详解】解:设原来弟弟身上有x元,则哥哥有5x元。
5x-80.5-(x+80.5)=21
5x-80.5-x-80.5=21
4x-161=21
4x=21+161
4x=182
x=182÷4
x=45.5
哥哥和弟弟身上各有一些钱,已知哥哥身上的钱是弟弟的5倍,如果哥哥给弟弟80.5元,则哥哥的钱还比弟弟多21元,原来弟弟身上有45.5元。
【点睛】根据方程的实际应用,利用哥哥和弟弟身上的钱数之间的关系,设出未知数,找出相关的量,列方程,解方程。
10.(2分)在演讲比赛中,评委给王明打出的分数分别是87分、93分、94分、95分、98分、85分、 92分、91分。按比赛规则,计算选手的平均得分要先去掉一个最高分和一个最低分,再计算。因此,王明的实际得分是( )分。
【答案】92
【分析】去掉最高分98分和最低分85分,根据平均数=总数÷数据个数,代入数据计算即可。
【详解】(87+93+94+95+92+91)÷6
=(180+94+95+92+91)÷6
=(274+95+92+91)÷6
=(369+92+91)÷6
=(461+91)÷6
=552÷6
=92(分)
在演讲比赛中,评委给王明打出的分数分别是87分、93分、94分、95分、98分、85分、 92分、91分。按比赛规则,计算选手的平均得分要先去掉一个最高分和一个最低分,再计算。因此,王明的实际得分是92分。
【点睛】本题主要考查平均数的意义和求法,关键是掌握平均数的相关公式。
二、选择题(共10分)
11.(2分)工厂计划本月生产一批零件。实际生产时发现上半月完成计划的,下半月完成计划的,下面说法正确的是( )。
A.本月生产计划没有完成 B.本月实际产量是计划的
C.本月实际产量超过计划的 D.本月产量超过计划的主要原因是上半月生产效率高
【答案】C
【分析】把本月生产计划产量看作单位“1”,把实际生产时上半月和下半月完成计划的分率相加,再与单位“1”比较即可。
【详解】+=
-1=
所以本月实际产量超过计划的。
故答案为:C
【点睛】本题考查了学生解决简单的分数加法与减法的应用题的能力。
12.(2分)一个长方体木块正好能锯成两个小正方体,如果每个小正方体的表面积是6平方分米,那么原来长方体的表面积是( )平方分米。
A.12 B.10 C.8 D.6
【答案】B
【分析】根据小正方体的表面积为6平方分米,可求出正方体每个面的面积,长方体木块锯成两个正方体后面积增加了两个正方形面积,将两个正方体表面积加起来减去两个正方形面的面积即可得到答案。
【详解】6÷6×2
=1×2
=2(平方分米)
6×2-2
=12-2
=10(平方分米)
原来长方体的表面积是10平方分米。
故答案为:B
13.(2分)下列算式结果最大的是( )。
A.× B.× C.+ D.-
【答案】C
【分析】根据分数加减法及分数乘法法则,分别求出各选项的结果,再比较即可。
【详解】A.×=;
B.×=;
C.+=;
D.-=。
因为<<<,所以,得数最大的算式是+。
故答案为:C
14.(2分)图中,甲、乙两个立体图形的表面积( ),体积( )。
A.甲>乙;甲<乙 B.甲<乙;甲>乙
C.甲<乙;甲=乙 D.无法判断;无法判断
【答案】C
【分析】甲乙都是由同样大小的小正方体组成的,那么它们的表面积可以利用小正方体的个数表示出来,分别从前后、上下、左右观察并计算出它们的小正方体的面的总和;然后进行比较;所占空间的大小就是这个立体图形的体积的大小,它们的体积分别等于组成它的小正方体的体积之和,由此数出各自的小正方体的个数即可进行比较。
【详解】甲的表面积由24个完全相同的正方形的面积组成,乙的表面积由26个完全相同的正方形的面积组成,所以甲的表面积<乙的表面积;
甲乙都是由7个小正方体组成的,所以它们的体积相等。
故答案为:C
15.(2分)图书馆在公园西偏南30°的方向,那么公园在图书馆( )的方向。
A.南偏西30° B.东偏北30° C.北偏东30° D.南偏西60°
【答案】B
【分析】根据位置的相对性可知,它们的方向相反,角度相等,距离相等,据此解答。
【详解】图书馆在公园西偏南30°的方向,那么公园在图书馆东偏北30°的方向。
故答案为:B
【点睛】本题主要考查了学生对位置相对性的掌握情况。
三、判断题(共10分)
16.(2分)一根绳子对折再对折,量得每段长米,这根绳子原来的长度是5米。( )
【答案】×
【分析】把这根绳子的长度看成单位“1”,对折一次,相当于把这根绳子平均分成2份,对折两次,相当于把这根绳子平均分成4份,每段占这根绳子的,量得每段长米,根据分数除法的意义,全长是:÷。
【详解】一根绳子对折再对折,相当于把这根绳子平均分成4份,每段占这根绳子的,所以:
÷=(米)
所以,这根这根绳子原来的长度是米。
故答案为:×
【点睛】本题考查分数的意义及分数除法的应用。
17.(2分)根据下图可列方程为。( )
【答案】√
【分析】观察图形可知,女生人数是x人,男生是女生的4倍,男生人数是4x人,女生和男生一共90人,列方程:x+4x=90,据此解答。
【详解】解:设女生人数是x人,则男生人数是4x人。
x+4x=90
5x=90
x=90÷5
x=18
原题干正确。
故答案为:√
【点睛】根据女生人数和男生人数之间的关系设出未知数,找出相关的量,列方程即可。
18.(2分)小丽参加“中英文风采”大赛,5个评委给她的评分是:97分,96分,88分,90分,93分,去掉最高分和最低分后她的平均得分是92分。( )
【答案】×
【分析】根据题目可知,去掉一个最高分97分和一个最低分88分,把剩下的分数相加,然后再利用分数总数÷总份数=平均分,把数代入公式即可判断。
【详解】(96+90+93)÷3
=279÷3
=93(分)
去掉最高分和最低分后她的平均得分是93分,所以原题说法错误。
故答案为:×
【点睛】解答此题先去掉最高分和最低分是解答的前提。
19.(2分)用两个棱长为1厘米的正方体拼成一个长方体,长方体的表面积是12平方厘米。( )
【答案】×
【分析】用2个棱长是1厘米的正方体拼成的长方体的长为2厘米、宽为1厘米、高为1厘米,根据“长方体表面积=(长×宽+长×高+宽×高)×2”,求出表面积即可。
【详解】(2×1+1×1+2×1)×2
=(2+1+2)×2
=5×2
=10(平方厘米)
所以,用两个棱长为1厘米的正方体拼成一个长方体,长方体的表面积是10平方厘米;原题干说法错误。
故答案为:×
【点睛】本题主要考查立体图形的切拼及长方体表面积公式,解题的关键是构想出拼成的长方体的长、宽、高。
20.(2分)x=1,那么x=。( )
【答案】√
【分析】方程两边同时乘,即可求得x的值,再进行判断。据此解答。
【详解】x=1
解:x=1×
x=
原题说法正确。
故答案为:√
【点睛】本题考查了倒数的认识。明确乘积为1的两个数互为倒数是解答本题的关键。
四、计算题(共12分)
21.(6分)用你喜欢的方法计算,并写出计算过程。
【答案】;;
【分析】(1)先根据减法的性质a-(b-c)=a-b+c把变成,然后交换“”和“”的位置,再按顺序计算;
(2)先根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c),把变成,再按顺序计算;
(3)根据分数乘分数的计算方法,分子和分子相乘的积作为分子,分母与分母相乘的积作为分母;在计算过程中能约分的先约分,再计算。
【详解】(1)
(2)
(3)
22.(6分)计算下列图形的表面积和体积。(单位:cm)
【答案】(1)216cm2;216cm3
(2)1980cm2;5400cm3
(3)62cm2;28cm3
【分析】(1)根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,把数据代入公式解答;
(2)根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,即可解答;
(3)通过观察图形可知,由于正方体和长方体粘合在一起,求表面积时,上面的正方体只求它的4个侧面的面积,下面的长方体求出表面积,然后合并起来,这个组合图形的体积等于正方体的体积加上长方体的体积。根据正方体的表面积公式:S=6a2,体积公式:V=a3,长方体的表面积公式:S=(ab+ah+bh)×2,体积公式:V=abh,把数据代入公式解答。
【详解】(1)6×6×6
=36×6
=216(cm2)
6×6×6
=36×6
=216(cm3)
它的表面积是216 cm2,体积是216 cm3。
(2)(30×12+30×15+15×12)×2
=(360+450+180)×2
=(810+180)×2
=990×2
=1980(cm2)
30×15×12
=450×12
=5400(cm3)
它的表面积是1980cm2,体积是5400 cm3。
(3)2×2×4+(4×2+4×2.5+2×2.5)×2
=4×4+(8+10+5)×2
=16+(18+5)×2
=16+23×2
=16+46
=62(cm2)
2×2×2+4×2.5×2
=4×2+10×2
=8+20
=28(cm3)
它的表面积是62 cm2,体积是28 cm3。
五、作图题(共6分)
23.(6分)根据笑笑提供的信息,画出笑笑从家到学校的路线图。
笑笑:我先从家向北偏东40°方向走200米到中国银行,再向正东方面走400米到达万达超市,最后向东偏南30°的方向走500米到学校。(1厘米表示100米)
【答案】见详解
【分析】结合题意,图上1厘米表示实际100米。先以家为观测点,向北偏东40°方向画一条2厘米的线段,线段末端表示中国银行;再以中国银行为观测点,向正东方向画一条4厘米长的线段,线段末端表示万达超市;再以万达超市为观测点,向东偏南30°画一条5厘米长的线段,线段末端表示学校。
【详解】如图:
200÷100=2(厘米)
400÷100=4(厘米)
500÷100=5(厘米)
【点睛】绘制路线图时,先明确单位长度,然后确定观测点、被观测点,要以观测点为参照物结合具体描述来绘制。
六、解答题(共42分)
24.(5分)中国土地资源总量丰富,土地利用类型齐全,其中耕地面积约占全国总面积的,草地面积比耕地面积多占全国总面积的,林地面积比草地面积少占全国总面积的,那么林地面积约占全国总面积的几分之几?
【答案】
【分析】已知草地面积比耕地面积多占全国总面积的,用耕地面积约占全国总面积的分率加上,求出草地面积约占全国总面积的几分之几;
已知林地面积比草地面积少占全国总面积的,用草地面积约占全国总面积的分率减去,即是林地面积约占全国总面积的几分之几。
【详解】
答:林地面积约占全国总面积的。
25.(5分)建设美丽校园,共享绿色文明。桃源小学在今年植树节活动中,共植树1050棵,其中是杨树,是槐树,哪种树种植得多?多多少棵?
【答案】槐树;70棵
【分析】将总棵数看作单位“1”,总棵数分别乘杨树和槐树的对应分率,即求出杨树和槐树的棵数,比较,求差即可。
【详解】1050×=350(棵)
1050×=420(棵)
420>350
420-350=70(棵)
答:槐树种植的多,多70棵。
26.(5分)将两盒糖果包装成一包,怎样包装才能最节省包装纸?(画出草图)需要包装纸的面积是多少平方厘米?
【答案】将上下两个面拼起来;画图见详解;1300平方厘米
【分析】
想最节省包装纸就是让拼起来的长方体表面积最小,将长方体最大的两个面拼起来表面积最小,观察示意图,上下面最大,将上下两个面拼起来即可。拼起来的大长方体长和宽不变,高=原长方体的高×2,根据长方体表面积=(长×宽+长×高+宽×高)×2,即可求出需要的包装纸的面积。
【详解】
5×2=10(厘米)
(20×15+20×10+15×10)×2
=(300+200+150)×2
=650×2
=1300(平方厘米)
答:将上下两个面拼起来最节省包装纸,需要包装纸的面积是1300平方厘米。
27.(5分)两袋大米,第二袋比第一袋重15千克,已知第一袋大米的恰好与第二袋的相等,两袋大米各重多少千克?(先写出等量关系式,再列方程解答问题)
等量关系式:
列方程解答:
【答案】第一袋大米的质量×=第二袋大米的质量×
第一袋15千克;第二袋30千克
【分析】第一袋大米的恰好与第二袋的相等,所以,第一袋大米的质量×=第二袋大米的质量×。第二袋比第一袋重15千克,设第一袋大米重千克,则第二袋大米重千克,列方程求解即可。
【详解】等量关系式:第一袋大米的质量×=第二袋大米的质量×
列方程解答:解:设第一袋大米重千克,则第二袋大米重千克,
(千克)
答:第一袋大米重15千克,则第二袋大米重30千克。
28.(5分)惠东南站是厦深铁路上18个客运站之一,距离深圳北站88千米,为沿线县级车站之最。已知甲动车从惠东南站出发,每分行驶2千米,行驶11分钟后,乙动车才从深圳北站出发,每分行驶1.3千米,乙动车出发多少分后两车相遇?
【答案】20分
【分析】根据相遇问题中“速度和×相遇时间=路程”可得出等量关系:甲动车的速度×甲先行驶的时间+(甲动车的速度+乙动车的速度)×乙动车出发后的相遇时间=惠东南站与深圳北站的距离,据此列出方程,并求解。
【详解】解:设乙动车出发分后两车相遇。
2×11+(2+1.3)=88
22+3.3=88
22+3.3-22=88-22
3.3=66
3.3÷3.3=66÷3.3
=20
答:乙动车出发20分后两车相遇。
29.(8分)AI智能模块化鱼缸是一款科技感十足的智能鱼缸,它拥有自动定时喂食、自动清洁等多种功能,让养鱼这件事变得更加简单。张大爷家的智能鱼缸是长60厘米,宽和高都是40厘米的长方体。
(1)鱼缸的四周是钢化玻璃,为了防止玻璃自爆,需要在玻璃上贴一层防爆膜,一共需要贴多少平方米的防爆膜?(损耗忽略不计)
(2)鱼缸中放有一块高为24厘米,体积为1100立方厘米的假山石(如图),如果向鱼缸内注水,那么至少需要注入多少立方分米的水才能将假山石完全淹没?
【答案】(1)0.8平方米
(2)56.5立方分米
【分析】(1)求四周需要贴防爆膜的面积,就是求这个长方体鱼缸的侧面积,根据长方体侧面积公式:侧面积=(长×高+宽×高)×2,代入数据,即可解答,注意单位名数的换算;
(2)水能将假山石完全淹没,鱼缸中水的高度等于假山石的高度;根据长方体体积公式:体积=长×宽×高,代入数据,求出高是24厘米的长方体的体积,再减去假山石的体积,即可求出水的体积,注意单位名数的换算。
【详解】(1)(60×40+40×40)×2
=(2400+1600)×2
=4000×2
=8000(平方厘米)
8000平方厘米=0.8平方米
答:一共需要贴0.8平方米的防爆膜。
(2)60×40×24-1100
=2400×24-1100
=57600-1100
=56500(立方厘米)
56500立方厘米=56.5立方分米
答:至少需要注入56.5立方分米的水才能将假山石完全淹没。
30.(9分)下面是某大药房2023年1-5月消毒液、感冒药的销售情况统计表。
(1)根据上表中的数据,画出折线统计图。
(2)( )月到( )月感冒药销售数量降低最多。
(3)消毒液销售数量的变化趋势是( ),消毒液平均每月销售( )箱。
【答案】(1)见详解
(2)1;2
(3)逐渐增加;46
【分析】(1)结合统计表中的数据,先在统计图中描出各点,然后把各点用线段顺次连接起来,完成折线统计图的绘制。
(2)把相邻两个月感冒药销售数量相减,差值最大的,这两个月感冒药销售数量降低最多。
(3)观察折线统计图中消毒液的折线变化情况,据此得出消毒液销售数量的变化趋势。
先用加法求出这五个月消毒液的销售数量总和,再除以5,即是消毒液平均每月的销售数量。
【详解】(1)如图:
(2)32-25=7(箱)
25-22=3(箱)
22-20=2(箱)
20-15=5(箱)
7>5>3>2
1月到2月感冒药销售数量降低最多。
(3)(15+48+52+55+60)÷5
=230÷5
=46(箱)
消毒液销售数量的变化趋势是逐渐增加,消毒液平均每月销售46箱。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
