人教版六年级数学下册期末考试满分冲刺质量检测卷一(含解析)
文档属性
| 名称 | 人教版六年级数学下册期末考试满分冲刺质量检测卷一(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 18:58:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版六年级数学下册期末考试满分冲刺质量检测卷一
一、填空题(共20分)
1.(2分)在比例尺是1∶500的图纸上,量得一个正方形草坪的边长是4厘米。这个草坪的实际面积是( )。
2.(2分)甲、乙两杯饮料的体积之比是4∶5,乙杯饮料的体积是甲杯的( )%,甲杯饮料的体积比乙杯饮料少( )%。
3.(2分)用完全一样的火柴棍拼图形(如图)。
按照这样的方法拼成第4个图形需要火柴棍( )根,拼成第n个图形需要火柴棍( )根。
4.(2分)2023年我国普通小学在校生约有108079000人,此数读作( ),初中生有五千二百四十三万六千九百人,此数写作( )。
5.(2分)=0.8==( )%=24∶( )。
6.(2分)一根长2米的圆柱形钢材截成三小段圆柱后,表面积比原来增加了36平方分米,这根钢材原来的体积是( )立方分米。
7.(2分)填上合适的单位。
明乐小学的劳动教育基地面积大约有1公顷,六(1)班分到一块长方形地并种植了黄瓜。大约经过3个月,收获的季节到了,萌萌摘下一根很大的黄瓜,长约3( ),体积约500( ),她称了一下重0.5( )。
8.(2分)根据各式的规律填空:
1=
1+3=
1+3+5=
1+3+5+7=
(1)1+3+5+7+9+11+13= 。
(2)从1开始, 个连续奇数相加的和是。
9.(2分)在一个比例里,两个内项互为倒数,一个外项是2.5,另一个外项是( )。如果一个内项是0.5,那么这个比例可能是( )。
10.(2分)按一定的规律写数:1、2、﹣3、4、5、﹣6、7、8、﹣9…,当写完第100个数停下来时,写的数中一共有( )个正数,( )个负数。
二、判断题(共10分)
11.(2分)在一定存期内,利率一定,利息和本金成正比例。( )
12.(2分)A×=B÷(A,B都不等于0),则A<B。( )
13.(2分)一根圆柱形木料,如果沿着底面直径切成两半,表面积增加120平方厘米。如果平行于底面截成两个小圆柱,表面积增加157平方厘米。则这根圆柱形木料原来的高是6厘米。( )
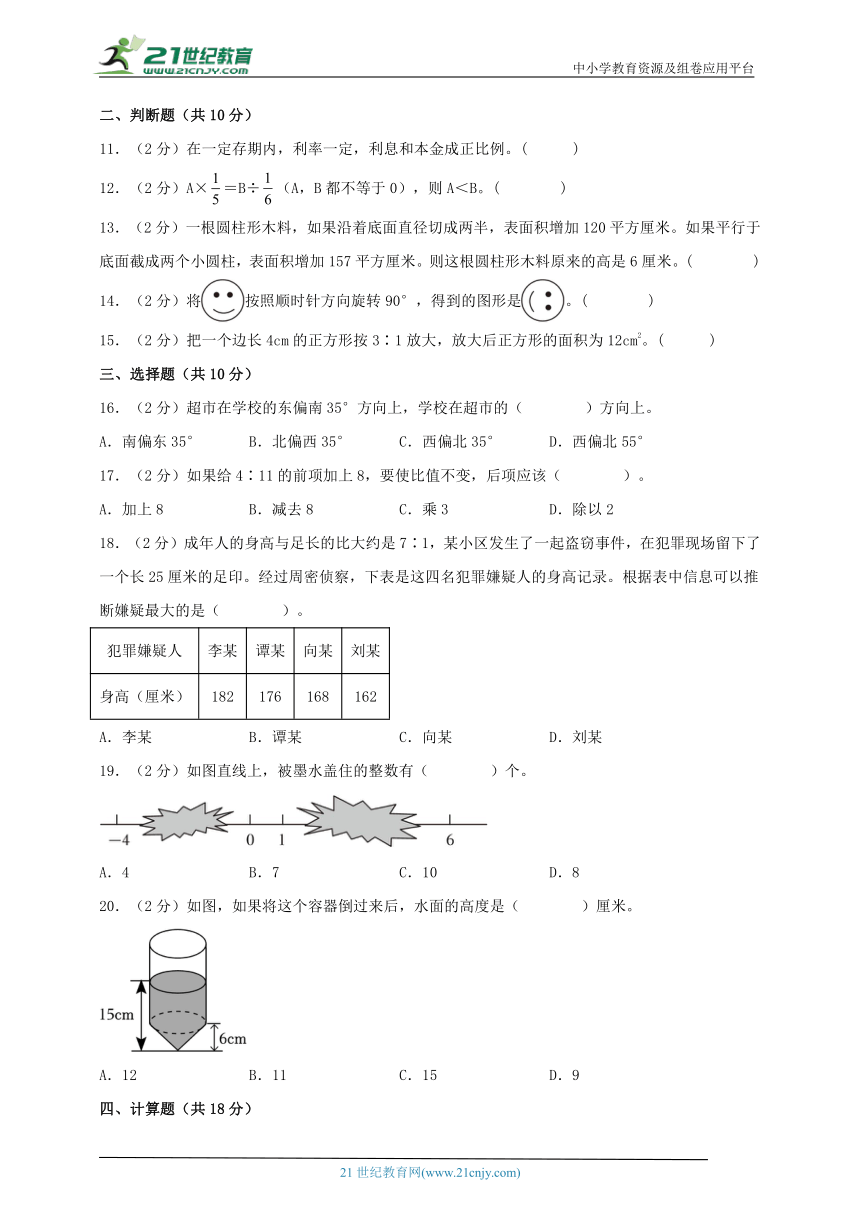
14.(2分)将按照顺时针方向旋转90°,得到的图形是。( )
15.(2分)把一个边长4cm的正方形按3∶1放大,放大后正方形的面积为12cm2。( )
三、选择题(共10分)
16.(2分)超市在学校的东偏南35°方向上,学校在超市的( )方向上。
A.南偏东35° B.北偏西35° C.西偏北35° D.西偏北55°
17.(2分)如果给4∶11的前项加上8,要使比值不变,后项应该( )。
A.加上8 B.减去8 C.乘3 D.除以2
18.(2分)成年人的身高与足长的比大约是7∶1,某小区发生了一起盗窃事件,在犯罪现场留下了一个长25厘米的足印。经过周密侦察,下表是这四名犯罪嫌疑人的身高记录。根据表中信息可以推断嫌疑最大的是( )。
犯罪嫌疑人 李某 谭某 向某 刘某
身高(厘米) 182 176 168 162
A.李某 B.谭某 C.向某 D.刘某
19.(2分)如图直线上,被墨水盖住的整数有( )个。
A.4 B.7 C.10 D.8
20.(2分)如图,如果将这个容器倒过来后,水面的高度是( )厘米。
A.12 B.11 C.15 D.9
四、计算题(共18分)
21.(6分)下面各题,怎样简便就怎样算。
12.5×32×0.25
22.(6分)解方程。
23.(6分)直接写得数。
0.4×20%= = = =
1÷0.2= 0.53= = =
五、作图题(共8分)
24.(8分)实践操作与应用。
(1)画出三角形ABC绕点B逆时针旋转90°后的图形。旋转后,C点的对应点的位置用数对表示是( )。
(2)以BC所在直线为对称轴,画出与三角形ABC对称的图形。
(3)画出三角形ABC按2∶1放大后的图形。
六、解答题(共34分)
25.(4分)2024年5月20日,盐城新地标建筑“串场之眼”揭开面纱,成了市民们休闲娱乐的“打卡”新去处。据介绍,该建筑总面积约21000平方米,比商业使用面积的3.2倍还多1800平方米。“串场之眼”商业使用面积约有多少平方米?(用方程解)
26.(4分)张大伯家有一个圆锥形小麦堆,量得它的底面周长是12.56米,高是1.5米,如果每立方米小麦的质量为700千克,这堆小麦的质量为多少千克?
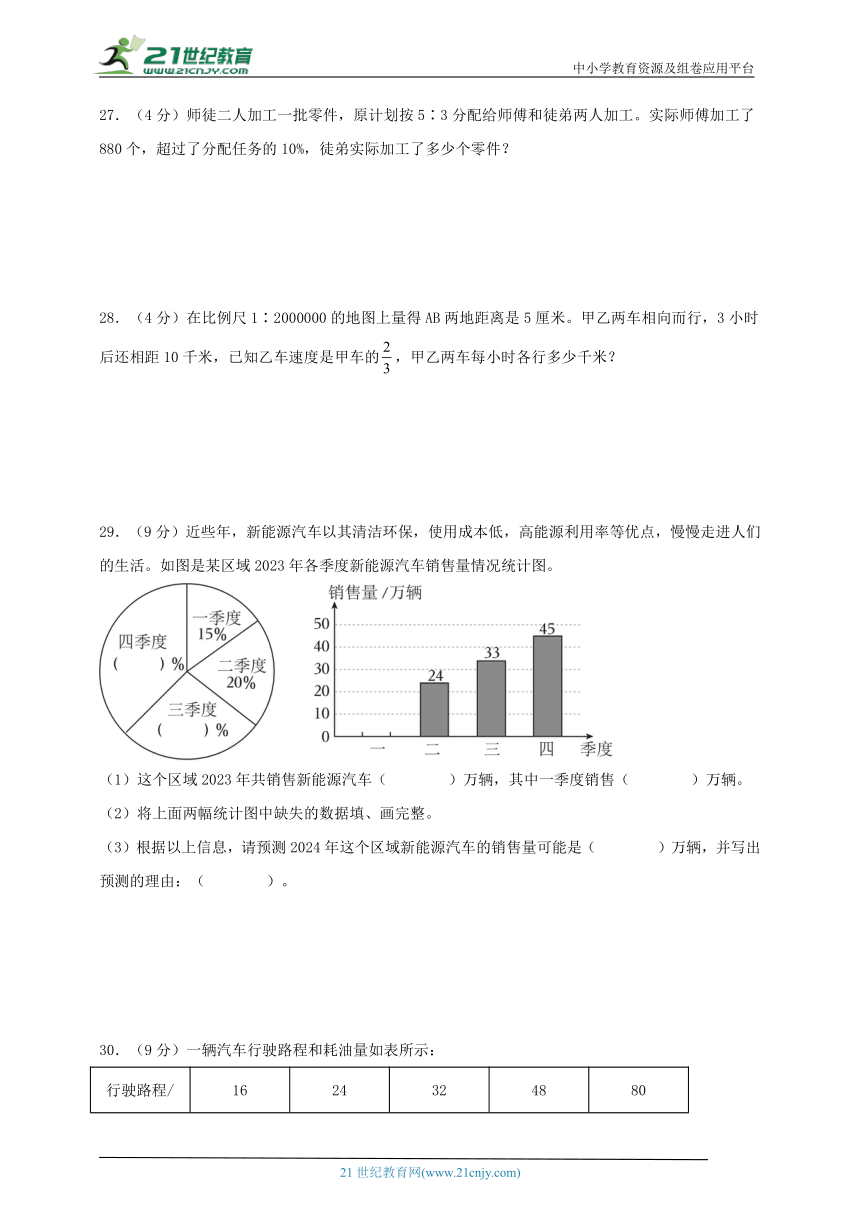
27.(4分)师徒二人加工一批零件,原计划按5∶3分配给师傅和徒弟两人加工。实际师傅加工了880个,超过了分配任务的10%,徒弟实际加工了多少个零件?
28.(4分)在比例尺1∶2000000的地图上量得AB两地距离是5厘米。甲乙两车相向而行,3小时后还相距10千米,已知乙车速度是甲车的,甲乙两车每小时各行多少千米?
29.(9分)近些年,新能源汽车以其清洁环保,使用成本低,高能源利用率等优点,慢慢走进人们的生活。如图是某区域2023年各季度新能源汽车销售量情况统计图。
(1)这个区域2023年共销售新能源汽车( )万辆,其中一季度销售( )万辆。
(2)将上面两幅统计图中缺失的数据填、画完整。
(3)根据以上信息,请预测2024年这个区域新能源汽车的销售量可能是( )万辆,并写出预测的理由:( )。
30.(9分)一辆汽车行驶路程和耗油量如表所示:
行驶路程/千米 16 24 32 48 80
耗油量/L 2 3 4 6 10
(1)表中的耗油量与行驶路程成( )比例关系。
(2)在图中描出表示行驶路程与对应耗油量的点,然后把它们连起来。
(3)李叔叔开这辆车从A城出发时,看到汽车里程表显示为370千米,到达B城时里程表显示为530千米。算一算这辆汽车从A城到B城耗油多少升?
答案解析
一、填空题(共20分)
1.(2分)在比例尺是1∶500的图纸上,量得一个正方形草坪的边长是4厘米。这个草坪的实际面积是( )。
【答案】400平方米
【分析】根据实际距离=图上距离÷比例尺,代入数据求出正方形草坪的实际边长,再根据正方形的面积=边长×边长解答即可。
【详解】4÷
=4×500
=2000(厘米)
2000厘米=20米
20×20=400(平方米)
所以这个草坪的实际面积是400平方米。
2.(2分)甲、乙两杯饮料的体积之比是4∶5,乙杯饮料的体积是甲杯的( )%,甲杯饮料的体积比乙杯饮料少( )%。
【答案】 125 20
【分析】把甲杯饮料的体积看作4升,把乙杯饮料的体积看作5升,根据求一个数是另一个数的百分之几,用除法解答,用5÷4列式解答;用乙杯饮料的体积减去甲杯饮料的体积的差除以乙杯饮料的体积求出甲杯饮料的体积比乙杯饮料少百分之几。
【详解】5÷4=1.25=125%
(5-4)÷5
=1÷5
=20%
所以乙杯饮料的体积是甲杯的125%,甲杯饮料的体积比乙杯饮料少20%。
3.(2分)用完全一样的火柴棍拼图形(如图)。
按照这样的方法拼成第4个图形需要火柴棍( )根,拼成第n个图形需要火柴棍( )根。
【答案】 34 (8n+2)/(2+8n)
【分析】根据题图可知:
第1个图形需要的火柴棍为:10根;
第2图形需要的火柴棍为:18根,18=10+8×1;
第3个图形需要的火柴棍为:26根,26=10+8×2;
第4个图形需要的火柴棍为:34根,26=10+8×3;
……
第n个图形需要的火柴棍根数为;10+8×(n-1)=8n+2。
据此解答。
【详解】下午第n个图形需要的火柴棍根数为;10+8×(n-1)=8n+2。
当n=4时,
8×4+2
=32+2
=34(根)
拼成第4个图形需要火柴棍34根,拼成第n个图形需要火柴棍(8n+2)或(2+8n)根。
4.(2分)2023年我国普通小学在校生约有108079000人,此数读作( ),初中生有五千二百四十三万六千九百人,此数写作( )。
【答案】 一亿零八百零七万九千 52436900
【分析】读数时,把数先分级,从高位读起,亿级或万级的数按照个级的读法去读,再在每级的末尾加一个“亿”或“万”字,每级末尾的0都不读,每一级的开头或中间无论有几个0,都读一个0;亿以内数的写法,从最高位写起,先写亿级再万级最后写个级,哪个数位上一个单位也没有,就在那个数位上写0;据此解答。
【详解】108079000:一亿零八百零七万九千
五千二百四十三万六千九百:52436900
2023年我国普通小学在校生约有108079000人,此数读作一亿零八百零七万九千,初中生有五千二百四十三万六千九百人,此数写作52436900。
5.(2分)=0.8==( )%=24∶( )。
【答案】10;16;80;30
【分析】将0.8转化为分数,再根据分数的基本性质,将分子和分母同时乘2和将分子和分母同时乘4;
先把0.8的小数点向右移动两位,再添上百分号就是80%。
根据分数与比的关系(分子对应前项,分母对应后项),将分数转化为比的形式,再根据比的基本性质将比的前项和后项同时乘6。
【详解】
=24∶30
6.(2分)一根长2米的圆柱形钢材截成三小段圆柱后,表面积比原来增加了36平方分米,这根钢材原来的体积是( )立方分米。
【答案】180
【分析】
如图所示,截开之后表面积比原来增加了4个截面的面积,求出一个截面的面积,再根据“圆柱的体积=底面积×高”求出这根钢材原来的体积,据此解答。
【详解】一根长2米的圆柱形钢材截成三小段圆柱后表面积比原来增加了4个截面的面积。
2米=20分米
36÷4×20
=9×20
=180(立方分米)
所以,这根钢材原来的体积是180立方分米。
7.(2分)填上合适的单位。
明乐小学的劳动教育基地面积大约有1公顷,六(1)班分到一块长方形地并种植了黄瓜。大约经过3个月,收获的季节到了,萌萌摘下一根很大的黄瓜,长约3( ),体积约500( ),她称了一下重0.5( )。
【答案】 分米/dm 立方厘米/cm3 千克/kg
【分析】常见的长度单位有米、分米、厘米、毫米等。黄瓜的长度通常不会太大,一般用厘米或者分米。
体积的单位常用的有立方米、立方分米、立方厘米。黄瓜的体积,500立方米的话太大了,不可能。500立方分米的话,等于0.5立方米,也就是相当于一个大水缸的体积,显然也不合适。而500立方厘米的话,相当于一个边长为约8厘米的正方体的体积,这比较符合黄瓜的体积。
常用吨、千克、克。0.5吨显然不可能,0.5千克的话是500克,而0.5克又太轻了。黄瓜的重量,普通的大约200克到300克,如果这根黄瓜很大,可能接近500克,也就是0.5千克。
【详解】根据分析可知:萌萌摘下一根很大的黄瓜,长约3分米,体积约500立方厘米,她称了一下重0.5千克
8.(2分)根据各式的规律填空:
1=
1+3=
1+3+5=
1+3+5+7=
(1)1+3+5+7+9+11+13= 。
(2)从1开始, 个连续奇数相加的和是。
【答案】(1)7
(2)20
【分析】(1)求1+3+5+7+9+11+13等于几的平方,我们看前面的式子1=,这里是1个奇数相加;1+3=,这里是2个奇数相加;1+3+5=,这里是3个奇数相加;1+3+5+7=,这里是4个奇数相加。那么对于1+3+5+7+9+11+13,我们数一下这里奇数的个数,一共有7个奇数相加,所以从1开始连续奇数相加的和等于奇数个数的平方。据此解答。
(2)根据(1)中的规律解答。
【详解】(1)根据前面发现的规律,从1开始连续奇数相加的和等于奇数个数的平方,所以1+3+5+7+9+11+13=。
(2)因为前面我们发现从1开始连续奇数相加的和等于奇数个数的平方。现在和是,那么根据这个规律,就可以知道是从1开始20个连续奇数相加的和是。
9.(2分)在一个比例里,两个内项互为倒数,一个外项是2.5,另一个外项是( )。如果一个内项是0.5,那么这个比例可能是( )。
【答案】 0.4/ 2.5∶0.5=2∶0.4
【分析】根据比例的基本性质:在比例中,两个外项的积等于两个内项的积,如果两个内项互为倒数,则两个内项之积等于1,用1÷2.5即可求出另一个外项。根据内项是0.5,用1÷0.5求出另一个内项,然后写出比例即可。
【详解】1÷2.5=0.4
1÷0.5=2
比例为:2.5∶0.5=2∶0.4
所以,两个内项互为倒数,一个外项是2.5,另一个外项是0.4。如果一个内项是0.5,那么这个比例可能是2.5∶0.5=2∶0.4(比例答案不唯一)。
10.(2分)按一定的规律写数:1、2、﹣3、4、5、﹣6、7、8、﹣9…,当写完第100个数停下来时,写的数中一共有( )个正数,( )个负数。
【答案】 67 33
【分析】将写的这一组数中每三个数分为一组,每组中前两个数为正数,后一个数为负数;用100除以3所得商为一共有几组数,余数为每组中的第几个数,最后用所得商乘2再加上这个余数,就是所有正数的个数,用100减去正数的个数,所得差即为负数的个数。
【详解】100÷3=33(组)……1(个)
余数为1,最后一个数在第34组的第1个,可知为正数。
正数:2×33+1
=66+1
=67(个)
负数:100-67=33(个)。
因此写的数中一共有67个正数,33个负数。
二、判断题(共10分)
11.(2分)在一定存期内,利率一定,利息和本金成正比例。( )
【答案】√
【分析】用判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,此题中是两个数量之间的积是一定的,据此判断即可。
【详解】因为本金×利率×存期=利息,即利息÷本金÷存期=利率(一定),是商一定,所以本金和利息成正比例。
原题说法正确。
故答案为:√
12.(2分)A×=B÷(A,B都不等于0),则A<B。( )
【答案】×
【分析】本题可先将等式A×=B÷进行变形,再比较A和B的大小。对等式进行变形,根据除法运算法则,除以一个数等于乘它的倒数,B÷=B×6,那么原等式A×=B÷可转化为A×=B×6。比较A和B的大小,在等式A×=B×6中,因为<6,当两个乘法算式的积相等时(A、B都不为0),一个因数越小,另一个因数就越大。
所以A>B,而题目中说A<B,该说法错误。
【详解】A×=B÷
即A×=B×6
因为<6,所以A>B。
故答案为:×
13.(2分)一根圆柱形木料,如果沿着底面直径切成两半,表面积增加120平方厘米。如果平行于底面截成两个小圆柱,表面积增加157平方厘米。则这根圆柱形木料原来的高是6厘米。( )
【答案】√
【分析】如果平行于底面截成两个小圆柱,则增加的表面积是两个底面圆的面积,用157÷2即可求得一个圆的面积,再根据变形得求得半径;将圆柱沿着底面直径切成两半,新增加的面是两个长方形,长方形的一条边是底面直径,另一条边是圆柱的高,用120÷2求出一个长方形的面积,再用长方形的面积除以直径,就可以求出圆柱的高;据此解答即可。
【详解】157÷2÷3.14
=78.5÷3.14
=25(平方厘米)
因为5×5=25,所以说这个圆柱形的木料的底面半径是5厘米。
120÷2÷(5×2)
=60÷10
=6(厘米)
所以,这根圆柱形木料的高是6厘米。
原题说法正确。
故答案为:√
14.(2分)将按照顺时针方向旋转90°,得到的图形是。( )
【答案】√
【分析】将图形按顺时针方向旋转90°,即将图形中的每一部分都按顺时针方向旋转90°,即可得到旋转后的图形,再进行判断即可。
【详解】
根据旋转的方法可知,将按顺时针方向旋转90°,得到的图形是;原说法正确。
故答案为:√
15.(2分)把一个边长4cm的正方形按3∶1放大,放大后正方形的面积为12cm2。( )
【答案】×
【分析】根据题意,将正方形按3∶1放大,即放大后的正方形边上是原来边长的3倍,据此计算出放大后正方形的边长,再根据正方形的面积=边长×边长,计算出面积即可判断。
【详解】4×3=12(cm)
12×12=144(cm2)
即放大后正方形的面积为144cm2,即原说法错误。
故答案为:×
三、选择题(共10分)
16.(2分)超市在学校的东偏南35°方向上,学校在超市的( )方向上。
A.南偏东35° B.北偏西35° C.西偏北35° D.西偏北55°
【答案】C
【分析】根据位置的相对性可知,它们的方向相反,角度相等,据此解答即可。
【详解】超市在学校的东偏南35°方向上,学校在超市的西偏北35°方向上。
故答案为:C
17.(2分)如果给4∶11的前项加上8,要使比值不变,后项应该( )。
A.加上8 B.减去8 C.乘3 D.除以2
【答案】C
【分析】比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
给4∶11的前项加上8得12,即前项乘3,根据比的基本性质,比的后项也要乘3,后项11乘3后再减去11,就是比的后项要增加的数,据此解答。
【详解】前项相当于乘:
(4+8)÷4
=12÷4
=3
后项也要乘3或加上:
11×3-11
=33-11
=22
如果给4∶11的前项加上8,要使比值不变,后项应该乘3或加上22。
故答案为:C
18.(2分)成年人的身高与足长的比大约是7∶1,某小区发生了一起盗窃事件,在犯罪现场留下了一个长25厘米的足印。经过周密侦察,下表是这四名犯罪嫌疑人的身高记录。根据表中信息可以推断嫌疑最大的是( )。
犯罪嫌疑人 李某 谭某 向某 刘某
身高(厘米) 182 176 168 162
A.李某 B.谭某 C.向某 D.刘某
【答案】B
【分析】已知成年人身高与足长比为7:1 ,犯罪现场足印长25厘米,根据这个比例关系,可列出比例7∶1=x∶25,根据比例的基本性质解出x,也就是理论身高;按照比的应用,在这个情境中,嫌疑人身高越接近根据足印和身高足长比例关系算出的理论身高,嫌疑就越大。
【详解】解:设长25厘米足印的人理论身高是x厘米。
7∶1=x∶25
x=25×7
x=175
所以长25厘米足印的人理论身高是175厘米。
A.李某身高182厘米,与175厘米相比,偏离了182-175=7厘米;
B.谭某身高176厘米,仅偏离理论身高176-175=1厘米;
C.向某身高168厘米,偏离了175-168=7厘米;
D.刘某身高162厘米,偏离达175-162=13厘米。
通过比较可知,谭某身高与根据比例算出的理论身高差值最小,所以谭某嫌疑最大。
故答案为:B
19.(2分)如图直线上,被墨水盖住的整数有( )个。
A.4 B.7 C.10 D.8
【答案】B
【分析】由图可知,直线上两个相邻的数之差是1,左边盖住的整数数值是:﹣3,﹣2,﹣1;右边盖住的整数数值是:2,3,4,5。负整数有3个,正整数有4个,把3个和4个加起来即可。
【详解】3+4=7(个)
所以如图直线上,被墨水盖住的整数有7个。
故答案为:B
20.(2分)如图,如果将这个容器倒过来后,水面的高度是( )厘米。
A.12 B.11 C.15 D.9
【答案】B
【分析】已知圆锥的高度是6厘米,因为等底等高的圆柱体积是圆锥体积的3倍,所以相同体积的水,在圆锥中高度为6厘米时,倒过来放在等底的圆柱中,高度就变为圆锥高度的,用6×列式求出与原来圆柱等底、高为6cm的圆锥变为圆柱后的水的高度,再加上原来容器内圆柱部分水的高度即可解答。
【详解】6×+(15-6)
=2+9
=11(厘米)
所以水面的高度是11厘米。
故答案为:B
四、计算题(共18分)
21.(6分)下面各题,怎样简便就怎样算。
12.5×32×0.25
【答案】7;100
3;
【分析】48×(+),根据乘法分配律,原式化为:48×+48×,再进行计算。
12.5×32×0.25,把32化为8×4,原式化为:12.5×8×4×0.25,再根据乘法结合律,原式化为:(12.5×8)×(4×0.25),再进行计算。
-2.25+-4.75,根据带符号搬家,原式化为:+-2.25-4.75,再根据加法结合律和减法性质,原式化为:(+)-(2.25+4.75),再进行计算。
÷[-(+)],根据减法性质,原式化为:÷[--],再根据带符号搬家,原式化为:÷[--],再按照运算顺序,进行计算。
【详解】48×(+)
=48×+48×
=4+3
=7
12.5×32×7.25
=12.5×8×4×0.25
=(12.5×8)×(4×0.25)
=100×1
=100
-2.25+-4.75
=+-2.25-4.75
=(+)-(2.25+4.75)
=10-7
=3
÷[-(+)]
=÷[--]
=÷[--]
=÷[1-]
=÷
=×4
=
22.(6分)解方程。
【答案】;
;
【分析】(1)先根据比例的基本性质将比例方程改写成,然后方程两边同时除以,求出方程的解;
(2)先把方程化简成,然后方程两边同时除以,求出方程的解;
(3)方程两边先同时减去,再同时除以,求出方程的解;
(4)方程两边先同时除以,再同时减去,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
(4)
解:
23.(6分)直接写得数。
0.4×20%= = = =
1÷0.2= 0.53= = =
【答案】0.08;9;;1;
5;0.125;;9
五、作图题(共8分)
24.(8分)实践操作与应用。
(1)画出三角形ABC绕点B逆时针旋转90°后的图形。旋转后,C点的对应点的位置用数对表示是( )。
(2)以BC所在直线为对称轴,画出与三角形ABC对称的图形。
(3)画出三角形ABC按2∶1放大后的图形。
【答案】(1)(2,6);图见详解
(2)图见详解
(3)图见详解
【分析】(1)根据旋转的特征,将三角形ABC绕点B逆时针旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此用数对表示旋转后C点对应点的位置。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,找到三角形ABC的各顶点关于对称轴BC所在直线的对称点后,依次连接各点得到三角形ABC对称的图形。
(3)三角形ABC按2∶1放大,则三角形ABC原来的底和高都乘2,即是放大后三角形的底和高,据此画出放大后的三角形。
【详解】(1)三角形ABC绕点B逆时针旋转90°,如下图。
C点的对应点的位置用数对表示是(2,6)。
(2)以BC所在直线为对称轴,画与三角形ABC对称的图形,如下图。
(3)放大后三角形的底:3×2=6
放大后三角形的高:2×2=4
画一个底为6、高为4的三角形。
如图:
六、解答题(共34分)
25.(4分)2024年5月20日,盐城新地标建筑“串场之眼”揭开面纱,成了市民们休闲娱乐的“打卡”新去处。据介绍,该建筑总面积约21000平方米,比商业使用面积的3.2倍还多1800平方米。“串场之眼”商业使用面积约有多少平方米?(用方程解)
【答案】6000平方米
【分析】设“串场之眼”商业使用面积是x平方米,商业使用面积×3.2+“串场之眼”的建筑总面积比商业使用面积的3.2倍多的面积=“串场之眼”的建筑总面积,据此列出方程为:3.2x+1800=21000,再解方程即可。
【详解】解:设“串场之眼”商业使用面积是x平方米。
3.2x+1800=21000
3.2x+1800-1800=21000-1800
3.2x=19200
3.2x÷3.2=19200÷3.2
x=6000
答:“串场之眼”商业使用面积约有6000平方米。
26.(4分)张大伯家有一个圆锥形小麦堆,量得它的底面周长是12.56米,高是1.5米,如果每立方米小麦的质量为700千克,这堆小麦的质量为多少千克?
【答案】4396千克
【分析】利用圆锥底周长公式:C=2πr,转化为r=C÷π÷2,计算其底面半径,再利用体积公式:V=πr2计算其体积,再乘700千克,计算小麦的质量即可。
【详解】12.56÷3.14÷2=2(m)
=3.14×4×1.5×
=6.28(m3)
6.28×700=4396(千克)
答:这堆小麦的质量为4396千克。
27.(4分)师徒二人加工一批零件,原计划按5∶3分配给师傅和徒弟两人加工。实际师傅加工了880个,超过了分配任务的10%,徒弟实际加工了多少个零件?
【答案】400个
【分析】先以师傅原计划任务量为单位“1”,根据师傅实际加工数及超产比例,用除法求出师傅原计划任务量;再依据原计划分配比例,可知师傅原计划任务量占总任务量的,通过除法求出零件总任务量;最后用零件总任务量减去师傅实际加工量就是徒弟实际加工数量。
【详解】880÷(1+10%)
=880÷(100%+10%)
=880÷110%
=880÷1.1
=800(个)
800÷
=800÷
=800×
=160×8
=1280(个)
1280-880=400(个)
答:徒弟实际加工了400个零件。
28.(4分)在比例尺1∶2000000的地图上量得AB两地距离是5厘米。甲乙两车相向而行,3小时后还相距10千米,已知乙车速度是甲车的,甲乙两车每小时各行多少千米?
【答案】甲车:18千米,乙车:12千米
【分析】先根据图上距离除以比例尺求出两地的距离,用两地距离减10可得行驶的路程,再根据路程和÷行驶时间求出速度和,把甲车速度看作单位“1”,则两车速度和占甲车的,根据已知一个数的几分之几是多少,求这个数用除法计算,进而求出甲车速度,再根据求一个数的几分之几是多少,用乘法计算即可。计算时单位统一为千米。
【详解】5÷
=5×2000000
=10000000(厘米)
10000000厘米=100千米
(100-10)÷3
=90÷3
=30(千米)
30÷(1+)
=30÷
=30×
=18(千米)
18×=12(千米)
答:甲车每小时行18千米,乙车每小时行12千米。
29.(9分)近些年,新能源汽车以其清洁环保,使用成本低,高能源利用率等优点,慢慢走进人们的生活。如图是某区域2023年各季度新能源汽车销售量情况统计图。
(1)这个区域2023年共销售新能源汽车( )万辆,其中一季度销售( )万辆。
(2)将上面两幅统计图中缺失的数据填、画完整。
(3)根据以上信息,请预测2024年这个区域新能源汽车的销售量可能是( )万辆,并写出预测的理由:( )。
【答案】(1)120;18;
(2)图见详解
(3)150;每一季度的销售量是逐渐增加的
【分析】(1)根据统计图可知,二季度的销售量是24万量,占这个区域2023年总销售量的20%,用24除以20%即可求出总销售量;再用总销售量乘一季度占的百分比,即可求出一季度的销售量;
(2)分别用三、四季度的销售量除以总销售量,分别求出三、四季度占的百分比,然后再把统计图补充完整。
(3)根据2023年销售量预测2024的销售量即可。(答案不唯一)
【详解】(1)24÷20%=120(万辆)
120×15%=18(万辆)
这个区域2023年共销售新能源汽车120万辆,其中一季度销售18万辆。
(2)33÷120×100%
=0.275×100%
=27.5%
45÷120×100%
=0.375×100%
=37.5%
统计图如下:
(3)预测2024年这个区域新能源汽车的销售量可能是150万辆,因为每一季度的销售量是逐渐增加的。(答案不唯一)
30.(9分)一辆汽车行驶路程和耗油量如表所示:
行驶路程/千米 16 24 32 48 80
耗油量/L 2 3 4 6 10
(1)表中的耗油量与行驶路程成( )比例关系。
(2)在图中描出表示行驶路程与对应耗油量的点,然后把它们连起来。
(3)李叔叔开这辆车从A城出发时,看到汽车里程表显示为370千米,到达B城时里程表显示为530千米。算一算这辆汽车从A城到B城耗油多少升?
【答案】(1)正;
(2)见详解
(3)20升
【分析】(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量叫做成正比例的量,它们的关系叫做正比例关系。
(2)根据表中的数据,描点、连线即可。
(3)用530减去370求出从A城到B城的路程,再除以行驶1千米的耗油量即可解答。
【详解】(1)16∶2=8
24∶3=8
32∶8
48∶6=8
80∶10=8
行驶路程∶耗油量=8(一定),所以表中的耗油量与行驶路程成正比例关系。
(2)
(3)530-370=160(千米)
160÷8=20(升)
答:这辆汽车从A城到B城耗油20升。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版六年级数学下册期末考试满分冲刺质量检测卷一
一、填空题(共20分)
1.(2分)在比例尺是1∶500的图纸上,量得一个正方形草坪的边长是4厘米。这个草坪的实际面积是( )。
2.(2分)甲、乙两杯饮料的体积之比是4∶5,乙杯饮料的体积是甲杯的( )%,甲杯饮料的体积比乙杯饮料少( )%。
3.(2分)用完全一样的火柴棍拼图形(如图)。
按照这样的方法拼成第4个图形需要火柴棍( )根,拼成第n个图形需要火柴棍( )根。
4.(2分)2023年我国普通小学在校生约有108079000人,此数读作( ),初中生有五千二百四十三万六千九百人,此数写作( )。
5.(2分)=0.8==( )%=24∶( )。
6.(2分)一根长2米的圆柱形钢材截成三小段圆柱后,表面积比原来增加了36平方分米,这根钢材原来的体积是( )立方分米。
7.(2分)填上合适的单位。
明乐小学的劳动教育基地面积大约有1公顷,六(1)班分到一块长方形地并种植了黄瓜。大约经过3个月,收获的季节到了,萌萌摘下一根很大的黄瓜,长约3( ),体积约500( ),她称了一下重0.5( )。
8.(2分)根据各式的规律填空:
1=
1+3=
1+3+5=
1+3+5+7=
(1)1+3+5+7+9+11+13= 。
(2)从1开始, 个连续奇数相加的和是。
9.(2分)在一个比例里,两个内项互为倒数,一个外项是2.5,另一个外项是( )。如果一个内项是0.5,那么这个比例可能是( )。
10.(2分)按一定的规律写数:1、2、﹣3、4、5、﹣6、7、8、﹣9…,当写完第100个数停下来时,写的数中一共有( )个正数,( )个负数。
二、判断题(共10分)
11.(2分)在一定存期内,利率一定,利息和本金成正比例。( )
12.(2分)A×=B÷(A,B都不等于0),则A<B。( )
13.(2分)一根圆柱形木料,如果沿着底面直径切成两半,表面积增加120平方厘米。如果平行于底面截成两个小圆柱,表面积增加157平方厘米。则这根圆柱形木料原来的高是6厘米。( )
14.(2分)将按照顺时针方向旋转90°,得到的图形是。( )
15.(2分)把一个边长4cm的正方形按3∶1放大,放大后正方形的面积为12cm2。( )
三、选择题(共10分)
16.(2分)超市在学校的东偏南35°方向上,学校在超市的( )方向上。
A.南偏东35° B.北偏西35° C.西偏北35° D.西偏北55°
17.(2分)如果给4∶11的前项加上8,要使比值不变,后项应该( )。
A.加上8 B.减去8 C.乘3 D.除以2
18.(2分)成年人的身高与足长的比大约是7∶1,某小区发生了一起盗窃事件,在犯罪现场留下了一个长25厘米的足印。经过周密侦察,下表是这四名犯罪嫌疑人的身高记录。根据表中信息可以推断嫌疑最大的是( )。
犯罪嫌疑人 李某 谭某 向某 刘某
身高(厘米) 182 176 168 162
A.李某 B.谭某 C.向某 D.刘某
19.(2分)如图直线上,被墨水盖住的整数有( )个。
A.4 B.7 C.10 D.8
20.(2分)如图,如果将这个容器倒过来后,水面的高度是( )厘米。
A.12 B.11 C.15 D.9
四、计算题(共18分)
21.(6分)下面各题,怎样简便就怎样算。
12.5×32×0.25
22.(6分)解方程。
23.(6分)直接写得数。
0.4×20%= = = =
1÷0.2= 0.53= = =
五、作图题(共8分)
24.(8分)实践操作与应用。
(1)画出三角形ABC绕点B逆时针旋转90°后的图形。旋转后,C点的对应点的位置用数对表示是( )。
(2)以BC所在直线为对称轴,画出与三角形ABC对称的图形。
(3)画出三角形ABC按2∶1放大后的图形。
六、解答题(共34分)
25.(4分)2024年5月20日,盐城新地标建筑“串场之眼”揭开面纱,成了市民们休闲娱乐的“打卡”新去处。据介绍,该建筑总面积约21000平方米,比商业使用面积的3.2倍还多1800平方米。“串场之眼”商业使用面积约有多少平方米?(用方程解)
26.(4分)张大伯家有一个圆锥形小麦堆,量得它的底面周长是12.56米,高是1.5米,如果每立方米小麦的质量为700千克,这堆小麦的质量为多少千克?
27.(4分)师徒二人加工一批零件,原计划按5∶3分配给师傅和徒弟两人加工。实际师傅加工了880个,超过了分配任务的10%,徒弟实际加工了多少个零件?
28.(4分)在比例尺1∶2000000的地图上量得AB两地距离是5厘米。甲乙两车相向而行,3小时后还相距10千米,已知乙车速度是甲车的,甲乙两车每小时各行多少千米?
29.(9分)近些年,新能源汽车以其清洁环保,使用成本低,高能源利用率等优点,慢慢走进人们的生活。如图是某区域2023年各季度新能源汽车销售量情况统计图。
(1)这个区域2023年共销售新能源汽车( )万辆,其中一季度销售( )万辆。
(2)将上面两幅统计图中缺失的数据填、画完整。
(3)根据以上信息,请预测2024年这个区域新能源汽车的销售量可能是( )万辆,并写出预测的理由:( )。
30.(9分)一辆汽车行驶路程和耗油量如表所示:
行驶路程/千米 16 24 32 48 80
耗油量/L 2 3 4 6 10
(1)表中的耗油量与行驶路程成( )比例关系。
(2)在图中描出表示行驶路程与对应耗油量的点,然后把它们连起来。
(3)李叔叔开这辆车从A城出发时,看到汽车里程表显示为370千米,到达B城时里程表显示为530千米。算一算这辆汽车从A城到B城耗油多少升?
答案解析
一、填空题(共20分)
1.(2分)在比例尺是1∶500的图纸上,量得一个正方形草坪的边长是4厘米。这个草坪的实际面积是( )。
【答案】400平方米
【分析】根据实际距离=图上距离÷比例尺,代入数据求出正方形草坪的实际边长,再根据正方形的面积=边长×边长解答即可。
【详解】4÷
=4×500
=2000(厘米)
2000厘米=20米
20×20=400(平方米)
所以这个草坪的实际面积是400平方米。
2.(2分)甲、乙两杯饮料的体积之比是4∶5,乙杯饮料的体积是甲杯的( )%,甲杯饮料的体积比乙杯饮料少( )%。
【答案】 125 20
【分析】把甲杯饮料的体积看作4升,把乙杯饮料的体积看作5升,根据求一个数是另一个数的百分之几,用除法解答,用5÷4列式解答;用乙杯饮料的体积减去甲杯饮料的体积的差除以乙杯饮料的体积求出甲杯饮料的体积比乙杯饮料少百分之几。
【详解】5÷4=1.25=125%
(5-4)÷5
=1÷5
=20%
所以乙杯饮料的体积是甲杯的125%,甲杯饮料的体积比乙杯饮料少20%。
3.(2分)用完全一样的火柴棍拼图形(如图)。
按照这样的方法拼成第4个图形需要火柴棍( )根,拼成第n个图形需要火柴棍( )根。
【答案】 34 (8n+2)/(2+8n)
【分析】根据题图可知:
第1个图形需要的火柴棍为:10根;
第2图形需要的火柴棍为:18根,18=10+8×1;
第3个图形需要的火柴棍为:26根,26=10+8×2;
第4个图形需要的火柴棍为:34根,26=10+8×3;
……
第n个图形需要的火柴棍根数为;10+8×(n-1)=8n+2。
据此解答。
【详解】下午第n个图形需要的火柴棍根数为;10+8×(n-1)=8n+2。
当n=4时,
8×4+2
=32+2
=34(根)
拼成第4个图形需要火柴棍34根,拼成第n个图形需要火柴棍(8n+2)或(2+8n)根。
4.(2分)2023年我国普通小学在校生约有108079000人,此数读作( ),初中生有五千二百四十三万六千九百人,此数写作( )。
【答案】 一亿零八百零七万九千 52436900
【分析】读数时,把数先分级,从高位读起,亿级或万级的数按照个级的读法去读,再在每级的末尾加一个“亿”或“万”字,每级末尾的0都不读,每一级的开头或中间无论有几个0,都读一个0;亿以内数的写法,从最高位写起,先写亿级再万级最后写个级,哪个数位上一个单位也没有,就在那个数位上写0;据此解答。
【详解】108079000:一亿零八百零七万九千
五千二百四十三万六千九百:52436900
2023年我国普通小学在校生约有108079000人,此数读作一亿零八百零七万九千,初中生有五千二百四十三万六千九百人,此数写作52436900。
5.(2分)=0.8==( )%=24∶( )。
【答案】10;16;80;30
【分析】将0.8转化为分数,再根据分数的基本性质,将分子和分母同时乘2和将分子和分母同时乘4;
先把0.8的小数点向右移动两位,再添上百分号就是80%。
根据分数与比的关系(分子对应前项,分母对应后项),将分数转化为比的形式,再根据比的基本性质将比的前项和后项同时乘6。
【详解】
=24∶30
6.(2分)一根长2米的圆柱形钢材截成三小段圆柱后,表面积比原来增加了36平方分米,这根钢材原来的体积是( )立方分米。
【答案】180
【分析】
如图所示,截开之后表面积比原来增加了4个截面的面积,求出一个截面的面积,再根据“圆柱的体积=底面积×高”求出这根钢材原来的体积,据此解答。
【详解】一根长2米的圆柱形钢材截成三小段圆柱后表面积比原来增加了4个截面的面积。
2米=20分米
36÷4×20
=9×20
=180(立方分米)
所以,这根钢材原来的体积是180立方分米。
7.(2分)填上合适的单位。
明乐小学的劳动教育基地面积大约有1公顷,六(1)班分到一块长方形地并种植了黄瓜。大约经过3个月,收获的季节到了,萌萌摘下一根很大的黄瓜,长约3( ),体积约500( ),她称了一下重0.5( )。
【答案】 分米/dm 立方厘米/cm3 千克/kg
【分析】常见的长度单位有米、分米、厘米、毫米等。黄瓜的长度通常不会太大,一般用厘米或者分米。
体积的单位常用的有立方米、立方分米、立方厘米。黄瓜的体积,500立方米的话太大了,不可能。500立方分米的话,等于0.5立方米,也就是相当于一个大水缸的体积,显然也不合适。而500立方厘米的话,相当于一个边长为约8厘米的正方体的体积,这比较符合黄瓜的体积。
常用吨、千克、克。0.5吨显然不可能,0.5千克的话是500克,而0.5克又太轻了。黄瓜的重量,普通的大约200克到300克,如果这根黄瓜很大,可能接近500克,也就是0.5千克。
【详解】根据分析可知:萌萌摘下一根很大的黄瓜,长约3分米,体积约500立方厘米,她称了一下重0.5千克
8.(2分)根据各式的规律填空:
1=
1+3=
1+3+5=
1+3+5+7=
(1)1+3+5+7+9+11+13= 。
(2)从1开始, 个连续奇数相加的和是。
【答案】(1)7
(2)20
【分析】(1)求1+3+5+7+9+11+13等于几的平方,我们看前面的式子1=,这里是1个奇数相加;1+3=,这里是2个奇数相加;1+3+5=,这里是3个奇数相加;1+3+5+7=,这里是4个奇数相加。那么对于1+3+5+7+9+11+13,我们数一下这里奇数的个数,一共有7个奇数相加,所以从1开始连续奇数相加的和等于奇数个数的平方。据此解答。
(2)根据(1)中的规律解答。
【详解】(1)根据前面发现的规律,从1开始连续奇数相加的和等于奇数个数的平方,所以1+3+5+7+9+11+13=。
(2)因为前面我们发现从1开始连续奇数相加的和等于奇数个数的平方。现在和是,那么根据这个规律,就可以知道是从1开始20个连续奇数相加的和是。
9.(2分)在一个比例里,两个内项互为倒数,一个外项是2.5,另一个外项是( )。如果一个内项是0.5,那么这个比例可能是( )。
【答案】 0.4/ 2.5∶0.5=2∶0.4
【分析】根据比例的基本性质:在比例中,两个外项的积等于两个内项的积,如果两个内项互为倒数,则两个内项之积等于1,用1÷2.5即可求出另一个外项。根据内项是0.5,用1÷0.5求出另一个内项,然后写出比例即可。
【详解】1÷2.5=0.4
1÷0.5=2
比例为:2.5∶0.5=2∶0.4
所以,两个内项互为倒数,一个外项是2.5,另一个外项是0.4。如果一个内项是0.5,那么这个比例可能是2.5∶0.5=2∶0.4(比例答案不唯一)。
10.(2分)按一定的规律写数:1、2、﹣3、4、5、﹣6、7、8、﹣9…,当写完第100个数停下来时,写的数中一共有( )个正数,( )个负数。
【答案】 67 33
【分析】将写的这一组数中每三个数分为一组,每组中前两个数为正数,后一个数为负数;用100除以3所得商为一共有几组数,余数为每组中的第几个数,最后用所得商乘2再加上这个余数,就是所有正数的个数,用100减去正数的个数,所得差即为负数的个数。
【详解】100÷3=33(组)……1(个)
余数为1,最后一个数在第34组的第1个,可知为正数。
正数:2×33+1
=66+1
=67(个)
负数:100-67=33(个)。
因此写的数中一共有67个正数,33个负数。
二、判断题(共10分)
11.(2分)在一定存期内,利率一定,利息和本金成正比例。( )
【答案】√
【分析】用判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,此题中是两个数量之间的积是一定的,据此判断即可。
【详解】因为本金×利率×存期=利息,即利息÷本金÷存期=利率(一定),是商一定,所以本金和利息成正比例。
原题说法正确。
故答案为:√
12.(2分)A×=B÷(A,B都不等于0),则A<B。( )
【答案】×
【分析】本题可先将等式A×=B÷进行变形,再比较A和B的大小。对等式进行变形,根据除法运算法则,除以一个数等于乘它的倒数,B÷=B×6,那么原等式A×=B÷可转化为A×=B×6。比较A和B的大小,在等式A×=B×6中,因为<6,当两个乘法算式的积相等时(A、B都不为0),一个因数越小,另一个因数就越大。
所以A>B,而题目中说A<B,该说法错误。
【详解】A×=B÷
即A×=B×6
因为<6,所以A>B。
故答案为:×
13.(2分)一根圆柱形木料,如果沿着底面直径切成两半,表面积增加120平方厘米。如果平行于底面截成两个小圆柱,表面积增加157平方厘米。则这根圆柱形木料原来的高是6厘米。( )
【答案】√
【分析】如果平行于底面截成两个小圆柱,则增加的表面积是两个底面圆的面积,用157÷2即可求得一个圆的面积,再根据变形得求得半径;将圆柱沿着底面直径切成两半,新增加的面是两个长方形,长方形的一条边是底面直径,另一条边是圆柱的高,用120÷2求出一个长方形的面积,再用长方形的面积除以直径,就可以求出圆柱的高;据此解答即可。
【详解】157÷2÷3.14
=78.5÷3.14
=25(平方厘米)
因为5×5=25,所以说这个圆柱形的木料的底面半径是5厘米。
120÷2÷(5×2)
=60÷10
=6(厘米)
所以,这根圆柱形木料的高是6厘米。
原题说法正确。
故答案为:√
14.(2分)将按照顺时针方向旋转90°,得到的图形是。( )
【答案】√
【分析】将图形按顺时针方向旋转90°,即将图形中的每一部分都按顺时针方向旋转90°,即可得到旋转后的图形,再进行判断即可。
【详解】
根据旋转的方法可知,将按顺时针方向旋转90°,得到的图形是;原说法正确。
故答案为:√
15.(2分)把一个边长4cm的正方形按3∶1放大,放大后正方形的面积为12cm2。( )
【答案】×
【分析】根据题意,将正方形按3∶1放大,即放大后的正方形边上是原来边长的3倍,据此计算出放大后正方形的边长,再根据正方形的面积=边长×边长,计算出面积即可判断。
【详解】4×3=12(cm)
12×12=144(cm2)
即放大后正方形的面积为144cm2,即原说法错误。
故答案为:×
三、选择题(共10分)
16.(2分)超市在学校的东偏南35°方向上,学校在超市的( )方向上。
A.南偏东35° B.北偏西35° C.西偏北35° D.西偏北55°
【答案】C
【分析】根据位置的相对性可知,它们的方向相反,角度相等,据此解答即可。
【详解】超市在学校的东偏南35°方向上,学校在超市的西偏北35°方向上。
故答案为:C
17.(2分)如果给4∶11的前项加上8,要使比值不变,后项应该( )。
A.加上8 B.减去8 C.乘3 D.除以2
【答案】C
【分析】比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
给4∶11的前项加上8得12,即前项乘3,根据比的基本性质,比的后项也要乘3,后项11乘3后再减去11,就是比的后项要增加的数,据此解答。
【详解】前项相当于乘:
(4+8)÷4
=12÷4
=3
后项也要乘3或加上:
11×3-11
=33-11
=22
如果给4∶11的前项加上8,要使比值不变,后项应该乘3或加上22。
故答案为:C
18.(2分)成年人的身高与足长的比大约是7∶1,某小区发生了一起盗窃事件,在犯罪现场留下了一个长25厘米的足印。经过周密侦察,下表是这四名犯罪嫌疑人的身高记录。根据表中信息可以推断嫌疑最大的是( )。
犯罪嫌疑人 李某 谭某 向某 刘某
身高(厘米) 182 176 168 162
A.李某 B.谭某 C.向某 D.刘某
【答案】B
【分析】已知成年人身高与足长比为7:1 ,犯罪现场足印长25厘米,根据这个比例关系,可列出比例7∶1=x∶25,根据比例的基本性质解出x,也就是理论身高;按照比的应用,在这个情境中,嫌疑人身高越接近根据足印和身高足长比例关系算出的理论身高,嫌疑就越大。
【详解】解:设长25厘米足印的人理论身高是x厘米。
7∶1=x∶25
x=25×7
x=175
所以长25厘米足印的人理论身高是175厘米。
A.李某身高182厘米,与175厘米相比,偏离了182-175=7厘米;
B.谭某身高176厘米,仅偏离理论身高176-175=1厘米;
C.向某身高168厘米,偏离了175-168=7厘米;
D.刘某身高162厘米,偏离达175-162=13厘米。
通过比较可知,谭某身高与根据比例算出的理论身高差值最小,所以谭某嫌疑最大。
故答案为:B
19.(2分)如图直线上,被墨水盖住的整数有( )个。
A.4 B.7 C.10 D.8
【答案】B
【分析】由图可知,直线上两个相邻的数之差是1,左边盖住的整数数值是:﹣3,﹣2,﹣1;右边盖住的整数数值是:2,3,4,5。负整数有3个,正整数有4个,把3个和4个加起来即可。
【详解】3+4=7(个)
所以如图直线上,被墨水盖住的整数有7个。
故答案为:B
20.(2分)如图,如果将这个容器倒过来后,水面的高度是( )厘米。
A.12 B.11 C.15 D.9
【答案】B
【分析】已知圆锥的高度是6厘米,因为等底等高的圆柱体积是圆锥体积的3倍,所以相同体积的水,在圆锥中高度为6厘米时,倒过来放在等底的圆柱中,高度就变为圆锥高度的,用6×列式求出与原来圆柱等底、高为6cm的圆锥变为圆柱后的水的高度,再加上原来容器内圆柱部分水的高度即可解答。
【详解】6×+(15-6)
=2+9
=11(厘米)
所以水面的高度是11厘米。
故答案为:B
四、计算题(共18分)
21.(6分)下面各题,怎样简便就怎样算。
12.5×32×0.25
【答案】7;100
3;
【分析】48×(+),根据乘法分配律,原式化为:48×+48×,再进行计算。
12.5×32×0.25,把32化为8×4,原式化为:12.5×8×4×0.25,再根据乘法结合律,原式化为:(12.5×8)×(4×0.25),再进行计算。
-2.25+-4.75,根据带符号搬家,原式化为:+-2.25-4.75,再根据加法结合律和减法性质,原式化为:(+)-(2.25+4.75),再进行计算。
÷[-(+)],根据减法性质,原式化为:÷[--],再根据带符号搬家,原式化为:÷[--],再按照运算顺序,进行计算。
【详解】48×(+)
=48×+48×
=4+3
=7
12.5×32×7.25
=12.5×8×4×0.25
=(12.5×8)×(4×0.25)
=100×1
=100
-2.25+-4.75
=+-2.25-4.75
=(+)-(2.25+4.75)
=10-7
=3
÷[-(+)]
=÷[--]
=÷[--]
=÷[1-]
=÷
=×4
=
22.(6分)解方程。
【答案】;
;
【分析】(1)先根据比例的基本性质将比例方程改写成,然后方程两边同时除以,求出方程的解;
(2)先把方程化简成,然后方程两边同时除以,求出方程的解;
(3)方程两边先同时减去,再同时除以,求出方程的解;
(4)方程两边先同时除以,再同时减去,求出方程的解。
【详解】(1)
解:
(2)
解:
(3)
解:
(4)
解:
23.(6分)直接写得数。
0.4×20%= = = =
1÷0.2= 0.53= = =
【答案】0.08;9;;1;
5;0.125;;9
五、作图题(共8分)
24.(8分)实践操作与应用。
(1)画出三角形ABC绕点B逆时针旋转90°后的图形。旋转后,C点的对应点的位置用数对表示是( )。
(2)以BC所在直线为对称轴,画出与三角形ABC对称的图形。
(3)画出三角形ABC按2∶1放大后的图形。
【答案】(1)(2,6);图见详解
(2)图见详解
(3)图见详解
【分析】(1)根据旋转的特征,将三角形ABC绕点B逆时针旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此用数对表示旋转后C点对应点的位置。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,找到三角形ABC的各顶点关于对称轴BC所在直线的对称点后,依次连接各点得到三角形ABC对称的图形。
(3)三角形ABC按2∶1放大,则三角形ABC原来的底和高都乘2,即是放大后三角形的底和高,据此画出放大后的三角形。
【详解】(1)三角形ABC绕点B逆时针旋转90°,如下图。
C点的对应点的位置用数对表示是(2,6)。
(2)以BC所在直线为对称轴,画与三角形ABC对称的图形,如下图。
(3)放大后三角形的底:3×2=6
放大后三角形的高:2×2=4
画一个底为6、高为4的三角形。
如图:
六、解答题(共34分)
25.(4分)2024年5月20日,盐城新地标建筑“串场之眼”揭开面纱,成了市民们休闲娱乐的“打卡”新去处。据介绍,该建筑总面积约21000平方米,比商业使用面积的3.2倍还多1800平方米。“串场之眼”商业使用面积约有多少平方米?(用方程解)
【答案】6000平方米
【分析】设“串场之眼”商业使用面积是x平方米,商业使用面积×3.2+“串场之眼”的建筑总面积比商业使用面积的3.2倍多的面积=“串场之眼”的建筑总面积,据此列出方程为:3.2x+1800=21000,再解方程即可。
【详解】解:设“串场之眼”商业使用面积是x平方米。
3.2x+1800=21000
3.2x+1800-1800=21000-1800
3.2x=19200
3.2x÷3.2=19200÷3.2
x=6000
答:“串场之眼”商业使用面积约有6000平方米。
26.(4分)张大伯家有一个圆锥形小麦堆,量得它的底面周长是12.56米,高是1.5米,如果每立方米小麦的质量为700千克,这堆小麦的质量为多少千克?
【答案】4396千克
【分析】利用圆锥底周长公式:C=2πr,转化为r=C÷π÷2,计算其底面半径,再利用体积公式:V=πr2计算其体积,再乘700千克,计算小麦的质量即可。
【详解】12.56÷3.14÷2=2(m)
=3.14×4×1.5×
=6.28(m3)
6.28×700=4396(千克)
答:这堆小麦的质量为4396千克。
27.(4分)师徒二人加工一批零件,原计划按5∶3分配给师傅和徒弟两人加工。实际师傅加工了880个,超过了分配任务的10%,徒弟实际加工了多少个零件?
【答案】400个
【分析】先以师傅原计划任务量为单位“1”,根据师傅实际加工数及超产比例,用除法求出师傅原计划任务量;再依据原计划分配比例,可知师傅原计划任务量占总任务量的,通过除法求出零件总任务量;最后用零件总任务量减去师傅实际加工量就是徒弟实际加工数量。
【详解】880÷(1+10%)
=880÷(100%+10%)
=880÷110%
=880÷1.1
=800(个)
800÷
=800÷
=800×
=160×8
=1280(个)
1280-880=400(个)
答:徒弟实际加工了400个零件。
28.(4分)在比例尺1∶2000000的地图上量得AB两地距离是5厘米。甲乙两车相向而行,3小时后还相距10千米,已知乙车速度是甲车的,甲乙两车每小时各行多少千米?
【答案】甲车:18千米,乙车:12千米
【分析】先根据图上距离除以比例尺求出两地的距离,用两地距离减10可得行驶的路程,再根据路程和÷行驶时间求出速度和,把甲车速度看作单位“1”,则两车速度和占甲车的,根据已知一个数的几分之几是多少,求这个数用除法计算,进而求出甲车速度,再根据求一个数的几分之几是多少,用乘法计算即可。计算时单位统一为千米。
【详解】5÷
=5×2000000
=10000000(厘米)
10000000厘米=100千米
(100-10)÷3
=90÷3
=30(千米)
30÷(1+)
=30÷
=30×
=18(千米)
18×=12(千米)
答:甲车每小时行18千米,乙车每小时行12千米。
29.(9分)近些年,新能源汽车以其清洁环保,使用成本低,高能源利用率等优点,慢慢走进人们的生活。如图是某区域2023年各季度新能源汽车销售量情况统计图。
(1)这个区域2023年共销售新能源汽车( )万辆,其中一季度销售( )万辆。
(2)将上面两幅统计图中缺失的数据填、画完整。
(3)根据以上信息,请预测2024年这个区域新能源汽车的销售量可能是( )万辆,并写出预测的理由:( )。
【答案】(1)120;18;
(2)图见详解
(3)150;每一季度的销售量是逐渐增加的
【分析】(1)根据统计图可知,二季度的销售量是24万量,占这个区域2023年总销售量的20%,用24除以20%即可求出总销售量;再用总销售量乘一季度占的百分比,即可求出一季度的销售量;
(2)分别用三、四季度的销售量除以总销售量,分别求出三、四季度占的百分比,然后再把统计图补充完整。
(3)根据2023年销售量预测2024的销售量即可。(答案不唯一)
【详解】(1)24÷20%=120(万辆)
120×15%=18(万辆)
这个区域2023年共销售新能源汽车120万辆,其中一季度销售18万辆。
(2)33÷120×100%
=0.275×100%
=27.5%
45÷120×100%
=0.375×100%
=37.5%
统计图如下:
(3)预测2024年这个区域新能源汽车的销售量可能是150万辆,因为每一季度的销售量是逐渐增加的。(答案不唯一)
30.(9分)一辆汽车行驶路程和耗油量如表所示:
行驶路程/千米 16 24 32 48 80
耗油量/L 2 3 4 6 10
(1)表中的耗油量与行驶路程成( )比例关系。
(2)在图中描出表示行驶路程与对应耗油量的点,然后把它们连起来。
(3)李叔叔开这辆车从A城出发时,看到汽车里程表显示为370千米,到达B城时里程表显示为530千米。算一算这辆汽车从A城到B城耗油多少升?
【答案】(1)正;
(2)见详解
(3)20升
【分析】(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量叫做成正比例的量,它们的关系叫做正比例关系。
(2)根据表中的数据,描点、连线即可。
(3)用530减去370求出从A城到B城的路程,再除以行驶1千米的耗油量即可解答。
【详解】(1)16∶2=8
24∶3=8
32∶8
48∶6=8
80∶10=8
行驶路程∶耗油量=8(一定),所以表中的耗油量与行驶路程成正比例关系。
(2)
(3)530-370=160(千米)
160÷8=20(升)
答:这辆汽车从A城到B城耗油20升。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
