北师大版六年级数学下册期末考试满分冲刺质量检测卷一(含解析)
文档属性
| 名称 | 北师大版六年级数学下册期末考试满分冲刺质量检测卷一(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 992.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-13 18:59:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版六年级数学下册期末考试满分冲刺质量检测卷一
一、填空题(共20分)
1.(2分)把一个长、宽、高分别为12厘米、6厘米、3厘米的长方体切成同样大小的正方体,切成的正方体棱长最大是( )厘米,最多可切成( )个。
2.(2分)作业本上获得15颗小星星就可以换3本连环画,小涛用60颗小星星换了本连环画,根据信息可以得到比例( )=( ),算一算,小涛换了( )本连环画。
3.(2分)一件外套的标价是500元,商家的优惠活动是“每满200元减100元”,这件外套实际是在打( )折出售,实际花费( )元就能买下这件外套。
4.(2分)在一个乡村中,柳树有64棵,杨树的棵数比柳树多,杨树有( )棵,柞树的棵数比柳树少,柞树有( )棵。
5.(2分)如图中,正方形的周长是16厘米,则平行四边形的面积是( )平方厘米,三角形的面积是( )平方厘米。
6.(2分)用黑、白两种颜色的正方形纸片按如图中的规律拼图案。
第15个图案有白色纸片( )张,第n个图案中有白色纸片121张,则n=( )。
7.(2分)两个分母相同的最简分数的和是,它们分子的比是7∶11,这两个数分别是( )和( )。
8.(2分)2023年我国普通小学在校生约有108079000人,此数读作( ),初中生有五千二百四十三万六千九百人,此数写作( )。
9.(2分)李师傅准备用左边的长方形铁皮卷成一个圆柱的侧面,再从右边的几个图形中选一个做底面,可直接选用的底面有( )个,选择( )号时容积最大。(单位:厘米)
10.(2分)如图,一个五边形的内角和是540°,试一试,推导出∠1+∠2+∠3+∠4+∠5=( )°。
二、判断题(共10分)
11.(2分)淘淘参加研学活动,他站在教官对面,教官整队喊口令“向右转”,他的身体应顺时针旋转。( )
12.(2分)5∶8的前项加上10,要使比值不变,后项应加上16。( )
13.(2分)长度分别是6cm、8cm、10cm的三根小棒,可以围成一个三角形。( )
14.(2分)小明和小红到图书馆看书,小明每6天去一次,小红每8天去一次,如果1月12日他们在图书馆相遇,则他们下一次在图书馆相遇是在2月4日。( )
15.(2分)鸡的只数比鸭多,也就是鸭的只数比鸡少。( )
三、选择题(共10分)
16.(2分)一个果园种植桃树和苹果树共2000棵,成活1760棵。其中桃树成活率为90%,苹果树成活率为85%。桃树、苹果树各有多少棵?解答时设桃树有x棵,则下列方程不正确的是( )。
A.90%x+(2000-x)×85%=1760 B.90%x+2000×85%=1760
C.(2000-x)×85%=1760-90%x D.2000×85%+(90%-85%)x=1760
17.(2分)下面的中国航天大事件,发生在闰年的是( )。
A.1970年中国自行研制的第一颗卫星“东方一号”发射成功。
B.2000年北斗卫星导航试验系统建成。
C.2007年我国首次月球探测工程取得圆满成功。
D.2019年“嫦娥四号”首次实现了航天器在月球背面软着陆。
18.(2分)小勇、小冬、小灵与小胖四人进行跑步比赛,小冬不是最慢的,但比小勇、小灵慢,小勇比小灵慢,获得第一名的是( )。
A.小勇 B.小冬 C.小灵 D.小胖
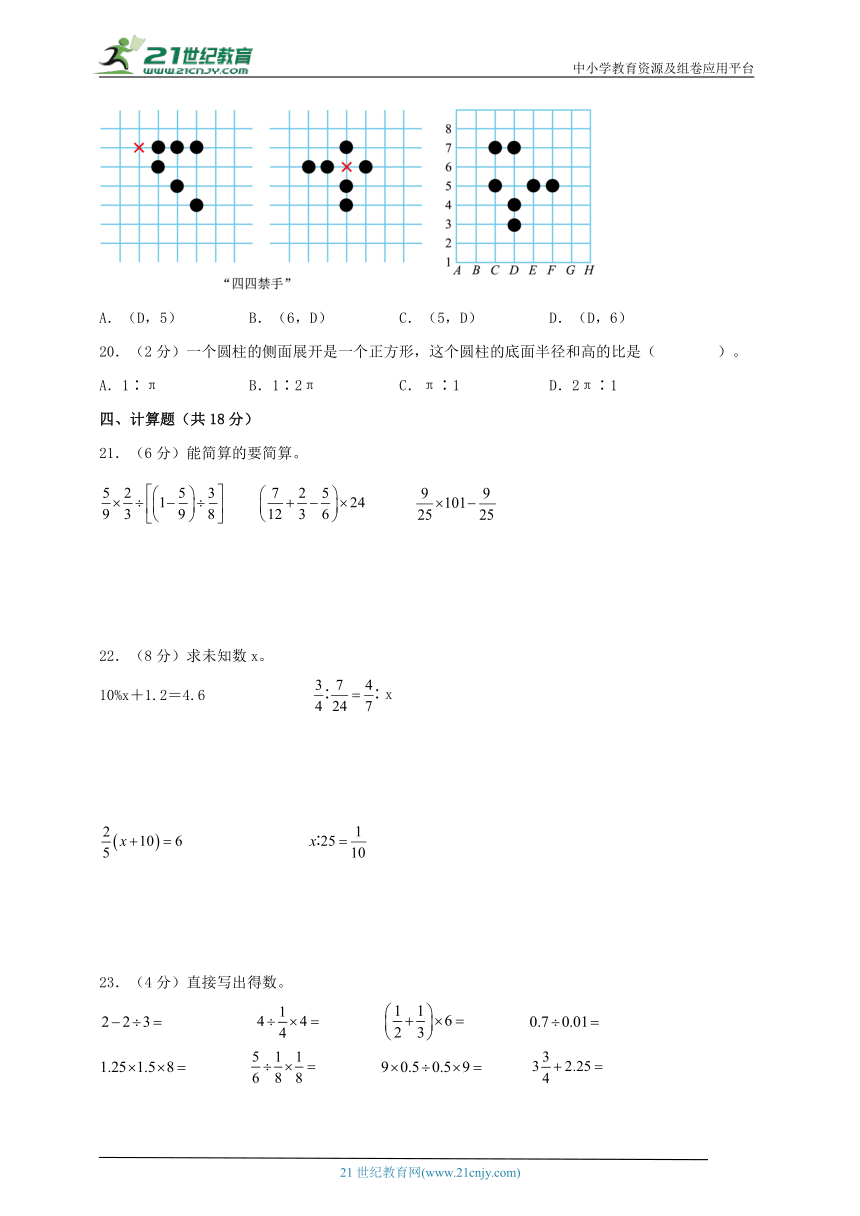
19.(2分)下五子棋时,黑方一子落下(如图中“×”的位置),同时形成两个或两个以上的“四”的情况,那么下一步黑棋应该落在哪个位置?这个位置用数对表示为( )。
A.(D,5) B.(6,D) C.(5,D) D.(D,6)
20.(2分)一个圆柱的侧面展开是一个正方形,这个圆柱的底面半径和高的比是( )。
A.1∶π B.1∶2π C.π∶1 D.2π∶1
四、计算题(共18分)
21.(6分)能简算的要简算。
22.(8分)求未知数x。
10%x+1.2=4.6
23.(4分)直接写出得数。
五、作图题(共8分)
24.(8分)在方格中根据要求画一画。
(1)把三角形绕A点逆时针旋转90°,画出旋转后的图形。
(2)将旋转后的三角形按2∶1的比放大,画出放大后的三角形。
(3)画出图①的另一半,使它成为一个轴对称图形。
六、解答题(共34分)
25.(4分)在比例尺1∶2000000的地图上量得AB两地距离是5厘米。甲乙两车相向而行,3小时后还相距10千米,已知乙车速度是甲车的,甲乙两车每小时各行多少千米?
26.(4分)某小学会议室需要装修,如果用面积为8平方分米的方砖铺地,需要360块。如果改用边长为3分米的方砖铺地,需要多少块?
27.(4分)学校体育室里,足球和篮球共有160个,体育课上用去足球个数的40%和16个篮球后,剩下的足球个数和篮球个数相等,原来体育室内有篮球和足球各多少个?
28.(4分)临近毕业,同学们和自己的好朋友互赠礼物。酷爱集卡的小华和小明互赠卡片。两人共有112张,小华拿出自己拥有卡片的送给小明,现在两人的卡片张数就同样多。原来小华和小明各有多少张卡片?(先把线段图补充完整,再解答)
29.(9分)端午节期间,学校就学生对端午节文化习俗的了解情况进行了随机调查(了解程度:A.很了解;B.比较了解;C.了解较少;D.不了解),并将调查结果绘制成如下统计图。
(1)调查时,如果在学校中任意抽样,那么( )是最好的。
A.从每个班中抽10名学生。
B.从女子舞蹈队中选一些队员。
C.从男子排球队中选一些队员。
D.选一些对端午节文化有了解的学生。
(2)本次调查共调查了( )人,被调查的学生中对端午节文化习俗“很了解”的占总人数的( )%。
(3)本次调查中对端午节文化习俗“了解较少”的学生有( )人。请将条形统计图补充完整。
30.(9分)如图,图象表示一幅地图图上距离和实际距离的关系。
(1)根据图象,可以求出这幅地图的比例尺是( )。
(2)图上距离和实际距离成( )比例。
(3)在这幅地图上量得甲、乙两城的图上距离是10厘米。一辆小汽车上午10:00从甲城开车到乙城,下午3:00到达。这辆小汽车平均每时行驶多少千米?
答案解析
一、填空题(共20分)
1.(2分)把一个长、宽、高分别为12厘米、6厘米、3厘米的长方体切成同样大小的正方体,切成的正方体棱长最大是( )厘米,最多可切成( )个。
【答案】 3 8
【分析】要切成同样大小的正方体,正方体棱长需是长方体长、宽、高的公因数,12、6、3的公因数有1、3 ,所以最大公因数是3,即切成的正方体棱长最大是3厘米;
分别计算长方体长、宽、高方向能切出的正方体个数:长方体长12厘米,12÷3=4,长的方向可切出4个;宽6厘米,6÷3=2,宽的方向可切出2个;高3厘米,3÷3=1,高的方向可切出1个; 最后将三个方向个数相乘,4×2×1=8,最多可切成8个。
【详解】12=2×2×3
6=2×3
12、6、3的最大公因数是3,所以小正方体的棱长最大就是3厘米;
(12÷3)×(6÷3)×(3÷3)
=4×2×1
=8×1
=8(个)
所以最多可切成8个。
2.(2分)作业本上获得15颗小星星就可以换3本连环画,小涛用60颗小星星换了本连环画,根据信息可以得到比例( )=( ),算一算,小涛换了( )本连环画。
【答案】 15∶3 60∶ 12
【分析】根据题意可知,小星星的颗数∶连环画的本数=1本连环画需小星星的颗数(一定),比值一定,那么小星星的颗数与连环画的本数成正比例关系,据此列出正比例方程,并求解。
【详解】15∶3=60∶
解:15=3×60
15=180
=180÷15
=12
根据信息可以得到比例15∶3=60∶,小涛换了12本连环画。
3.(2分)一件外套的标价是500元,商家的优惠活动是“每满200元减100元”,这件外套实际是在打( )折出售,实际花费( )元就能买下这件外套。
【答案】 六 300
【分析】根据题意,先用除法求出500元里面有几个200,就可以减去几个100元,据此求出这件外套的现价;
然后用这件外套的现价除以标价,求出现价是标价的百分之几,再根据折扣的意义,把百分数化成折扣即可。
【详解】500÷200=2(个)……100(元)
500-100×2
=500-200
=300(元)
300÷500×100%
=0.6×100%
=60%
60%=六折
这件外套实际是在打六折出售,实际花费300元就能买下这件外套。
4.(2分)在一个乡村中,柳树有64棵,杨树的棵数比柳树多,杨树有( )棵,柞树的棵数比柳树少,柞树有( )棵。
【答案】 72 54
【分析】根据题意,杨树的棵数比柳树多,可将柳树棵数看作单位“1”,则此时杨树棵树为,已知柳树有64棵,运用分数乘法计算得出杨树棵数;柞树的棵数比柳树少,将柳树数量看作单位“1”,则柞树有,且已知柳树数量,运用分数乘法计算得出答案。
【详解】杨树棵数为:
64×(1+)
=64×
=72(棵)
柞树棵树为:
(棵)
所以在一个乡村中,柳树有64棵,杨树的棵数比柳树多,杨树有72棵,柞树的棵数比柳树少,柞树有54棵。
5.(2分)如图中,正方形的周长是16厘米,则平行四边形的面积是( )平方厘米,三角形的面积是( )平方厘米。
【答案】 16 8
【分析】已知正方形周长16厘米,由“正方形周长=边长×4”,用周长除以4可算出边长;平行四边形底和高都等于正方形边长,依据“平行四边形面积=底×高”,把数值代入可求面积;三角形底和高等于正方形边长,根据“三角形面积=底×高÷2” ,代入数值就能算出面积。
【详解】16÷4=4(厘米)
4×4=16(平方厘米)
4×4÷2
=16÷2
=8(平方厘米)
所以平行四边形的面积是16平方厘米,三角形的面积是8平方厘米。
6.(2分)用黑、白两种颜色的正方形纸片按如图中的规律拼图案。
第15个图案有白色纸片( )张,第n个图案中有白色纸片121张,则n=( )。
【答案】 46 40
【分析】观察图案可知,第1个图案中有白色纸片4张,即(3×1+1)张;第2个图案中有白色纸片7张,即(3×2+1)张;第3个图案中有白色纸片10张,即(3×3+1)张。由此可推出第n个图案中有白色纸片(3n+1)张;把n=15代入3n+1计算即可求出第15个图案有白色纸片的张数,令3n+1=121,方程两边同时减去1,再同时除以3即可解答。
【详解】(1)3×15+1
=45+1
=46(张)
所以第15个图案有白色纸片46张。
(2)由分析可得:
3n+1=121
3n+1-1=121-1
3n=120
3n÷3=120÷3
n=40
所以第40个图案中有白色纸片121张,则n=40。
7.(2分)两个分母相同的最简分数的和是,它们分子的比是7∶11,这两个数分别是( )和( )。
【答案】
【分析】因为两个分数是分母相同的最简分数,所以分子的比就是这两个分数的比,即7∶11,因此这两个分数共11+7=18份,其中的一份是÷(7+11)。然后求出这两个分数即可。
【详解】÷(7+11)
=÷18
=×
=
×11=
×7=
所以这两个数分别是和。
8.(2分)2023年我国普通小学在校生约有108079000人,此数读作( ),初中生有五千二百四十三万六千九百人,此数写作( )。
【答案】 一亿零八百零七万九千 52436900
【分析】读数时,把数先分级,从高位读起,亿级或万级的数按照个级的读法去读,再在每级的末尾加一个“亿”或“万”字,每级末尾的0都不读,每一级的开头或中间无论有几个0,都读一个0;亿以内数的写法,从最高位写起,先写亿级再万级最后写个级,哪个数位上一个单位也没有,就在那个数位上写0;据此解答。
【详解】108079000:一亿零八百零七万九千
五千二百四十三万六千九百:52436900
2023年我国普通小学在校生约有108079000人,此数读作一亿零八百零七万九千,初中生有五千二百四十三万六千九百人,此数写作52436900。
9.(2分)李师傅准备用左边的长方形铁皮卷成一个圆柱的侧面,再从右边的几个图形中选一个做底面,可直接选用的底面有( )个,选择( )号时容积最大。(单位:厘米)
【答案】 2 4
【分析】根据题意,用一张长方形铁皮卷成一个圆柱的侧面,那么会有两个形状不同的圆柱,一个圆柱是把长方形的长作为圆柱的底面周长,宽作为圆柱的高;另一个圆柱是把长方形的宽作为圆柱的底面周长,长作为圆柱的高;
根据圆的周长公式C=2πr,可知r=C÷π÷2,由此求出圆柱的底面半径,据此得出可直接选用的底面有几个;
根据圆柱的体积(容积)公式V=πr2h,分别计算出两个圆柱的容积,再比较,得出选择几号作为圆柱的底面时容积最大。
【详解】以长作为圆柱的底面半径是:25.12÷3.14÷2=4(厘米)
以宽作为圆柱的底面半径是:12.56÷3.14÷2=2(厘米)
所以,可直接选用的底面有2号和4号,有2个。
选择2号作为底面时圆柱的容积:
3.14×22×25.12
=3.14×4×25.12
=315.5072(立方厘米)
选择4号作为底面时圆柱的容积:
3.14×42×12.56
=3.14×16×12.56
=631.0144(立方厘米)
631.0144>315.5072
可直接选用的底面有(2)个,选择(4)号时容积最大。
10.(2分)如图,一个五边形的内角和是540°,试一试,推导出∠1+∠2+∠3+∠4+∠5=( )°。
【答案】360
【分析】从图中可知,∠1和∠6、∠2和∠7、∠3和∠8、∠4和∠9、∠5和∠10都组成平角180°,且五边形的内角和是540°,即∠6+∠7+∠8+∠9+∠10=540°,据此求出∠1+∠2+∠3+∠4+∠5的度数之和。
【详解】因为∠1+∠6=180°,∠2+∠7=180°,∠3+∠8=180°,∠4+∠9=180°,∠5+∠10=180°,则:
∠1+∠2+∠3+∠4+∠5
=(180°-∠6)+(180°-∠7)+(180°-∠8)+(180°-∠9)+(180°-∠10)
=180°+180°+180°+180°+180°-∠6-∠7-∠8-∠9-∠10
=180°×5-(∠6+∠7+∠8+∠9+∠10)
=900°-540°
=360°
所以,∠1+∠2+∠3+∠4+∠5=360°。
二、判断题(共10分)
11.(2分)淘淘参加研学活动,他站在教官对面,教官整队喊口令“向右转”,他的身体应顺时针旋转。( )
【答案】√
【分析】根据旋转的意义:把一个图形绕着某一点转动一个角度的图形变换叫做旋转,由此结合实际可知,教官整队喊口令向左或者向右都是旋转了90°,向右是顺时针,向左是逆时针,据此解答即可。
【详解】淘淘参加研学活动,他站在教官对面,教官整队喊口令“向右转”,他的身体应顺时针旋转。原题说法正确。
故答案为:√
12.(2分)5∶8的前项加上10,要使比值不变,后项应加上16。( )
【答案】√
【分析】比的性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
据此将前项加上10,再除以原来的前项,求出前项乘几。要使比值不变,那么后项也乘几。将变化后的后项减去原来的后项,求出后项应加上几。
【详解】前项相当于乘:
(5+10)÷5
=15÷5
=3
后项也应乘3,或加上:
8×3-8
=24-8
=16
5∶8的前项加上10,要使比值不变,后项应乘3或加上16。
原题说法正确。
故答案为:√
13.(2分)长度分别是6cm、8cm、10cm的三根小棒,可以围成一个三角形。( )
【答案】√
【分析】三角形两边之和大于第三边,据此解答。
【详解】6+8>10,8+10>6,6+10>8,所以用三根长度分别为6厘米、8厘米和10厘米的小棒可以围成一个三角形。原题说法正确。
故答案为:√
14.(2分)小明和小红到图书馆看书,小明每6天去一次,小红每8天去一次,如果1月12日他们在图书馆相遇,则他们下一次在图书馆相遇是在2月4日。( )
【答案】×
【分析】求下一次他们俩都到图书馆是几月几日,先求出他俩再次都到图书馆所需要的天数,也就是求6和8的最小公倍数,6和8的最小公倍数是24;所以1月12日他们在图书馆相遇,再过24日他俩就都到图书馆,1月有31天,也就是下一次都到图书馆是2月5日。
【详解】6=2×3
8=2×2×2
6和8的最小公倍数是2×2×2×3=24,2×3×4=24
1月12日+24日=2月5日
他们下一次在图书馆相遇是在2月5日。
故答案为:×
15.(2分)鸡的只数比鸭多,也就是鸭的只数比鸡少。( )
【答案】×
【分析】根据题意,鸡的只数比鸭多,把鸭的只数看作单位“1”,那么鸡的只数是鸭的1+=,可得鸡的只数占6份,鸭的只数占5份,再根据求A比B少几分之几,用(B-A)÷B计算。
【详解】1+=
(6-5)÷6
=1÷6
=
所以鸡的只数比鸭多,也就是鸭的只数比鸡少,原题说法错误。
故答案为:×
三、选择题(共10分)
16.(2分)一个果园种植桃树和苹果树共2000棵,成活1760棵。其中桃树成活率为90%,苹果树成活率为85%。桃树、苹果树各有多少棵?解答时设桃树有x棵,则下列方程不正确的是( )。
A.90%x+(2000-x)×85%=1760 B.90%x+2000×85%=1760
C.(2000-x)×85%=1760-90%x D.2000×85%+(90%-85%)x=1760
【答案】B
【分析】分析题目,设桃树有x棵,则苹果树有(2000-x)棵,结合成活率的意义可知:桃树成活的棵数是90%x,苹果树成活的棵数是85%×(2000-x),桃树成活的棵数+苹果树成活的棵数=1760,据此逐项分析即可。
【详解】A.根据“桃树成活的棵数+苹果树成活的棵数=1760”可列出方程:90%x+(2000-x)×85%=1760;
B.90%x表示桃树成活的棵数,2000是桃树和苹果树的总棵数,85%是苹果树的成活率,2000×85%不能计算出苹果树的成活棵数,所以方程90%x+2000×85%=1760不正确;
C.根据“桃树成活的棵数+苹果树成活的棵数=1760”可知:苹果树的成活棵数=1760-桃树的成活棵数,据此可列出方程:(2000-x)×85%=1760-90%x;
D.假设2000棵全部是苹果树,则成活的总棵数是2000×85%,实际其中有x棵是桃树,x棵桃树比x棵苹果树成活的棵数多了(90%-85%)x ,据此可列出方程:2000×85%+(90%-85%)x=1760。
所以不正确的方程是:90%x+2000×85%=1760。
故答案为:B
17.(2分)下面的中国航天大事件,发生在闰年的是( )。
A.1970年中国自行研制的第一颗卫星“东方一号”发射成功。
B.2000年北斗卫星导航试验系统建成。
C.2007年我国首次月球探测工程取得圆满成功。
D.2019年“嫦娥四号”首次实现了航天器在月球背面软着陆。
【答案】B
【分析】公历年份是4的倍数的一般都是闰年,但年份是100的倍数时,必须是400的倍数才是闰年,据此分析。
【详解】1970÷4=492……2
2000÷400=5
2007÷4=501……3
2019÷4=504……3
A.1970不是4的倍数,不是闰年;
B.2000是4的倍数,是闰年;
C.2007不是4的倍数,不是闰年;
D.2019不是4的倍数,不是闰年。
故答案为:B
18.(2分)小勇、小冬、小灵与小胖四人进行跑步比赛,小冬不是最慢的,但比小勇、小灵慢,小勇比小灵慢,获得第一名的是( )。
A.小勇 B.小冬 C.小灵 D.小胖
【答案】C
【分析】根据“小冬不是最慢的,但比小勇、小灵慢”说明最慢的是小胖,小胖是第四名,小东是第三名,又因为“小勇比小灵慢”,所以最快的是小灵,那么小勇是第二名,小灵是第一名。据此推理即可解答。
【详解】据分析可知,最快的是小灵,所以获得第一名的是小灵。
故答案为:C
19.(2分)下五子棋时,黑方一子落下(如图中“×”的位置),同时形成两个或两个以上的“四”的情况,那么下一步黑棋应该落在哪个位置?这个位置用数对表示为( )。
A.(D,5) B.(6,D) C.(5,D) D.(D,6)
【答案】A
【分析】数对的第一个数表示列,第二个数表示行,如下图,要使盘中棋局成为“四四禁手”,下一步黑棋应该落在红“×”位置,这个位置用数对表示为(D,5),据此即可解答。
【详解】根据分析可知,下五子棋时,黑方一子落下,同时形成两个或两个以上的“四”的情况,那么下一步黑棋应该落的位置用数对表示为(D,5)。
故答案为:A
20.(2分)一个圆柱的侧面展开是一个正方形,这个圆柱的底面半径和高的比是( )。
A.1∶π B.1∶2π C.π∶1 D.2π∶1
【答案】B
【分析】因为圆柱的侧面展开是一个正方形,那么圆柱的底面周长和高相等,由圆的周长公式C=2πr,可得出2πr=h;根据比的意义写出这个圆柱的底面半径和高的比为r∶h,用2πr代替h,再化简比即可。
【详解】设圆柱的底面半径是r,高是h;
因为圆柱的侧面展开图是个正方形,所以h=2πr。
r∶h
=r∶2πr
=(r÷r)∶(2πr÷r)
=1∶2π
这个圆柱的底面半径和高的比是1∶2π。
故答案为:B
四、计算题(共18分)
21.(6分)能简算的要简算。
【答案】;10;36
【分析】(1)先算小括号里面的减法,再算中括号里面的除法,然后再计算括号外的乘法,最后计算括号外的除法,注意除以一个数相当于乘这个数的倒数;
(2)按照乘法分配律,用括号里面的数分别与括号外面的数相乘,再把积相加;
(3)按照乘法分配律,提出,再将剩下数相减计算。
【详解】
=×÷[×]
=÷
=×
=
=×24+×24-×24
=14+16-20
=10
=×(101-1)
=×100
=36
22.(8分)求未知数x。
10%x+1.2=4.6
【答案】x=34;x=;
x=5;x=
【分析】(1)先根据等式的基本性质1给方程两边同时减去 1.2,再根据等式的基本性质2给方程两边同时除以10%即可;
(2)先根据比例的基本性质把方程写成x=×,再根据等式的基本性质2给方程两边同时除以即可;
(3)先根据等式的基本性质2给方程两边同时除以,再根据等式的基本性质1给方程两边同时减去10即可;
(4)根据比的前项=比值×比的后项得到x=×25,进一步计算即可。
【详解】10%x+1.2=4.6
解:10%x+1.2-1.2=4.6-1.2
10%x=3.4
0.1x÷0.1=3.4÷0.1
x=34
∶=∶x
解:x=×
x=
x÷=÷
x÷=×
x=
(x+10)=6
解:(x+10)÷=6÷
x+10=6×
x+10=15
x+10-10=15-10
x=5
x∶25=
解:x=×25
x=
23.(4分)直接写出得数。
【答案】;64;5;70;
15;;81;6
五、作图题(共8分)
24.(8分)在方格中根据要求画一画。
(1)把三角形绕A点逆时针旋转90°,画出旋转后的图形。
(2)将旋转后的三角形按2∶1的比放大,画出放大后的三角形。
(3)画出图①的另一半,使它成为一个轴对称图形。
【答案】见详解
【分析】(1)根据旋转的特征,将三角形绕A点逆时针旋转90°,点A位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(2)将旋转后的三角形按2∶1的比放大,则三角形的底和高都要乘2,那么放大后三角形的底是6,高是4,据此画出放大后的三角形。
(3)一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴,据此找到关键的对称点依次连接,即可画出对称图形。
【详解】如图:
六、解答题(共34分)
25.(4分)在比例尺1∶2000000的地图上量得AB两地距离是5厘米。甲乙两车相向而行,3小时后还相距10千米,已知乙车速度是甲车的,甲乙两车每小时各行多少千米?
【答案】甲车:18千米,乙车:12千米
【分析】先根据图上距离除以比例尺求出两地的距离,用两地距离减10可得行驶的路程,再根据路程和÷行驶时间求出速度和,把甲车速度看作单位“1”,则两车速度和占甲车的,根据已知一个数的几分之几是多少,求这个数用除法计算,进而求出甲车速度,再根据求一个数的几分之几是多少,用乘法计算即可。计算时单位统一为千米。
【详解】5÷
=5×2000000
=10000000(厘米)
10000000厘米=100千米
(100-10)÷3
=90÷3
=30(千米)
30÷(1+)
=30÷
=30×
=18(千米)
18×=12(千米)
答:甲车每小时行18千米,乙车每小时行12千米。
26.(4分)某小学会议室需要装修,如果用面积为8平方分米的方砖铺地,需要360块。如果改用边长为3分米的方砖铺地,需要多少块?
【答案】320块
【分析】根据题意可知,每块方砖的面积×需要的块数=会议室地面总面积(一定),每块方砖的面积和需要的块数成反比例关系,列方程解答即可。
【详解】解:设用边长为3分米的方砖铺地,需要x块。
3×3×x=8×360
9x=8×360
9x÷9=8×(360÷9)
x=8×40
x=320
答:用边长为3分米的方砖铺地,需要320块。
27.(4分)学校体育室里,足球和篮球共有160个,体育课上用去足球个数的40%和16个篮球后,剩下的足球个数和篮球个数相等,原来体育室内有篮球和足球各多少个?
【答案】篮球70个;足球90个
【分析】把原有足球的个数看作单位“1”,用160减去16个篮球后得到的是足球的总数和篮球剩下的个数,即得到的数量占原有足球个数的,根据已知一个数的百分之几是多少,求这个数用除法计算可得原有足球的数量,再用160减原有足球的数量可得篮球的数量。
【详解】(160-16)÷(1-40%+1)
=144÷1.6
=90(个)
160-90=70(个)
答:原来体育室内有篮球70个,足球90个。
28.(4分)临近毕业,同学们和自己的好朋友互赠礼物。酷爱集卡的小华和小明互赠卡片。两人共有112张,小华拿出自己拥有卡片的送给小明,现在两人的卡片张数就同样多。原来小华和小明各有多少张卡片?(先把线段图补充完整,再解答)
【答案】小华72张;小明40张
【分析】根据题意,设小华有张,则小明有(112-)张卡片;小华拿出自己拥有卡片的送给小明,即送给小明张,那么小华还剩张,小明则有张,现在两人的卡片张数就同样多,所以可以列出方程,解出未知数即是小华卡片的张数,再用两人卡片的总张数减去小华的张数,求出小明卡片的张数。
【详解】如图:
解:设小华有张,则小明有(112-)张卡片。
=72
112-72=40(张)
答:小华有72张卡片,小明有40张卡片。
29.(9分)端午节期间,学校就学生对端午节文化习俗的了解情况进行了随机调查(了解程度:A.很了解;B.比较了解;C.了解较少;D.不了解),并将调查结果绘制成如下统计图。
(1)调查时,如果在学校中任意抽样,那么( )是最好的。
A.从每个班中抽10名学生。
B.从女子舞蹈队中选一些队员。
C.从男子排球队中选一些队员。
D.选一些对端午节文化有了解的学生。
(2)本次调查共调查了( )人,被调查的学生中对端午节文化习俗“很了解”的占总人数的( )%。
(3)本次调查中对端午节文化习俗“了解较少”的学生有( )人。请将条形统计图补充完整。
【答案】(1)A
(2) 400 35
(3)80;作图见详解
【分析】(1)抽样调查时,样本要具有代表性,据此选择。
(2)从两幅统计图中可知,对端午节文化习俗“比较了解”的有160人,占调查总人数的40%,把调查的总人数看作单位“1”,单位“1”未知,根据百分数除法的意义求出调查总人数;已知对端午节文化习俗“很了解”的有140人,用“很了解”的人数除以总人数,即是被调查的学生中对端午节文化习俗“很了解”的占总人数的百分之几。
(3)用调查的总人数减去对端午节文化习俗“很了解”、“比较了解”、“不了解”的人数,即是对端午节文化习俗“了解较少”的人数,据此将条形统计图补充完整。
【详解】(1)调查时,如果在学校中任意抽样,那么从每个班中抽10名学生是最好的。
故答案为:A
(2)160÷40%
=160÷0.4
=400(人)
140÷400
=0.35
=35%
本次调查共调查了400人,被调查的学生中对端午节文化习俗“很了解”的占总人数的35%。
(3)400-140-160-20
=260-160-20
=100-20
=80(人)
本次调查中对端午节文化习俗“了解较少”的学生有80人。
30.(9分)如图,图象表示一幅地图图上距离和实际距离的关系。
(1)根据图象,可以求出这幅地图的比例尺是( )。
(2)图上距离和实际距离成( )比例。
(3)在这幅地图上量得甲、乙两城的图上距离是10厘米。一辆小汽车上午10:00从甲城开车到乙城,下午3:00到达。这辆小汽车平均每时行驶多少千米?
【答案】(1)1∶4000000
(2)正
(3)80千米
【分析】(1)从图中可知,图上距离是1厘米时,对应的实际距离是40千米;根据“图上距离∶实际距离=比例尺”以及进率“1千米=100000厘米”,求出这幅地图的比例尺。
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。
(3)已知甲、乙两城的图上距离是10厘米,根据“实际距离=图上距离÷比例尺”,求出甲、乙两城的实际距离;
已知一辆小汽车上午10:00从甲城开车到乙城,下午3:00(即15:00)到达,用到达时刻减去出发时刻,求出小汽车行驶的时间;再根据“速度=路程÷时间”求出这辆小汽车的速度。
【详解】(1)1厘米∶40千米
=1厘米∶(40×100000)厘米
=1∶4000000
根据图象,可以求出这幅地图的比例尺是(1∶4000000)。
(2)图上距离∶实际距离=(一定),比值一定,则图上距离和实际距离成(正)比例。
(3)下午3:00=15:00
15时-10时=5(小时)
10÷
=10×4000000
=40000000(厘米)
40000000厘米=400千米
400÷5=80(千米)
答:这辆小汽车平均每时行驶80千米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版六年级数学下册期末考试满分冲刺质量检测卷一
一、填空题(共20分)
1.(2分)把一个长、宽、高分别为12厘米、6厘米、3厘米的长方体切成同样大小的正方体,切成的正方体棱长最大是( )厘米,最多可切成( )个。
2.(2分)作业本上获得15颗小星星就可以换3本连环画,小涛用60颗小星星换了本连环画,根据信息可以得到比例( )=( ),算一算,小涛换了( )本连环画。
3.(2分)一件外套的标价是500元,商家的优惠活动是“每满200元减100元”,这件外套实际是在打( )折出售,实际花费( )元就能买下这件外套。
4.(2分)在一个乡村中,柳树有64棵,杨树的棵数比柳树多,杨树有( )棵,柞树的棵数比柳树少,柞树有( )棵。
5.(2分)如图中,正方形的周长是16厘米,则平行四边形的面积是( )平方厘米,三角形的面积是( )平方厘米。
6.(2分)用黑、白两种颜色的正方形纸片按如图中的规律拼图案。
第15个图案有白色纸片( )张,第n个图案中有白色纸片121张,则n=( )。
7.(2分)两个分母相同的最简分数的和是,它们分子的比是7∶11,这两个数分别是( )和( )。
8.(2分)2023年我国普通小学在校生约有108079000人,此数读作( ),初中生有五千二百四十三万六千九百人,此数写作( )。
9.(2分)李师傅准备用左边的长方形铁皮卷成一个圆柱的侧面,再从右边的几个图形中选一个做底面,可直接选用的底面有( )个,选择( )号时容积最大。(单位:厘米)
10.(2分)如图,一个五边形的内角和是540°,试一试,推导出∠1+∠2+∠3+∠4+∠5=( )°。
二、判断题(共10分)
11.(2分)淘淘参加研学活动,他站在教官对面,教官整队喊口令“向右转”,他的身体应顺时针旋转。( )
12.(2分)5∶8的前项加上10,要使比值不变,后项应加上16。( )
13.(2分)长度分别是6cm、8cm、10cm的三根小棒,可以围成一个三角形。( )
14.(2分)小明和小红到图书馆看书,小明每6天去一次,小红每8天去一次,如果1月12日他们在图书馆相遇,则他们下一次在图书馆相遇是在2月4日。( )
15.(2分)鸡的只数比鸭多,也就是鸭的只数比鸡少。( )
三、选择题(共10分)
16.(2分)一个果园种植桃树和苹果树共2000棵,成活1760棵。其中桃树成活率为90%,苹果树成活率为85%。桃树、苹果树各有多少棵?解答时设桃树有x棵,则下列方程不正确的是( )。
A.90%x+(2000-x)×85%=1760 B.90%x+2000×85%=1760
C.(2000-x)×85%=1760-90%x D.2000×85%+(90%-85%)x=1760
17.(2分)下面的中国航天大事件,发生在闰年的是( )。
A.1970年中国自行研制的第一颗卫星“东方一号”发射成功。
B.2000年北斗卫星导航试验系统建成。
C.2007年我国首次月球探测工程取得圆满成功。
D.2019年“嫦娥四号”首次实现了航天器在月球背面软着陆。
18.(2分)小勇、小冬、小灵与小胖四人进行跑步比赛,小冬不是最慢的,但比小勇、小灵慢,小勇比小灵慢,获得第一名的是( )。
A.小勇 B.小冬 C.小灵 D.小胖
19.(2分)下五子棋时,黑方一子落下(如图中“×”的位置),同时形成两个或两个以上的“四”的情况,那么下一步黑棋应该落在哪个位置?这个位置用数对表示为( )。
A.(D,5) B.(6,D) C.(5,D) D.(D,6)
20.(2分)一个圆柱的侧面展开是一个正方形,这个圆柱的底面半径和高的比是( )。
A.1∶π B.1∶2π C.π∶1 D.2π∶1
四、计算题(共18分)
21.(6分)能简算的要简算。
22.(8分)求未知数x。
10%x+1.2=4.6
23.(4分)直接写出得数。
五、作图题(共8分)
24.(8分)在方格中根据要求画一画。
(1)把三角形绕A点逆时针旋转90°,画出旋转后的图形。
(2)将旋转后的三角形按2∶1的比放大,画出放大后的三角形。
(3)画出图①的另一半,使它成为一个轴对称图形。
六、解答题(共34分)
25.(4分)在比例尺1∶2000000的地图上量得AB两地距离是5厘米。甲乙两车相向而行,3小时后还相距10千米,已知乙车速度是甲车的,甲乙两车每小时各行多少千米?
26.(4分)某小学会议室需要装修,如果用面积为8平方分米的方砖铺地,需要360块。如果改用边长为3分米的方砖铺地,需要多少块?
27.(4分)学校体育室里,足球和篮球共有160个,体育课上用去足球个数的40%和16个篮球后,剩下的足球个数和篮球个数相等,原来体育室内有篮球和足球各多少个?
28.(4分)临近毕业,同学们和自己的好朋友互赠礼物。酷爱集卡的小华和小明互赠卡片。两人共有112张,小华拿出自己拥有卡片的送给小明,现在两人的卡片张数就同样多。原来小华和小明各有多少张卡片?(先把线段图补充完整,再解答)
29.(9分)端午节期间,学校就学生对端午节文化习俗的了解情况进行了随机调查(了解程度:A.很了解;B.比较了解;C.了解较少;D.不了解),并将调查结果绘制成如下统计图。
(1)调查时,如果在学校中任意抽样,那么( )是最好的。
A.从每个班中抽10名学生。
B.从女子舞蹈队中选一些队员。
C.从男子排球队中选一些队员。
D.选一些对端午节文化有了解的学生。
(2)本次调查共调查了( )人,被调查的学生中对端午节文化习俗“很了解”的占总人数的( )%。
(3)本次调查中对端午节文化习俗“了解较少”的学生有( )人。请将条形统计图补充完整。
30.(9分)如图,图象表示一幅地图图上距离和实际距离的关系。
(1)根据图象,可以求出这幅地图的比例尺是( )。
(2)图上距离和实际距离成( )比例。
(3)在这幅地图上量得甲、乙两城的图上距离是10厘米。一辆小汽车上午10:00从甲城开车到乙城,下午3:00到达。这辆小汽车平均每时行驶多少千米?
答案解析
一、填空题(共20分)
1.(2分)把一个长、宽、高分别为12厘米、6厘米、3厘米的长方体切成同样大小的正方体,切成的正方体棱长最大是( )厘米,最多可切成( )个。
【答案】 3 8
【分析】要切成同样大小的正方体,正方体棱长需是长方体长、宽、高的公因数,12、6、3的公因数有1、3 ,所以最大公因数是3,即切成的正方体棱长最大是3厘米;
分别计算长方体长、宽、高方向能切出的正方体个数:长方体长12厘米,12÷3=4,长的方向可切出4个;宽6厘米,6÷3=2,宽的方向可切出2个;高3厘米,3÷3=1,高的方向可切出1个; 最后将三个方向个数相乘,4×2×1=8,最多可切成8个。
【详解】12=2×2×3
6=2×3
12、6、3的最大公因数是3,所以小正方体的棱长最大就是3厘米;
(12÷3)×(6÷3)×(3÷3)
=4×2×1
=8×1
=8(个)
所以最多可切成8个。
2.(2分)作业本上获得15颗小星星就可以换3本连环画,小涛用60颗小星星换了本连环画,根据信息可以得到比例( )=( ),算一算,小涛换了( )本连环画。
【答案】 15∶3 60∶ 12
【分析】根据题意可知,小星星的颗数∶连环画的本数=1本连环画需小星星的颗数(一定),比值一定,那么小星星的颗数与连环画的本数成正比例关系,据此列出正比例方程,并求解。
【详解】15∶3=60∶
解:15=3×60
15=180
=180÷15
=12
根据信息可以得到比例15∶3=60∶,小涛换了12本连环画。
3.(2分)一件外套的标价是500元,商家的优惠活动是“每满200元减100元”,这件外套实际是在打( )折出售,实际花费( )元就能买下这件外套。
【答案】 六 300
【分析】根据题意,先用除法求出500元里面有几个200,就可以减去几个100元,据此求出这件外套的现价;
然后用这件外套的现价除以标价,求出现价是标价的百分之几,再根据折扣的意义,把百分数化成折扣即可。
【详解】500÷200=2(个)……100(元)
500-100×2
=500-200
=300(元)
300÷500×100%
=0.6×100%
=60%
60%=六折
这件外套实际是在打六折出售,实际花费300元就能买下这件外套。
4.(2分)在一个乡村中,柳树有64棵,杨树的棵数比柳树多,杨树有( )棵,柞树的棵数比柳树少,柞树有( )棵。
【答案】 72 54
【分析】根据题意,杨树的棵数比柳树多,可将柳树棵数看作单位“1”,则此时杨树棵树为,已知柳树有64棵,运用分数乘法计算得出杨树棵数;柞树的棵数比柳树少,将柳树数量看作单位“1”,则柞树有,且已知柳树数量,运用分数乘法计算得出答案。
【详解】杨树棵数为:
64×(1+)
=64×
=72(棵)
柞树棵树为:
(棵)
所以在一个乡村中,柳树有64棵,杨树的棵数比柳树多,杨树有72棵,柞树的棵数比柳树少,柞树有54棵。
5.(2分)如图中,正方形的周长是16厘米,则平行四边形的面积是( )平方厘米,三角形的面积是( )平方厘米。
【答案】 16 8
【分析】已知正方形周长16厘米,由“正方形周长=边长×4”,用周长除以4可算出边长;平行四边形底和高都等于正方形边长,依据“平行四边形面积=底×高”,把数值代入可求面积;三角形底和高等于正方形边长,根据“三角形面积=底×高÷2” ,代入数值就能算出面积。
【详解】16÷4=4(厘米)
4×4=16(平方厘米)
4×4÷2
=16÷2
=8(平方厘米)
所以平行四边形的面积是16平方厘米,三角形的面积是8平方厘米。
6.(2分)用黑、白两种颜色的正方形纸片按如图中的规律拼图案。
第15个图案有白色纸片( )张,第n个图案中有白色纸片121张,则n=( )。
【答案】 46 40
【分析】观察图案可知,第1个图案中有白色纸片4张,即(3×1+1)张;第2个图案中有白色纸片7张,即(3×2+1)张;第3个图案中有白色纸片10张,即(3×3+1)张。由此可推出第n个图案中有白色纸片(3n+1)张;把n=15代入3n+1计算即可求出第15个图案有白色纸片的张数,令3n+1=121,方程两边同时减去1,再同时除以3即可解答。
【详解】(1)3×15+1
=45+1
=46(张)
所以第15个图案有白色纸片46张。
(2)由分析可得:
3n+1=121
3n+1-1=121-1
3n=120
3n÷3=120÷3
n=40
所以第40个图案中有白色纸片121张,则n=40。
7.(2分)两个分母相同的最简分数的和是,它们分子的比是7∶11,这两个数分别是( )和( )。
【答案】
【分析】因为两个分数是分母相同的最简分数,所以分子的比就是这两个分数的比,即7∶11,因此这两个分数共11+7=18份,其中的一份是÷(7+11)。然后求出这两个分数即可。
【详解】÷(7+11)
=÷18
=×
=
×11=
×7=
所以这两个数分别是和。
8.(2分)2023年我国普通小学在校生约有108079000人,此数读作( ),初中生有五千二百四十三万六千九百人,此数写作( )。
【答案】 一亿零八百零七万九千 52436900
【分析】读数时,把数先分级,从高位读起,亿级或万级的数按照个级的读法去读,再在每级的末尾加一个“亿”或“万”字,每级末尾的0都不读,每一级的开头或中间无论有几个0,都读一个0;亿以内数的写法,从最高位写起,先写亿级再万级最后写个级,哪个数位上一个单位也没有,就在那个数位上写0;据此解答。
【详解】108079000:一亿零八百零七万九千
五千二百四十三万六千九百:52436900
2023年我国普通小学在校生约有108079000人,此数读作一亿零八百零七万九千,初中生有五千二百四十三万六千九百人,此数写作52436900。
9.(2分)李师傅准备用左边的长方形铁皮卷成一个圆柱的侧面,再从右边的几个图形中选一个做底面,可直接选用的底面有( )个,选择( )号时容积最大。(单位:厘米)
【答案】 2 4
【分析】根据题意,用一张长方形铁皮卷成一个圆柱的侧面,那么会有两个形状不同的圆柱,一个圆柱是把长方形的长作为圆柱的底面周长,宽作为圆柱的高;另一个圆柱是把长方形的宽作为圆柱的底面周长,长作为圆柱的高;
根据圆的周长公式C=2πr,可知r=C÷π÷2,由此求出圆柱的底面半径,据此得出可直接选用的底面有几个;
根据圆柱的体积(容积)公式V=πr2h,分别计算出两个圆柱的容积,再比较,得出选择几号作为圆柱的底面时容积最大。
【详解】以长作为圆柱的底面半径是:25.12÷3.14÷2=4(厘米)
以宽作为圆柱的底面半径是:12.56÷3.14÷2=2(厘米)
所以,可直接选用的底面有2号和4号,有2个。
选择2号作为底面时圆柱的容积:
3.14×22×25.12
=3.14×4×25.12
=315.5072(立方厘米)
选择4号作为底面时圆柱的容积:
3.14×42×12.56
=3.14×16×12.56
=631.0144(立方厘米)
631.0144>315.5072
可直接选用的底面有(2)个,选择(4)号时容积最大。
10.(2分)如图,一个五边形的内角和是540°,试一试,推导出∠1+∠2+∠3+∠4+∠5=( )°。
【答案】360
【分析】从图中可知,∠1和∠6、∠2和∠7、∠3和∠8、∠4和∠9、∠5和∠10都组成平角180°,且五边形的内角和是540°,即∠6+∠7+∠8+∠9+∠10=540°,据此求出∠1+∠2+∠3+∠4+∠5的度数之和。
【详解】因为∠1+∠6=180°,∠2+∠7=180°,∠3+∠8=180°,∠4+∠9=180°,∠5+∠10=180°,则:
∠1+∠2+∠3+∠4+∠5
=(180°-∠6)+(180°-∠7)+(180°-∠8)+(180°-∠9)+(180°-∠10)
=180°+180°+180°+180°+180°-∠6-∠7-∠8-∠9-∠10
=180°×5-(∠6+∠7+∠8+∠9+∠10)
=900°-540°
=360°
所以,∠1+∠2+∠3+∠4+∠5=360°。
二、判断题(共10分)
11.(2分)淘淘参加研学活动,他站在教官对面,教官整队喊口令“向右转”,他的身体应顺时针旋转。( )
【答案】√
【分析】根据旋转的意义:把一个图形绕着某一点转动一个角度的图形变换叫做旋转,由此结合实际可知,教官整队喊口令向左或者向右都是旋转了90°,向右是顺时针,向左是逆时针,据此解答即可。
【详解】淘淘参加研学活动,他站在教官对面,教官整队喊口令“向右转”,他的身体应顺时针旋转。原题说法正确。
故答案为:√
12.(2分)5∶8的前项加上10,要使比值不变,后项应加上16。( )
【答案】√
【分析】比的性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
据此将前项加上10,再除以原来的前项,求出前项乘几。要使比值不变,那么后项也乘几。将变化后的后项减去原来的后项,求出后项应加上几。
【详解】前项相当于乘:
(5+10)÷5
=15÷5
=3
后项也应乘3,或加上:
8×3-8
=24-8
=16
5∶8的前项加上10,要使比值不变,后项应乘3或加上16。
原题说法正确。
故答案为:√
13.(2分)长度分别是6cm、8cm、10cm的三根小棒,可以围成一个三角形。( )
【答案】√
【分析】三角形两边之和大于第三边,据此解答。
【详解】6+8>10,8+10>6,6+10>8,所以用三根长度分别为6厘米、8厘米和10厘米的小棒可以围成一个三角形。原题说法正确。
故答案为:√
14.(2分)小明和小红到图书馆看书,小明每6天去一次,小红每8天去一次,如果1月12日他们在图书馆相遇,则他们下一次在图书馆相遇是在2月4日。( )
【答案】×
【分析】求下一次他们俩都到图书馆是几月几日,先求出他俩再次都到图书馆所需要的天数,也就是求6和8的最小公倍数,6和8的最小公倍数是24;所以1月12日他们在图书馆相遇,再过24日他俩就都到图书馆,1月有31天,也就是下一次都到图书馆是2月5日。
【详解】6=2×3
8=2×2×2
6和8的最小公倍数是2×2×2×3=24,2×3×4=24
1月12日+24日=2月5日
他们下一次在图书馆相遇是在2月5日。
故答案为:×
15.(2分)鸡的只数比鸭多,也就是鸭的只数比鸡少。( )
【答案】×
【分析】根据题意,鸡的只数比鸭多,把鸭的只数看作单位“1”,那么鸡的只数是鸭的1+=,可得鸡的只数占6份,鸭的只数占5份,再根据求A比B少几分之几,用(B-A)÷B计算。
【详解】1+=
(6-5)÷6
=1÷6
=
所以鸡的只数比鸭多,也就是鸭的只数比鸡少,原题说法错误。
故答案为:×
三、选择题(共10分)
16.(2分)一个果园种植桃树和苹果树共2000棵,成活1760棵。其中桃树成活率为90%,苹果树成活率为85%。桃树、苹果树各有多少棵?解答时设桃树有x棵,则下列方程不正确的是( )。
A.90%x+(2000-x)×85%=1760 B.90%x+2000×85%=1760
C.(2000-x)×85%=1760-90%x D.2000×85%+(90%-85%)x=1760
【答案】B
【分析】分析题目,设桃树有x棵,则苹果树有(2000-x)棵,结合成活率的意义可知:桃树成活的棵数是90%x,苹果树成活的棵数是85%×(2000-x),桃树成活的棵数+苹果树成活的棵数=1760,据此逐项分析即可。
【详解】A.根据“桃树成活的棵数+苹果树成活的棵数=1760”可列出方程:90%x+(2000-x)×85%=1760;
B.90%x表示桃树成活的棵数,2000是桃树和苹果树的总棵数,85%是苹果树的成活率,2000×85%不能计算出苹果树的成活棵数,所以方程90%x+2000×85%=1760不正确;
C.根据“桃树成活的棵数+苹果树成活的棵数=1760”可知:苹果树的成活棵数=1760-桃树的成活棵数,据此可列出方程:(2000-x)×85%=1760-90%x;
D.假设2000棵全部是苹果树,则成活的总棵数是2000×85%,实际其中有x棵是桃树,x棵桃树比x棵苹果树成活的棵数多了(90%-85%)x ,据此可列出方程:2000×85%+(90%-85%)x=1760。
所以不正确的方程是:90%x+2000×85%=1760。
故答案为:B
17.(2分)下面的中国航天大事件,发生在闰年的是( )。
A.1970年中国自行研制的第一颗卫星“东方一号”发射成功。
B.2000年北斗卫星导航试验系统建成。
C.2007年我国首次月球探测工程取得圆满成功。
D.2019年“嫦娥四号”首次实现了航天器在月球背面软着陆。
【答案】B
【分析】公历年份是4的倍数的一般都是闰年,但年份是100的倍数时,必须是400的倍数才是闰年,据此分析。
【详解】1970÷4=492……2
2000÷400=5
2007÷4=501……3
2019÷4=504……3
A.1970不是4的倍数,不是闰年;
B.2000是4的倍数,是闰年;
C.2007不是4的倍数,不是闰年;
D.2019不是4的倍数,不是闰年。
故答案为:B
18.(2分)小勇、小冬、小灵与小胖四人进行跑步比赛,小冬不是最慢的,但比小勇、小灵慢,小勇比小灵慢,获得第一名的是( )。
A.小勇 B.小冬 C.小灵 D.小胖
【答案】C
【分析】根据“小冬不是最慢的,但比小勇、小灵慢”说明最慢的是小胖,小胖是第四名,小东是第三名,又因为“小勇比小灵慢”,所以最快的是小灵,那么小勇是第二名,小灵是第一名。据此推理即可解答。
【详解】据分析可知,最快的是小灵,所以获得第一名的是小灵。
故答案为:C
19.(2分)下五子棋时,黑方一子落下(如图中“×”的位置),同时形成两个或两个以上的“四”的情况,那么下一步黑棋应该落在哪个位置?这个位置用数对表示为( )。
A.(D,5) B.(6,D) C.(5,D) D.(D,6)
【答案】A
【分析】数对的第一个数表示列,第二个数表示行,如下图,要使盘中棋局成为“四四禁手”,下一步黑棋应该落在红“×”位置,这个位置用数对表示为(D,5),据此即可解答。
【详解】根据分析可知,下五子棋时,黑方一子落下,同时形成两个或两个以上的“四”的情况,那么下一步黑棋应该落的位置用数对表示为(D,5)。
故答案为:A
20.(2分)一个圆柱的侧面展开是一个正方形,这个圆柱的底面半径和高的比是( )。
A.1∶π B.1∶2π C.π∶1 D.2π∶1
【答案】B
【分析】因为圆柱的侧面展开是一个正方形,那么圆柱的底面周长和高相等,由圆的周长公式C=2πr,可得出2πr=h;根据比的意义写出这个圆柱的底面半径和高的比为r∶h,用2πr代替h,再化简比即可。
【详解】设圆柱的底面半径是r,高是h;
因为圆柱的侧面展开图是个正方形,所以h=2πr。
r∶h
=r∶2πr
=(r÷r)∶(2πr÷r)
=1∶2π
这个圆柱的底面半径和高的比是1∶2π。
故答案为:B
四、计算题(共18分)
21.(6分)能简算的要简算。
【答案】;10;36
【分析】(1)先算小括号里面的减法,再算中括号里面的除法,然后再计算括号外的乘法,最后计算括号外的除法,注意除以一个数相当于乘这个数的倒数;
(2)按照乘法分配律,用括号里面的数分别与括号外面的数相乘,再把积相加;
(3)按照乘法分配律,提出,再将剩下数相减计算。
【详解】
=×÷[×]
=÷
=×
=
=×24+×24-×24
=14+16-20
=10
=×(101-1)
=×100
=36
22.(8分)求未知数x。
10%x+1.2=4.6
【答案】x=34;x=;
x=5;x=
【分析】(1)先根据等式的基本性质1给方程两边同时减去 1.2,再根据等式的基本性质2给方程两边同时除以10%即可;
(2)先根据比例的基本性质把方程写成x=×,再根据等式的基本性质2给方程两边同时除以即可;
(3)先根据等式的基本性质2给方程两边同时除以,再根据等式的基本性质1给方程两边同时减去10即可;
(4)根据比的前项=比值×比的后项得到x=×25,进一步计算即可。
【详解】10%x+1.2=4.6
解:10%x+1.2-1.2=4.6-1.2
10%x=3.4
0.1x÷0.1=3.4÷0.1
x=34
∶=∶x
解:x=×
x=
x÷=÷
x÷=×
x=
(x+10)=6
解:(x+10)÷=6÷
x+10=6×
x+10=15
x+10-10=15-10
x=5
x∶25=
解:x=×25
x=
23.(4分)直接写出得数。
【答案】;64;5;70;
15;;81;6
五、作图题(共8分)
24.(8分)在方格中根据要求画一画。
(1)把三角形绕A点逆时针旋转90°,画出旋转后的图形。
(2)将旋转后的三角形按2∶1的比放大,画出放大后的三角形。
(3)画出图①的另一半,使它成为一个轴对称图形。
【答案】见详解
【分析】(1)根据旋转的特征,将三角形绕A点逆时针旋转90°,点A位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(2)将旋转后的三角形按2∶1的比放大,则三角形的底和高都要乘2,那么放大后三角形的底是6,高是4,据此画出放大后的三角形。
(3)一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴,据此找到关键的对称点依次连接,即可画出对称图形。
【详解】如图:
六、解答题(共34分)
25.(4分)在比例尺1∶2000000的地图上量得AB两地距离是5厘米。甲乙两车相向而行,3小时后还相距10千米,已知乙车速度是甲车的,甲乙两车每小时各行多少千米?
【答案】甲车:18千米,乙车:12千米
【分析】先根据图上距离除以比例尺求出两地的距离,用两地距离减10可得行驶的路程,再根据路程和÷行驶时间求出速度和,把甲车速度看作单位“1”,则两车速度和占甲车的,根据已知一个数的几分之几是多少,求这个数用除法计算,进而求出甲车速度,再根据求一个数的几分之几是多少,用乘法计算即可。计算时单位统一为千米。
【详解】5÷
=5×2000000
=10000000(厘米)
10000000厘米=100千米
(100-10)÷3
=90÷3
=30(千米)
30÷(1+)
=30÷
=30×
=18(千米)
18×=12(千米)
答:甲车每小时行18千米,乙车每小时行12千米。
26.(4分)某小学会议室需要装修,如果用面积为8平方分米的方砖铺地,需要360块。如果改用边长为3分米的方砖铺地,需要多少块?
【答案】320块
【分析】根据题意可知,每块方砖的面积×需要的块数=会议室地面总面积(一定),每块方砖的面积和需要的块数成反比例关系,列方程解答即可。
【详解】解:设用边长为3分米的方砖铺地,需要x块。
3×3×x=8×360
9x=8×360
9x÷9=8×(360÷9)
x=8×40
x=320
答:用边长为3分米的方砖铺地,需要320块。
27.(4分)学校体育室里,足球和篮球共有160个,体育课上用去足球个数的40%和16个篮球后,剩下的足球个数和篮球个数相等,原来体育室内有篮球和足球各多少个?
【答案】篮球70个;足球90个
【分析】把原有足球的个数看作单位“1”,用160减去16个篮球后得到的是足球的总数和篮球剩下的个数,即得到的数量占原有足球个数的,根据已知一个数的百分之几是多少,求这个数用除法计算可得原有足球的数量,再用160减原有足球的数量可得篮球的数量。
【详解】(160-16)÷(1-40%+1)
=144÷1.6
=90(个)
160-90=70(个)
答:原来体育室内有篮球70个,足球90个。
28.(4分)临近毕业,同学们和自己的好朋友互赠礼物。酷爱集卡的小华和小明互赠卡片。两人共有112张,小华拿出自己拥有卡片的送给小明,现在两人的卡片张数就同样多。原来小华和小明各有多少张卡片?(先把线段图补充完整,再解答)
【答案】小华72张;小明40张
【分析】根据题意,设小华有张,则小明有(112-)张卡片;小华拿出自己拥有卡片的送给小明,即送给小明张,那么小华还剩张,小明则有张,现在两人的卡片张数就同样多,所以可以列出方程,解出未知数即是小华卡片的张数,再用两人卡片的总张数减去小华的张数,求出小明卡片的张数。
【详解】如图:
解:设小华有张,则小明有(112-)张卡片。
=72
112-72=40(张)
答:小华有72张卡片,小明有40张卡片。
29.(9分)端午节期间,学校就学生对端午节文化习俗的了解情况进行了随机调查(了解程度:A.很了解;B.比较了解;C.了解较少;D.不了解),并将调查结果绘制成如下统计图。
(1)调查时,如果在学校中任意抽样,那么( )是最好的。
A.从每个班中抽10名学生。
B.从女子舞蹈队中选一些队员。
C.从男子排球队中选一些队员。
D.选一些对端午节文化有了解的学生。
(2)本次调查共调查了( )人,被调查的学生中对端午节文化习俗“很了解”的占总人数的( )%。
(3)本次调查中对端午节文化习俗“了解较少”的学生有( )人。请将条形统计图补充完整。
【答案】(1)A
(2) 400 35
(3)80;作图见详解
【分析】(1)抽样调查时,样本要具有代表性,据此选择。
(2)从两幅统计图中可知,对端午节文化习俗“比较了解”的有160人,占调查总人数的40%,把调查的总人数看作单位“1”,单位“1”未知,根据百分数除法的意义求出调查总人数;已知对端午节文化习俗“很了解”的有140人,用“很了解”的人数除以总人数,即是被调查的学生中对端午节文化习俗“很了解”的占总人数的百分之几。
(3)用调查的总人数减去对端午节文化习俗“很了解”、“比较了解”、“不了解”的人数,即是对端午节文化习俗“了解较少”的人数,据此将条形统计图补充完整。
【详解】(1)调查时,如果在学校中任意抽样,那么从每个班中抽10名学生是最好的。
故答案为:A
(2)160÷40%
=160÷0.4
=400(人)
140÷400
=0.35
=35%
本次调查共调查了400人,被调查的学生中对端午节文化习俗“很了解”的占总人数的35%。
(3)400-140-160-20
=260-160-20
=100-20
=80(人)
本次调查中对端午节文化习俗“了解较少”的学生有80人。
30.(9分)如图,图象表示一幅地图图上距离和实际距离的关系。
(1)根据图象,可以求出这幅地图的比例尺是( )。
(2)图上距离和实际距离成( )比例。
(3)在这幅地图上量得甲、乙两城的图上距离是10厘米。一辆小汽车上午10:00从甲城开车到乙城,下午3:00到达。这辆小汽车平均每时行驶多少千米?
【答案】(1)1∶4000000
(2)正
(3)80千米
【分析】(1)从图中可知,图上距离是1厘米时,对应的实际距离是40千米;根据“图上距离∶实际距离=比例尺”以及进率“1千米=100000厘米”,求出这幅地图的比例尺。
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。
(3)已知甲、乙两城的图上距离是10厘米,根据“实际距离=图上距离÷比例尺”,求出甲、乙两城的实际距离;
已知一辆小汽车上午10:00从甲城开车到乙城,下午3:00(即15:00)到达,用到达时刻减去出发时刻,求出小汽车行驶的时间;再根据“速度=路程÷时间”求出这辆小汽车的速度。
【详解】(1)1厘米∶40千米
=1厘米∶(40×100000)厘米
=1∶4000000
根据图象,可以求出这幅地图的比例尺是(1∶4000000)。
(2)图上距离∶实际距离=(一定),比值一定,则图上距离和实际距离成(正)比例。
(3)下午3:00=15:00
15时-10时=5(小时)
10÷
=10×4000000
=40000000(厘米)
40000000厘米=400千米
400÷5=80(千米)
答:这辆小汽车平均每时行驶80千米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
