第19章一次函数章末测试卷(含答案)-2024-2025学年数学八年级下册人教版
文档属性
| 名称 | 第19章一次函数章末测试卷(含答案)-2024-2025学年数学八年级下册人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 824.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第19章一次函数章末测试卷-2024-2025学年数学八年级下册人教版
一.选择题(共8小题)
1.小亮爸爸到加油站加油,如图是所用的加油机上的数据显示牌,金额随着数量的变化而变化,则下列判断正确的是( )
A.金额是因变量
B.单价是自变量
C.7.76和31是常量
D.金额是随着数量的增大而减少
2.函数y中,自变量x的取值范围是( )
A.x B.x C.x D.x
3.已知一个函数的函数值y与自变量x的几组对应值如表,这个函数的表达式可以是( )
x … ﹣1 0 1 2 …
y … ﹣3 0 3 6 …
A.y=3x B.y=x﹣2 C. D.y=3x2
4.如果y=x+2a﹣1是正比例函数,则a的值是( )
A. B.0 C. D.﹣2
5.如图1,在平行四边形ABCD中,点P沿A→B→C方向从点A移动到点C,设点P移动路程为x,线段AP的长为y,图2是点P运动时y随x变化的关系图象,则BC的长为( )
A.4.4 B.4.8 C.5 D.6
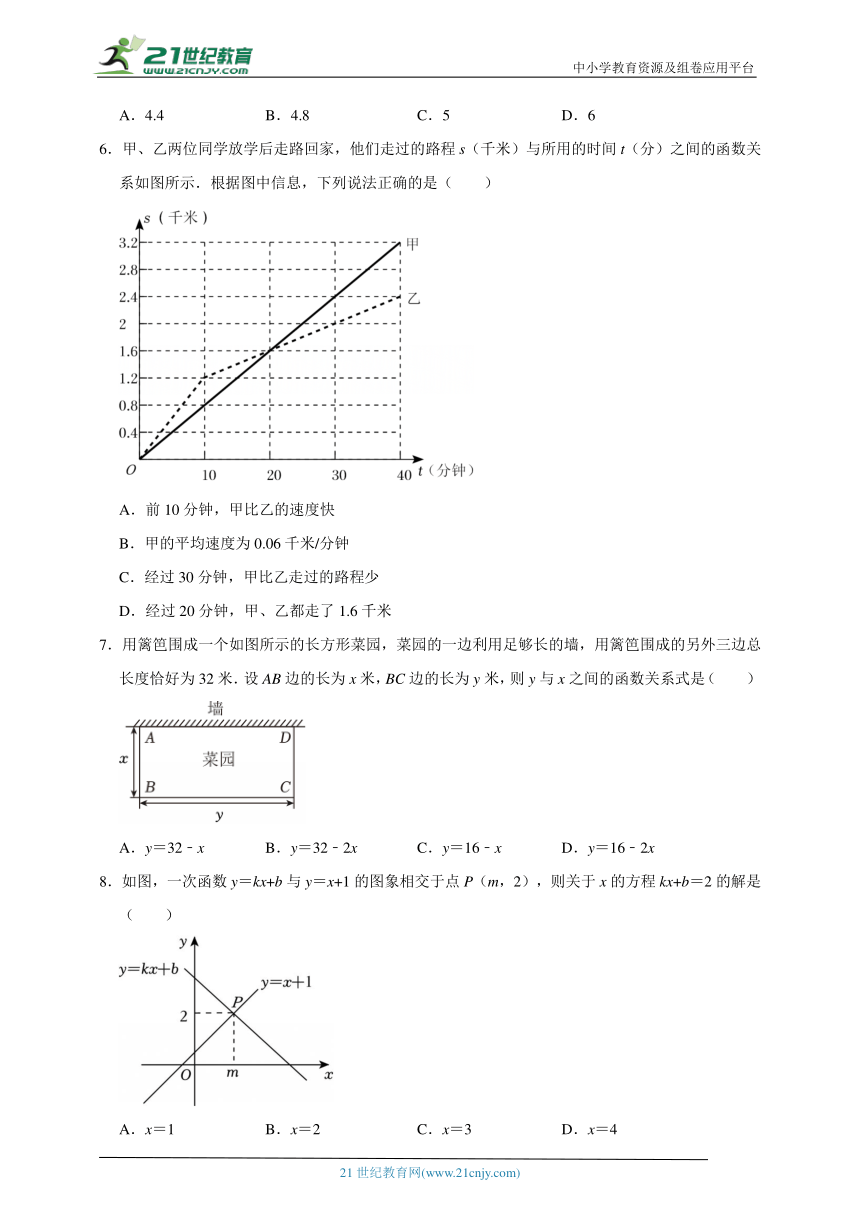
6.甲、乙两位同学放学后走路回家,他们走过的路程s(千米)与所用的时间t(分)之间的函数关系如图所示.根据图中信息,下列说法正确的是( )
A.前10分钟,甲比乙的速度快
B.甲的平均速度为0.06千米/分钟
C.经过30分钟,甲比乙走过的路程少
D.经过20分钟,甲、乙都走了1.6千米
7.用篱笆围成一个如图所示的长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为32米.设AB边的长为x米,BC边的长为y米,则y与x之间的函数关系式是( )
A.y=32﹣x B.y=32﹣2x C.y=16﹣x D.y=16﹣2x
8.如图,一次函数y=kx+b与y=x+1的图象相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x=1 B.x=2 C.x=3 D.x=4
二.填空题(共6小题)
9.在函数中,自变量x的取值范围是 .
10.铁的密度为7.9g/cm3,铁块的质量m(单位:g)与它的体积V(单位:cm3)之间的函数关系式为m=7.9V,当V=8cm3时,m= g.
11.元朝朱世杰的《算学启蒙》一书记载了一个驾马先行的问题,其中良马与劣马行走路程s(单位:里)关于行走时间t(单位:日)的函数图象如图所示,则劣马比良马早出发 日;良马的速度比劣马的速度快 里/日.
12.函数y=(3﹣m)x+n(m,n为常数,m≠3)若2m﹣n=2,当﹣1≤x≤1时,函数有最大值0,则n= .
13.某品牌鞋子的长度y cm与鞋子的码数x(码)之间满足一次函数关系.如果22码鞋子的长度为16cm,44码鞋子的长度为27cm,那么长度为24cm的鞋子码数是 码.
14.若整数a使关于z的不等式组有且仅有5个整数解,且使一次函数y=(a+1)x+a﹣5的图象不经过第二象限,则满足条件的所有整数a的和为 .
三.解答题(共5小题)
15.下表反映的是M市用电量x(千瓦时)与应缴电费y(元)之间的关系:
用电量(千瓦时) 1 2 3 4 5 ……
应缴电费(元) 0.55 1.1 1.65 2.2 2.75 ……
(1)请直接写出应缴电费y与用电量x之间的函数关系式;
(2)如果小明家某月缴纳电费40.7元,则用电量是多少?
16.某公司每月生产甲、乙两种型号的果汁共20万瓶,且所有果汁当月全部卖出,其中成本、售价如表:
甲 乙
成本 12元/瓶 4元/瓶
售价 18元/瓶 6元/瓶
(1)设甲种型号的果汁有x万瓶,公司所获利润为W元,如果该公司四月份投入成本不超过216万元,应该怎样安排甲、乙两种型号果汁的产量,可使该月公司所获利润最大?并求出最大利润.
(2)“五一”黄金周期间,为扩大销量,该公司对乙种型号果汁进行优惠,优惠方案如下:
方案一:购买乙种型号果汁一律打9折;
方案二:购买168元会员卡后,乙种型号果汁一律8折.
某超市到该公司购买乙种型号果汁,请帮该超市设计出合适的购买方案.
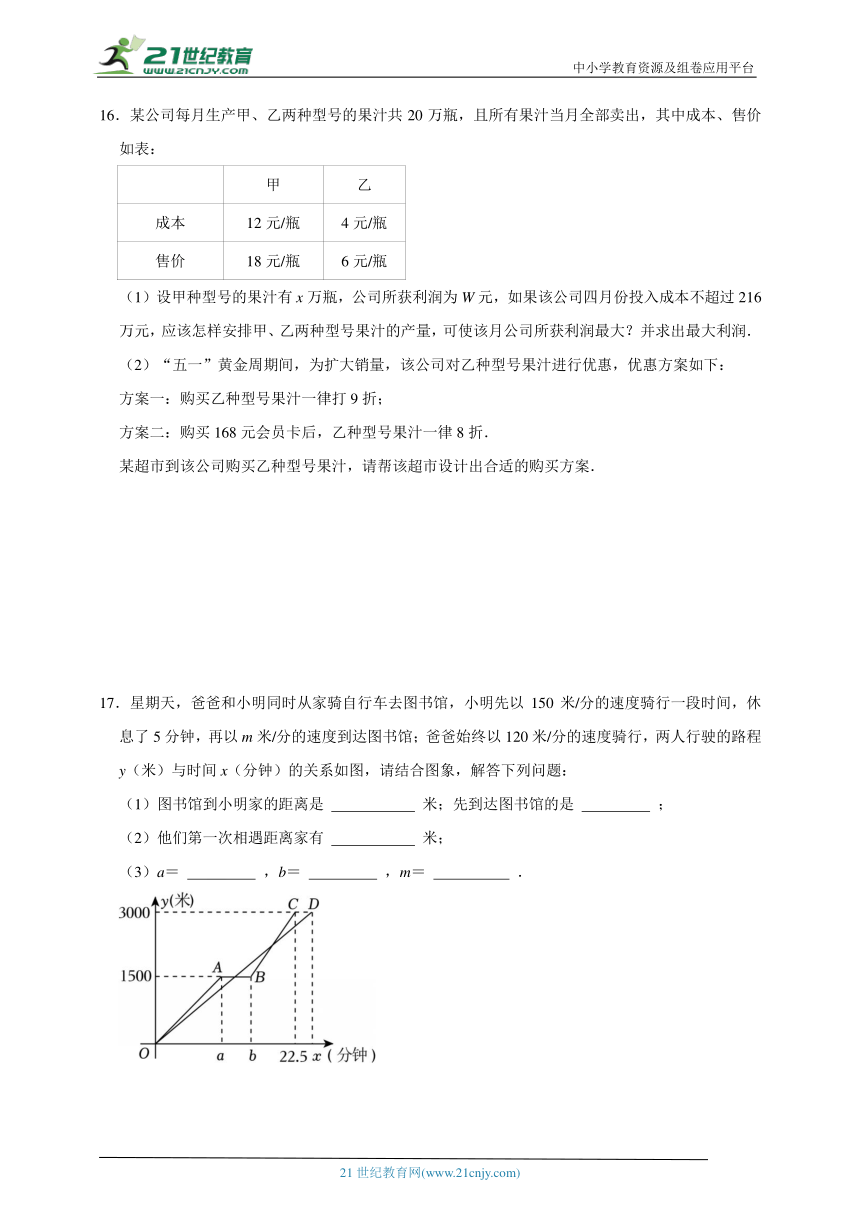
17.星期天,爸爸和小明同时从家骑自行车去图书馆,小明先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆;爸爸始终以120米/分的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)图书馆到小明家的距离是 米;先到达图书馆的是 ;
(2)他们第一次相遇距离家有 米;
(3)a= ,b= ,m= .
18.如图,在直角坐标系中,直线与x轴交于A,与直线交于,直线l2分别与x轴、y轴交于C、D,连接AD.
(1)直接根据图象写出关于x的不等式的解集;
(2)求出m、n的值;
(3)求出△ABD的面积.
19.如图,在平面直角坐标系xOy中,直线y=﹣x+m分别交x轴,y轴于A,B两点,已知点C(2,0).
(1)当直线AB经过点C时,点O到直线AB的距离是 .
(2)设点P为线段OB的中点,连接PA,PC,若∠CPA=∠ABO,求m的值.
(3)如图,D为A点右侧x轴上一点,E为x轴负半轴上一点,连接BE,BD,DF⊥BE于点F,线段AB与DF相交于点G,恰有BE=DG.若GD=5,GF=3,求G点的坐标.
第19章一次函数章末测试卷-2024-2025学年数学八年级下册人教版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A A A A C D B A
一.选择题(共8小题)
1.小亮爸爸到加油站加油,如图是所用的加油机上的数据显示牌,金额随着数量的变化而变化,则下列判断正确的是( )
A.金额是因变量
B.单价是自变量
C.7.76和31是常量
D.金额是随着数量的增大而减少
【解答】解:∵金额随着数量的变化而变化,
∴数量是自变量,金额是因变量,单价是常量,
∴金额是随着数量的增大而增大.
故选:A.
2.函数y中,自变量x的取值范围是( )
A.x B.x C.x D.x
【解答】解:根据题意得:2﹣3x>0,
解得:x.
故选:A.
3.已知一个函数的函数值y与自变量x的几组对应值如表,这个函数的表达式可以是( )
x … ﹣1 0 1 2 …
y … ﹣3 0 3 6 …
A.y=3x B.y=x﹣2 C. D.y=3x2
【解答】解:这是一个正比例函数,且函数关系式是y=3x;
故选:A.
4.如果y=x+2a﹣1是正比例函数,则a的值是( )
A. B.0 C. D.﹣2
【解答】解:∵y=x+2a﹣1是正比例函数,
∴2a﹣1=0.
解得:a.
故选:A.
5.如图1,在平行四边形ABCD中,点P沿A→B→C方向从点A移动到点C,设点P移动路程为x,线段AP的长为y,图2是点P运动时y随x变化的关系图象,则BC的长为( )
A.4.4 B.4.8 C.5 D.6
【解答】解:如图1,过A点作AE⊥BC于E,连接AC,
根据图2知:当点P与点B重合时,AP=AB=3,
当P与E重合时,AB+BP=4.8,
∴BP=BE=1.8,
∴AE,
当点P到达点C时,AP=AC=4,
∴EC,
∴BC=BE+EC=1.85.
故选:C.
6.甲、乙两位同学放学后走路回家,他们走过的路程s(千米)与所用的时间t(分)之间的函数关系如图所示.根据图中信息,下列说法正确的是( )
A.前10分钟,甲比乙的速度快
B.甲的平均速度为0.06千米/分钟
C.经过30分钟,甲比乙走过的路程少
D.经过20分钟,甲、乙都走了1.6千米
【解答】解:A.前10分钟,甲走了0.8千米,乙走了1.2千米,所以乙比甲的速度快,故此选项错误,不符合题意;
B.根据图象可知,甲40分钟走了3.2千米,所以甲的平均速度为0.08千米/分钟,故此选项错误,不符合题意;
C.经过30分钟,甲走了2.4千米,乙走了2千米,所以甲比乙走过的路程多,故此选项错误,不符合题意;
D.经过20分钟,由函数图象可知,甲、乙都走了1.6千米,故此选项正确,符合题意.
故选:D.
7.用篱笆围成一个如图所示的长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为32米.设AB边的长为x米,BC边的长为y米,则y与x之间的函数关系式是( )
A.y=32﹣x B.y=32﹣2x C.y=16﹣x D.y=16﹣2x
【解答】解:由题意得:2x+y=32,
∴y=﹣2x+32,即y=32﹣2x.
故选:B.
8.如图,一次函数y=kx+b与y=x+1的图象相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x=1 B.x=2 C.x=3 D.x=4
【解答】解:由条件可得:m+1=2,解得m=1,
∴点P的坐标为P(1,2),
∵点P(1,2)在一次函数y=kx+b的图象上,
∴k+b=2,
∴关于x的方程kx+b=2的解是x=1,
故选:A.
二.填空题(共6小题)
9.在函数中,自变量x的取值范围是 x≠﹣4 .
【解答】解:根据分式有意义的条件可得:
x+4≠0,
解得:x≠﹣4,
故答案为:x≠﹣4.
10.铁的密度为7.9g/cm3,铁块的质量m(单位:g)与它的体积V(单位:cm3)之间的函数关系式为m=7.9V,当V=8cm3时,m= 63.2 g.
【解答】解:当V=8时,m=7.9×8=63.2.
故答案为:63.2.
11.元朝朱世杰的《算学启蒙》一书记载了一个驾马先行的问题,其中良马与劣马行走路程s(单位:里)关于行走时间t(单位:日)的函数图象如图所示,则劣马比良马早出发 12 日;良马的速度比劣马的速度快 90 里/日.
【解答】解:由图象可知,劣马从第0日出发,良马从第12日出发.劣马比良马早出发12日;
由图象可知,当t=32时,两直线有交点,代表良马追上劣马,此时良马出发32﹣12=20(日),
良马行走4800里用了20日,故速度为4800÷20=240(里/日),劣马行走4800里用了32日,故速度为4800÷32=150(里/日),
所以良马的速度比劣马的速度快240﹣150=90(里/日).
故答案为:12,90.
12.函数y=(3﹣m)x+n(m,n为常数,m≠3)若2m﹣n=2,当﹣1≤x≤1时,函数有最大值0,则n= ﹣4 .
【解答】解:①当3﹣m>0,即m<3时,
当x=1时,y取到最大值,y最大=(3﹣m)+n=0,即﹣m+n=﹣3.
故.
解得.
②当3﹣m<0,即m>3时,
当x=﹣1时,y取到最大值,y最大=﹣(3﹣m)+n=0,即m+n=3.
故,
解得(舍去).
综上所述,n的值是﹣4.
故答案是:﹣4.
13.某品牌鞋子的长度y cm与鞋子的码数x(码)之间满足一次函数关系.如果22码鞋子的长度为16cm,44码鞋子的长度为27cm,那么长度为24cm的鞋子码数是 38 码.
【解答】解:设y与x之间的函数关系式为y=kx+b(k、b为常数,且k≠0),
将x=22,y=16和x=44,y=27分别代入y=kx+b,
得,
解得,
∴y与x之间的函数关系式为yx+5,
当y=24时,得x+5=24,
解得x=38,
∴长度为24cm的鞋子码数是38码.
故答案为:38.
14.若整数a使关于z的不等式组有且仅有5个整数解,且使一次函数y=(a+1)x+a﹣5的图象不经过第二象限,则满足条件的所有整数a的和为 12 .
【解答】解:解不等式组得,
∵不等式组有且仅有5个整数解,
∴﹣10,
∴2<a≤9,
∵关于x的一次函数y=(a+1)x+a﹣5的图象不经过第二象限,
∴,
∴﹣1<a≤5,
∴2<a≤5,
∴满足条件的所有整数a为3,4,5,
∵3+4+5=12,
∴满足条件的所有整数a的和为12.
故答案为:12.
三.解答题(共5小题)
15.下表反映的是M市用电量x(千瓦时)与应缴电费y(元)之间的关系:
用电量(千瓦时) 1 2 3 4 5 ……
应缴电费(元) 0.55 1.1 1.65 2.2 2.75 ……
(1)请直接写出应缴电费y与用电量x之间的函数关系式;
(2)如果小明家某月缴纳电费40.7元,则用电量是多少?
【解答】解(1)根据表中数据可知:用电量每增加1千瓦时,电费增加0.55元,
∴应缴电费y与用电量x之间的函数关系式为y=0.55x.
(2)∵小明家某月缴纳电费40.7元,
∴y=40.7,即0.55x=40.7,
解得,x=74,
答:如果小明家某月缴纳电费40.7元,则用电量是74千瓦时.
16.某公司每月生产甲、乙两种型号的果汁共20万瓶,且所有果汁当月全部卖出,其中成本、售价如表:
甲 乙
成本 12元/瓶 4元/瓶
售价 18元/瓶 6元/瓶
(1)设甲种型号的果汁有x万瓶,公司所获利润为W元,如果该公司四月份投入成本不超过216万元,应该怎样安排甲、乙两种型号果汁的产量,可使该月公司所获利润最大?并求出最大利润.
(2)“五一”黄金周期间,为扩大销量,该公司对乙种型号果汁进行优惠,优惠方案如下:
方案一:购买乙种型号果汁一律打9折;
方案二:购买168元会员卡后,乙种型号果汁一律8折.
某超市到该公司购买乙种型号果汁,请帮该超市设计出合适的购买方案.
【解答】解:(1)∵该公司每月生产甲、乙两种型号的果汁共20万瓶,且甲种型号的果汁生产了x万瓶,
∴乙种型号的果汁生产了(20﹣x)万瓶.
根据题意得:12x+4(20﹣x)≤216,
解得:x≤17.
∵公司所获利润为W元,
∴W=(18﹣12)x+(6﹣4)(20﹣x),
∴W=4x+40,
∵4>0,
∴W随x的增大而增大,
∴当x=17时,W取得最大值,最大值为4×17+40=108,此时20﹣x=20﹣17=3.
答:当甲种型号的果汁生产了17万瓶,乙种型号的果汁生产了3万瓶时,该月公司所获利润最大,最大利润为108万元;
(2)设该超市到该公司购买乙种型号果汁y瓶,则选择方案一所需费用为6×0.9y=5.4y元;选择方案二所需费用为168+6×0.8y=(168+4.8y)元.
若5.4y<168+4.8y,则y<280,
∴当0<y<280时,选择方案一购买更合算;
若5.4y=168+4.8y,则y=280,
∴当y=280时,选择两优惠方案所需费用相同;
若5.4y>168+4.8y,则y>280,
∴当y>280时,选择方案二购买更合算.
答:当0<y<280时,选择方案一购买更合算;当y=280时,选择两优惠方案所需费用相同;当y>280时,选择方案二购买更合算.
17.星期天,爸爸和小明同时从家骑自行车去图书馆,小明先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆;爸爸始终以120米/分的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)图书馆到小明家的距离是 3000 米;先到达图书馆的是 小明 ;
(2)他们第一次相遇距离家有 1500 米;
(3)a= 10 ,b= 15 ,m= 200 .
【解答】解:(1)由题意,图书馆到小明家的距离是3000米;先到达图书馆的是小明;
故答案为:3000;小明.
(2)由题意,结合图象,可得他们第一次相遇距离家有1500米;
故答案为:1500;
(3)由题意,a=1500÷150=10(分钟),
b=10+5=15(分钟),
m=(3000﹣1500)÷(22.5﹣15)=200(米/分).
故答案为:10;15;200.
18.如图,在直角坐标系中,直线与x轴交于A,与直线交于,直线l2分别与x轴、y轴交于C、D,连接AD.
(1)直接根据图象写出关于x的不等式的解集;
(2)求出m、n的值;
(3)求出△ABD的面积.
【解答】解:(1)∵x+mx+1,
∴x;
(2)∵直线yx+1经过B(,n),
∴n1.
∵直线yx+m经过B(,),
∴m,
∴m=3;
(3)由(2)得直线l2的解析式为yx+3,
令x=0,则yx+1,
∴H(0,1),
令x=0,则0x+3,
∴y=3,
∴D(0,3),
∴△ABD的面积=△AHD的面积+△HBD的面积(3﹣1)×2(3﹣1).
19.如图,在平面直角坐标系xOy中,直线y=﹣x+m分别交x轴,y轴于A,B两点,已知点C(2,0).
(1)当直线AB经过点C时,点O到直线AB的距离是 .
(2)设点P为线段OB的中点,连接PA,PC,若∠CPA=∠ABO,求m的值.
(3)如图,D为A点右侧x轴上一点,E为x轴负半轴上一点,连接BE,BD,DF⊥BE于点F,线段AB与DF相交于点G,恰有BE=DG.若GD=5,GF=3,求G点的坐标.
【解答】解:(1)∵直线y=﹣x+m经过点C(2,0),
∴0=﹣2+m,
解得m=2,
∴直线AB解析式为y=﹣x+2,
在y=﹣x+2中,令x=0得y=2,令y=0得x=2,
∴A(2,0),B(0,2),
∴AB2,
设点O到直线AB的距离是h,
∵2S△AOB=OA OB=AB h,
∴h,
∴点O到直线AB的距离是;
故答案为:;
(2)在y轴负半轴上取点D,使OD=OC=2,连接CD,则∠PDC=45°,CD=2,如图,
由y=﹣x+m可得A(m,0),B(0,m),
∴OA=OB=m,ABm,
∴∠OBA=∠OAB=45°,
当m<0时,B在y轴负半轴,∠APC>∠ABO=45°,此时∠CPA=∠ABO不成立,
∴m>0,
∵∠CPA=∠ABO=45°,
∴∠BPA+∠OPC=∠BAP+∠BPA=135°,
∴∠OPC=∠BAP,
∵∠PDC=45°=∠ABP,
∴△PCD∽△APB,
∴,
∵点P为线段OB的中点,
∴OPm=PB,
∴,
解得m=12,
∴m的值为12;
(3)过G作GK⊥x轴于K,如图:
设GK=t,
∵∠BAO=45°,
∴△GKA是等腰直角三角形,
∴AK=GK=t,
∴OK=OA﹣AK=m﹣t,
∵DF⊥BE,
∴∠DFE=90°,
∴∠GDK=90°﹣∠FEO=∠EBO,
∵BE=DG,∠BOE=90°=∠DKG,
∴△BOE≌△DKG(AAS),
∴OE=GK=t,OB=DK=m,BE=DG=5,
∴DE=DK+OK+OE=m+m﹣t+t=2m,
∵GD=5,GF=3,
∴DF=8,
∵∠GDK=∠EDF,∠GKD=90°=∠EFD,
∴△GKD∽△EFD,
∴,即,
解得m=2(负值已舍去),
∴OA=OB=2,
∴GK=t=OE,
∴OK=m﹣t=2,
∴G(,).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第19章一次函数章末测试卷-2024-2025学年数学八年级下册人教版
一.选择题(共8小题)
1.小亮爸爸到加油站加油,如图是所用的加油机上的数据显示牌,金额随着数量的变化而变化,则下列判断正确的是( )
A.金额是因变量
B.单价是自变量
C.7.76和31是常量
D.金额是随着数量的增大而减少
2.函数y中,自变量x的取值范围是( )
A.x B.x C.x D.x
3.已知一个函数的函数值y与自变量x的几组对应值如表,这个函数的表达式可以是( )
x … ﹣1 0 1 2 …
y … ﹣3 0 3 6 …
A.y=3x B.y=x﹣2 C. D.y=3x2
4.如果y=x+2a﹣1是正比例函数,则a的值是( )
A. B.0 C. D.﹣2
5.如图1,在平行四边形ABCD中,点P沿A→B→C方向从点A移动到点C,设点P移动路程为x,线段AP的长为y,图2是点P运动时y随x变化的关系图象,则BC的长为( )
A.4.4 B.4.8 C.5 D.6
6.甲、乙两位同学放学后走路回家,他们走过的路程s(千米)与所用的时间t(分)之间的函数关系如图所示.根据图中信息,下列说法正确的是( )
A.前10分钟,甲比乙的速度快
B.甲的平均速度为0.06千米/分钟
C.经过30分钟,甲比乙走过的路程少
D.经过20分钟,甲、乙都走了1.6千米
7.用篱笆围成一个如图所示的长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为32米.设AB边的长为x米,BC边的长为y米,则y与x之间的函数关系式是( )
A.y=32﹣x B.y=32﹣2x C.y=16﹣x D.y=16﹣2x
8.如图,一次函数y=kx+b与y=x+1的图象相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x=1 B.x=2 C.x=3 D.x=4
二.填空题(共6小题)
9.在函数中,自变量x的取值范围是 .
10.铁的密度为7.9g/cm3,铁块的质量m(单位:g)与它的体积V(单位:cm3)之间的函数关系式为m=7.9V,当V=8cm3时,m= g.
11.元朝朱世杰的《算学启蒙》一书记载了一个驾马先行的问题,其中良马与劣马行走路程s(单位:里)关于行走时间t(单位:日)的函数图象如图所示,则劣马比良马早出发 日;良马的速度比劣马的速度快 里/日.
12.函数y=(3﹣m)x+n(m,n为常数,m≠3)若2m﹣n=2,当﹣1≤x≤1时,函数有最大值0,则n= .
13.某品牌鞋子的长度y cm与鞋子的码数x(码)之间满足一次函数关系.如果22码鞋子的长度为16cm,44码鞋子的长度为27cm,那么长度为24cm的鞋子码数是 码.
14.若整数a使关于z的不等式组有且仅有5个整数解,且使一次函数y=(a+1)x+a﹣5的图象不经过第二象限,则满足条件的所有整数a的和为 .
三.解答题(共5小题)
15.下表反映的是M市用电量x(千瓦时)与应缴电费y(元)之间的关系:
用电量(千瓦时) 1 2 3 4 5 ……
应缴电费(元) 0.55 1.1 1.65 2.2 2.75 ……
(1)请直接写出应缴电费y与用电量x之间的函数关系式;
(2)如果小明家某月缴纳电费40.7元,则用电量是多少?
16.某公司每月生产甲、乙两种型号的果汁共20万瓶,且所有果汁当月全部卖出,其中成本、售价如表:
甲 乙
成本 12元/瓶 4元/瓶
售价 18元/瓶 6元/瓶
(1)设甲种型号的果汁有x万瓶,公司所获利润为W元,如果该公司四月份投入成本不超过216万元,应该怎样安排甲、乙两种型号果汁的产量,可使该月公司所获利润最大?并求出最大利润.
(2)“五一”黄金周期间,为扩大销量,该公司对乙种型号果汁进行优惠,优惠方案如下:
方案一:购买乙种型号果汁一律打9折;
方案二:购买168元会员卡后,乙种型号果汁一律8折.
某超市到该公司购买乙种型号果汁,请帮该超市设计出合适的购买方案.
17.星期天,爸爸和小明同时从家骑自行车去图书馆,小明先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆;爸爸始终以120米/分的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)图书馆到小明家的距离是 米;先到达图书馆的是 ;
(2)他们第一次相遇距离家有 米;
(3)a= ,b= ,m= .
18.如图,在直角坐标系中,直线与x轴交于A,与直线交于,直线l2分别与x轴、y轴交于C、D,连接AD.
(1)直接根据图象写出关于x的不等式的解集;
(2)求出m、n的值;
(3)求出△ABD的面积.
19.如图,在平面直角坐标系xOy中,直线y=﹣x+m分别交x轴,y轴于A,B两点,已知点C(2,0).
(1)当直线AB经过点C时,点O到直线AB的距离是 .
(2)设点P为线段OB的中点,连接PA,PC,若∠CPA=∠ABO,求m的值.
(3)如图,D为A点右侧x轴上一点,E为x轴负半轴上一点,连接BE,BD,DF⊥BE于点F,线段AB与DF相交于点G,恰有BE=DG.若GD=5,GF=3,求G点的坐标.
第19章一次函数章末测试卷-2024-2025学年数学八年级下册人教版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A A A A C D B A
一.选择题(共8小题)
1.小亮爸爸到加油站加油,如图是所用的加油机上的数据显示牌,金额随着数量的变化而变化,则下列判断正确的是( )
A.金额是因变量
B.单价是自变量
C.7.76和31是常量
D.金额是随着数量的增大而减少
【解答】解:∵金额随着数量的变化而变化,
∴数量是自变量,金额是因变量,单价是常量,
∴金额是随着数量的增大而增大.
故选:A.
2.函数y中,自变量x的取值范围是( )
A.x B.x C.x D.x
【解答】解:根据题意得:2﹣3x>0,
解得:x.
故选:A.
3.已知一个函数的函数值y与自变量x的几组对应值如表,这个函数的表达式可以是( )
x … ﹣1 0 1 2 …
y … ﹣3 0 3 6 …
A.y=3x B.y=x﹣2 C. D.y=3x2
【解答】解:这是一个正比例函数,且函数关系式是y=3x;
故选:A.
4.如果y=x+2a﹣1是正比例函数,则a的值是( )
A. B.0 C. D.﹣2
【解答】解:∵y=x+2a﹣1是正比例函数,
∴2a﹣1=0.
解得:a.
故选:A.
5.如图1,在平行四边形ABCD中,点P沿A→B→C方向从点A移动到点C,设点P移动路程为x,线段AP的长为y,图2是点P运动时y随x变化的关系图象,则BC的长为( )
A.4.4 B.4.8 C.5 D.6
【解答】解:如图1,过A点作AE⊥BC于E,连接AC,
根据图2知:当点P与点B重合时,AP=AB=3,
当P与E重合时,AB+BP=4.8,
∴BP=BE=1.8,
∴AE,
当点P到达点C时,AP=AC=4,
∴EC,
∴BC=BE+EC=1.85.
故选:C.
6.甲、乙两位同学放学后走路回家,他们走过的路程s(千米)与所用的时间t(分)之间的函数关系如图所示.根据图中信息,下列说法正确的是( )
A.前10分钟,甲比乙的速度快
B.甲的平均速度为0.06千米/分钟
C.经过30分钟,甲比乙走过的路程少
D.经过20分钟,甲、乙都走了1.6千米
【解答】解:A.前10分钟,甲走了0.8千米,乙走了1.2千米,所以乙比甲的速度快,故此选项错误,不符合题意;
B.根据图象可知,甲40分钟走了3.2千米,所以甲的平均速度为0.08千米/分钟,故此选项错误,不符合题意;
C.经过30分钟,甲走了2.4千米,乙走了2千米,所以甲比乙走过的路程多,故此选项错误,不符合题意;
D.经过20分钟,由函数图象可知,甲、乙都走了1.6千米,故此选项正确,符合题意.
故选:D.
7.用篱笆围成一个如图所示的长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为32米.设AB边的长为x米,BC边的长为y米,则y与x之间的函数关系式是( )
A.y=32﹣x B.y=32﹣2x C.y=16﹣x D.y=16﹣2x
【解答】解:由题意得:2x+y=32,
∴y=﹣2x+32,即y=32﹣2x.
故选:B.
8.如图,一次函数y=kx+b与y=x+1的图象相交于点P(m,2),则关于x的方程kx+b=2的解是( )
A.x=1 B.x=2 C.x=3 D.x=4
【解答】解:由条件可得:m+1=2,解得m=1,
∴点P的坐标为P(1,2),
∵点P(1,2)在一次函数y=kx+b的图象上,
∴k+b=2,
∴关于x的方程kx+b=2的解是x=1,
故选:A.
二.填空题(共6小题)
9.在函数中,自变量x的取值范围是 x≠﹣4 .
【解答】解:根据分式有意义的条件可得:
x+4≠0,
解得:x≠﹣4,
故答案为:x≠﹣4.
10.铁的密度为7.9g/cm3,铁块的质量m(单位:g)与它的体积V(单位:cm3)之间的函数关系式为m=7.9V,当V=8cm3时,m= 63.2 g.
【解答】解:当V=8时,m=7.9×8=63.2.
故答案为:63.2.
11.元朝朱世杰的《算学启蒙》一书记载了一个驾马先行的问题,其中良马与劣马行走路程s(单位:里)关于行走时间t(单位:日)的函数图象如图所示,则劣马比良马早出发 12 日;良马的速度比劣马的速度快 90 里/日.
【解答】解:由图象可知,劣马从第0日出发,良马从第12日出发.劣马比良马早出发12日;
由图象可知,当t=32时,两直线有交点,代表良马追上劣马,此时良马出发32﹣12=20(日),
良马行走4800里用了20日,故速度为4800÷20=240(里/日),劣马行走4800里用了32日,故速度为4800÷32=150(里/日),
所以良马的速度比劣马的速度快240﹣150=90(里/日).
故答案为:12,90.
12.函数y=(3﹣m)x+n(m,n为常数,m≠3)若2m﹣n=2,当﹣1≤x≤1时,函数有最大值0,则n= ﹣4 .
【解答】解:①当3﹣m>0,即m<3时,
当x=1时,y取到最大值,y最大=(3﹣m)+n=0,即﹣m+n=﹣3.
故.
解得.
②当3﹣m<0,即m>3时,
当x=﹣1时,y取到最大值,y最大=﹣(3﹣m)+n=0,即m+n=3.
故,
解得(舍去).
综上所述,n的值是﹣4.
故答案是:﹣4.
13.某品牌鞋子的长度y cm与鞋子的码数x(码)之间满足一次函数关系.如果22码鞋子的长度为16cm,44码鞋子的长度为27cm,那么长度为24cm的鞋子码数是 38 码.
【解答】解:设y与x之间的函数关系式为y=kx+b(k、b为常数,且k≠0),
将x=22,y=16和x=44,y=27分别代入y=kx+b,
得,
解得,
∴y与x之间的函数关系式为yx+5,
当y=24时,得x+5=24,
解得x=38,
∴长度为24cm的鞋子码数是38码.
故答案为:38.
14.若整数a使关于z的不等式组有且仅有5个整数解,且使一次函数y=(a+1)x+a﹣5的图象不经过第二象限,则满足条件的所有整数a的和为 12 .
【解答】解:解不等式组得,
∵不等式组有且仅有5个整数解,
∴﹣10,
∴2<a≤9,
∵关于x的一次函数y=(a+1)x+a﹣5的图象不经过第二象限,
∴,
∴﹣1<a≤5,
∴2<a≤5,
∴满足条件的所有整数a为3,4,5,
∵3+4+5=12,
∴满足条件的所有整数a的和为12.
故答案为:12.
三.解答题(共5小题)
15.下表反映的是M市用电量x(千瓦时)与应缴电费y(元)之间的关系:
用电量(千瓦时) 1 2 3 4 5 ……
应缴电费(元) 0.55 1.1 1.65 2.2 2.75 ……
(1)请直接写出应缴电费y与用电量x之间的函数关系式;
(2)如果小明家某月缴纳电费40.7元,则用电量是多少?
【解答】解(1)根据表中数据可知:用电量每增加1千瓦时,电费增加0.55元,
∴应缴电费y与用电量x之间的函数关系式为y=0.55x.
(2)∵小明家某月缴纳电费40.7元,
∴y=40.7,即0.55x=40.7,
解得,x=74,
答:如果小明家某月缴纳电费40.7元,则用电量是74千瓦时.
16.某公司每月生产甲、乙两种型号的果汁共20万瓶,且所有果汁当月全部卖出,其中成本、售价如表:
甲 乙
成本 12元/瓶 4元/瓶
售价 18元/瓶 6元/瓶
(1)设甲种型号的果汁有x万瓶,公司所获利润为W元,如果该公司四月份投入成本不超过216万元,应该怎样安排甲、乙两种型号果汁的产量,可使该月公司所获利润最大?并求出最大利润.
(2)“五一”黄金周期间,为扩大销量,该公司对乙种型号果汁进行优惠,优惠方案如下:
方案一:购买乙种型号果汁一律打9折;
方案二:购买168元会员卡后,乙种型号果汁一律8折.
某超市到该公司购买乙种型号果汁,请帮该超市设计出合适的购买方案.
【解答】解:(1)∵该公司每月生产甲、乙两种型号的果汁共20万瓶,且甲种型号的果汁生产了x万瓶,
∴乙种型号的果汁生产了(20﹣x)万瓶.
根据题意得:12x+4(20﹣x)≤216,
解得:x≤17.
∵公司所获利润为W元,
∴W=(18﹣12)x+(6﹣4)(20﹣x),
∴W=4x+40,
∵4>0,
∴W随x的增大而增大,
∴当x=17时,W取得最大值,最大值为4×17+40=108,此时20﹣x=20﹣17=3.
答:当甲种型号的果汁生产了17万瓶,乙种型号的果汁生产了3万瓶时,该月公司所获利润最大,最大利润为108万元;
(2)设该超市到该公司购买乙种型号果汁y瓶,则选择方案一所需费用为6×0.9y=5.4y元;选择方案二所需费用为168+6×0.8y=(168+4.8y)元.
若5.4y<168+4.8y,则y<280,
∴当0<y<280时,选择方案一购买更合算;
若5.4y=168+4.8y,则y=280,
∴当y=280时,选择两优惠方案所需费用相同;
若5.4y>168+4.8y,则y>280,
∴当y>280时,选择方案二购买更合算.
答:当0<y<280时,选择方案一购买更合算;当y=280时,选择两优惠方案所需费用相同;当y>280时,选择方案二购买更合算.
17.星期天,爸爸和小明同时从家骑自行车去图书馆,小明先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆;爸爸始终以120米/分的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)图书馆到小明家的距离是 3000 米;先到达图书馆的是 小明 ;
(2)他们第一次相遇距离家有 1500 米;
(3)a= 10 ,b= 15 ,m= 200 .
【解答】解:(1)由题意,图书馆到小明家的距离是3000米;先到达图书馆的是小明;
故答案为:3000;小明.
(2)由题意,结合图象,可得他们第一次相遇距离家有1500米;
故答案为:1500;
(3)由题意,a=1500÷150=10(分钟),
b=10+5=15(分钟),
m=(3000﹣1500)÷(22.5﹣15)=200(米/分).
故答案为:10;15;200.
18.如图,在直角坐标系中,直线与x轴交于A,与直线交于,直线l2分别与x轴、y轴交于C、D,连接AD.
(1)直接根据图象写出关于x的不等式的解集;
(2)求出m、n的值;
(3)求出△ABD的面积.
【解答】解:(1)∵x+mx+1,
∴x;
(2)∵直线yx+1经过B(,n),
∴n1.
∵直线yx+m经过B(,),
∴m,
∴m=3;
(3)由(2)得直线l2的解析式为yx+3,
令x=0,则yx+1,
∴H(0,1),
令x=0,则0x+3,
∴y=3,
∴D(0,3),
∴△ABD的面积=△AHD的面积+△HBD的面积(3﹣1)×2(3﹣1).
19.如图,在平面直角坐标系xOy中,直线y=﹣x+m分别交x轴,y轴于A,B两点,已知点C(2,0).
(1)当直线AB经过点C时,点O到直线AB的距离是 .
(2)设点P为线段OB的中点,连接PA,PC,若∠CPA=∠ABO,求m的值.
(3)如图,D为A点右侧x轴上一点,E为x轴负半轴上一点,连接BE,BD,DF⊥BE于点F,线段AB与DF相交于点G,恰有BE=DG.若GD=5,GF=3,求G点的坐标.
【解答】解:(1)∵直线y=﹣x+m经过点C(2,0),
∴0=﹣2+m,
解得m=2,
∴直线AB解析式为y=﹣x+2,
在y=﹣x+2中,令x=0得y=2,令y=0得x=2,
∴A(2,0),B(0,2),
∴AB2,
设点O到直线AB的距离是h,
∵2S△AOB=OA OB=AB h,
∴h,
∴点O到直线AB的距离是;
故答案为:;
(2)在y轴负半轴上取点D,使OD=OC=2,连接CD,则∠PDC=45°,CD=2,如图,
由y=﹣x+m可得A(m,0),B(0,m),
∴OA=OB=m,ABm,
∴∠OBA=∠OAB=45°,
当m<0时,B在y轴负半轴,∠APC>∠ABO=45°,此时∠CPA=∠ABO不成立,
∴m>0,
∵∠CPA=∠ABO=45°,
∴∠BPA+∠OPC=∠BAP+∠BPA=135°,
∴∠OPC=∠BAP,
∵∠PDC=45°=∠ABP,
∴△PCD∽△APB,
∴,
∵点P为线段OB的中点,
∴OPm=PB,
∴,
解得m=12,
∴m的值为12;
(3)过G作GK⊥x轴于K,如图:
设GK=t,
∵∠BAO=45°,
∴△GKA是等腰直角三角形,
∴AK=GK=t,
∴OK=OA﹣AK=m﹣t,
∵DF⊥BE,
∴∠DFE=90°,
∴∠GDK=90°﹣∠FEO=∠EBO,
∵BE=DG,∠BOE=90°=∠DKG,
∴△BOE≌△DKG(AAS),
∴OE=GK=t,OB=DK=m,BE=DG=5,
∴DE=DK+OK+OE=m+m﹣t+t=2m,
∵GD=5,GF=3,
∴DF=8,
∵∠GDK=∠EDF,∠GKD=90°=∠EFD,
∴△GKD∽△EFD,
∴,即,
解得m=2(负值已舍去),
∴OA=OB=2,
∴GK=t=OE,
∴OK=m﹣t=2,
∴G(,).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
