沪科版九年级数学上册第21章二次函数与反比例函数21.1 二次函数(1)
文档属性
| 名称 | 沪科版九年级数学上册第21章二次函数与反比例函数21.1 二次函数(1) |  | |
| 格式 | ppt | ||
| 文件大小 | 682.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 07:20:16 | ||
图片预览






文档简介
(共14张PPT)
知识点
二次函数
1
二次函数的定义
一般地,表达式形如 y=ax2+bx+c ( a, b, c 是常数,且 a ≠ 0 )的函数叫做 x 的二次函数,其中 x 是自变量 .
2. 二次函数的三要素
(1)自变量的最高次数必须是 2;
(2)等号右边的 ax2+bx+c 是关于自变量 x 的整式;
(3)二次项系数 a 不等于零 .
3. 二次函数的一般形式 y=ax2+bx+c ( a, b, c 是常数,且 a ≠ 0 )是二次函数的一般形式 .ax2 是二次项, a 是二次项系数; bx是一次项, b 是一次项系数; c 是常数项 .
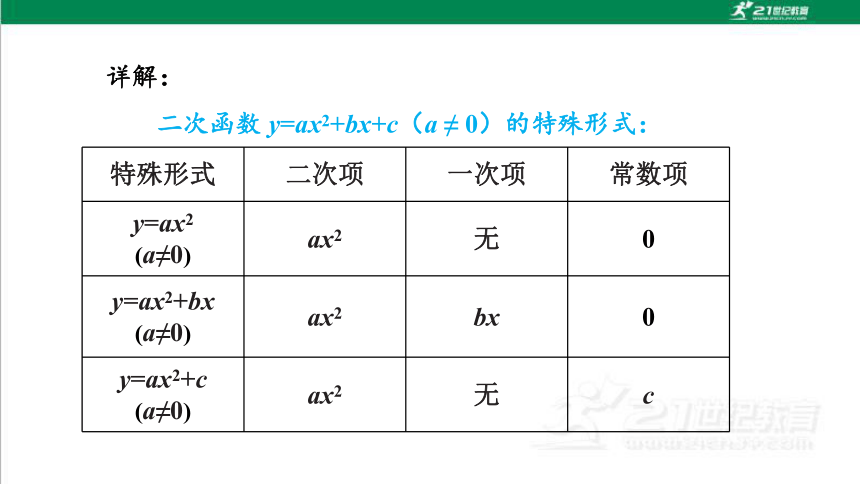
详解:
二次函数 y=ax2+bx+c(a ≠ 0)的特殊形式:
特殊形式 二次项 一次项 常数项
y=ax2 (a≠0) ax2 无 0
y=ax2+bx (a≠0) ax2 bx 0
y=ax2+c (a≠0) ax2 无 c
例 1
[ 中考·北京改编 ] 如图 21.1-1,用绳子围成周长为 10 m 的矩形,记矩形的一边长为 x m,它的邻边长为 y m,矩形的面积为S m2.当 x 在一定范围内变化时, S 随 x 的变化而变化,则 S 与 x 满足的函数关系是( )
A.二次函数关系 B. 无函数关系
C. 正比例函数关系 D. 一次函数关系
解题秘方:理清题中的数量关系,矩形的周长为 2 ( x+y ) =10 m,矩形的面积 S=xy,化简即可得到 S 关于 x 的函数关系式.
解: 由题意得,2(x+y) =10,
∴ x+y=5,
∴ y=5-x,
∴ S=xy=x(5-x) =-x2+5x,
∴ S 关于 x 的函数关系式为 S=-x2+5x,
即满足二次函数关系.
答案: A
知识点
建立二次函数模型表示变量间的关系
2
建立二次函数模型的一般步骤:
审清题意
找出问题中的已知量(常量)和未知量(变量) ,把问题中的文字或图形语言转化成数学语言 .
2. 找相等关系
分析常量和变量之间的关系,列出等式 .
3. 列二次函数表达式
设出表示变量的字母,把相等关系用含字母的式子表示,并把它整理成二次函数的一般形式 .
4. 确定自变量的取值范围
根据自变量所表示的实际意义确定其取值范围 .
特别提醒:
1. 建立二次函数模型与建立一元二次方程模型类似,不同的是需将它转化为用含一个变量的代数式表示另一个变量 .
2. 自变量的取值范围应使实际问题有意义 .
例2
[ 中考·淮安改编 ] 某超市经销一种商品,每件
成本为50 元 . 经市场调研,当该商品每件的销售价为 60 元时,每个月可销售 300 件,若每件的销售价每增加 1 元,则每个月的销售量将减少 10件.设该商品每件的销售价为 x 元,每个月的销售量为 y件.
解题秘方:熟悉利润问题中的基本数量关系“利润 = (售价 -进价) × 销量”是列出函数表达式的关键.
方法点拨:
在实际问题中建立二次函数关系时,关键要找出两个变量之间的数量关系,用类似建立一元二次方程模型的方法,借助方程思想求出二次函数的表达式 .
(1)求 y 与 x 的函数表达式,并写出自变量的取值范围;
(2)设每个月的销售利润为 W 元,求 W 与 x 之间的函数表达式 .
解:根据题意,得y=300-10( x-60) =
-10x+900(60 ≤ x < 90) .
由(1)知:W=( x-50) (-10x+900) =
-10x2+1 400x-45 000.
二次函数
二次函数
定义
表达式
三要素
自变量的
取值范围
y=ax2
y=ax2+c
y=ax2+bx
y=ax2+bx+c
知识点
二次函数
1
二次函数的定义
一般地,表达式形如 y=ax2+bx+c ( a, b, c 是常数,且 a ≠ 0 )的函数叫做 x 的二次函数,其中 x 是自变量 .
2. 二次函数的三要素
(1)自变量的最高次数必须是 2;
(2)等号右边的 ax2+bx+c 是关于自变量 x 的整式;
(3)二次项系数 a 不等于零 .
3. 二次函数的一般形式 y=ax2+bx+c ( a, b, c 是常数,且 a ≠ 0 )是二次函数的一般形式 .ax2 是二次项, a 是二次项系数; bx是一次项, b 是一次项系数; c 是常数项 .
详解:
二次函数 y=ax2+bx+c(a ≠ 0)的特殊形式:
特殊形式 二次项 一次项 常数项
y=ax2 (a≠0) ax2 无 0
y=ax2+bx (a≠0) ax2 bx 0
y=ax2+c (a≠0) ax2 无 c
例 1
[ 中考·北京改编 ] 如图 21.1-1,用绳子围成周长为 10 m 的矩形,记矩形的一边长为 x m,它的邻边长为 y m,矩形的面积为S m2.当 x 在一定范围内变化时, S 随 x 的变化而变化,则 S 与 x 满足的函数关系是( )
A.二次函数关系 B. 无函数关系
C. 正比例函数关系 D. 一次函数关系
解题秘方:理清题中的数量关系,矩形的周长为 2 ( x+y ) =10 m,矩形的面积 S=xy,化简即可得到 S 关于 x 的函数关系式.
解: 由题意得,2(x+y) =10,
∴ x+y=5,
∴ y=5-x,
∴ S=xy=x(5-x) =-x2+5x,
∴ S 关于 x 的函数关系式为 S=-x2+5x,
即满足二次函数关系.
答案: A
知识点
建立二次函数模型表示变量间的关系
2
建立二次函数模型的一般步骤:
审清题意
找出问题中的已知量(常量)和未知量(变量) ,把问题中的文字或图形语言转化成数学语言 .
2. 找相等关系
分析常量和变量之间的关系,列出等式 .
3. 列二次函数表达式
设出表示变量的字母,把相等关系用含字母的式子表示,并把它整理成二次函数的一般形式 .
4. 确定自变量的取值范围
根据自变量所表示的实际意义确定其取值范围 .
特别提醒:
1. 建立二次函数模型与建立一元二次方程模型类似,不同的是需将它转化为用含一个变量的代数式表示另一个变量 .
2. 自变量的取值范围应使实际问题有意义 .
例2
[ 中考·淮安改编 ] 某超市经销一种商品,每件
成本为50 元 . 经市场调研,当该商品每件的销售价为 60 元时,每个月可销售 300 件,若每件的销售价每增加 1 元,则每个月的销售量将减少 10件.设该商品每件的销售价为 x 元,每个月的销售量为 y件.
解题秘方:熟悉利润问题中的基本数量关系“利润 = (售价 -进价) × 销量”是列出函数表达式的关键.
方法点拨:
在实际问题中建立二次函数关系时,关键要找出两个变量之间的数量关系,用类似建立一元二次方程模型的方法,借助方程思想求出二次函数的表达式 .
(1)求 y 与 x 的函数表达式,并写出自变量的取值范围;
(2)设每个月的销售利润为 W 元,求 W 与 x 之间的函数表达式 .
解:根据题意,得y=300-10( x-60) =
-10x+900(60 ≤ x < 90) .
由(1)知:W=( x-50) (-10x+900) =
-10x2+1 400x-45 000.
二次函数
二次函数
定义
表达式
三要素
自变量的
取值范围
y=ax2
y=ax2+c
y=ax2+bx
y=ax2+bx+c
