沪科版九年级数学上册第21章二次函数与反比例函数21.3 二次函数与一元二次方程课件
文档属性
| 名称 | 沪科版九年级数学上册第21章二次函数与反比例函数21.3 二次函数与一元二次方程课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 07:25:01 | ||
图片预览











文档简介
(共31张PPT)
知识点
二次函数与一元二次方程之间的关系
1
1. 二次函数图象与 x 轴的交点横坐标与一元二次方程根的关系一般地,从二次函数 y=ax2+bx+c 的图象可知:如果抛物线y=ax2+bx+c 与 x 轴有交点,交点的横坐标是 x0,那么当 x=x0时,函数值是 0,因此 x=x0 是方程 ax2+bx+c=0 的一个根 .
2. 二次函数与一元二次方程的联系与区别
一元二次方程 ax2+bx+c=0 与二次函数y=ax2+bx+c 之间的内在联系列表如下:
b2-4ac 的符号 b2-4ac>0 b2-4ac=0 b2-4ac<0
一元二次方程ax2+bx+c=0的根的情况 有两个不等实根 x1= x2= 没有实根
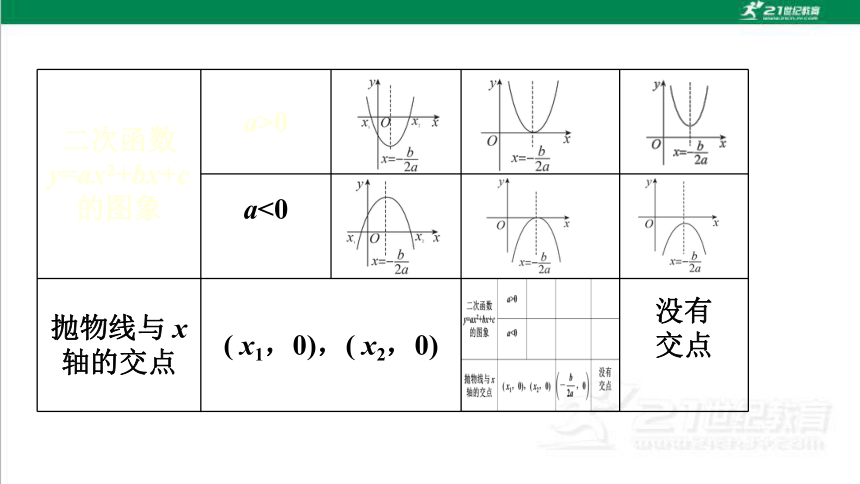
二次函数 y=ax2+bx+c 的图象 a>0
a<0
抛物线与 x 轴的交点 ( x1,0),( x2,0) 没有
交点
拓宽视野
1. 已 知 二 次 函数 y=ax2+bx+c, 求当 y=m 时自变量 x 的值, 可 以 解 一 元 二次 方 程 ax2+bx+c=m;反之,解一元二次方程 ax2+bx+c=m 可 以 看成 是 已 知y=ax2+bx+c的函数值 y=m,求自变 量 x 的 值 . 方 程ax2+bx+c=m 的解是抛物线 y=ax2+bx+c 与 直 线y=m 的交点的横坐标 .
2. 二 次 函 数y=ax2+bx+c 与一元二次方程 ax2+bx+c=0 的关系密切,二者可以相互转化 .
例 1
[ 中考·乐山 ] 已知关于 x 的一元二次方程 x2+x-m=0.
(1)若方程有两个不相等的实数根,求 m 的取值范围;
解题秘方:由 Δ 即可列不等式得到答案;
(2)二次函数 y=x2+x-m 的部分图象如图21.3-1 所示,求一元二次方程 x2+x-m=0 的解.
解题秘方:根据抛物线的对称性可得抛物线与 x 轴的另一个交点,即可得到答案.
知识点
二次函数图象法求解一元二次方程
2
利 用 二 次 函 数 y=ax2+bx+c 的 图 象 与 x 轴 的 交 点 求 一 元 二 次 方 程ax2+bx+c=0 的解
(1)作出二次函数 y=ax2+bx+c 的图象,确定图象与 x 轴的交点的横坐标;
(2)函数图象与 x 轴的交点的横坐标就是一元二次方程ax2+bx+c=0 的解;
(3)当函数图象与 x 轴的交点的横坐标不是整数时,可通过不断缩小解所在的范围估计一元二次方程的解 .
方法提醒
估计一元二次方程的解的方法:
在难以读出交点的坐标时,我们可以通过不断缩小解所在范围估计一元二次方程的解 .
2. 利用二次函数 y=ax2 的图象与直线 y= - bx - c 的交点求方程 ax2+bx+c=0的解
(1)将一元二次方程 ax2+bx+c=0 化为 ax2= - bx - c 的形式;
(2)在 平 面 直 角 坐 标 系 中 画 出 抛 物 线 y=ax2 和 直 线 y=-bx-c,并确定抛物线与直线的交点的横坐标;
(3)交点的横坐标即为一元二次方程 ax2+bx+c=0 的解 .
例2
利用二次函数的图象求一元二次方程 -x2+2x-3=-8的近似解(结果精确到 0.1) .
解题秘方:画出二次函数 y=-x2+2x+5 的图象, 利用二次函数的图象求方程的近似解 .
解题通法
用图象法求一元二次方程的近似解:
用图象法求一元二次方程的近似解时,一般先作出相应的二次函数的图象,确定其图象与 x 轴交点的横坐标的大致范围,即一元二次方程的解的大致范围;
然后利用取平均数的方法缩小解所在的范围,通过反复计算求出满足精确度要求的近似解 .
解:整理方程,得 -x2+2x+5=0.
作函数 y=-x2+2x+5 的图象如图 21.3-2 所示 .
由图象可知,抛物线与 x 轴交点的横坐标分别在 -2 和
-1,3 和 4 之间,即方程 -x2+2x-3=-8 的两个实数解分别在-2 和 -1,3 和 4 之间,用取平均数
的方法不断缩小解的取值范围,从而确定方程
的近似解 .
由图象可知,当 x=3 时, y>0;当 x=4 时, y<0,
取 3 和 4 的平均数 3.5,当 x=3.5 时, y=-0.25,
与 x=3时的函数值异号,所以方程的这个解在 3 和 3.5 之间 .
取 3 和 3.5 的平均数 3.25,当 x=3.25 时, y=0.937 5,与x=3.5 时的函数值异号,所以方程的这个解在 3.25 和 3.5 之间 .
取 3.25 和 3.5 的 平 均 数 3.375, 当 x=3.375 时, y=
0.359 375,与 x=3.5 时的函数值异号,所以方程的这个解在3.375 和 3.5 之间 .
由此方法可得到原方程的一个近似解为 3.4.
用同样的方法可得到原方程的另一个近似解为 -1.4.
所以方程 -x2+2x-3=-8 的解为 x1 ≈ -1.4, x2 ≈ 3.4.
特别提醒
用图象法解一元二次方程是数形结合思想的具体应用,通过画函数图象解一元二次方程是数的直观化的体现,但由于作图或观察存在误差,因此通过这种方法求得的方程的解一般是近似的 .
知识点
二次函数与一元二次不等式之间的关系
3
求 不 等 式 ax2+bx+c>0(a ≠ 0) 的 解 集, 就 是 求 x 为何 值 时, 二 次 函 数 y=ax2+bx+c 的 函 数 值 y>0; 求 不 等 式ax2+bx+c<0( a ≠ 0)的解集,就是求 x 为何值时,二次函数y=ax2+bx+c 的函数值 y<0. 列表如下:(以 a>0 为例)
b2-4ac 的符号 b2-4ac>0 b2-4ac=0 b2-4ac<0
y=ax2+bx+c(a>0) 的图象与 x 轴的交 点个数
ax2+bx+c=0 (a>0)的根 两不等实数根 x1= x2= 没有实数根
一元二次不等式的解集 ax2+bx+c>0(a>0) xx2 全体实数
ax2+bx+c >0(a>0) x1深度理解
二次函数与一元二次不等式的关系:
二 次 函 数y=ax2+bx+c 的 图 象 在 x轴 上 方 的 部 分 对 应 的自 变 量 取 值 范 围 就 是ax2+bx+c > 0 的 解 集,在 x 轴下方的部分对应的自变量取值范围就是ax2+bx+c < 0 的解集 .
当抛物线开口向上且与x轴无交点时,ax2+bx+c>0 的解集是全体实数,ax2+bx+c<0无解;当抛物线开口向下且 与 x 轴 无 交 点 时,ax2+bx+c > 0 无 解,ax2+bx+c < 0 的解集是全体实数 .
例 3
[ 期 末· 高 邮 ] 二 次 函 数 y=ax2+bx+c 的 图 象 如 图
21.3-3 所示,根据图象解答下列问题:
(1)方程 ax2+bx+c=0 的两个根为 ________,不等式
ax2+bx+c > 0 的解集为 _______;
解题秘方:根据抛物线与 x 轴的交点即可得出方程与不等式的解或解集;
特别提醒
根据二次函数与一元二次不等式之间的关系,结合题目中的图象即可求解.
解:∵抛物线开口向下,抛物线与 x 轴的交点为
(1,0),(3,0),
∴方程 ax2+bx+c=0 的两个根为 x1=1, x2=3;
不等式 ax2+bx+c > 0 的解集为 1 < x < 3.
答案: x1=1, x2=3;1 < x < 3
(2)若关于 x 的一元二次方程ax2+bx+c=k 有两个不相等的实数根,则 k的取值范围为 _________;
解题秘方:结合函数图象,利用直线 y=k 与抛物线有 2 个交点得到 k 的取值范围;
解:∵抛物线的顶点的纵坐标为 2,
∴抛物线 y=ax2+bx+c=0 与直线 y=2 只有一个公共点,∴当 k < 2 时,抛物线 y=ax2+bx+c=0 与直线 y=k 有两个公共点,即方程 ax2+bx+c=k 有两个不相等的实数根,满足条件的 k 的取值范围为 k < 2.
答案: k < 2
(3)若关于 x 的一元二次方程ax2+bx+c-t=0 在 1 < x < 4 的范围内有实数根,求 t 的取值范围.
解题秘方:根据待定系数法求得抛物线的表达式,结合函数图象,写出 t 的取值范围.
解:设抛物线的表达式为 y=a(x-2) 2+2,
把点(1,0)的坐标代入得,0=a+2,
∴ a=-2,∴ y=-2( x-2) 2+2,
把 x=4 代入得 y=-6,∴ t 的取值范围是 -6 < t ≤ 2.
二次函数与一元二次方程
有两个交点
有两个不相
等的实数根
有一个交点
二次函数图象与
x 轴的交点个数
二次函数与一
元二次方程之
间的关系
有两个相等
的实数根
没有实数根
没有交点
一元二次方
程根的情况
知识点
二次函数与一元二次方程之间的关系
1
1. 二次函数图象与 x 轴的交点横坐标与一元二次方程根的关系一般地,从二次函数 y=ax2+bx+c 的图象可知:如果抛物线y=ax2+bx+c 与 x 轴有交点,交点的横坐标是 x0,那么当 x=x0时,函数值是 0,因此 x=x0 是方程 ax2+bx+c=0 的一个根 .
2. 二次函数与一元二次方程的联系与区别
一元二次方程 ax2+bx+c=0 与二次函数y=ax2+bx+c 之间的内在联系列表如下:
b2-4ac 的符号 b2-4ac>0 b2-4ac=0 b2-4ac<0
一元二次方程ax2+bx+c=0的根的情况 有两个不等实根 x1= x2= 没有实根
二次函数 y=ax2+bx+c 的图象 a>0
a<0
抛物线与 x 轴的交点 ( x1,0),( x2,0) 没有
交点
拓宽视野
1. 已 知 二 次 函数 y=ax2+bx+c, 求当 y=m 时自变量 x 的值, 可 以 解 一 元 二次 方 程 ax2+bx+c=m;反之,解一元二次方程 ax2+bx+c=m 可 以 看成 是 已 知y=ax2+bx+c的函数值 y=m,求自变 量 x 的 值 . 方 程ax2+bx+c=m 的解是抛物线 y=ax2+bx+c 与 直 线y=m 的交点的横坐标 .
2. 二 次 函 数y=ax2+bx+c 与一元二次方程 ax2+bx+c=0 的关系密切,二者可以相互转化 .
例 1
[ 中考·乐山 ] 已知关于 x 的一元二次方程 x2+x-m=0.
(1)若方程有两个不相等的实数根,求 m 的取值范围;
解题秘方:由 Δ 即可列不等式得到答案;
(2)二次函数 y=x2+x-m 的部分图象如图21.3-1 所示,求一元二次方程 x2+x-m=0 的解.
解题秘方:根据抛物线的对称性可得抛物线与 x 轴的另一个交点,即可得到答案.
知识点
二次函数图象法求解一元二次方程
2
利 用 二 次 函 数 y=ax2+bx+c 的 图 象 与 x 轴 的 交 点 求 一 元 二 次 方 程ax2+bx+c=0 的解
(1)作出二次函数 y=ax2+bx+c 的图象,确定图象与 x 轴的交点的横坐标;
(2)函数图象与 x 轴的交点的横坐标就是一元二次方程ax2+bx+c=0 的解;
(3)当函数图象与 x 轴的交点的横坐标不是整数时,可通过不断缩小解所在的范围估计一元二次方程的解 .
方法提醒
估计一元二次方程的解的方法:
在难以读出交点的坐标时,我们可以通过不断缩小解所在范围估计一元二次方程的解 .
2. 利用二次函数 y=ax2 的图象与直线 y= - bx - c 的交点求方程 ax2+bx+c=0的解
(1)将一元二次方程 ax2+bx+c=0 化为 ax2= - bx - c 的形式;
(2)在 平 面 直 角 坐 标 系 中 画 出 抛 物 线 y=ax2 和 直 线 y=-bx-c,并确定抛物线与直线的交点的横坐标;
(3)交点的横坐标即为一元二次方程 ax2+bx+c=0 的解 .
例2
利用二次函数的图象求一元二次方程 -x2+2x-3=-8的近似解(结果精确到 0.1) .
解题秘方:画出二次函数 y=-x2+2x+5 的图象, 利用二次函数的图象求方程的近似解 .
解题通法
用图象法求一元二次方程的近似解:
用图象法求一元二次方程的近似解时,一般先作出相应的二次函数的图象,确定其图象与 x 轴交点的横坐标的大致范围,即一元二次方程的解的大致范围;
然后利用取平均数的方法缩小解所在的范围,通过反复计算求出满足精确度要求的近似解 .
解:整理方程,得 -x2+2x+5=0.
作函数 y=-x2+2x+5 的图象如图 21.3-2 所示 .
由图象可知,抛物线与 x 轴交点的横坐标分别在 -2 和
-1,3 和 4 之间,即方程 -x2+2x-3=-8 的两个实数解分别在-2 和 -1,3 和 4 之间,用取平均数
的方法不断缩小解的取值范围,从而确定方程
的近似解 .
由图象可知,当 x=3 时, y>0;当 x=4 时, y<0,
取 3 和 4 的平均数 3.5,当 x=3.5 时, y=-0.25,
与 x=3时的函数值异号,所以方程的这个解在 3 和 3.5 之间 .
取 3 和 3.5 的平均数 3.25,当 x=3.25 时, y=0.937 5,与x=3.5 时的函数值异号,所以方程的这个解在 3.25 和 3.5 之间 .
取 3.25 和 3.5 的 平 均 数 3.375, 当 x=3.375 时, y=
0.359 375,与 x=3.5 时的函数值异号,所以方程的这个解在3.375 和 3.5 之间 .
由此方法可得到原方程的一个近似解为 3.4.
用同样的方法可得到原方程的另一个近似解为 -1.4.
所以方程 -x2+2x-3=-8 的解为 x1 ≈ -1.4, x2 ≈ 3.4.
特别提醒
用图象法解一元二次方程是数形结合思想的具体应用,通过画函数图象解一元二次方程是数的直观化的体现,但由于作图或观察存在误差,因此通过这种方法求得的方程的解一般是近似的 .
知识点
二次函数与一元二次不等式之间的关系
3
求 不 等 式 ax2+bx+c>0(a ≠ 0) 的 解 集, 就 是 求 x 为何 值 时, 二 次 函 数 y=ax2+bx+c 的 函 数 值 y>0; 求 不 等 式ax2+bx+c<0( a ≠ 0)的解集,就是求 x 为何值时,二次函数y=ax2+bx+c 的函数值 y<0. 列表如下:(以 a>0 为例)
b2-4ac 的符号 b2-4ac>0 b2-4ac=0 b2-4ac<0
y=ax2+bx+c(a>0) 的图象与 x 轴的交 点个数
ax2+bx+c=0 (a>0)的根 两不等实数根 x1= x2= 没有实数根
一元二次不等式的解集 ax2+bx+c>0(a>0) x
ax2+bx+c >0(a>0) x1
二次函数与一元二次不等式的关系:
二 次 函 数y=ax2+bx+c 的 图 象 在 x轴 上 方 的 部 分 对 应 的自 变 量 取 值 范 围 就 是ax2+bx+c > 0 的 解 集,在 x 轴下方的部分对应的自变量取值范围就是ax2+bx+c < 0 的解集 .
当抛物线开口向上且与x轴无交点时,ax2+bx+c>0 的解集是全体实数,ax2+bx+c<0无解;当抛物线开口向下且 与 x 轴 无 交 点 时,ax2+bx+c > 0 无 解,ax2+bx+c < 0 的解集是全体实数 .
例 3
[ 期 末· 高 邮 ] 二 次 函 数 y=ax2+bx+c 的 图 象 如 图
21.3-3 所示,根据图象解答下列问题:
(1)方程 ax2+bx+c=0 的两个根为 ________,不等式
ax2+bx+c > 0 的解集为 _______;
解题秘方:根据抛物线与 x 轴的交点即可得出方程与不等式的解或解集;
特别提醒
根据二次函数与一元二次不等式之间的关系,结合题目中的图象即可求解.
解:∵抛物线开口向下,抛物线与 x 轴的交点为
(1,0),(3,0),
∴方程 ax2+bx+c=0 的两个根为 x1=1, x2=3;
不等式 ax2+bx+c > 0 的解集为 1 < x < 3.
答案: x1=1, x2=3;1 < x < 3
(2)若关于 x 的一元二次方程ax2+bx+c=k 有两个不相等的实数根,则 k的取值范围为 _________;
解题秘方:结合函数图象,利用直线 y=k 与抛物线有 2 个交点得到 k 的取值范围;
解:∵抛物线的顶点的纵坐标为 2,
∴抛物线 y=ax2+bx+c=0 与直线 y=2 只有一个公共点,∴当 k < 2 时,抛物线 y=ax2+bx+c=0 与直线 y=k 有两个公共点,即方程 ax2+bx+c=k 有两个不相等的实数根,满足条件的 k 的取值范围为 k < 2.
答案: k < 2
(3)若关于 x 的一元二次方程ax2+bx+c-t=0 在 1 < x < 4 的范围内有实数根,求 t 的取值范围.
解题秘方:根据待定系数法求得抛物线的表达式,结合函数图象,写出 t 的取值范围.
解:设抛物线的表达式为 y=a(x-2) 2+2,
把点(1,0)的坐标代入得,0=a+2,
∴ a=-2,∴ y=-2( x-2) 2+2,
把 x=4 代入得 y=-6,∴ t 的取值范围是 -6 < t ≤ 2.
二次函数与一元二次方程
有两个交点
有两个不相
等的实数根
有一个交点
二次函数图象与
x 轴的交点个数
二次函数与一
元二次方程之
间的关系
有两个相等
的实数根
没有实数根
没有交点
一元二次方
程根的情况
